[ Article ]

Transactions of the Korean Society for Noise and Vibration Engineering - Vol. 33, No. 3, pp.313-325

ISSN: 1598-2785 (Print) 2287-5476 (Online)

Print publication date 20 Jun 2023

Received 05 Apr 2023 Revised 27 Apr 2023 Accepted 04 May 2023

DOI: https://doi.org/10.5050/KSNVE.2023.33.3.313

좁은 주파수 대역의 랜덤 가진을 받는 블레이드 어셈블리에서 인위적인 미스튜닝에 의한 마찰 댐퍼의 성능 변화

차덕순^†

The Performance of Friction Dampers on the Intentionally Mistuned Bladed Disk Assembly Subjected to Narrow Band Random Excitation

Douksoon Cha^†

Correspondence to: ^†Member, Korea University of Technology & Education, Department of Mechanical Design Engineering, Assistant Professor E-mail : dscha@koreatech.ac.kr ‡ Recommended by Editor Seung Hun Baek

Abstract

In this study, the effects of intentional mistuning on the performance of B–B friction dampers are investigated in an inherently mistuned bladed disk assembly subjected to narrow band random excitation. The intentional large mistuning and inherent small mistuning are modeled by the additional mass and perturbations in the stiffness of the blade, respectively. Notably, the performance of B–B friction dampers improved owing to the intentional mistuning of the correlated excitations. Based on a simple model of an intentionally and inherently mistuned bladed disk assembly, the analytical technique offers an efficient method to evaluate the effects of intentional mistuning and friction dampers.

Keywords:

Intentional Mistuning, Inherent Mistuning, Bladed Disk Assembly, Friction Damper, Narrow Band Random Excitation, Excitation Correlation

키워드:

인위적인 미스튜닝, 고유의 미스튜닝, 블레이드 어셈블리, 마찰 댐퍼, 좁은 주파수 대역의 랜덤 가진, 가진의 상관성

1. 서 론

터빈 블레이드는 가공 및 조립 과정에서 미세한 오차로 인하여 개별 블레이드의 모달 특성이 동일하지 않고 미세한 차이가 발생하는데, 그 결과로 작동과정에서 일부 블레이드의 진동이 매우 크게 발생하는 현상이 발생한다. 이러한 현상을 미스튜닝(mistuning) 효과라고 하는데, 가스 터빈 엔진의 경우에 피로 수명을 단축시키고, 작동중의 고장을 초래하므로 많은 연구가 이루어져 왔다^(1~6).

미스튜닝 효과를 저감하는 하나의 방법으로 인위적으로 큰 크기의 동특성의 편차를 유발하는 방법이 있는데, 매우 큰 폭의 진동 저감 효과가 있는 것으로 알려져 있다^(7~11). 블레이드의 진동이 작은 크기의 고유의 미스튜닝에는 둔감해지고, 인위적으로 부가된 큰 크기의 미스튜닝에 주로 영향을 받는다고 하였다. 이러한 결과는 외력의 주파수와 위상이 일정한 엔진오더 가진(engine-order-excitation)일 때의 결과이다. 그러나 많은 경우에서 외력의 특성은 랜덤 가진의 특성을 가지는 것으로 알려져 있다^(1,5,12~15).

외력이 랜덤 가진인 상황에서는 인위적인 미스튜닝의 영향에 대하여는 별다른 연구가 진행되지 않았다.

마찰 댐퍼도 블레이드의 진폭을 줄이기 위하여 많이 사용되는데^{(2,3,13,14,16~20)}, 인접한 블레이드를 서로 연결하는 B-B(blade-to-blade, 블레이드와 블레이드 사이) 마찰 댐퍼가 간단한 구조로 인하여 많이 사용되고 있다. 그러나 B-B 마찰 댐퍼의 성능은 외력의 특성에 따라 많은 차이가 있다. 외력의 특성이 불규칙한 주기의 랜덤 가진인 상태에서 외력이 서로 코릴레이션(correlation)이 있는 상황에서는 특정 주파수 대역에서 B-B 마찰 댐퍼의 효과는 아주 약해지는 것이 밝혀졌다⁽¹⁴⁾.

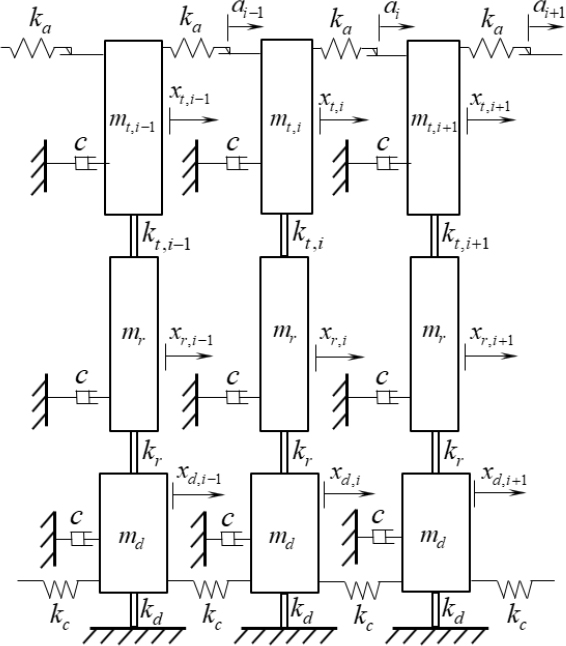
이 논문에서는 외력의 특성이 랜덤 가진인 상태에서 단순한 패턴의 인위적인 미스튜닝을 이용하여 B-B 마찰 댐퍼의 성능을 향상시키는 방법을 연구하였다. 왜냐하면 인위적인 미스튜닝만으로는 랜덤 가진상태에서는 블레이드의 진동 저감에 대한 효과가 없는 것으로 나타났기 때문이다. 그러나 인위적인 미스튜닝과 B-B 마찰 댐퍼를 동시에 사용하는 경우에는 랜덤 가진의 모든 주파수 대역에서 블레이드의 진동을 저감할 수 있는 것으로 나타났다. 미스튜닝 효과는 외력의 주파수가 넓은 백색소음(white noise)가진에서는 매우 작기 때문에^(5,13~15), 랜덤 가진의 주파수 대역이 좁은 경우만을 고려하였고, 외력의 주파수 대역의 변환과 코릴레이션은 밴드패스 필터(band pass filter)를 사용하여 처리하였다⁽⁵⁾. 블레이드 어셈블리의 모델은 Fig. 1에 나타나 있다⁽²¹⁾. 어셈블리에서 하나의 섹터는 디스크에 해당하는 하나의 질량과 블레이드를 표현하는 두개의 질량으로 이루어져 있다. 이 모델은 블레이드의 첫번째와 두 번째의 굽힘 모드를 표현하고 있다. 인위적인 미스튜닝과 고유의 작은 미스튜닝은 상부 블레이드에 부가적인 질량과 강성에 작은 크기의 변수를 추가하여 표현하였다. 먼저 이론적인 해석방법에 대하여 설명하고 인위적인 미스튜닝에 의한 B-B 마찰 댐퍼의 성능 변화에 대하여 설명하였다.

Fig. 1

Model of bladed disk assembly with friction dampers

2. 모델링 및 해석

블레이드의 i번째 상부 및 하부의 질량과 강성은 각각 m_t,i, m_r, k_t,i, 및 k_r로 표현된다. 블레이드의 하부 질량과 강성은 모두 동일하다고 가정하고, 인위적인 미스튜닝과 고유의 미스튜닝은 식 (1)과 식 (2)로 모델링하였다.

m t, i = m t + d m i

(1)

k t, i = k t + δ k i, i = 1, 2, ⋯, n

(2)

여기서 dm_i는 인위적인 미스튜닝을 위한 부가적인 질량이고, δk_i는 고유의 미스튜닝 에 의한 강성의 편차이다. m_t와 k_t는 가공오차가 없는 이상적인 블레이드의 상부의 질량과 강성을 표현한다. δk_i는 평균값이 0이고 가우스 분포를 가진 독립적인 랜덤 변수라고 가정한다.

디스크 부분의 질량과 강성은 각각 m_d와 k_d로 표현된다. 디스크 부분에 의하여 서로 인접한 블레이드 사이에 발생하는 강성은 k_c로 표현되고 마찰댐퍼의 강성은 k_a로 표현된다.

댐핑 계수 c는 블레이드에 가해지는 공기역학적인 댐핑과 구조적인 댐핑의 영향을 표현하였다. 외력 f_i(t)은 블레이드의 상부 질량에 가해진다고 가정하였다. 그러면 i번째 블레이드 어셈블리의 운동 방정식은 식 (3) ~ 식 (5)와 같이 나타난다.

m t, i x ¨ t, i + c x ˙ t, i + k t, i x t, i - x r, i + f a, i - f a, i - 1 = f i t

(3)

m r x ¨ r, i + c x ˙ r, i + k t, i x r, i - x t, i + k r x r, i - x d, i = 0

(4)

m d x ¨ d, i + c x d, i ˙ + k d x d, i + k r x d, i - x r, i + k c 2 x d, i - x d, i + 1 - x d, i - 1 = 0

(5)

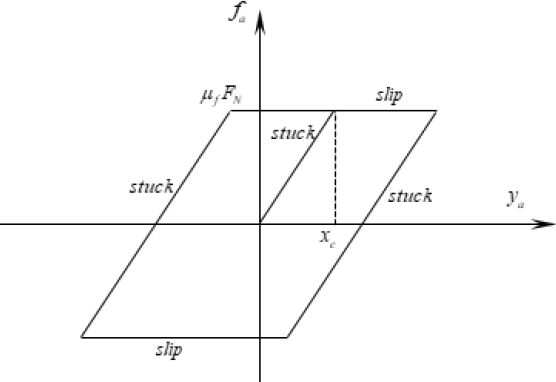
여기서, f_i(t)는 평균값이 0인 정상상태의 랜덤 가진이다. Fig. 2는 블레이드에 가해지는 마찰 댐퍼의 비선형적인 히스테레시스 마찰력 f_a,i를 표현한 것으로 식 (6) ~ (10)과 같이 나타낼 수 있다⁽²²⁾.

Fig. 2

Hysteretic characteristic of friction damper

f a, i x ˙ a, i, y a, i = k a y a, i U y a, i + x a c - U y a, i - x a c + k a x a c U y a, i - x a c U x ˙ a, i - U - y a, i - x a c U - x ˙ a, i

(6)

y ˙ a, i = h a, i x ˙ a, i, y a, i = x ˙ a, i U y a, i + x a c - U y a, i - x a c + U y a, i - x a c U - x ˙ a, i + U - y a, i - x a c U x ˙ a, i

(7)

x a, i = x t, i - x t, i + 1

(8)

y a, i = x t, i - a i

(9)

x a c = μ f F N a k a

(10)

여기서 μ_f는 마찰계수를 표현하고, $F N a$ 는 마찰 댐퍼의 수직하중을 표현한다. U(•)는 식 (11)과 같은 스텝 함수를 표현한다.

U x = 1 i f x > 0 0 i f x ≤ 0

(11)

이러한 운동 방정식을 등가선형화법(equivalent linearization method)을 사용하면, 식 (12) ~ 식 (19)과 같은 선형 방정식으로 표현된다.

m t, i x ¨ t, i + c x ˙ t, i + k t, i x t, i - x r, i + c a, i x x ˙ a, i + k a, i x y a, i - c a, i - 1 x x ˙ a, i - 1 + k a, i - 1 x y a, i - 1 = f i t

(12)

m r x ¨ r, i + c x ˙ r, i + k t, i x r, i - x t, i + k r x r, i - x d, i + c b, i x x ˙ b, i + k b, i x y b, i - c b, i - 1 x x ˙ b, i - 1 + k b, i - 1 x y b, i - 1 = 0

(13)

m d x ¨ d, i + c x ˙ d, i + k d x d, i + k r x d, i - x r, i + k c 2 x d, i - x d, i + 1 - x d, i - 1 = 0

(14)

y ˙ a, i = c a, i y x ˙ a, i + k a, i y y a, i

(15)

여기서,

c a, i x = E ∂ f a, i ∂ x ˙ a, i

(16)

k a, i x = E ∂ f a, i ∂ y a, i

(17)

c a, i y = E ∂ h a, i ∂ x ˙ a, i

(18)

k a, i y = E ∂ h a, i ∂ y a, i

(19)

E[•]는 평균값을 나타낸다. 그리고 각 계수에 대한 상세한 표현은 Appendix A에 나타나 있다. 외력의 주요한 특성인 주요 주파수와 코릴레이션은 백색소음을 입력으로 하는 밴드패스 필터를 이용하여 결정할 수 있다⁽⁵⁾. 전체의 운동 방정식은 식 (20) ~ (27)과 같은 선형방정식으로 표현할 수 있다.

f ¨ + C F f ˙ + K F f = K F w t

(20)

M x ¨ + C + C x x ˙ + K x + K x y = D f t

(21)

y ˙ = C y x ˙ + K y y

(22)

여기서

C F = 2 ξ F ω F C R

(23)

K F = ω F 2 I

(24)

f = f 1 f 2 ⋯ f n T

(25)

x = x t, 1 x r, 1 x d, 1 ⋯ x t, n x r, n x d, n T

(26)

y = y a, 1 ⋯ y a, n T

(27)

M, K와 C는 마찰 댐퍼가 없는 시스템의 질량, 강성 및 댐핑 행렬을 나타내고, D는 f와 x의 크기를 조정하기 위한 행렬이다. 밴드패스 필터의 댐핑 계수 ξ_F와 고유진동수 ω_F는 외력의 주요 주파수와 주파수 대역을 조정하는 데 사용된다. 그리고 C_R은 외력의 코릴레이션을 결정하는 데 사용된다⁽⁵⁾. 마찰 댐퍼의 선형화에 사용된 행렬 C_x, K_x, C_y와 K_y는 Appendix B에 나타나 있다.

운동 방정식을 상태(state) 변수를 이용하여 1차 미분방정식의 행렬로 식 (28)과 같이 표현할 수 있다.

z ˙ = A z + B w t

(28)

식 (29) ~ 식 (31)에서

z = f f ˙ x x ˙ y T

(29)

A = 0 I 000 - K F - C F 000 000 I 0 M -1 D 0 - M -1 K - M -1 C + C x - M -1 K x 000 C y K y

(30)

B = 0 K F 0 0 0 T

(31)

밴드패스 필터의 입력인 백색소음의 코릴레이션은 식 (32)와 같이 정의된다.

R w τ = E w t w T t + τ = Q 0 δ τ I

(32)

여기서 Q₀는 입력의 강도를 표현하고, δ(τ)는 dirac-delta 함수이다. E[w(t)]=0이므로, 정상상태에서는 E[z(t)]=0이다.

상태 변수의 코릴레이션 행렬이 P이면,

P = E z t z T t

(33)

정상상태에서 행렬 P는 식 (34) Lyapunov 방정식에서 구할 수 있다.

A P + P A T = - B Q 0 B T

(34)

선형화 계수의 값은 행렬 P의 값을 이용하므로 식 (33)은 수치적인 반복법으로 계산할 수 있다^(13,14). 상부 블레이드의 진동 응답은 식 (35)와 같이 행렬 P로부터 얻을 수 있다.

E x t, i 2 = P j, j, j = 2 n + 3 i - 2

(35)

dm_i의 값은 인위적으로 이미 결정된 값이므로, 블레이드의 응답은 변수 δk_i에 의하여 변화된다.

Lyapunov 방정식의 해는 테일러 급수(Taylor-series-expansion)를 이용하여 식 (36)과 같은 근사식으로부터 구할 수 있다. 테일러 급수의 고차항은 무시하였다.

P = P t + ∑ i = 1 n ∂ P ∂ k i δ k i

(36)

여기서 P_t는 인위적으로 미스튜닝된 상태에서의 상태 변수의 코릴레이션 행렬이다. 행렬 ∂P/∂k_i는 아래의 방정식으로부터 구할 수 있다.

A t ∂ P ∂ k i + ∂ P ∂ k i A t T = - ∂ A ∂ k i P t + P t ∂ A T ∂ k i

(37)

여기서 ∂P/∂k_i에 대한 표현은 Appendix C에 나타나 있다. 식 (37)로부터 상부 블레이드의 랜덤 가진에 대한 응답 분산(variance)의 평균값과 표준편차를 구할 수 있다.

μ t, i = E P j, j

(38)

σ t, i = E P j, j 2 - μ t, i 2

(39)

식 (38)과 식 (39)에서 μ_t,i와 σ_t,i에 대한 표현은 Appendix D에 나타나 있다.

3. 수치 해석 결과

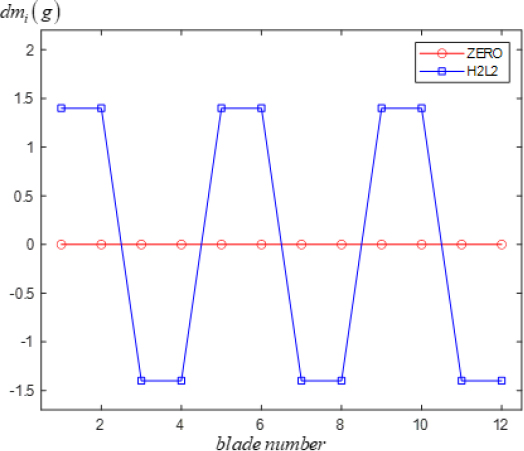
수치해석을 위한 시스템의 계수는 Table 1에 나타나 있다⁽²¹⁾. 블레이드의 개수는 12개로 선정하였다. 인위적인 미스튜닝은, Fig. 3과 같이 모든 상부 블레이드가 동일한 질량을 가지는 ZERO 패턴과 두개의 연속적인 블레이드를 무겁거나 가볍게 하는 H2L2 패턴을 사용하였다.

Table 1

System parameters

Fig. 3

Additional mass patterns for intentional mistuning

인위적인 미스튜닝에 사용된 부가적인 질량은 1.4 g으로 하였다. 그래서 dm_i는 식 (40)과 같이 표현할 수 있다.

d m i = 0.00140.0014 - 0.0014 - 0.0014 ⋯ : H 2 L 2 0 : Z E R O

(40)

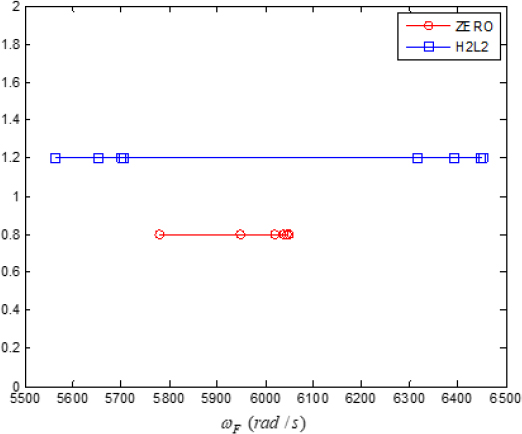
마찰 댐퍼가 제거된 상태에서, 두 가지 패턴에 대한 블레이드 어셈블리의 고유진동수는 Fig. 4에 나타나 있다. H2L2 패턴의 경우에는 ZERO 패턴보다 고유진동수간 주파수 간격이 넓어지면서 두 개의 그룹으로 분리되는 현상이 나타난다.

Fig. 4

Modal frequencies of the upper blade with additional mass

고유의 미스튜닝을 표현하기 위한 δk_i의 표준편차는 8600 N/m로 하였다. 이 값은 블레이드 어셈블리의 첫번째 고유진동수에서 약 1 %에 해당하는 표준편차를 발생시킨다. MATLAB 프로그램에서 ‘randn” 명령어를 사용하여 평균값이 0이고 요구되는 표준편차를 가지는 변수를 생성시켜서 블레이드의 강성 변화에 사용하였다. 외력 f_i(t)의 주요 주파수는 w_F를 이용하여 변화시키고, 밴드폭(bandwidth)은 0.01이 되도록 ξ_F의 값을 선정하였다. 식 (41)과 같이, 외력의 코릴레이션은 필터의 내부 구조를 표현하는 행렬 C_R에 의하여 원하는 값으로 결정될 수 있다⁽⁵⁾.

R f = E f t f t T = Q 0 ω F 4 ξ F C R - 1

(41)

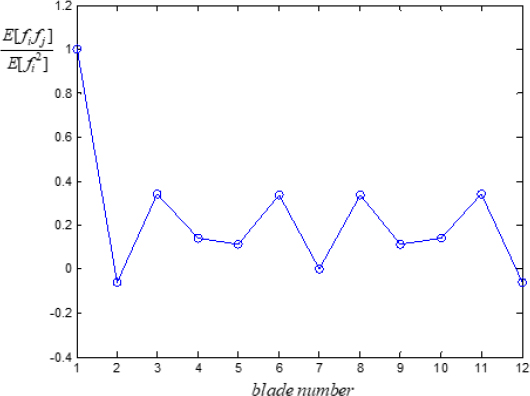
예를 들어, 외력이 서로 독립적이고 코릴레이션이 없다면 C_R은 단위행렬이 된다. Fig. 5에 나타난 외력 상호간의 코릴레이션을 이용하여 외력의 코릴레이션의 영향을 살펴보았다. 이것은 전통적인 엔진오더 가진(engine-order-excitation)의 관점에서 보면, 첫 번째와 다섯 번째의 엔진오더 가진(engine-order-excitation)이 합해진 경우의 외력의 특성과 유사하다고 할 수 있다. 필터가 입력을 증폭하기 때문에, 백색소음의 강도는 10^-6N²으로 정하였다. 마찰 댐퍼의 성능을 외력의 특성에 관계없이 표현하기 위하여 $μ t R s t, σ t R s t 와 x a c σ s t$ 의 무차원 변수를 이용하였다^(14,23).

Fig. 5

Correlation example of narrow band excitation

R s t = E x s t 2

(42)

σ s t = R s t

(43)

식 (42)와 식 (43)에서 x_st는 마찰 댐퍼의 미끄러짐이 없고, 미스튜닝이 없는 상태에서, 상부 블레이드의 최대 진폭을 나타낸다. 마찰 댐퍼가 완전히 고정되는 상태에서는 마찰 댐퍼는 인접하는 블레이드를 연결하는 커플링 강성과 정확하게 동일한 역할을 한다. 이론적인 해석의 정확도는 1000개의 블레이드 어셈블리를 사용한 몬테카를로(Monte-Carlo) 시뮬레이션의 통계 결과와 비교하여 평가하였다.

3.1 외력이 독립적인 경우

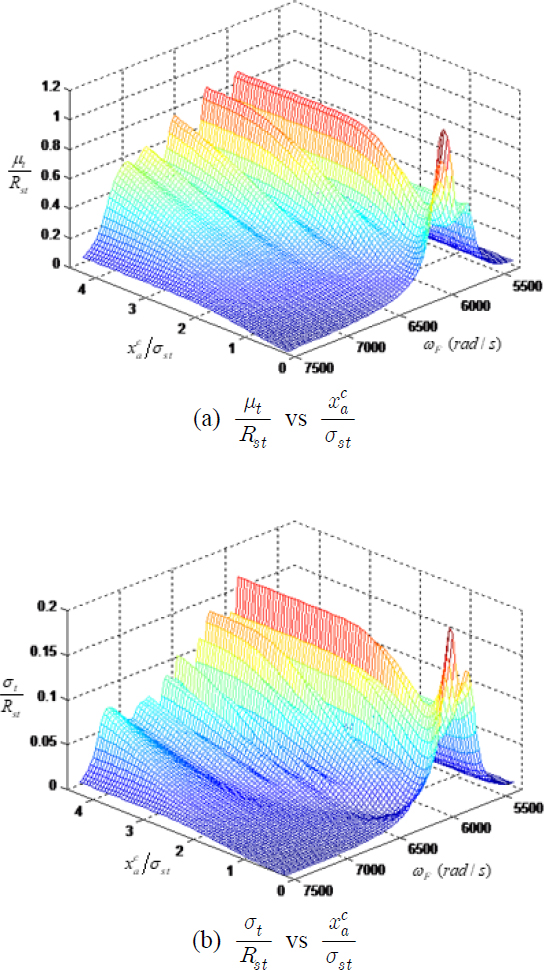
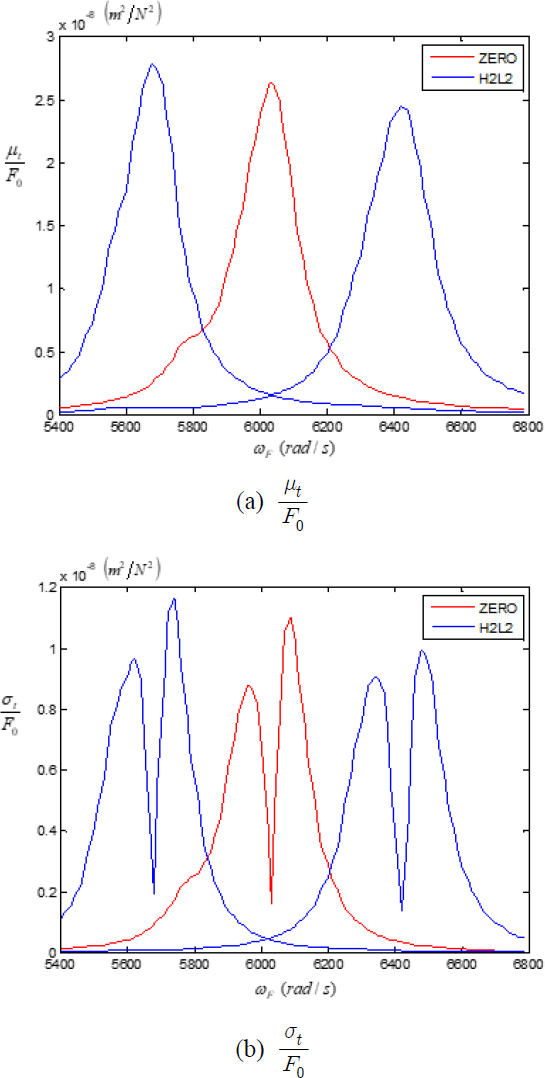
외력이 서로 독립적으로 코릴레이션이 없는 경우에 ZERO와 H2L2 패턴에 대한 이론적인 해석 결과가 Figs. 6, 7에 나타나 있다. 블레이드의 응답에서 μ_t의 값은 고유의 미스튜닝이 없는 상태에서의 분산을 나타내고, σ_t의 값은 고유의 미스튜닝에 의한 분산의 표준편차를 나타낸다. 그리고 ZERO 패턴은 인위적인 미스튜닝이 없는 상태와 동일하므로, 인위적인 H2L2 패턴으로 미스튜닝된 시스템의 결과를 분석하는데 기준이 될 수 있다. 식 (10)에 나타난 바와 같이, $x a c$ 는 마찰 댐퍼의 미끄럼이 발생하기 시작할 때의 마찰 댐퍼의 변형으로 댐퍼에 가해지는 수직하중과 비례한다. $x a c$ 와 x_st 및 σ_st는 동일한 차원이므로, 외력의 주요 주파수와 댐퍼의 수직하중의 변화에 대한 블레이드 시스템의 응답 분산을 무차원으로 표현할 수 있다.

Fig. 6

Uncorrelated, ZERO pattern

ZERO 패턴은 인위적인 미스튜닝이 없고 고유의 작은 미스튜닝에 의한 영향만 나타나 있다. H2L2 패턴에서는 인위적으로 부가되는 질량으로 인하여, 블레이드의 응답은 두 개의 그룹으로 나누어진다. 이러한 두 그룹의 응답은 최대 진폭을 쉽게 나타낼 수 있도록 서로 겹쳐서 하나의 그림에 나타나 있다.

마찰 댐퍼의 $x a c$ 의 값이 증가하면, 댐퍼의 커플링 강성의 효과도 동시에 증가하므로, μ_t와 σ_t의 값은 하나의 피크에서 여러 개의 피크로 변화한다.

Fig. 7에서 $x a c$ 의 값이 작은 경우에 나타나는 두 개의 피크는 H2L2 패턴에서 무거운 블레이드와 가벼운 블레이드의 해석결과가 중첩이 되어 표현된 것이다. $x a c$ 의 값이 최적으로 결정되면, 모든 패턴에서 마찰 댐퍼에 의하여 진동이 효과적으로 저감되는 것을 알 수 있다.

Fig. 7

Uncorrelated, H2L2 pattern

첫 번째 모달 주파수에서 H2L2 패턴의 μ_f와 σ_t의 값이 ZERO 패턴의 경우보다 더욱 큰 값이기 때문에, 부적절한 값의 $x a c$ 가 정해지는 경우에는 H2L2 패턴에서 더욱 심각한 진동이 발생한다. 그러므로 외력이 독립적인 경우에는 인위적인 미스튜닝은 별다른 장점이 없다고 판단된다.

3.2 외력의 Correlation이 있는 경우

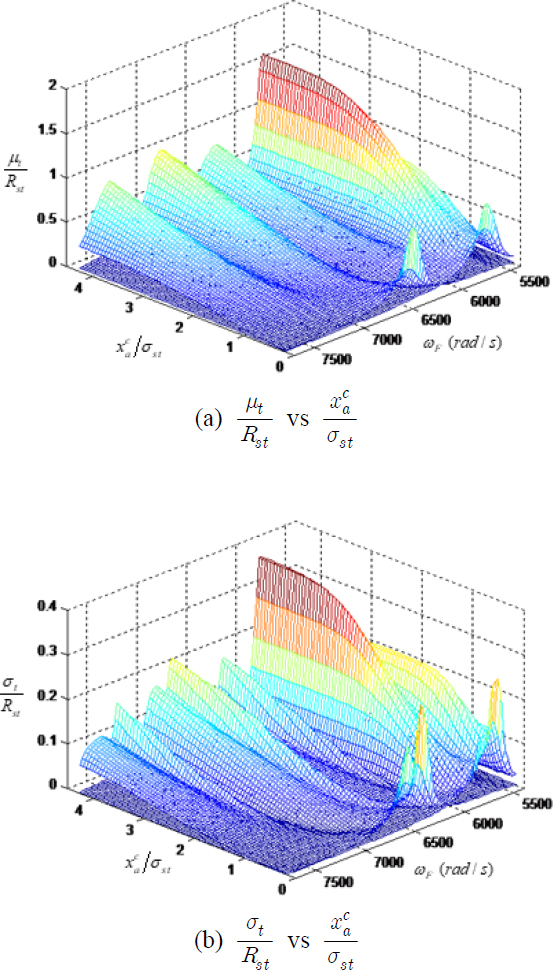
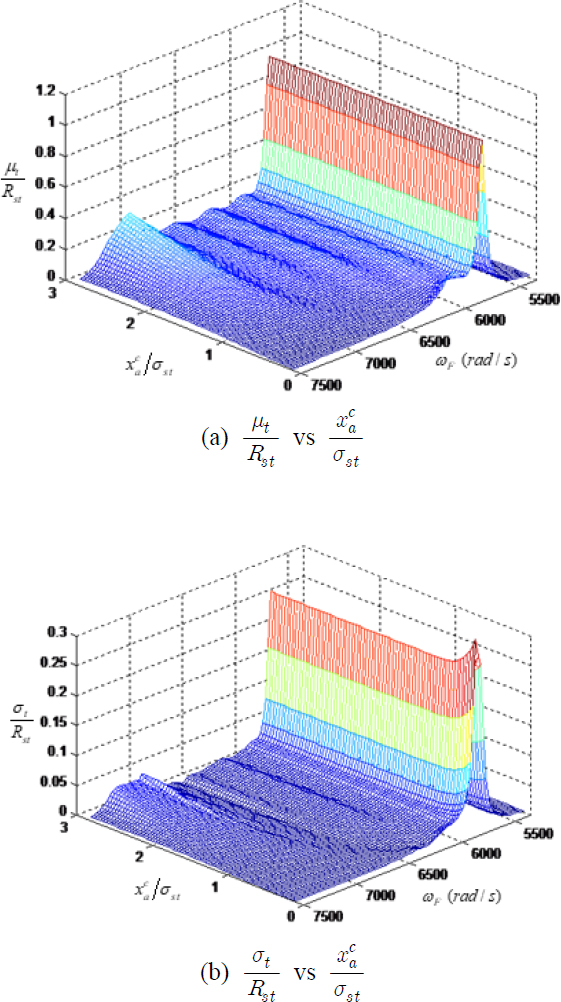
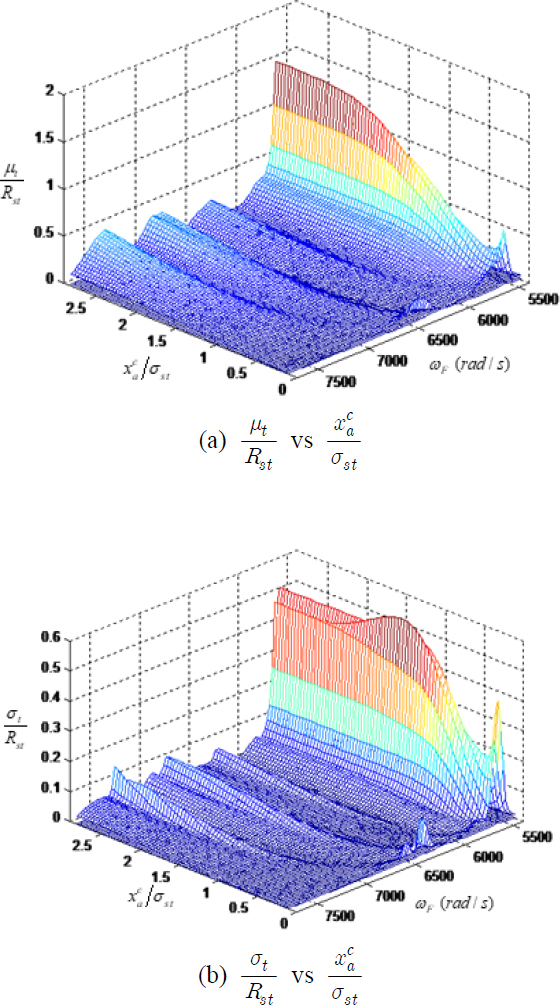
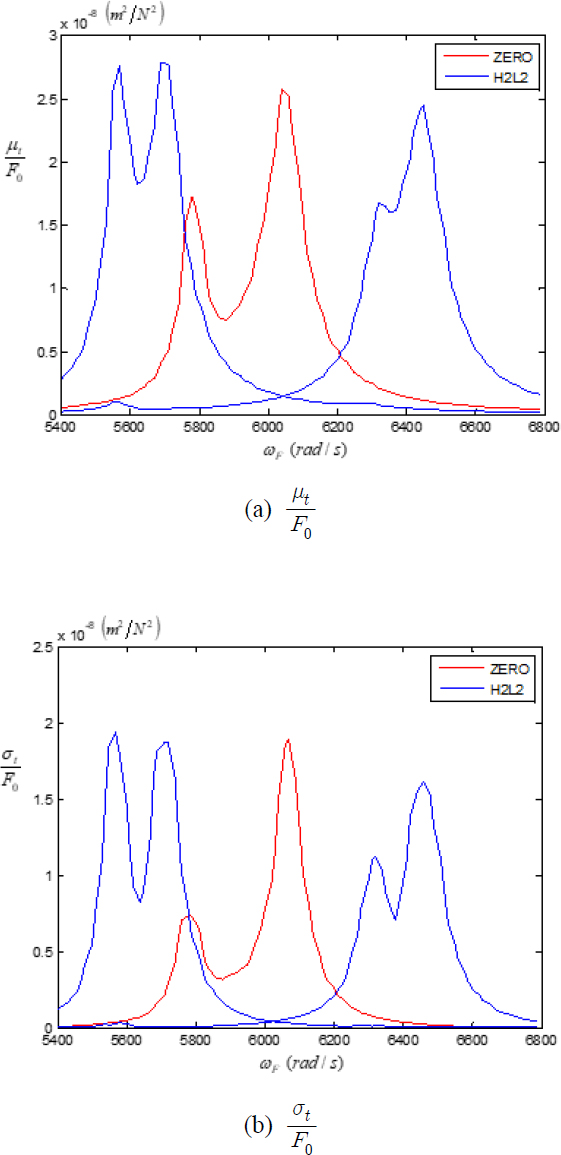
외력의 코릴레이션이 있는 경우에는, 인위적인 미스튜닝에 의하여 마찰 댐퍼의 성능은 매우 달라진다. Fig. 8을 보면, ZERO 패턴의 경우에는 마찰 댐퍼의 기능이 첫 번째 모달 주파수(5775 $r a d s$ )에서 거의 작동하지 않는 것으로 나타난다. B-B 마찰 댐퍼는 인접한 블레이드의 상대 운동에 의하여 효과를 발휘하는데 외력의 코릴레이션이 있는 경우에는 첫 번째 모달 주파수에서 모든 블레이드가 거의 동일한 방향으로 움직여서 상대 운동이 작아지기 때문이다. 이러한 경우에 B-B 마찰 댐퍼의 작동은 매우 제한되고, 효율은 매우 낮아진다.

Fig. 8

Correlation example, ZERO pattern

그 반면에 H2L2 패턴에서는 Fig. 9에 나타난 바와 같이, 적절한 값의 $x a c$ 가 정해지면 μ_t는 모든 주파수 대역에서 낮은 값을 유지할 수 있다. 비록 최적의 $x a c$ 가 결정되어도 σ_t의 값은 ZERO 패턴과 비교하여 낮아지지 않는데, 이것은 고유의 작은 미스튜닝에 의한 영향이 인위적인 미스튜닝에 의하여 크게 변동하지 않기 때문이다. 또한 $x a c$ 가 최적의 값에서 벗어나면 μ_t와 σ_t의 값이 매우 빠르게 증가하는 현상이 발견된다. 따라서 마찰 댐퍼의 설계에서 수직 하중의 선정은 매우 중요한 것을 알 수 있다.

Fig. 9

Correlation example, H2L2 pattern

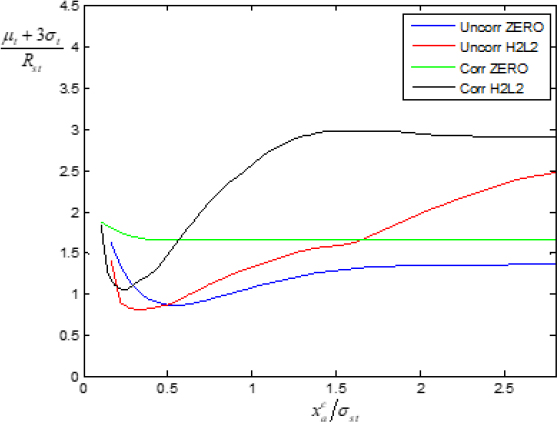
3.3 인위적인 Mistuning의 효과

외력의 특성에 따른 인위적인 미스튜닝과 마찰 댐퍼의 성능을 분석하기 위하여, 블레이드 응답의 3시그마 값을 사용하여 Fig. 10에 나타내었다. H2L2 패턴에서는 항상 무거운 블레이드에서 더 큰 진동이 발생하여 무거운 블레이드의 응답만 선택되었다. 모든 주파수 대역에서 가장 큰 값의 μ_t + 3σ_t이 선정되어 $x a c σ s t$ 의 변수와 같이 그려졌다. 인위적인 미스튜닝과 마찰 댐퍼가 함께 사용되면 외력의 특성에 관계없이 블레이드의 진동을 효과적으로 저감할 수 있다. 적절한 $x a c$ 가 정해지면 H2L2 패턴의 경우에서 ZERO 패턴보다 블레이드의 진동이 더욱 작아지는 것이 발견된다. 그럼에도 불구하고, $x a c$ 가 최적의 영역을 벗어나는 경우에는 블레이드의 진동이 H2L2 패턴에서 빠르게 증가하므로 마찰 댐퍼의 설계에는 많은 주의가 필요하다.

Fig. 10

μt+3σtRst vs xacσst

3.4 해석 결과의 정확도

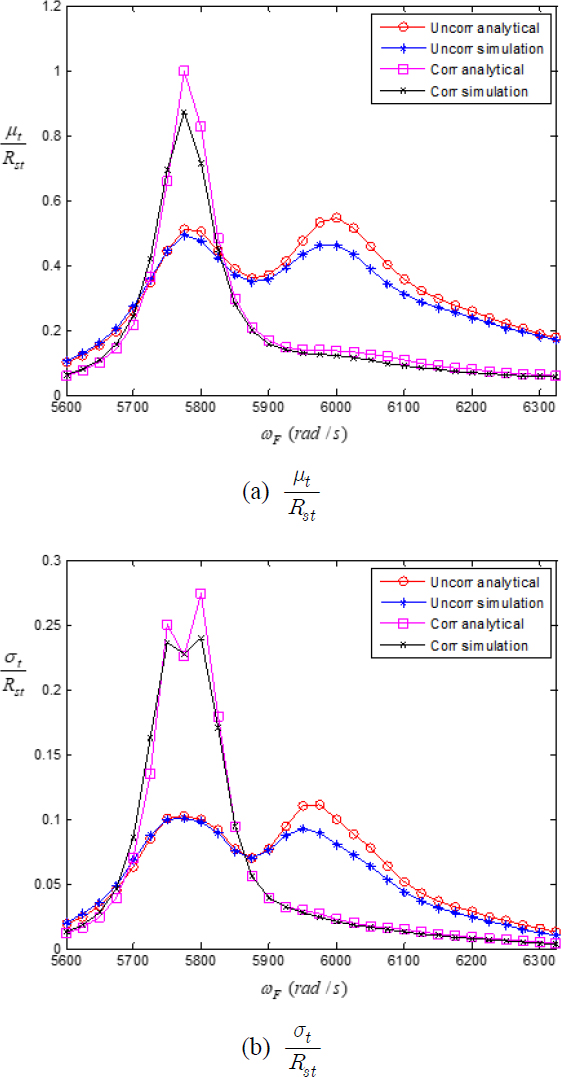
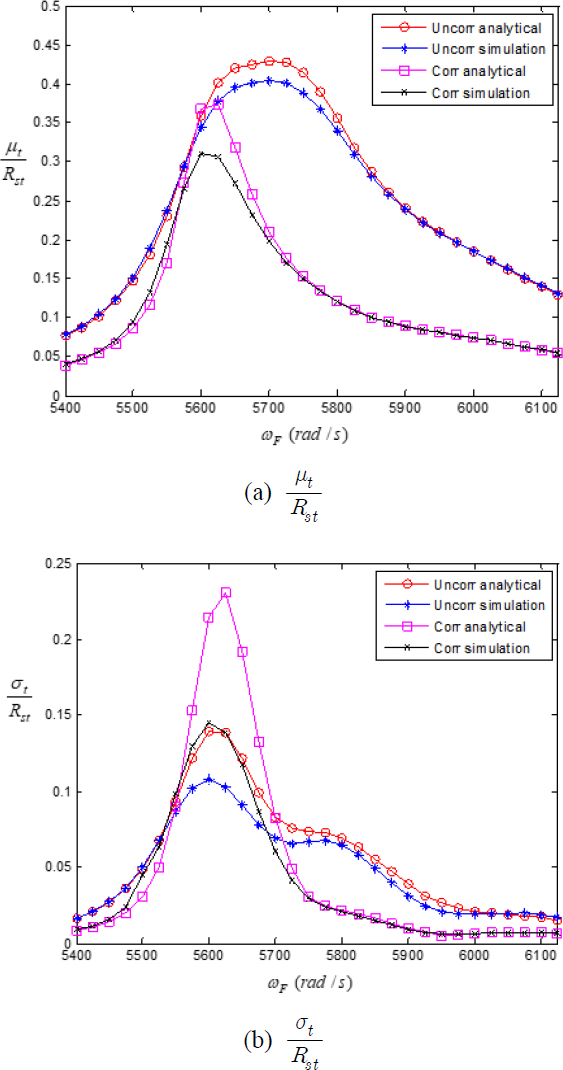
이론적인 해석의 정확도를 검증하기 위하여 몬테카를로 시뮬레이션의 결과와 비교하였다. 첫 번째 모달 주파수 대역에서 Table 2에 나타난 최적의 $x a c$ 를 선택하여 Figs. 11, 12에 ZERO 패턴과 H2L2 패턴에 대한 비교 결과를 각각 나타내었다. 인위적인 미스튜닝은 μ_t의 오차에는 많은 영향을 미치지 않으나, σ_t의 오차는 외력의 코릴레이션이 있을 때는 많이 증가하여 약 40 %의 오차를 보이고 있다. H2L2 패턴에서 σ_t의 오차가 상당히 크게 발생하기는 하지만, 외력의 코릴레이션이 있는 경우에 인위적인 미스튜닝이 마찰 댐퍼의 성능을 향상시키는 점은 명백한 것으로 나타나고 있다. 몬테카를로 시뮬레이션의 결과를 보면, H2L2 패턴에서는 μ_t와 σ_t의 값이 외력의 특성 변화에 크게 영향을 받지 않고 있는 것을 알 수 있다.

Table 2

Optimal value of xacσst for Monte-Carlo simulations

Fig. 11

ZERO pattern, xac=1.58e-5

Fig. 12

H2L2 pattern, xac=1.58e-5

비록 이론적인 해석 결과가 몬테카를로 시뮬레이션의 결과와 비교적 많은 오차를 나타내고 있으나, 몬테카를로 시뮬레이션보다는 계산시간이 매우 짧기 때문에, 마찰 댐퍼의 최적의 수직하중을 구하는 과정에는 아주 효과적으로 사용될 수 있다고 할 수 있다.

3.5 마찰 댐퍼가 제거된 경우

마찰 댐퍼가 제거된 상태에서 인위적인 미스튜닝의 효과를 검토하였다. 외력의 크기에 관계없이 μ_t와 σ_t의 값을 나타내기 위하여 식 (44)와 같이 외력의 강도를 사용하였다.

F 0 = E f 2 t

(44)

ZERO 패턴과 H2L2 패턴에 대하여, μ_t와 σ_t의 값이 외력의 강도(intensity)에 따라 Figs. 13, 14에 나타나 있다.

Fig. 13

Uncorrelated

H2L2 패턴은 가벼운 블레이드와 무거운 블레이드의 두 개의 그룹으로 이루어져 있으므로, 진동의 응답도 두 개의 피크로 이루어진 공진 특성을 나타내고 있다. 커플링 강성은 디스크 부분만을 통하여 연결되고, 상부 블레이드는 다른 블레이드와 직접 연결되지는 않으므로 분리된 하나의 블레이드와 유사한 진동 특성을 보인다. 따라서 Fig. 14와 같이 외력의 코릴레이션의 영향이 μ_t에서는 뚜렷하게 나타나지는 않으나 σ_t에서는 첫 번째와 다섯 번째의 모달 주파수에서 뚜렷하게 나타난다.

Fig. 14

Correlation example

결론적으로 인위적인 미스튜닝은 고유의 미스튜닝의 영향을 줄이지 못하고 있으며, 외력의 코릴레이션(correlation)이 있는 경우에는 더욱 악화시키는 것으로 보인다.

4. 결 론

블레이드 어셈블리의 단순한 모델을 이용하여 인위적인 미스튜닝과 B-B 마찰 댐퍼의 영향을 살펴보았다. 인위적인 미스튜닝이 없는 상태에서는, 모든 블레이드는 모달 주파수에서 공진이 동시에 발생한다. 만약 외력의 코릴레이션이 있는 상태에서, 외력의 주요 주파수가 시스템의 첫 번째 모달 주파수와 비슷한 경우에는 인접한 블레이드간의 상대운동이 매우 줄어들기 때문에 B-B 댐퍼의 성능도 급격하게 떨어진다. 이러한 현상은 블레이드의 쉬라우드(shroud)나 스누브(snubber)의 형상을 수정하는 인위적인 미스튜닝을 사용하여 제거할 수 있다. 왜냐하면 인위적인 미스튜닝으로 인하여 인접한 블레이드의 모달 특성이 공진 상태에서 매우 달라지고 인접한 블레이드 사이의 상대운동도 증가하므로, 외력의 코릴레이션 특성에 관계없이 마찰 댐퍼는 매우 효율적으로 작동될 수 있다.

이 연구에서는 인위적인 미스튜닝과 마찰댐퍼를 동시에 적용했을 때 블레이드 진동 저감 효과를 이론적으로 분석하여 댐퍼의 설계에 필요한 최적의 수직하중을 블레이드의 진폭을 이용하여 나타내었다. 그리고 마찰 댐퍼가 없는 상태에서 인위적인 미스튜닝만으로는 진동 저감 효과가 없다는 것이 밝혀졌는데, 이러한 결과는 전통적인 엔진오더 가진(engine-order-excitation)에서의 다른 결과이다. 터빈 시스템에서 외력은 비주기적인 특성을 가지므로, 블레이드의 진동 제어를 위하여는 인위적인 미스튜닝과 더불어 마찰댐퍼를 같이 적용하는 것이 반드시 필요하다.

기 호 설 명


A :	블레이드 시스템의 상태 공간 행렬
B :	입력 힘의 상태 공간 행렬
a_i :	i번째 마찰 댐퍼의 변위
C :	시스템 모델의 댐핑 행렬
C_F :	밴드패스 필터(band pass filter)의 댐핑 행렬
C_R :	밴드패스 필터의 연결 구조 행렬
C_x, K_x, C_y, K_y :	마찰 댐퍼의 선형화 행렬
c :	블레이드 시스템의 댐핑 계수
$c a, i x, k a, i x, c a, i y, k a, i y$ :	i번째 마찰 댐퍼의 선형화 계수
D :	차원 일치용 행렬
E[ ] :	평균
$F N a$ :	마찰 댐퍼의 수직하중
F₀ :	f(t)의 강도
f_a,i :	마찰 댐퍼의 히스테레시스 마찰력
f_i(t) :	i번째 블레이드에 작용하는 외력
I :	단위 행렬
K :	시스템 모델의 강성 행렬
K_F :	밴드패스 필터의 강성 행렬
k_a :	마찰 댐퍼의 강성
k_c :	블레이드의 커플링(coupling) 강성
k_d :	디스크 부의 강성
k_r :	하부 블레이드의 강성
k_t :	상부 블레이드의 강성
δk_i :	i번째 블레이드의 고유한 미스튜닝 강성
M :	시스템 모델의 질량 행렬
m_d :	디스크 부의 질량
m_r :	하부 블레이드의 질량
m_t :	상부 블레이드의 질량
dm_i :	i번째 블레이드의 인위적인 미스튜닝 질량
n :	블레이드의 개수
P :	상태 변수의 코릴레이션(correlation) 행렬
Q₀ :	w(t)의 강도
R_w :	w(t)의 코릴레이션(correlation) 행렬
R_f :	f_i(t)의 코릴레이션(correlation) 행렬
R_st :	x_st의 응답 분산(variance)
U( ) :	단위 스텝 함수
w(t) :	백색소음(white noise) 가진력
x_a,i :	i번째 상부 블레이드의 상대 변위
x_d,i :	i번째 디스크 부의 변위
x_st :	마찰 댐퍼가 고착된 상태에서 상부 블레이드의 최대 진폭
x_t,i :	i번째 상부 블레이드의 변위
x_r,i :	i번째 하부 블레이드의 변위
$x a c$ :	마찰 댐퍼의 미끄럼 발생 거리
y_a,i :	i번째 마찰 댐퍼의 상대 변위
z :	블레이드 시스템의 상태 벡터
μ_f :	마찰 댐퍼의 마찰 계수
μ_t,i :	상부 블레이드의 응답 분산(variance)의 평균
σ_st :	x_st의 표준 편차
σ_t,i :	상부 블레이드의 응답 분산(variance)의 표준편차
ξ_F :	밴드패스 필터의 댐핑 비
ω_F :	밴드패스 필터의 공진 주파수

Acknowledgments

이 논문은 2021년도 한국기술교육대학교 교수 교육연구진흥과제 지원에 의하여 연구되었음.

References

Whitehead, D. S., 1960, The Analysis of Blade Vibration Due To Random Excitation, Reports and Memoranda No. 3253, Cambridge University.
Griffin, J. H. and Sinha, A., 1985, The Interaction Between Mistuning and Friction in the Forced Response of Bladed Disk Assemblies, ASME Journal of Engineering for Gas Turbines and Power, Vol. 107, pp. 205~211. [https://doi.org/10.1115/1.3239684]
Sinha, A., 1990, Friction Damping of Random Vibration in Gas Turbine Engine Airfoils, International Journal of Turbo and Jet Engines, Vol. 7, No. 1-2, pp. 95~102. [https://doi.org/10.1515/TJJ.1990.7.1-2.95]
Castanier, M. P. and Pierre, C., 2006, Modeling and Analysis of Mistuned Bladed Disk Vibration: Status and Emerging Directions, Journal of Propulsion and Power, Vol. 22, No. 2, pp. 384~396. [https://doi.org/10.2514/1.16345]
Cha, D., 2017, Effects of Correlations of Narrow Band Random Excitations on the Response of a Mistuned Bladed Disk Assembly, International Journal of Precision Engineering and Manufacturing, Vol. 18, No. 6, pp. 853~862. [https://doi.org/10.1007/s12541-017-0101-9]
Cha, D., 2021, Mistuning Effects Caused by the Blade Assembling Conditions, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 31, No. 5, pp. 529~534. [https://doi.org/10.5050/KSNVE.2021.31.5.529]
Castanier, M. P. and Pierre, C., 1998, Investigation of the Combined Effects of Intentional and Random Mistuning on the Forced Response of Bladed Disks, AIAA Paper 98-3720, Vol. 126. [https://doi.org/10.2514/6.1998-3720]
Mignolet, M. P., Hu, W. and Jadic, I., 2000, On the Forced Response of Harmonically and Partially Mistuned Bladed Disks. Part I: Harmonic Mistuning, International Journal of Rotating Machinery, Vol. 6, No. 1, pp. 29~41. [https://doi.org/10.1155/S1023621X0000004X]
Mignolet, M. P., Hu, W. and Jadic, I., 2000, On the Forced Response of Harmonically and Partially Mistuned Bladed Disks. Part II: Partial Mistuning and Applications, International Journal of Rotating Machinery, Vol. 6, No. 1, pp. 43~56. [https://doi.org/10.1155/S1023621X00000051]
Castanier, M. P. and Pierre, C., 2002, Using Intentional Mistuning in the Design of Turbomachinery Rotors, AIAA Journal, Vol. 40, No. 10, pp. 2077~2086. [https://doi.org/10.2514/2.1542]
Beirow, B., Kühhorn, A., Figaschewsky, F., Bornhorn, A. and Repetckii, O. V., 2019, Forced Response Reduction of a Blisk by Means of Intentional Mistuning, ASME Journal of Engineering for Gas Turbines and Power, Vol. 141, No. 1, 011008. [https://doi.org/10.1115/1.4040715]
Choi, Y. S. and Lee, K.-H., 2010, Investigation of Blade Failure in a Gas Turbine, Journal of Mechanical Science and Technology, Vol. 24, No. 10, pp. 1969~1974. [https://doi.org/10.1007/s12206-010-0614-y]
Cha, D. and Sinha, A., 2006, Statistics of Response of a Mistuned and Frictionally Damped Bladed Disk Assembly Subjected to White Noise and Narrow Band Excitation, Probabilistic Engineering Mechanics, Vol. 21, pp. 384~396. [https://doi.org/10.1016/j.probengmech.2006.01.001]
Cha, D., 2018, Performance of Friction Dampers in Geometric Mistuned Bladed Disk Assembly Subjected to Random Excitations, Journal of Sound and Vibration, Vol. 426, pp. 34~53. [https://doi.org/10.1016/j.jsv.2018.04.012]
Cha, D., 2020, Response of Large Mistuned Bladed Disk Assembly Subjected to Random Excitations, Journal of Mechanical Science and Technology, Vol. 34, No. 2, pp. 603~615. [https://doi.org/10.1007/s12206-020-0108-5]
Griffin, J. H., 1980, Friction Damping of Resonant Stresses in Gas Turbine Engine Airfoils, ASME Journal of Engineering for Gas Turbines and Power, Vol. 102, pp. 329~333. [https://doi.org/10.1115/1.3230256]
Sinha, A. and Griffin, J. H., 1984, Effects of Static Friction on the Forced Response of Frictionally Damped Turbine Blades, ASME Journal of Engineering for Gas Turbines and Power, Vol. 106, No. 1, pp. 65~69. [https://doi.org/10.1115/1.3239552]
Panning, L., Sextro, W. and Popp, K., 2003, Spatial Dynamics of Tuned and Mistuned Bladed Disks with Cylindrical and Wedge-shaped Friction Dampers, International Journal of Rotating Machinery, Vol. 9, No. 3, pp. 219~228. [https://doi.org/10.1155/S1023621X03000198]
Petrov, E. P. and Ewins, D. J., 2003, Analytical Formulation of Friction Interface Elements for Analysis of Nonlinear Multi-harmonic Vibrations of Bladed Disks, ASME Journal of Turbomachinery, Vol. 125, No. 2, pp. 364~371. [https://doi.org/10.1115/1.1539868]
Petrov, E. P. and Ewins, D. J., 2005, Method for Analysis of Nonlinear Multi-harmonic Vibrations of Mistuned Bladed Disks with Scatter of Contact Surface Characteristics, ASME Journal of Turbomachinery, Vol. 127, No. 1, pp. 128~136. [https://doi.org/10.1115/1.1812781]
Griffin, J. H. and Hoosac, T. M., 1984, Model Development and Statistical Investigation of Turbine Blade Mistuning, ASME Journal of Vibration, Acoustics, Stress and Reliability in Design, Vol. 106, No. 2, pp. 204~210. [https://doi.org/10.1115/1.3269170]
Asano, K. and Iwan, W. D., 1984, An Alternative Approach to the Random Response of Bilinear Hysteretic Systems, Earthquake Engineering and Structural Dynamics, Vol. 12, No. 2, pp. 229~236. [https://doi.org/10.1002/eqe.4290120207]
Cha, D. and Sinha, A., 2003, Computation of the Optimal Normal Load of a Friction Damper Under Different Types of Excitation, ASME Journal of Engineering for Gas Turbines and Power, Vol. 125, No. 4, pp. 1042~1049. [https://doi.org/10.1115/1.1584474]

부 록

A. Expressions for equivalent linear coefficients of friction dampers

등가선형화법(equivalent linearization method)을 사용하고, joint gauss 확률 분포를 가진다고 가정하면 식 (16)에서 식 (19)의 계수는 아래와 같이 나타난다⁽²²⁾.

$c a, i x = k a x a c σ x ˙ a, i 2 π e r f c x a c σ y a, i 2 1 - ρ a, i 2 k a, i x = k a e r f x a c σ y a, i 2 - k a x a c σ y a, i 2 π e x p - x a c 2 2 σ y a, i 2 e r f c ρ a, i x a c σ y a, i 2 1 - ρ a, i 2 c a, i y = 12 1 + e r f x a c σ y a, i 2 - 1 π ∫ x a c 2 σ y a, i ∞ e - ν 2 e r f ρ a, i ν 1 - ρ a, i 2 d ν k a, i y = - ρ a, i x a c σ x ˙ a, i σ y a, i 2 2 π e x p - x a c 2 2 σ y a, i 2 × 1 + e r f ρ a, i x a c σ y a, i 2 1 - ρ a, i 2 - σ x ˙ a, i 1 - ρ a, i 2 σ y a, i π e x p - x a c 2 2 1 - ρ a, i 2 σ y a, i 2$

여기서

$σ x ˙ a, i 2 = E x ˙ t, i 2 + E x ˙ t, i + 1 2 - 2 E x ˙ t, i x ˙ t, i + 1 σ y a, i 2 = E y a, i 2 ρ a, i = E x ˙ t, i y a, i - E x ˙ t, i + 1 y a, i σ x ˙ a, i σ y a, i$

$c a, i y$ 는 ρ_a,i의 값이 작은 경우에는 수치적인 적분을 하지 않고 아래와 같이 근사적으로 구할 수 있다.

$c a, i y = 12 1 + e r f x a c σ y a, i 2 - 1 π ρ a, i 1 - ρ a, i 2 e x p - x a c 2 2 σ y a, i 2$

B. Expression of equivalent linear matrices of friction dampers

$C x = c a, 1 x + c a, n x 00 - c a, 1 x 00 ⋯ - c a, n x 00 0 c b, 1 x + c b, n x 00 - c b, 1 x 0 ⋯ 0 - c b, n x 0 000000 ⋯ 000 - c a, 1 x 00 c a, 2 x + c a, 1 x 00 ⋯ 000 0 - c b, 1 x 00 c b, 2 x + c b, 1 x 0 ⋯ 000 000000 ⋯ 000 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋱ ⋮ ⋮ ⋮ - c a, n x 00000 ⋯ c a, n x + c a, n - 1 x 00 0 - c b, n x 0000 ⋯ c b, n x + c b, n - 1 x 0 000000 ⋯ 000 C x = c a, 1 y 00 - c a, 1 y 00 ⋯ 000 0 c b, 1 y 00 - c b, 1 y 0 ⋯ 000 000 c a, 2 y 00 ⋯ 000 0000 c b, 2 y 0 ⋯ 000 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋱ ⋮ ⋮ ⋮ - c a, n y 00000 ⋯ c a, n y 00 0 - c b, n y 0000 ⋯ 0 c b, n y 0$

Douksoon Cha is an assistant professor of the Korea University of Technology & Education, Cheonan, Korea. He received his Ph.D. in Mechanical Engineering from Pennsylvania State University. His research interests include vibration of turbine blade, friction damper and nonlinear dynamic.