와류기인진동과 소프트갤러핑 응답에서 원통형 실린더의 유체력 추정연구
© The Korean Society for Noise and Vibration Engineering
Abstract
Different types of flow-induced vibrations are caused by fluid flows. Vortex-induced vibrations (VIV) generally occur in circular cylinders, while galloping is observed in non-circular ones. In the present study, VIV and soft galloping were investigated using a circular cylinder. To initiate soft galloping by changing the geometry of the circular cylinder, a passive turbulence control mechanism was attached to the surface of the circular cylinder. As the flow speed increased, a transition of VIV to soft galloping and its responses were observed. The maximum amplitude of the VIV and soft galloping responses were approximately 0.9 A/D and 2.8 A/D, respectively. The oscillation frequency of the circular cylinder at soft galloping was approximately the same as the natural frequency of the system. Additionally, a mathematical model was used to estimate the fluid forces during VIV and soft galloping.
Keywords:
Flow-induced Vibrations, Soft Galloping, Hard Galloping, Vortex-induced Vibrations, Fluid Force키워드:
유동기인진동, 소프트 갤러핑, 하드 갤러핑, 와류기인진동, 유체력1. 서 론
진동은 다양한 원인으로 발생을 하며, 진동의 발생은 기계부품의 마모, 피로, 파괴, 소음 등 기계에 나쁜 영향을 미친다. 유동기인진동(flow-induced vibrations)은 바람(wind)이나 조류(current) 같은 유동이 구조물을 지날 때, 구조물이 진동하는 현상을 의미한다. 유동기인진동은 구조물의 형상, 유속, 시스템의 질량, 감쇠비 등에 따라서 다양한 종류로 발생하며, 유동기인중에서 가장 많이 알려진 형태는 와류기인진동 혹은 와류유발진동(vortex-induced vibrations)이다. 와류기인진동은 원통형 구조물에서 자주 발생하며, 유동이 구조물을 지날 때, 구조물에서 생긴 와류(vortex)가 떨어져 나가면서 구조물에 양력을 번갈아 가면서 발생시키며, 결과적으로 구조물의 진동을 발생시키는 현상이다(1,2). 또 다른 형태의 유동기인진동으로 비원통형 구조물에 자주 발생하는 갤러핑(galloping)이 있다. 와류기인진동은 진동의 최대 진폭이 제한되는 반면, 갤러핑의 경우 진동의 최대 진폭에 제한이 없다(3). 즉, 임계유속(critical flow speed)에서 갤러핑이 시작하며, 임계유속 보다 유속이 더 증가함에 따라서 진폭도 함께 증가하며 결국 시스템의 파괴를 불러일으킨다. 갤러핑이 자연적으로 발생하는지 외부의 입력이 필요한지에 따라서 소프트 갤러핑(soft galloping)과 하드 갤러핑(hard galloping)으로 나누어진다(4). 소프트 갤러핑은 유속이 증가함에 따라서 자연적으로 갤러핑이 발생하는 현상이며, 하드 갤러핑은 유속이 증가하더라도 갤러핑이 발생하지 않으며, 갤러핑을 발생시키기 위해서는 인위적인 임계값(threshold amplitude)이 필요하다. 그 외에도 후류 갤러핑(wake galloping), 간섭 갤러핑(interference galloping), 근접 갤러핑(proximity galloping)등 다양한 형태의 유동기인진동이 존재한다(5).
유동기인진동은 구조물에 지속적인 진동을 발생시켜 시스템을 파괴시킬 수 있다. 특히, 갤러핑은 와류기인진동에 비해서 진폭의 크기가 훨씬 크기 때문에, 다리, 건물, 해양구조물 설계에 각별한 주의가 필요하다. 최근 과학기술의 발달로 인해서 전산유체역학(computational fluid dynamics : CFD)이나 유체구조 상호작용(fluid-structure interaction: FSI) 해석 소프트웨어를 이용해서, 유동기인진동에 의한 유체력 추정은 가능하나 시뮬레이션 검증을 위해서 여전히 실험 데이터가 필요하다. 특히, 유체력은 mass ratio와 Reynolds number에 많은 영향을 받으며, 이 실험이 이루어진 Reynolds 영역대는 3 × 104<Re<1.2 × 105이다. 정지한 원통형 실린더에 대해서 이는 TrSL3(transition to shear layer 3)에 속하는 영역대이다. 이 영역은 shear layer가 완전히 난류(turbulent) 영역이 되는 곳이면서 유체의 양력이 가장 강한 곳이다(5). 원통형 실린더의 유체력 측정을 위한 많은 연구들은 정지한 실린더에 대해서 행해졌으며, Table 1에 나타난 것처럼, 자유롭게 움직이는 실린더에 대해서 유체력을 측정한 연구는 적은 편이며, 특히 아주 높은 Reynolds 영역대인 TrsL3에서 유체력을 측정한 실험은 제한적이다. 따라서, 구조물의 안전한 설계를 위해서 갤러핑에 의한 유체력을 산정하기 위한 연구가 필수적이다. 실험실에서 구조물에 가해지는 정확한 유체력을 측정하기 위해서는 로드셀(load cell)이나 센서처럼 측정장치가 필요하다. 이번 연구에서는 물속에 잠긴 구조물에서 발생한 유동기인진동의 유체력을 측정장비 없이 실험에서 계측한 진폭과 진동수비를 이용해서 유체력을 추정하는 방법을 이용했다. 이를 위해서 구조물의 운동방정식으로부터 유도된 수학적 모델이 사용되었다.
섹션 2에서 와류기인진동과 소프트 갤러핑 반응을 실험하고 측정하기 위한 진동장치와 회류수조가 소개되었다. 섹션 3에서는 실험을 통해서 측정한 와류기인진동과 소프트 갤러핑의 진폭과 진동수 반응이 소개되었다. 또한, 수학적 모델을 이용해서 계산한 와류기인진동과 소프트 갤러핑의 유체력계수 와 위상차 결과들이 제시되었다.
2. 실험 방법
이 섹션에서는 유동기인진동을 실험하기 위한 실험 장치와 진동장치를 설명한다.
2.1 회류 수조
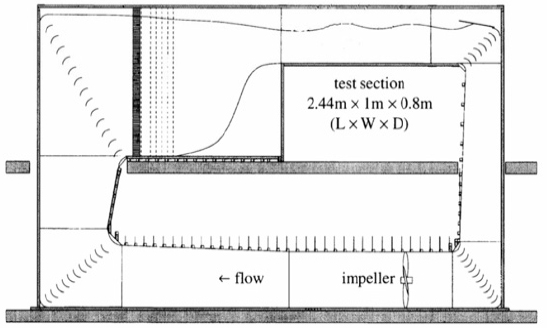
이번 실험은 회류수조에서 물이 흘러갈 때 원통형 실린더의 응답을 측정하는 형식으로 진행되었으며, 실험은 미국 미시건대학교(University of Michigan)에서 행해졌다. Fig. 1에 나타난 것처럼, 회류 수조는 2층으로 이루어져 있다. 1층에는 20 HP(horse power)을 가진 모터와 임펠러(impeller)가 설치되어 있으며, 2층에는 실험구역(test section)이 위치하고 있다. 실험구역의 치수는 2.44 m × 1 m × 0.8 m(L × W × D)이며 1층에 있는 모터를 구동 시켜 물이 일정한 유속으로 실험구역을 지나도록 회류수조가 설계되었다. 회류 수조의 최대 유속은 1.6 m/s이며, 자유표면(free surface)에서의 난류강도(turbulence intensity)는 0.1 %보다 낮도록 설계되었다(13).
2.2 진동장치
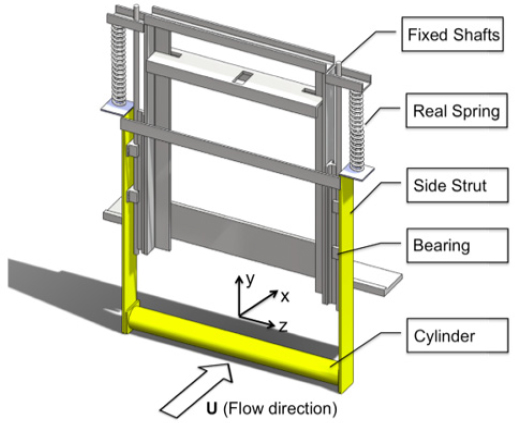
유동기인진동은 구조물에 수직과 수평방향 모두 움직임을 발생시킬 수 있다. 다만, 와류기인진동과 소프트 갤러핑에서는 수평방향으로의 움직임은 수평방향의 움직임에 비해서 미비하며, 힘의 크기도 수직방향이 수평방향 보다 훨씬 크게 나타난다(14,15). 따라서, 이 연구에서는 실린더의 움직임을 1 자유도로 제한을 두었다. Fig. 2는 진동 장치의 개략도를 보여준다. 유체가 원통형 실린더를 지나가면, 실린더는 유체의 흐름방향에 수직으로 움직이도록 설계가 되었다. 실린더 양쪽에는 버팀목(strut)이 붙어있으며, 버팀목의 끝에는 스프링이 연결되어 있다. 스프링은 원통형 실린더의 진폭 범위내에서 선형적으로 변형하는 스프링이 선택되었다. 따라서, 실험에서 스프링은 선형스프링으로 가정된다. 스프링의 스프링계수와 시스템의 감쇠계수는 자유 감쇠 실험(free decay test)을 통해서 측정되었다. 자유 감쇠 실험은 10번 수행되었으며, 10번에 대한 평균값이 실험에 사용되었다. 스프링 상수(k)와 감쇠계수(c)는 각각 763 kN/m와 3.44 Ns/m이며, 실험에 사용된 진동 장치의 물성치는 Table 2에 요약되어있다.
실린더는 원통형 모양의 실린더가 사용되었다. 원통형 실린더의 직경(D)은 0.0889 m이고 길이(L)는 0.914 m이다. 원통형 실린더 움직임을 계측하기 위해서 Celesco사의 cable-extension 선형 위치 변환기(linear position transducer)가 사용되었다. 선형 위치 변환기의 케이블은 원통형 실린더에 연결되었으며, 원통형 실린더가 움직임에 따라서, 케이블의 길이 변화가 전압으로 표시되었다. 표시된 전압은 실시간으로 변위로 변환되어서 기록되었다. 기록된 데이터의 샘플링 주파수(sampling frequency)는 100 Hz였다. 실험에서 유속을 0.45 m/s부터 1.5 m/s까지 일정한 간격으로 증가시켰으며, 고정된 유속에서 원통형 실린더의 움직임을 60초 동안 기록하였다. 실린더의 진폭은 측정된 움직임에서 가장 큰 양의 진폭과 음의 진폭 60개를 RMS(root mean square)을 이용해서 구하였다. 원통형 실린더의 움직임 진동수(oscillation frequency)는 60초 동안 기록된 시계열 값을 PSD(power spectrum density)를 사용해서 계산하였다.
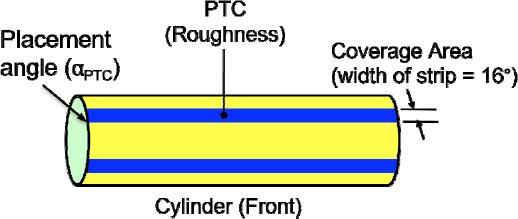
일반적으로 원통형 실린더에서는 와류기인진동만 발생하지 갤러핑은 발생하지 않는다. 갤러핑을 발생시키기 위해서 PTC(passive turbulence control)라는 새로운 장치가 원통형 실린더에 부착되었다. Fig. 3에 보여진 것처럼, PTC는 얇은 두께로 가진 사포(sand paper)이며, 실린더에 대칭으로 부착이 되었다. PTC부착으로 인해서, 원통형 실린더는 기하학적으로 더 이상 원통형 실린더가 아니며, 실험결과 와류기인진동뿐만 아니라 소프트 갤러핑도 함께 발생하였다. 실험에서 사용된 PTC는 박리점으로부터 40° 위치에 설치가 되며, PTC의 높이는 실린더 직경의 1 %가 사용되었다.
3. 실험 결과
이 섹션에서는 진동응답에서 측정된 진폭과 진동수에 대한 결과가 제시되었다. 또한, 수학적 모델을 이용해서 계산한 와류기인진동과 소프트 갤러핑의 유체력상수, 위상차 결과도 함께 제시되었다.
3.1 진폭 및 진동수 반응
유속에 따른 실린더의 진폭은 무차원변수인 U*와 A*로 표현되었으며, 실린더의 진동수는 f*로 표현되었다. f*와 U* 정의에는 added mass가 포함되었다.
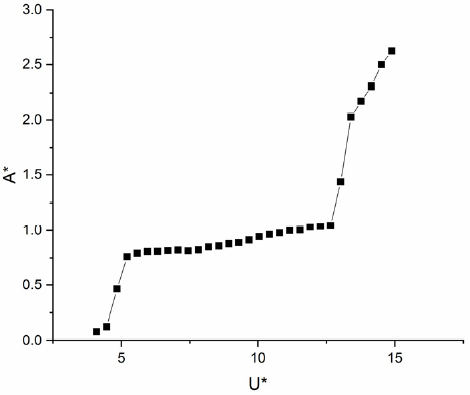
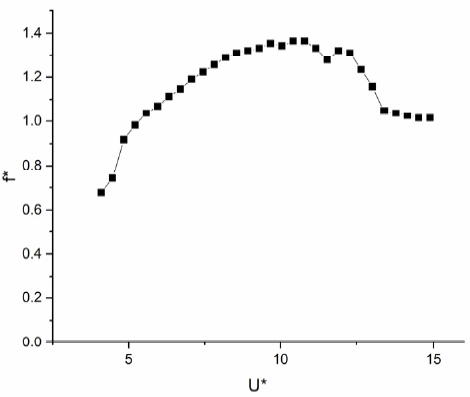
Fig. 4와 Fig. 5는 유속에 따른 진폭응답과 진동수응답을 보여준다. 실린더의 진폭응답반응은 와류기인진동, 와류기인진동-소프트갤러핑 과도단계, 소프트 갤러핑 순으로 나타났다. U*<5인 구간은 와류가 떨어지는 진동수(vortex shedding frequency)와 원통형 실린더의 진동주파수(oscillation frequency)가 같아지기 전이기 때문에, 진폭이 미미하다. U*~5에서 실린더의 Strouhal number(=fnD/U)가 0.2가 된다. 즉, 와류가 떨어지는 진동수와 원통형 실린더의 고유진동수 같아지면서, 이때부터 본격적인 와류기인진동이 시작된다. 이번 실험에서 5<U*<11이 이 구간에 해당하며, 와류기인진동은 가장 큰 진폭응답을 보이며, 유속이 증가함에 따라서 실린더의 진폭은 서서히 증가한다. Fig. 5에 나타난 것처럼, 와류기인진동 영역에서 유속이 증가함에 진동수도 함께 증가한다. 이러한 반응은 일반적인 와류기인진동과 다른 반응이며, PTC의 영향으로 간주된다. 유속을 더 증가시킴에 따라서, 11<U*<12.5에서 와류기인진동-소프트 갤러핑의 과도구간이 발생한다. 이 구간은 와류기인진동이 갤러핑으로 바뀌는 중간단계의 과정이다. Fig. 4에 나타난 것처럼 과도구간에서의 진폭은 와류기인진동의 진폭과 비슷하다. 그러나, Fig. 5에 나타난 것처럼 진동수 반응은 서서히 떨어지기 시작한다. U*>12.5부터는 본격적인 소프트 갤러핑 반응이 시작되면서, 실린더의 진폭이 급격하게 증가하며, 최대진폭은 약 2.8 A* 이다. Fig. 5에 보여진 것처럼, 실린더의 진동수 반응은 거의 일정한 값을 유지한다. 특히, 소프트 갤러핑에서의 실린더의 움직임 진동수는 시스템의 고유진동수와 같은 값을 가진다. 실험실의 제한조건으로 인해서 U*>15구간은 데이터를 측정할 수 없었다.
3.2 시계열 및 주파수 반응
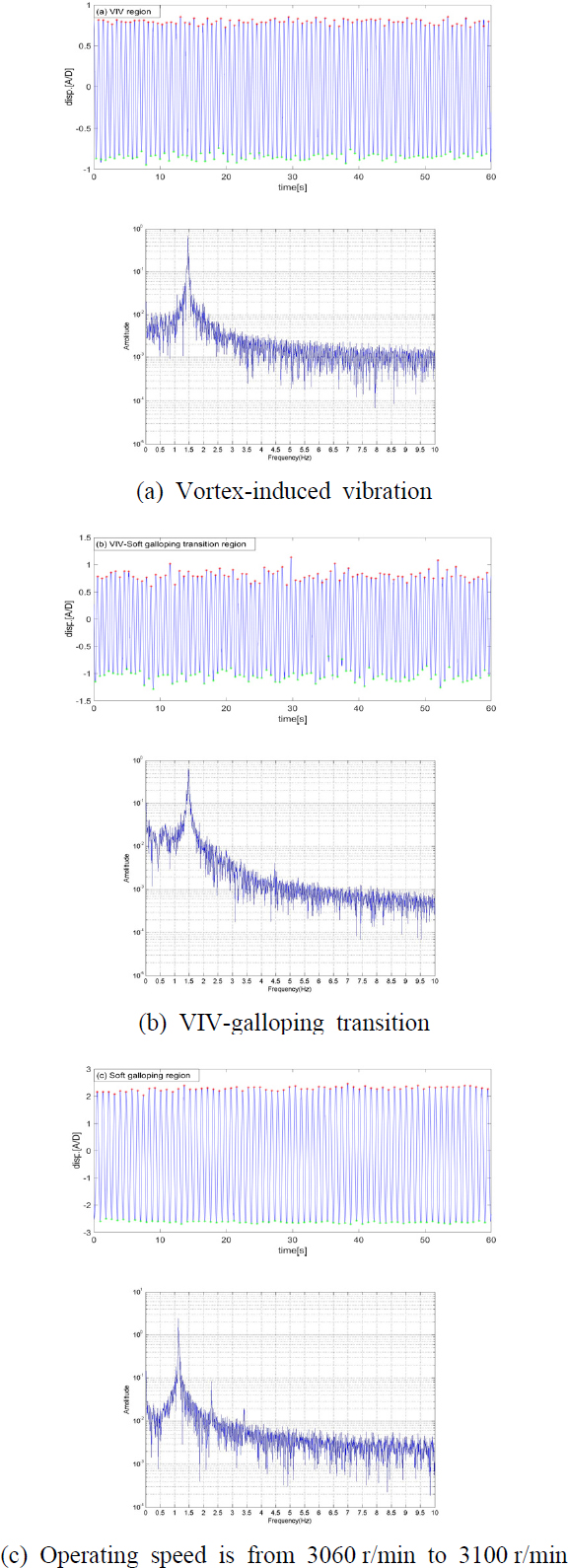
Fig. 6은 와류기인진동, 와류기인진동과 소프트 갤러핑의 과도단계, 소프트 갤러핑 영역에서 시간에 따른 실린더의 진폭반응과 PSD 해석 반응을 보여준다. Fig. 6(a)에 나타난 것처럼, 와류기인진동에서는 실린더의 시계열 반응은 규칙적인 정현응답(sinusoidal response)을 가지며, PSD 해석에도 하나의 peak 주파수가 나타난다. 유속을 증가시켜서 와류기인진동과 소프트 갤러핑의 과도단계에 도달하면(Fig. 6(b)), 와류기인진동 보다 불규칙적인 실린더 응답이 발생하며, 4.5 Hz에서 두 번째 peak이 발생한다. 즉, 와류기인진동 응답과 소프트 갤러핑 응답이 섞여서 나오는 것을 확인할 수 있다. Fig. 6(c)에 나타난 것처럼, 유속을 더 증가시키면 온전히 소프트 갤러핑 응답이 발생하며 실린더의 시계열 반응은 다시 규칙적인 정현응답을 보인다. 여기서 주목할 점은, 실린더의 시계열 반응은 규칙적인 정현응답이지만, PSD 반응에서 2, 3번째의 peak 주파수가 발생한다. 와류기인진동에 비해서 갤러핑에서는 다수의 와류가 발생을 하기때문에 다수의 와류가 한 사이클에서 같이 떨어지기 때문에 2, 3번째 peak을 만든 것으로 유추된다.
3.3 유체력 계산
와류기인진동은 원통형 구조물에서 주로 발생하는 진동현상이다. 원통형 구조물은 크게 강체형태와 유연체 형태로 나눌 수 있다. 해양산업에서 바다의 원유를 채취하기 위해서 많이 쓰이는 라이저(riser)는 최대 2 km의 길이를 가진 원통형 구조물이다. 라이저의 긴 길이와 유연한 재질로 인해서, 라이저에서 발생하는 와류기인진동을 해석하기 위해서는 라이저를 유연체 형태로 모델링을 해야한다. 이번 연구에 사용된 원통형 실린더는 aspect ratio가 10.28이기 때문에 라이저와 다르게 강체로 가정하고 해석되어야한다. 따라서, 선형 스프링에 매달린 원통형 실린더의 움직임은 식 (1)과 같이 질량-감쇠-스프링(mass-dashpot-spring) 운동방정식으로 표현될 수 있다(3). 식 (1)에서 유체력 F는 시간에 따라서 변화며 비선형적인 특성을 가지고 있다.
| (1) |
식 (1)에서 실린더의 움직임을 정현파로 가정하면, 실린더의 변위와 유체력은 식 (2), (3)처럼 표현할 수 있다.
| (2) |
| (3) |
식 (2), 식 (3)을 식 (1)에 대입한 후, sin항과 cos항으로 정리를 하면, 두 개의 식을 얻는다. 이 식들을 무차원 변수로 변환하면 식 (4), 식 (5)를 얻게 된다.
| (4) |
| (5) |
식 (4)와 식 (5)를 변형하면, 유체력 계수와 위상차를 계산 할 수 있는 식 (6), 식 (7)을 얻게 된다.
| (6) |
| (7) |
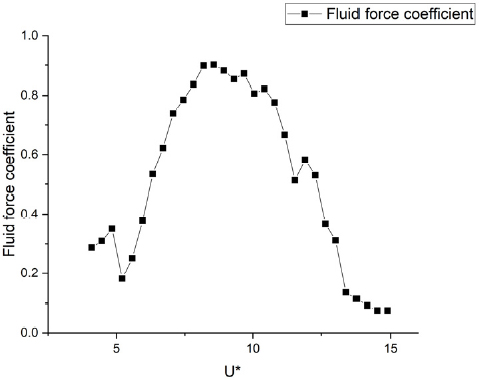
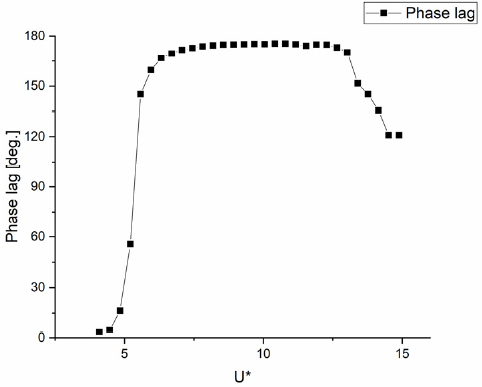
식 (6), (7)을 이용하면, 시스템의 물성치와 실험에서 측정한 유동기인진동의 진폭과 진동수를 이용해서 유동기인진동의 유체력계수 및 위상차를 계산할 수 있다. 단, 유의할 점은 이 식들은 실린더의 움직임을 정현파로 가정했기 때문에, 와류기인진동과 소프트 갤러핑의 과도구간에서는 정확도가 떨어진다. Figs. 7, 8은 섹션 3.1에서 얻어진 데이터를 바탕으로 계산한 와류기인진동, 와류기인진동-소프트 갤러핑 과도단계, 소프트 갤러핑에서의 유체력계수 및 위상차 결과이다.
와류기인진동 구간인 5<U*<11에서, 유체력계수는 U* ~ 8.5까지 빠르게 증가한다. 그리고 와류기인진동의 나머지 구간까지 거의 일정한 값을 유지한다. 와류기인진동이 시작되는 지점인 U* ~ 5.3 지점에서 위상차는 90°를 통과한다. 선형진동시스템에서 위상차 90°는 공진에서 발생을 하며, 와류기인진동에서 이 지점은 와류가 실린더에서 떨어지는 진동수와 시스템의 고유진동수가 같아지는 지점(U* ~ 5)과 유사하다. 와류기인진동 구간에서 위상차는 약 175°까지 증가한 후, 일정한 값을 유지한다. 6<U*<9 구간에서 와류기인진동의 유체력 계수는 꾸준히 증가하지만, 유체력과 실린더 속도의 위상차가 90° 차이를 보이기 때문에 와류기인진동의 진폭은 유체력계수의 증가에 비례해서 증가하지 않는다. 오히려 와류기인진동의 진폭은 제한적인 특징을 보여준다. 와류기인진동 과 소프트 갤러핑의 과도단계에서(11<U*<12.5) 위상차는 일정한 값을 가지지만, 유체력 계수는 급격하게 줄어들기 시작한다. Fig. 6에 나타난 것처럼, 이 구간에서 원통형 실린더의 움직임이 덜 규칙적인 정현파의 모습을 보이기 때문에, 결과의 정확도가 떨어질 것으로 예상된다. 그리고 소프트 갤러핑이 발생한 순간부터(U* ~ 12.5) 유체력 계수는 낮아지기 시작하며, U* ~ 15에서는 유체력 계수는 0.09 값에 수렴하는 경향이 있다. 가지나, 유속 전 범위에 대해서 가장 낮은 값을 가진다. 또한, 소프트 갤러핑에서 위상차도 유체력 계수와 비슷하게 소프트 갤러핑이 발생한 순간부터(U* ~ 12.5) 낮아지기 시작해서 U* ~ 15에서는 위상차가 120°에 수렴하는 경향을 보인다. 유체력 계수와 위상차를 분석한 결과, 실린더의 진폭은 소프트 갤러핑에서 가장 크게 발생하나, 유체력 계수는 와류기인진동에서 최대값이 발생하였다. 특히, 소프트 갤러핑에서의 유체력 계수는 전체 실험 범위 중에서 가장 낮은 값을 보여준다. 즉, 실린더의 진폭 반응은 유체력계수 와 위상차의 영향을 모두 받으며, 특히 위상차가 더 큰 영향을 준다는 것을 보여준다.
4. 결 론
일반적으로 원통형 실린더에서는 와류기인진동만 발생하며, 소프트 갤러핑은 발생하지 않는다. 원통형 실린더에서 소프트 갤러핑을 발생시키기 위해서 얇은 사포로 이루어진 PTC가 대칭으로 실린더 표면에 부착되었다. 이 연구에서는 PTC가 부착된 실린더의 진폭반응과 진동수 반응을 실험적으로 연구하였다. 실험에서 측정한 실린더의 진폭과 진동수 반응은 실린더에 가해지는 유체력계수와 유체력의 위상차를 추정하기 위한 수학적 모델의 입력 값으로 사용되었다. 이번 연구를 통해서 아래와 같은 결론이 도출되었다.
(1) PTC를 실린더 표면에 부착함에 따라서, 실린더의 진폭반응은 와류기인진동, 와류기인진동-소프트 갤러핑 과도반응, 소프트 갤러핑 반응 순으로 나타났다. 소프트 갤러핑에서는 최대 진폭이 약 2.8 A*까지 증가했으며, 실린더의 움직임 진동수는 시스템의 고유 진동수랑 거의 같은 값을 유지하였다.
(2) 실린더의 움직임을 시계열에서 분석한 결과, 와류기인진동과 소프트 갤러핑에서는 원통형 실린더는 규칙적인 정현파 움직임을 보인다. 그러나 와류기인진동과 소프트 갤러핑의 과도단계에서는 두 유동기인진동이 섞여 있기 때문에 불규칙적인 움직임이 나타났다.
(3) 유체력 계수와 유체력의 위상차를 계산하기 위해서, 실린더의 변위를 규칙적인 정현파로 가정한 수학적 모델이 사용되었다. 이 모델은 실험에서 측정한 실린더의 진폭과 실린더의 움직임 진동수를 이용해서 유동기인진동이 실린더에 가하는 유체력을 추정할 수 있다. 실린더의 진폭은 유체력 계수와 유체력의 위상차 모두 영향을 주었으며, 특히 위상차가 유체력 계수 보다 더 많은 영향을 주었다.
기 호 설 명
| A : | 원통형 실린더의 진폭 [m] |
| A*(=N/D) : | 무차원화 된 진폭 [-] |
| c : | 시스템의 감쇠 계수 [Ns/m] |
| C : | 유체력 계수 [-] |
| D : | 원통형 실린더의 지름 [m] |
| fosc : | 구조물의 움직임 진동수 [Hz] |
| fn,w : | () 물속에서 구조물의 고유진동수 [Hz] |
| f* : | 무차원화된 진동수 [-] |
| F : | 실린더에 가해지는 유체력 [N] |
| k : | 시스템의 강성 계수 [N/m] |
| L : | 원통형 실린더의 길이 [m] |
| m : | 장치에서 움직이는 부품들의 총 질량 [kg] |
| ma : | 원통형 실린더의 부가 질량 [kg] |
| mcylinder : | 실린더의 질량 [kg] |
| m* : | () 질량비 [-] |
| U : | 유속 [m/s] |
| U* : | () 감소 속도 [-] |
| S : | 실린더의 단면적 [m2] |
| y : | 실린더의 변위 [m] |
| : | 실린더의 속도 [m/s] |
| : | 실린더의 가속도 [m/s2] |
| ρ : | 물의 밀도 [kg/m3] |
| ζ : | 감쇠비 [-] |
Acknowledgments
이 연구는 2023년도 계명대학교 비사연구기금으로 이루어졌음(20230192).
References
- Hwang, J.-S., 2005, Vortex-induced Vibrations and Their Suppression in Slender Structure, Journal of KSNVE, Vol. 15, No. 6, pp. 25~29.
- Jang, H. K., Kim, S. H., Rhee, J. H. and Yang, J. R., 1999, Reduction of Flow-induced Vibration in the Heat Exchanger, Journal of KSNVE, Vol. 9, No. 6, pp. 1200~1209.
- Blevins, R. D., 1990, Flow-induced Vibration, 2nd edition, Van Nostrand Reinhold, New York.
-
Nakamura, Y. and Tomonari, Y., 1977, Galloping of Rectangular Prisms in a Smooth and Turbulent Flow, Journal of Sounds and Vibrations, Vol. 52, No. 2, pp. 233~241.
[https://doi.org/10.1016/0022-460X(77)90642-3]

- Zdravkovich, M. M., 2003, Flow Around Circular Cylinders, Oxford University Press, Oxford.
-
Zhou, B., Wang, X., Gho, W. M. and Tan, S. K., 2015, Force and Flow Characteristics of a Circular Cylinder with Uniform Surface Roughness at Subcritical Reynolds Numbers, Applied Ocean Research, Vol. 49, pp. 20~26.
[https://doi.org/10.1016/j.apor.2014.06.002]

-
Tsutsui, T. 2012, Experimental Study on the Instantaneous Fluid Force Acting on Two Circular Cylinders Closely Arranged in Tandem, Journal of Wind Engineering and Industrial Aerodynamics, Vol. 109, pp. 46~54.
[https://doi.org/10.1016/j.jweia.2012.06.005]

-
Naito, H. and Fukagata, K., 2012, Numerical Simulation of Flow Around a Circular Cylinder Having Porous Surface, Physics of Fluids, Vol. 24, No. 11, 117102.
[https://doi.org/10.1063/1.4767534]

-
Assi, G. R. S., Bearman, P. W. and Meneghini, J. R., 2010, On the Wake-induced Vibration of Tandem Circular Cylinders: The Vortex Interaction Excitation Mechanism, Journal of Fluid Mechanics, Vol. 661, pp. 365~401.
[https://doi.org/10.1017/S0022112010003095]

-
Morse, T. L. and Williamson, C. H. K., 2009, Fluid Forcing, Wake Modes, and Transitions for a Cylinder Undergoing Controlled Oscillations, Journal of Fluids and Structures, Vol. 25, No. 4, pp. 697~712.
[https://doi.org/10.1016/j.jfluidstructs.2008.12.003]

-
Morse, T. L. and Williamson, C. H. K., 2006, Employing Controlled Vibrations To Predict Fluid Forces on a Cylinder Undergoing Vortex-induced Vibration, Journal of Fluids and Structures, Vol. 22, No. 6-7, pp. 877~884.
[https://doi.org/10.1016/j.jfluidstructs.2006.04.004]

-
Brankovic, M. and Bearman, P. W., 2006, Measurement of Transverse Forces on Circular Cylinder Undergoing Vortex-induced Vibration, Journal of Fluids and Structures, Vol. 22, No. 6-7, pp. 829~836.
[https://doi.org/10.1016/j.jfluidstructs.2006.04.022]

-
Walker, D. T., Lyzenga, D. R., Ericson, E. A. and Lund, D. E., 1996, Radar Backscatter and Surface Roughness Measurements for Stationary Breaking Waves, Proceedings of the Royal Society A, Vol. 452, No. 1952, pp. 1953~1984.
[https://doi.org/10.1098/rspa.1996.0104]

-
Williamson, C. H. K. and Govardhan, R., 2004, Vortex-induced Vibrations, Annual Review of Fluid Mechanics, Vol. 36, pp. 413~455.
[https://doi.org/10.1146/annurev.fluid.36.050802.122128]

-
Bearman, P. W., 2011, Circular Cylinder Wake and Vortex-induced Vibrations, Journal of Fluids and Structures, Vol. 27, No. 5-6, pp. 648~658.
[https://doi.org/10.1016/j.jfluidstructs.2011.03.021]


Hongrae Park is received a Ph.D. in Mechanical Engineering from University of Michigan, Ann Arbor and is currently working at Keimyung University as a professor at the department of mechanical engineering. His research interest is renewable energy using flow-induced vibrations.