[ Article ]

Transactions of the Korean Society for Noise and Vibration Engineering - Vol. 33, No. 4, pp.360-371

ISSN: 1598-2785 (Print) 2287-5476 (Online)

Print publication date 20 Aug 2023

Received 19 Feb 2023 Revised 23 Apr 2023 Accepted 12 Jun 2023

DOI: https://doi.org/10.5050/KSNVE.2023.33.4.360

우주쓰레기 능동제거를 위한 우주그물 설계 변수에 따른 전개 특성 비교 연구

김형모^* ; 송다한^* ; 조해성^† ; 박재상^**

Comparative Study on Deployment Characteristics upon Space-net Design Parameters for Active Space Debris Removal

Hyeongmo Kim^* ; Dahan Song^* ; Haeseong Cho^† ; Jae-Sang Park^**

*Jeonbuk National University, Student
**Chungnam National University, Professor

Correspondence to: ^†Member, Jeonbuk National University, Assistant Professor E-mail : hcho@jbnu.ac.kr # A part of this paper was presented at the KSNVE 2022 Annual Autumn Conference‡ Recommended by Editor Joong-Kwan Kim

Abstract

As the era of private space development has begun in earnest, the amount of space debris is also increasing rapidly. Therefore, active debris removal methods are being studied. In this study, the contact-type space debris active removal method using the space net was analyzed for the tendency of the space net design variables through the structural dynamics analysis of the ejection-deployment behavior using the finite element method-based software, LS-DYNA. Boundary conditions were configured considering the injection situation, and concentrated mass, cable element, self-contact condition, and Kevlar 49 material were used. Subsequently, the storage form was simulated by folding the net. Through simulation, the design variables, ejection speed, ejection angle, and mass of the capture projectile were confirmed when the space net was completely deployed. In addition, additional simulations were performed by assuming the disturbance caused by the ejection device.

Keywords:

Active Debris Removal, Space Debris Removal Satellite, Net Deployment Simulation, Structural Dynamics Analysis, Space Net

키워드:

능동 쓰레기 제거, 청소 위성, 그물 전개 시뮬레이션, 구조 동역학 해석, 우주그물

1. 서 론

현재 우주 산업의 생태계는 기존의 정부 주도 사업(old space era)에서 민간 기업이 주도하는 뉴스페이스 시대(new space era)로 전환되어가고 있다. 대표적인 민간우주 기업인 스페이스x사의 스타링크 프로젝트는 2022년 기준 1000~2000개의 위성을 발사하였다. 이에 여러 경쟁 업체들 또한 수천 개의 위성을 쏘아 올리고 있다⁽¹⁾. 활발한 우주 개발의 양상에 따라 그 부산물로 수많은 우주쓰레기가 발생할 것으로 예상하고 있다.

우주쓰레기란, 수명이 다한 위성, 발사체 잔해물, 로켓의 파편 등을 의미한다. 2022년 12월 기준, 유럽 우주국(european space agency)에 따르면, 고도 200 km 이상에서 약 10500톤 이상의 우주쓰레기가 지구 저궤도를 초속 7 k m/s~8 k m/s로 돌고 있는 것으로 알려져 있으며, 이들은 우주선이나 인공위성과 충돌할 우려가 있다⁽²⁾. 실제로 미국항공우주국(NASA)에 따르면, 국제우주정거장(ISS)은 2020년에만 우주쓰레기로 인해 3차례 긴급 회피 기동했다⁽³⁾.

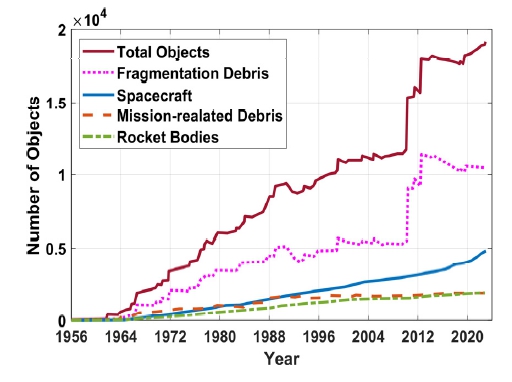
Fig. 1과 같이 우주쓰레기의 수는 급격히 증가하는 경향을 보인다. 지속 가능한 우주 개발 산업을 위하여 우주쓰레기의 경감 필요성이 대두되고 있다⁽⁴⁾. 최근 각 국가 주도 차원에서 우주쓰레기를 줄일 수 있는 청소 위성(space debris removal satellite)을 이용하여 우주쓰레기를 포획 및 제거하는 기술에 대해 적극적으로 연구되고 있다^(5~8).

Fig. 1

Monthly number of objects in earth orbit with respect to object type

우주쓰레기를 포획 및 제거하는 방법은 접촉식과 비접촉식으로 구분할 수 있다. 접촉식 제거 기법은 작살, 로봇팔, 우주그물 등이 있다. 이외에도 비접촉식 제거 기법으로 전자기장, 레이저 등을 이용한 방법이 있다. 접촉식 제거 방법 중, 작살을 이용하여 우주쓰레기를 제거하는 방법은 지상에서 많은 측면의 유효성 검사를 진행하여 다양한 설계 문제를 극복하고 특성화할 수 있지만, 우주쓰레기와 작살이 다시 청소 위성에 충돌하여 임무의 매우 높은 위험을 줄 수 있다⁽⁵⁾. 또한, 로봇 팔을 이용한 방법은 궤도상 서비싱 기술과 더불어 많은 주목을 받고 있으나, 비우호적인 우주쓰레기를 포획할 경우 로봇 팔의 조인트에 높은 토크를 가할 수 있어 포획의 어려움이 존재한다⁽⁶⁾.

한편, 우주그물을 이용하여 우주쓰레기를 포획 및 제거하는 방법은 다른 기법들과 달리 추가적인 우주쓰레기를 생성할 가능성이 적고, 정밀한 센서나 구동기가 필요하지 않으며 우주쓰레기의 크기를 고려한 우주그물의 형상 설계를 통하여 다양한 크기 및 비우호적 운동을 하는 우주쓰레기를 포획할 때 상대적으로 유리하다⁽⁷⁾. 이때 우주그물을 이용한 사출 방식의 경우 성공적으로 우주쓰레기를 제거하기 위해서는 우주그물이 원활하게 사출장치 수납형태에서 완전 전개가 이루어져야 한다. 그러나 우주그물 사출-전개 시뮬레이션의 경우 목표하는 완전 전개 형태를 얻기 위해서 고반복의 시험이 요구되며, 비용 또한 추가적으로 발생할 수 있다. 또한 국내 우주그물을 이용한 제거방법의 경우 포획과 포획 이후 우주그물에 대한 연구는 진행된 바 있으나 사출-전개에 관한 연구는 미진한 실정이다^(8,9).

따라서, 이 논문에서는 다양한 제거 방법 중 우주그물을 이용한 우주쓰레기 능동 제거 방법(active debris removal)의 사출 - 전개 시험에 대해 시뮬레이션 모델을 이용한 구조 동역학 해석을 고려하였다. 이때, 우주그물의 사출 및 전개 거동을 예측하기 위하여 우주그물에 대해 구조 동역학 해석 모델을 생성하고 이를 기반으로 시간에 따른 우주그물의 전개 거동을 사출-전개 시뮬레이션을 통해 분석하였다.

2. 연구 방법

2.1 그물 사출-전개 해석을 위한 문제 정의

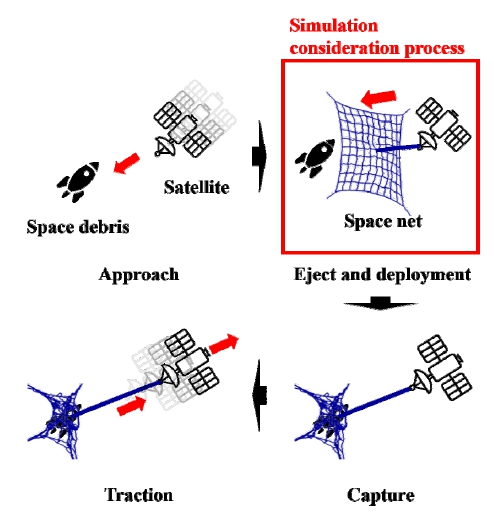
우주그물을 이용한 우주쓰레기 제거 과정은 Fig. 2와 같이 접근, 우주그물 사출, 우주그물 전개, 우주쓰레기 포획 및 우주쓰레기 견인의 5단계로 구성될 수 있다. 이 연구에서는 우주그물을 이용한 우주쓰레기 제거 과정 중 사출-전개 과정을 고려하였다. 이때, 우주쓰레기의 견인을 위한 견인줄(tether)을 생략하였으며, 사출 장치에서 포획 projectile이 발사된 상황을 가정하여 별도의 사출장치 모델을 고려하지 않았다. 하지만 우주그물의 청소위성 수납을 고려하여 그물이 접힌 형태로 초기 형상을 가정하였으며, 운용환경을 고려하여 무중력 조건을 적용하였다.

Fig. 2

Sequence of active debris removal using space net

이 연구에서는 상용 유한요소 해석 소프트웨어 Ansys⁽¹⁰⁾와 LS-DYNA⁽¹¹⁾를 사용하여 우주그물의 사출-전개 시뮬레이션 연구를 수행하였다. 유한요소법 기반 상용 소프트웨어 Ansys를 이용하여 초기 시뮬레이션 모델을 생성한다. 초기 시뮬레이션 모델은 LS-DYNA의 전처리 소프트웨어인 LS-PrePost⁽¹²⁾의 airbag folding 기능을 사용하여 우주그물의 사출 전 수납형태를 모사한다. 이후 각각의 경계조건에 따른 그물의 사출-전개 구조 동역학 해석을 LS-DYNA를 이용하여 수행하였다. 이때 사출-전개 과정에서 발생할 수 있는 우주그물 간의 자가 접촉을 고려하였다.

2.2 우주그물의 유한요소해석

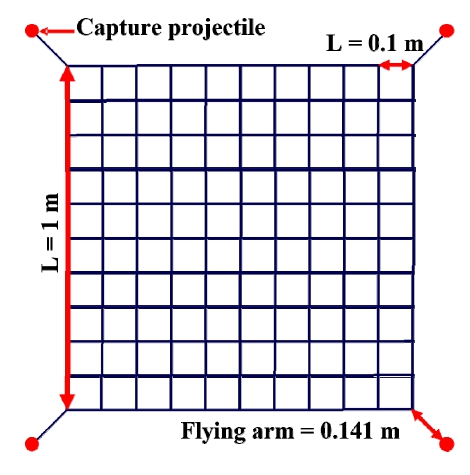
우주그물은 그물망, 포획 projectile, flying arm으로 구성되며 이 연구에서는 선행연구⁽⁹⁾를 참조하여 우주그물의 형상을 Fig. 3과 같이 설정하였다. 그물망은 우주쓰레기를 직접적으로 감싸는 그물 포획 projectile은 그물의 사출 시 발사되는 물체이며, flying arm은 그물망과 포획 projectile을 연결하는 줄이다. 그물망은 1 m×1 m 크기의 정사각형 그물이며, 각 모서리 끝단에 연결된 flying arm을 통해 포획 projectile과 결합된다. 우주그물의 격자 크기는 0.1 m로 설정하였으며, 우주그물의 단면은 1 mm의 크기를 가지는 원형 단면으로 가정하였다. Flying arm 또한 동일한 크기의 원형 단면으로 가정하였으며, 길이는 0.141 m로 설정하였다.

Fig. 3

Geometry of space net

이 연구에서 줄을 해석할 때, 축 방향 거동을 고려함에 따라 비틀림과 굽힘 강성은 무시하는 것으로 가정한다. 따라서 줄의 동적 모델을 1차원 선 요소로 단순화 가능하며, 그물망과 flying arm을 줄(cable) 요소로 모델링하였다. 각 몸체 별 요소 수 10개로 이산화 하여 총 2240개의 줄 요소로 구성하였다. 또한 줄 요소는 인접한 두 줄 요소의 끝점과 시작점이 서로 접착되어 있는 것으로 가정하였으며, 각 요소는 시작점과 끝점을 질량이 집중된 얇은 막대로 가정한 다중 강체 시스템으로 모사할 수 있다⁽¹⁴⁾. 줄 요소는 다음의 식 (1)~(3)을 통해 내력, 변위, 강성 계수가 정의된다.

F = K ⋅ m a x (△ L, 0)

(1)

Δ L = L - L 0 - d L

(2)

K = E A L 0 - d L

(3)

이때 F는 0이 아니며 요소에 가해지는 장력이다. ∆L은 줄 요소의 길이 변화량이며, K는 요소의 강성을 의미한다. L, L₀, dL은 각각 현재 요소의 길이, 초기 길이, 미소 변위이다.

포획 projectile은 구 형태를 가지는 집중질량으로 flying arm 끝단에 모사하였다. 이때 포획 projectile의 질량 관성모멘트는 선행연구⁽⁹⁾와 동일한 2.45×10^-4kg⦁m²으로 설정하였다. 우주그물의 그물망과 flying arm의 재료는 축 강성이 우수한 Kevlar 49 소재로 설정하였으며 자세한 물성치는 Table 1에 정리하였다.

Table 1

Material property of Kevlar 49

2.3 우주그물의 수납형태 정의

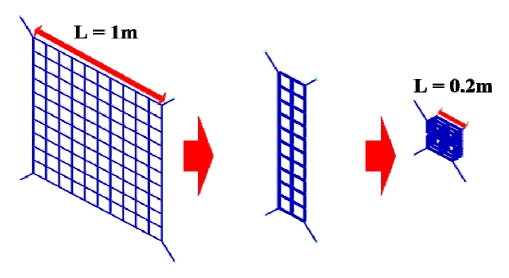
우주그물을 이용한 접촉식 우주쓰레기 능동 제거 방법의 경우 한정된 수납공간을 활용하기 위해 우주그물을 접어서 수납한다. 수납되어 있는 우주그물은 사출 단계에서 포획 projectile이 사출됨에 따라 우주그물은 수납 상태에서 전개가 진행된다. 이 연구에서는 LS-PrePost의 airbag folding 기능을 이용하여 우주그물의 수납형태를 정의하였다.

Airbag folding 기능의 접힘 정의 방식 중, thick fold 기법을 고려하였다. Airbag folding의 접힘 정의는 두 절점을 선택하여 접히는 모서리를 정의하고, 이를 기준으로 접히는 면의 절점을 선택하여 접힘 면을 정의한다. Thick fold는 Fig. 4와 같이 접힘 모서리의 반지름 값과 면 사이 두께 값을 입력하여 접힘 형태를 정의한다⁽¹²⁾. 또한 이후의 그물 접기 정의에서는 앞선 그물 접기에 의해 변형된 형상을 기준으로 접는 면이 정의된다. 앞서 기술한 방식을 이을 접는 순서를 정의하였으며, 이를 통해 그물의 초기 면적 1 m²에서 약 4 %의 면적을 가지도록 수납형태를 정의하였다. 상세한 우주그물의 수납형태 모사 과정과 최종 형태는 Fig. 5에 정리하였다.

Fig. 4

Thick fold in LS-PrePost

Fig. 5

Schematic of net folding

2.4 사출-전개 거동에 관한 그물 설계 변수

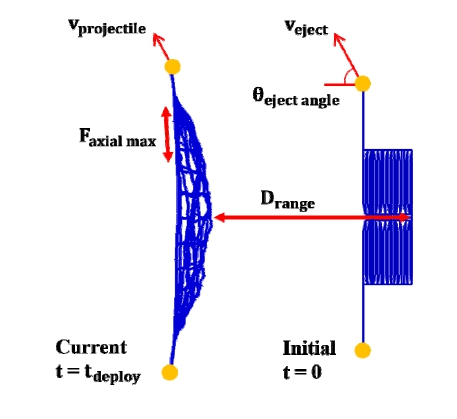
이 연구에서는 우주그물 그물망의 안정성과 구체적인 임무 설계에 앞서 사출 및 전개 시, 우주그물을 이용한 우주쓰레기 제거 선행연구에서^(13~15) 제시된 우주그물의 설계변수와 비교지표를 통해 그물의 사출 전개 시 미치는 영향을 구조 동역학 해석을 통해 확인한다. 설계변수로 우주그물 사출 각도, 사출속도, 포획 projectile 질량을 고려하였으며, 전개 특성에 관한 비교지표로 완전 전개 시 이동거리, 완전 전개 소요 시간, 줄 요소의 최대 축 하중, 완전 전개 시 포획 projectile의 속도를 비교하였다. 추가적으로 비대칭적인 우주그물 사출 속도를 부여하여 비정상적인 사출 상황을 가정하였으며, 마찬가지로 완전 전개 시 비교지표와 우주그물의 전개 형상을 확인하였다. 각 설계변수와 비교 지표를 Fig. 6에 정리하였다. 우주그물 완전 전개 상태는 그물망의 끝단 사이 거리가 최대일 때를 기준으로 하였다.

Fig. 6

Definition of parameters

3. 수치 해석 결과

3.1 경계조건 및 비교 지표 측정 위치

우주그물 사출-전개 시뮬레이션 모델의 경계조건과 설계 변수 범위는 선행연구를^(13~16) 참조하였다. 초기 경계조건으로, 포획 projectile이 사출된 상황을 가정하여 사출속도를 집중질량이 위치한 flying arm 끝단 절점에 부여하였다. 사출속도는 2.5 m/s에서 12 m/s까지, 사출각도 30°에서 70°까지, 포획 projectile 질량 0.1 kg에서 1 kg까지로 설정하여 LS-DYNA의 외연적 동역학 해석자(explicit dynamic analysis)를 사용하여 천이응답해석을 수행한다.

추가적으로 마찰 등 외란에 의한 비대칭 사출 상황 가정하여 각 포획 projectile의 사출 속도를 0 %에서 10 %까지 외란을 갖도록 설정하였다. 각 설계변수와 값의 범위는 Table 2에 정리하였다.

Table 2

Parameters in the present numerical analysis

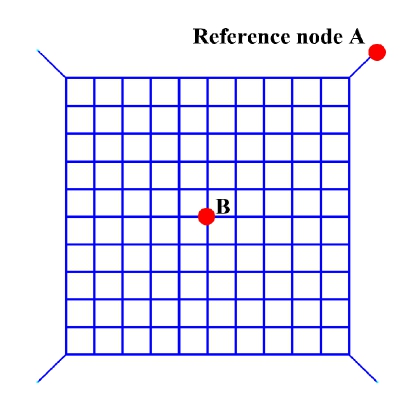
포획 projectile의 완전 전개 시 속도는 A 위치에서 이동 거리는 B위치에서 획득하였으며, 각각의 절점 위치는 Fig. 7에 나타내었다. 또한, 우주그물의 사출 - 전개 단계 과정에서 각 설계변수 별 비교지표에 대한 영향을 직관적으로 확인하기 위해 각 비교지표의 최소값과 최대값을 이용한 선형 기울기를 고려하였다. 이때, 최소값과 최대값의 기울기는 식 (4)를 이용하여 구하였다.

Fig. 7

Reference node at geometry

a = ∑ i = 1 n P i - P - C d i - C d - ∑ i = 1 n C d i - C d - 2

(4)

여기에서 a는 추세선의 기울기, P는 우주그물 설계변수, $P -$ 는 우주그물 설계변수 값의 평균, C_d는 비교지표이며, $C d ¯$ 는 비교지표의 평균이다.

3.2 우주그물 사출 속도 변화

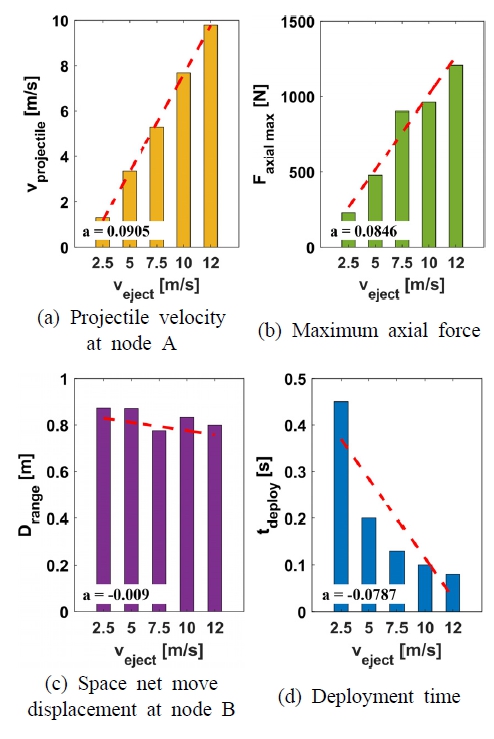
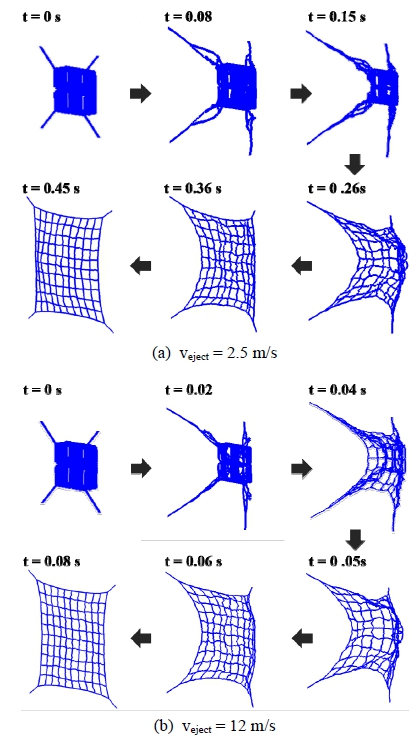
먼저 우주그물 사출속도 변화에 의한 우주그물의 사출-전개 시 영향을 확인하였다. 사출각도는 50° 및 포획 projectile 질량은 0.5 kg으로 고정하여 초기조건을 부여하였고, 사출속도는 2.5 m/s에서 12 m/s까지 변화시키며 우주그물의 사출-전개 시뮬레이션을 수행하였다.

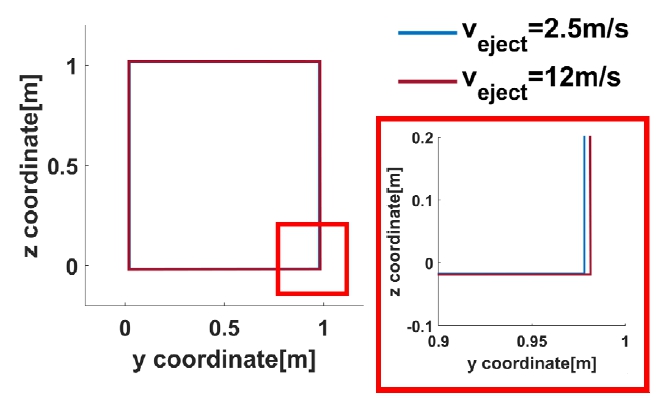
Fig. 8은 사출속도 변화에 따른 각각의 비교지표 결과이다. 사출속도 증가에 따라 완전전개 시 포획 projectile의 최종속도는 Fig. 8(a)와 같이 사출속도 2.5 m/s 조건과 비교하여 약 658 % 증가하였으며, Fig. 8(b)와 같이 최대 축 하중은 434 % 증가하였다. 반면 이동거리는 Fig. 8(c)와 같이 8 % 감소하였으며, 완전 전개 소요 시간은 Fig. 8(d)와 같이 82 % 감소함을 확인하였다. 따라서 Fig. 8(a)와 Fig. 8(c)에서 제시한 것과 같이 사출속도 증가에 따른 각 비교지표 별 영향은 최종속도의 변화율(a=0.0905)이 가장 크고 이동거리 변화율(a=-0.009)이 가장 작은 것을 확인하였다. 또한 그물의 이동거리의 경우 사출속도가 커짐에 따라 대체로 감소하는 경향을 보이나 요소 간 자가접촉 등 비우호적 거동에 의해 선형적 경향을 크게 벗어나는 것을 확인하였다. 마지막으로 Fig. 9와 같이 완전 전개 시 그물망의 2차원 평면 상 넓이는 사출속도 2.5 m/s 조건 대비 0.7 % 증가함을 확인하였다. Fig. 10(a)와 Fig. 10(b)는 각각 사출속도 2.5 m/s 및 12 m/s의 전개 과정을 나타낸다.

Fig. 8

Simulation results with respect to variation of ejection velocity

Fig. 9

Comparison of in-plane configuration of deployed space net by varying ejection velocity

Fig. 10

History of net deployment by varying ejection velocity, veject

결과적으로 사출속도와 최대 축 하중, 최종속도는 비례 관계이며, 이동거리 및 전개 소요 시간은 반비례 관계임을 수치적으로 도출하였다.

3.3 우주그물 사출 각도 변화

이 절에서는 사출각도를 변화에 의한 우주그물의 사출-전개 시 영향을 확인하였다. 사출속도는 10 m/s, 포획 projectile 질량은 0.5 kg으로 초기조건을 부여하였으며, 사출각도는 30°에서 70°까지 변화시키며 우주그물의 사출-전개 시뮬레이션을 수행하였다.

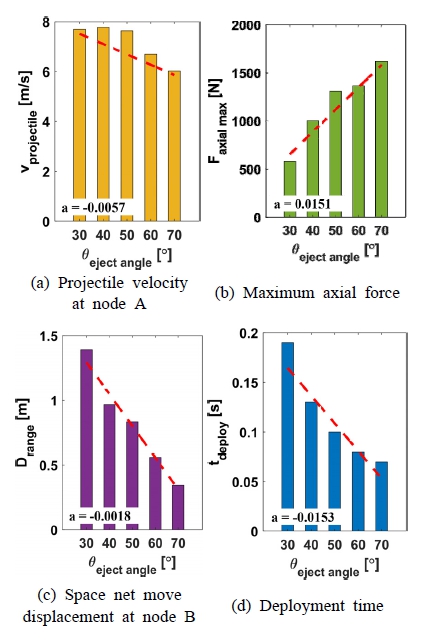
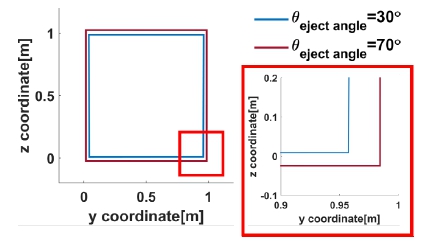
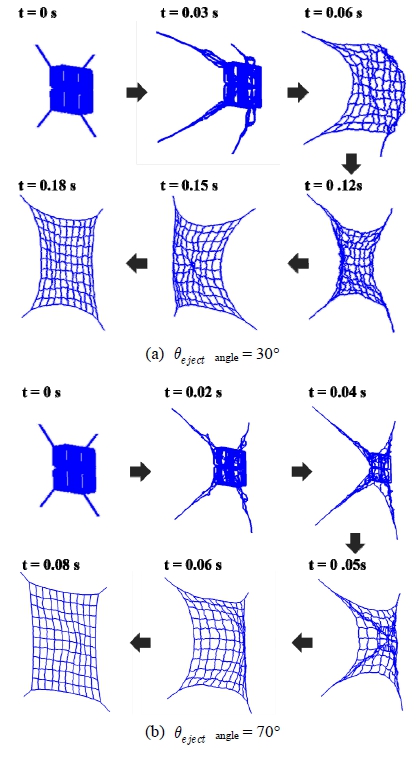
Fig. 11은 사출각도 변화에 따른 각각의 비교 지표 결과이다. 사출각도 증가에 따라 포획 projectile의 최종 속도는 Fig. 11(a)와 같이 사출각도 30° 조건과 비교하여 21 % 감소하였다. Fig. 11(b)와 같이 최대 축 하중은 약 166 % 증가하였으며, 그물망의 이동 거리는 Fig. 11(c)와 같이 75 % 감소하였다. 또한 Fig. 11(d)와 같이 전개 소요 시간은 63 % 감소함을 확인하였다. Fig. 11(a)와 Fig. 11(d)에 제시한 것과 같이 사출각도 변화에 따른 각 비교지표 별 영향은 완전 전개 소요시간의 변화율(a=-0.0153)이 가장 크고 최종속도 변화율(a=-0.0057)이 가장 작은 것을 확인하였다. 마지막으로 Fig. 12 처럼 완전 전개 시 그물망의 2차원 평면상 넓이는 사출각도 30° 조건과 비교하여 13 % 증가하였다. Fig. 13(a)와 Fig. 13(b)는 각각 사출각도 30° 및 70°일 때의 전개 과정을 나타낸다. 결과적으로 우주그물 사출각도와 최대 축 하중은 비례 관계이며, 이동거리, 포획 projectile의 최종속도, 전개 소요 시간은 반비례 관계임을 수치적으로 도출하였다.

Fig. 11

Simulation results with respect to variation of ejection angle

Fig. 12

Comparison of in-plane configuration of deployed space net by varying ejection angle

Fig. 13

History of net deployment by varying ejection angle, θeject angle

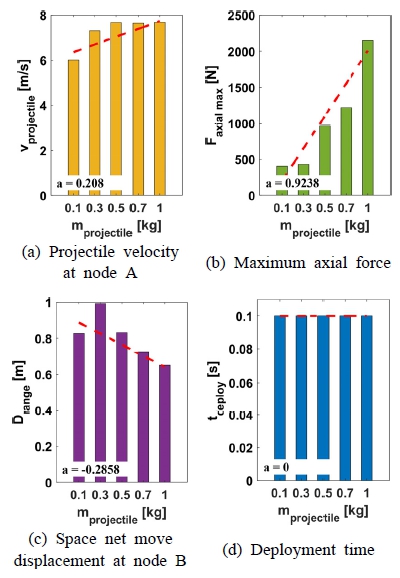
3.4 우주그물 포획 projectile 질량 변화

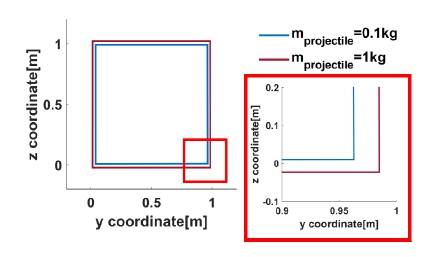
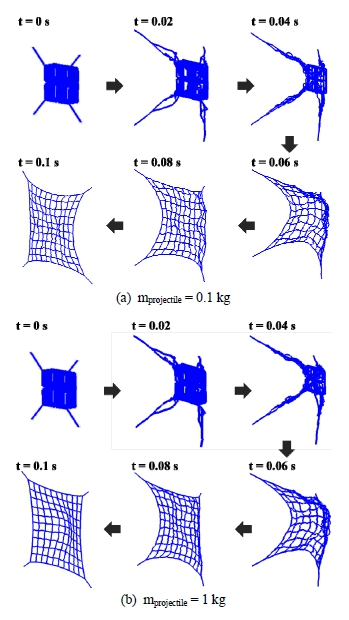
이 절에서는 포획 projectile의 질량 변화에 따른 우주그물 사출-전개 시 영향을 확인하였다. 사출각도는 50° 사출속도는 10 m/s로 고정하여 초기조건을 부여하였으며, 포획 projectile의 질량은 0.1 kg에서 1 kg까지 변화시키며 사출-전개 시뮬레이션을 수행하였다. Fig. 14는 포획 projectile의 질량 변화에 따른 각각의 비교지표 결과이다. 포획 projectile의 질량이 증가에 따라 포획 projectile의 질량 0.1 kg 조건과 비교하였을 때 최종속도는 Fig. 14(a)처럼 약 27 %, 최대 축 하중은 Fig. 14(b)와 같이 435 % 증가하였다. 반면 이동거리는 Fig. 14(c)처럼 21 % 감소하였으며, 완전 전개에 소요되는 시간은 Fig. 14(d)와 같이 0.1 s로 일정하였다. 따라서 Fig. 14(a)와 Fig. 14(b)에서 제시한 것과 같이 포획 projectile 질량에 따른 각 비교지표 별 영향은 최대 축 하중의 변화율(a=0.9238)이 가장 크고 최종속도 변화율(a=0.208)이 가장 작았다. 또한 질량에 따른 전개 소요 시간의 변화는 없었다. 추가적으로 그물의 이동거리의 경우 포획 projectile의 질량이 커짐에 따라 감소하는 경향을 보이나 요소간 자가접촉 등 비우호적 거동에 따라 비선형적 관계임을 확인하였다. 마지막으로 Fig. 15처럼 완전 전개 시 그물망의 2차원 평면상 넓이는 포획 projectile의 질량 0.1 kg 조건과 비교하여 12 % 증가하였다. Fig. 16(a)와 Fig. 16(b)는 각각 포획 projectile의 질량 0.1 kg 및 1 kg일 때의 전개 과정을 나타낸다.

Fig. 14

Simulation results with respect to variation of mass of projectile

Fig. 15

Comparison of in-plane configuration of deployed space net by varying mass of projectile

Fig. 16

History of net deployment by varying mass of projectile, mprojectile

결과적으로 포획 projectile 질량과 그물망 완전 전개 시 최종속도, 최대 축 하중은 비례관계이며, 이동거리는 반비례 관계이고 전개 소요 시간은 관계가 없음을 수치적으로 도출하였다.

3.5 우주그물 사출 시 외란 발생

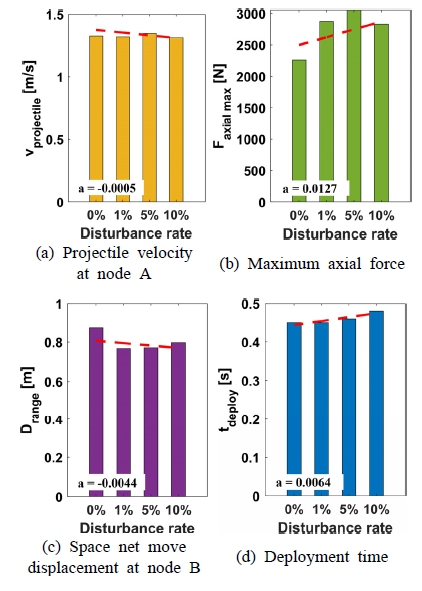
우주그물을 이용한 우주쓰레기 능동 제거 방법의 경우 사출장치의 공차 혹은 사출 시 마찰에 의한 사출속도 오차가 존재할 수 있다. 따라서 이 절에서는 정상 사출 속도는 2.5 m/s 및 사출각도 50°으로 고정하여 초기조건을 부여하였고, 비정상 사출 속도와 정상 사출 속도 간 외란을 0 %에서 10 %까지 변화시키며 우주그물의 사출-전개 시뮬레이션을 수행하였다. 이때, 비정상 사출 상황을 가정하여 Fig. 17과 같은 양 대각 포획 projectile에 감속이 발생한 상황을 가정하였다.

Fig. 17

Position of nodes with velocity disturbance

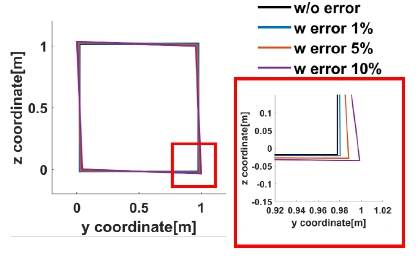
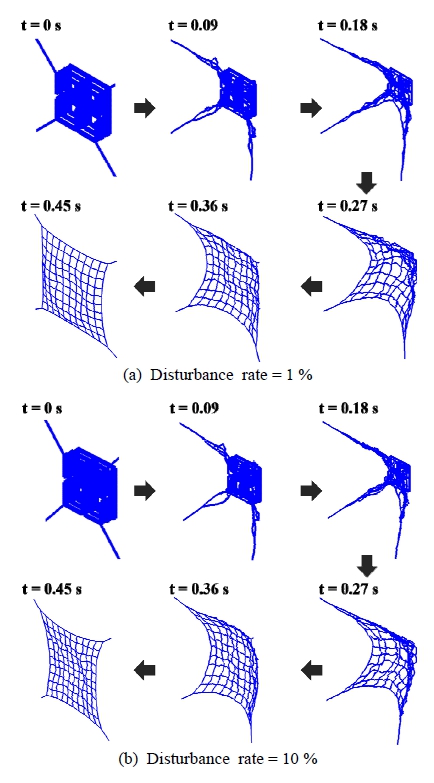
Fig. 18은 사출속도 외란에 따른 각각의 비교지표 결과이다. Fig. 18(a)와 같이 사출 속도의 외란이 커짐에 따라 최대 축 하중은 Fig. 18(b)와 같이 5 % 외란조건에서 약 3000N으로 도출되었으며, 외란이 없는 경우와 비교하여 50 % 증가하였다. 또한 최대 10 % 외란 조건에서는 외란이 없는 정상 사출 조건과 비교하여 약 25 % 증가함을 확인하였다. 다음으로 전개 소요시간은 Fig. 18(d)와 같이 10 % 외란 조건에서 정상사출 조건과 비교하여 약 6 % 증가하였으며, 이동거리는 Fig. 18(c)와 같이 8 % 감소하였다. 따라서 Fig. 18(a)와 Fig. 18(b)에서 제시한 것과 같이 사출속도 외란에 따른 각 비교지표 별 영향은 최대 축 하중의 변화율(a=0.0127)이 가장 크고 최종속도 변화율(a=0.0005)이 가장 작은 것을 확인하였다. 추가적으로 그물의 최대 축 하중 및 이동 거리의 경우 외란에 의한 전개 불균형, 그물 요소의 자가접촉 등에 의한 비우호적 거동으로 인해 일반적인 경향을 보이지 않았다. 마지막으로 Fig. 19처럼 완전 전개 시 그물망의 2차원 평면상 넓이는 사출 속도 외란이 커질수록 전개 형상의 비대칭성이 커지는 것을 확인하였다. Fig. 20(a)와 Fig. 20(b)는 각각 사출 속도 외란 1 % 및 10 %의 전개 과정을 나타낸다.

Fig. 18

Simulation results with respect to variation of disturbance rate

Fig. 19

Comparison of in-plane configuration of deployed space net by varying disturbance rate

Fig. 20

History of net deployment by varying disturbance rate

결과적으로 사출속도의 외란과 그물망 완전 전개 시 소요시간, 최대 축 하중은 비례 관계이며, 이동거리, 최종 속도는 반비례 관계임을 수치적으로 도출하였다.

4. 결 론

이 연구에서는 우주그물을 이용한 우주쓰레기 능동 제거 방법의 우주그물 사출-전개 시뮬레이션 연구를 수행하였다. 사출-전개 시뮬레이션은 유한요소법 기반 상용 소프트웨어인 Ansys와 LS-DYNA를 사용하였으며, 선행연구에서⁽⁹⁾ 제시된 1 m²의 정사각 형태의 우주그물을 LS-PrePost의 airbag folding 기법을 적용하여 평면상의 넓이가 4 %가 되도록 수납형태를 모사하였다. 해당 시뮬레이션 모델을 바탕으로 우주그물의 설계 변수 중 사출 각도, 사출 속도, 포획 projectile의 질량을 변경하여 비교지표인 우주그물 이동거리, 완전 전개 시 소요 시간 및 전개 넓이, 우주그물 이동거리, 최대 축 하중을 시뮬레이션을 통해 각 설계 변수의 사출-전개 시 미치는 영향을 확인하였다.

사출 각도는 최대 축 하중과 비례, 완전 전개 시 포획 projectile의 속도, 이동거리, 전개 소요시간과 반비례하였다. 사출 속도는 완전 전개 시 포획 projectile의 속도, 최대 축 하중, 전개 소요시간과 비례하였으며, 이동거리, 전개 소요 시간과 반비례 관계임을 확인하였다. 포획 projectile 질량은 완전 전개 시 포획 pro-jectile 속도, 최대 축 하중과 비례하였으며, 이동거리와 반비례하였다. 완전 전개에 소요되는 시간은 동일하였다. 추가적으로 공정 혹은 발사 시 발생할 수 있는 외란에 의한 사출속도의 감속 상황을 가정하여, 비정상 사출 상황에서의 사출-전개 시뮬레이션을 수행하였다. 사출 속도 오차율이 커질수록 최대 축 하중, 전개 소요 시간이 커지는 경향을 보였으며, 이동거리의 경우 감소하는 경향을 보였다. 앞선 수치해석 결과들에 따라서 우주쓰레기 제거를 위한 랑데부 거리를 설계 시, 수치해석 결과를 고려하였을 때 사출각도와 포획 projectile의 질량의 민감도가 높음을 확인하였다 또한 그물의 사출 – 전개 시 파단을 방지하기 위해서는 최대 축 하중의 민감도가 높은 사출 속도 및 각도와 포획 projectile의 질량을 적절히 설계해야 한다.

향후 시뮬레이션 모델의 타당성 검증을 위하여 축소 실험 장치를 이용한 우주그물 사출-전개 지상 시험을 통해 검증할 예정이다. 또한 이 연구에서 생략한 견인줄이 결합된 시뮬레이션 모델에서의 설계변수 영향을 확인할 예정이다. 추가적으로 다양한 형상 및 재료의 우주그물을 제시하고 해당 그물에 대한 사출-전개 시뮬레이션을 통해 최적 설계를 수행할 예정이다.

기 호 설 명


A :	단면적
a :	추세선의 기울기
C_d :	비교지표 무차원 값
$C d ¯$ :	비교지표 무차원 값의 평균
D_range :	우주그물 이동 거리
dL :	줄 요소 미소 변화 길이
E :	탄성 계수
F :	줄 요소 축 하중
F_axialmax :	줄 요소 최대 축 하중
K :	강성 계수
L₀ :	줄 요소 초기 길이
ΔL :	줄 요소 변화 길이
m_projectile :	포획 projectile의 질량
P :	우주그물 설계 변수
$P -$ :	우주그물 설계 변수 평균
t :	시뮬레이션 시간
t_deploy :	완전 전개 소요 시간
v_eject :	우주그물 사출 속도
v_projectile :	완전 전개 시 포획 projectile 속도
θ_{eject angle} :	우주그물 사출 각도

Acknowledgments

이 논문은 2022년 정부(과학기술정보통신부)의 재원으로 한국연구재단 스페이스챌린지사업(No.2022 m1A3B8076744)의 지원을 받아 수행된 연구입니다.

References

BBC News, 2022, Starlink: Why is Elon Musk Launching Thousands of Satellites?, https://www.bbc.com/news/technology-62339835
The European Space Agency, 2022, Space Debris by the Numbers, https://www.esa.int/Space_Safety/Space_Debris/Space_debris_by_the_numbers
National Aeronautics and Space Administration, 2020, Orbital Debris Quarterly News, Volume 24, Issue 1, pp. 1~16.
NASA Orbital Debris Program Office, 2022, Legend: 3D/OD Evolutionary Model, https://orbitaldebris.jsc.nasa.gov/modeling/legend.html, (accessed December 30, 2022).
Forshaw, J. L., Aglietti, G. S., Navarathinam, N., Kadhem, H., Salmon, T., Pisseloup, A. et al., 2016, RemoveDEBRIS: An In-Orbit Active Debris Removal Demonstration Mission, Acta Astronautica, Vol. 127, pp. 448~463. [https://doi.org/10.1016/j.actaastro.2016.06.018]
Biesbroek, R., Innocenti, L., Wolahan, A. and Serrano, S. M., 2017, E. Deorbit - ESA’s Active Debris Removal Mission, Presented at the 7th European Conference on Space Debris.
Forshaw, J. L., Aglietti, G. S., Fellowes, S., Salmon, T., Retat, I., Hall, A. et al., 2020, The Active Space Debris Removal Mission Remove Debris. Part 1: From Concept to Launch, Acta Astronautica, Vol. 168, pp. 293~309. [https://doi.org/10.1016/j.actaastro.2019.09.002]
Lim, J. and Chung, J., 2018, Dynamic Analysis of a Tethered Space-tug System, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 28, No. 1, pp. 83~91. [https://doi.org/10.5050/KSNVE.2018.28.1.083]
Hwang, U.-J., Jang, M., Lim, J.-H., Shin, H.-C., Sim, C.-H. and Park, J.-S., 2022, Capture Simulation Study for Space Debris Using Space-nets, Journal of the Korean Society for Aeronautical & Space Sciences, Vol. 50, No. 6, pp. 435~444. [https://doi.org/10.5139/JKSAS.2022.50.6.435]
Ansys M. Element Library, 2020, Ansys Element Reference.
Livermore Software Technology, 2021, LS-DYNA User’s Manual, Vol. 1.
Taylor, R. and Hayashi, S., 2015, Using JFOLD & LS-DYNA to Study the Effects of Folding on Airbag Deployment, Presented at the 10th European LS-DYNA Conference 2015.
Shan, M., Gua, J. and Gill, E., 2017, Deployment Dynamics of Tethered-Net for Space Debris Removal, Acta Astronautica, Vol. 132, pp. 293~302. [https://doi.org/10.1016/j.actaastro.2017.01.001]
Yang, L., Zhang, Q., Zhen, M. and Liu, H., 2017, Dynamics and Design of Space Nets for Orbital Capture, 1 st Edition, Springer, Newyork, pp.44~45. [https://doi.org/10.1007/978-3-662-54064-0_1]
Botta, E. M., 2018, Deployment and Capture Dynamics of Tether-nets for Active Space Debris Removal, Doctoral Dissertation, McGill University, Canada.
Brown, I. F. and Burgoyne, C. J., 1999, The Friction and Wear of Kevlar 49 Sliding against Aluminium at Low Velocity Under High Contact Pressures, Wear, Vol. 236, No. 1-2, pp. 315~327. [https://doi.org/10.1016/S0043-1648(99)00293-8]

Hyeongmo Kim received his B.S. degree in Mechanical System Engineering from Jeonbuk National University in 2022. He is currently a M.S. candidate at Department of Aerospace Engineering, Jeonbuk National University. His research interests include computer-aided engineering for structural dynamics and rotorcraft fuselage structure.

Dahan Song will receive her B.S. degree in Department of Aerospace Engineering from Jeonbuk National University in 2023. In the future, she plans to be M.S. candidate at Department of Aerospace Engineering, Jeonbuk National University. Her research interests include computer-aided engineering for structural dynamics and active debris removal mechanism.

Haeseong Cho received his B.S. degree in Aerospace Engineering from Korea Aerospace University in 2011 and his M.S. and Ph.D. in Mechanical and Aerospace Engineering from Seoul National University in 2013 and 2017, respectively. He is currently an assistant professor of Aerospace Engineering at Jeonbuk National University. His research interests include computational methods in structures, structural dynamics and aeroelasticity, multiphysics/multiscale simulation.

Jae-Sang Park received Ph.D. degree in Mechanical and Aerospace engineering, from Seoul National University, Seoul, Korea in 2006. Dr. Park is currently a professor, Department of Aerospace engineering, Chungnam National University, Daejeon, Korea. His research interests include aerospace structural analyses and rotorcraft aeromechanics analyses.

Kevlar 49
Density	1440 kg/m³
Young's modulus	112 GPa
Poisson's ratio	0.36

Parameter	Value	Comparison index
θ_{eject angle}	30° ~ 70°	D_range t_deploy F_{axial max} v_projectile
v_eject	2.5 m/s ~ 12 m/s
m_proejctile	0.1 kg ~ 1 kg
Disturbance rate	0 % ~ 10 %