로켓 장착 상태에 따른 항공용 발사대 동특성 분석

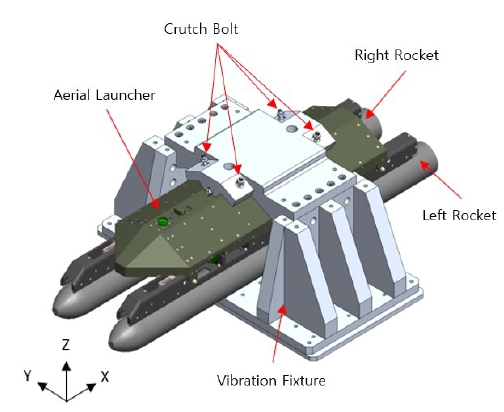
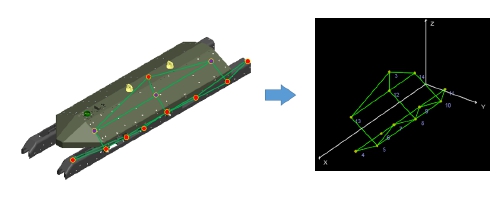
로켓 장착 상태에 따른 항공용 발사대의 동특성을 분석하기 위해 세 가지 시험을 준비하였다. 시험 경우의 수는 Table 1과 같으며 이 중 3번 시험의 시료 형상은 Fig. 1과 같다.

Table 1

Case test configuration

Fig. 1

Test configuration (case 3)

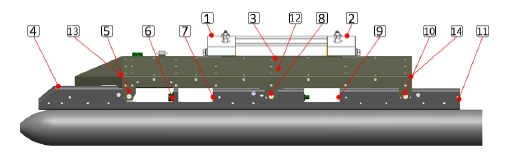
센서 부착현상은 Fig. 2와 같으며 실제 가진기에 장착한 현상은 Fig. 3과 시료 형상은 진동시험치구 하부판에서 가진이 시작되어 상부판에 전달되고, 상부판에서 항공용 발사대로 전달되는 구조이다. 따라서 원하는 가진을 항공용 발사대에 전달하기 위해서는 진동시험치구의 크러치 볼트(crutch bolt) 근처에 센서 2개(No. 1, 2)를 부착하여 계측의 평균값으로 제어할 필요가 있었으며, 이와 동시에 관찰을 수행하였다.

Fig. 2

Sensor measurement position configuration

Fig. 3

Test configuration (case 2, z-axis)

항공용 발사대의 두 러그 사이에 센서 1개(No. 3)를 부착하여 진동시험치구에서 크러치 볼트와 러그를 통해 항공용 발사대로 전달되는 응답을 계측하였다. 항공용 발사대 내부에 장착되는 전자장비의 응답을 확인하기 위해 센서 1개(No. 12)를 부착하였다. 항공용 발사대의 몸체 구조물에서 로켓이 장착되는 레일 구조물로 전달되는 응답을 계측하기 위해 몸체 구조물과 레일 구조물의 연결부에 센서 3개(No. 5, 8, 10)를 부착하였고, 몸체 구조물의 최전방과 최후방 위치에 각각 센서 1개씩(No. 13, 14)을 부착하여 응답을 계측하였다. 레일 구조물은 로켓을 장착하는 위치와 가까운 곳과 최전방과 최후방 위치에 센서 5개(No. 4, 6, 7, 9, 11)를 부착하여 응답을 계측하였다. 데이터 수집 장치는 DEWESOFT사의 SIRIUS-HD-16xACC를 사용하였고 데이터 계측 센서는 DYTRAN사의 3220E 1축 가속도 센서를 사용하였다.

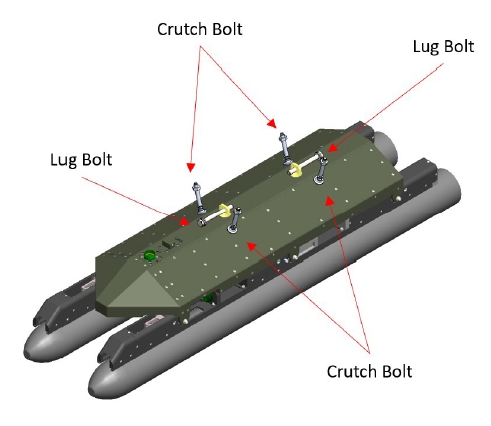
진동시험치구와 항공용 발사대는 스웨이브레이스-러그(swaybrace-lug) 장착 경계 조건을 가지고 있다. Fig. 4와 같이 진동시험치구의 러그 고정 볼트는 항공용 발사대의 러그 홈을 관통하여 항공용 발사대를 매달며, 4개의 크러치 볼트를 항공용 발사대에 맞닿게 조여 축력으로 고정하게 된다. 크러치 볼트의 끝 부분에는 볼 압입 형태로 자유롭게 회전운동을 할 수 있는 스웨이브레이스 패드(pad)가 항공용 발사대의 표면에 평행한 각도로 맞닿아 장착된다. 이는 크러치 볼트의 조임 축력에 의한 반작용력으로 고정되는 경계 조건이다. 항공용 발사대는 크러치 볼트 조임 축력에 의한 압축력만을 받기 때문에 크러치 볼트의 풀림 방향으로는 움직일 수 없게 고정되지만, 클러치 볼트 조임 방향으로는 자유롭게 움직일 수 있다. 러그 고정 볼트와 크러치 볼트는 진동시험치구 상부판에 결합한다.

Fig. 4

BC of vibration fixture & aerial launcher

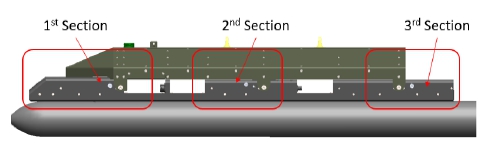
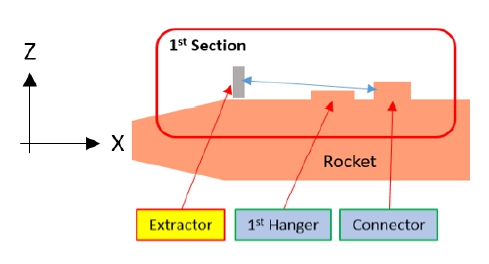
항공용 발사대와 로켓의 장착 상태는 비선형 경계 조건을 가지고 있다⁽⁶⁾. 로켓은 로켓 상단의 행거(hanger)를 항공용 발사대 레일 구조물 내부에 넣어 장입한다. 항공용 발사대의 레일 구조물은 로켓의 행거를 일정 간격의 홈 안에서만 움직이도록 제한하고, 로켓의 행거가 레일 구조물의 레버(lever)와 스누버(snubber)의 스프링 강성에 의한 비선형 접촉 및 고정을 유도한다. 항공용 발사대는 로켓을 세 구역에서 고정하며 이는 Fig. 5와 같다.

Fig. 5

Boundary condition of aerial launcher & rocket

첫 번째 구역은 로켓과 항공용 발사대의 전면부 고정이다. 로켓 행거는 항공용 발사대 레일 구조물의 홈 안에서 움직이게 된다. 로켓의 커넥터는 항공용 발사대 커넥터 분리 장치(extractor)에 고정된다. 커넥터 분리 장치는 로켓이 +X 방향으로 움직이지 않도록 고정한다. 이는 Fig. 6과 같다.

Fig. 6

1st Section BC of aerial launcher & rocket

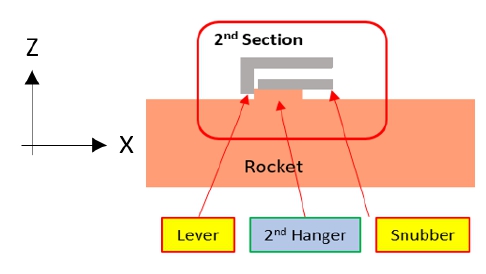
두 번째 구역은 로켓과 항공용 발사대의 중앙부 고정이다. 로켓 행거는 항공용 발사대 레일 구조물의 홈 안에서 움직이게 되면서, 항공용 발사대의 레버와 스누버를 이용해서 고정된다. 레버는 로켓이 -X 방향으로 움직이지 않도록 하며, 스누버는 로켓이 +Z 방향으로 움직이지 않도록 고정한다. 이는 Fig. 7과 같다.

Fig. 7

2nd Section BC of aerial launcher & rocket

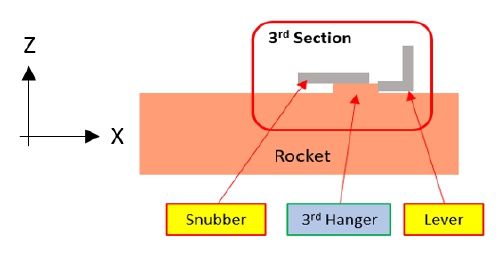
세 번째 구역은 로켓과 항공용 발사대의 후방부 고정이다. 로켓 행거는 항공용 발사대 레일 구조물의 홈 안에서 움직이게 되면서, 항공용 발사대의 레버와 스누버를 이용해서 고정된다. 레버는 로켓이 +X축 방향으로 움직이지 않도록 하며, 스누버는 로켓이 +Z 방향으로 움직이지 않도록 한다. 이는 Fig. 8과 같다.

Fig. 8

3rd Section BC of aerial launcher & rocket

항공용 발사대 몸체 주 구조물과 레일 주 구조물은 A7075-T651을 적용하였고, 레버는 STS630-H1025를 적용하여 제작하였다. 스누버를 포함한 항공용 발사대의 나머지 구조물은 A6061-T651을 사용하여 제작하였다. 로켓 동체 주 구조물은 A6061BD-T6511을 사용하였다. 로켓의 첫 번째와 세 번째 행거는 A7075-T651을 적용하였고 로켓의 두 번째 행거는 STS630-H1025를 적용하여 제작하였다. 각 재료의 물성 정보는 Table 2와 같다.

Table 2

Material property

MIL-STD-810 규격에 의하면 저속 회전익 항공기의 외부 장착물의 경우 500 Hz 내에서 내구성 시험을 시행해야 한다. 진동시험치구의 영향성을 최소화하기 위해서 진동시험치구 공진주파수가 내구성 시험의 주파수를 회피하는 설계가 수행되어야 한다.

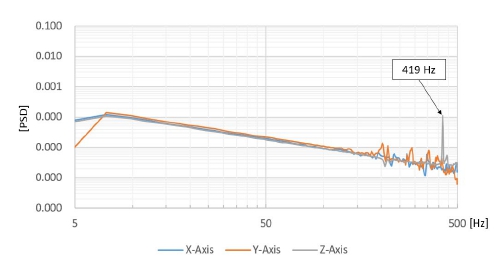
가진기에 진동시험치구만을 장착하고 3축 방향에 대해 편도 방향 공진 탐색(5 Hz~500 Hz, 0.1 g)을 6분씩 수행하였다. 제어는 가진기에 부착된 가속도 센서를 사용하였고, 공진 탐색은 진동시험치구 크러치 볼트 근처에 있는 센서 2개(No. 1, 2)의 응답 평균으로 판단하였다. X축과 Y축의 경우 500 Hz 이하에서 피크(peak) 응답이 계측되지 않았으나, Z축의 경우 Fig. 9와 같이 419 Hz에서 높은 피크 응답이 발생했다. 진동시험치구의 공진주파수는 Table 3과 같다.

Fig. 9

Vibration fixture resonance search

Table 3

Vibration fixture resonance search

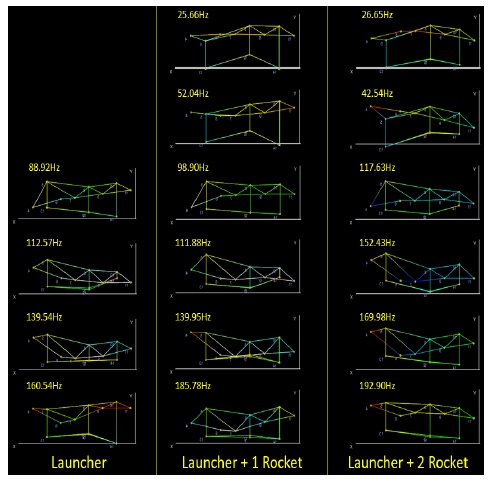
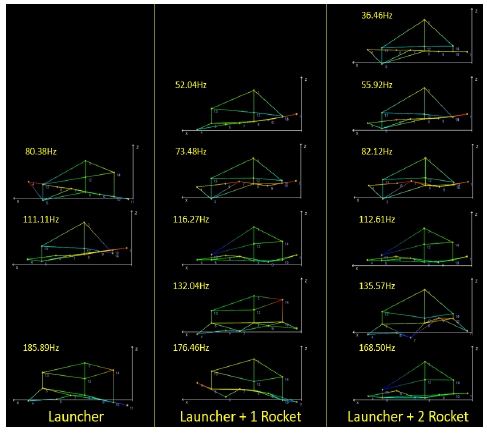
세 가지 시료 모두 3축 방향에 대해 편도 방향 공진 탐색(5 Hz~500 Hz, 0.1 g)을 6분씩 수행하였다. 가진기의 모니터링은 1번 센서 근처에서 측정하였다. 항공용 발사대에 부착한 가속도 센서의 응답을 통해 로켓 장착 수량에 따른 항공용 발사대의 주파수 응답 변화를 확인할 수 있다. 1번 센서는 항공용 발사대에 가진이 시작되는 지점이다. 따라서 1번 센서의 전달함수를 기준으로 모든 센서의 주파수 응답 함수(FRF, frequency response function)와 전달함수(TF, transfunction)를 산출하였다. 로켓 수량 변화에 따른 모드 형상(mode shape) 변화를 확인하기 위해 작동 중 변형 형상(ODS, operating deflection shape)을 계산하였다. 항공용 발사대에 부착한 센서 위치를 Fig. 10과 같이 모드 형상 절점(node)으로 설정하였다.

Fig. 10

Mode shape node configuration

항공용 발사대는 X축 방향으로 길이가 긴 형상 특성으로 인하여 공진주파수 차이에 대한 분석은 Y축과 Z축에 대해서만 수행하였다. 각 시료에 대해 공진주파수를 판단하기 위해서는 감쇠비가 안정화되는 특정 주파수를 구분해야 한다. 이를 위해 주파수 응답 함수와 전달함수를 통해 복소수 최소 제곱 기법(least squares complex exponential method)으로 공진주파수 분석(modal analysis)을 수행하였다. 안정화를 판단하기 위한 최대 차수는 40으로 설정하였다.

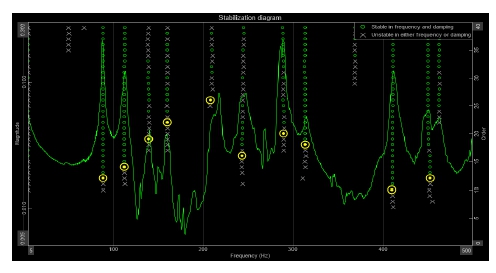
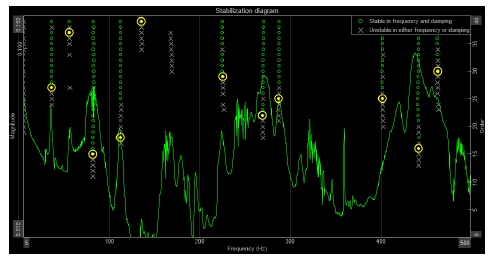
1번 센서를 기준으로 관심 영역 주파수에의 안정화 도표(stabilization diagram)를 구하여 3 % 미만의 추정 감쇠비를 갖는 특정 안정 주파수를 구분하였다. 로켓을 장착하지 않은 상태에서의 Y축 안정화 도표는 Fig. 11과 같으며, 이때 안정화된 감쇠비는 Table 4와 같다. 각 시료에 대한 Y축 공진주파수 차이는 Table 5와 같다.

Fig. 11

Stabilization diagram(launcher, y-axis)

Table 4

Stabilization table (launcher, y-axis)

Table 5

Stabilization table (launcher, y-axis)

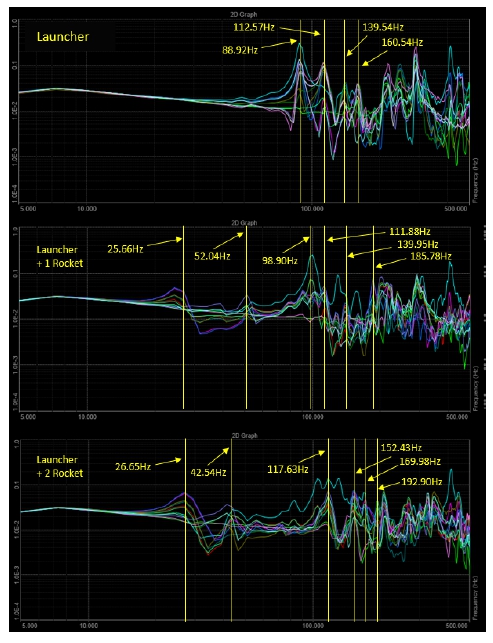
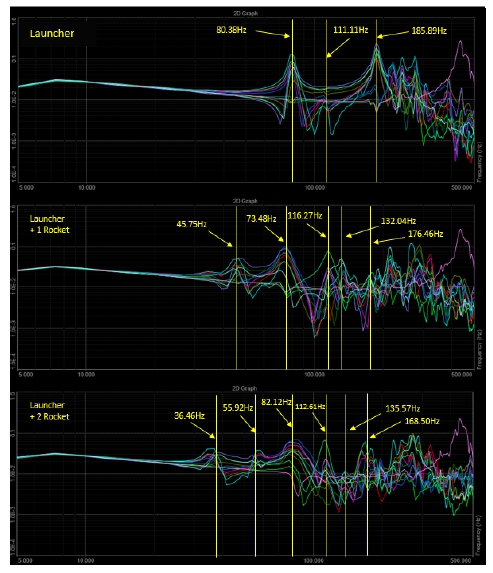
로켓 장착 상태에 따른 항공용 발사대의 Y축 동특성 차이를 분석하기 위해 Fig. 12와 같이 가속도 응답도표(acceleration response graph)를 비교하였다. 3번부터 14번까지 총 12개의 센서에 대한 응답을 중첩하였고, 200 Hz까지 영역에서 전체적으로 가속도 응답이 높은 주파수를 식별하였다. 가속도 응답이 높은 주파수는 모든 시료에서 모드 형상 분석의 주파수와 일치하였음을 확인하였고, 로켓 장착 상태에 따라 항공용 발사대의 공진주파수가 달라짐을 확인하였다.

Fig. 12

Sensor response graph (Y-axis)

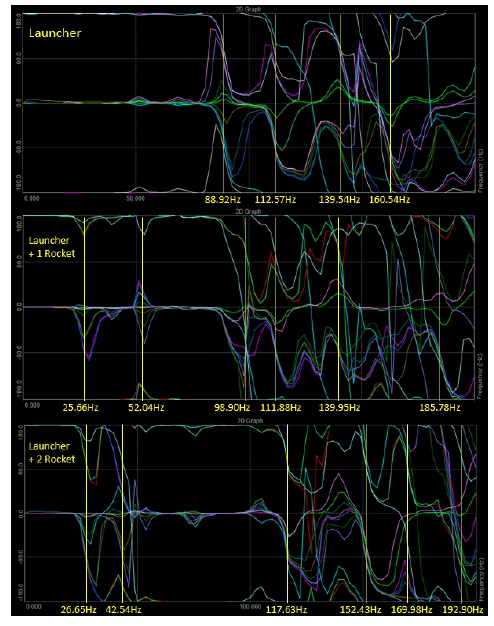
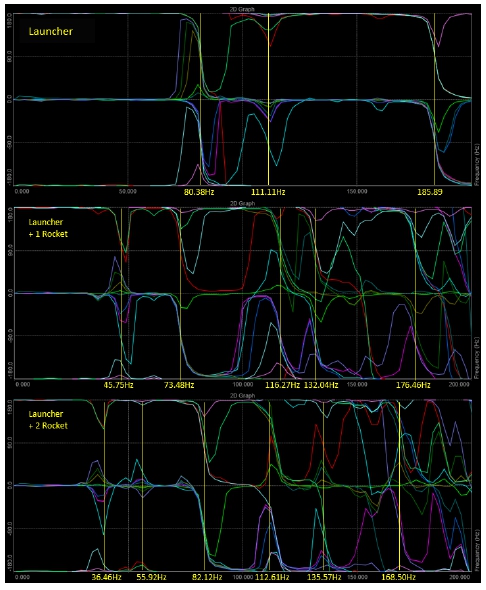
위상 변화 도표(phase shift graph)로 Y축 동특성 차이를 분석하였다. 3번부터 14번까지 센서 응답의 위상 변화를 Fig. 13과 같이 작성하여 비교하였다. 위상이 180° 변화할 때 해당 주파수에서 공진이 발생했다고 판단할 수 있다. 위상 변화 도표와 가속도 응답 도표의 공진주파수가 일치하였음을 확인하였다.

Fig. 13

Sensor phase shift graph (Y-axis)

항공용 발사대 공진주파수에 대해 Y축에 대한 모드 형상은 Fig. 14와 같다. 로켓을 장착하였을 때 첫 번째와 두 번째를 제외하고 유사한 모드 형상에 대해 공진주파수가 달라짐을 확인하였다.

Fig. 14

Mode shape (Y-axis)

로켓을 모두 장착한 상태에서 1번 센서를 기준으로 관심 영역 주파수에서의 Z축 안정화 도표는 Fig. 15와 같으며, 이때 안정화된 감쇠비는 Table 6과 같다. 각 시료에 대한 Z축 공진주파수 차이는 Table 7과 같다.

Fig. 15

Stabilization diagram (launcher + 2 rocket, Z-axis)

Table 6

Stabilization table (launcher + 2 rocket, Z-axis)

Table 7

Aerial launcher resonance search (Z-axis)

로켓 장착 상태에 따른 항공용 발사대의 Z축 동특성 차이를 분석하기 위해 Y축 분석과 동일하게 가속도 센서 응답 도표를 비교하여 200 Hz까지 영역에서 전체적으로 가속도 응답이 높은 주파수를 Fig. 16과 같이 식별하였다. 가속도 응답이 높은 주파수는 모든 시료에서 모드 형상 분석의 주파수와 일치하였음을 확인하였고, 로켓 장착 상태에 따라 항공용 발사대의 공진주파수가 달라짐을 확인하였다.

Fig. 16

Sensor response graph (Z-axis)

Z축에 대한 항공용 발사대의 각 시료에 대한 위상 변화 도표를 Fig. 17과 같이 비교하였다. 위상 변화 도표의 공진주파수와 가속도 응답 도표의 공진주파수가 일치하였음을 확인하였다.

Fig. 17

Sensor phase shift graph (Z-axis)

항공용 발사대 공진주파수에 대해 Z축에 대한 모드 형상은 Fig. 18과 같다. 로켓을 장착하였을 때 첫 번째와 두 번째를 제외하고 유사한 모드 형상에 대해 공진주파수가 달라짐을 확인하였다. 또한 로켓이 장착됨에 따라 다섯 번째의 새로운 공진주파수와 모드형상이 추가됨을 확인하였다.

Fig. 18

Mode shape (Z-axis)

Y축과 Z축 모두 로켓이 장착되었을 때 1차 주파수 응답이 하락했다. Y축은 항공용 발사대 레일 구조물의 홈 안에서 로켓이 움직이게 되는 경계 구조이기 때문에 25 Hz, 40 Hz~50 Hz 근처에서 병진 운동이 발생하는 것으로 판단된다. Z축도 로켓이 장착됨에 따라 주파수의 응답은 낮아졌으며 36 Hz, 53 Hz, 133 Hz 근처에서 공진주파수가 추가됨을 확인했다. 이를 통해 공진주파수 기준 로켓 장착 상태에 따른 항공용 발사대의 동특성 변화를 확인했다.

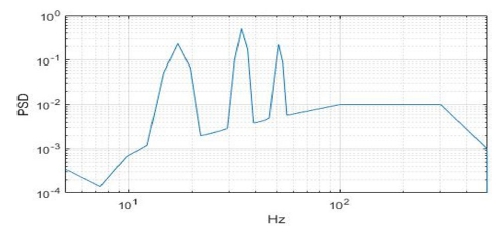
회전익 항공기 외부 장착물의 시험 프로파일은 광대역 랜덤 영역에 사인 피크가 포함된 사인 온 랜덤(SoR, sine on random)이며, 주파수에 대한 파워 스펙트럼 밀도(PSD, power spectrum density) 함수로 나타낼 수 있다. 이는 Fig. 19와 같다.

Fig. 19

Reference SoR PSD profile

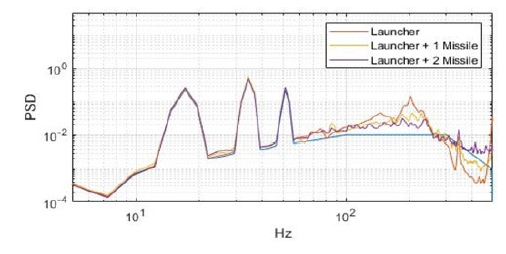
가진은 진동시험치구 하부판에서 시작되어 상부판을 거친 뒤 크러치 볼트와 러그 볼트를 통해 항공용 발사대에 전달되게 된다. 따라서 1번과 2번 센서에서 계측되는 평균 가속도 응답이 설정한 가진 입력과 유사하도록 가진을 제어하였다. 항공용 발사대로 입력되는 가속도 표준 편차(GRMS, gravity root mean square)를 계산하고자 3번 센서의 응답 가속도를 축 별로 분석하였고, 이 중 X축 응답은 Fig. 20과 같다.

Fig. 20

Sensor(No. 3) SoR response PSD (x-axis)

가속도 표준 편차는 중력 가속도와 표준 편차가 합쳐진 단위이며 랜덤 가진 시 가속도 센서를 통해 얻는 음과 양의 값이 섞인 중력 가속도의 크기를 정량적으로 나타낼 때 주로 사용하는 기법이다. 시간에 대한 중력 가속도 크기로 나타나는 계측 데이터를 고속 푸리에 변환(FFT, fast Fourier transform)을 통해 주파수에 대한 파워 스펙트럼 밀도 함수로 나타낼 수 있다. 가속도 표준 편차는 주파수에 대한 파워 스펙트럼 밀도 곡선 아래의 면적을 적분하여 얻을 수 있으며 면적의 제곱근과 같다.

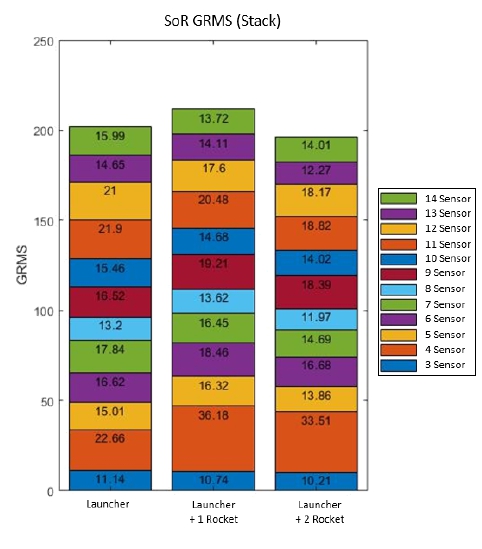
Fig. 21과 Table 8에서의 X1은 기준 사인 온 랜덤 파워 스펙트럼 밀도 가속도 표준 편차이며 각 축에 대한 가진 입력이다. X2, X4, X6은 제어 기준 사인 온 랜덤 파워 스펙트럼 밀도 가속도 표준 편차이며 센서 1번과 2번에서 계측된 값의 평균이다. X3, X5, X7은 입력 기준 센서 3번에서 계측된 사인 온 랜덤 파워 스펙트럼 밀도 가속도 표준 편차이다. 결과를 분석해보면 제어 기준 사인 온 랜덤 파워 스펙트럼 밀도 가속도 표준 편차는 약 6 % 이내로 제어가 되어 기대 입력 가속도 표준 편차가 가진 되었다고 판단할 수 있다. 입력 기준 사인 온 랜덤 파워 스펙트럼 밀도 가속도 표준 편차는 로켓이 없을 때 항공용 발사대의 가속도 응답이 가장 높았으며 로켓의 수량이 증가할 수록 가속도 응답이 낮아졌다.

Fig. 21

Sensor(No. 3) SoR response GRMS

Table 8

Sensor(No. 3) SoR response GRMS

3축을 모두 분석하였을 때, 로켓이 장착되지 않은 항공용 발사대의 가진 제어가 가장 어려웠으며 로켓이 추가되면서 점차 안정적으로 되었다. 이는 로켓이 추가되면서 전체적인 질량이 증가하고 감쇠비가 증가하여 제어가 잘 되었다고 판단된다.

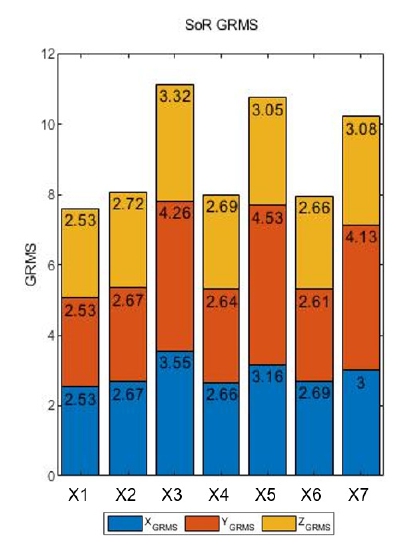
항공용 발사대에 부착한 가속도 센서의 응답을 통해 입력 가속도 대비 해당 위치에서의 가속도 응답을 확인할 수 있다. 항공용 발사대에 장착된 로켓은 경계 조건에 의해 축 방향으로 가진할 때, 해당 방향으로 주거동이 나올 것으로 가정하였다. 각 축 방향으로 가진하였을 때 항공용 발사대의 가속도 응답을 분석하였고 이는 Fig. 22와 Table 9와 같다.

Fig. 22

All sensor SoR response GRMS

Table 9

Sensor(3) SoR response GRMS

항공용 발사대에 대한 가속도 응답 총합은 항공용 발사대에 로켓을 1개 장착했을 때 가장 높았다. 축별로 분석했을 때 X축으로 가진 시, 센서 대부분은 로켓의 수량이 증가함에 따라 가속도 응답이 낮아졌다. 하지만 Y축과 Z축의 경우 대부분의 센서는 로켓의 수량이 증가함에 따라 가속도 응답이 높아졌으며, 로켓을 1개 장착했을 때 그 증가폭이 더 높았다. 특히 4번 센서의 가속도 응답이 크게 증가하였으며 6번, 9번의 센서 응답도 상대적으로 증가하였다. 이 센서들의 위치는 항공용 발사대와 로켓의 접촉부에서 거리가 먼 곳이다. 로켓의 장착됨에 따라 로켓의 동특성에 의해 접촉부가 절점이 되어 상대적으로 거리가 먼 위치에서 가속도 응답이 높아진 것으로 분석된다.

항공용 발사대의 동특성을 수치상으로 표현하고 로켓 장착 수량에 따른 항공용 발사대의 동특성 차이를 정량적으로 비교하기 위해 모드상관계수(MAC, modal assurance criterion)로 분석하였다⁽⁷⁾. 모드상관계수는 두 종류 이상의 시료에서 특정 모드의 유사도를 분석하는 기법이다. 형상 정보는 복소수 형태의 고유 벡터 값으로 표현할 수 있으며 모드상관계수의 일반적인 계산식은 식 (1)과 같다.

일반적인 계산식은 질량 분포가 형상학적으로 대칭인 구조물에 적용할 수 있지만, 항공용 발사대와 같이 질량 분포가 비대칭적이며 형상학적으로도 비대칭적인 복합 구조물의 경우에는 수정된 계산식이 필요하다. 수정된 계산식은 식 (2)와 같다.

두 종류의 시료가 동일한 위치에서 계측한 센서 응답이 있다면 모드 유사도를 판별할 수 있다.

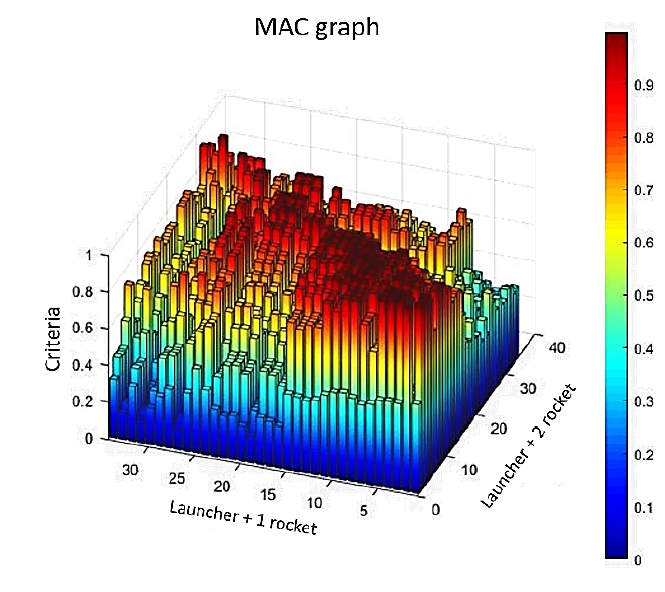
로켓 장착 상태에 따른 항공용 발사대의 전체 동특성 차이를 분석하기 위해 특정 모드의 유사도 판별이 아닌 모든 주파수에 대해 고유 벡터 값을 추출하여 동특성 유사도를 판별하였다. 세 종류의 시료에 대해 각 축에 대한 고유 벡터 값을 추출하였고, 이를 모드상관계수 계산식에 적용하였다. 동특성 유사도 확인은 기준 사인 온 랜덤 파워 스펙트럼 밀도 가속도 표준 편차를 5 Hz~500 Hz까지 가진하였을 때의 응답으로 비교하였다. 실제 계측은 2.44 Hz 간격으로 204개 주파수에 대한 응답을 측정하였으나 모든 값을 다 적용하기엔 너무 표본수가 많아 약 14.65 Hz 간격의 34개 주파수에 대한 응답으로 표본을 압축하여 모드상관계수 계산식에 적용하였다. 항공용 발사대에 로켓 1개를 장착했을 때와 로켓 2개를 장착했을 때의 X축 방향 모드상관계수는 Fig. 23과 같으며 이를 정리한 결과는 Table 10과 같다.

Fig. 23

MAC calculation result

Table 10

MAC calculation result

계산된 행렬의 대각 행렬은 두 시료의 동일 모드 및 동일 절점에서의 모드 유사성을 표현한다. 대각 행렬이 0.9 이상이면 동특성이 유사하다고 판단할 수 있다⁽⁸⁾. 정리한 결과는 Table 11과 같다.

Table 11

MAC diagonal matrix

항공용 발사대에 로켓을 하나 장착했을 때와 두 개 장착했을 때 X축 방향으로의 동특성 유사도는 41.50 Hz 이하에서 낮게 나왔다. 그 이후 일부 주파수에서도 동특성 유사도가 낮게 나왔다. 항공용 발사대 전체 중량에 있어서 큰 비중을 차지하는 로켓으로 인하여, 장착된 로켓의 수량이 항공용 발사대 동특성에 큰 영향을 크게 주는 것으로 판단하였다.

항공용 발사대 모드상관계수 대각 행렬의 숫자는 모든 시료에서 34개로 같으며 동일한 주파수에서 계산되었다. 모드상관계수 기준 동특성 차이를 분석하기 위해 각 시료에 대한 대각 행렬의 총합을 구한 뒤 34개의 대각 행렬 숫자로 나눈 값을 동특성 유사도로 판단하였다. 이는 Table 12와 같다.

Table 12

Dynamic characteristic similarity

X축의 경우 로켓 수량의 차이가 동특성에 미치는 영향이 상대적으로 적었으며, Y축과 Z축의 경우 동특성 차이가 상대적으로 컸다. 이는 Y축과 Z축이 X축에 비해 비선형 요소가 더 많은 경계조건이며, 로켓의 형상이 강체이며 로켓 동특성이 항공용 발사대에 미치는 영향이 크기 때문이라고 판단하였다.