[ Article ]

Transactions of the Korean Society for Noise and Vibration Engineering - Vol. 33, No. 5, pp.480-490

ISSN: 1598-2785 (Print) 2287-5476 (Online)

Print publication date 20 Oct 2023

Received 21 Mar 2023 Revised 26 May 2023 Accepted 23 Jun 2023

DOI: https://doi.org/10.5050/KSNVE.2023.33.5.480

저속 RFV 측정장비의 드럼 직경에 따른 휠타이어 반경방향하중 영향 측정 및 분석

이충현^* ; 김동준^* ; 윤기훈^* ; 신현재^* ; 이계상^** ; 나형준^** ; 심규호^†

Measurement and Analysis of Effect of Radial Force Variation on Tires According to Drum Diameter of Low-speed RFV Measuring Equipment

Choonghyun Lee^* ; Dong-Jun Kim^* ; Kihoon Yoon^* ; Hyunjae Shin^* ; Kyesang Lee^** ; Hyungjoon Na^** ; Kyuho Sim^†

*Member, Department of Mechanical System Design Engineering, Seoul National University of Science and Technology, Student
**Safety Part of Manufacturing Engineering Team, Kia, Researcher

Correspondence to: ^†Member, Department of Mechanical System Design Engineering, Seoul National University of Science and Technology, Professor E-mail : khsim@seoultech.ac.kr ‡ Recommended by Editor Seunghun Baek

Abstract

This study evaluated the effect of drum diameter on radial force variation (RFV) by comparing laboratory development equipment with a drum diameter of 240 mm and commercial equipment with 1707 mm. When measuring RFV, a large drum is suitable for imitating the flatness of the actual road surface, but it is economically advantageous to utilize a small drum. The results of the RFV measurement depend on the drum diameter and tire stiffness. Therefore, several tests have been performed to evaluate the effect of measurement conditions such as drum diameter, air pressure, and static load on RFV. The main factors of RFV are runout and tire radial stiffness; therefore, wheel samples were made by imitating wheel runout. The RFV of the same tire was measured on two different diameter equipment, and the results for the larger diameter equipment were estimated to be approximately 13.8 % greater.

Keywords:

Tire Uniformity, Uniformity Machine Drum Diameter, Tire Radial Force Variation, Tire Radial Stiffness, Tire Radial Runout

키워드:

타이어 유니포미티, 유니포미티 장비 드럼 직경, 타이어 반경방향 하중 변동, 타이어 반경방향 강성, 타이어 반경방향 형상불균일

1. 서 론

최근 자동차의 고급화 및 전동화로 타이어 진동에 대한 관심이 높아지고 있다. 타이어는 자동차와 지면 사이에 위치하는 회전 접촉 부로 진동 하중이 타이어를 통해 차체로 전달된다⁽¹⁾. 특히 반경 방향 하중 변동(radial force variation, 이하 RFV)은 타이어 반경 방향으로 발생하는 힘의 변동으로 저속에서 타이어 반경 방향 형상 변동(radial runout, 이하 RRO)에 의해 주로 발생한다. RFV는 차량 진동의 주요 원인 중 하나로 타이어 및 완성차 제조사는 생산/조립 과정에서 품질검사를 통해 RFV가 일정 수준 이하가 되도록 관리하고 있다. 그러나 품질검사를 통과한 타이어를 장착한 차량임에도 진동 이슈가 지속적으로 발생하여 보다 정확한 RFV 측정 관리가 필요한 실정이다.

RFV는 타이어에 노면을 모사하는 드럼(drum)을 접촉시켜 하중을 가한 뒤 저속 회전(60 r/min ~ 120 r/min)하며 발생하는 힘을 측정해 평가한다. 그러나 실제 노면은 평평한 반면 드럼은 곡률을 가지기 때문에 구동 조건의 차이가 발생한다.

드럼 직경이 클수록 곡률이 작아져 평평한 노면 모사에는 적합하지만 큰 사이즈로 인해 비용이 높고 공간 차지가 커서 단기간에 많은 타이어를 평가하는 산업 현장에서 사용하기에 적합하지 않다. 이렇듯 타이어 품질 관리 환경은 실제 주행 환경과 달라 양품으로 평가된 타이어가 실제 주행 환경에서 문제가 될 소지가 있다. 이에 따라 장비의 드럼 직경에 따른 RFV와 타이어 반경 반향 강성(K_r, 이하 타이어 강성)의 거동을 규명하는 연구들이 수행되었다.

Phromjan은⁽²⁾ 드럼 직경과 타이어 강성 간의 관계를 FEM 구조해석을 통해 규명하였다. 연구에 따르면 동일 하중에 대해 드럼 직경이 증가하면서 드럼-타이어 간 접촉면적이 커져 변형량이 모두 감소하는데, 드럼 직경이 950 mm보다 커지면 접촉면적과 변형량이 일정해진다는 것을 해석적으로 예측하였다. 결과적으로 드럼 직경이 커짐에 따라 접촉 면적이 넓어지며 변형량이 감소해 타이어 강성이 증가하다가 접촉 조건이 평지와 유사해져 일정해진다는 것을 밝혔다.

Nordeen은⁽³⁾ 드럼 직경과 타이어에 가해지는 하중에 따라 동일 타이어의 RFV 측정값이 달라짐을 실험적으로 규명하였다. 동일 하중에 대해 드럼 직경이 203 mm에서 762 mm로 약 3.75배로 증가할 때 RFV는 110.9 N에서 129.5 N으로 약 15 % 증가함을 확인하였다. 또한 드럼 직경 762 mm일 때 하중이 1765.8 N에서 5297.4 N으로 증가하면 RFV는 평균적으로 132.4 N에서 104.0 N으로 약 21% 감소하는 경향을 확인하였다.

Stutts는⁽⁴⁾ RFV를 타이어 강성과 타이어 RRO에 지배된다는 것을 실험적으로 검증하였으며, 이러한 물리적 배경에 의거해 선행 연구 결과들을 종합하면 드럼 직경에 따라 접촉형상이 달라지고 이에 따라 타이어 강성도 달라지기 때문에 RFV가 달라진다는 것을 알 수 있다. 특히 타이어 공기압(이하 공기압)과 가해지는 정하중(static load) 조건도 타이어 강성을 변화시켜 RFV에 복합적으로 영향을 미칠 수 있다.

이 연구에서는 드럼 직경이 서로 다른 2대의 RFV 측정장비를 이용해 다양한 공기압, 정하중 조건에서 드럼 직경이 RFV에 미치는 영향을 비교 분석하였다. 또한 타이어 RRO 변화에 따른 RFV 경향성을 파악하기 위해 휠의 비드면에 금속 시트(metal sheet)를 부착하여 RRO를 모사하는 방법을 개발하여 적용하였다. 더불어 다양한 실험 조건에 따른 측정 RFV는 타이어 강성과 RRO에 기반하는 RFV 이론 모델을 통해 비교/검증하였으며 RFV 조화성분 중 가장 큰 영향을 미치는 R1H(RFV 1st harmonic)를 중심으로 분석하였다.

2. 저속 RFV 이론 모델

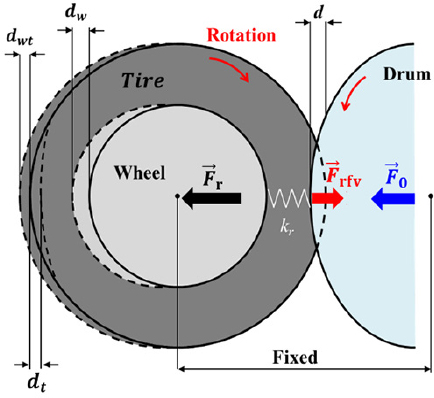
Fig. 1은 드럼으로 하중을 가할 때 저속에서 측정되는 휠&타이어 assembly(이하 휠타이어)의 RFV에 대한 이론 모델의 개념도를 보여준다. 타이어와 드럼이 고정된 이상적인 접촉 조건에서 타이어를 하나의 강성 요소로 고려할 때, 타이어를 통해 허브베어링 중심(O_hub)으로 전달되는 반경 방향 하중( $F → r$ )은 식 (1)과 같다.

F → r = F → 0 + F → r f v

(1)

Fig. 1

Conceptual diagram of RFV theoretical model for drum and tire contact condition

$F → 0$ 는 타이어에 가하는 정하중으로 시험 조건에 해당하며, $F → r f v$ 는 RFV를 의미한다. RFV는 훅의 법칙에 의해 타이어 강성과 휠타이어 RRO를 곱한 식 (2)와 같이 나타낼 수 있다.

F → r f v = k r d → w t

(2)

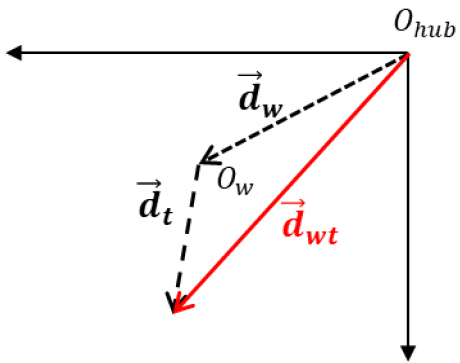
여기서 $d → w t$ 는 휠과 타이어를 조립했을 때 발생하는 휠타이어 RRO를 의미한다. Fig. 2는 휠타이어 RRO를 벡터 다이어그램으로 표현한 것으로 허브베어링 중심으로부터 휠의 RRO ( $d → w$ , 이하 휠 RRO)에 타이어의 내재된 RRO( $d → t$ , 이하 타이어 RRO)가 더해져 나타나며 식 (3)과 같이 표현할 수 있다.

d → w t = d → w + d → t

(3)

Fig. 2

Vector diagram of wheel and tire assembly RRO

이론 모델은 RFV가 휠타이어 RRO와 타이어 강성에 의해 결정된다는 것을 의미한다. 이와 같이 단순한 형태를 가진 이론 모델의 타당성 검증을 위해 타이어 강성과 RRO의 측정을 통해 예측된 RFV를 RFV 측정값과 비교 검증하였다.

3. 실험 장비

3.1 Lab-scale RFV 측정장비

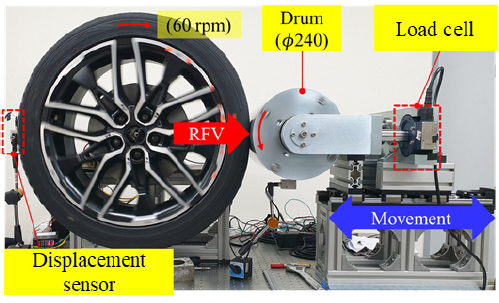
드럼 직경에 따른 RFV를 평가하기 위해 본 연구실에서 개발한 드럼 직경 240 mm인 Lab-scale RFV 측정장비(이하 lab. 장비)와 드럼 직경 1707 mm인 상용 RFV 측정장비(이하 상용 장비)를 사용하였다. Fig. 3은 lab. 장비의 구성 사진을 보여준다. DC 모터를 이용해 휠타이어 조립체를 60 r/min으로 정속 회전시킬 수 있으며, 드럼은 리드 스크류를 이용해 좌측으로 움직이며 타이어를 밀어 하중을 가한다. 레이저 변위센서의 분해능은 1 μm로 휠 RRO와 휠타이어 RRO를 측정할 수 있다. 2개의 1축 로드셀을 이용해 드럼 접촉에 의한 타이어의 반경 방향 하중을 총 9810 N까지 측정 가능하다. 타코미터(tachometer)에서 1회전 마다 발생하는 펄스 신호를 이용해 타이어의 회전속도 및 위상을 측정하였다.

Fig. 3

Front view of lab-scale RFV measuring equipment

3.2 상용 RFV 측정장비

Fig. 4는 드럼 직경은 1707 mm인 상용 장비를 보여준다. 상용 장비는 RFV 측정 시퀀스가 자동화되어 있다. 장비의 시험 조건(정하중, 공기압 등)을 설정한 후 측정 버튼을 누르면 드럼이 타이어 쪽으로 이송되면서 설정한 하중을 가하고, 타이어를 시계 방향과 반시계 방향으로 각 30초씩 120 r/min으로 회전시키면서 RFV를 측정한 후 자동으로 정지한다. Table 1은 lab. 장비와 상용 장비의 사양을 보여준다. 두 장비는 드럼 직경 이외에 회전속도가 서로 다르다. 120 r/min 수준의 저속에서는 질량 불균일의 효과가 매우 작아 두 장비의 속도 차이가 RFV 측정값에 주는 영향이 매우 작다.

Fig. 4

Front view of commercial RFV measuring equipment

Table 1

Specifications for two RFV measuring equipment

3.3 타이어 비드 안착성 검증

평가 신뢰성을 확보하기 위해 비드 안착성 검증을 진행하였다. 타이어를 휠에 장착할 때 조립 및 비드 안착에 도움을 주는 이형제를 바르는데, 작업자에 따라 이형제의 양이 달라진다. 타이어 비드 안착성은 RFV 측정 반복성에 영향을 주어 휠타이어를 동일한 위상으로 매칭하여 조립해도 RFV 측정 결과가 매번 다를 수 있다.

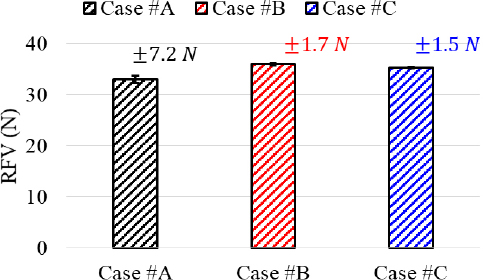
Fig. 5는 이형제 양이 적음(#A), 중간(#B), 많음(#C) 조건에 대해 RFV를 각 5회 반복 측정한 결과로 평균값과 표준편차를 보여준다. RFV 평균값은 중간과 많음 케이스 결과는 거의 같으며, 이형제가 적은 경우 약 3.0 N의 차이가 난다. 결과적으로 충분히 바른 이형제는 표준편차, 즉, 실험 반복오차를 ±7.2 N에서 ±1.5 N으로 크게 감소시킨다. 그러므로 실험 반복오차를 최소화하기 위해 이형제를 충분히 발라 실험을 수행하였다.

Fig. 5

Results of measured RFV by amount of releasing agent

3.4 웜업(warm-up)을 통한 RFV 데이터 신뢰성 확보

웜업은 휠타이어 조립 후 안정적인 비드 안착을 위해 드럼으로 휠타이어에 하중을 가해 일정 시간 동안 회전 구동시키는 것을 말한다. 휠타이어 조립 후 RFV를 곧바로 측정하게 되면 구동 시간에 따라 값이 조금씩 변화하는 것을 확인할 수 있다. 조립된 휠과 타이어는 웜업 과정에서 서로 강하게 밀착되어 회전하며 비드 안착이 점차 안정화되는 과도 상태를 거치는데, 이 때 RFV 값이 시간에 따라 변화하다 수렴하는 경향을 보인다.

RFV 측정데이터의 높은 신뢰성을 위해서는 일반적으로 10분 ~ 15분의 웜업을 통한 비드 안착 과정이 필요하다. 그러므로 이 연구의 모든 RFV 데이터는 신뢰성 확보를 위해 10분간의 웜업 후 측정하였다.

Lab. 장비는 매뉴얼하게 작동할 수 있어 연속으로 10분 간 웜업이 가능하지만, 상용 장비는 1분 간 장비 구동 후 정지되는 자동화 시퀀스로 연속적인 구동이 불가능하여 10회 반복 구동을 통해 웜업하여 데이터 신뢰성을 확보하였다.

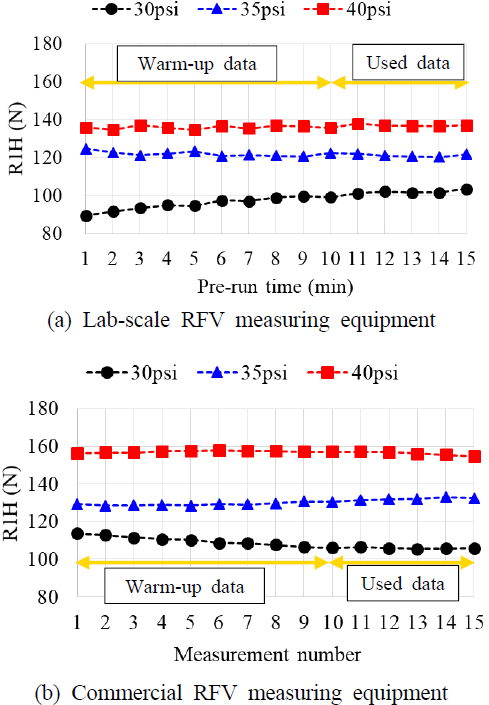
Fig. 6은 공기압 조건 별로 반복 측정된 R1H로 Fig. 6(a)는 lab. 장비, Fig. 6(b)는 상용 장비로 측정한 결과를 나타낸다. Lab. 장비는 15분 연속 구동을 통해 1분에 1회씩 R1H를 측정하였다. 모든 공기압 조건에서 웜업 시간에 따라 R1H가 미세하게 변하다가 약 10분부터 일정한 값으로 수렴하는 것을 확인할 수 있다. 공기압 30 psi의 경우 웜업에 따른 R1H값은 변화폭이 약 14.7 N으로 큰 것을 볼 수 있다. 따라서 lab. 장비를 이용한 R1H 측정 데이터는 동일 실험 조건에 대해 10분간의 웜업 후 5분간 측정한 데이터 5개의 평균값을 사용하였다. 상용 장비는 1회 측정 시 약 1분이 소요되므로 10회 반복 측정 시 10분 간의 웜업 효과를 얻을 수 있다. 따라서 상용 장비를 이용한 RFV 측정 데이터는 총 15회 측정하여, 전반부 10회 구동으로 웜업과 동일한 효과를 주었고, 후반부 5회 측정의 평균값을 평가 데이터로 사용하였다.

Fig. 6

Measured RFV with warm-up time for air pressure of 30 psi, 35 psi, and 40 psi with static load of 4905 N and RRO of 1 mm

4. 실험 방법

4.1 타이어 실험인자 및 실험방법

장비 드럼 직경과 타이어의 실험 조건에 따른 RFV 거동을 평가하기 위한 실험을 수행하였다. 실험 인자는 휠 RRO, 공기압, 정하중으로 Table 2는 실험 계획을 보여준다. 실험은 휠 RRO 3가지 케이스에 대해 공기압과 정하중을 각각 3수준으로 변화시키며 수행하였다. 휠 RRO의 크기에 따라 # 00, # 11, # 22 실험케이스로 구분하였으며, 각각 0, 0.5, 1 mm 수준이다.

Table 2

Experimental design for RRO, static load, and tire air pressure

공기압과 정하중 조건의 기준은 각각 30 psi, 4905 N이다. 참고로 중대형급 차량 기준 타이어 1본에 가해지는 공차 하중은 약 4415 N ~ 5396 N이고, 공기압은 약 33 psi ~ 40 psi 수준이다(Table 4).

Table 3

Wheel RRO level controlled by metal sheet

Table 4

Curb weight and tire standard air pressure for various mid-large vehicles

휠 RRO 케이스에 대한 실험 프로세스는 다음과 같고, 3가지 케이스에 대한 실험을 위해 프로세스를 3회 반복하였다.

(1) 휠에 RRO를 모사하는 금속 시트를 부착하고, lab. 장비를 이용해 휠 RRO를 측정하여 크기/위상을 확인한다.

(2) 조립 재현성을 위해 RRO 모사 휠과 타이어의 매칭 방향을 일정하게 조립한다.

(3) Lab. 장비를 이용하여 계획한 모든 공기압과 정하중 조건에 대한 타이어 RRO와 강성을 측정한다.

(4) Lab. 장비와 상용장비를 이용해 계획한 모든 정하중과 공기압 조건에 대해 휠타이어의 RFV를 측정한다

모든 실험 케이스에 대해서 휠과 타이어 RRO, 타이어 반경방향 강성을 측정하는데 상용 장비는 해당 기능을 지원하지 않아 lab. 장비만을 이용해 측정하였다. 모사 휠 RRO에 대한 영향을 명확하게 확인하기 위해 휠 RRO와 타이어 RFV가 매우 작은 샘플을 각각 1본씩 추출해 이 실험에 사용하였다. 사용한 휠과 타이어 규격은 각각 19인치, 245/40ZR19이다.

4.2 RRO 모사법 개발

휠 RRO는 타이어 RFV 발생에 가장 큰 영향을 미치는 인자이다^(4,5). 실험에 사용할 특정 RRO를 가진 휠을 구하기 위해서는 수많은 휠의 RRO를 직접 측정하여 추출해야 한다. 하지만 이 작업은 많은 시간과 비용을 소모하므로, 타이어 비드가 안착되는 휠 외면에 금속 시트를 원주방향으로 일정 범위에만 부착하여 원하는 휠 RRO를 모사하는 방법을 개발하였다.

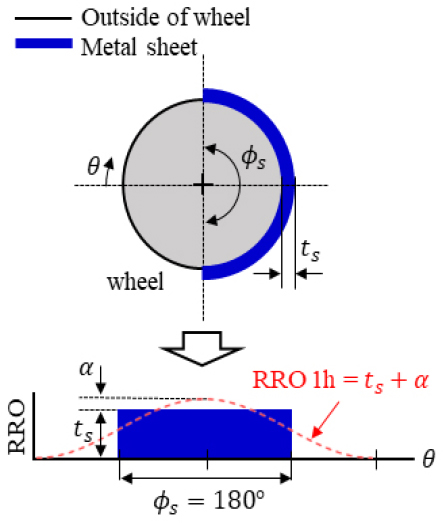
Fig. 7은 금속 시트를 이용한 휠 RRO 모사법의 개념도를 보여준다. 금속 시트 부착 범위(ϕ_s)는 휠 편심 불균형인 RRO 1 h(1st harmonic)를 모사하기 위해 원주길이의 180°만큼 부착하였다. 두께가 t_s인 금속 시트를 부착했을 때 실제 RRO 1h의 크기는 부착한 두께보다 ɑ만큼 크게 측정된다. 이는 사각파형(square wave)의 1st harmonic 진폭이 사각파형의 높이보다 약 25 % 크기 때문에 발생하는 현상이다⁽⁶⁾. Fig. 8은 휠 내면 비드부(wheel in)에 금속 시트를 부착한 사진을 보여준다. 금속 시트는 두께 0.5 mm인 알루미늄 테이프를 사용하였다.

Fig. 7

Concept diagram of wheel RRO control method using metal sheet

Fig. 8

Photo of wheel with metal sheet on wheel in

4.3 모사 휠 RRO 측정

Fig. 3은 휠 내외면에 금속 시트를 붙여 RRO를 모사한 케이스를 나타낸다. 실험케이스 # 00은 휠에 금속 시트를 부착하지 않은 경우이고, # 11과 # 22는 각각 0.5 mm, 1 mm 두께의 금속 시트를 휠 내외면 모두 동일 위상에 부착하였다.

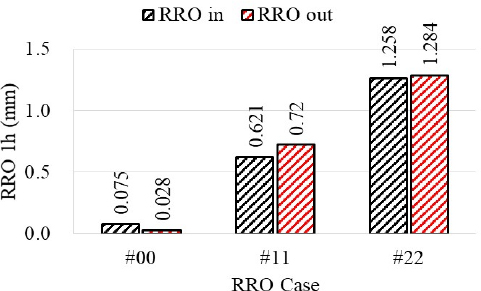
Fig. 9는 RRO 모사 휠 내외의 RRO 1h를 측정한 결과를 보여준다. 실험케이스 # 00 측정 결과로 휠 내외의 RRO 1h는 각각 0.075 mm, 0.028 mm로로 매우 작은 것을 알 수 있다. # 11과 # 22의 RRO 1h는 사각파 특성으로 인해 부착한 금속 시트 두께보다 약 25 % 더 크게 측정되었다. 결과적으로 모사 휠의 RRO는 휠 자체의 잔류 RRO와 금속 시트 두께의 약 125 %를 합한 값을 가지는 것을 확인함으로써 RRO 모사법을 이용해 RRO의 크기와 위상을 효율적으로 제어할 수 있음을 확인하였다.

Fig. 9

Measured RRO 1 h of in/out of controlled wheel for 3 cases of RRO using lab. equipment

4.4 RRO 모사 타이어 RFV 측정

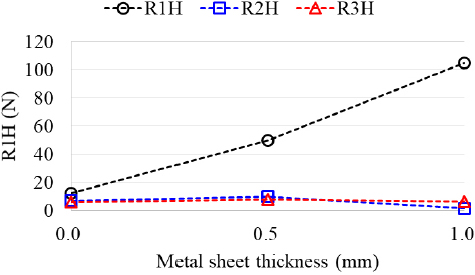
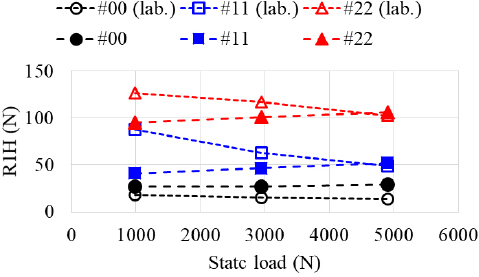
Fig. 10은 lab. 장비를 이용해 측정한 RRO 1h 증가에 따른 타이어 R1H, R2H, R3H를 보여준다. R2H와 R3H는 각각 RFV의 2차, 3차 조화성분이다. 공기압과 정하중 조건은 각각 30 psi, 4905 N이다. R1H는 휠 RRO 1h가 증가함에 따라 선형적으로 증가하는 반면 R2H, R3H는 휠 RRO 1h와는 관계없이 매우 작은 값으로 유지된다. 이를 통해 RRO 1h는 R1H에만 영향을 미친다는 것을 확인하였다.

Fig. 10

Measured R1H, R2H, and R3H for wheel RRO level using lab. equipment

5. 실험결과 및 분석

5.1 접촉조건에 따른 타이어 강성 측정

타이어 강성은 lab. 장비의 드럼이 타이어에 하중을 가한 상태에서 드럼을 좌우로 움직일 때 발생하는 변위와 하중 변화를 이용해 측정하였다(Fig. 3). 드럼의 변위는 레이저 변위센서로 계측하였고, 타이어 반력은 로드셀로 측정하였다. 타이어 강성은 트레드 셸(tread shell) 형상에 의한 구조강성과 공기압에 의한 압력강성으로 구분되는데, 본 실험에서는 구조강성과 압력강성의 합한 값을 측정하였다.

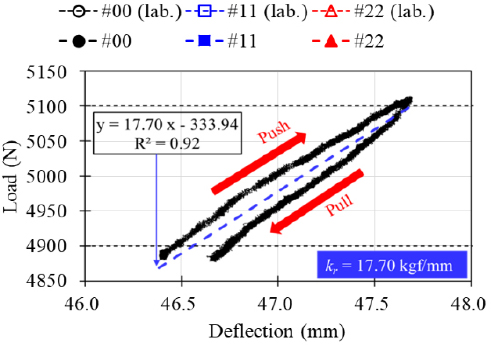
Fig. 11은 드럼이 타이어에 정하중 4905 N을 가한 상태에서 ±98.1 N 만큼 하중이 변화하도록 드럼을 좌우로 움직이며 측정한 하중-변위 선도이다. 하중-변위 선도의 기울기는 강성을 의미한다. 타이어 강성은 드럼을 좌우로 움직일 때 나타나는 곡선의 선형 회귀분석으로 계산되는 기울기로 정의하였다. 참고로 드럼의 변위 방향에 따라 타이어 강성이 달라지는데, 이는 타이어 고무 분자가 압축과 복원을 반복하면서 발생하는 히스테리시스 현상을 나타낸다.

Fig. 11

Force-displacement test with air pressure of 30 psi and static load of 4905 N

Fig. 12는 정하중 변화에 따른 drum-tire(이하 DT) 강성과 flat-tire(이하 FT) 강성의 측정 결과를 보여준다. DT 강성은 드럼과 타이어를 직접 접촉시켜 측정한 것이고, FT 강성은 평평한 노면 접촉을 모사하기 위해 드럼과 타이어 사이에 금속 평판을 두고 측정한 것이다. 참고로 드럼 직경이 1707 mm일 경우 곡률이 작아 FT 강성과 유사할 것으로 판단된다.

Fig. 12

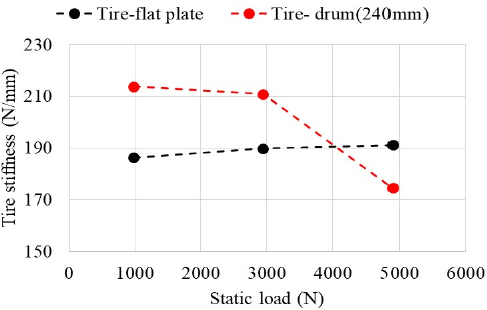
Measured TD and FT stiffness for static load of 981 N, 2943 N, and 4905 N at air pressure of 30 psi using lab. equipment

DT 강성은 하중 증가에 따라 비선형적으로 감소한다. 이는 타이어가 직경이 작은 드럼에 의해 국부적으로 눌리면서 크게 변형해 트레드 셸 구조 형상이 찌그러져 강성이 약해지기 때문에 발생하는 현상으로 추정된다. 반대로 FT 강성은 하중 증가에 따라 미세하게 증가한다. 이는 하중이 증가하면서 타이어와 평판 간의 접촉면적이 넓어져 접촉압력이 분산되어 변형량이 감소하기 때문으로 보인다.

5.2 타이어 공기압/정하중에 따른 R1H 측정

Fig. 13은 정하중 4905 N 조건에서 두 장비를 이용하여 공기압 변화에 대한 R1H 측정결과를 보여준다. 두 장비에서 측정된 R1H는 모두 공기압과 함께 증가하는 경향을 보인다. 공기압은 압력강성을 증가시키므로 타이어 강성과 비례하는 R1H가 동시에 증가한다. 그러나 # 00 케이스와 같이 강성이 커지더라도 RRO 1h가 매우 작다면 R1H의 증가는 제한되며, # 11, # 22로 증가하면서 공기압에 따른 R1H 변화의 기울기가 증가하는 것을 확인할 수 있다. 또한 R1H는 드럼 직경이 큰 경우에 더 크게 측정되었다. 하중이 동일할 때 드럼-타이어 간 접촉면적은 드럼 직경이 작을 수록 감소해 변형량이 커지기 때문에 측정 강성이 감소해 R1H는 상대적으로 작게 측정된다.

Fig. 13

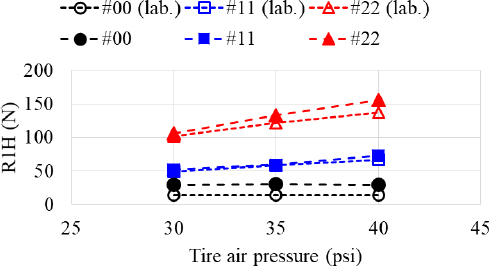
Measured R1H for air pressure of 30 psi, 35 psi, and 40 psi at static load of 4905 N using lab. and commercial equipment

Fig. 14는 공기압 30 psi 조건에서 두 장비를 이용하여 정하중 변화에 대해 R1H를 측정한 결과를 보여준다. 드럼 직경 240 mm일 때 R1H는 정하중 증가에 따라 감소하는 반면 드럼 직경 1707 mm일 때 R1H는 미세하게 증가한다. 이러한 반대 경향은 드럼 직경 차이로 인해 발생하는 강성의 차이 때문으로 Fig. 10의 강성 경향과 동일하다. 이를 통해 참고문헌 2의 드럼 직경과 관계없이 정하중 증가에 따라 R1H는 감소한다는 결론은 드럼 직경 1707 mm일 때 R1H 측정결과를 근거로 틀린 것을 알 수 있다.

Fig. 14

Measured R1H for static load of 981 N, 2943 N, and 4905 N at air pressure of 30 psi using lab. and commercial equipment

5.3 이론 모델을 통한 R1H 예측 및 실험 비교

앞서 측정한 타이어 강성과 RRO를 곱해 계산된 R1H와 실험결과를 비교해 이론 모델의 타당성을 검증하였다. 타당성 검증은 이론 모델에 사용되는 타이어 강성과 RRO를 측정할 수 있는 lab. 장비에 대해서만 수행하였다.

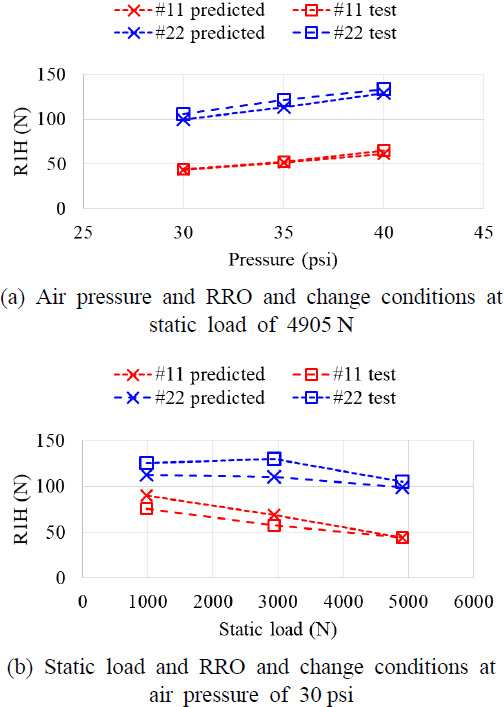
Fig. 15는 이론 모델을 통해 예측된 R1H와 측정결과를 비교한 그래프로, Fig. 15(a)는 공기압과 RRO 변화, Fig. 15(b)는 정하중과 RRO 변화 조건에 대해 비교하였다. 전체적으로 예측과 측정값은 경향이 동일하고 크기가 높은 수준으로 일치함을 확인할 수 있다. 다만 저하중 영역에서 타이어 구조 강성의 비선형 효과로 인해 오차가 비교적 크게 발생하였다. 하지만 981 N, 2943 N은 실제 주행 시 타이어가 받는 하중에 비해 매우 작으며, 주행 조건 근방에서는 이론 모델을 이용해 높은 정확도로 R1H를 예측할 수 있다.

Fig. 15

Comparison of predicted R1H of theoretical model with measured RFV using lab. equipment

5.4 드럼 직경에 따른 R1H 경향 분석

앞서 5.2절에서는 드럼 직경, 공기압, 정하중, 타이어 RRO에 대한 R1H의 전반적인 경향성을 확인했다. 이 절에서는 측정 데이터를 기반으로 타이어 규격 사양과 유사한 공기압, 정하중 조건에서 드럼 직경에 따른 R1H 경향성을 분석했다. Table 4에 제조사에서 제공하는 중대형급 차량의 공차 중량과 타이어 공기압을 나타냈다^(7,8). 이에 따라 정하중과 공기압은 Table 4에서 제시된 19인치 타이어를 장착하는 중대형급 차량의 사양을 기준으로 결정하였다. 정하중은 차량 무게의 1/4 수준인 4905 N으로 고정하고, 공기압 30 psi, 35 psi, 40 psi의 범위에서 드럼 직경과 RFV의 상관성을 분석하였다. RRO는 타이어 유니포미티 품질이 가장 나쁜 # 22로 선정하였다.

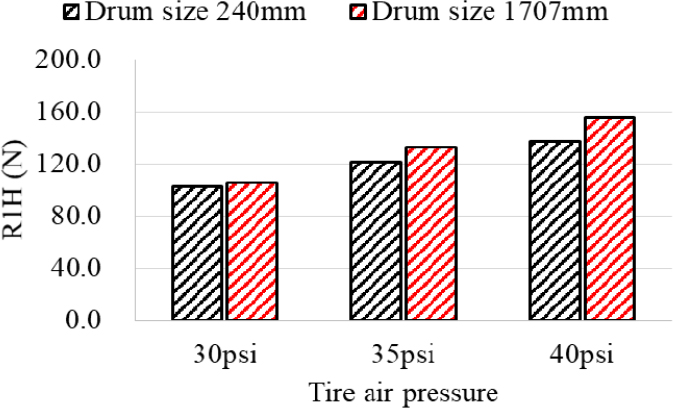
Fig. 16은 위에서 결정한 실험조건에서 서로 다른 드럼 직경으로 측정된 R1H의 비교 결과를 보여준다. 모든 공기압 범위에서 드럼 직경이 클 때 R1H는 3.5 % ~ 13.8 % 더 크게 측정되었다. 이는 참고문헌 3 결과의 경향과 동일하다. 평평한 노면 조건과 유사한 드럼 직경 1707 mm의 R1H 측정값을 기준으로 볼 때 드럼 직경 240 mm인 장비를 이용해 R1H의 품질을 관리할 때는 보수적으로 R1H를 15 % 가량 크게 보는 것이 타당하다. 또한 공기압이 증가할수록 두 장비의 R1H 차이가 커지므로 낮은 공기압 조건에서 R1H를 측정하는 것이 드럼 직경이 미치는 영향을 줄이는 방법이 될 수 있다.

Fig. 16

Comparison measured R1H with respect to air pressure changes using lab. and commercial equipment

6. 결 론

이 연구에서는 드럼 직경이 서로 다른 2대의 RFV 측정장비를 이용해 다양한 실험 조건에서 드럼 직경이 R1H에 미치는 영향을 분석하였다. 실험은 1본의 휠타이어(245/40ZR19)에 대해 휠 RRO, 정하중, 공기압과 같은 조건을 변화시키면서 R1H를 측정하였고, 이 연구의 결론은 다음과 같다.

(1) RRO는 RFV와 선형적 비례관계이다. 다만 RRO 1 h는 R1H와만 선형비례 관계이고 R2H, R3H와는 독립적이다.

(2) 타이어 강성과 RRO로 정의되는 단순한 형태의 RFV 이론 모델은 실험결과와 비교해 타이어 규격사양 근방의 4905 N 하중에서 높은 예측 정확도를 보인다. 다만 2943 N 이하의 저하중 영역에서는 타이어 강성의 비선형성으로 인해 예측 정확도가 떨어진다.

(3) 공기압과 R1H의 상관관계는 드럼 직경에 관계없이 공기압 증가에 따라 R1H가 일정하게 증가한다. 공기압은 타이어 강성을 증가시켜 타이어 강성과 비례하는 R1H를 증가시킨다.

(4) 정하중과 R1H의 상관관계는 드럼 직경에 따라 달라진다. 드럼 직경이 240 mm일 때 정하중이 증가할수록 RFV가 감소하는 반면 1707 mm일 때는 정하중에 따라 RFV가 증가한다. 이는 드럼 곡률 차이로 인해 발생하는 타이어의 구조적 강성 차이 때문이다. 실제 차량은 평지를 주행하므로 정하중이 증가할 때 RFV가 증가한다는 것이 타당하다.

(5) 타이어 규격 조건 근방의 공기압, 정하중 조건에서 RFV는 드럼 직경이 클 때 모든 공기압 조건에서 상대적으로 3.5 % ~ 13.8 % 크게 측정되고, 공기압이 40 psi에서 30 psi로 작아질 때 드럼 직경에 따른 RFV 격차는 13.8 %에서 3.5 %까지 감소함을 확인하였다.

기 호 설 명


d :	타이어 변형량 [mm]
$d → t$ :	타이어 반경 방향 치수 변동 [mm]
$d → w$ :	휠 반경 방향 치수 변동 [mm]
$d → w t$ :	휠타이어 반경 방향 치수 변동 [mm]
$F → r$ :	반경 방향 하중 [N]
$F → r f v$ :	반경 방향 하중 변동 [N]
$F → 0$ :	정하중 [N]
r :	반경 방향
R :	반경 방향 치수 변동 [mm]
k_r :	타이어 반경 방향 강성 [N/mm]
n :	하모닉 차수
O_hub :	허브베어링 중심
O_w :	휠 중심
t :	타이어
t_s :	금속 시트 두께 [mm]
w :	휠
wt :	휠타이어
δ :	반경 방향 하중 변동의 크기 [N]
ϕ :	반경 방향 하중 변동의 위상 [°]
ϕ_s :	금속 시트 부착 위상 [°]

Acknowledgments

이 연구는 2021년 기아(KIA)의 연구비 지원에 의한 연구임.

References

Park, J.-P., Choi, J. and Lee, S.-J., 2007, Vehicle Vibration Study by Tire Flat Spot, Proceedings of the Korean Society for Noise and Vibration Engineering Conference, pp. 1395~1400.
Phromjan, J. and Suvanjumrat, C., 2020, The Contact Patch Analysis of Solid Tire on Drum Testing by Finite Element Method, IOP Conference Series: Materials Science and Engineering, Vol. 886, 012049. [https://doi.org/10.1088/1757-899X/886/1/012049]
Nordeen, D. L. and Rasmussen, R. E., 1966, Factors Influencing the Measurement of Tire Uniformity, SAE Transactions, Vol. 74, pp. 466~475. [https://doi.org/10.4271/650734]
Stutts, D. S., Soedel, W. and Jha, S. K., 1991, Fore‐aft Forces in Tire‐wheel Assemblies Generated by Unbalances and the Influence of Balancing, Tire Science and Technology, Vol. 19, No. 3, pp. 142~162. [https://doi.org/10.2346/1.2141713]
Dorfi, H. R., 2005, Tyre Non-uniformities: Comparison of Analytical and Numerical Tyre Models and Correlation to Experimentally Measured Data, Vehicle System Dynamics, Vol. 43, No. sup1, pp. 223~240. [https://doi.org/10.1080/00423110500140906]
Tantrigoda, D. A. and Rodrigo, D. S., 2014, Numerical Implementation of Fourier Transforms and Associated Problems, International Journal of Multidisciplinary Studies, Vol. 1, No. 1, pp. 1~10. [https://doi.org/10.4038/ijms.v1i1.27]
Genesis: Vehicle Specifications, Catalog, 2022, https://www.genesis.com/kr/ko/models/luxury-sedan-genesis/g80/specs.html.
Kia: Vehicle Specifications, Catalog, 2022, https://www.kia.com/kr/shopping-tools/catalog-price.html, .

Choonghyun Lee received a B.S. degree in Dept. of Automotive Engineering and M.S. degree in Dept. of Mechanical System Design Engineering from Seoul National University of Science and Technology in 2018 and 2022, respectively.

Kyuho Sim received the M.S. degree in mechanical engineering from Korea Advanced Institute of Science and Technology(KAIST), Daejon, Korea, in 2002 and PhD degree in mechanical engineering from Texas A&M University, College Station, TX, in 2007. He joined Samsung Advanced Institute of Technology, Suwon, Korea, in 2009, and Korea Institute of Science and Technology, Seoul, Korea, in 2010, on development of oil-free rotating systems such as high speed permanent magnet motor/generator and high temperature micro gas turbines. Currently, he is working as a associate professor at Seoul National University of Science and Technology. His research interests are lying on the analysis, design and testing of rotordynamic and thermal systems such as high speed turbomachinery, electric motors, Stirling engines, etc.

Equipment	Drum diameter	Rotating speed	Loadcell		Laser displacement sensor
Equipment	Drum diameter	Rotating speed	Range	Resolution	Range	Resolution
Lab-scale	240 mm	60 r/min	Max 4905 N	10 N	10 mm ~ 20 mm	0.001 mm
Commercial	1707 mm	120 r/min	-	-	-	-

	Net weight [kg]	Air pressure [psi]
Genesis G80	1785 ~ 2265	36 ~ 40
Genesis G90	2020 ~ 2225	35
Genesis GV70	1820 ~ 2010	33 ~ 41
Genesis GV80	2040 ~ 2150	33 ~ 42
Kia Sorento	1840 ~ 1889	34

Test RRO case (# 00, # 11, # 22)		Inflated air pressure [psi]
Test RRO case (# 00, # 11, # 22)		30	35	40
Static load (N)	981	O	-	-
	2943	O	-	-
	4905	O	O	O