Canny Edge검출 기법과 합성곱 신경망을 이용한 심층학습 기반 터보차저 진동 분석
© The Korean Society for Noise and Vibration Engineering
Abstract
This study proposes a novel method for analyzing turbocharger vibration utilizing a combination of the convolutional neural networks (CNN) technique and the Canny edge detection technique. The conventional 1D machine-learning techniques exhibit poor accuracies due to the irregularly changing rotating speeds of the turbine and compressor, which are inherent to turbochargers. To address the issue, the adoption of a 2D CNN accompanied by the Canny edge detection technique has been proposed here. First, the experimental vibration data of the turbocharger have been created and labeled. To augment the limited number of experimental data, the data augmentation technique is applied, resulting in a sufficient amount of data. Subsequently, various preprocessing and machinelearning techniques have been applied for the analysis. By comparing the accuracy and loss data of these analyses, the 2D CNN accompanied by the Canny edge detection technique has been confirmed as the most effective approach for analyzing turbocharger vibration.
Keywords:
Turbo Charger, Vibration, Fast Fourier Transformation, Convolutional Neural Network, Canny Edge Detection, Data Augmentation키워드:
터보차저, 진동, 고속 푸리에 변환, 합성곱 신경망, Canny 엣지 검출, 데이터 증강1. 서 론
딥러닝(deep learning: DL)은 머신러닝(machine learning: ML) 기법 중 하나이며, 인공 신경망을 기반으로 규칙을 학습하는 다양한 방법들을 종합적으로 지칭한다. 최근 딥러닝을 적용하면서 머신러닝 기술이 다시 각광받고 있는데 이는 다음과 같은 2가지 환경 변화에 기인한 것이다. 첫 번째, 머신러닝 학습에 사용되는 데이터가 폭발적으로 증가했다. 두 번째, CPU, GPU, 메모리를 포함한 컴퓨터 하드웨어 성능이 빠르게 발전했다(1). 이러한 머신러닝 기술의 발전으로 인해 활용 영역이 확대되고 있으며, 소음 진동 분야에서는 수집된 소음 진동 데이터를 활용하여 학습시킨 머신러닝 모델이 시스템의 고장 및 상태 진단 등에 활용되고 있다. 기존에는 고장 및 상태 진단을 위해 crest factor, synchronous average, impact index, correlation 등 시간 영역 신호 처리 기술을 적용하거나 대역폭 분석, 차수 분석, 3차원 spectral mapping, cepstrum 분석 등 주파수 영역 신호처리 기술을 적용하여 데이터를 분석했다(2). 하지만 모든 진동 신호를 수동으로 분석할 경우 시간이 많이 걸리고 사람에 의한 오류가 존재하기 때문에 진동 분석 전문가에 의한 고장 및 상태 진단은 한계가 있다(3). 따라서, 데이터 전처리 및 특징 추출 기법을 적용하고 이를 데이터 세트로 구성하여 머신러닝 모델에 학습시키고 학습된 모델의 정확도를 전문가의 정확도와 비슷하거나 그 이상으로 높이고자 하는 연구가 진행 중이다(4,5). 딥러닝 알고리즘 중의 하나인 합성곱 신경망 모델은 이미지 데이터에 대한 분류 작업에 우수한 성능을 보이며, 특히 진동 분야에서는 진동 데이터의 복잡한 패턴을 효과적으로 학습하여 효과적인 분석이 가능하다는 것이 검증되었다(6).
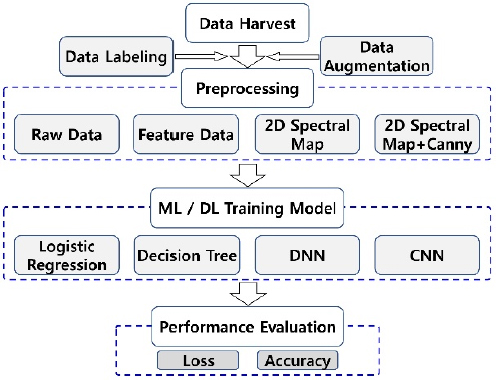
터보차저 작동 중 발생되는 소음과 진동은 다양한 원인에 의해 발생되며 원인에 따라 서로 다른 회전 차수 성분을 나타낸다(7). 그 중 터보차저 컴프레서 블레이드 수에 해당하는 차수의 소음(whine noise)은 차량 주행 중 심각한 NVH 문제를 발생시킬 수 있어 반드시 저감이 필요하다(7). 또한, 이 소음은 일반적으로 동일한 차수의 진동을 동반하는 것으로 알려져 있어 진동 측정 결과를 이용하여 소음 발생을 예측할 수 있는 방법이 필요하다(7). 그러나 시간에 따라 진폭이 변화하고 회전수 측정이 불가능한 터보차저 진동 데이터에 대해 기존 방법을 적용한 결과, 차수 성분의 영향으로 분류가 잘 이루어지지 않아 정확도가 낮아지는 현상이 발생한다. 따라서, 분석 모델의 성능을 높이기 위해 데이터 전처리 및 특징 추출에 대한 개선이 필요하다. 이 논문에서는 spectral map에 Canny edge 검출법을 적용하여 합성곱 신경망의 훈련 성능을 높임으로써 결함 성분 감지 능력을 제고하는 방법을 제안한다. 우선 실험을 통해 12초 동안 측정된 터보차저 진동 데이터에 대한 주파수 분석과 동반되는 소음에 대한 관능 평가를 수행하여 결함 여부를 판단한다. 분석 및 평가 결과를 근거로 데이터 라벨링(labeling)을 진행하고, 데이터를 증강한다. 증강된 데이터에 대해 Fig. 1에 설명된 시간 또는 주파수 영역전처리를 적용하여 데이터 세트를 준비하고 훈련, 테스트, 검증 데이터 세트로 나누어 머신러닝 모델 훈련을 준비한다. 다음으로, 훈련이 완료된 머신러닝 모델의 정확도 및 손실을 분석하여 머신러닝 모델의 성능을 평가한다. 마지막으로 제안된 기법의 정확도를 다른 머신러닝 기법, 전처리 및 특징 추출 방식을 적용한 결과와 비교하여 제안 기법의 성능을 확인한다.
Flowchart for vibration analysis using deep learning
2. 데이터 세트 준비
2.1 시간 영역 데이터 획득
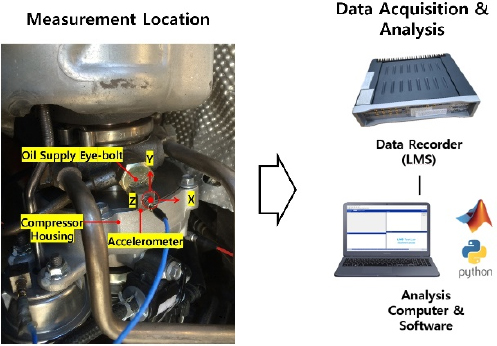
이 연구에 사용된 데이터는 차량 가속주행 중 터보차저 컴프레서 하우징 부위의 Z축 방향(차량 기준 상하 방향) 진동 데이터이다. 측정 시간은 12초, 샘플링 주파수는 51200 Hz이며 터보차저를 정지 상태에서 속도를 점차 증가시키며 진동을 측정한다. 이와 같은 진동 데이터 수집과정과 측정 방향은 Fig. 2에 설명되어 있다. 터보차저에서 발생된 진동은 가속도계를 통해 전압 신호로 변환되어 데이터 수집 장비인 LMS로 전달된다. 측정된 신호 길이는 613897 ~ 614653 (11.990초 ~ 12.005초) 사이로 측정 길이가 일정하지 않다. 따라서, 측정 길이를 일정하게 변환하는 작업이 필요하다. 변환된 전압 신호는 LMS Test Lab, MATLAB 및 Python으로 작성한 프로그램을 사용하여 분석하였다.
Process for measuring turbocharger vibration
이 연구의 데이터 분석에는 NVIDIA GeForce GTX 1650 with Max-Q Design 11.9GB의 GPU를 장착한 ASUS사의 ZenBook UX534FTC laptop 컴퓨터가 사용되었다. 또한, Python으로 작성한 프로그램에서 사용된 라이브러리는 목적 및 version과 함께 Table 1에 정리하였다.
List of libraries used
2.2 시간영역 데이터 증강
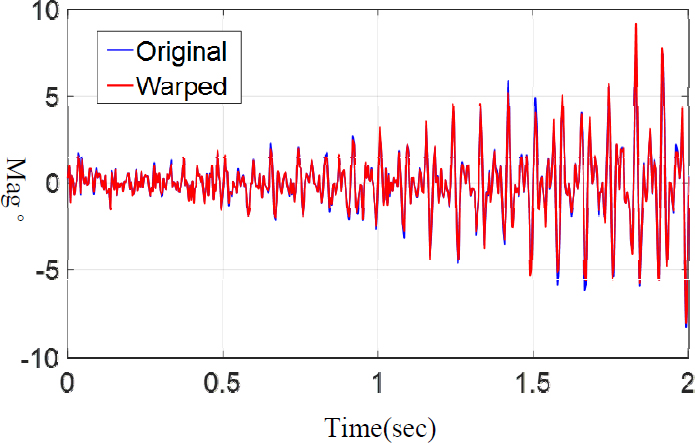
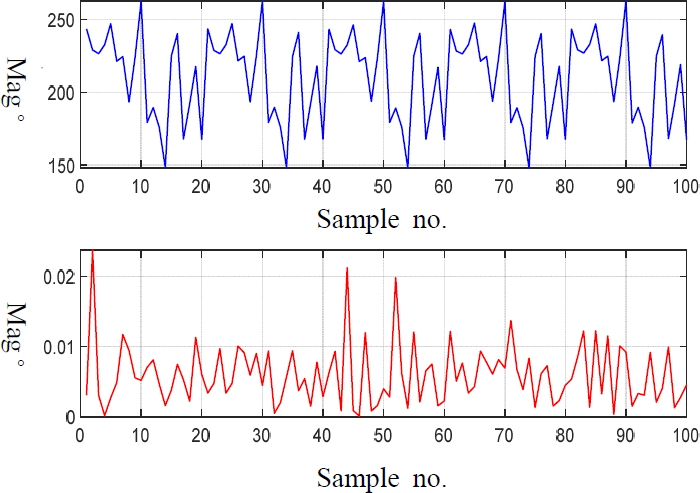
실험을 통해 생성된 진동 데이터는 샘플 개수가 20개로 충분치 않아 데이터 세트를 나누는데 어려움이 있다. 따라서, 원본 데이터의 특징을 잘 반영한 새로운 데이터를 만드는 데이터 증강 기법을 이용하여 충분한 데이터 세트를 확보하였다. 데이터 증강 기법은 샘플링 편향을 발생시키지 않으면서, 데이터 개수를 증가시킬 수 있는 장점이 있다. 일반적으로 사용되는 시계열 데이터 증강 기법은 random transformation, pattern mixing, generative models, decomposition 등 4가지이다(8). 이 연구에서는 random transformation의 magnitude warping데이터 증강 기법을 사용하였다. magnitude warping은 데이터 크기를 무작위로 조절하여 새로운 데이터를 만드는 기법으로 진폭이 점차 증가하는 데이터에 대해 적절하다고 판단되어 사용하였다. 측정된 진동 데이터 값마다 0.95 ~ 1.05 범위에서 생성된 난수를 곱하여 기존 데이터 수의 4배를 증가시켰다. magnitude warping를 적용한 예를 Fig. 3에 설명하였다.
Comparison of the original data with the augmented data
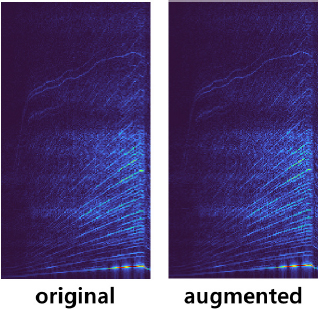
데이터 증강 기법을 통해 증강된 데이터는 원본 데이터 특성을 잘 반영하므로 이전에 부여한 라벨은 유지 하였다. 증강된 데이터는 원본 데이터와 비슷한 경향을 보이기 때문에 증강된 데이터에 spectral mapping을 적용해도 기존 데이터와 유사한 결과가 나타났다. 원본 데이터와 증강된 데이터의 유사성을 확인하기 위하여 두 데이터의 2D spectral map을 비교한 결과가 Fig. 4에 설명되어 있다.
Original and augmented spectral mapping results
그림에서 보는 바와 같이 두 데이터는 전체 영역에서 거의 동일한 특성을 나타냄을 확인할 수 있었다. 따라서 증강된 데이터를 이용하여 spectral map을 생성하여도 이전에 부여한 라벨을 유지할 수 있다고 판단되었다.
2.3 시간영역 데이터 Scaling
실험을 통해 얻어진 터보차저 진동 데이터는 그 특성 상 scale이 일정하지 않다. 이처럼 입력 데이터 범위가 샘플 별로 각각 다른 경우, 특성 값의 크기에 의존하는 머신러닝 학습 과정에서 잘못된 학습을 수행할 가능성이 있어서 입력 데이터를 정규화하는 것이 필요하다. 이와 같은 문제점을 개선하기 위하여 이 연구에서는 식 (1)과 같은 min-max scaling을 사용하여 데이터 범위를 0 ~ 1사이로 정규화 작업을 수행하였다.
| (1) |
샘플 별 정규화 전, 최소 및 최대 값의 분포가 Fig. 5에 설명되어 있다. 그림에서 보는 바와 같이 정규화 전에는 샘플에 따른 최소 및 최대값의 변동이 다소 크게 나타나지만 정규화 후에는 최대값은 1로 최소값은 0으로 수렴한다.
Min & Max values before scaling(Key: ━━Max, ━━ Min)
3. Data Labeling 및 전처리
3.1 Data Labeling
준비된 data를 대상으로 전문가의 소음 평가 결과를 참조하여 3종류로 분류하고 각각 0, 1, 2로 labeling한다. Table 2에 label이 의미하는 상태와 각 label에 대한 데이터 개수를 정리하였다.
Labeling result
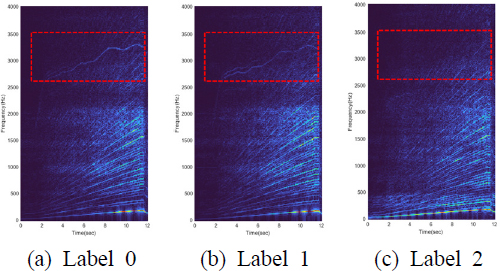
Table 2에서 defect 1 상태는 whine 성분의 소음과 진동 수준이 상대적으로 높은 상태이고 defect 2는 해당 소음과 진동이 상대적으로 낮으며 normal은 소음과 진동이 허용 범위 내에 있음을 의미한다. Fig. 6은 라벨에 따른 2D color map을 비교한 것으로 분석 결과 2.5kHz ~ 3.5kHz 영역의 진동 데이터의 특성에 따라 라벨이 결정되었다.
2D color map for each label
3.2 전처리
측정된 시간 영역 데이터는 두 형태로 딥러닝 분석에 사용되었다. 우선 앞 장에서 얻어진 데이터를 전처리 없이 그대로 사용하는 경우로 전체 길이의 시간 영역 데이터를 그대로 분석하였다. 전처리를 하는 경우에는 시간영역 데이터를 분석하여 얻어지는 9개의 통계적, 물리적 특성을 이용하여 머신러닝/딥러닝 분석을 수행하였다. 분석에 사용된 특성과 특성값을 계산하기 위한 수식을 Table 3에 설명하였다(10).
Statistical & physical features formula
앞 장에서 설명한 데이터 증강을 통하여 얻은 100개의 데이터 세트에 대해 위 표의 식들을 적용하여 얻어진 100 × 9 행렬을 이용하여 머신러닝 분석을 수행하였다.
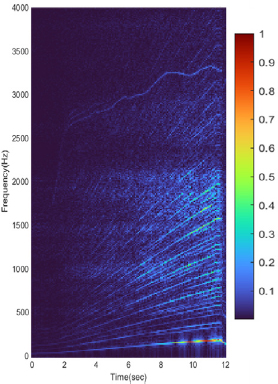
주파수영역의 전처리는 이차원(2D) 형태로 수행되었다. 2D 전처리에서는 시간 영역 데이터를 일정한 길이로 slicing이 완료된 데이터를 0.08초씩 일정한 시간 간격으로 나누어 4096 × 149으로 2차원 배열 데이터로 변환한다. 이렇게 변환된 배열은 열 방향으로 주파수 분석을 수행한다. 상기 과정을 거치면 데이터는 0kHz ~ 25.6kHz의 주파수 범위와 0초 ~ 12초의 시간 범위를 가지는 2048 × 149 크기의 2차원 spectral map을 얻을 수 있었다. 이 연구에서는 관심있는 주파수 범위와 분석 편의성을 고려하여 주파수 범위를 0 Hz ~ 4,000 Hz로 축소하여 분석하였다. Fig. 7은 이러한 과정을 통하여 얻어진 2D color spectral map의 예로 진동의 크기가 color로 표현되어 진폭 확인이 용이하다.
An example of 2D color map for turbo charger vibration
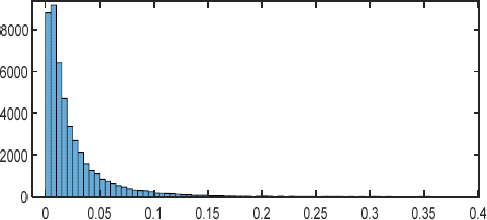
Canny edge detection은 이미지에서 edge를 찾는 알고리즘이다. Gaussian 필터를 사용하여 잡음을 제거한 뒤, 이미지 전체를 스캔하면서 사용자가 설정한 한계(threshold) 값인 maxVal과 minVal을 기준으로 edge가 아니라고 판단된 픽셀은 0, edge라고 판단된 픽셀은 1로 변환하는 작업을 수행한다(9). 일반적으로 maxVal와 minVal을 결정하는 건 여러 번의 시행착오를 거쳐야 하는 힘든 작업이다. 이 작업을 위해 데이터 세트에서 무작위로 추출된 샘플들의 분포를 히스토그램으로 표시하면 Fig. 8과 같다.
Histogram of original data
321 × 149 크기의 spectral mapping 이미지에는 47829개의 픽셀이 있으며 Fig. 8에서 알 수 있는 바와 같이 대부분 픽셀 값이 0 ~ 0.1 범위에서 분포되어 있다. 이 영역은 잡음 등 불필요한 정보가 있을 가능성이 높다고 판단하여 Canny edge detection에서 파라미터를 max Val=0.1, minVal=0.05으로 설정했다. Fig. 9는 상기 파라미터로 설정한 Canny edge detection을 적용한 결과를 보여준다.
2D spectral map with application of Canny edge technique
Fig. 9를 Fig. 7과 비교했을 때, 주위의 잡음으로 인해 육안으로는 whine 성분이 잘 보이지 않지만, whine 진동 성분의 경계선이 두드러지게 되어 신경망 학습 성능이 향상되는 것으로 판단된다.
3.3 데이터 세트 준비
Python의 train_test_split() method를 이용하여 데이터 세트를 훈련 세트, 테스트 세트, 검증 세트로 분할했다. 총 데이터 수 100개 중 60개는 훈련 세트, 20개는 테스트 세트, 20개는 검증 세트로 나누어서 데이터 세트를 준비했다. 데이터를 무작위로 골라서 세트를 구성하는 경우 특정 라벨의 샘플이 과도하게 많은 샘플링 편향이 발생할 수 있어 좋은 성능의 머신러닝 모델을 만들 수 없다. 따라서 원본 데이터에서 라벨의 비율(2:2:1)을 맞추면서 데이터 세트를 나누기 위해 ‘stratify=target’ 파라미터를 설정했다. 또한, 동일한 데이터 세트를 이용하여 여러가지 전처리 기법 및 특징 추출을 비교하기 위해 ‘random_state’ 파라미터를 일정한 값으로 설정했다. 나누어진 데이터 세트는 Table 4와 같다.
Dataset preparation
4. 머신러닝 모델 훈련
4.1 모델 훈련
로지스틱 회귀(logistic regression)는 선형방정식을 학습하고 분류하는 모델이다. 이 연구에서는 적절한 규제를 위하여 C(규제) 및 max_iter(가중치 갱신 횟수)를 각각 10으로 설정하였다. 그리고 fit() method를 사용하여 훈련 세트의 데이터와 타겟을 로지스틱 회귀 모델에 전달하여 훈련을 진행하고, 테스트 세트의 데이터와 타겟을 통해 테스트 세트의 데이터에 대한 분류 능력을 확인하는 과정을 진행했다.
결정 트리(decision tree)는 이진 트리 구조로 데이터의 특징을 바탕으로 데이터 분류를 수행하는 모델이다. 이 연구에서는 훈련 데이터에 대한 과적합을 방지하기 위하여 max_depth=3으로 깊이를 제한하였다. 또한, fit() Method를 사용하여 훈련 세트의 데이터와 타겟을 결정 트리 모델에 전달하여 훈련을 진행하고, 테스트 세트의 데이터와 타겟을 통해 테스트 세트의 데이터에 대한 분류 능력을 확인하였다.
심층 신경망(deep neural network; DNN)은 완전연결신경망을 2개 층 이상을 사용하여 신경망 층을 깊게 만들어 비선형 데이터 분포를 가지는 복잡한 문제를 해결할 수 있는 딥러닝 모델이다. 이 연구에서는 dense의 매개변수인 unit을 50으로 설정한 다음 2개 층을 쌓고 출력층을 클래스 개수인 3으로 지정한 DNN모델을 적용했다. 마지막 출력 층을 제외한 나머지 층은 ReLU 활성화 함수를 사용하고 출력 층의 활성화 함수는 클래스가 3개이므로 다중분류에서 사용되는 ‘softmax’를 사용했다. 모델 compile에서 optimizer는 ‘adam’을 사용했고 다중 분류에 사용되는 손실함수 ‘sparse categorical crossentropy’을 사용했다. 모델 훈련에서는 epoch=10, 훈련세트와 타겟을 전달해주었으며 epoch마다 검증 세트의 정확도와 손실을 계산하기 위해 validation data 매개변수에 검증 세트와 검증 세트의 타겟을 설정하여 결함 분류를 위한 훈련을 진행했다. Table 5는 model.summary() method를 이용하여 출력된 훈련에 사용된 심층 신경망 구조, 출력 형태, 파라미터 개수를 나타낸 것이다.
Deep neural network model
합성곱 신경망은 합성곱 연산을 사용하여 이미지에서 유용한 특성을 추출하고 이를 인공신경망과 연결하여 이미지 분류를 수행하는 딥러닝 모델이다. 이 연구에서는 이미지로 표현된 spectral map에 대해 합성곱 신경망을 이용하여 훈련을 진행했다. Table 6은 model. summary() method를 이용하여 출력된 훈련에 사용된 합성곱 신경망의 구조, 출력 형태, 파라미터 개수를 요약한 것이다.
Convolutional neural network model
합성곱 층은 3개를 사용했으며 필터 개수는 각각 16, 32, 64로 지정했다. 각각의 합성곱 층은 same padding, kernel_size=(3,3) 조건을 동일하게 사용했고 합성곱 층 다음에는 MaxPooling을 추가하여 특성맵의 크기를 줄이는 작업을 수행했다. flatten 층은 3번째 MaxPooling-2D 층 다음에 위치하여 2차원 특성맵을 1차원으로 펼쳐 인공신경망의 입력으로 사용했다. 완전연결신경망의 뉴런 개수는 50과 3을 각각 사용했다. 마지막 출력 층을 제외한 나머지 층은 ReLU 활성화 함수를 사용하고 출력 층의 활성화 함수는 클래스가 3개이므로 다중분류에서 사용되는 ‘softmax’를 사용했다. 모델 compile에서 optimizer는 ‘adam’을 사용했고 다중 분류에 사용되는 손실함수 ‘sparse categorical crossentropy’을 사용했다. 모델 훈련에서는 epoch=10, 훈련세트와 타겟을 전달했다. epoch마다 검증 세트의 정확도와 손실함수 값을 계산하기 위해, 검증 데이터 매개변수에 검증 세트와 그에 해당하는 타겟을 설정하여 결함 분류를 위한 모델 훈련을 진행했다.
4.2 정확도 및 손실
훈련이 완료되면 Canny 전처리가 적용된 데이터에 대한 훈련, 테스트 및 검증 세트에 대한 분석을 실시하여 분석 모델의 정확도를 계산하였다. 로지스틱 회귀 분석에서는 검증세트를 나누지 않고 훈련세트 80 %, 테스트 세트 20 %를 사용하여 정확도를 계산하였다. 로지스틱 회귀 분석 결과는 Table 7에 설명되어 있다.
Accuracy of logistic regression model
결정 트리도 훈련 세트 80 %, 테스트 세트 20 %에 대해 분석을 진행하였다. 결정 트리 모델의 분석 결과는 Table 8과 같다.
Accuracy of decision tree model
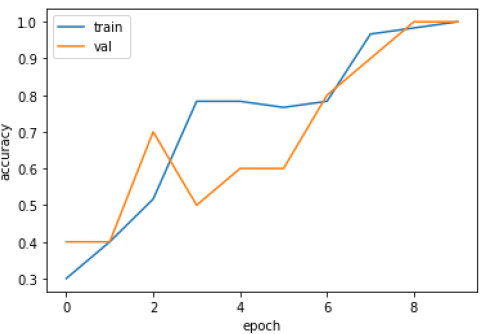
심층 신경망(DNN) 모델의 경우, history.history 딕셔너리(dictionary) 자료형에 훈련세트, 검증세트에 대한 정확도 결과가 저장된다. 딕셔너리에 저장된 값을 이용하여 훈련 성능을 평가하기 위해 각 epoch의 훈련 세트, 검증 세트의 정확도를 Fig. 10에 그래프로 나타냈다.
Accuracy per epoch in DNN analysis
훈련 세트에 대해서는 정확도가 5 epoch 이후로 1로 수렴하지만 검증 세트에 대해서는 2 epoch 이후로 0.8에 정확도가 일정하게 나타나며 과적합(overfitting) 문제가 발생하였다.
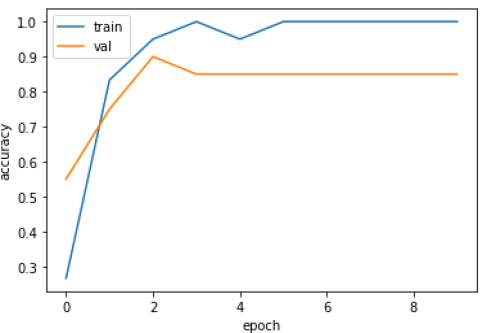
CNN 모델도 history.history 딕셔너리 자료형에 epoch마다 훈련세트, 검증세트에 대한 정확도 및 손실함수 값이 저장된다. 딕셔너리에 저장된 값을 이용, 훈련 성능을 평가하기 위해 epoch마다 훈련 세트, 검증 세트의 정확도 결과를 Fig. 11에 그래프로 나타냈다.
Accuracy per epoch in CNN analysis
그래프를 통해 7 epoch 이후로 정확도가 1에 근접한 결과가 나타났으며 이를 통해 합성곱 신경망 모델이 잘 훈련되었음을 확인할 수 있다.
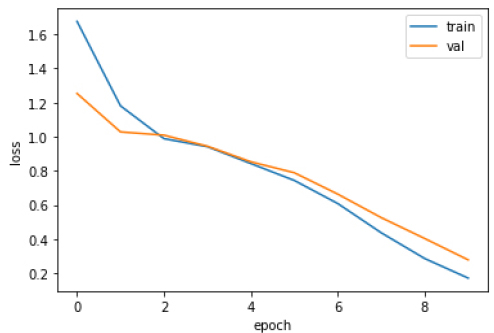
머신러닝 모델의 훈련 성능 평가를 위한 방법으로 데이터에 따른 손실함수 값을 사용할 수 있다. 이 연구에서는 정확도가 낮은 로지스틱 회귀, 결정 트리를 제외하고, 심층신경망(DNN)과 합성곱 신경망(CNN)의 손실함수 값의 변화를 조사했다. 상기 DNN 모델에서 각각의 epoch마다 훈련 세트, 검증 세트의 loss를 평가한 결과가 아래 Fig. 12에 설명되어 있다.
Loss per epoch in DNN analysis
그래프를 통해 훈련 세트에 대한 손실은 안정적으로 0에 수렴하나 검증 세트에 대한 손실은 2 epoch 이후로 증가하고 있는 것을 확인할 수 있다. 정확도와 손실 그래프를 통해 심층신경망 모델은 새로운 진동 데이터에 대해 분석하지 못할 가능성이 크다는 것을 확인할 수 있다.
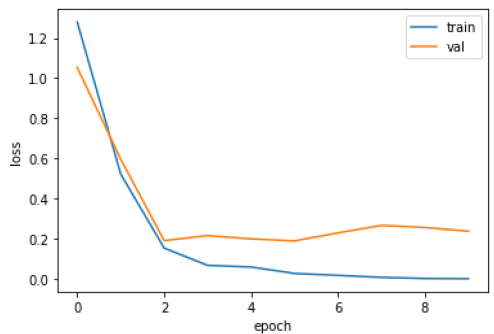
합성곱 신경망 모델에서 epoch마다 훈련 세트, 검증 세트의 손실함수 값을 분석한 결과가 다음 Fig. 13에 설명되어 있다.
Loss per epoch in CNN analysis
그래프를 통해 훈련 세트와 검증 세트에 대한 손실이 안정적으로 0에 수렴하고 있는 것을 확인할 수 있다. 손실이 훈련 도중 증가하는 발산이 발생하지 않았으므로 모델 훈련이 잘 이루어지고 있음을 알 수 있다. 또한, 이는 모델을 실제 데이터에 적용했을 때, 모델이 추정하는 오차가 많이 줄어들 수 있음을 확인할 수 있다.
5. 결과 비교
5.1 전처리 효과 분석
앞에서 설명된 전처리의 효과를 분석하기 위하여 서로 다른 전처리를 적용하는 경우 나타나는 정확도를 분석하였다. 시간영역 데이터, 시간영역 데이터로부터 추출한 물리적 및 통계적 특징, 2D spectral Map 데이터 및 2D spectral map에 Canny방법을 적용한 데이터 등 4종류의 데이터에 대해 정확도를 비교하였다. 시간영역 데이터, 시간영역 데이터의 물리, 통계적 특징과 같은 1D데이터는 1D CNN을, 나머지 두 데이터에 대해서는 2D CNN을 사용하여 분석한 결과를 Table 9에 비교하였다.
Accuracy comparison by data preprocessing
Table 9에서 알 수 있는 바와 같이, 1D CNN을 사용하여 분석한 정확도는 2D CNN을 사용한 결과에 비해 매우 낮다. 또한, 2D spectral map의 경우 Canny 전처리를 적용함에 따라 정확도가 더 높아졌다.
Table 10은 전처리 기법 별로 정확도와 손실함수 값을 비교한 것으로, Canny 전처리 기법을 적용함에 따라 정확도는 증가하고 손실함수 값이 감소하는 것을 확인했다.
Accuracy and loss by data preprocessing
5.2 머신러닝 모델 별 훈련 성능 비교
Table 10에 설명된 전처리 방식에 대해 합성곱 신경망과 다른 머신러닝 모델들을 사용하여 결함 분류를 진행하고 전체 데이터 세트에 대해 정확도 분석 결과를 정리하면 Table 11과 같다.
Comparison of accuracies of ML models
각각의 머신러닝 모델은 다양한 파라미터를 가지고 있기 때문에, 같은 입력 데이터에 대해서도 다양한 모델에서 우수한 성능을 보이는 전처리를 찾는 것은 쉽지 않지만, 이 연구에 사용된 머신러닝 모델들에서는 ‘Canny’ 전처리를 적용하면 성능이 향상된다는 사실을 확인했다. 이를 통해 ‘Canny’ 전처리는 합성곱 신경망 모델뿐 아니라 머신러닝 모델의 학습 성능을 향상시킬 수 있는 유효한 전처리 기법임을 Table 11을 통해 확인할 수 있다.
6. 결 론
이 연구에서는 터보차저 진동 데이터에 대한 머신러닝 분석 성능 향상을 위하여 Canny edge 검출 전처리와 합성곱 신경망을 적용하는 방법을 제시하였다. Canny를 이용하여 데이터 전처리를 진행한 spectral map 이미지는 결함여부 결정에 영향을 주는 2500 Hz ~ 3500 Hz 영역을 집중적으로 학습시킬 수 있어 머신러닝의 성능이 향상되는 사실을 epoch별 정확도와 손실 그래프를 통해 확인할 수 있었다. Table 10을 통해 어떠한 전처리도 적용하지 않은 spectral map 이미지에서는 전체 데이터 세트에 대해 평균 손실함수 값이 0.6323인 반면에 Canny전처리를 적용한 경우 손실함수의 평균 값이 0.0516으로 학습 성능이 더 우수함을 확인할 수 있었다. 정확도 확인 및 epoch별 그래프 분석 기법들을 통해 Canny전처리를 적용하는 것이 머신러닝 모델의 성능 향상에 기여한다는 것을 확인했다.
향후에 추가적인 소음 데이터 및 진동 데이터를 확보해서 이 논문에서 적용한 데이터 증강 기법을 사용하지 않고 제안된 방법을 추가로 검증할 예정이다. 또한, 제시된 방법 이외에 구조를 복잡하게 구성하지 않고 높은 학습 성능을 보일 수 있는 최적의 입력 데이터를 찾는 연구를 통해 구조 단순화 및 소형화 연구를 진행할 것이다.
Acknowledgments
이 논문에 사용된 터보차저 실험 결과를 제공해주신 ㈜계양정밀에 감사드립니다.
References
- Ji, Y. M., Yoo, J. J. and Lee, S. H., 2017, Internet of Things, Big-data and Artificial Intelligence, Communications of the Korean Institute of Information Scientists and Engineers, Vol. 35, No. 7, pp. 43~50.
- Eun, H. J., 1984, Machine Condition Diagnosis and Defect Detection by Vibration Signal Processing, Journal of the Korean Society of Mechanical Engineers, Vol. 24, No. 6, pp. 428~436.
-
Jung, S.-M. and Choi, W.-J., 2022, A Study on Deep Learning-based Fault Diagnosis Using Vibration Data of Wind Generator, Journal of KIIT, Vol. 20, No. 6, pp. 129~136.
[https://doi.org/10.14801/jkiit.2022.20.6.129]
- Lee, J.-D. and Kim, J. H., 2020, A Study on the Denoising Method of Gearbox Vibration Signal Using Auto-encoder, Journal of the Korea Society of Information Technology Policy & Management, Vol. 12, No. 5, pp. 2017~2023.
-
Jung, I., Lee, D., Noh, K. and Chang, J.-H., 2022, Development of AI-based Diagnosis Technology Using Noise/Vibration Data of Automobile Powertrain, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 32, No. 1, pp. 37~44.
[https://doi.org/10.5050/KSNVE.2022.32.1.037]
- Lee, S., Ko, S. and Lee, S., 2022, Fault Classification Model Based on Deep Learning Using Vibration Data of Mechanical Equipment, The Journal of Korean Institute of Next Generation Computing, Vol. 18, No. 2, pp. 36~46.
-
Lee, H., 2010, Noise Diagram of an Automotive Turbo Charger and Its Applications, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 20, No. 5, pp. 502~509.
[https://doi.org/10.5050/KSNVE.2010.20.5.502]
-
Iwana, B. K. and Uchida, S., 2021, An Empirical Survey of Data Augmentation for Time Series Classification with Neural Networks, PLoS ONE, Vol. 16, No. 7, e0254841.
[https://doi.org/10.1371/journal.pone.0254841]
-
Canny, J., 1986, A Computational Approach to Edge Detection, IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 8, No. 6, pp. 679~698.
[https://doi.org/10.1109/TPAMI.1986.4767851]
-
Kim, S., Noh, Y., Kang, Y., Park, S. and Ahn, B., 2021, Fault Classification Model Based on Time Domain Feature Extraction of Vibration Data, Journal of the Computational Structural Engineering Institute of Korea, Vol. 34, No. 1, pp. 25~33.
[https://doi.org/10.7734/COSEIK.2021.34.1.25]
Yun-Hyeok Lim He is an undergraduate student in the Department of Automotive Engineering at Kyungpook National University. He is currently pursuing a bachelor’s degree.
Hyung-Ju Cho Ph.D. in computer science and Professor in the Department of Software, Kyungpook National University. His current research interests include moving object databases, query processing in mobile peer-to-peer networks and real-time maintenance of the high-definition digital map for autonomous vehicles.
Hyeong-Ill Lee Ph.D. in mechanical engineering and Professor in the School of Automotive Engineering, Kyungpook National University. Prof. Lee is teaching Dynamics, Automatic Control and Mechanical Vibration, etc. He has academic interests in automotive NVH, Brake squeal, Sound radiation from vibrating structures, etc.