해상풍력발전 블레이드 진동기반 이상 진단을 위한 전산 축소 모델 개발

1. 서 론

2050년 탄소중립 시나리오가 발표됨에 따라 재생에너지의 목표 비중이 대폭 상향되었으며, 태양광에 이어 두 번째로 높은 전력 공급(2030년 17.7 GW 공급 목표)을 위해 대규모 해상풍력 단지 건설이 추진되고 있다. 단지 확대와 더불어 개별 풍력발전기의 발전 용량 확대를 위해 핵심요소인 블레이드가 대형화되고 있으며, 국내에선 8 MW 해상풍력터빈 실증 사업이 진행중이다. 하지만 블레이드의 대형화로 인해 블레이드 제조공정에서 발생할 수 있는 층간분리(delamination), 복합 층간의 주름(wrinkle), 균열(crack) 등의 결함 발생 확률 및 운전 중 발생할 수 있는 층간분리, 낙뢰에 의한 파손(lighting damage), debonding접착분리(debonding)⁽¹⁾ 등의 손상 확률이 증가할 수 있으며 이미 국내에서도 이와 관련된 블레이드 사고가 수차례 발생하였다.

블레이드와 같이 육안으로 확인이 불가능한 결함, 층간분리 등은 초음파 탐상 검사(ultrasonic testing, UT)⁽²⁾, 음향 방출 검사(acoustic emission techniques, AE)^(3,4) 등을 통해 제작 및 유지보수 과정에서의 신뢰도를 높일 수 있으나 분해능 확보의 어려움, 운용 중 측정 불가, 두께 및 측정조건 제약 등의 한계로 인해 여전히 운용 현장에서의 적용에 어려움이 많다.

해상풍력발전 블레이드의 운용 중 중대결함의 사전 탐지를 위해선 블레이드의 진동을 상시 계측하고, 계측된 데이터를 정확도가 높은 유한요소해석 모델 해석결과와 비교하여 이상 여부를 진단하는 방법을 사용할 수 있다. 이러한 방법은 최근 주목받고 있는 디지털 트윈 기반 구조물 상태감시 방법과 유사하며, 이를 위해서 정확한 유한요소 해석모델 구축뿐만 아니라 실시간 데이터 비교 분석을 위해 연산량이 대폭 저감된 해석 모델을 확보해야 한다⁽⁵⁾. 이 논문에서는 다양한 전산 축소 모델(reduced order model, ROM) 개발 기법을 활용하여 블레이드의 상태감시에 활용될 수 있는 전산 축소 모델을 개발하였다. 2장에서는 축소 모델 개발 기법들의 이론적 배경 비교·분석을 간단하게 기술하였으며, 3장에는 다양한 기법들을 기반으로 예제 블레이드에 대해 구축한 전산 축소 모델들을 활용하여 모달해석, 조화해석, 시간이력 해석을 수행한 결과를 유한요소해석 결과와 비교 분석한 내용을 기술하였으며, 4장에는 결론을 기술하였다.

2. 전산 축소 모델 구축 기법

일반적인 전산 해석 모델의 경우 식 (1)과 식 (2)와 같이 감쇠 시스템으로 표현할 수 있다.

여기서 M, C, K는 각각 질량, 감쇠, 강성 행렬을 의미하며 F는 시스템에 가해지는 하중을 의미한다. 시스템의 응답을 나타내는 x를 식 (2)와 같이 변환행렬 T를 도입하여 z라는 새로운 변수로 치환한다면 식 (1)은 식 (3)과 같이 변환할 수 있다.

M, C, K 행렬의 경우 좌변에 T^T를 곱해줌으로써 축소된 행렬인 M_z, C_z, K_z로 변환되며 F 행렬 또한 축소된 F_z로 변환이 가능하다. T의 열 개수를 통해 축소 행렬의 크기가 자유롭게 바꿀 수 있으며, 모드확장법(modal expansion)에 사용되는 고유벡터(eigenvector)가 대표적인 T의 예시이다. T를 구성하는 방법에 따라 축소 행렬의 형태가 달라지며, 이를 통해 얻을 수 있는 응답 정확도의 차이가 발생한다. 이 논문에서는 가장 많이 활용되는 정적축소(static reduction), 동적축소(dynamic reduction), 크릴로프 부분공간(Krylov subspace), 등가 축소 확장 과정(system equivalent reduction expansion process, SEREP)에 대해 간략히 다루고자 한다.

3. 예제 블레이드를 활용한 축소 모델 구축 및 해석 결과

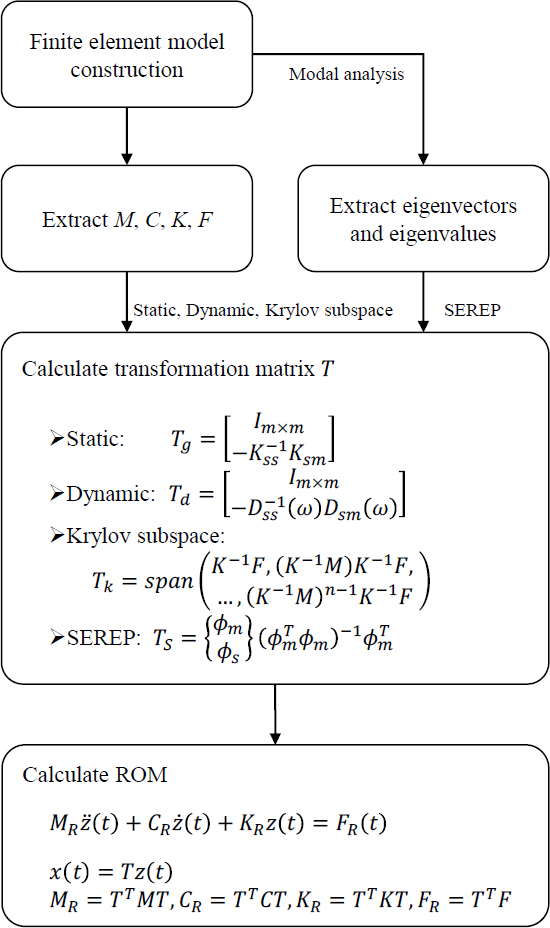
이 장에선 앞서 소개한 4가지 기법을 활용하여 축소 모델을 구축하고, 해당 모델들을 활용하여 해석 수행 및 결과 분석 내용을 다루고자 한다. 축소 모델을 구축하기 위해 수행하는 과정들은 Fig. 1과 같다.

Fig. 1

Schematic diagram for the reduced order model construction

상용 유한요소해석 프로그램을 활용하여 유한요소 격자(mesh) 생성, 경계조건 입력 등의 전처리 과정을 수행하면 M, C, K, F 행렬을 추출할 수 있게 된다. SEREP을 제외한 나머지 기법의 경우 상기 정보를 활용하여 축소 모델을 구축할 수 있으며, SEREP의 경우 고유치 해석을 수행하여 고유치, 고유벡터를 추가적으로 필요로 한다. 추출한 행렬들을 활용하여 모달 해석을 수행할 수도 있지만, 상용 프로그램의 최적화된 수치해석 알고리즘을 활용하는 것이 보다 빠르기 때문에 이와 같이 해석 결과를 추출하는 방식을 사용하였다.

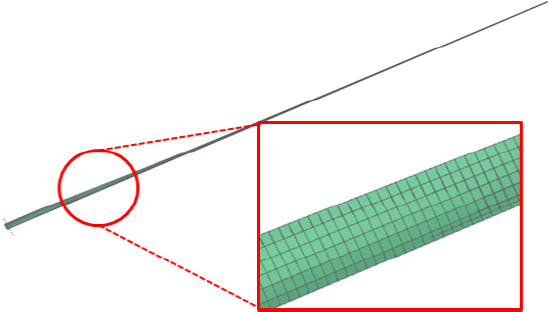
이 연구에선 상용 유한요소해석 프로그램으로 Simcenter 3D를, 축소 모델 생성 및 연산에는 Python 3.8을 활용하였다. 예제로 사용한 블레이드 모델은 Fig. 2와 같으며, 상세 정보는+8- Table 1에 기술하였다. Polycarbonate 물성으로 구성된 예제 블레이드 모델을 사용하였고, 시스템의 단순화를 위해 감쇠 행렬은 제거하였다. 블레이드 허브에 자유도를 구속하는 경계조건을 사용하였으며, 경계조건을 제외한 M, K 행렬의 크기는 60966 × 60966이다. 2장에 기술한 4가지 기법을 사용하여 축소 모델을 구축하는데 소요된 시간은 Table 2와 같다.

Fig. 2

Finite element model of wind turbine blade (full model)

Table 1

Details of finite element model

Table 2

ROM construction time

블레이드에 센서를 설치하더라도 다수의 센서를 설치할 수 없어 10개의 센서를 설치하였다고 가정하고, FEM 상에서 이를 구현하게 되면 6 자유도 값을 확인할 수 있어 축소모델의 크기를 60 × 60으로 설정하였다. Krylov subspace 기법을 제외한 나머지 기법의 경우 Fig. 3에서 파란색 점으로 표시된 10개 절점에서의 6 자유도를 고려하였고, Krylov subspace는 60개의 벡터를 추출하여 M_R, K_R 크기를 60 × 60로 통일하였다. Table 2에서 살펴볼 수 있듯이, SEREP이 변환행렬 연산 속도 측면에서 가장 우수하였으며 Krylov기법이 가장 느린 속도를 보였다. 이는 역행렬 계산에 따른 연산 부하에 의한 현상으로, SEREP의 경우 generalized inverse를 사용하여 역행렬 길이가 모드 수로 작아진 반면 static, dynamic reduction의 경우 (전체 dof–master node dof)로 소폭 축소되어 SEREP 대비 연산 부하가 큰 것을 알 수 있다. Krylov의 경우 K^-1 연산을 위해 LU 분해 기법을 사용하고, arnoldi iteration 과정을 거치면서 타 기법에 비해 연산 부하가 크고 더 많은 시간이 소요됨을 확인할 수 있다. 참고사항으로 Table 2의 SEREP 연산 시간에는 모달 해석에 소요된 시간이 배제되었으며, 그 외 모든 연산은 python 3.8에서 수행되었다. 만약 요소, 절점 수가 많은 해석모델을 활용하여 ROM을 구축하는 경우 모달 해석 수행에 많은 시간이 소요될 수 있으며, 역행렬 계산에 있어 보다 최적화된 알고리즘을 사용하는 상용 유한요소해석 소프트웨어를 활용한다면 시간이 단축될 수 있을 것이다. 실제 블레이드의 경우 예제 블레이드와 달리 이방성 재료들이 적층된 구조이지만, 각 element 별 M, K 행렬 내 구성이 달라질 뿐 이후 연산 과정은 동일하기 때문에 상기 기법들의 적용이 가능하다.

Fig. 3

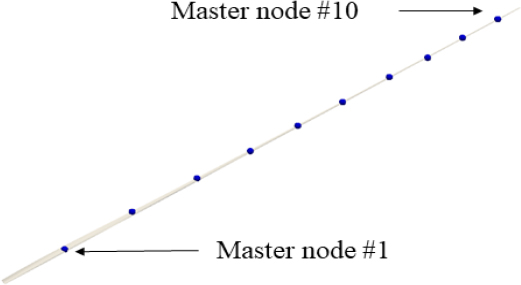
Comparison of full model and reduced order model of wind turbine blade (blue circle: master nodes of reduced order model)

3.1 모달 해석(modal analysis)

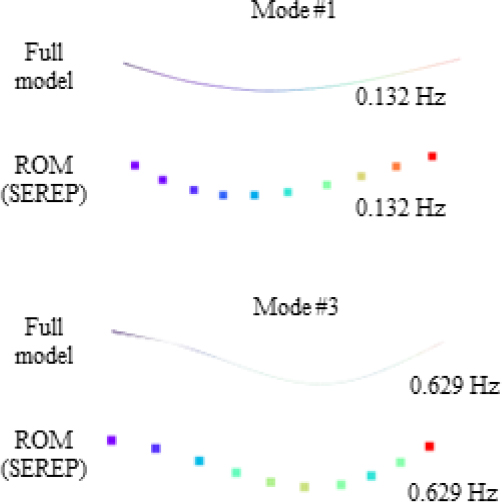
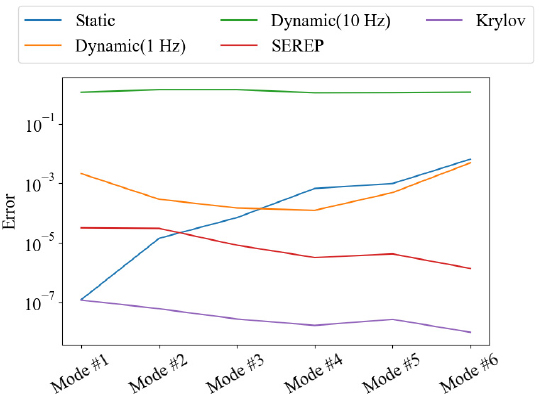
구축한 전산 축소 모델의 정확도 분석을 위해 모달 해석을 수행하였다. 처음 6개 모드에 대해 모드 형상 및 고유진동수 비교를 수행하였으며, 이를 Figs. 4, 5와 Table 3 ~ Table 8에 정리하였다. SEREP 기법 적용 축소 모델을 대표 예시로 도시한 Fig. 4에서와 같이 full 모델과 ROM의 모드 형상이 동일함을 알 수 있다. Full 모델의 고유진동수를 기준으로 오차 분석 시 Krylov subspace의 오차가 가장 작은 것을 확인할 수 있으며, static reduction은 저주파 대역에선 우수한 성능을 보이지만 고주파로 갈수록 오차가 커짐을 알 수 있다. Dynamic reduction의 경우 ω값에 따라 확연히 편차가 큰 것을 확인할 수 있다. Dynamic reduction을 활용하여 광대역 진동 해석을 수행할 경우, 정확한 해석을 위해선 협대역 별 T_d를 연산하여 해석을 수행해야 하고 다수의 모드가 중첩되는 고주파 대역에선 이 방법조차도 큰 수치 오류로 이어질 수 있어 권장되지 않는다. 반면 Krylov subspace 기법은 타 기법 대비 우수한 성능을 갖으며, 6차 모드까지 편차가 작은 것을 확인할 수 있다. 다만 해석 시간을 감안한다면 SEREP 기법 또한 축소 모델 구현에 효과적인 기법이라 할 수 있다. 더불어 SEREP은 Fig. 4와 같이 축소 모델로부터 얻은 변위 응답이 full 모델의 응답과 일치하기 때문에 변환과정 없이 직관적으로 이를 해석할 수 있지만, Krylov subspace는 필히 변환행렬을 사용해야만 응답을 해석할 수 있다는 차이가 있다.

Fig. 4

Comparison of mode shapes between full model and reduced order model

Fig. 5

Natural frequency error compared to full model

Table 3

Natural frequency comparison between full model and reduced order model(unit: Hz)

Table 4

MAC between full model and ROM using static reduction (column: full model, row: ROM)

Table 5

MAC between full model and ROM using dynamic reduction (ω = 1Hz, column: full model, row: ROM)

Table 6

MAC between full model and ROM using dynamic reduction (ω = 10Hz, column: full model, row: ROM)

Table 7

MAC between full model and ROM using SEREP (column: full model, row: ROM)

Table 8

MAC between full model and ROM using Krylov subspace method (column: full model, row: ROM)

Modal assurance criterion (MAC)을 사용하여 Full 모델과 축소 모델의 모드 형상의 일치 여부를 정량적으로 판별한 결과는 Table 4 ~ Table 8과 같다. 고유진동수와 동일하게 10 Hz로 설정한 dynamic reduction 모델은 대각 행렬의 값이 낮으며, SEREP과 Krylov subspace 기법이 가장 우수한 것을 확인할 수 있다.

3.2 조화 해석(harmonic analysis)

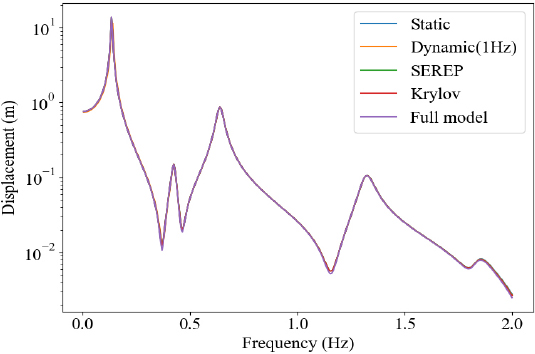
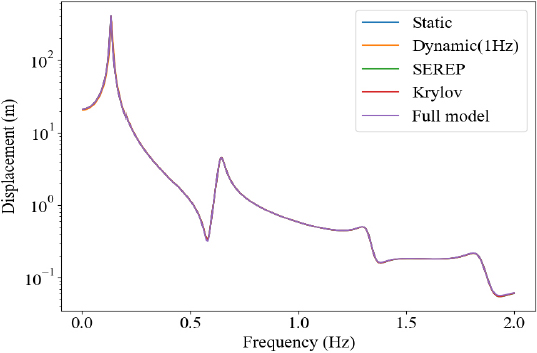
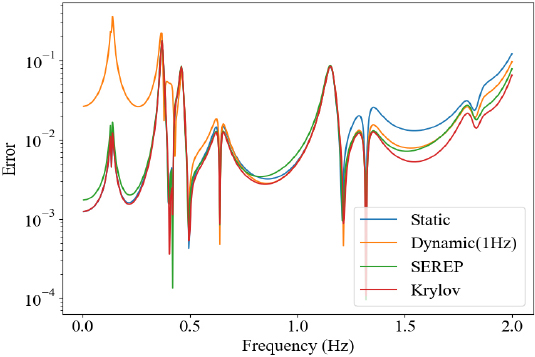
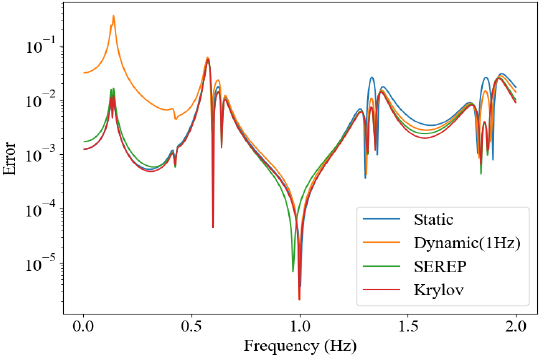
다음으로 전산 축소 모델로부터 연산된 변위 응답의 정확도 분석을 위해 조화 해석을 수행하였다. 비교 분석을 위한 해석이기에 단순한 형태의 하중을 입력하였다. Fig. 3에 도시된 10개의 master node들에 y 방향으로 1 N의 힘을 입력하였고, numerical damping을 0.05로 설정하였을 때 master node # 2와 slave node 중 하나를 선정하여 해당 위치에서의 변위 응답을 추출하였다. 주파수 범위는 0.005 Hz 간격으로 0 Hz ~ 2 Hz로 설정하였으며 해석 결과는 Fig. 6 ~ Fig. 9와 같다. Fig. 6, Fig. 9과 같이 구축한 MOR들의 master node 변위 응답과 변환행렬을 활용하여 구한 slave node 변위 응답 모두 full 모델의 결과와 매우 유사함을 확인할 수 있다. Full model과의 오차 분석 시 Figs. 8, 9에서와 같이 Krylov subspace 기법의 성능이 가장 우수하였으며, dynamic 기법의 경우 주파수 선정에 따라 상당한 오차가 발생함을 확인할 수 있었다. Dynamic reduction의 경우 특정 주파수에서의 시스템 동특성만이 변환행렬에 반영되었기에, 목표 주파수(1 Hz)에서는 Krylov subspace 기법과 유사한 정확도를 보이나 해당 주파수에서 벗어날수록 정확도가 타 기법에 비해 떨어짐을 확인할 수 있다. Static 기법의 경우 모달 해석 분석 결과와 유사하게 고주파 대역에서 성능이 저하됨을 확인할 수 있으며, SEREP의 경우 Krylov subspace와 유사한 수준의 정확도를 갖음을 확인할 수 있다. 해석에 소요된 시간의 경우 Table 9와 같이 full 모델 대비 4가지 기법 모두 연산 속도에 있어 강점을 갖음을 확인할 수 있다.

Fig. 6

Harmonic analysis result at master node # 2

Fig. 7

Harmonic analysis result at node 6830 (middle of master node # 7 and # 8)

Fig. 8

Numerical error between full model and MOR for harmonic analysis result at master node # 2

Fig. 9

Numerical error between full model and MOR for harmonic analysis result at node 6830

Table 9

Runtime of harmonic analysis

3.3 시간 이력 해석(transient analysis)

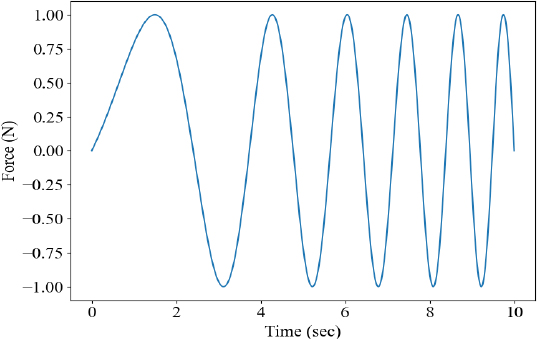
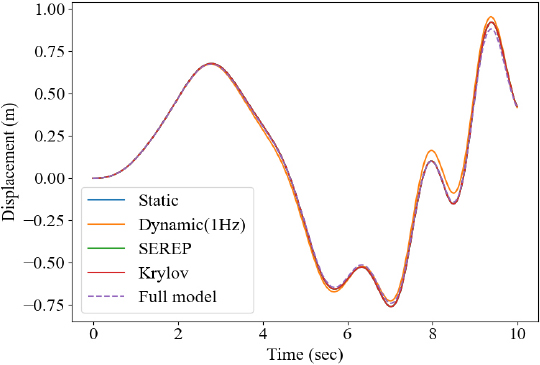
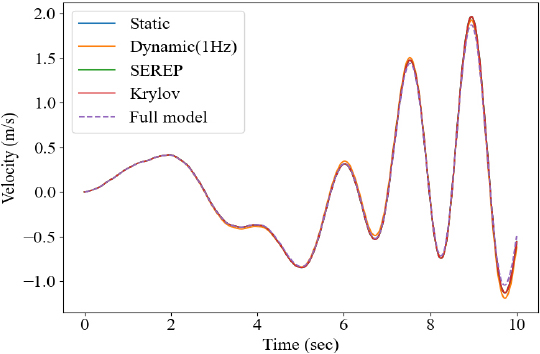
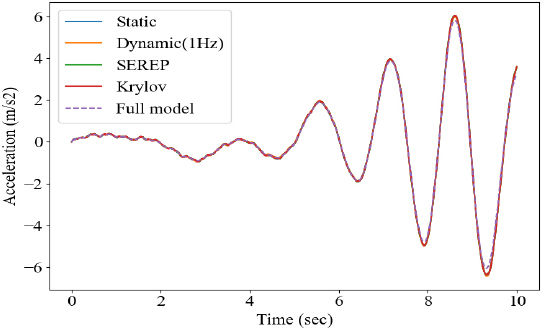
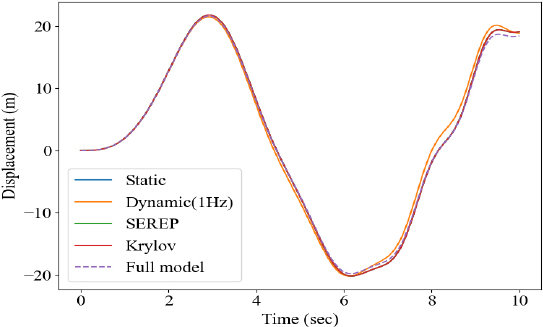
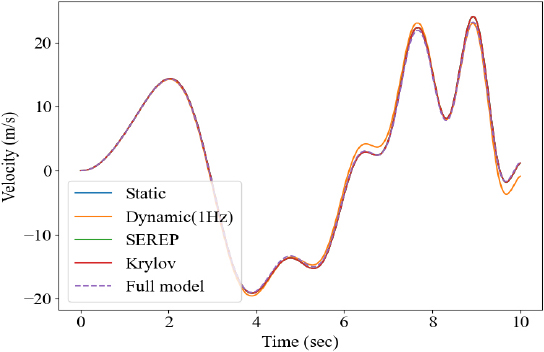
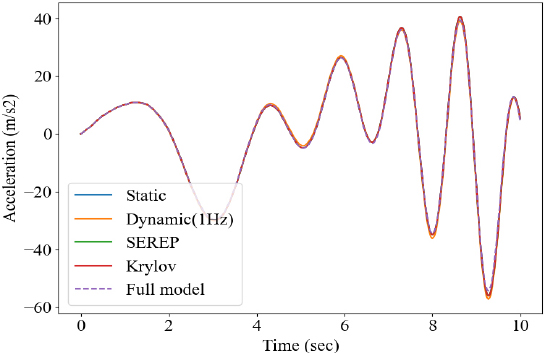
마지막으로 전산 축소 모델을 활용하여 시간 이력 해석을 수행하였다. Fig. 10과 같이 sine sweep을 입력 파형으로 선정하였으며, 조화 해석과 동일하게 Fig. 4에 도시된 10개 지점에 동일한 힘을 인가하였다. 수치해석 기법으로는 뉴마크 기법을 활용하였으며, β = 0.25, γ = 0.5를 활용하여 해석을 수행하였다. 초기조건으로 변위와 속도 값 모두 0을 활용하였으며, 앞서 구축한 4개의 축소 모델의 해석 시간과 결과는 Table 10과 Fig. 11 ~ Fig. 16과 같다.

Fig. 10

Input force used in transient analysis

Table 10

Runtime of transient analysis

Fig. 11

Transient analysis result (displacement) at master node # 2

Fig. 12

Transient analysis result(velocity) at master node # 2

Fig. 13

Transient analysis result (acceleration) at master node # 2

Fig. 14

Transient analysis result (displacement) at node 6830

Fig. 15

Transient analysis result (velocity) at node 6830

Fig. 16

Transient analysis result (acceleration) at node 6830

앞선 해석결과와 유사하게 dynamic 기법을 활용하여 구축한 모델의 정확도가 상대적으로 타 기법보다 낮음을 확인할 수 있으며, SEREP과 Krylov subspace 기법 활용 모델의 해석결과가 FEM 결과와 가장 유사함을 확인할 수 있다. 입력으로 사용된 힘의 주파수 성분이 1 Hz 이하의 성분들로 구성되어 있어, Figs. 8, 9에서 확인한 dynamic 기법의 오차와 같이 목표 주파수에서 벗어날수록 왜곡된 변환행렬로 인해 시간 이력 해석의 연산 정확도 또한 타 기법에 낮음을 확인할 수 있다. Table 10과 같이 모든 축소 기법 사용 시 full 모델 대비 해석 시간이 현저히 적게 소요됨을 확인할 수 있고, 특정 회전 주파수로 동작하는 기계 시스템의 경우엔 그에 맞춰 구성한 변환행렬을 사용하여 dynamic 기법을 적용할 수 있으나, 다양한 주파수 성분이 존재한다면 Krylov subspace와 SEREP 기법 사용이 권장된다. 모든기법들에 대해 요약한 정보는 Table 11과 같다.

Table 11

Summary of ROM constructing methods

4. 결 론

이 논문에선 해상풍력발전 블레이드의 진동기반 이상 진단을 위한 수단으로써 블레이드의 진동을 묘사할 수 있는 전산 축소 모델을 구축하고, 이를 활용하여 진동 해석을 수행한 결과가 유한요소해석 결앞서 언급한 바와 같이 이 연구에서 소개한 모든 기법들에 대해 요약한 정보를 Table 11에 기재하였으며, 특정 회전 주파수로 동작하는 기계류에서는 dynamic, SEREP, Krylov subspace 기법을, 두 개 이상의 회전 주파수 성분을 관측해야 하는 경우에는 SEREP, Krylov subspace 기법을, 분석 대상체의 모드 형상을 계측할 수 있는 경우에는 SEREP 기법의 사용을 권장한다. 해당 방법들을 활용할 경우 실시간 해석을 수행할 수 있을 만큼 유한요소해석 대비 해석 시간을 상당히 단축할 수 있음을 확인하였다. 비록 이 논문에서 활용한 입력 힘의 크기, 형태가 실제 블레이드에 인가되는 공력과는 차이가 있어 진동 응답의 크기가 비현실적인 부분이 있지만, 이 연구를 통해 정확하면서도 빠른 연산이 가능한 축소 모델을 확보하였음에 큰 의의가 있다. 추후 실제 공력과 유사한 입력을 산정하여 해석한 결과와 실제 블레이드의 진동을 계측한 값을 비교 검증하는 연구를 진행할 계획이다.

Acknowledgments

이 논문은 한국기계연구원의 기본사업(NK244B)과 산업통상자원부의 재원으로 한국에너지기술평가원의 지원(No. 20213030020120, 해상풍력발전 블레이드의 전주기 신뢰성 향상을 위한 생산품질 및 유지 관리 기술 개발)을 받아 수행된 연구임.

References

• Kong, K., Dyer, K., Payne, C., Hamerton, I. and Weaver, P. M., 2022, Progress and Trends in Damage Detection Methods, Maintenance, and Data-driven Monitoring of Wind Turbine Blades - A Review, Renewable Energy Focus, Vol. 44, pp. 390~412. [https://doi.org/10.1016/j.ref.2022.08.005]
• Jasinien, E., Raiutis, R., Literis, R., Voleiis, A., Vladiauskas, A., Mitchard, D. and Amos, M., 2009, NDT of Wind Turbine Blades Using Adapted Ultrasonic and Radiographic Techniques, Insight, Vol. 51, No. 9, pp. 477~483. [https://doi.org/10.1784/insi.2009.51.9.477]
• Liu, Z., Wang, X. and Zhang, L., 2020, Fault Diagnosis of Industrial Wind Turbine Blade Bearing Using Acoustic Emission Analysis, IEEE Transactions on Instrumentation and Measurement, Vol. 69, No. 9, pp. 6630~6639. [https://doi.org/10.1109/TIM.2020.2969062]
• Han, B.-H., Yoon, D.-J., Huh, Y.-H. and Lee, Y.-S., 2014, Damage Assessment of Wind Turbine Blade under Static Loading Test Using Acoustic Emission, Journal of Intelligent Material Systems and Structures, Vol. 25, No. 5, pp. 621~630. [https://doi.org/10.1177/1045389X13508329]
• Oh, S., Park, D., Baek, H., Kim, S., Lee, J.-K. and Kim, J.-G., 2020, Virtual Sensing System of Structural Vibration Using Digital Twin, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 30, No. 2. pp. 149~160. [https://doi.org/10.5050/KSNVE.2020.30.2.149]
• Guyan, R. J., 1965, Reduction of Stiffness and Mass Matrices, AIAA Journal, Vol. 3, No. 2, p. 380. [https://doi.org/10.2514/3.2874]
• Flodén, O., Persson, K. and Sandberg, G., 2014, Reduction Methods for the Dynamic Analysis of Substructure Models of Lightweight Building Structures, Computers & Structures, Vol. 138, pp. 49~61. [https://doi.org/10.1016/j.compstruc.2014.02.011]
• O’Callahan, J. C., 1989, System Equivalent Reduction Expansion Process, Proceedings of the 7th International Modal Analysis Conference, pp. 29~37.
• Sastry, C. V. S., Mahapatra, D. R., Gopalakrishnan, S. and Ramamurthy, T. S., 2003, An Iterative System Equivalent Reduction Expansion Process for Extraction of High Frequency Response from Reduced Order Finite Element Model, Computer Methods in Applied Mechanics and Engineering, Vol. 192, No. 15, pp. 1821~1840. [https://doi.org/10.1016/S0045-7825(03)00204-4]
• Krylov, A. N., 1931, On the Numerical Solution of the Equation by which in Technical Questions Frequencies of Small Oscillations of Material Systems are Determined, Izvestija AN SSSR (News of Academy of Sciences of the USSR), Otdel. mat. i estest. nauk, Vol. 7, No. 4, pp. 491~539.
• Freund, R. W., 2003, Model Reduction Methods Based on Krylov Subspaces, Acta Numerica, Vol. 12, pp. 267~319. [https://doi.org/10.1017/S0962492902000120]