바닥 가진 시 PH15-7Mo 브라켓 진동 피로 파괴에 따른 모달 파라미터 추정

1. 서 론

모빌리티 및 에너지 산업 분야에서 진동, 내진 시험은 전자식이나 유압식 쉐이커를 활용하여 수행되고 있다. 전자식의 경우 유압식에 비해 높은 가속도와 진동수 범위를 가지고 있어 모빌리티에서 발생되는 진동을 바닥 가진으로 재현하여 시험하는 분야에 사용되며, 유압식의 경우 높은 스트로크 가진력을 기반으로 내진 및 토목 분야에 주로 사용되고 있다. 바닥 가진을 사용하는 경우 임팩트 해머를 사용하는 모달 테스트에 비해서, 가진력의 크기를 정해진 시험기 규격 내에서 자유롭게 가진할 수 있다. 이러한 장점 때문에 시스템에 부여할 수 있는 에너지가 크고 비선형적인 현상을 관찰하기 용이하며, 다량의 데이터 획득이 용이하여 정규화된 데이터를 얻기에 유리하다. 하지만 힘을 측정할 수 있는 해머와 달리 가속도계를 활용하여 시험을 수행하기 때문에 전달함수가 무차원이며, 서클 피팅 시 전달함수가 완벽한 원이 아니다. 이러한 문제에도 불구하고 바닥 가진 시 모달 파라미터를 추출하려는 시도는 Béliveau에 의해 시험에서 구한 전달함수의 대수적인 처리를 통해 상용 프로그램에 적용하여 고유진동수와 감쇠를 추정한 바 있으며⁽¹⁾, M Link의 경우 모달 테스트의 대체안으로써 질량행렬을 알고 있을 때 시스템 파라미터를 구하는 방법을 제시한 바 있다⁽²⁾.

전자식 쉐이커를 활용한 진동 내구 연구는 다음과 같다. 시스템의 내구성을 평가하기 위한 연구로 입력 가진과 시험을 통해 얻은 시스템의 동특성을 이용하여 진동 피로 수명을 계산하는 연구가 수행되었다⁽³⁾. 또한 입력 가진을 랜덤, 조화, SOR (sine-on-random) 조건으로 수행하여 계측한 가속도 데이터를 활용하여 피로 손상도를 구하는 연구가 수행되었다⁽⁴⁾. 진동 시험을 통해 얻어진 모달 파라미터는 해석 검증에 사용되거나 해석 모델을 개선하는 데에 사용되는데, 랜덤 진동으로 모드 시험을 수행하여 유한요소모델을 개선하거나⁽⁵⁾, 해석 모델을 검증하고 이를 기반으로 내구성 평가에 활용되고 있다⁽⁶⁾. 시스템이 손상을 받을 때 모달 파라미터의 변화를 기반으로 하여 손상을 식별하는 연구도 진행되었다. 일반적으로 손상을 받게 되면 강성이 감소하여 고유진동수가 낮아지고 모드 형상이 변화한다고 알려져 있다. 이를 바탕으로 손상이 있는 외팔보의 고유진동수와 강성계수를 사용하여 손상을 검출하는 방법이 제시되었다⁽⁷⁾. 또한 감쇠를 고려하여 손상된 강성을 예측하는 방법을 제안하여 손상을 예측할 수 있는 방법 등이 연구되었다⁽⁸⁾.

이 연구에서는 가속도 시험을 통해 얻은 데이터를 바탕으로 시편의 전달함수를 서클 피팅하고 모달 파라미터를 추출하는 방법을 제시한다. 또한, 가진시험 동안 모달 파라미터의 변화를 가시화 함으로써 시편에 파단이 발생하는 과정에서 모달 파라미터의 변화를 기술 하고자 한다. Modal identification 방법 중 서클 피팅은 해머를 사용하여 획득한 모빌리티 전달함수가 완전한 원 형태를 가지는 특성을 사용하여 시스템의 특성치들을 추정하는 방법이다. 하지만 가진기를 이용한 시험의 경우 시험 방법의 특성상 모달 서클이 완벽한 원의 형태를 이룰 수 없는 문제가 수반되는데, 이 연구에서 이를 보완한 방법론을 제시하고자 한다. 우선, 다자유도계 바닥 가진 운동방정식에서 시험기 강체 운동의 기하벡터를 모드 좌표계로 변환하여 직교화를 수행하였다. 이후 바닥 가진 전달률의 실수부와 허수부를 특정 조건에서 원의 방정식 형태로 변환하여 서클 피팅 하였다. 시험체는 볼팅으로 인한 마찰감쇠가 포함된 브라켓 구조를 사용하였다.

2. 바닥 가진 서클 피팅 이론 및 실험

2.1 1자유도 바닥 가진 서클 피팅

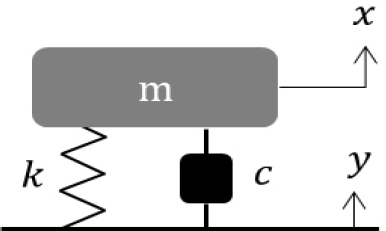
진동 시험 시 바닥 가진으로 입력될 때 1자유도 운동 방정식은 식 (1)과 같다. m은 질량, c는 점성감쇠계수, k는 강성을 의미하며, 이를 도식화하면 Fig. 1과 같다.

$\[ m\ddot{x}+c\left(\dot{x}-\dot{y}\right)+k\left(x-y\right)=0 \]$

(1)

Fig. 1

1-DOF system

식 (1)에서 x는 시편에서의 변위, y는 기초의 변위를 의미한다. 입력 가진을 정현파로 가정하였을 때 변위는 변위의 진폭과 위상으로 식 (2)와 같이 표현할 수 있다.

$\[ x\left(t\right)=X_0{e}^{i\left(\omega t-\varphi \right)},y\left(t\right)=Y_0{e}^{i\omega t} \]$

(2)

식 (2)에서 X₀은 시편에서의 변위 진폭, Y₀은 기초의 변위 진폭, ϕ는 시편과 기초 변위의 위상차를 의미한다.

진동 내구 시험을 진동테이블을 사용하여 시험하면, 테이블이나 지그에 부착된 센서를 기준으로 시험하기 때문에 힘이 아닌 가속도만을 얻을 수 있다. 이 때문에 바닥 가진이 있는 진동 내구 시험에서 서클 피팅을 적용하기 위해 식 (1)로부터 감쇠와 고유진동수를 추정한다. 식 (1)에 식 (2)를 대입하여 기초의 변위 y(t)에 대한 시편 변위 x(t)의 전달함수를 구하면 식 (3)과 같다. 여기서 r은 진동수비를 의미한다.

$\[ \begin{array}{l}G\left(r\right)=\frac{X_0}{Y_0}{e}^{i\varphi }=\frac{1+i2\xi r}{1-r^2+i2\xi r},\\ r=\omega /{\omega }_n\end{array} \]$

(3)

식 (3)의 실수부와 허수부를 각각 G_R, G₁로 두고 각각을 제곱하여 더하면 식 (4)와 같다.

$\[ G_R^2+G_I^2=\frac{1+{\left(2\xi r\right)}^2}{{\left(1-r^2\right)}^2+{\left(2\xi r\right)}^2} \]$

(4)

식 (4)를 활용하여 원의 형태로 변경하면 식 (5)와 같으며, r ≅ 1일 때 원의 형태를 가지게 된다. 여기서 P는 전달함수의 데이터로 결정되는데, 식 (3)을 사용하여 만들어진 이산 데이터를 서클 피팅하면 P는 0.75이다. 일반적인 모달 서클 식과 달리 이산 데이터에 의해 P가 결정되며, 이는 서클의 반지름에도 영향을 미친다.

$\[ \begin{array}{c}{\left(G_R-P\right)}^2+{\left(G_I+\frac{1}{4\xi r}\right)}^2\\ {=\left(P-1\right)}^2+\frac{1}{16r^2{\xi }^2}\\ +\frac{r^2\left(r^2-1\right)\left(2P-1\right)}{1-r^4+r^2\left(4{\xi }^2-2\right)}\end{array} \]$

(5)

따라서 피팅한 원의 반지름이나 y축 원의 중심으로 감쇠비 ξ를 추정할 수 있다. 이 논문에서는 y축 원의 중심을 사용하여 감쇠비를 추정하였다. 고유진동수의 위치는 주파수 공간 기법을 활용하여 구할 수 있다⁽⁹⁾. 단, 전달함수는 무차원이므로 감쇠비와 고유진동수만 추정이 가능하고 시스템의 모달 강성 k와 모달 질량 m 등은 추정할 수 없다.

2.2 다자유도 직교화 및 서클 피팅

일반적인 다자유도 시스템의 경우 이를 확장하면, 시스템을 식 (6)과 같이 쓸 수 있다. 해석을 위한 방법에서는 상대좌표를 활용하여 우변의 감쇠행렬과 강성행렬을 질량 행렬로 도치시켜 지배방정식을 수정하지만, 가속도 신호를 활용할 경우 상대좌표에서 가속도 신호의 오차가 커질 소지가 있으므로 식 (6)의 형태를 사용한다. 여기서 [M], [C], [K]는 질량, 감쇠, 강성행렬이며, a는 시험기 테이블의 변위, {x}는 시험체의 변위, {y}는 시험기의 운동으로 발생하는 강체 운동을 정의하기 위해 시스템 자유도 중 강체 운동 성분만을 1로 두는 벡터, {q}는 모드좌표계의 응답이다.

$\[ \begin{array}{c}\left[M\right]\left\{\ddot{x}\right\}+\left[C\right]\left\{\dot{x}\right\}+\left[K\right]\left\{x\right\}\\ =\dot{a}\left(t\right)\left[C\right]\left\{y\right\}+a\left(t\right)\left[K\right]\left\{y\right\}\end{array} \]$

(6)

여기서 모드행렬을 [ϕ]라 두고, 시험체의 변위를 {x} = [ϕ]{q}, 강체 운동의 기하벡터를 모드행렬을 활용하여 {y} = [ϕ]{b}로 변환하면 식 (7)과 같이 직교화가 가능하다. 이때 {b}는 모드 좌표에서 강체 운동 {y}를 표현하는 벡터이다.

$\[ \begin{array}{c}\left[m_j\right]\left\{\ddot{q}\right\}+\left[c_j\right]\left\{\dot{q}\right\}+\left[k_j\right]\left\{q\right\}\\ =\dot{a}\left[c_j\right]\left\{b\right\}+a\left[k_j\right]\left\{b\right\}\end{array} \]$

(7)

여기서, [m_j], [c_j], [k_j]는 대각 행렬이다. 식 (7)을 분리된 1자유도 방정식으로 변경하면 j번째 모드의 운동방정식은 식 (8)과 같이 표현된다.

$\[ m_j{\ddot{q}}_j+c_j{\dot{q}}_j+k_j{q}_j=\dot{a}{c}_j{b}_j+a{k}_j{b}_j \]$

(8)

식 (8)에서 q_j의 주파수 응답 Q(ω)을 구하고 모드 벡터 ϕ를 곱해서 {x}를 구하면 전체 시스템의 응답을 구할 수 있다. 이중 {x}의 n번째 성분 x_n의 주파수 응답 X_n(ω)와 바닥하중 a의 주파수 응답 A(ω)의 전달률은 식 (9)와 같이 정의된다. 여기서 ϕ_nj는 [ϕ]의 j차 행, n차 열 성분이다.

$\[ G_n\left(r\right)\begin{array}{l}=\frac{X_n\left(\omega \right)}{A\left(\omega \right)}\\ =\sum _{j=1} {\varphi }_{nj}{b}_j\left(\frac{1+i2{\xi }_j{r}_j}{1-r_j^2+i2{\xi }_j{r}_j}\right)\end{array} \]$

(9)

식 (9)는 식 (3)과 같이 1자유도계의 조합으로 구성되어 있으며, 식 (6)에 ϕ_njb_j이 곱해져 있는 형태로 표기된다. 따라서 ϕ_njb_j를 실수 상수 Z로 두고 식 (3)에 곱해서, 전달 함수의 실수부와 허수부를 G_R, G₁ 원형 식으로 표현하면 식 (10)과 같다.

$\[ \begin{array}{c}{\left(G_R-PZ\right)}^2+{\left(G_I+\frac{Z}{4\xi r}\right)}^2\\ =Z^2{\left(P-1\right)}^2+\frac{Z^2}{16r^2{\xi }^2}\\ +\frac{Z^2{r}^2\left(r^2-1\right)\left(2P-1\right)}{1-r^4+r^2\left(4{\xi }^2-2\right)}\end{array} \]$

(10)

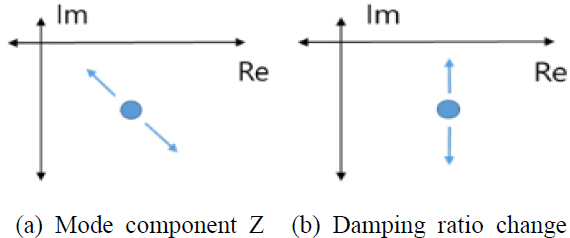
위 식에서 x축 원의 중심 PZ는 모드에 영향을 받고, y축 원의 중심 $$ -\frac{z}{4\xi r}$$는 모드 ϕ_hj와 b_j, 감쇠비 ξ에 의해 영향을 받는다. b_j의 경우 모드에 의해 결정되므로 모드가 비교적 일정한 경우 Z 또한 비교적 일정하다 할 수 있다. 시험 시 모드가 유지되고 감쇠비가 변경되는 경우 Fig. 2(b)와 같이 y축 원 중심의 위치만 변경되며, 모드가 변경될 시 Fig. 2(a)와 같이 원의 중심이 -1의 기울기를 따라 이동할 것이라 추정할 수 있다.

Fig. 2

Two distinct scenarios of the circle’s center shifting

3. 시험 및 분석 결과

3.1 시험 셋업

시편은 석출경화형 스테인레스강 PH15-7Mo 소재의 브라켓 형상으로 제작하였으며 Fig. 3과 같다. PH15-7Mo 소재의 1.6 mm 두께 sheet를 열처리하여 브라켓을 제작하였다. PH15-7Mo 소재는 열처리 방법에 의해 재료의 특성이 달라지는데 해당 시편 제작에는 Condition TH1050을 사용하였다. Condition TH1050은 풀림 상태에서 열을 가해 오스테나이트에서 마르텐자이트 상태로 변화 시키고, 1050 ℉에서 석출경화 열처리를 하는 방법이다. Fig. 3에서 홀이 한 개인 쪽인 A side는 더미 질량과 체결하고 홀이 두 개인 B side는 지그와 체결하였다. 동일한 브라켓 두 개를 한 세트로 시험하였다.

Fig. 3

Specimens before the test

브라켓의 무게는 개당 0.05 kg이고, 스테인리스 스틸로 제작된 더미 질량의 무게는 2.5 kg이다. 알루미늄으로 제작된 지그는 9 kg으로 시험 대상의 무게는 총 11.6 kg이다. x축 방향으로 단축 진동 시험을 진행할 수 있도록 지그의 방향을 고정시켰다. 가진 방향은 랜덤 진동 해석과 모달 해석을 통해 응력과 모드 형상을 고려하여 시험을 가속화하기 위해 x축으로 가진하였다. 시험 시 가진의 제어는 지그 바닥부에 부착한 가속도 센서를 사용하였다. 시편의 응답은 왼쪽 브라켓에서 가까운 쪽의 더미 질량 상단에 가속도 센서를 부착하여 확인하였다. 가속도 센서의 위치는 Fig. 4와 같다.

Fig. 4

Test set-up

랜덤 진동 시험의 입력 가진은 PSD (power spectral density)로 표현된다. 주어진 주파수 영역에서 PSD는 측정 대역폭으로 나눈 가속도 값의 제곱 평균 값으로 G²/Hz의 단위를 가진다. 랜덤 진동 시험의 입력 프로파일은 MIL-STD-810G를 참고하였다. 소요 시간을 고려하여 21.48 Grms로 15 Hz ~ 2000 Hz의 범위에서 x축 방향으로 가진하였다. Grms 단위는 중력 가속도의 제곱평균제곱근으로 랜덤 진동의 가진 크기를 나타내기 위해 사용한다. 랜덤 진동 시험의 프로파일은 Table 1과 같다.

Table 1

Random vibration test profile

3.2 시험 결과

시험은 육안으로 파단이 확인될 때까지 수행하였다. Table 1의 입력 가진으로 동일한 시험을 3회 수행하였으며, 각 시험 소요시간은 38분, 49분, 36분이다. Fig. 5와 같이 파단이 발생한 위치는 A side에서 가까운 굽힘부이며, 시험마다 양쪽에 설치된 브라켓 중 하나가 파단되면 시험을 중단하였다. 시편 체결 시, 볼트에 일정한 토크를 주어 시험 전후로 볼트 풀림이 없는 것을 확인하며 시험하였다.

Fig. 5

Specimens (right brackets) after random vibration test

3.3 분석 결과

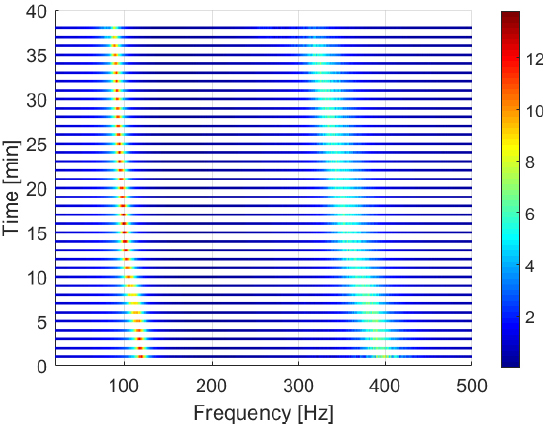
시험 중 동특성 변화를 확인하기 위해 가속도계로 계측한 데이터를 Fig. 6과 같이 1분 단위의 전달함수로 분석하였다. 그래프의 색상은 전달함수 응답의 크기로 G/G 단위를 가진다. 1차 고유진동수는 120 Hz, 2차 고유진동수는 400 Hz 부근에서 시작하여 감소하는 것을 확인할 수 있다.

Fig. 6

Transfer function in random # 1

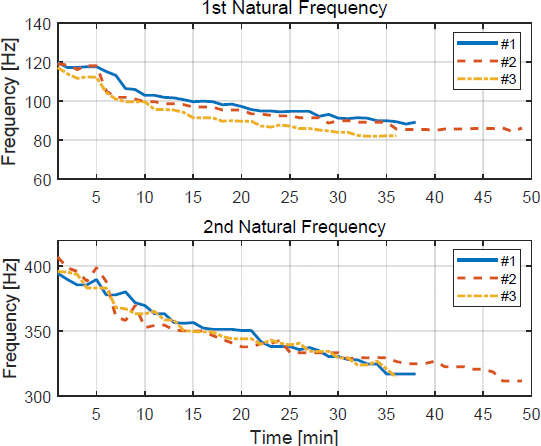
Fig. 7은 Fig. 6에서의 첫 번째 피크값이며 시스템의 고유진동수 변화를 나타낸다. 전달함수의 첫 번째 피크를 1차 고유진동수로 두고 변화를 추적하였을 때, 시험 전후의 고유진동수는 25.47 %, 27.67 %, 29.85 %로 25 % 이상이 감소하였다. 시험 시작 후 10분 이내에 1차 고유진동수가 급격히 감소하는 것을 확인할 수 있었는데, 이는 전체 감소량의 54.92 %, 59.09 %, 50 %로 시험 시작 후 10분 동안 전체 감소량의 50 % 이상이 감소한 것이다. 1차 고유진동수와 비교하였을 때 2차 고유진동수의 시험 전후 감소량이 더 크다.

Fig. 7

Changes of natural frequencies (1st, 2nd)

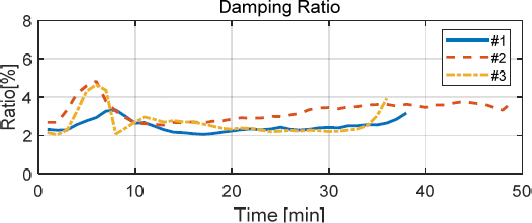
1차 고유진동수에서 서클 피팅을 통해 추정한 감쇠비는 Fig. 8과 같다. 감쇠비는 시험 초반에 값이 증가하나 시험 전후로 보았을 때 대략 3 %를 유지하였다. 파단 직전 감쇠비가 증가하는 것이 확인되었다.

Fig. 8

Damping ratio estimated by circle fitting method

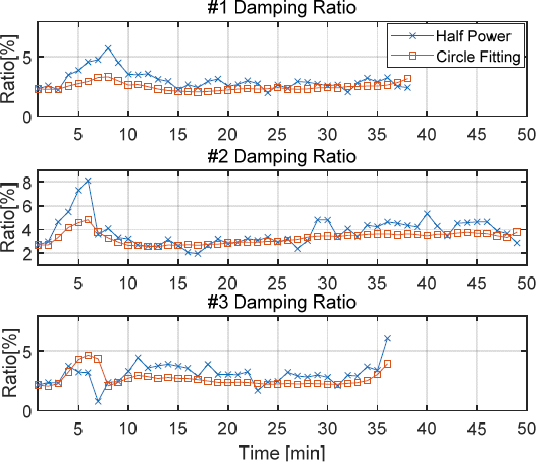
서클 피팅을 통해 추정한 감쇠비는 하프 파워 방법으로 추정한 감쇠를 초기값으로 참고하여 값을 계산하였다. 하프 파워의 경우 전달함수에서 피크점을 찾아 해당 주파수를 고유진동수로 두고, 고유진동수에서의 응답을 $$ \sqrt{2}$$로 나눈 값을 가지는 두 점의 주파수를 찾아서 감쇠비를 추정하는 방법이다. 하프 파워 방법의 경우 노이즈의 영향을 크게 받아 서클 피팅 방법과 비교하였을 때 감쇠비의 추정값에 변동성이 비교적 큰 것을 Fig. 9에서 확인할 수 있다.

Fig. 9

Comparison between half power method and circle fitting method in estimating damping ratio

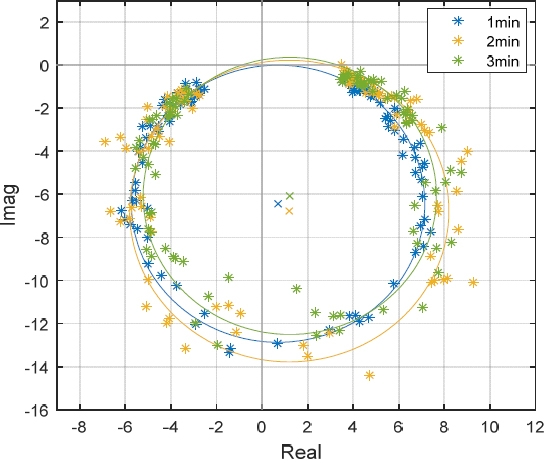
식 (5)에서 r ≅ 1일 때 원의 형태를 가지게 되므로, r값이 0.9에서 1.1 사이의 데이터를 바탕으로 구한 전달함수를 서클 피팅 하면 Fig. 10과 같다.

Fig. 10

Circle fitting method

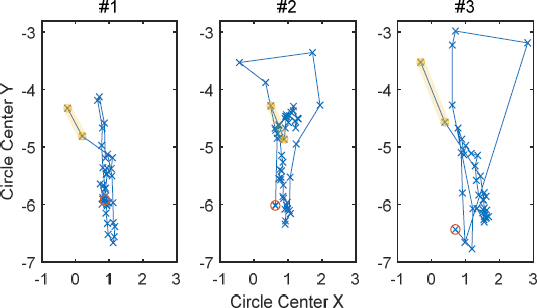
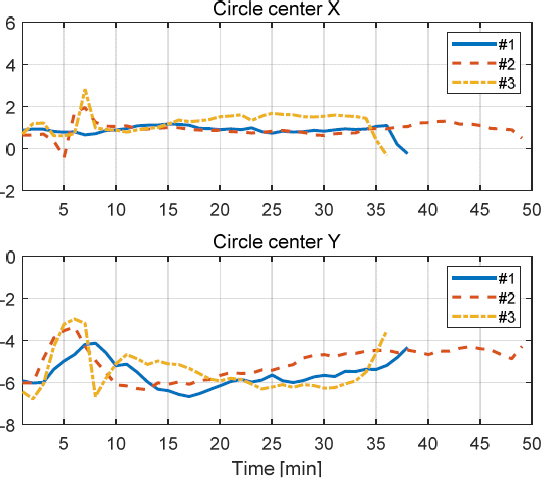
서클 피팅 방법에서 원의 중심은 시스템 특성인 고유진동수, 감쇠, 모드에 의해 결정된다. 시험 중 원의 중심의 이동은 Fig. 11, Fig. 12와 같다. Fig. 2에서 모드가 변화할 때는 (a)와 같이 중심이 이동하고, 감쇠가 변화할 때는 (b)와 같이 y축 원의 중심만 이동하는 방향으로 변화하는 것을 식을 통해 확인하였다. Fig. 11에서 원의 중심은 원으로 마킹된 점에서 시작하여 하이라이트된 값에서 종료된다. Fig. 11에서 나타나는 시험에서 원의 중심은 대체적으로 Fig. 2(b)와 같은 움직임이 나타나는 것을 통해 모드가 일정하고 감쇠가 변화하는 것을 추정할 수 있다. 시험이 종료되기 전 Fig. 2(a)와 같은 움직임이 나타나는 것으로 보아 파단으로 인한 모드의 변화가 반영되는 것을 알 수 있다. 초반 10분 동안 원의 중심이 크게 이동하는 것을 통해 시스템 특성의 변화를 추정할 수 있고 이때 감쇠, 고유진동수가 변화하며 원의 중심 이동이 x축으로 일어나는 것을 보면 모드 또한 변화하는 양상을 추정할 수 있다.

Fig. 11

Location changes of circle center in circle fitting

Fig. 12

Changes of circle center (X-Y) in circle fitting

4. 결 론

이 논문에서는 랜덤 진동 실험을 통해 얻은 전달 함수를 서클 피팅 방법으로 감쇠비를 산출하고, 서클 피팅 중심 점의 변화를 바탕으로 모달 파라미터 값의 변화 추이를 분석하였다. 랜덤 시험 시 발생하는 노이즈의 영향을 극복하기 위해 가속도 센서만을 사용하고, 완벽한 원으로 표현되지 않는 전달률 식을 근사화 하여 r이 1에 가까운 데이터만으로 서클 피팅하는 방법을 제시하였다. 또한 유도된 식을 통해 원의 중심이 계측점의 모드 벡터 성분과 감쇠비 변화에 따라 이동하는 양상이 다름을 확인하였다. 진동 내구 시험 과정에서 원의 중심 이동 양상을 통해 다음과 같은 결과를 확인하였다. 첫번째, 시험 중 감쇠 변화의 영향으로 원 중심이 위아래로 이동하였다. 두번째, 파단 직전에 감쇠비가 소폭 증가하였다. 세번째, 파단이 발생한 후에는 모드가 변화한다. 시험 초반에 원의 중심이 불규칙하게 이동하는 양상은 볼팅에 의한 마찰 조건이 진동내구 시험 진행 도중 변화함에 따라 모드와 감쇠에 영향을 주어 발생하는 것이라 추정된다. 향후 카메라를 활용한 계측이나 마찰부의 조도, 압축력 변화 등을 통해 마찰 조건 변화를 확인 가능하다 판단된다.

이와 같은 결과는 진동 내구 시험에서 가속도 센서만을 사용하여 볼트로 고정된 시험 대상의 동적 특성의 변화를 추정하고, 결함이 없는 상태에서 파단에 이르기까지의 감쇠비와 모드 벡터의 비선형적인 특성을 보여준다.

Acknowledgments

이 연구는 2022년도 산업통상자원부 및 한국산업기술평가관리원(KEIT)의 연구비 지원(20019096)과 2023년 한국기계연구원 기본사업(NK224C) 지원으로 수행하였음.

References

• Béliveau, J.-G., Vigneron, F. R., Soucy, Y. and Draisey, S., 1986, Modal Parameter Estimation from Base Excitation, Journal of Sound and Vibration, Vol. 107, No. 3, pp. 435~449. [https://doi.org/10.1016/S0022-460X(86)80117-1]
• Link, M. and Vollan, A., 1978, Identification of Structural System Parameters from Dynamic Response Data, Zeitschrift fuer Flugwissenschaften und Weltraumforschung, Vol. 2, pp. 165~174.
• Kim, C.-J., Bae, C.-H. and Lee, B.-H., 2006, Verification on Damage Calculating Method of Vibration Fatigue Using Uni-axial Vibration Test, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 16, No. 5, pp. 521~528. [https://doi.org/10.5050/KSNVN.2006.16.5.521]
• Kim, C.-J., 2015, Damage Count Method Using Acceleration Response for Vibration Test Over Multi-spectral Loading Pattern, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 25, No. 11, pp. 739~746. [https://doi.org/10.5050/KSNVE.2015.25.11.739]
• Kim, S., 2012, Modal Test and Finite Element Model Update of Aircraft with High Aspect Ratio Wings, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 22, No. 5, pp. 480~488. [https://doi.org/10.5050/KSNVE.2012.22.5.480]
• Ryu, J. and Yang, W., 2022, Durability Analysis for Vibration Characteristics of EGR System Considering Fluid-structure Interaction, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 32, No. 6, pp. 552~559. [https://doi.org/10.5050/KSNVE.2022.32.6.552]
• Son, I.-S., Ahn, S.-J. and Yoon, H.-I., 2009, Study on Detection of Crack and Damage for Cantilever Beams Using Vibration Characteristics, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 19, No. 9, pp. 935~942. [https://doi.org/10.5050/KSNVN.2009.19.9.935]
• Lee, J. Y., 2012, Prediction of the Damage in the Structure with Damping Using the Modified Dynamic Characteristics, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 22, No. 11, pp. 1144~1151. [https://doi.org/10.5050/KSNVE.2012.22.11.1144]
• Klosterman, A. L., 1971, On the Experimental Determination and Use of Modal Representations of Dynamic Characteristics, Doctoral Dissertation, University of Cincinnati, Cincinnati, OH.