원구형 관절을 갖는 ER 햅틱 인터페이스의 2자유도 힘반향 제어
© The Korean Society for Noise and Vibration Engineering
Abstract
This paper presents the design and control of a haptic interface using a smart fluid. Recently, there has been active research on interfaces incorporating the third human sense, i.e., the sense of touch, into master-slave systems. Therefore, to realize 2-DOF haptic reflections in the master, this study develops a smart haptic interface featuring active force feedback using a spherical joint, which mimics biological articulation by employing smart materials such as electrorheological fluids. The proposed haptic system is designed and manufactured through torque modeling, which is then validated through a comparison with the generated torque levels of the manufactured interface. The main control challenge is to control the field to achieve the desired force. A sliding mode controller is designed to address this issue by considering hysteresis as the uncertainty. To demonstrate the effectiveness of the proposed haptic control algorithm, its tracking control performance is evaluated via experiments.
Keywords:
Master-slave System, Haptic Interface, Electrorheological Fluid, Spherical Joint, 2-DOF Motion, Force-reflecting Control키워드:
마스터-슬레이브 시스템, 햅틱 인터페이스, ER 유체, 원구형 조인트, 2자유도 운동, 힘반향 제어1. 서 론
최근 로봇 기술 분야에서는 원격통신과 암호화 기술을 접목함으로써 원격지의 슬레이브 로봇을 근거리 또는 원거리에서 마스터 장치로 조작하는 마스터-슬레이브 원격조작 기술이 발달하고 있다. 여기에서 사용자는 마스터 장치를 직접적으로 조종하게 되며 그 동작에 기초하여 슬레이브 장치는 원격으로 제어될 수 있다. 예를 들어, 마스터-슬레이브 장치는 미세한 작업을 요구하는 수술 현장, 무인드론을 활용하는 전장 환경, 원자로 혹은 우주공간과 같은 극한환경에 주로 사용된다(1).
이러한 원격 조작을 위한 장치를 구동하기 위해서는 인간의 감각 기관을 통한 인간과 기계 시스템 간의 커뮤니케이션이 무엇보다 중요하게 강조된다. 따라서 이러한 인간의 감각에 정보를 전달하기 위해 다양한 기계 시스템들이 개발되어왔다. 오감 중에서 현재 인간과 기계 시스템간의 인터페이스 역할을 하는 대표적인 감각으로는 사물을 보는 시각과 소리를 듣는 청각이 이용되고 있다. 하지만 시각과 청각 인터페이스 만으로는 근거리 혹은 원거리 원격지 로봇의 제어에는 한계가 있다. 따라서 최근 촉각 인터페이스에 대한 연구가 활발히 진행되고 있다(1,2).
일반적으로 햅틱은 사용자에게 피부압력, 근골격력, 진동 등의 촉감을 제공하는 기술이며, 이러한 햅틱 기술은 촉감을 통해 정보를 전달함으로써 시각 및 청각 정보에 대한 집중을 유지하면서도 추가적인 정보를 받아들이기 쉽고, 나아가 더 직관적이고 명료하게 기기를 조작할 수 있도록 한다. 현재 햅틱 기술은 웨어러블 장치와 접목되면서 가전, 자동차, 의료, 군사 등 다양한 분야로의 적용이 가속화되고 있다. 하지만 인간의 감각 중에서 촉각은 매우 민감한 감각으로 여기에 정보를 전달하는 인터페이스는 아직 많은 연구를 필요로 하고 있다(3,4).
지능유체, 압전재료, 형상기억합금 등으로 대표되는 지능재료는 우수한 설계 유연성과 제어 용이성 등으로 인해 최근 차량이나 구조물의 진동제어 뿐만 아니라 힘 또는 위치 추적을 위한 다양한 메카트로닉스 시스템의 작동기로서 응용되고 있다(5,6). 일반적으로 마스터-슬레이브 장치에서 운동의 전달과 힘 반향을 위해 가장 널리 사용되는 것은 전기모터이지만 낮은 정밀도와 높은 관성은 작은 힘의 정밀제어에는 큰 단점으로 작용하고 있다. 이를 극복하기 위해 최근 압전재료와 같은 지능재료를 이용한 햅틱 작동기가 활발히 진행되고 있으며, 실제 관절과 유사한 구조를 갖도록 설계할 수 있는 지능유체를 활용한 햅틱 인터페이스에 대한 관심도 점점 커지고 있다(7~10).
따라서 이 연구에서는 다자유도 능동 힘 반향이 가능한 관절형 햅틱 마스터를 제안하였다. 이를 위해 원구형(spherical type) 클러치 메커니즘을 고안하고, 반향력을 조절하기 위한 지능유체를 도입하였다. 그리고 제안된 원구형 관절 메커니즘을 마스터 장치에 적용하여 2자유도 운동 및 힘반향이 가능한 햅틱 마스터 장치를 구성하고 시스템의 토크 모델링으로부터 주요 설계변수의 영향을 검토하고 설계를 수행하였다. 마지막으로 제안된 햅틱 마스터 시스템을 실제 제작하였으며, ER유체의 히스테리시스를 불확실성으로 간주한 슬라이딩모드 제어알고리즘을 적용하였으며, 햅틱 힘반향 제어를 통해 제안된 시스템의 유효성을 실험적으로 검증하였다.
2. ER 햅틱 마스터
대표적인 지능유체의 하나인 ER(electrorheological) 유체는 전기유변유체로서 전기장이 인가에 반응하여 그 유변학적 거동이 변화하는 물질이며, 분극화가 가능한 마이크로 크기의 전도성 입자들이 비전도성 용매에 분산되어 있는 현탁액이다. Fig. 1과 같이 용매에 분산되어 자유롭게 운동하던 입자들이 전기장 부하 시에 체인 형상의 구조를 형성함으로써 마치 고체와 같이 항복응력을 갖는 빙햄(bingham) 유체의 거동을 나타내게 된다. 이는 일반적으로 빙햄모델로 표현되며 수학적으로 나타내면 식 (1)과 같다(10).
| (1) |
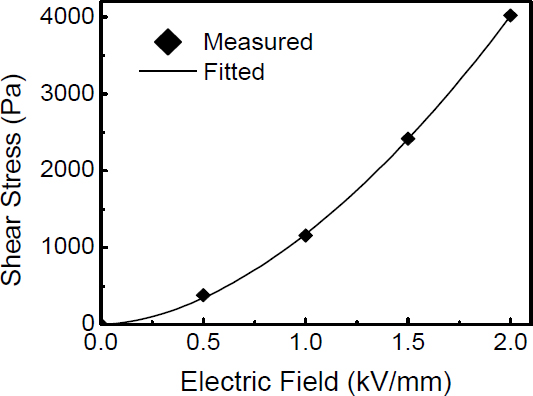
여기서, η는 유체의 점성계수, 은 유체의 전단속도비, E는 부하되는 전기장을 나타낸다. 이 때 항복응력은 전기장에 따라 지수적으로 증가한다. 그리고 a와 b값은 유체의 고유 특성치이다. 이 값은 용매의 종류와 용매 점도, 입자 종류, 입자 중량비, 입자에 함유된 수분량, 등 다양한 변수에 의해 영향을 받는다. 이 연구에서 이러한 빙햄 특성은 실험을 통해 측정되었다. 이 연구에서는 BaTi2계 ER 유체를 적용하였으며, 입자체적비는 50 %이다. Fig. 2는 토크 측정결과로부터 도출한 빙햄 특성치를 나타낸 것이다. 약 2 kV/mm 인가 시 최대 약 4 kPa의 항복전단응력이 발생하며, 측정된 항복응력은 1188E1.8 Pa, 점성계수는 0.53 Pa·s이다.
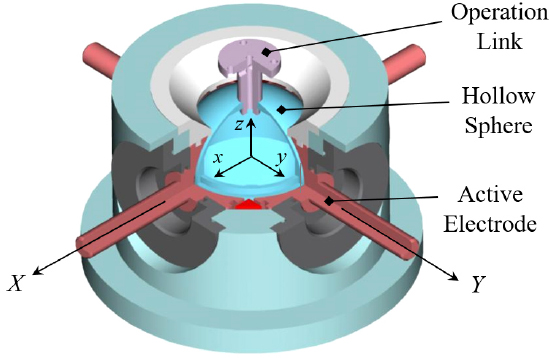
이 연구에서는 능동 힘 구현을 가능토록 하기 위해서 클러치를 응용한 능동 조인트를 제안하였으며, 이를 원구형 조인트와 연계하여 다자유도 힘 구현을 가능토록 하였다. Fig. 3은 제안된 원구형 마스터 장치를 나타낸 것이다. 도시된 바와 같이 제안된 시스템은 회전운동이 가능한 원구형 조인트로서, 고정되어 있는 외측 원구 내에 자유로이 운동할 수 있는 내측 원구가 있고, 외측 및 내측 원구 사이에는 ER 유체가 채워져 있다. 제안된 시스템의 능동 힘 구현부는 2축 회전운동이 가능한 원구형 조인트를 가운데에 두고 있으며, 양방향(bi-directional) 클러치 시스템을 구축하기 위해 일반 AC모터에 의해 양쪽에서 반대 방향으로 구동되는 2개의 1/4반구형 능동전극으로 구성된다. 따라서 양방향 클러치에서 전기장의 인가 방향에 따라 정/역의 힘을 구현한다. 이러한 양방향 클러치 2세트를 x축과 y축 각각에 설치함으로써 2자유도의 힘 반향을 실현할 수 있다.
제안된 ER 햅틱마스터는 원구형 조인트에 능동형 클러치 메커니즘을 이용한 전극을 추가하여 구성되었다. 이러한 ER 능동조인트의 전달 토크는 식 (2)와 같이 전기장에 의해 조절이 가능한 제어토크 Tc와 유체점성에 의해 발생하는 점성토크 Tη, 그리고 시스템 구성요소 사이의 마찰에 의해 발생하는 마찰토크 Tf의 합으로 구성된다.
| (2) |
먼저 항복응력에서 기인하는 Tc는 구면 좌표계를 도입하여 구면상의 미소면적에 대해 계산할 수 있다. 먼저 구면상의 한 점 p는 식 (3)과 같이 구면좌표계에서 나타낼 수 있다.
| (3) |
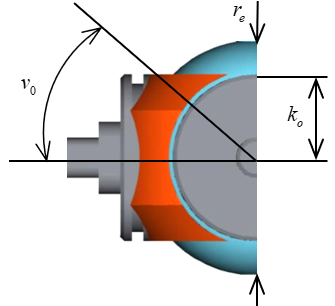
여기서, u와 v는 구면좌표계의 방위각과 편각을 나타내며, re는 전극의 유효반경이다. 따라서 Tc는 식 (4)와 같이 구할 수 있다.
| (4) |
여기서 v0는 능동전극의 반경을 나타내는 각이며, rc는 토크를 발생시키는 축의 회전반경을 의미한다. 또한 항복전단응력 τy는 전기장 E의 함수이며, 첨자 cw와 ccw는 각각 시계방향 및 반시계 방향을 의미한다. ER 유체의 점성에 기인하는 Tη는 정/역 방향으로 구동 모터에 의해 ω의 속력으로 회전하고 있는 능동전극과 의 회전각속도를 가지는 내측원구에 대해 식 (5)와 같이 정리할 수 있다.
| (5) |
마지막으로 마찰 토크를 고려하면 제안된 시스템에서 발생하는 전체 토크는 식 (6)과 같이 수학적으로 표현될 수 있다.
| (6) |
식 (6)의 토크 모델에서 나타낸 바와 같이 ER 클러치 전극의 유효 반경(re), 외측 능동전극의 최대반경을 나타내는 각(v0)와 전극간극(h) 등의 설계변수를 갖고 있고, 주요 변수값들은 Table 1에 나타내었다. 이 때 ER 유체의 최대항복응력의 값은 4.02 kPa이며, 점성계수는 0.53 Pa·s이다. 또한, 설정된 모터의 회전속도는 최대 1.5 rad/s이며, 내측원구의 회전각속도 은 축간의 간섭을 방지하기 위해 0 rad/s로 설정하였다. 따라서 식 (6)은 식 (7)과 같이 나타낼 수 있다.
| (7) |
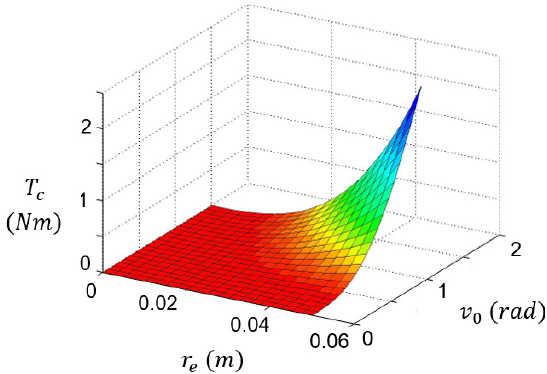
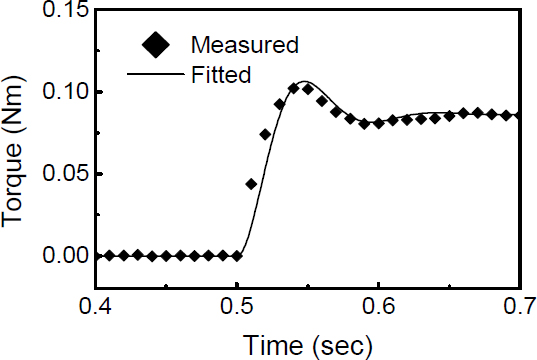
Fig. 4는 식 (7)의 토크모델에 기반하여 설계변수에 따른 제어토크 Tc의 변화를 나타낸 것이며, 발생 토크의 크기에 미치는 각 설계변수의 영향을 고찰하였다. 먼저, 전극 간극 h를 1 mm로 가정한 상태에서 설계 변수인 re와 v0값을 변화시켰다. re는 실제 제작을 감안하여 0 cm에서 5 cm까지, ER 장치에서 능동전극의 크기를 나타내는 각도 v0는 0 rad에서 1.5 rad까지 변화시켰다. 결과에 나타난 바와 같이 re와 v0에 따라 토크가 처음에는 서서히 증가하다가 차츰 증가 폭이 커지고 있음을 알 수 있다. 따라서 효율적인 토크 생성을 위한 전극의 설계를 위해서는 v0는 2.5 cm, re는 0.5 rad 이상의 값을 필요로 한다. 하지만 각 축에 위치한 능동전극의 상호 간섭으로 인해 v0는 1.57 rad의 공간적인 한계를 갖게되며 실제 제작을 위한 구조물을 고려하면 그 한계는 0.78 rad에 이르게 된다. 따라서 최종 결정된 설계변수는 0.72 rad, 유효반경은 3 cm이며, 모델로부터 예상되는 설계토크는 0.076 Nm이다. Fig. 5는 실제 제작된 ER 마스터 장치의 사진이며, Fig. 6은 마스터로부터 측정된 토크를 도시한 것이다. 측정된 토크는 X 방향의 능동 토크이며, 최대 0.079 Nm의 토크가 발생하였다. 이상의 실험 결과로부터 제작된 조인트에서 실제 발생하는 토크가 모델링 결과와 잘 일치하고 있음을 알 수 있다.
3. 힘 반향 제어
이 연구에서는 햅틱 마스터에 존재하는 히스테리시스 비선형성과 마찰 등에 의한 영향을 불확실성으로 간주하고 슬라이딩모드 제어기법을 도입하였다. 전술한 Fig. 6의 측정 결과에서 보는 바와 같이 ER 조인트는 2차의 동적거동을 보여주고 있으며, 이는 ER 유체의 빠른 응답속도와 형성된 체인의 탄성효과 등에 기인하는 것이다. 따라서 전기장 인가에 따라 발생하는 토크를 식 (8)과 같이 2차의 동적 모델로 표현할 수 있다.
| (8) |
여기서 E는 전기장, ωn은 고유진동수, ζ는 감쇠계수이며, Ks는 식 (7)로부터 결정되는 입력 전기장과 출력토크간의 관계를 나타내는 영향계수로서 0.000 019의 값은 갖는다. 또한 Fig. 6의 동적 응답으로부터 감쇠계수 ζ=0.42와 고유진동수 ωn=73 rad/s를 얻을 수 있다.
Fig. 3에서 오퍼레이션링크가 연결된 내측원구가 고정되어 있고, 두쌍의 양방향 클러치에 의해 발생하는 토크는 각각 고정좌표축 X, Y에 대한 각운동 방향으로 발생한다. 따라서, 능동 햅틱 마스터의 동적지배방정식은 식 (9)와 같다.
| (9) |
이 때 제어입력의 방향이 일반화힘의 방향과 일치하지 않는다. 따라서 고정좌표계와 회전좌표계 회전운동 사이의 오일러각 관계와 가상일정리로부터 외측클러치 고정좌표 X, Y에서의 토크입력과 내측원구 이동좌표 x, y에서의 일반화힘 출력의 관계를 식 (10)과 같이 정의할 수 있다.
| (10) |
여기서 내측 원구의 회전은 요(yaw) θ3와 피치(pitch) θ2회전을 한다. 햅틱마스터의 지배방정식을 오퍼레이터에게 전달되는 힘에 대해 다시 표현하면 식 (11)과 같이 나타낼 수 있다.
| (11) |
여기서 L은 오퍼레이션 링크의 길이, 영향계수 Ii는 식 (12)와 같이 나타낼 수 있다.
| (12) |
이 연구에서 제어하고자 하는 것은 마스터의 내부 전극에 연결된 오퍼레이션 링크에서 오퍼레이터에게 전달되는 힘이 요구궤적을 추종하도록 하는 것이다. 하지만 이미 전술한 바와 같이 제안된 시스템은 마찰 뿐 만 아니라 ER 유체의 히스테리시스와 같은 비선형성을 갖고 있다. 따라서 이러한 비선형적인 요소를 불확실성으로 고려한 강건한 제어기법을 필요로 한다. 먼저 제안된 시스템에서 나타나는 불확실성은 식 (13)과 같이 영향계수의 변화로 표현할 수 있다.
| (13) |
여기서, I0는 공칭 영향계수이고, δIi는 변수 변화이며 제어기 설계를 용이하게 하기 위해 다시 가중함수(ai)를 이용하여 나타낼 수 있다.
이 연구에서 도입된 슬라이딩모드 제어기는 외란 및 변수변화에 강건한 제어기이며, 이를 설계하기 위해서 먼저 안정한 슬라이딩 평면을 식 (14)와 같이 정의하여야 한다.
| (14) |
여기서 식 (15)는,
| (15) |
이 때 슬라이딩모드가 발생하기 위해서는 식 (16)과 같은 슬라이딩모드 존재조건을 만족하여야 한다.
| (16) |
따라서 제어기는 식 (17)과 같이 표현할 수 있다.
| (17) |
여기서, Ki는 불연속 제어 게인이다. 도출된 제어기의 실제 적용에 있어서 불연속 제어 입력은 채터링 등을 유발하므로, 포화함수를 이용한 연속적인 입력으로 근사화 할 수 있다. 식 (17)에 의해 제어입력이 결정되면 이는 각 양방향 클러치 작동기에 의해 구현된다. 이때 인가되는 전기장은 식 (18)과 같이 오일러 관계를 고려하여 결정할 수 있다.
| (18) |
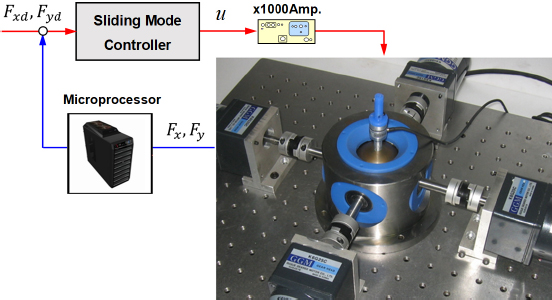
Fig. 7은 햅틱 마스터 인터페이스의 힘 반향 실험장치 구성을 나타낸 것이다. 능동전극을 이루는 클러치를 15 r/min으로 구동하기 위해 120:1 기어비를 갖는 4개의 AC 모터가 장착되어 있고, 컴퓨터에서 계산된 제어입력은 고전압 증폭기를 통해 각 전극에 인가되도록 하였다. 그리고 조인트에서 발생하는 반력은 ATI사의 6축 힘센서(Nano25)를 이용하여 측정하였다.
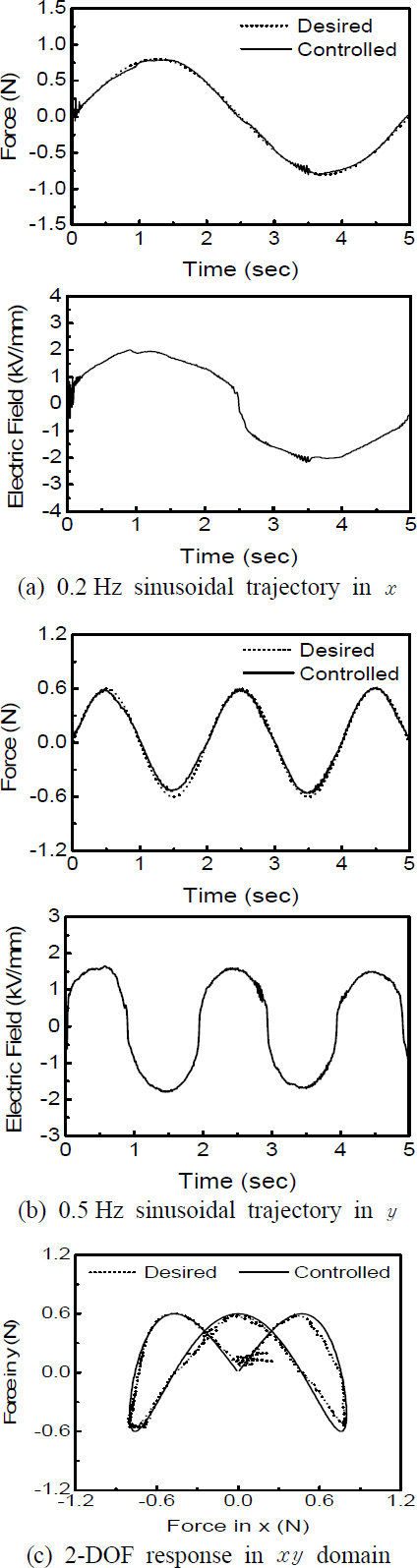
Fig. 8은 능동 힘반향에 대한 슬라이딩 모드 제어결과로서 사인파형의 궤적에 대한 2자유도 힘반향 추종성능을 나타낸 것이다. 이때 슬라이딩 평면의 기울기는 38이며, 불연속 이득은 4800이다. 이때 x 방향의 요구 궤적의 주파수는 0.2 Hz, 진폭은 0.8 N이며, y 방향의 요구 궤적의 주파수는 0.5 Hz, 진폭은 0.6 N이며, 오퍼레이션 링크는 임의의 지점에 고정되어 있다. Fig. 8(a)와 Fig. 8(b)의 결과로부터 제어기가 요구궤적을 매우 잘 추종하고 있음을 알 수 있으며, 최대 추종오차는 약 0.05 N이다. 또한 해당 제어입력으로 부터 적절한 크기의 전기장이 인가되고 있음을 알 수 있다. 하지만 그 크기가 시뮬레이션으로 예측된 값이 비해 다소 크게 나타나고 있는데 이는 히스테리시스와 마찰 등에 의한 불확실성의 영향인 것으로 판단된다. 마지막으로 Fig. 8(c)는 2자유도 힘반향 결과를 xy 영역에서 표현한 것이다. 제어 결과에 나타난 바와 같이 제안된 제어기가 큰 오차 없이 요구궤적을 매우 잘 추종하고 있으며, 오일러 관계식에 따라 각 회전방향에 대해 적절한 전기장이 인가되고 있다. 이로부터 제안된 시스템이 실제 환경에서도 우수한 힘반향 환경을 제공할 수 있음을 확인할 수 있다.
4. 결 론
이 연구에서는 원격지의 슬레이브 장치를 제어하는 마스터 장치에서 햅틱 힘 반향을 구현하기 위해 ER 햅틱마스터를 제안하였다. 특히 근골격적인 힘 반향을 위해 원구형 관절 메커니즘을 제안하고 지능유체인 ER유체를 클러치 형태로 적용하여 능동 힘 반향이 가능하도록 구성하였다. 수학적인 토크 모델에 기반으로 제어토크를 최적화함으로써 마스터 장치를 설계 및 제작하였고, 실험적으로 토크를 측정하여 모델의 타당성을 입증하였다. 또한 실험적으로 고찰된 시스템의 동적특성을 기반으로 동적 모델을 구축하고 슬라이딩모드 제어 기법을 적용하여 0.2 Hz에서 0.5 Hz에 이르는 사인파형의 요구궤적에 대해 안정적인 추종성능을 확인하였다. 이로부터 제안된 햅틱 인터페이스 시스템의 2자유도 힘 반향을 실험적으로 고찰하여 우수한 제어성능을 입증하였다. 이를 바탕으로 향후 오퍼레이션 링크에 연결된 포셉을 실제 조작하는 환경하에서 힘반향 제어를 수행할 예정이다.
References
-
Abovitz, R., 2001, Digital Surgery: The Future of Medicine and Human-robot Symbiotic Interaction, Industrial Robot, Vol. 28, No. 5, pp. 401~406.
[https://doi.org/10.1108/EUM0000000005842]

-
Shazhaev, I., Mihaylov, D. and Shafeeg, A., 2023, A Review of Haptic Technology Applications in Healthcare, Open Journal of Applied Sciences, Vol. 13, No. 2, pp. 163~174.
[https://doi.org/10.4236/ojapps.2023.132013]

- Bar-Cohen, Y., Mavroidis, C., Pfeiffer, C., Culbert, C. and Magruder, D. F., 2000, Automation, Miniature Robotics and Sensors for Nondestructive Testing and Evaluation, The American Society for Nondestructive Testing, Columbus, 10.3, Haptic Interfaces, pp. 461~468.
-
van Wegen, M., Herder, J. L., Adelsberger, R., Pastore-Wapp, M., van Wegen, E. E. H., Bohlhalter, S., Nef, T., Krack, P. and Vanbellingen, T., 2023, An Overview of Wearable Haptic Technologies and Their Performance in Virtual Object Exploration, Sensors, Vol. 23, No. 3, p. 1563.
[https://doi.org/10.3390/s23031563]

-
Choi, S. B., Choi, Y. T. and Park, D. W., 2000, A Sliding Mode Control of a Full-car Electrorheological Suspension System via Hardware-in-the-loop Simulation, Journal of Dynamic Systems, Measurement, and Control, Vol. 122, No. 1, pp. 114~121.
[https://doi.org/10.1115/1.482435]

-
Han, Y.-M and Choi, S.-B., 2018, Performance Investigation of Piezoelectric Ultrasonic Vibrator for Uniform Atomization Application, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 28, No. 6, pp. 752~758.
[https://doi.org/10.5050/KSNVE.2018.28.6.752]

-
Stevens, N. G., Sproston, J. L. and Stanway, R., 1988, An Experimental Study of Electro-rheological Torque Transmission, Journal of Mechanisms, Transmissions, and Automation in Design, Vol. 110, No. 2, pp. 182~188.
[https://doi.org/10.1115/1.3258924]

- Salunkhe, H., Kolekar, A. and Thikane, S., 2023, Electrorheological Fluids: Properties, Technology and Modern Applications, International Research Journal of Engineering and Technology, Vol. 10, No. 2, pp. 129~134.
-
Bullough, W. A., Johnson, A. R., Hosseini-Sianaki, A., Makin, J. and Firoozian, R., 1993, The Electro-rheological Clutch: Design, Performance Characteristics and Operation, Proceedings of the Institution of Mechanical Engineers, pp. 87~95.
[https://doi.org/10.1243/PIME_PROC_1993_207_322_02]

- Han, Y. M., 2005, Design and Control of Haptic Interface Utilizing Smart Materials, Doctoral Dissertation, Inha University, Incheon.

Young-Min Han received the Ph.D. degree in mechanical engineering from Inha University, Incheon, Korea in 2005. Since 2011, he has been a Professor at Ajou Motor College, Chungman, Korea. His current research interest includes design and control of functional mechanisms utilizing smart materials.