고정단 평판의 전 주파수 대역 고유치 추출이 가능한 NDIF법 개발: 제1부(이론 정립 및 검증)
© The Korean Society for Noise and Vibration Engineering
Abstract
In the eigenvalue analysis of clamped plates, the original NDIF method cannot extract low-order eigenvalues and eigenmodes when the number of nodes is increased. Recently, the author developed a practical method to solve this problem for eigenvalue analysis of membranes and acoustic cavities. In the study, the practical method is applied and extended to clamped plates, and the exact solution obtained for a verification example of a clamped circular plate shows that the proposed method can extract all the eigenvalues across the entire frequency range irrespective of the number of nodes. In addition, the eigenvalues obtained using the proposed method are compared with those using the original NDIF method, exact solution, and finite element method (FEM;ANSYS). Evidently, the proposed method, which uses only 30 nodes, provides more accurate results than the FEM, which uses 1835 nodes for extracting eigenvalues and eigenmodes.
Keywords:
Clamped Plate, Spurious Eigenvalue, Eigenvalue, Eigenmode, NDIF Method, Matrix Rank, Finite Element Method, Boundary Element Method키워드:
고정단 평판, 허위 고유치, 고유치, 고유모드, 무차원 동영향 함수법, 행렬 랭크, 유한요소법, 경계요소법1. 서 론
NDIF법(non-dimensional dynamic influence function method 또는 무차원 동영향 함수법)은 저자가 임의 형상 고정단 평판의 고정밀도 자유진동해석을 위해 개발한 고유치 해석 기법이다(1). 저자는 혼합 경계 조건을 가진 임의 형상 평판과 자유단 평판의 고정밀도 고유치 해석을 위한 NDIF법도 성공적으로 개발하였다(2~4). 이후, 저자는 평판의 고유치 해석에 있어서 NDIF법의 해석 효율성과 정확도를 높이기 위한 다양한 연구를 수행하였다(5~8).
NDIF법은 해석 대상 평판의 내부를 요소(element)로 분할하는 유한요소법(FEM)과는(9) 달리 해석 대상 평판의 경계만을 이산화하기 때문에, 이산화 방법의 관점에서는 경계요소법(BEM)과(10) 유사하다고 말할 수 있다. 하지만, 경계요소법과는 달리 NDIF법은 평판의 경계를 요소 없이 노드로만 이산화하기 때문에 노드와 노드 사이에 설정된 보간 함수의 특이치 적분 과정이 필요 없는 특징을 가진다. 이러한 특징 덕분에, NDIF법의 이론이 간결하고 그 해석 결과도 유한요소법 및 경계요소법에 비해 더 정확한 장점을 가진다.
그러나 NDIF법은 평판의 고차 고유치와 고유 모드를 추출하기 위해 노드의 개수를 증가시킬 경우 저주파수 영역에서 시스템 행렬이 발산하여 저차 고유치가 구해지지 않는 단점이 존재한다. 그래서 NDIF법에서는 고차 고유치를 추출할 때, 저차 고유치 추출을 위한 별도의 이산화 과정이 추가로 필요한 비효율성이 존재한다.
이 논문에서는 상기의 비효율성을 제거하기 위한 연구가 수행된다. 임의 형상 멤브레인과 음향 공동에 대해 최근에 수행된 연구에서는(11,12), 노드의 개수를 증가시켰을 때 저주파수 고유치가 구해지지 않는 문제점이 개선된 NDIF법이 성공적으로 개발되었다. 이번 논문에서는 위의 연구 결과를 평판으로 확장하는 시도가 이루어졌다.
이 논문에서는 평판의 시스템 행렬이 노드의 개수와 상관없이 전 주파수 대역에서 정확한 고유치와 고유모드를 제공하는 NDIF법 이론이 성공적으로 개발되었으며, 엄밀해가 존재하는 고정단 원형 평판에 개발된 이론을 적용하여 그 타당성과 정확성이 검증되었다. 참고로, 이 논문의 2부에서는 다양한 형상의 고정단 평판에 대해 개발된 이론을 적용하는 예제 연구가 수행되었다.
2. 평판에 대한 NDIF 법 이론
2.1 고정단 평판 지배방정식 및 경계조건
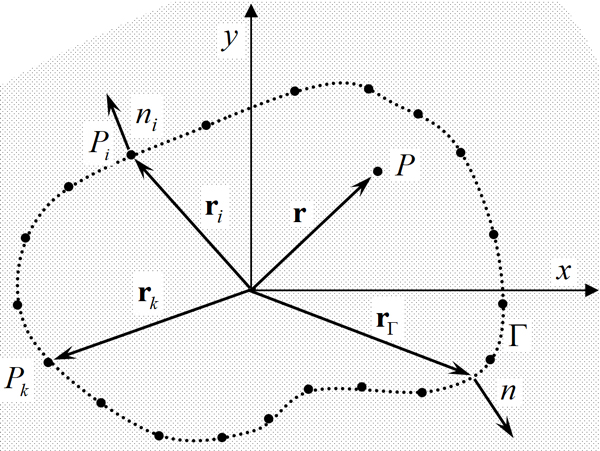
Fig. 1에서 점선으로 표시한 임의 형상 평판의 자유 진동 변위는 식 (1)을 만족한다.
| (1) |
여기서 w(r, t)는 위치 벡터 r의 종점 P에서의 진동 변위, ρs는 평판의 면밀도, D는 평판의 강성으로 식 (2)와 같다.
| (2) |
여기서 E는 평판의 영률(Young’s modulus), h와 v는 각각 평판의 두께와 푸아송 비(Poisson’s ratio)를 의미한다.
평판이 조화 진동한다고 가정하면, 평판 진동 변위는 식 (3)과 같이 나타낼 수 있다.
| (3) |
여기서 W(r)는 평판의 조화 진동 변위, ω는 조화 진동각주파수(angular frequency)를 의미한다. 식 (3)을 식 (1)에 대입하면 자유 진동 지배 방정식 식 (4)를 얻을 수 있다.
| (4) |
여기서 Λ = (ρsω2 / D)1/4는 주파수 파라미터이다.
다음으로, 고정단 평판의 경계 조건은 평판의 경계 Γ에서 평판 변위와 기울기가 0임을 뜻하며, 식 (5)와 식 (6)과 같이 두 개의 식으로 주어진다.
| (5) |
| (6) |
여기서 n은 평판 경계에서의 법선 방향을 의미한다.
2.2 고정단 평판의 자유진동해 가정 및 경계조건 이산화
Fig. 1에서 점선으로 표시된 해석 대상 고정단 평판의 경계는 N개의 노드들 P1, P2, ... , PN로 이산화 된다. 평판 내부의 한 점 P에서의 진동 변위, 즉 자유 진동해는 무차원 동영향 함수들의 선형 결합으로 식 (7)과 같이 가정된다(1).
| (7) |
여기서 J0와 I0는 각각 제1종 0차 베셀 함수(Bessel function)와 수정 베셀 함수를 나타내며, Ak와 Bk는 미지 기여도 계수이다. 그리고 rk는 Fig. 1에서 알 수 있듯이 평판 경계 노드 Pk에 대한 위치 벡터를 뜻한다.
가정된 자유 진동 해 식 (7)이 평판의 경계 노드에서 고정단 경계 조건을 만족하도록 하기 위해, 고정단 경계 조건 식 (5)와 식 (6)을 식 (8)과 식 (9)와 같이 각각 이산화한다.
| (8) |
| (9) |
여기서 ri와 ni는 평판의 경계 노드 Pi의 위치벡터와 법선 방향을 각각 나타낸다.
2.3 시스템 행렬 추출 및 고유치 계산식
자유 진동 해 식 (7)을 이산 경계 조건 식 (8)과 식 (9)에 대입하면 각각 식 (10)과 식 (11)을 얻을 수 있다.
| (10) |
| (11) |
식 (10)과 식 (11)은 각각 식 (12)와 식 (13)처럼 시스템 행렬식으로 표현 가능하다.
| (12) |
| (13) |
여기서 로컬 시스템 행렬 SM(J), SM(I), ,의 i행, k열 위치의 성분(element)은 식 (14) ~ (17)과 같이 각각 구해진다.
| (14) |
| (15) |
| (16) |
| (17) |
식 (12)와 식 (13)으로 주어진 2개의 시스템 행렬식을 하나의 시스템 행렬식으로 머지(merge)하기 위해 식 (12)를 식 (18)과 같이 변형한다.
| (18) |
식 (12)를 식 (13)에 대입하면 식 (19)와 같은 최종 시스템 행렬식이 추출된다.
| (19) |
여기서 SMN은 크기 N으로 축약된 정사각 시스템 행렬이며 식 (20)에 의해 구해진다.
| (20) |
고정단 평판의 고유치는 시스템 행렬 SMN의 판별식이 0을 만족하는 주파수 파라미터에 해당되며, 식 (21)의 해로부터 구해진다(1).
| (21) |
고정판 평판의 i번째 고유모드 형상을 구하기 위해, 먼저 식 (21)로부터 구한 i번째 고유치 Λi를 식 (19)에 대입하여 기여도 계수 Ai를 구한다. 다음으로 Ai를 식 (18)에 대입하여 기여도 계수 Bi를 구한다. 마지막으로 Ai와 Bi의 성분을 식 (7)에 대입한 후 식 (7)에 의해 i번째 고유모드 형상을 그릴 수 있다.
한편, 식 (21)을 만족하는 주파수 파라미터 값들 속에는 멤브레인의 고유치에 해당하는 허위 고유치가 포함되어 있다(1). 그래서 SMN은 식 (22)와 같이 멤브레인의 시스템 행렬 SM(J)가 곱해져 있다고 가정할 수 있다.
| (22) |
식 (22)의 양변의 판별식 값을 구하면 식 (23)과 같이 된다.
| (23) |
| (24) |
| (25) |
식 (23)에서 det(SMmembrane) = 0의 해는 멤브레인의 고유치(허위 고유치)에 해당되며, det(SMplate)의 해는 허위 고유치가 제거된 평판의 고유치에 해당된다. 최종적으로 허위 고유치가 제거된 평판의 고유치는 식 (26)의 해로 구해진다.
| (26) |
2.4 기존 NDIF법의 문제점 분석
식 (26)의 타당성을 확인하기 위해 Fig. 2와 같이 엄밀해가 존재하는 고정단 원형 평판의 경계를 24개와 30개의 노드로 각각 이산화 한다. 식 (26)을 이용하여, 24개 노드로 이산화된 평판에 대한 판별식 곡선을 그리면 Fig. 3의 점선과 같다. 점선 판별식 곡선에 표시된 Λ1, Λ2,⋯, Λ6은 고정단 원형 평판의 고유치에 해당되며, M2, M3,⋯, M7은 원형 멤브레인의 고유치, 즉 허위 고유치에 해당된다. 참고로, 첫번째 허위 고유치 M1은 2.405로 3보다 작아서 Fig. 3에 나타나지 않는다.
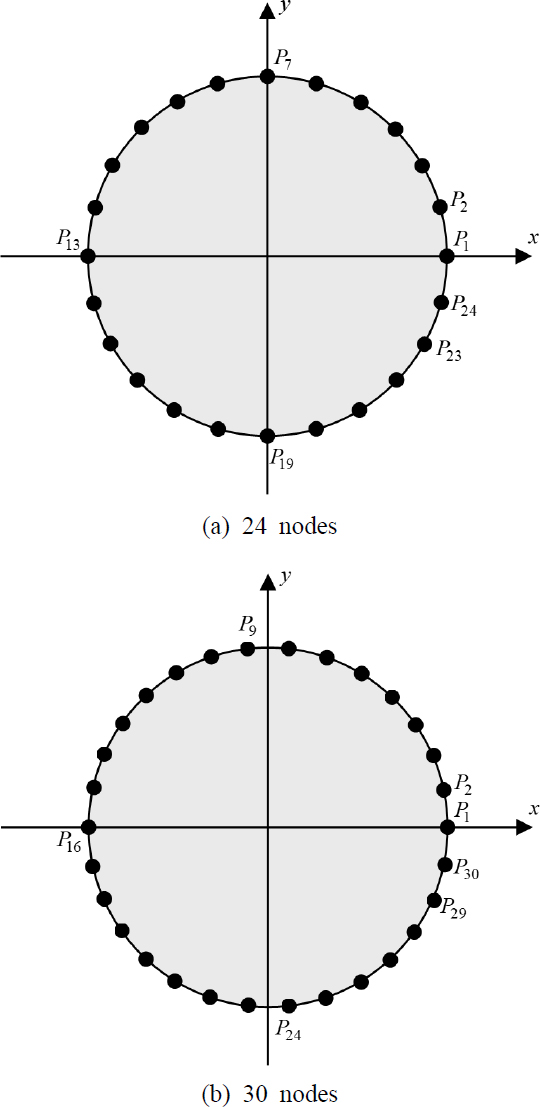
Clamped circular plates of unit radius whose boundary are discretized with 24 and 30 nodes, respectively
Fig. 3에서 구해진 고정단 원형 평판(24 노드)의 고유치들은 Table 1에 요약되었다. 이들 고유치들은 엄밀해와 오차 없이 정확히 일치함을 확인할 수 있다. 반면에, 1835개의 많은 노드를 사용한 FEM (ANSYS) 고유치들은 엄밀해와 오차가 있음을 확인할 수 있다. Fig. 3에서 실선으로 표시된 판별식 곡선은 고정단 원형 평판의 경계를 30개의 노드로 이산화한 경우에 대한 것이다. 이 곡선을 살펴보면, 저주파수 영역에서 시스템 행렬이 발산하여, 저차 고유치 Λ1와 Λ2가 구해지지 않음을 확인할 수 있다. 이 곡선에 의해 구해진 고유치 Λ3, Λ4,⋯, Λ6도 Table 1에 요약되었다.
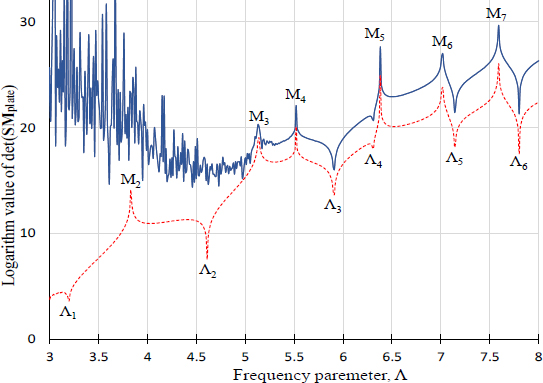
Determinant curve for the clamped circular plate by the original NDIF method (dotted line: 24 nodes, solid line: 30 nodes)

Eigenvalues of the clamped circular plate by the original NDIF method, the exact solution, and ANSYS (parenthesized values denote errors (%) with respect to the exact solution)
Fig. 3과 Table 1에서 확인한 바와 같이, 고유치가 엄밀해에 이미 수렴한 상태에서 노드의 개수를 증가시키면 시스템 행렬이 발산하여 저주파수 고유치들이 구해지지 않음이 기존 NDIF법에서 확인된다. 이번 논문에서는 이러한 문제점을 극복할 수 있는 방안이 제안된다.
3. 기존 NDIF법 문제점 해결 방안 제안
이전의 멤브레인에 관한 연구(11)에서 시스템 행렬의 랭크가 시스템 행렬의 크기 보다 작을 경우에는 시스템 행렬의 판별식 값이 발산함이 확인되었다. 그래서 이러한 발산 문제를 없애기 위해 이전 연구에서 제안한, 시스템 행렬의 랭크를 고려한 시스템 행렬 판별식 계산 방법(11)을 고려하면, 고정단 원형 평판의 고유치 추출 식인 식 (26)의 좌변, 즉 시스템 행렬((SMplate(Λ)))의 판별식은 식 (27)의 방법에 의해 계산 가능하다.
| (27) |
여기서 R(Λ)은 주파수 파라미터 Λ의 함수로 주어지는 시스템 행렬 SMplate(Λ)의 랭크이며, λi(Λ)는 식 (28)과 같은 SMplate(Λ)에 대한 대수 고유치 문제에서 i번째 고유치를 의미한다.
| (28) |
여기서 vi는 i번째 고유 벡터를 의미한다.
더 나아가, 식 (27)을 이용하여 시스템 행렬의 판별식 곡선을 그릴 경우, 시스템 행렬의 랭크가 불연속적으로 변하는 주파수 파라미터 값들 위치에서 판별식 곡선도 불연속적으로 변하는 현상이 발생한다(11,12). 이러한 판별식 곡선의 불연속 현상을 제거하기 위해, 랭크의 변화에 의해 추가로 곱해지는 고유치들의 곱들을 식 (27)의 판별식 계산식에서 나누어 주는 방안(11,12)인 식 (29)가 이용된다.
| (29) |
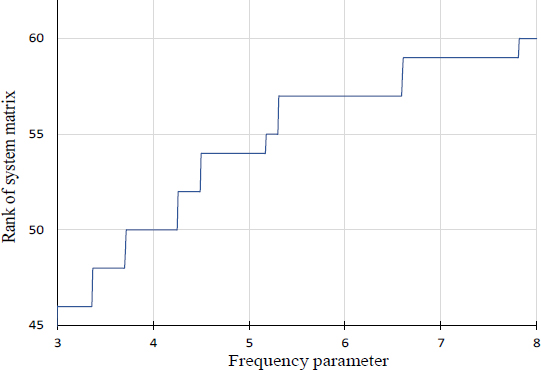
식 (29)를 이용하여 30개의 노드로 이산화한 고정단 원형 평판의 시스템 행렬(SMplate)에 대한 판별식 곡선을 그린 결과는 Fig. 3의 실선과 일치하는 것으로 확인되었다. 그 이유는 식 (24)에 의해 주어지는 SMplate의 랭크가 전체 주파수 구간에서 30으로 일정하기 때문인 것으로 분석되었다.
위에서 살펴본 바와 같이, 식 (29)를 이용하는 최근의 연구 방법(11)으로는 평판 시스템 행렬의 저주파수 발산 문제를 해결할 수 없음을 알 수 있다. Fig. 3의 실선으로 주어진 판별식 곡선의 저주파수 영역에서의 발산 문제를 해결하기 위해선, 저주파수 영역에서 시스템 행렬의 랭크의 크기가 시스템 행렬의 크기보다 작아야 한다. 그런데 앞에서 설명한 바와 같이, 현재의 경우는 시스템 행렬의 랭크의 크기가 시스템 행렬의 크기와 일치하기 때문에, 식 (29)가 그 효용성을 발휘하지 못하는 것으로 판단된다.
SMplate의 랭크가 30으로 일정한 원인은, 식 (24)에서 SMplate을 계산할 때 로컬 시스템 행렬의 역행렬이 사용되었기 때문으로 판단된다. 그래서 논문에서는 시스템 행렬을 다른 방법으로 구할 방안이 제안된다. 식 (12)와 식 (13)에 의해 주어진 로컬 시스템 행렬식은 다음과 같이 역행렬을 사용한 행렬 축약 과정 없이 식 (30)과 같은 하나의 시스템 행렬식으로 나타낸다.
| (30) |
식 (31, 32)는 여기서,
| (31, 32) |
식 (30)에서 위첨자 2N은 시스템 행렬의 크기를 의미한다. 참고로, 식 (24)와 같이 역행렬을 이용해서 구해진 시스템 행렬은 축약이 되어서 그 크기가 N이다. 식 (30)의 시스템 행렬을 식 (29)에 대입하면 식 (33)과 같다.
| (33) |
식 (33)을 이용하여 판별식 곡선을 구하면 Fig. 4와 같다. 이 곡선에 의해 구해진 고유치 값들은 Fig. 4에 표시되어 있으며, 이들 값들은 Table 1의 엄밀해와 정확히 일치함이 확인된다. 이러한 사실은, 이 논문에서 제안된 방법이 노드의 개수가 증가하더라도 전 주파수 대역에서 고정단 평판의 고유치들을 정확하게 추출할 수 있음을 보여준다. 참고로 Fig. 5를 보면, 시스템 행렬의 랭크가 저주파수 영역에서 시스템 행렬의 크기보다 작은 정상적인 현상을 확인할 수 있다.
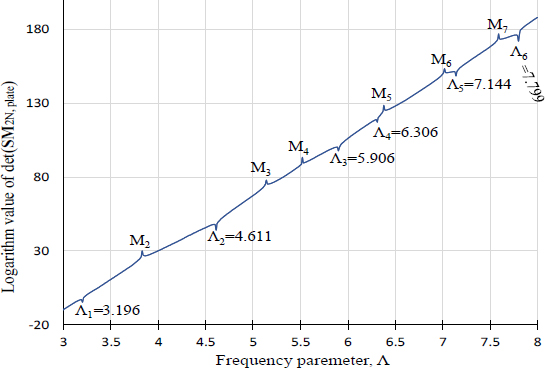
Determinant curve for the clamped circular plate with 30 boundary nodes, obtained by the proposed method using Eq. (33)
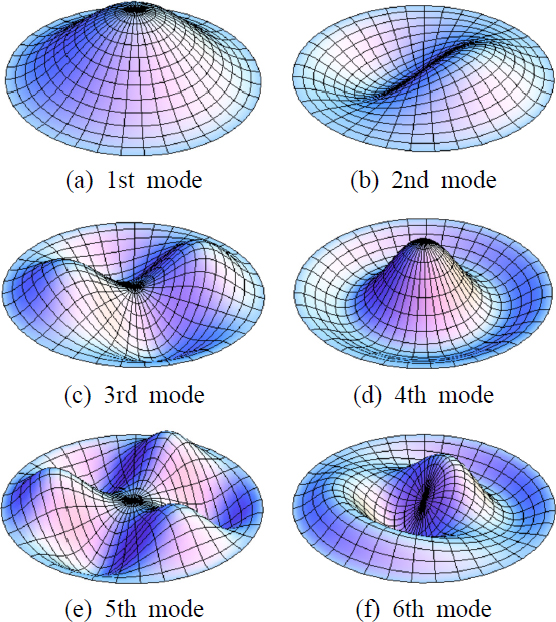
제안된 방법에 의해 구해진 고유모드 형상은 Fig. 6에 제시되었으며 이들 형상은 엄밀해 고유모드 형상과 정확히 일치함이 확인되었다.
4. 결 론
기존의 NDIF법에서 고정단 평판의 고유치를 추출할 때, 노드의 수를 증가시키면 저주파수 영역에서 시스템 행렬이 발산하여 저차 고유치가 구해지지 않는 문제점이 존재한다. 이 논문에서는 상기의 문제점을 개선하기 위하여 시스템 행렬의 판별식을 계산할 때 시스템 행렬의 랭크를 고려하는 방안이 새로이 제안되었다. 제안된 방법의 타당성과 정확성은 엄밀해가 존재하는 고정단 원형 평판에 대한 예제 검증을 통해 확인되었다. 논문의 2부에서는 다양한 형상을 가진 임의 형상 고정단 평판에 대한 예제 연구들이 수행되었다.
Acknowledgments
이 연구는 한성대학교 교내학술연구비 지원 과제임.
References
-
Kang, S. W. and Lee J. M., 2001, Free Vibration Analysis of Arbitrarily Shaped Plates with Clamped Edges Using Wave-type Functions, Journal of Sound and Vibration, Vol. 242, No. 1, pp. 9~26.
[https://doi.org/10.1006/jsvi.2000.3347]

-
Kang, S. W., 2002, Free Vibration Analysis of Arbitrarily Shaped Plates with a Mixed Boundary Condition Using Non-dimensional Dynamic Influence Functions, Journal of Sound and Vibration, Vol. 256, No. 3, pp. 533~549.
[https://doi.org/10.1006/jsvi.2002.5009]

-
Kang, S. W., 2007, Free Vibration Analysis of Arbitrarily Shaped Polygonal Plates with Free Edges by Considering the Phenomenon of Stress Concentration at Corners, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 17, No. 3, pp. 220~225.
[https://doi.org/10.5050/KSNVN.2007.17.3.220]

-
Kang, S. W., Kim, I. S. and Lee, J. M., 2008, Free Vibration Analysis of Arbitrarily Shaped Plates with Smoothly Varying Free Edges Using NDIF Method, Journal of Vibration and Acoustics, Vol. 130, No. 4, 041010.
[https://doi.org/10.1115/1.2730531]

-
Kang, S. W. and Kim, J. G., 2009, A Formulation of NDIF Method to the Algebraic Eigenvalue Problem for Efficiently Extracting Natural Frequencies of Arbitrarily Shaped Plates with the Simply Supported Boundary Condition, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 19, No. 6, pp. 607~613.
[https://doi.org/10.5050/KSNVN.2009.19.6.607]

-
Kang, S. W. and Yoon, J. I., 2012, Development of the NDIF Method Using a Sub-domain Approach for Extracting Highly Accurate Natural Frequencies of Arbitrarily Shaped Plates, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 22, No. 9, pp. 830~836.
[https://doi.org/10.5050/KSNVE.2012.22.9.830]

-
Kang, S. W., 2015, Efficient Meshless Method for Accurate Eigenvalue Analysis of Clamped Plates, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 25, No. 10, pp. 653~659.
[https://doi.org/10.5050/KSNVE.2015.25.10.653]

-
Kang, S. W., 2017, New Formulation of NDIF Method for Highly Accurate Eigenvalue Analysis of Arbitrarily Shaped Plates, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 27, No. 5, pp. 622~628.
[https://doi.org/10.5050/KSNVE.2017.27.5.622]

- Bathe, K. J., 1982, Finite Element Procedures in Engineering Analysis, Prentice-hall, New Jersey.
-
Brebbia, C. A., Telles, J. C. F. and Wrobel, L. C., 1984, Boundary Element Techniques, Springer-verlag, Berlin, Heidelberg.
[https://doi.org/10.1007/978-3-642-48860-3]

-
Kang, S. W., 2022, Efficient Higher-order Eigenvalue Analysis of Arbitrarily Shaped Membranes Using NDIF Method, Transactions of the Korean Society of Mechanical Engineers A, Vol. 46, No. 1, pp. 57~63.
[https://doi.org/10.3795/KSME-A.2022.46.1.057]

-
Kang, S. W., 2023, Development of Modified NDIF Method for Extracting Eigenvalues in Entire Frequency Range of Arbitrarily Shaped Acoustic Cavities: Part 1 (Theoretical Formulation), Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 33, No. 1, pp. 44~50.
[https://doi.org/10.5050/KSNVE.2023.33.1.044]

- Blevins, R. D., 1979, Formulas for Natural Frequency and Mode Shape, Van Nostrand Reinhold, New York.

Sang Wook Kang received a B.S., M.S. and Ph.D. degrees in Dept. of Mechanical Design Engineering from Seoul National University. He is working in Hansung University