차량용 조향 모터의 가상센서 시스템 및 홀로렌즈 시각화

1. 서 론

최근 자동차 산업의 동향은 내연기관에서 전동화 시스템으로 전환되고 있다. 이에 따라 해당 시스템의 핵심 부품 중 하나인 구동 모터의 진동 성분은 전동화 시스템의 성능을 결정하는 주요한 지표 중 하나로 여겨지고 있다. 이러한 이유로 구동 모터의 모니터링 시스템은 진동 성분을 사전에 예측하고 평가하는데 사용된다. 또한 모니터링 시스템에서 계측된 데이터는 NVH 성능분석, 사전 고장 감지, 시스템 설계 등 다양한 측면에서 활용된다^(1~5). 하지만 접촉식 센서를 사용한 모터의 응답 계측은 센서부착이 어려운 지점에서 응답을 얻기 제한되는 뿐만 아니라 여러 응답을 얻으려면 각각 대응되는 센서가 필요하기 때문에 비용적인 제한점이 존재한다.

이러한 제한을 극복하기 위해 최근 축소모델링 기법을^(6,7) 통한 유한요소모델을 기반으로 시간적분기 및 역동역학적 하중 추정법을 적용한 가상센싱 기술이 개발 및 적용되었다^(8~12). 해당 기술을 적용하면, 소수의 계측 데이터를 활용하여 구조물 전반의 미계측 응답 및 응력장, 상호작용력 등 부가 정보를 간접적으로 추정할 수 있다. 그러나 해당 기술의 단순 적용에 의한 추정 정보의 분석을 위해서는 해당 분야의 전문성을 지닌 전문인력을 필요로 하는 등 실제 산업 현장에서의 활용도가 제한될 수 있다.

이 연구에서는 위 가상센싱 기술을 적용하여 모터 구조물의 미계측 진동 응답 및 모터와 지그 구조물 사이 결합 반발력을 추정하였으며, 추정된 결과는 동일한 지점에서 센서를 통해 측정된 계측값과 비교하여 정확성을 검증하였다. 나아가, 추정 결과를 시각적인 자료를 통해 직관적으로 사용자에게 전달하기 위해 혼합 현실(mixed reality) 기반 모니터링 시스템을 제안하였다. 구축된 모니터링 시스템은 Unity 3D 게임엔진 프로그램과 증강현실 기기인 HoloLens 2를 활용하여, 혼합현실 상에서 구조물의 동작 상태를 직관적으로 이해할 수 있도록 구성하였다. 이를 위하여 모터의 유한요소 모델의 정보를 메쉬 구조체로 변환해 3차원 그래픽스 상에서 렌더링을 진행하였다. 또한 가상센서 시스템에서 실시간으로 연산되는 모터의 응답 데이터를 실시간 전송하기 위하여 server와 client 사이 TCP/IP 데이터 통신 프로세스를 구축하였으며, client에서 전달받은 축소 응답 벡터를 시각화 메쉬 구조체로 실시간 투영하기 위한 연산 자원을 최적화하기 위하여 GPU 병렬 연산 알고리즘을 적용하였다. 이를 통해 구동 모터의 실시간 변위 및 모터와 지그 사이 반발력을 혼합현실에서 시각화하여 구동 모터의 모니터링 시스템 활용도를 높였다.

2. 유한요소 모델링 및 가상센싱 기술

2.1 BLAC 모터 모델링

영구 자석 동기 전동기(permanent magnet synchronous motor, PMSM)로 불리는 brushless AC(BLAC) 모터는 전류를 6개의 사다리꼴 형태로 제어하는 brushless DC(BLDC) 모터에 비해 연속된 3상의 정현파로 제어한다. 이러한 이유로 BLDC 모터에 비해 비교적 설계 난이도는 높지만 속도제어, 위치제어, 토크의 직접 제어가 가능하다는 등 효율적인 측면에서 장점이 있어 최근 전동화 시스템에서 많이 사용된다^(13,14).

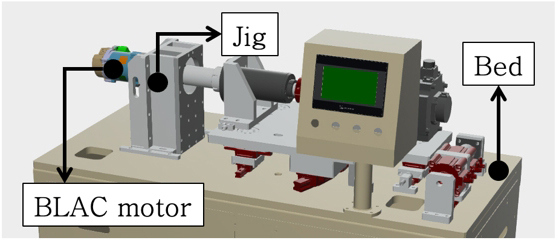
이 연구에서는 역동역학적 하중 추정법을⁽¹⁵⁾ 적용하여 BLAC 모터의 하우징에서 계측한 데이터로 미계측 지점에 대한 응답을 추정하였다. BLAC 모터의 작동중인 환경을 모사하기 위해 시뮬레이터를 사용하여 Fig. 1과 같이 테스트 환경을 구축하였다. 구축된 테스트 환경을 바탕으로 Fig. 2의 BLAC 모터를 이산화하여 물리적 특성을 모사할 수 있는 유한요소모델을 구축하였다. 또한 베드와 지그의 유한요소 모델링을 통해 테스트 환경에서 실질적인 응답을 모사할 수 있도록 하였다. 해당 시스템의 유한요소 정보는 Table 1에 표기된 바와 같다.

Fig. 1

Geometry of system

Fig. 2

Permanent magnet synchronous motor

Table 1

FE information of target system

위 과정에서 구축된 BLAC 모터의 유한요소모델은 식 (1)과 같이 비감쇠 운동방정식으로 표현할 수 있다.

$\[ \mathbf{M}\ddot{\mathbf{u}}+\mathbf{K}\mathbf{u}=\mathbf{f} \]$

(1)

M과 K는 시스템의 질량, 강성행렬을 의미하고 $$ \ddot{\mathbf{u}},\mathbf{ }\mathbf{u},\mathbf{ }\mathbf{f}$$는 가속도, 변위, 하중을 의미한다.

하지만 생성된 유한요소 모델의 직접 연산은 상당한 연산량을 요구할 수 있으며, 이는 구축된 모니터링 시스템의 실시간 연산을 제한할 수 있다.

이 연구에서는 해당 모델을 실시간 모니터링 가능한 시스템으로 구축하기 위하여 Craig-bampton(CB) 기법을 사용하여 모델을 축소하였다. CB 기법을 사용하기 위하여 기존 자유도를 경계자유도(boundary DoFs)와 내부자유도(internal DoFs)로 나누어 주었다. 이를 고려하면 식 (1)은 식 (2)와 같이 표현된다.

$\[ \left[\begin{array}{c}{\mathbf{M}}_b\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}{\mathbf{M}}_c^T\\ {\mathbf{M}}_c\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}{\mathbf{M}}_s\end{array}\right]\left[\begin{array}{c}{\ddot{\mathbf{u}}}_b\\ {\ddot{\mathbf{u}}}_s\end{array}\right]+\left[\begin{array}{c}{\mathbf{K}}_b{\mathbf{K}}_c^T\\ {\mathbf{K}}_c{\mathbf{K}}_s\end{array}\right]\left[\begin{array}{c}{\mathbf{u}}_b\\ {\mathbf{u}}_s\end{array}\right]=\left[\begin{array}{c}{\mathbf{f}}_b\\ 0\end{array}\right] \]$

(2)

하첨자 b, s는 경계자유도, 내부자유도를 의미하며 c는 경계자유도와 내부자유도 사이 결합항(coupling term)을 의미한다.

CB 기법은 경계자유도에 정적 응축(static condensation) 기법을 적용하는 한편, 모드 합성법(mode superposition)을 이용해 내부 자유도의 진동특성을 반영할 수 있다. 이를 통해 변위벡터는 식 (3)과 같이 근사할 수 있다^(16,17).

$\[ \mathbf{u}\approx \mathbf{T}\widehat{\mathbf{u}} \]$

(3a)

$\[ \mathbf{T}=\left[\begin{array}{cc}\mathbf{I}& 0\\ -{\left({\mathbf{K}}_s\right)}^{-1}{\mathbf{K}}_c& {\mathit{\varphi }}_d\end{array}\right], \widehat{\mathbf{u}}=\left[\begin{array}{c}{\mathbf{u}}_b\\ {\mathbf{q}}_d\end{array}\right] \]$

(3b)

여기서 $$ \widehat{\mathbf{u}}$$은 축소된 변위벡터, T는 변환행렬을 의미한다. 식 (3)을 식 (1)에 적용하면 식 (4)와 같이 축소된 운동방정식을 얻을 수 있다.

$\[ \widehat{\mathbf{M}}\ddot{\widehat{\mathbf{u}}}+\widehat{\mathbf{K}}\widehat{\mathbf{u}}=\widehat{\mathbf{f}} \]$

(4a)

$\[ \widehat{\mathbf{M}}={\mathbf{T}}^T\mathbf{M}\mathbf{T}, \widehat{\mathbf{K}}={\mathbf{T}}^T\mathbf{K}\mathbf{T}, \widehat{\mathbf{f}}={\mathbf{T}}^T\mathbf{f} \]$

(4b)

위 과정을 통해 기존 3 982 760 자유도의 행렬을 506 자유도로 축소시켜 해당 시스템의 실시간성을 확보하였다.

또한 구조물의 감쇠를 고려하기 위하여 질량 및 강성 비례 감쇠 행렬을 생성하였으며, 이를 포함한 전체 운동방정식은 식 (5)와 같이 표현할 수 있다.

$\[ \widehat{\mathbf{M}}\ddot{\widehat{\mathbf{u}}}+\widehat{\mathbf{C}}\dot{\widehat{\mathbf{u}}}+\widehat{\mathbf{K}}\widehat{\mathbf{u}}=\widehat{\mathbf{f}} \]$

(5a)

$\[ \widehat{\mathbf{C}}=a_1\widehat{\mathbf{M}}+a_2\widehat{\mathbf{K}} \]$

(5b)

여기서 a₁, a₂는 각각 질량 및 강성 비례감쇠 계수를 의미한다.

2.3 실험 및 결과분석

앞서 언급한 과정에서 구축한 시스템 검증을 위하여 2000 r/min으로 작동 중인 상태에서 실험을 진행하였다. 역동역학적 하중 추정 시스템에서 입력 가속도 데이터는 3축 가속도계(356A15, PCB piezoelectronics)를 통해 계측하여 모터와 지그 사이 결합 반발력을 추정하였다.

실제 결합 반발력은 하중 센서(PCB-261A01, PCB piezoelectronics)를 사용하여 계측하였고, 해당 하중 센서의 동적 특성을 모사하기 위하여 Table 2와 Fig. 3의 센서 규격 정보를 바탕으로 하중 센서의 요소행렬을 구축하였다. 구축된 행렬은 식 (1)에서 모터와 지그 사이 체결 지점의 자유도에 대하여 결합하는 방식을 사용하여 부착된 하중 센서의 동적 특성을 모사하였다.

Table 2

PCB-261A01 physical information

Fig. 3

Sensor position

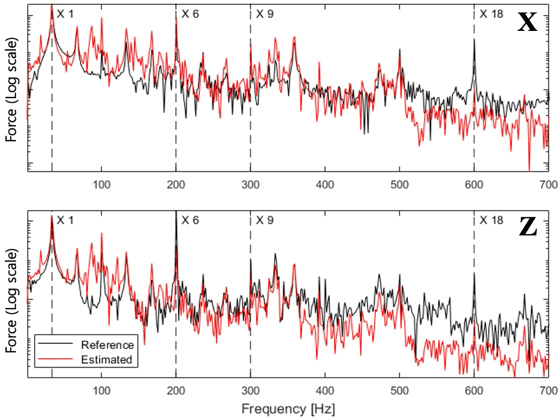
Fig. 4는 주파수 대역에서 결합 반발력에 대한 계측 값과 추정 값을 비교한 결과이다. 작동 환경의 회전 주파수 33.3 Hz를 기준으로 모터의 극 수, 슬롯 수의 고조파 성분인 1차, 6차, 9차, 18차 성분에서 주파수 응답의 절대값에 대한 상대 오차를 Table 3에 정리하였다.

Fig. 4

Comparison of reaction force

Table 3

Relative amplitude error

회전체의 가진력이 주요하게 작용하는 저주파 대역 1차, 6차, 9차 성분에 대해서는 평균 오차가 참조 값 대비 37.57 %로 나타났다. 하지만 전자기력의 영향을 받는 고주파 대역인 18차 성분에 대해서는 평균 오차가 94.27 %로 저주파에 비해 낮은 정확도를 확인했다. 이는 이 연구에서 FE모델 구축 시, 모터의 전자기 성분을 고려하지 않고 기계적 성분만 고려하여 모델링했기 때문이라 추론된다.

3. 실시간 모니터링 시스템

이 장에서는 역동역학적 하중 추정 시스템에서 연산한 모터의 변위와 모터, 지그 사이 결합 반발력을 실시간으로 시각화였다.

해당 시스템은 Unity 3D 게임엔진 프로그램을 사용해 개발하였다. 또한 개발된 환경을 혼합 현실에서 구현하기 위하여 홀로렌즈(Microsoft HoloLens 2)를 사용하여 실시간 모니터링 시스템을 구축하였다.

3.1 유한요소 모델 그래픽 렌더링

이 장에서는 유한요소로 구축된 BLAC 모터를 그래픽 렌더링을 통해 3차원 상에 표현하였다.

3차원 컴퓨터 그래픽스에서 입체적인 객체는 2차원 상의 절점(vertex)과 폴리곤(triangle)의 조합을 UV mapping을 통해 3차원 상에서 표현된다. 하나의 객체를 표현하는 절점과 폴리곤의 조합이 많을수록 부드러운 표면 및 움직임을 모사할 수 있지만 연산량이 증가하는 단점이 존재한다.

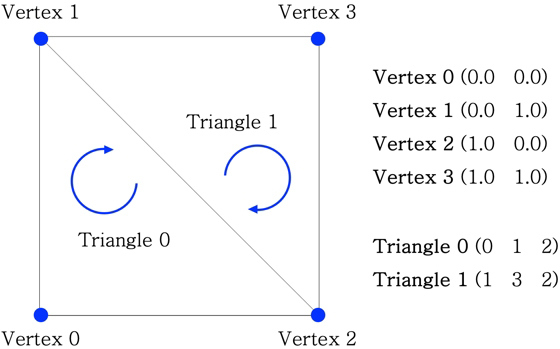
이 연구에서는 Unity 3D 메쉬 구조체를 활용하여 그래픽 렌더링을 진행하였다. 메쉬 구조체에서는 각 절점과 절점을 시계방향으로 매개해주는 폴리곤의 조합으로 UV mapping이 이루어진다. 해당 구조체의 예시는 Fig. 5와 같다.

Fig. 5

Mesh object example in 2D plane

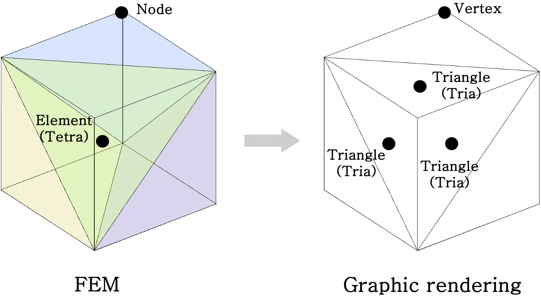
2장에서는 모터에 대한 유한요소 정보(node, element)를 구하였다. 해당 유한요소 정보를 메쉬 구조체로 표현해주기 위하여 Fig. 6과 같이 3차원 사면체 요소(3D tetrahedron element)의 표면을 2차원 삼각형요소(2D triangular element)로 분할하여 그래픽 렌더링을 진행하였다.

Fig. 6

FEM to graphic rendering

3.2 데이터 통신 및 연산

역동역학적 하중 추정 기술을 통해 laptop(server)에서 실시간으로 모터와 지그 사이 결합 반발력과 축소된 응답벡터를 연산하였다.

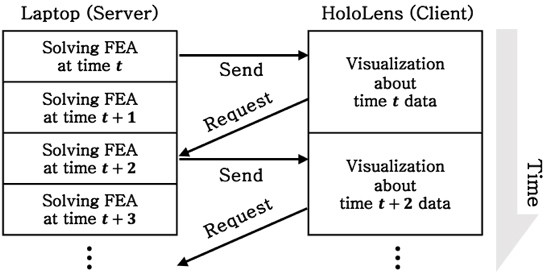
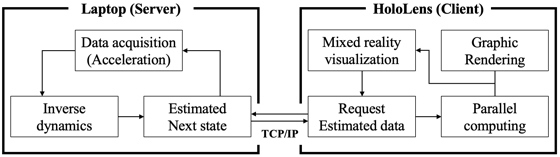
이 장에서는 laptop에서 연산된 결합 반발력과 축소된 변위벡터를 실시간 TCP/IP 통신을 통하여 홀로렌즈(client)로 데이터를 전송하였다. laptop과 홀로렌즈는 별개의 시스템으로 구성해주었고, 홀로렌즈에서 한 단계에 대한 시각화가 진행되면 다음 단계의 데이터를 laptop에 요청하여 데이터를 전송 받도록 시스템을 구축하였다. 해당 시스템의 흐름도는 Fig. 7에 표현된 바와 같다.

Fig. 7

Communication workflow

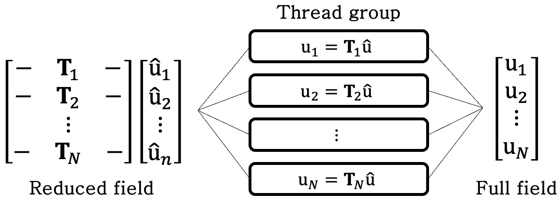
위 과정에서 전송받은 축소된 변위벡터를 전체 자유도에 대하여 시각화하기 위해 홀로렌즈 내에서 식 (3)의 추가적인 연산이 필요하다. 모터의 높은 자유도를 실시간으로 연산하기 위하여 그래픽 처리 장치(graphics processing unit, GPU)를 활용한 병렬연산알고리즘을 구축하였다. 병렬연산 알고리즘 및 데이터 통신 절차는 Fig. 8과 Fig. 9에 표기된 바와 같다.

Fig. 8

GPU parallel computing

Fig. 9

Data processing procedure

3.3 시각화 시스템 구성

이 장에서는 3.2장에서 구성한 절차를 바탕으로 Fig. 10과 같이 시스템을 구성해주었다.

Fig. 10

System setup

또한 Fig. 11 및 Fig. 12와 같이 시스템의 활용도를 높이기 위해 clipping plane으로 장면의 일부만 렌더링 하여 베어링과 같은 모터의 내부 요소를 시각화하였다. 결합 반발력은 하중의 방향 및 크기를 화살표와 그래프로 시각화하여 모니터링 및 상태진단이 가능한 시스템을 구축하였다.

Fig. 11

Motor internal visualization

Fig. 12

GUI setup

4. 결 론

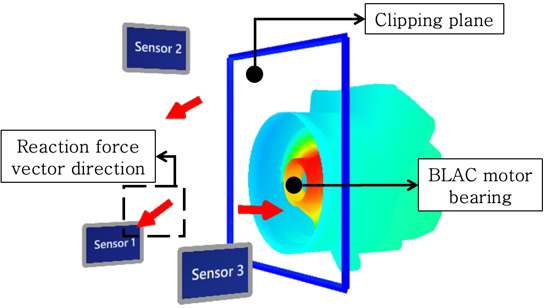
이 연구에서는 BLAC 모터의 미계측 동특성을 혼합현실에서 시각화하여 실시간 모니터링 시스템 절차를 제안하였다. 이를 위하여 BLAC 모터의 물리적 특성을 모사할 수 있는 유한요소모델 기반 축소모델을 구축하였으며, 이를 역동역학적 하중 추정 알고리즘과 결합하여 모터의 실시간 응답을 추정하였다. 추정된 값은 TCP/IP 통신을 통하여 데이터를 혼합현실 내에 전송하였으며 실제 모터에 추정 응답을 투영하였다. 나아가 clipping plane으로 베어링과 같은 내부 응답 표현, 결합 반발력의 벡터방향과 그래프에 대한 기능을 추가하여 직관적으로 응답에 대하여 모니터링할 수 있는 시스템을 구축하였다.

향후 연구 방향성은 크게 두가지로 기대하고 있다. 이 연구에서 계측데이터는 접촉식 가속도 센서로 계측된다. 하지만 구조물에 직접적으로 센서를 부착하여 데이터를 계측하는 방식은 구조물의 감쇠와 같은 물리적 특성에 영향을 줄 수 있는 제한점이 있다^(20,21). 이는 digital image correlation(DIC)을 활용한 데이터 계측을 통해 위 제한점 극복을 기대할 수 있다^(22,23). 또한 구조진동뿐만 아니라 전자기 영역까지 연구범위를 확장하여 가진원에 대한 전자기 성분 검증이 가능하다면, 모터의 NVH 성능 평가에 큰 활용성이 있을 것이라 판단한다.

Acknowledgments

이 연구는 현대모비스 디지털 트윈 및 메타모델을 활용한 구조물의 동특성 추출 연구 및 연구재단 기초연구실 과제(과제번호: RS-2023-00219052)의 지원을 받아 수행되었음.

References

• Kim, B., Hong, J., Yun, S., Shin, G., Min, G. and Chung, J., 2019, Noise Reduction of an In-wheel Motor System for an Electric Vehicle, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 29, No. 3, pp. 422~428. [https://doi.org/10.5050/KSNVE.2019.29.3.422]
• Lee, S.-J., Kim, D.-J., Lee, B.-H. and Hong, J.-P., 2013, Electrical Characteristics and Electromagnetic Excitation Force Comparison of PM Motor according to the Driving Method, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 23, No. 2, pp. 144~151. [https://doi.org/10.5050/KSNVE.2013.23.2.144]
• Schoen, R. R., Habetler, T. G., Kamran, F. and Bartfield, R. G., 1995, Motor Bearing Damage Detection using Stator Current Monitoring, IEEE Transactions on Industry Applications, Vol. 31, No. 6, pp. 1274~1279. [https://doi.org/10.1109/28.475697]
• Ostojic, P., Banerjee, A., Patel, D. C., Basu, W. and Ali, S., 2014, Advanced Motor Monitoring and Diagnostics, IEEE Transactions on Industry Applications, Vol. 50, No. 5, pp. 3120~3127. [https://doi.org/10.1109/TIA.2014.2303252]
• Liu, M., Gu, F. and Zhang, Y., 2017, Ride Comfort Optimization of In-wheel-motor Electric Vehicles with In-wheel Vibration Absorbers, Energies, Vol. 10, No. 10, p. 1647. [https://doi.org/10.3390/en10101647]
• Guyan, R. J., 1965, Reduction of Stiffness and Mass Matrices, AIAA Journal, Vol. 3, No. 2, p. 380. [https://doi.org/10.2514/3.2874]
• Craig, R. R. Jr., and Bampton, M. C. C., 1968, Coupling of Substructures for Dynamic Analyses, AIAA Journal, Vol. 6, No. 7, pp. 1313~1319. [https://doi.org/10.2514/3.4741]
• Oh, S., Park, D., Baek, H., Kim, S., Lee, J.-K. and Kim, J.-G., 2020, Virtual Sensing System of Structural Vibration Using Digital Twin, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 30, No. 2, pp. 149~160. [https://doi.org/10.5050/KSNVE.2020.30.2.149]
• Oh, S., Lee, K.-H., Ahn, K., Yu, Y., Kim, K. and Kim, J.-G., 2021, Development of Vibro-acoustic Virtual Sensing System for Pipeline Structure Using Digital Twin, Transactions of the Korean Society of Mechanical Engineers A, Vol. 45, No. 9, pp. 805~815. [https://doi.org/10.3795/KSME-A.2021.45.9.805]
• Ahn, C.-U., Oh, S., Kim, H.-S., Park, D. I. and Kim, J.-G., 2022, Virtual Thermal Sensor for Real-time Monitoring of Electronic Packages in a Totally Enclosed System, IEEE Access, Vol. 10, pp. 50589~50600. [https://doi.org/10.1109/ACCESS.2022.3174208]
• Oh, S., Lee, H., Lee, J.-K., Yoon, H. and Kim, J.-G., 2023, Real-time Response Estimation of Structural Vibration with Inverse Force Identification, Structural Control and Health Monitoring, Vol. 2023, 2691476. [https://doi.org/10.1155/2023/2691476]
• Jiang, J., Luo, S., Mohamed, M. S. and Liang, Z., 2020, Real-time Identification of Dynamic Loads Using Inverse Solution and Kalman Filter, Applied Sciences, Vol. 10, No. 19, p. 6767. [https://doi.org/10.3390/app10196767]
• Lee, T.-Y., Seo, M.-K., Kim, Y.-J. and Jung, S.-Y., 2016, Motor Design and Characteristics Comparison of Outer-rotor-type BLDC Motor and BLAC Motor Based on Numerical Analysis, IEEE Transactions on Applied Superconductivity, Vol. 26, No. 4, 5205506. [https://doi.org/10.1109/TASC.2016.2548079]
• Miyamasu, M. and Akatsu, K., 2013, Efficiency Comparison between Brushless DC Motor and Brushless AC Motor Considering Driving Method and Machine Design, IEEJ Journal of Industry Applications, Vol. 2, No. 1, pp. 79~86. [https://doi.org/10.1541/ieejjia.2.79]
• Oh, S., Baek, H., Lee, K.-H., Jang, D.-S., Jun, J. and Kim, J.-G., 2023, A Real-time Unmeasured Dynamic Response Prediction for Nuclear Facility Pressure Pipeline System, Nuclear Engineering and Technology, Vol. 55, No. 7, pp. 2642~2649. [https://doi.org/10.1016/j.net.2023.03.030]
• Kim, J.-G. and Lee, P.-S., 2015, An Enhanced Craig-bampton Method, International Journal for Numerical Methods in Engineering, Vol. 103, No. 2, pp. 79~93. [https://doi.org/10.1002/nme.4880]
• Kim, J.-G., Lee, K.-H. and Lee, P.-S., 2014, Estimating Relative Eigenvalue Errors in the Craig-bampton Method, Computers & Structures, Vol. 139, pp. 54~64. [https://doi.org/10.1016/j.compstruc.2014.04.008]
• Chopra, A. K., 1995, Dynamics of Structures: Theory and Applications to Earthquake Engineering, Prentice Hall, Englewood Cliffs. NJ, United States.
• Oh, S., Ahn, C., Ahn, K. and Kim, J.-G., 2023, Implicit Inverse Force Identification Method for Vibroacoustic Finite Element Model, Journal of Sound and Vibration, Vol. 556, 117713. [https://doi.org/10.1016/j.jsv.2023.117713]
• Kondoh, S., Yatomi, C. and Inoue, K., 1990, The Positioning of Sensors and Actuators in the Vibration Control of Flexible Systems, JSME International Journal, Series III, Vol. 33, No. 2, pp. 145~152. [https://doi.org/10.1299/jsmec1988.33.145]
• Kumar, K. R. and Narayanan, S., 2007, The Optimal Location of Piezoelectric Actuators and Sensors for Vibration Control of Plates, Smart Materials and Structures, Vol. 16, No. 6, p. 2680. [https://doi.org/10.1088/0964-1726/16/6/073]
• McCormick, N. and Lord, J., 2010, Digital Image Correlation, Materials Today, Vol. 13, No. 12, pp. 52~54. [https://doi.org/10.1016/S1369-7021(10)70235-2]
• Helfrick, M. N., Niezrecki, C., Avitabile, P. and Schmidt, T., 2011, 3D Digital Image Correlation Methods for Full-field Vibration Measurement, Mechanical Systems and Signal Processing, Vol. 25, No. 3, pp. 917~927. [https://doi.org/10.1016/j.ymssp.2010.08.013]