전산해석을 통한 질량동조감쇠기 적용 슬래브의 바닥충격음 저감 성능 검증
© The Korean Society for Noise and Vibration Engineering
Abstract
Floor impact sound, which occurs when children run, is primarily caused by the vibro-acoustic coupling effect. This effect involves the transmission of vibrations from the upper slab to the lower floor through the slab, which is then converted into sound at the ceiling surface. By reducing the vibration, it is possible to reduce the sound transmitted to the lower floor. In this study, a tuned mass damper (TMD) was designed to investigate its vibration and sound reduction performance. Computational analysis was performed to evaluate the effectiveness of the TMD. This study also compared the performance of slabs with and without the TMD as well as investigated the effect of the mass ratio, which is a design parameter of the TMD. The analysis results showed that installing the TMD led to an overall reduction in vibration. Specifically, the noise reduction of the 1st mode reached up to 42 %. However, when the mass ratio of the TMD was increased over a certain level (20 %), noise control performance was not significant.
Keywords:
Floor Impact Sound, Tuned Mass Damper, Computational Analysis키워드:
바닥충격음, 동조질량감쇠기, 전산해석1. 서 론
2022년 8월부터 시행된 층간소음 사후확인제도는 준공 전 바닥충격음 측정을 통해 경량과 중량충격음에 대해 단일수치평가량 기준 각각 49 dB 이하의 성능을 만족하도록 규정하고 있다(1). 감사원 조사에서 기존의 바닥충격음 공법을 적용한 공동주택의 바닥충격음 저감 성능을 측정한 결과는 사후확인제도 이전의 중량충격음 슬래브 성능 기준인 50 dB 만족도 만족시키지 못하는 것으로 나타났다(2). 따라서 사후확인제도가 시행되는 현재는 기존 기술 외의 성능 강화가 가능한 기술이 필요한 실정이다.
슬래브에 작용하는 충격력이 진동으로 전환되어 슬래브와 벽체를 통해 전달된 후 수음실에서 소리로 방사되어 발생하는 바닥충격음은 진동과 소리가 연계된 계(system)의 특성을 보인다. 따라서 바닥충격음 저감을 위해서는 충격력이 발생한 실의 슬래브를 통해 전달되는 진동을 제어하거나 전파된 진동이 소리로 방사되는 것을 음장 조정을 통해 제어하는 두 가지 방안이 있다.
음원실의 진동 전달 제어를 통해 바닥충격음 저감을 하는 연구에는 먼저, 공동주택의 바닥 구조 형식인 뜬바닥 구조에 관한 연구를 통해 기존 구조가 질량법칙에 따라 저주파 대역이 주요한 바닥충격음에 불리한 구조임이 나타났다(3). 제진층 삽입을 통해 진동 저감을 조사한 연구(4), 건식바닥구조의 고무층 경도를 통한 저감 연구(5), 슬래브 구조에서 모르타르와 경계조건 조사를 통해 충격음 저감에 관한 연구 등(6)에서 바닥충격음의 원인과 해결책을 제시했으나 충분한 저감 성능 확보에는 어려움이 있었다. 천장 구조를 통해 방사된 소리를 제어하는 연구에는 Kim et al.의 연구에서 공기층 190 mm정도에서 63 Hz가 증폭함이 나타났고(7), 흡음 석고보드 천장을 통해 1 dB ~ 4 dB 정도 저감이 가능하며(8), 공명기형 흡음기의 원리를 이용한 타공 석고보드를 통한 수음실 음장 변화를 통한 저감 방안 등이(9~11) 있었지만 충분한 성능확보에는 한계가 있었다. 바닥마감재에 관한 연구는 동탄성계수의 영향(12), 슬래브나 천장에 완충재·흡음재를 적용한 연구(13), 마감재와 매트의 소음저감 특성을 조사한 연구가(14) 있었으나 앞서 연구들과 마찬가지로 저감 성능에 관해 주거자가 만족할 만한 성능 확보를 위해서는 추가적인 저감 방안이 필요한 것으로 나타났다. 이와 같이, 기존의 연구에서 재료의 물성, 구조 등을 활용한 기술들은 바닥충격음 저감에 있어 한계가 있었기 때문에 보다 진동 저감에 특화된 기술이 필요하다고 판단된다.
이 연구에서는 슬래브의 진동을 원천적으로 저감함으로서 이로부터 유발되는 소음을 줄이는 대안으로써 진동저감장치의 하나인 질량동조질량감쇠기를 적용한다. 질량동조감쇠기(tuned mass damper)는 구조물의 고유진동수에 부가 질량을 동조(tuning)시켜 관성력을 통해 에너지를 소산시켜 감쇠효과를 얻는 흡진기(absorber)이다. 이 원리를 바닥 슬래브에 적용하여 진동과 소리가 연계된 특성을 갖는 바닥충격음의 근본적 원인이라 할 수 있는 진동을 소산시켜 수음층에 발생하는 소리의 음압을 감소시킬 수 있다. Santos et al.에서(15) 다중질량동조감쇠기(multi tuned mass damper)를 슬래브에 설치하여 변위를 10 %까지 감소시켜 진동저감 효과가 있는 것으로 나타났고, Hwang et al.의 연구에서(16) 다중질량동조감쇠기를 전산해석을 통해 슬래브에 적용 시 충격음이 저감되며 동조 조건에 따라 63.5 Hz 대역에서 최대 11.0 dB 저감 효과가 있는 것으로 나타났다. 따라서 바닥충격음 저감 기술로 질량동조감쇠기(이하 TMD)는 효과가 있으며, 적용을 위해 해당 구조물의 공진주파수를 통한 설계와 부착 위치에 대한 추가적 연구가 진행된다면 충분한 저감 성능을 갖춘 기술이 될 수 있을 것으로 판단된다.
이 연구는 전산해석을 통해 목업주택 구조물에 적용하여 TMD의 바닥충격음 저감 성능을 분석하였다. 4면이 내력벽으로 구성된 박스형 구조물의 모드 주파수를 파악하고, 고무공을 모사한 충격력으로 인해 진동이 발생하였을 때 상부 슬래브에 나타나는 진동저감효과를 파악하였다.
슬래브의 변위에 영향을 미치는 4개의 모드 주파수와 모드 형상을 고려하여 TMD를 설계 및 배치하고 전산해석을 수행하여 효과를 검증하고 추가적으로 TMD 설계 요소인 슬래브 대비 질량비에 따라 저감 성능과 경향을 파악하여 이를 통해 TMD의 소음 저감 기술 가능성에 대해 분석하였다.
2. 슬래브와 질량동조감쇠기 해석 모델링
2.1 질량동조감쇠기 설계
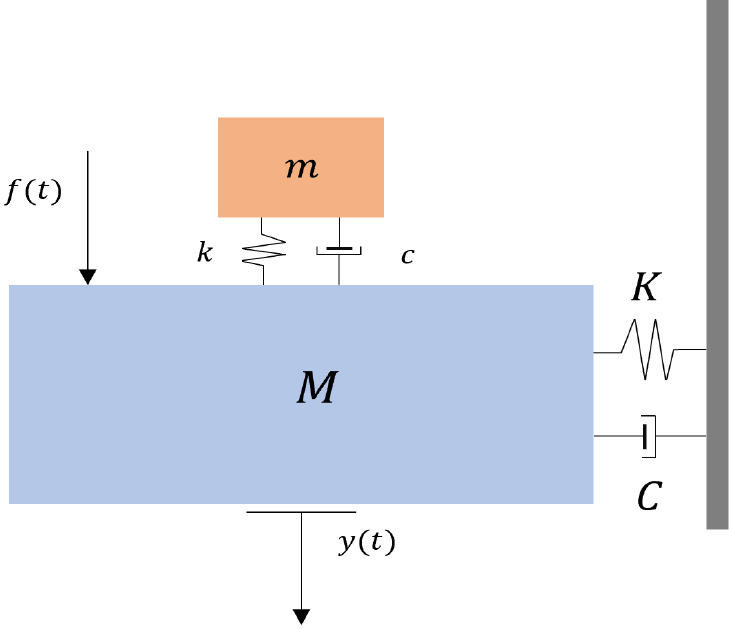
TMD는 동적 하중이 발생했을 때, 구조 부재들의 에너지 분산을 감소시켜 진동을 저감하는 원리의 감쇠기이다. TMD는 질량-스프링-감쇠기로 구성된 시스템 구조를 가지고 있다. Fig. 1과 같이 단자유도 시스템이 질량 M, 감쇠 C, 강성 K를 갖고, 동하중 f(t)가 가해지고 있을 때, 이 시스템에 질량 m, 감쇠 c, 강성 k를 갖는 TMD가 설치되어 있으면 운동방정식은 식 (1), 식 (2)와 같이 정의된다.
| (1) |
| (2) |
: 단자유도 시스템의 가속도
: 단자유도 시스템의 속도
y(t) : 단자유도 시스템의 변위
z(t) : TMD와 단자유도 시스템 사이 상대변위
f(t) : 동적하중
식 (1)을 통해 고유값을 구하면 공진주파수를 찾을 수 있게 된다. 구해진 공진주파수를 반영하여 TMD를 설계하는데 질량(m), 강성(k), 감쇠계수(c)를 입력 변수로 한다. 질량과 대상 공진주파수가 결정되면 식 (3) ~ 식 (5)를 통해 강성과 감쇠계수를 계산할 수 있다.
| (3) |
| (4) |
| (5) |
(w: 각진동수, f: 공진주파수, k: TMD 강성, m: 질량, c: TMD 감쇠계수, r: 감쇠비[%])
계산된 값을 반영하여 제작된 TMD의 설치를 통해 바닥판은 등가감쇠 증가효과를 가지게 되며 이를 통해 충격력에 대한 저항력 증가를 통해 진동을 저감하게 된다. 한편 증가된 질량은 고유진동수의 주파수 대역을 더 낮은 대역으로 이동하게 하여 가청영역에서 벗어날 수 있는 효과 또한 확보할 수 있다. TMD의 구성 요소인 감쇠기는 시스템의 감쇠를 증가시켜 진동에너지 흡수를 통해 진동 감소 효과를 얻게 된다.
이 연구의 TMD는 바닥슬래브에 부착하여 위의 원리로 진동 저감효과를 발휘하게 된다. 대상 공간을 전산해석하여 슬래브 위치별 변위에 영향을 주는 주파수 맞춤 TMD를 설계하고 슬래브 중량의 16 %로 설계하였다.
2.2 전산 해석 모델링
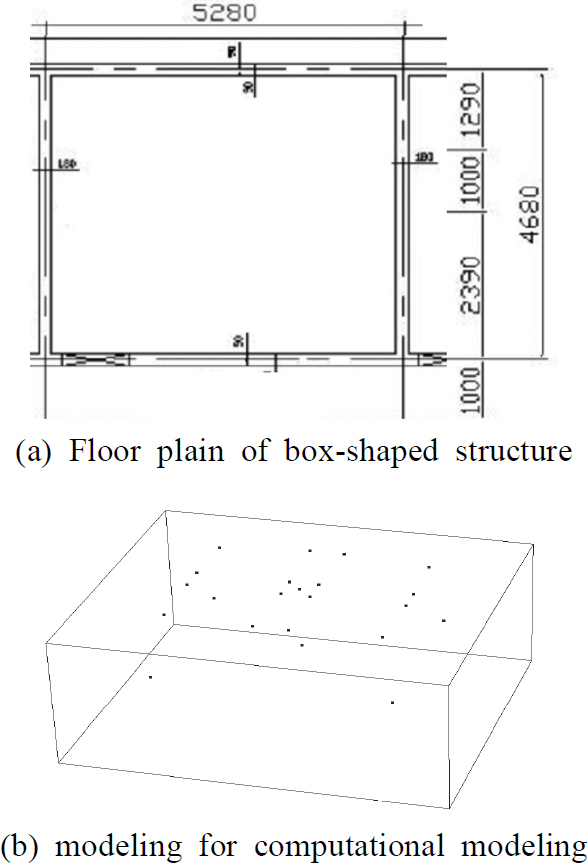
이 연구의 대상 구조물의 평면과 해석용 모델링은 Fig. 2와 같다. 가로 5.28 m, 세로 4.68 m, 높이 2.25 m의 구조를 가진 콘크리트 구조물이고, 슬래브 두께는 0.18 m, 벽체 두께는 0.15 m였다. 해석용 모델링은 평면도를 토대로 상부 슬래브와 4개의 벽면은 쉘구조로 모델링하였고, 내부 공간은 공기층으로 모델링하였다. 해석은 COMSOL multiphysics 5.6 version을 사용하였고, 전산해석을 위해 입력한 재료의 물성은 Table 1과 같다. COMSOL을 통해 고유진동수와 모드 형상을 계산하여 모드 형상에 따른 변위에서 슬래브의 변위만을 발생하게 하는 주파수를 선별하면 Fig. 3의 1차 ~ 4차 모드에 해당하는 슬래브의 모드형상을 나타내는 것으로 각각 39.19 Hz, 73.12 Hz, 84.30 Hz, 114.74 Hz이다. 선별된 주파수를 식 (3) ~ 식 (5)에 대입하여 계산한 TMD 설계값은 Table 2와 같다.
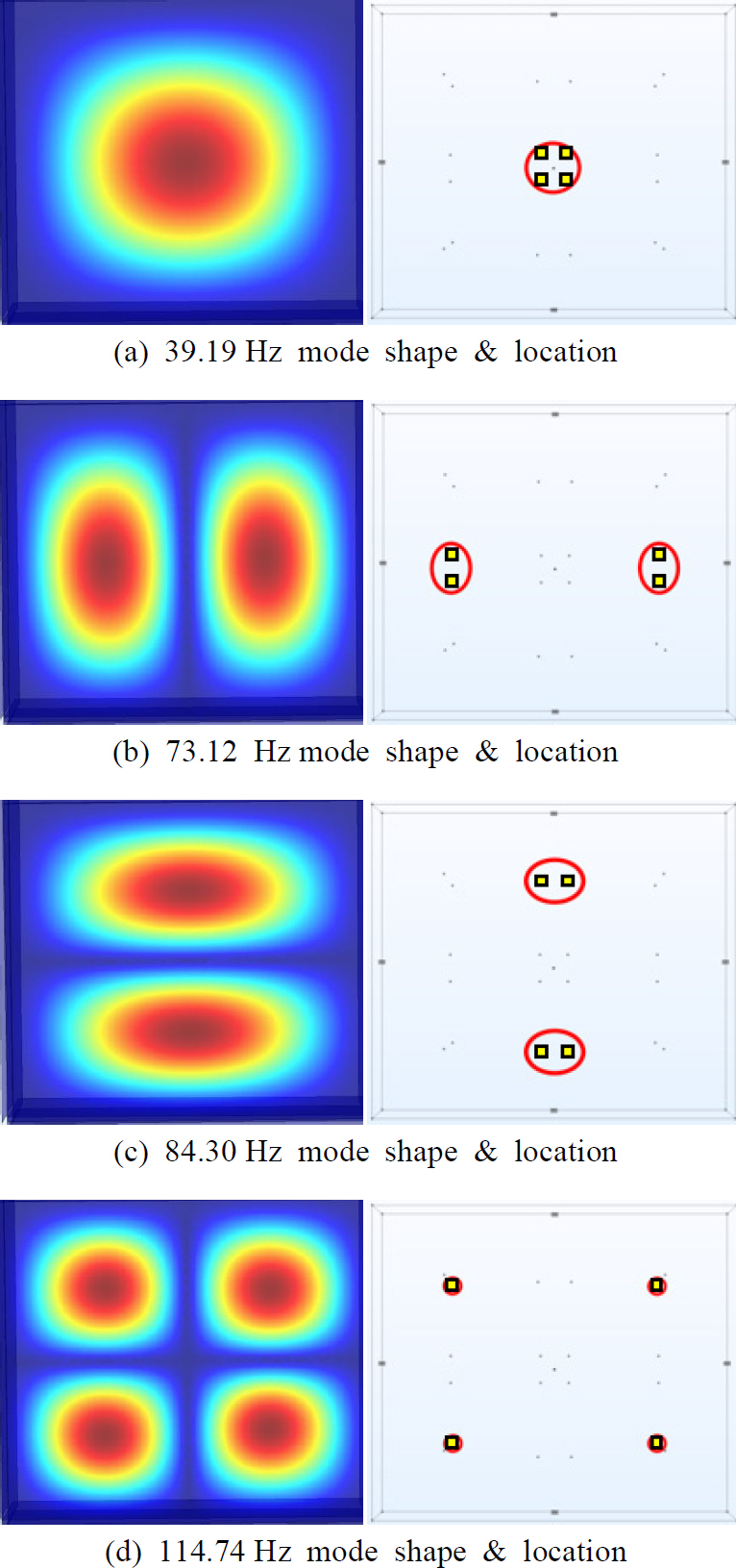
Natural frequencies, mode shape and deformation location of slab from analysis(black rectangle : installation points of TMD)
TMD의 설계값 뿐만 아니라 설치 위치도 성능에 영향을 미치는 요소로 작용한다. 이를 모델링에 적용하기 위해 상부 슬래브에 Fig. 3의 결과를 토대로 각 공진주파수 별 슬래브에 변위가 나타나는 지점에 해당 공진주파수 저감 목적으로 설계된 TMD를 설치하도록 Fig. 3(a) ~ Fig. 3(d)의 오른쪽 그림에 나타난 것과 같이 해당 지점에 TMD를 설계하였다. TMD의 질량비는 슬래브 질량 10 674.90 kg을 기준으로 16 %로 설계하였고 슬래브 적용 시 해석 상 구조적 안정성은 확보된 것으로 나타났고, 케이스 별 설계에 대한 상세는 Table 3과 같다.
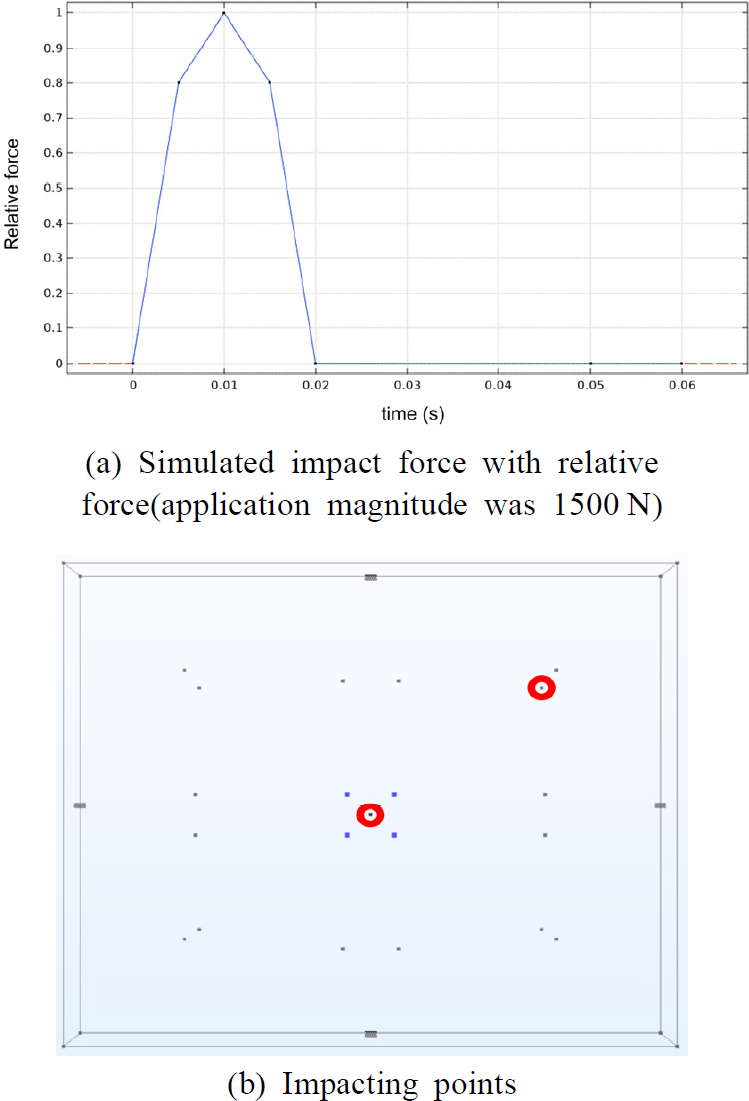
TMD의 크기는 가로와 세로가 각각 30 cm인 정사각형 형태로 가정하여 COMSOL multiphysics version 5.6에서 제공하는 기능인 lumped mechanical system을 활용하여 모델링하였다. Lumped mechanical system에서 각 지점에 설치된 TMD는 슬래브 상부와 강접합점(fixed node)으로 연결되어 거동하도록 하였고, 질량점을 자유단(free node)로 설정하고 강접합점과 질량점 사이에 강성 반영을 위한 스프링과 감쇠계수를 반영할 대쉬포트로 결합시켰다. 슬래브의 가해진 충격력은 KS F 2810-2에(17) 규정된 고무공 충격원을 기준으로 Fig. 4(a)와 같이 충격력 곡선을 모사한 최대 크기 1로 모델링된 사인파를 1500 N의 크기로 슬래브에 적용되도록 하였다. 충격력의 작용 위치는 중앙지점 외에 벽체로의 진동전달이 중앙지점보다 상대적으로 크다고 예상되는 구석 지점도 고려하여 Fig. 4(b)에서 빨간 원으로 표시된 지점과 같이 중앙점과 구석 지점 각각 1지점씩 선정하였다.
TMD 설치 전과 후의 소음 저감 성능을 비교하여 TMD가 슬래브에 설치되었을 때 저감 성능을 확보할 수 있는지 확인하였다. 진동 레벨과 음압 레벨의 차이를 비교하기 위해서 해석상 진동계와 마이크로폰을 나타내는 수음점을 슬래브와 내부 음장에 각각 설치하여 데이터를 추출했다. 가속도 센서는 슬래브 상부에 16개를 설치하였고, 음압 수음점의 경우 KS F 2810-2를 참고하여 수음실의 바닥에서 1.2 m 높이로 5지점 지정하였다.
전산해석은 충격력이 가해진 후 시간이 지남에 따른 거동을 확인하기 위해 시간이력해석(time dependent)을 수행하였고, 총 해석 시간은 고무공 충격원의 충격 시 충격력의 지속시간을 고려하여 0.125초를 0.5 밀리초 단위로 해석하였다.
3. 해석 결과 및 토의
3.1 시간이력해석
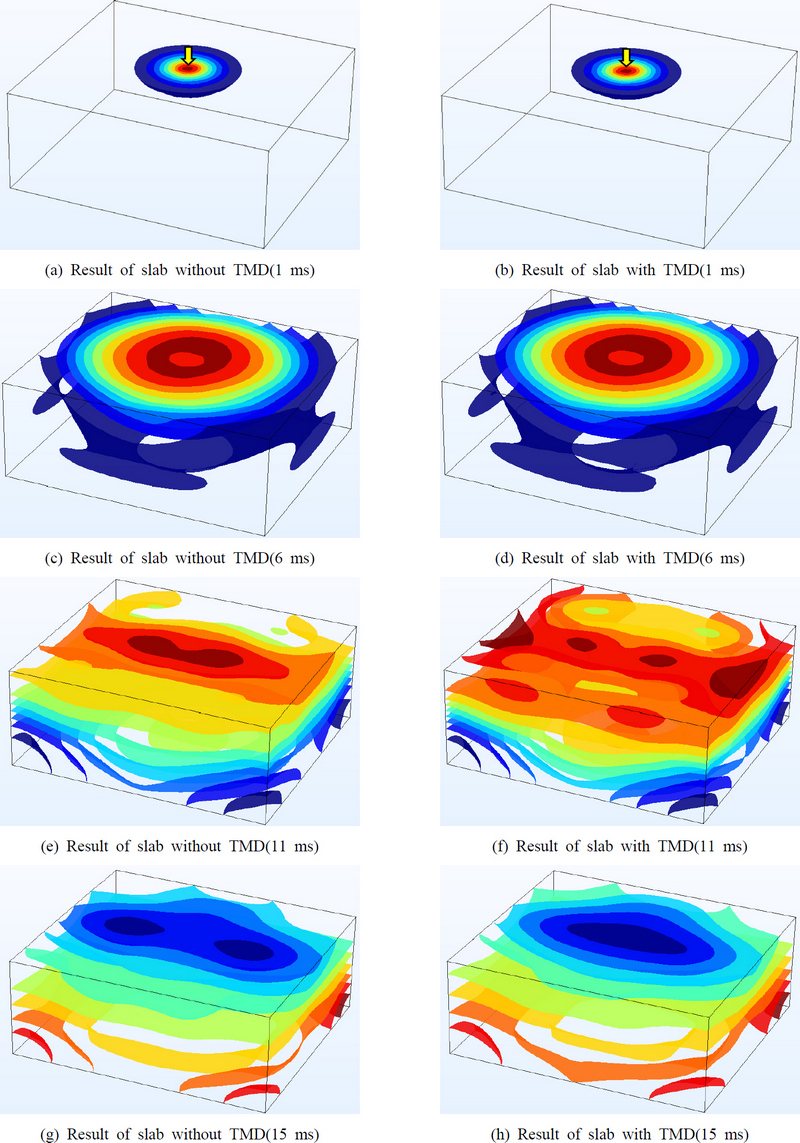
충격력의 작용으로 인한 진동이 슬래브를 통해 전파된 진동이 수음실의 천장면에서 내부 음장으로 방사되는 음압의 확산 경향을 알아보기 위해 시간이력해석을 수행하였다. 확산의 경향을 알아보기 위해 TMD는 설치하지 않은 조건과 설치한 조건에서 Fig. 4(b)에서 중앙 지점에서의 충격력 작용 시의 시간이력해석을 COMSOL의 acoustic pressure(actd) 기능을 이용하여 나타낸 결과는 Fig. 5와 같이 나타났다. 두 조건 모두 충격력이 작용한 지점에서 충격력 작용 후 1 ms에는 충격점 주위에 음압이 국부적으로 충격점 주위에 발생한다. 6 ms까지는 거의 유사한 경향을 보였고 점차 작용지점에서 전체 공간으로 퍼져나가게 되어 11 ms가 흐르면 전체 공간으로 퍼지는 것을 확인할 수 있었다. 11 ms 부터 TMD 설치 유무에 따라 거동이 달리 나타났는데 11 ms에서 TMD가 설치된 경우 1차모드가 주요하게 나타나는 중앙 부분에서 짙은 적색 영역이 감소하는 효과가 있는 것으로 나타났다. 15 ms에서도 다른 경향을 보였는데 전체적으로 짙은 파란색의 영역에서 차이를 보였고, 이외의 같은 등압 영역 색상에서는 TMD가 설치된 경우 등압 영역이 감소하는 경향을 보여 TMD가 설치된 경우 설치되지 않은 경우에 비해 시간이 지남에 따라 음압이 감소하는 경향이 나타나 충격음 감소에 영향을 미치는 것으로 나타났다.
3.2 TMD의 소음 저감 효과
TMD 설치 전후의 저감 효과를 알아보기 위해 Table 3의 case 1에서 감쇠계수 0.10, 질량 100 kg의 데이터를 반영한 해석 결과와 설치하지 않았을 때의 결과를 비교하였다. 충격원의 가진지점은 Fig. 4의 중앙점과 상단우측 지점 중 중앙점을 선정해 전산해석을 수행하였다. 결과는 음압레벨과 스펙트럼상의 진동가속도에 대해 분석하였고, 음압 레벨을 위한 수음점은 충격원이 가진한 지점 아래쪽에 모델링한 수음점의 해석치를 제시했고 진동가속도는 슬래브 상의 16개를 모두 조사하였다. 해석 결과는 바닥충격음의 평가 방식에 있어 주파수 상의 최대값인 Lmax나 바닥충격음 차단 성능 단일수치평가량을 나타내는 L′iA,Fmax를 고려하여 주파수 대역의 최대값 위주로 분석했고, 이러한 요소를 반영한 진동스펙트럼 및 음압레벨 결과는 Fig. 6과 같이 나타났다.
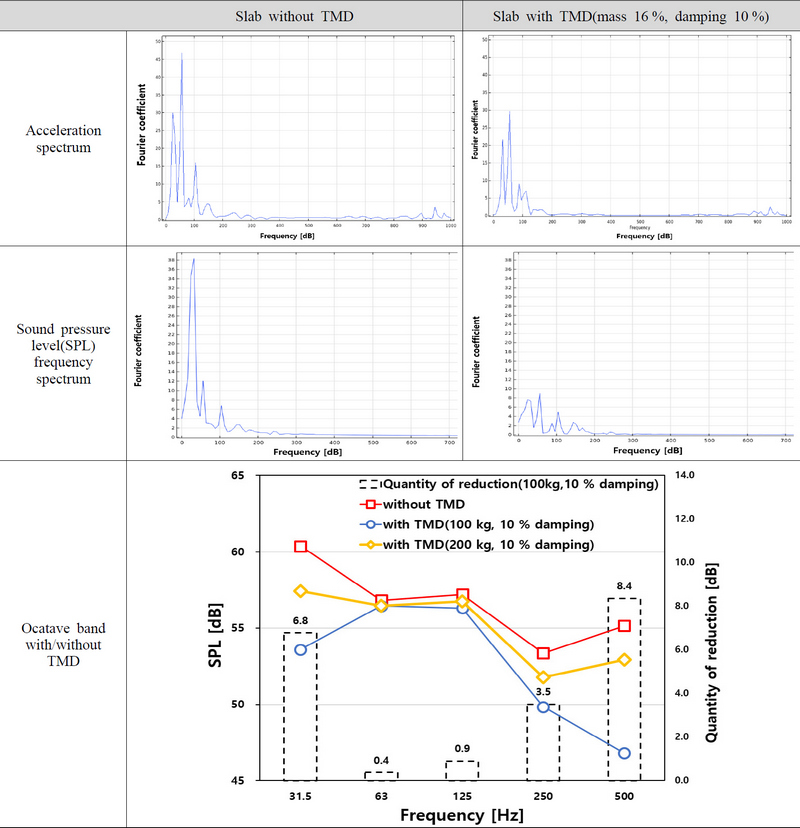
The comparison result of SPL, acceleration spectrum with and without TMD(mass 16 %, damping 10 %), and octave band among slab without TMD, with TMD(mass 16 %, damping 10 %), and TMD(mass 20 %, damping 10 %); time step was 0.5 ms and entire analysis time was 0.125 s
먼저, 진동 가속도 결과를 보면 일반슬래브는 최대값 39 Hz 부근에서 해석치 47.4를 보였고, TMD를 설치한 경우 최대값은 29.7로 감소하여 약 37 % 저감효과가 나타났다. 다른 주파수 대역에서도 전체적으로 감소하는 결과가 나타났으나 100.0 Hz 영역에서 증폭이 일어났다. 이는 TMD가 설치된 슬래브는 강성증가와 감쇠의 증가로 충격력에 의한 슬래브의 변위가 감소하게 되어 대부분의 주파수에서 저감효과가 나타나지만 일부 주파수 대역에서 TMD의 질량 증가로 인한 공진주파수의 저주파 대역 이동으로 인해 증폭이 일어날 수 있는 것으로 판단된다.
다음으로, 음압결과는 TMD의 설치 유무에 따라 큰 차이를 보였다. Fig. 6의 음압 스펙트럼을 보면 TMD를 설치하지 않은 경우 1차모드 대역에서 38.2로 큰 수치를 보였으나 TMD를 설치한 경우 2, 3차모드의 부근의 주파수에서 해석치 2 ~ 3 정도의 감소량을 보였지만 1차모드에서는 38.2에서 7.7으로 약 80 %의 저감량을 보여 해당 주파수 대역에서 큰 효과가 있음이 나타났다. Fig. 6의 1/3옥타브밴드 데이터를 1/1 옥타브밴드로 계산한 결과에서는 TMD를 설치하기 전에는 31.5 Hz에서 최대값을 보였으나 설치 후에는 125 Hz에서 최대값을 보였다. 저감량을 분석하면 31.5 Hz와 500 Hz에서 각각 6.8 dB, 8.4 dB로 저감효과가 명확하게 나타났고 250 Hz에서도 3.5 dB의 저감을 보였으나 63 Hz와 125 Hz에서는 0.4 dB, 0.9 dB로 상대적으로 적은 저감 수치를 보였다. 진동의 감소로 인해 슬래브를 통해 전달되어 방사된 음압이 전체 대역에서 감소할 것이라는 예상에 상반된 결과였다. 이는 실내 음장에 의한 룸모드 영향으로 인해 63 Hz ~ 125 Hz 대역 부근의 저감이 감소하여 이러한 결과가 나타난 것으로 판단된다.
3.3 질량비에 따른 TMD의 소음 저감 효과
추가적으로 슬래브 대비 TMD의 질량이 바닥충격음 저감 효과에 미치는 영향을 조사하기 위해 Table 3의 case 1(슬래브 대비 질량비 16 %)과 2(슬래브 대비 질량비 20 %)의 감쇠계수 0.10 기준으로 설계한 모델을 각각 해석하였다. 질량 증가는 1차모드(39.19 Hz)의 질량을 2배로 적용하고 해석을 수행하였다. 해석한 진동 및 음압 결과는 Fig. 6의 옥타브밴드 분석 결과와 같이 나타났다. 슬래브 대비 질량비 16 %, 20 %의 경우 모두 TMD가 없는 경우보다 낮은 음압레벨을 보였다. 하지만 저감 성능에 있어 질량비 16 %인 경우가 20 %인 경우와 250 Hz까지 큰 차이를 보이지 않았고, 500 Hz에서는 오히려 질량비 16 %가 더 큰 저감량을 보였다. 이는 TMD의 질량 증가가 오히려 Table 4에서 나타낸 고유진동수와 같이 바닥슬래브의 고유진동수 대역을 저주파수 대역으로 이동시키는 변화를 불러오게 되어 연성효과가 나타나는 음향모드 주파수에 영향을 미쳐 옥타브밴드 기준 31.5 Hz 영역에 영향을 준 것으로 해석된다. 단, 2차 ~ 4차 고유진동수들의 이동은 연성효과를 통해 음향모드 주파수의 이동을 발생시키지만 옥타브밴드 상의 63 Hz, 125 Hz에서의 효과가 31.5 Hz에 비해 작은 것으로 분석된다. 옥타브밴드 상의 250 Hz, 500 Hz 대역은 31.5 Hz와 마찬가지로 고유진동수의 이동으로 인한 음압저감 효과가 크게 나타난 것으로 판단된다. 슬래브 설치 후 질량비 16 %와 20 %의 고유진동수가 비슷하나 성능 차이가 나타나는 것은 이 연구의 대상 쉘구조물의 슬래브가 4면이 벽면에 의해 구속되어 일반적으로 TMD가 적용되는 빌딩에서 보이는 구조물 대비 질량비 증가가 성능의 향상으로 나타나는 것과는(18) 다른 거동을 보이는 것으로 판단된다. 따라서 음장과 구조를 고려한 종합적 분석이 필요하다고 판단되며 추후, 이에 대한 추가적인 연구를 수행할 예정이다.
전산해석 결과를 통해 TMD의 질량의 단순 증가보다는 설치할 슬래브의 질량과 고유주파수를 면밀히 분석하여 질량비를 설정해야 할 것으로 사료된다. 이 연구에서의 단순한 슬래브 대비 질량비로 산출한 질량비는 1.6 t으로 큰 수치를 보였으나 모드질량을 고려한 설계를 할 경우 TMD의 질량을 크게 줄일 수 있을 것으로 예상되며 이를 통해 125 Hz 주변 대역에서의 저감 성능을 확보할 수 있을 것으로 기대된다. 또한, TMD의 디튜닝 기법 적용 방안과 질량비·감쇠비 등의 TMD 설계 파라미터에 대한 영향을 향후 더욱 면밀히 검토하여 최적 설계화를 진행할 예정이다.
3.4 단일평가지수
이 연구의 TMD는 바닥충격음의 저감을 위한 목적으로 설계되었다. 이러한 효과를 확인하기 위해 전산해석상의 데이터를 토대로 단일수치평가량을 산출하였다. 단일수치평가량은 KS F ISO 717-2 : 2020을(19) 토대로 TMD가 적용되지 않은 경우와 case 1(질량비 16 %, 감쇠비 10 %)의 결과를 토대로 산출하였다. TMD를 적용한 경우와 적용하지 않은 경우의 1/1 옥타브밴드 값과 산출한 단일수치평가량은 Table 5와 같았다. 단일평가지수(LiA,Fmax 50-630)는 TMD가 없는 경우 53 dB로 나타났고, TMD가 설치된 경우 47 dB로 나타나 약 6 dB 저감이 나타났다. 단일수치평가량 분석을 통해 공동주택 슬래브에 적용할 경우 슬래브용 TMD가 바닥충격음에 있어 저감 효과를 거둘 수 있으며 전산해석 상 이 연구의 구조물과 같이 실제 공동주택에 비해 바닥충격음에 불리한 얇은 슬래브(180 mm) 조건에서도 높은 저감 성능을 확보할 수 있을 것으로 기대된다.
4. 결 론
이 연구는 바닥충격음의 저감을 위한 방안으로 질량동조감쇠기(TMD)의 슬래브 적용 시 효과를 전산해석을 통해 분석하였다. 또한 추가적으로 TMD의 슬래브 대비 질량비의 영향을 살펴보았다.
전산해석 결과 TMD를 설치하면 진동의 경우 특정 주파수에서는 효과가 미미할 수 있으나 대부분의 주파수 대역에서 감소하는 경향을 보였고, 음압은 1차모드의 경우 42 %까지 충격음의 저감이 나타났다. TMD의 진동저감효과 및 구조-음향 연성효과 고려 시 슬래브의 고유진동수 변화에 따른 영향에서 비롯된 것으로 사료된다. 따라서 바닥슬래브에 적용된 TMD가 바닥충격음 저감에 있어 효과적인 방안이 될 수 있는 것으로 판단된다.
TMD 설계 요소인 슬래브 대비 질량비의 영향조사를 통해 슬래브 대비 질량비 16 %와 20 %, 비적용 슬래브 비교 시 TMD를 설치한 경우가 확실히 저감성능을 나타냈고 특히 16 %의 저감성능 더 좋은 것으로 나타났다. 단순히 TMD의 질량 증가보다는 음장 및 구조를 고려한 종합적인 분석이 수행되어야 할 것으로 판단되며 이에 대해 추가적 연구가 필요하다고 판단된다.
이 연구의 결과는 TMD의 설계의 기초적인 연구로 더 다양한 조건에서의 결과를 통해 이 연구에서 제시한 설계요소 이외의 요소인 감쇠비나 기타 파라미터와 같은 요소의 영향을 조사하고 최적화하는 연구가 필요하다. 또한 전산해석의 결과만을 나타내었기에 실제 공동주택에서의 적용 시 효과에 대한 검증이 필요하다. 추후, 실제 공동주택과 유사한 공간을 갖는 시험주택을 대상으로 TMD를 설치하고 진동과 소리를 계측하여 TMD의 저감 효과를 검증하고 설계 요소의 확정 및 최적화 연구를 수행할 예정이다.
Acknowledgments
이 연구는 국토교통부/국토교통과학기술진흥원(과제번호 RS-2022-00144050)과 산업통상자원부 및 산업기술평가관리원(과제번호 20023556)의 지원으로 수행되었음.
References
- Ministry of Land, Infrastructure and Transport, 2023, Housing Act, Article 41-2, Sejong city, Korea.
- The Board of Audit and Inspection of Korea, 2019, Operating Status of the Floor Impact Sound Reduction System in Apartments, Audit Report, Seoul, Korea.
- Jeon, J. Y., Jeong, J. H. and Park, H. J., 2002, Subjective Evaluation of Floor Impact Noise Isolation Construction for Floor, Wall and Ceiling, Journal of the Architectural Institute of Korea Planning & Design, Vol. 18, No. 12, pp. 169~176.
-
Jeong, Y. and Jeon, J. Y., 2006, Vibration Characteristics of the Floor Structures Inserted with Damping Materials, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 16, No. 10, pp. 1036~1043.
[https://doi.org/10.5050/KSNVN.2006.16.10.1036]

-
Yeon, J., Kim, K., Choi, H., Yang, K. and Kim, K., 2013, Experiment Evaluation for the Heavy-weight Impact Sound of Dry Double-floor System - Effect of Rubber Hardness and Ceiling Structure, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 23, No. 1, pp. 34~40.
[https://doi.org/10.5050/KSNVE.2013.23.1.034]

-
Park, H. S., Oh, B. K., Kim, Y. and Cho, T., 2015, Low-frequency Impact Sound Transmission of Floating Floor: Case Study of Mortar Bed on Concrete Slab with Continuous Interlayer, Building and Environment, Vol. 94, Part 2, pp. 793~801.
[https://doi.org/10.1016/j.buildenv.2015.06.005]

-
Kim, K.-W., Kang, J.-S., Lee, S.-E. and Yang, K.-S., 2005, Floor Impact Sound Isolation Performance by Composition of Ceiling and Wall, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 15, No. 4, pp. 465~473.
[https://doi.org/10.5050/KSNVN.2005.15.4.465]

- Song, H.-S. and Ryu, J.-K., 2018, Effects of Sound Absorbent Gypsum Board in the Ceiling on Low-frequency Heavyweight Floor Impact Sound, The Journal of the Acoustical Society of Korea, Vol. 37, No. 5, pp. 323~330.
-
Shin, H. K. and Kim, K. W., 2019, Analysis Effects of Perforated Gypsum Board Ceiling Structure for Floor Impact Sound Reduction, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 29, No. 4, pp. 511~517.
[https://doi.org/10.5050/KSNVE.2019.29.4.511]

-
Ryu, J., Song, H. and Kim, Y., 2018, Effect of the Suspended Ceiling with Low-frequency Resonant Panel Absorber on Heavyweight Floor Impact Sound in the Building, Building and Environment, Vol. 139, pp. 1~7.
[https://doi.org/10.1016/j.buildenv.2018.05.004]

-
Kim, Y.-H., 2022, Acoustic Retrofit Approach of an Apartment Living Room Using Multi-perforated Gypsum Boards in Terms of Heavy-weight Impact Sounds, Sustainability, Vol. 14, No. 9, p. 5007.
[https://doi.org/10.3390/su14095007]

-
Kim, K.-W., Jeong, G.-C. and Sohn, J., 2008, Evaluation of the Dynamic Stiffness and Heavy-weight Floor Impact Sound Reduction by Composition of Resilient Materials, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 18, No. 2, pp. 247~254.
[https://doi.org/10.5050/KSNVN.2008.18.2.247]

-
Kim, K.-W., Choi, G.-S., Choi, H. and Yang, K.-S., 2004, Evaluation of Floor Impact Sound Performance According to the Reduction Methods, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 14, No. 9, pp. 811~818.
[https://doi.org/10.5050/KSNVN.2004.14.9.811]

-
Mun, D.-H., Song, G.-G., Lee, C.-S. and Park, H.-G., 2014, Reduction of Floor Impact Noise and Impact Force for PVC Floor Covering and Floor Mat, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 24, No. 7, pp. 501~508.
[https://doi.org/10.5050/KSNVE.2014.24.7.501]

-
Souza dos Santos, M. D., Fiuza Lima, D. V., Campuzano Carmona, J. E., Moreira Avila, S. and Doz de Carvalho, G. N., 2013, Vibration Control of a Gym Floor Using Tuned Mass Dampers: A Numerical Analysis, Modern Mechanical Engineering, Vol. 3, No. 3A, pp. 9~16.
[https://doi.org/10.4236/mme.2013.33A002]

-
Hwang, J.-S., Hong, G.-H. and Park, H.-G., 2008, Vibration and Noise Control of the Simply Supported Slab Using the Multi-tuned Mass Damper, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 18, No. 10, pp. 1006~1013.
[https://doi.org/10.5050/KSNVN.2008.18.10.1006]

- Korean Standard Association, 2022, Field Measurements of Floor Impact Sound Insulation of Buildings - Part 2: Method Using Standard Heavy Impact Sources, Korean Standard Association, Seoul, Korea. KS F 2810-2:2022.
- Woo, S.-S., Lee, S.-H., Hwang, J.-H. and Chung, L., 2013, Vertical Vibration Control of 39-story Steel Structure with Tuned Mass Damper, Journal of the Architectural Institute of Korea Structure & Construction, Vol. 29, No. 1, pp. 41~48.
- Korean Standard Association, 2020, Acoustics - Rating of Sound Insulation in Buildings and of Building Elements - Part 2: Impact Sound Insulation, Korean Standard Association, Seoul, Korea. KS F ISO 717-2:2020.

Suhong Kim graduated from Chonnam National University, Gwangju, Korea in 2020. He is currently a Ph.D. candidate in the school of architecture at Chonnam National University. His research interests are in the area of architectural acoustics, computational analysis and machine learning.

Jongkwan Ryu received his Ph.D. in Dept. of Architectural Engineering from Hanyang University, Seoul. He is currently as a professor in the school of architecture at Chonnam National University. His research interests are in the area of architectural acoustics, psycho-acoustics, acoustic barrier-free and machine learning authors’ bios be included. Others are optional.

Jae-Seung Hwang received a B.S., M.S. and Ph.D in Dept. of Architecture from Seoul National University in 1992, 1994 and 1998, respectively. He is currently working for Chonnam National University in the school of architecture as a professor. His main research area is vibration control and health monitoring, wind resistant design, analysis and control of structure-borne sound.