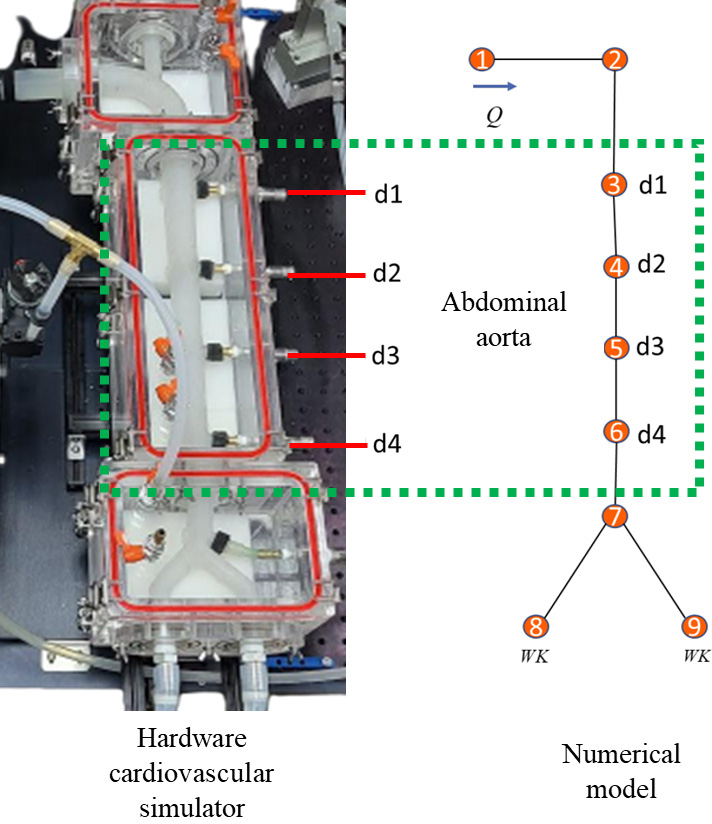
혈류역학 기반 1-D Flow Model을 이용한 복부 대동맥에서의 인체 맥파 전파 과정 재현
© The Korean Society for Noise and Vibration Engineering
Abstract
Human blood pressure is influenced by various factors in the arterial system, including arterial stiffness, wall thickness, cardiovascular diseases, heart rate, and cardiac output. When blood pressure propagates from the central aorta to peripheral arteries, the pulse pressure magnitude and waveform change. Understanding the pulse propagation mechanism in arteries can aid in the diagnosis and treatment of cardiovascular diseases. In this study, we modeled the human aorta using hemodynamic equations, assuming incompressible Newtonian blood and simplified cylindrical arterial vessels. Our model accurately represented the length and properties of the human aorta, including the ascending aorta, iliac arteries, and aortic bifurcation. Comparing the simulation results with cardiovascular hardware experiments, we confirmed the matching trends in pressure pulse wave propagation.
Keywords:
Hemodynamics, Blood Pressure, Abdominal Aorta, Propagation키워드:
혈류역학, 혈압, 복부대동맥, 전파1. 서 론
혈압은 심혈관계 건강 상태와 밀접한 관련이 있는 중요한 생리학적 지표로, 동맥 내에서 혈압이 어떻게 전파되는지에 대한 이해는 심혈관계 질환의 진단과 치료에 있어서 매우 중요하다. 이에 대해 혈관 경직도, 벽 두께, 심혈관 질환, 심박수, 심박출량과 같은 다양한 요소들은 혈압의 형성과 조절에 복합적으로 작용하고 있음이 알려져 있다(1).
0-D windkessel 모델을 이용하여 혈압 전파를 모델링하는 방법은 혈관 경직도와 혈압 증가에 대한 현상은 잘 반영하나, 혈압이 전파되는 과정에서 발생하는 현상들을 무시함으로써, 중첩 현상을 포함한 맥파 전파 과정에 대한 혈압 파형의 형상 변화를 확인하는 데에는 한계가 있다. 이러한 한계를 극복하기 위해 연구자들이 1-D 유동 모델을 도입하여 인체 동맥계를 더 정확하게 모델링하고자 했다(1). 그러나 무른 혈관에서의 혈압 전파로 인한 전진파와 후진파의 중첩 현상을 중점으로 한 실험적 검증은 진행되지 않았다.
이 연구는 1-D 혈류역학 지배방정식을 기반으로 하여 상행대동맥, 복부대동맥, 장골동맥까지를 포함한 하드웨어 심혈관계 시뮬레이터에(2,3) 상응하는 1차원 유동 수치 모델을 모델링함으로써 위의 한계를 극복하고자 했다. 하드웨어 시뮬레이터의 복부대동맥의 여러 위치에서 압력 파형을 측정하여 수치 모델의 혈압 전파 과정이 제대로 반영되었는지 확인했다. 이를 통해 이 연구는 혈류역학 기반 1-D 유동 모델을(4) 이용하여 인체 주요 동맥들을 모델링함으로써 복부 대동맥에서의 인체 맥파 전파 과정 및 압력 파형 중첩에 따른 형상 변화를 재현하는 것을 목표로 한다.
2. 연구 방법
2.1 1-D flow model
이 연구는 동맥 혈관에서의 혈압 전파 및 혈관 벽의 변형과 관련된 주요 현상을 반영하기 위해 인체 심혈관계의 특성을 고려하여 몇 가지 가정을 적용하였다.
인체 동맥의 주요 특징은 다음과 같다. 첫째, 인체 혈관은 매우 무르기 때문에 맥동에 의한 혈관 외내압 차이에 의해 혈관 벽의 많은 변형이 일어난다. 둘째, 동맥 혈관 벽은 투과가 거의 일어나지 않는다. 셋째, 혈관 단면은 거의 원형에 가깝다.
위의 특징을 바탕으로 다음과 같은 가정을 수립하였다. 첫째, 동맥 혈관은 가늘고 긴 원통형이며 비투과성이다. 둘째, 혈관은 곧게 뻗어있으며 혈관 벽은 선형 탄성 계수를 갖는다. 셋째, 혈관의 원주 방향 변위는 고려하나 길이 방향 변위는 무시될 수 있다. 넷째, 혈액은 비압축성 뉴터니안 유체이다(4).
혈류역학 지배방정식은 혈액과 혈관 벽의 상호작용과 관련하며 앞선 가정들을 반영하여 길이 방향으로 1차원화 한 수식은 식 (1) ~ 식 (3)과 같다(4).
| (1) |
| (2) |
| (3) |
식 (1)은 비압축성 유체의 연속방정식으로서 혈관의 시간에 따른 단면적 변화량과 길이 방향 변위에 따른 용적 유량률에 관한 식이다. 식 (2)는 나비에-스토크스 방정식을 나타낸다. 이는 유동의 운동량 보존을 나타내는 식이다. 유체의 시간에 따른 변화와 이동에 의한 변화, 압력의 공간적 변화에 따른 영향, 점성에 의한 영향, 항력에 의한 영향이 고려된 운동량 보존 법칙에 관련되어있다. 식 (3)은 외내압 차이와 혈관 단면적 관계를 나타낸다. 혈관의 탄성 계수가 클수록 압력 변화에 의한 혈관 벽의 변형이 작다.
말단 경계 조건으로는 1개의 저항과 1개의 캐패시터로 구성된 2-element windkessel 모델을 활용하였다(5). Windkessel 모델은 혈액이 말초혈관을 흐르는 동안의 혈액의 흐름을 설명하는 모델이다. Windkessel 모델은 동맥에 이어진 말초 혈관과 정맥계의 말초 저항과 컴플라이언스를 통합한 것이다. 말초 저항이 클수록 평균 혈압이 상승하는 효과가 있다. 컴플라이언스는 혈압의 급격한 변화를 완화시켜주는 역할을 한다.
2.2 하드웨어 심혈관계 시뮬레이터
하드웨어 심혈관계 시뮬레이터는(2,3,6) 인체 주요 대동맥을 모사하고 있다. 맥파 전파 과정 및 혈압 파형의 형성을 인체와 비슷한 조건에서 맞추기 위해 대동맥 혈관을 인체 혈관 물성을 참고하여 같은 크기 스케일로 제작한 것이다. 실험에 사용된 실리콘 관의 탄성계수는 310 kPa로, 건강한 40세 남성의 혈관 내 맥파 전파 속도를 맞추기 위해 제작되었다(2,7). 혈관벽 두께는 2 mm, 대동맥궁 내경은 14 mm, 분기점 이후 장골동맥 내경은 7 mm의 테이퍼드(tapered) 형상을 적용하였다. 복부대동맥 직선 길이는 551 mm이다.
펌프를 통해 물을 순환시키며 맥동에 의해 각 동맥 혈관 위치별로 압력이 전파된다. 물의 점도는 혈액에 비해 약 4배 가량 낮지만, 현실적인 실험 여건 상 혈액 유사한 점도의 유체를 사용하는 데는 제약이 있었다. 다만 수치 모델과 실험 모두에서 동일하게 물의 점도를 적용하여 일관된 비교가 가능하였으며, 각 위치에서의 압력 파형이 정성적, 정량적으로 잘 재현되었기에 혈액 점도에서도 유사한 경향성을 보일 것으로 예측할 수 있다(8). 그럼에도 혈액 점성을 직접 구현하지 못한 것은 이 연구의 한계로 남는다.
하드웨어 시뮬레이터는 상행대동맥, 복부대동맥, 장골동맥이 모사되어 있으며, 복부 대동맥의 각 위치에 4개의 압력 센서가 위치해있어, 혈압 전파에 의한 파형 형상의 변화를 측정하였다.
혈관의 물성과 치수, 대동맥 유량 등을 직접 측정하기 까다로운 인체에 비해 각 파라미터 값을 통제하여 결과를 확인할 수 있기 때문에 flow model을 이용한 수치적 재현 결과와 직접 비교하는 것이 가능했다.
2.3 복부 대동맥 혈압 전파 수치 모델링
1-D flow model을 이용하여 복부 대동맥에서의 맥파 전파 과정을 재현한 결과를 직접 검증하기 위해 하드웨어 시뮬레이터의 수치 정보와 실리콘 물성 정보를 이용하여 수치 모델을 구성했다. 심박수 60 BPM 1회 박출량 70 mL에 대해 계산된 복부대동맥 중심부에서의 평균 레이놀즈 수는 약 0.9975이다. 모델의 입력단 경계 조건으로는 실험에서 좌심실 펌프의 변위 정보를 통해 추정한 용적 유량률을 설정하였다. 말단 경계 조건으로는 장골 동맥에 해당하는 부분에서 2-elem windkessel 모델을 활용하였다. 저항 값은 3.89 × 108 Pa⋅s⋅m3, 컴플라이언스 값은 m3⋅Pa-1이다. 수치 모델의 해를 구하기 위한 솔버로는 OpenBF를 활용하였다(13).
Fig. 1은 하드웨어 시뮬레이터와 수치 모델을 나타내며, 복부대동맥의 네 위치의 압력을 측정 및 계산하여 맥파 전파 과정을 비교하였다.
3. 결 과
Fig. 2는 복부대동맥의 네 위치에서의 혈압 파형을 하드웨어 시뮬레이터를 통한 실측 결과와 수치 모델을 이용한 계산 결과와 비교한 것이다. 파형의 중첩 현상에 의한 실제 형상 변화를 정성적으로 비교하였을 때 수치 모델이 잘 재현한다는 것을 확인할 수 있다.
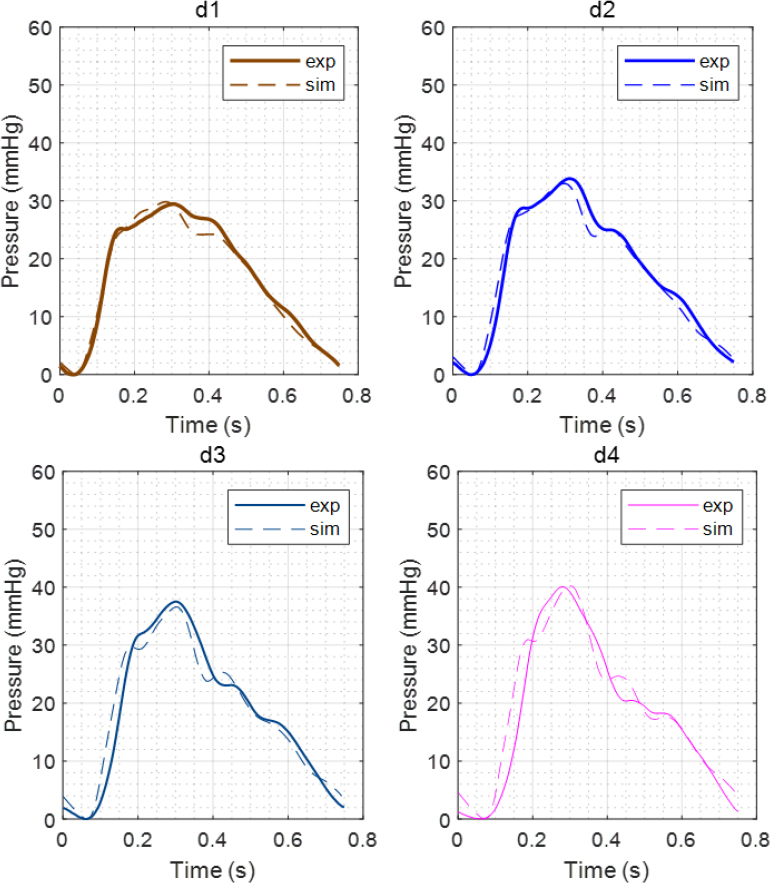
Pressure waveforms at each location on abdominal aorta; solid line: experiment result, dashed line: numerical simulation result
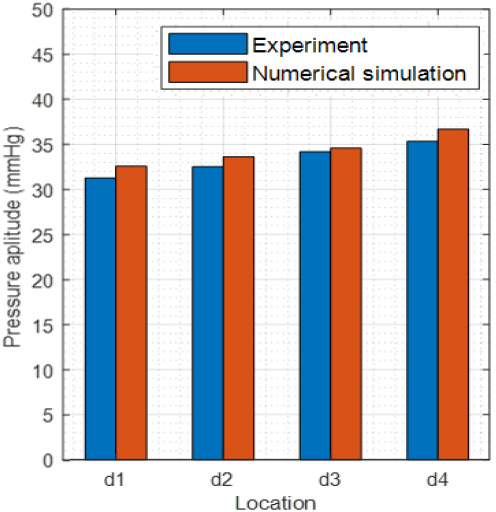
Fig. 3은 복부대동맥의 네 위치에서의 맥압 크기를 비교한 것이다. 수치 모델을 실측 결과와 동일하게 말단부로 갈수록 맥압 크기가 증가하는 경향을 보였다.
4. 결 론
이 연구에서는 1차원 유동 모델을 통해 복부대동맥에서의 맥파 전파 과정을 수치적으로 모사하고, 이를 실측 결과와 비교하였다. 수치 모델을 통해 재현한 혈압 파형의 형상과 맥압의 크기는 실측 결과와 유사한 경향성을 나타내었다. 이는 수치 모델이 복부대동맥에서의 맥파 전파 과정을 잘 모사하고 있음을 의미한다.
수치 모델과 실측 결과 모두에서 심장에서 멀어질수록 맥압의 크기가 증가하는 경향을 확인할 수 있었다. 이는 대동맥 분기점과 말단 부분에서 압력이 반사되고, 반사 지점에서 멀어질수록 전진파와 후진파 간의 중첩 구간이 줄어들기 때문인 것으로 해석된다. 또한, 맥파 전파 과정에서 전진파와 후진파의 중첩 시간차로 인해 혈관의 위치에 따라 압력 파형의 형상이 변화하는 것을 관찰할 수 있었다.
이러한 결과는 기존의 0차원 windkessel 모델로는 설명할 수 없었던 현상으로, 1차원 유동 모델의 유용성을 보여준다. 수치 모델을 통해 대동맥에서의 맥파 전파 과정을 성공적으로 모사함으로써, 맥파 전파 메커니즘에 대한 이해를 심화시킬 수 있었다. 나아가 이는 혈압 파형 분석을 통해 심혈관 상태를 역으로 진단할 수 있는 가능성을 시사한다.
다만, 이 연구에서 사용된 수치 모델은 혈관과 혈액 흐름에 대한 몇 가지 가정을 전제로 하고 있다. 혈관을 완전한 원통형으로 가정하고 벽 탄성을 일정하게 보았으나, 실제 대동맥은 주변 조직의 영향으로 단면이 원형에서 다소 벗어나며 위치에 따라 탄성의 차이가 있을 수 있다(9,10). 또한 혈액을 뉴턴 유체로 간주하였지만, 실제 혈액은 전단 변형률에 따라 점도가 변하는 비뉴턴 특성을 갖는다(11,12). 이러한 요소들이 혈류 및 맥파 전파에 미치는 영향을 고려하기 위해서는 보다 정교한 모델링이 필요할 것으로 보인다.
이상의 한계에도 불구하고 이 연구의 1차원 모델은 맥파 전파의 주요 메커니즘을 포착하고 실험 결과를 합리적으로 설명할 수 있었다는 점에서 그 의의를 찾을 수 있다. 향후에는 관 형상과 물성치, 경계조건 등에 대한 가정을 보완하고 실제 혈액 물성에 근접한 환경에서의 실험을 수행함으로써 모델의 예측 성능을 한층 개선할 수 있을 것으로 기대된다. 이를 통해 심혈관계 질환의 진단과 치료에 기여할 수 있는 연구로 발전시켜 나가고자 한다.
기 호 설 명
| A : | 혈관 단면적 |
| A0 : | 초기 혈관 단면적 |
| E : | 혈관벽 탄성 계수 |
| h0 : | 혈관벽 두께 |
| P : | 혈관 내 압력 |
| Pext : | 혈관 외 압력 |
| Q : | 용적 유량률 |
| a : | 코리올리 계수 |
| ρ : | 유체 밀도 |
| μ : | 유체 점도 |
| γυ : | 유체 프로파일 파라미터 |
| ν : | 혈관벽 푸아송비 |
Acknowledgments
이 연구는 2024년도 정부(산업통상자원부)의 재원으로 한국산업기술진흥원의 지원을 받아 수행된 연구임(P0017006, 2024년 산업혁신인재성장지원사업).
References
-
Reymond, P., Merenda, F., Perren, F., Rüfenacht, D. and Stergiopulos, N., 2009, Validation of a One-dimensional Model of the Systemic Arterial Tree, American Journal of Physiology-heart and Circulatory Physiology, Vol. 297, No. 1, pp. H208~H222.
[https://doi.org/10.1152/ajpheart.00037.2009]

-
Jeong, J.-H., Lee, B., Hong, J., Yang, T.-H. and Park, Y.-H., 2023, Reproduction of Human Blood Pressure Waveform using Physiology-based Cardiovascular Simulator, Scientific Reports, Vol. 13, No. 1, 7856.
[https://doi.org/10.1038/s41598-023-35055-1]

-
Jeong, J. H., Lee, B., Hong, J., Min, C. and Park, Y.-H., 2023, A Cardiovascular Simulator for the Reproduction of Blood Pressure Waveform and Magnitude, Trnasactions of the Korean Society of Mechanical Engineers A, Vol. 47, No. 8, pp. 627~633.
[https://doi.org/10.3795/KSME-A.2023.47.8.627]

- Melis, A., 2017, Gaussian Process Emulators for 1D Vascular Models, Doctoral Dissertation, University of Sheffield, Sheffield, England.
-
Westerhof, N., Lankhaar, J. and Westerhof, B. E., 2009, The Arterial Windkessel, Medical & Biological Engineering & Computing, Vol. 47, pp. 131~141.
[https://doi.org/10.1007/s11517-008-0359-2]

-
Jeong, J.-H., Kim, Y.-M., Lee, B., Hong, J., Kim, J. et al., 2020, Design and Evaluation of Enhanced Mock Circulatory Platform Simulating Cardiovascular Physiology for Medical Palpation Training, Applied Sciences, Vol. 10, No. 16, 5433.
[https://doi.org/10.3390/app10165433]

-
Hickson, S. S., Butlin, M., Graves, M., Taviani, V., Avolio, A. P. et al., 2010, The Relationship of Age with Regional Aortic Stiffness and Diameter, JACC: Cardiovascular Imaging, Vol. 3, No. 12, pp. 1247~1255.
[https://doi.org/10.1016/j.jcmg.2010.09.016]

-
Kung, E. O., Les, A. S., Figueroa, C. A., Medina, F., Arcaute, K. et al., 2011, In Vitro Validation of Finite Element Analysis of Blood Flow in Deformable Models, Annals of Biomedical Engineering, Vol. 39, pp. 1947~1960.
[https://doi.org/10.1007/s10439-011-0284-7]

-
Crosetto, P., Reymond, P., Deparis, S., Kontaxakis, D., Stergiopulos, N. et al., 2011, Fluid-structure Interaction Simulation of Aortic Blood Flow, Computers & Fluids, Vol. 43, No. 1, pp. 46~57.
[https://doi.org/10.1016/j.compfluid.2010.11.032]

-
Kim, H. J., Vignon-Clementel, I. E., Figueroa, C. A., LaDisa, J. F., Jansen, K. E. et al., 2009, On Coupling a Lumped Parameter Heart Model and a Three-dimensional Finite Element Aorta Model, Annals of Biomedical Engineering, Vol. 37, No. 11 pp. 2153~2169.
[https://doi.org/10.1007/s10439-009-9760-8]

- Yilmaz, F. and Gundogdu, M. Y., 2008, A Critical Review on Blood Flow in Large Arteries; Relevance to Blood Rheology, Viscosity Models and Physiologic Conditions, Korea-Australia Rheology Journal, Vol. 20, No. 4, pp. 197~211.
-
Bessonov, N., Sequeira, A., Simakov, S., Vassilevskii, Y. and Volpert, V., 2016, Methods of Blood Flow Modelling, Mathematical Modelling of Natural Phenomena, Vol. 11, No. 1, pp. 1~25.
[https://doi.org/10.1051/mmnp/201611101]

- Melis, A., 2018, openBF: Julia Software for 1D Blood Flow Modelling, Posted on Julia, Figshare.

Junki Hong received B.S. degree in mechanical engineering from Hanyang University in 2020 and M.S. degree in mechanical engineering from Korea Advanced Institute of Science and Technology(KAIST) in 2022. His research interests include cardiovascular system, hemodynamic model and neural operators.

Yong-Hwa Park joined KAIST in 2016 as an Associate Professor of the department of mechanical engineering devoting to research on vibration, acoustics, vision sensors and recognitions for human-machine interactions. His research interests include structural vibration; event/condition recognition from sound and vibration signatures utilizing AI; blood pressure and health monitoring sensors; 3D sensors, and lidar for motion measurements.