CFRP 스페이서의 허용한계 설정을 위한 구조해석 연구
© The Korean Society for Noise and Vibration Engineering
Abstract
A study was conducted to establish allowable limits for carbon fiber reinforced plastic (CFRP) spacers and improve analysis reliability by incorporating variable factors. First, stress-strain relationships were established for unidirectional lamina and for lamina in arbitrary directions. Classical laminated theory (CLT), a general CFRP analysis model, assumes thin laminated plates with constant in-plane strain across thickness, suitable for unidirectional laminates but inadequate for different direction laminates due to neglect of lateral shear deformation. Therefore, to account for lateral shear deformation effects, the first-order shear deformation theory (FSDT) was applied, addressing bending or twisting of laminates due to normal stress in the x-direction. Design limits were then set for torsional shear strength, buckling strength, and critical speed to establish standards for CFRP spacer products. Analytical verification of these design limits was performed to ensure compliance with established standards.
Keywords:
Carbon Fiber Reinforced Plastic(CFRP), Laminate, Spacer Structural Analysis키워드:
탄소강화플라소틱 소재, 적층판넬, 스페이서 구조해석1. 서 론
CFRP(carbon fiber reinforced plastic)는 저비중에 높은 비강도(specific strength) 특성을 가지고 있어 우주항공, 자동차, 선박, 건설, 스포츠 용품 등 산업 전반적으로 확대적용 되고 있다. 하지만 CFRP는 탄소섬유의 방향에 따라 기계적강도가 크게 달라지는 이방성을 갖고 있는 비선형 특성때문에 강도를 예측하기가 매우 어렵다. 또한, 탄소섬유를 적층 하거나 와인딩을 하여 성형을 하게 되는데 적층 방법에 따라 구조물의 거동 특성이 크게 달라진다. 따라서, 이러한 특성을 갖는 CFRP 제품을 해석을 통해 성능을 예측하기 위한 연구가 활발히 이루어 지고 있다.
최근 몇년간 CFRP 제품의 다양한 특성에 대한 연구가 활발히 이루어지고 있다. CFRP 제품의 탄소섬유를 평직(plainweave), 능직(twillweave), 단축(unidirectional), 다축(multidirectional)을 사용하여 적층 조건을 변경하며 정적 동적특성 분석 연구가 대표적이다(1). 탄소섬유 적층 각도에 따른 CFRP 평판의 실내소음을 이론적, 실험적인 방법을 통하여 적층 조건에 대한 더욱 정밀한 접근을 한 연구도 존재한다(2). 일반적으로 CFRP의 격자구조에 따른 강도 해석은 유한요소 방법을 적용하는데 등방성 격자구조 원통형 셸에 대한 와인딩 각도에 따른 압축성능에 대한 비선형 유한요소 해석을 실시하고 이를 시험과 비교 검증을 한 연구사례가 있다(3). 또한, 모드 해석법을 통해 알루미늄 평판과 CFRP 평판 재료에 대한 복합재료의 방향성에 따른 특성비교 연구와(4) 3-방향 직물 복합재료 붐 구조물을 CLT(classical laminated theory)이론으로 ABD 강성 행렬을 적용한 해석 연구는 해석이 어려운 CFRP 구조를 해석한 대표적인 사례이다(5). 이 외에도 일방향 프리프레그를 사용하여 원형 단면을 갖는 복합재 구조 부재를 이용한 충격 압궤 해석 연구(6), 외부 수압을 받는 복합재 원통 셸에 대한 복합재 적층 방향 변경에 따른 좌굴압력 거동을 확인하는 연구 등(7) 다양한 연구들이 수행 되고 있으나 적층판의 횡전단 변형을 고려한 연구는 진행되고 있지 않다. 따라서, 이러한 횡전단 특성을 반영한 CFRP의 구조물 특성을 해석을 통해 예측하고 실험으로 검증하며 해석의 신뢰성 향상을 위한 변수인자 반영 연구가 필요하다.
기존의 일반적인 CFRP 해석모델인 CLT이론은 적층판이 얇고 평판 두께에 대해 면내 변형률이 일정하다고 가정하기 때문에 일방향 적층판에 적용할 수는 있어도 각각 다른 방향으로 적층된 적층판 해석에는 적합하지 않다. 따라서 적층판의 횡전단 변형을 무시할 수 없는 경우일때는 FSDT(first-order shear deformation theory) 이론을 적용하여 해석의 정확도를 높히는 연구가 필요하다.
이 연구에서는 CFRP 소재로 설계된 스페이서(spacer) 제품을 설계최적화를 하기 위해 적층라미나의 응력-변형률 관계식과 전체 적층판의 구성방정식을 정립하고 회전에 의해 힘이 전달되는 스페이서 제품의 설계기준을 설정하기 위한 비틀림 전단강도, 좌굴강도, 임계속도에 대한 설계한도를 설정하고 설계기준의 해석적 고찰을 통해 설계한도를 검증하였다.
2. 스페이서 구조해석
2.1 일방향 섬유적층박판(lamina)에 대한 응력-변형률 관계식
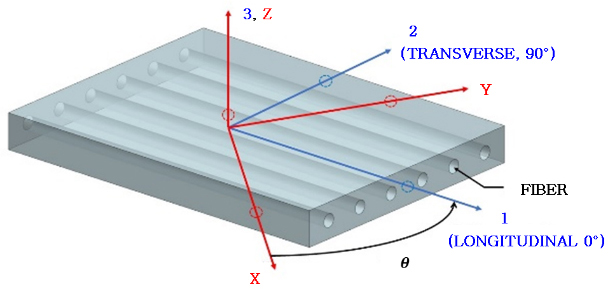
일방향 섬유적층박판의 경우 응력-변형률 관계식은 적층판이 직교 이방성 재료이고 평면응력 상태에 있는 것으로 간주하여 유도할 수 있다. Fig. 1은 3개 재료 특성 대칭면이 존재함을 보여준다. 따라서, 섬유적층박판은 직교 이방성 이므로, 일방향 2차원 섬유적층박판에 대한 응력-변형률 관계식은 식 (1)과 같다.
| (1) |
변환행렬의 각 요소는 Q11=E11/(1-ν12ν21), Q12=Q21=ν12E22/(1-ν12ν21), Q22=E22/(1-ν12ν21) 그리고 Q66=G12를 나타낸다. 식 (1)은 응력-변형률에 대한 관계식을 컴플라이언스로 식 (2)와 같이 표현 가능하며,
| (2) |
각 요소는 S111/E1, S221/E2, S66=1/G12, S12=S21=-ν12/E1을 나타낸다. 따라서, 면내 응력-변형률 관계식의 경우 단일 직교 섬유적층박판은 4개의 독립상수 Q11, Q22, Q12, Q66 또는 S11, S22, S12, S66 혹은 E1, E2, G12, ν12로 완전히 특성화 될 수 있다. ν21은 Betti’s reciprocal theorem, ν21E11=ν12E22에 의해 독립상수가 아니다.
즉, 평면응력하에서 직교 이방성 섬유적층박판에 대한 평면내 응력-변형률 관계식은 4개의 독립적인 탄성 매개변수(Q11, Q22, Q12, Q66 또는 S11, S22, S12, S66)로 표현할 수 있다. 그러나 평면응력하에서 0이 아닌 평면외 변형률 ε3은 순응매개변수 S13과 S23을 통하여 면내 응력 σ1과 σ2와 관련이 있다. 이 관련성 때문에 면내 응력-변형률 관계식에는 위의 4개 독립변수 외에 추가로 2개의 독립탄성매개 변수가 필요하다.
2.2 임의 방향을 갖는 섬유적층박판의 응력-변형률 관계
식 (1)의 응력-변형률 관계는 법선응력과 전단변형 사이에 아무런 연관이 없으며 전단응력과 법선변형률 사이에도 아무런 관련이 없음을 나타낸다. 그러나 섬유적층박판이 Fig. 1에서 처럼 임의의 x-y축을 따라 하중을 받게 될 때의 관계식을 변환행렬 T를 사용하여 식 (3) 및 식 (4)와 같이 표현할 수 있다.
| (3) |
| (4) |
식 (1)을 식 (3)에 대입하여 정리하면 식 (5)를 얻을 수 있다.
| (5) |
따라서, 식 (5)을 통해 임의 각을 갖는 x-y축에 관한 섬유적층박판의 응력-변형률에 대한 관계식은 식 (6)과 같이 표현된다.
| (6) |
응력-변형률에 대한 관계식을 컴플라이언스로 표현하면 식 (7)과 같다.
| (7) |
여기서 변환 행렬의 각 원소들은
| (8a) |
그리고,
| (8b) |
각각 식 (8a), 식 (8b)로 정의된다. 또한, 컴플라이언스의 변환 행렬을 식 (9)로 정리가 가능한데,
| (9) |
여기서, 변환행렬의 각 요소들은 식 (10)을 만족한다.
| (10) |
따라서, 재료 주축(1-2축)으로부터 임의의 각을 갖는 섬유적층박판의 탄성계수는 식 (10)으로부터 결정할 수 있다.
2.3 CLT 해석절차
Classical laminate theory(CLT)는 적층판의 해석을 위한 방법으로 널리 알려져 있고 광범위하게 사용되고 있는 방법이다. 이 이론의 목적은 적층판을 구성하는 개별 섬유적층박판 내의 응력을 계산하는 것이다. 개별 섬유적층박판 내의 응력을 결정하기 위해, 섬유적층박판의 탄성 거동이 먼저 결정되어야 한다. 따라서 전체 적층판은 개별 섬유적층박판의 탄성 거동의 단순한 병렬화를 나타낸다. 전체 변형으로부터 개별 섬유적층박판의 변형률을 계산하고 이어서 개별 섬유적층박판의 응력을 계산하게 된다. 강도해석을 수행하기 전에 전체 좌표계로 표현된 섬유적층박판의 응력은 국부 좌표계로 변환해야한다. CLT는 판 요소와 2D 맴브레인의 결합된 이론을 사용한다. 횡등방성 물질 거동을 보이는 개별 섬유적층박판은 일축 응력 상태에서 전단 응력을 유발하지 않기 때문에 법선 응력은 전단 변형을 수반하지 않는다. 그러나 서로 다른 방향으로 적층된 적층판에는 흥미로운 현상이 관찰된다. 적층판의 x-방향 법선 응력은 적층판을 구부리거나 심지어 비트는 현상까지 구현된다. 연결 강성 행렬(B-행렬)을 사용하면 해석에서 이러한 현상의 구현이 가능해진다. 전체 적층판에 대한 강성 행렬은 일반적으로 ABD-행렬로 알려져 있다. Kirchhoff 가정하에 성립하는 CLT는 횡 전단 해석을 할 수 없게 된다. 이는 층 내부의 전단응력을 고려하지 않기 때문이다. 일차 전단 변형론(FSDT)에서는 kinematic으로부터 개별 층 내부의 전단 변형을 고려한다. 만약 복합재의 횡전단 변형을 더 이상 무시할 수 없으면, 전단 변형을 고려하는 FSDT를 적용하여야 한다. 섬유적층박판은 횡등방성 재료 거동을 갖는 연속체로서 간주된다. 그러므로 그 구성 거동을 표현하는 Hooke의 법칙을 사용한다. Kirchhoff 변형률 관계식을 사용하여 섬유적층박판 내의 응력을 축소 강성행렬 식 (6)을 이용하여 계산한다.
적층판 내 임의의 점에서의 변형률은 식 (11)과 같이 정의된다.
| (11) |
식 (7)에 대입하면, 식 (12)와 같이 표현이 가능하다.
| (12) |
적층판을 구성하는 k번째 섬유적층박판의 합응력과 합모멘트는 식 (13)과 같이 정의한다.
| (13) |
여기서 zk와 zk-1은 k번째 섬유적층박판의 위, 아래 표면까지의 z-방향 거리를 나타낸다. 식 (12)에 표현된 섬유적층박판의 응력과 모멘트 합을 식 (13)에 대입하여 정리하면 식 (14)와 같다.
| (14) |
여기서, 식 (15)를 만족하고, 식 (14)와 식 (15)를 결합하면 식 (16)과 같이 전체 적층판 구성방정식을 표현할 수 있다.
| (15) |
| (16) |
적층판의 변형률은 ABD행렬의 역행렬을 통하여 식 (17)과 같이 결정된다.
| (17) |
팽창강성행렬 [A]에 정의된 요소들은 식 (18)과 같이 축방향 탄성계수 Ex와 후프방향 탄성계수 Eh를 계산하는데 사용되며, 이때 t는 구동축의 전체 두께를 나타낸다.
| (18) |
2.4 설계 기준의 해석적 고찰
동력 전달 축은 토크 전달 능력과 좌굴 토크 능력 그리고 측면 고유주파수 3가지 설계기준을 만족해야 한다. 스페이서는 탄소섬유로 제작되며 길이 4000 mm, 외경 260 mm, 두께 6 mm이며, 섬유적층박판 두께는 0.5 mm, 적층은 [(±10)5/(90)2]이다. 재료 특성 값은 Table 1과 같다.
비틀림 좌굴의 해석적 계산은 초기 설계가 목적과 용도에 적합한지 여부를 결정하기 위해 사용될 수 있다. 해석 결과는 설계하고자 하는 구동 축이 좌굴을 시작하는 토크를 나타낸다. 이러한 좌굴 토크는 스페이서 설계에서 임계 하중이 되며, 설계 전에 그 크기를 결정하는 것이 중요하다.
스페이서가 비틀림을 받을 때 비틀림과 비틀림 각 사이의 관계는 식 (19)와 같은 비틀림 방정식으로 표현된다.
| (19) |
여기서, T는 전달되는 토크이고, G는 전단계수이며, J는 극관성모멘트로 식 (20)과 같다.
| (20) |
만약, 스페이서의 허용비틀림각을 5°라고 한다면, 스페이서의 전단계수는 3.4 Gpa이므로 스페이서에 의해 전달되는 토크 T는 9595.5 Nm가 된다.
스페이서는 길고 얇은 장축이기 때문에 비틀림 좌굴에 취약하다. 따라서 스페이서를 이방성 원통 셸로 간주하여 좌굴 가능성을 확인한다. 좌굴 토크는 식 (21)과 같다.
| (21) |
여기서, Ex, Ey는 각각 x방향과 y방향의 탄성계수로 스페이서는 각각 83.31 Gpa, 10.2 Gpa값을 갖는다. 계산된 Tcr값은 32 000 Nm로 앞서 계산된 토크 값 9595.5 Nm를 초과하여 스페이서의 기본설계는 안전하다고 판단할 수 있다.
마지막으로 스페이서가 전달할 수 있는 최대 토크는 스페이서의 전단강도와 스페이서의 geometry 사이에 식 (22)와 같은 상관관계가 성립한다.
| (22) |
여기서 τ12는 스페이서의 전단강도 그리고 r0는 스페이서의 외경을 나타낸다.
모드 해석은 스페이서의 최대 허용 회전속도를 결정하기 위해 필요하다. 스페이서의 회전 속도는 구조물 손상을 예방하기 위해 첫 번째 고유주파수 보다 낮아야 한다. 고유주파수는 구조물의 치수와 비탄성계수의 함수이다. 양단 핀지지 경계조건의 비틀림 진동을 받는 중공형 원주 보의 고유주파수(fnb)는 식 (23)으로 구할 수 있다.
| (23) |
여기서 ms은 스페이서 단위 길이 당 질량으로 위와 같이 주어진다. 따라서 스페이서의 임계속도(Ncr)는 분당 회전수 즉 r/min으로 계산해야 하므로 초당 고유주파수인 Hz에 변환상수 60을 곱한 식 (24)로 계산된다.
| (24) |
3. 유한요소 해석
3.1 형상 및 유한요소 유형
ABAQUS standard 프로그램을 이용하여 셸 요소를 사용한 유한요소 해석을 수행하였다. 스페이서는 범용 S4 셸 요소로 구현하였다. 이 요소는 6개 자유도를 갖는 모서리 절점 4개가 있으며, 유한 막 변형과 대 회전을 포함하는 해석에 적합하다. 정확한 결과를 얻고 잔류응력의 선형 분포를 근사화시키기 위해 원주 방향 24 000개 요소와 길이 방향 360 000개 요소를 사용하였다. 이 요소는 1차 전단 변형론에 기초하며 대변형 해석에 우수한 성능을 갖는다. z-축은 스페이서 길이 방향에 해당하며 x-축은 반경방향 y-축은 원주방향을 나타낸다. 절점변위는 전체 좌표계에 대해 병진변위와 회전변위로 이루어진다. 말단 지점은 일련의 절점들을 주 절점에 연결시키는 kinematic coupling constraints를 이용하여 구현하였다. 이렇게 함으로서 셸 모델에 사용되는 말단 경계조건은 주 절점에만 요구되며, 토크 M 역시 주 절점에만 작용되어 응력집중을 방지할 수 있다. 이러한 구속을 사용함으로, 스페이서 끝 단면은 고정되고 다른 끝 단면에 대해서는 회전만을 허락할 수 있게 된다. 스페이서의 처짐, 응력, 진동 그리고 좌굴거동을 해석하였다.
3.2 경계조건
해석유형, 즉 모드해석 혹은 탄성좌굴해석에 따라 적합한 경계조건이 스페이서 유한요소 모델에 부여되어야 한다. 모드해석에서는 경계조건으로 모드 형상과 상응하는 고유주파수를 얻기 위해 스페이서의 일단은 고정되고, 타단은 회전만 허용된다. 좌굴해석에서는 스페이서 일단은 완전 고정되고 타단은 토크를 작용 시킴으로서 좌굴모드와 하중이 계산되며 최저 값이 임계 토크 좌굴하중이 된다.
3.3 파단강도 해석
스페이서의 토크 전달 능력은 설계 적용 가능성을 확인하는 첫 번째 특성이다. 실제 사용에서 스페이서의 양단은 삽입형 이음으로 동력계에 부착된다. 이러한 이음을 나타내기 위하여 모멘트는 스페이서 양단에서 각각 66 mm 만큼의 스페이서 내면에 작용되어지도록 한다. 만약 토크가 스페이서 양단 변에 작용하게 되면, 집중하중의 발생으로 불균일 응력분포를 발생시킨다. 토크 전달 능력을 결정하기 위해 최대응력 파손기준과 Tsai-Wu 파손기준을 적용하였다. 즉 적층 내 임의의 섬유적층박판이 파손되면 스페이서는 파손된 것으로 가정하고 그 때의 응력을 전단강도로 규정하였다. 유한요소 모델은 스페이서의 거동을 예측할 수 있도록 생성하였다.
Table 2는 최대응력 파손기준과 Tsai-Wu 파손기준을 적용하여 5000 N-m 토크를 작용시켰을 때 스페이서 각 플라이의 파손지표를 나타낸다. 이 파손 지표가 1을 초과하면 파손이 발생한 것으로 본다.
Table 2에서 확인할 수 있듯이 어떤 플라이에서도 파손지표는 1에 못 미치고 있다. 위 파손 지표 값을 기준으로 스페이서의 전단강도는 식 (25)와 같이 추정할 수 있다.
| (25a) |
또는
| (25b) |
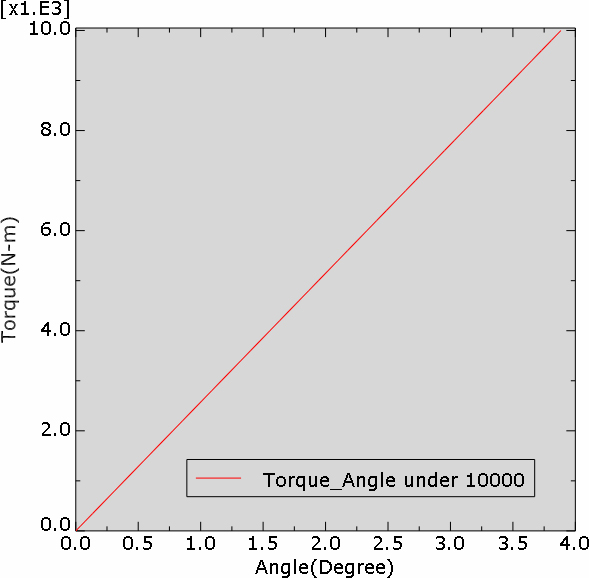
수치해석 결과 5000 N-m의 토크가 작용했을 때 각 변위는 대략 2° 만큼 발생함을 Fig. 2에서 확인할 수 있다.
3.4 비틀림 좌굴 해석(고유치 좌굴 해석)
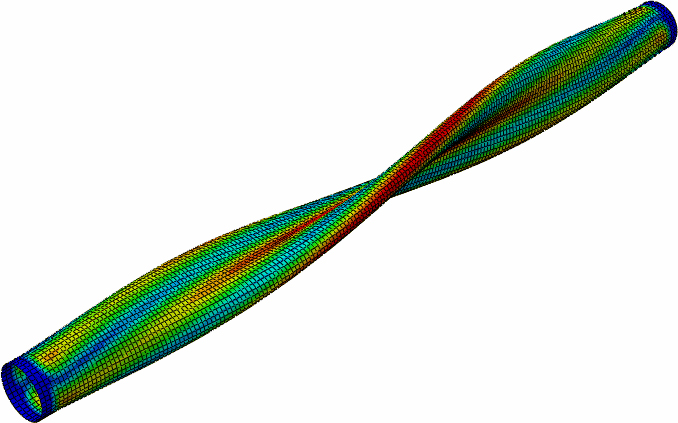
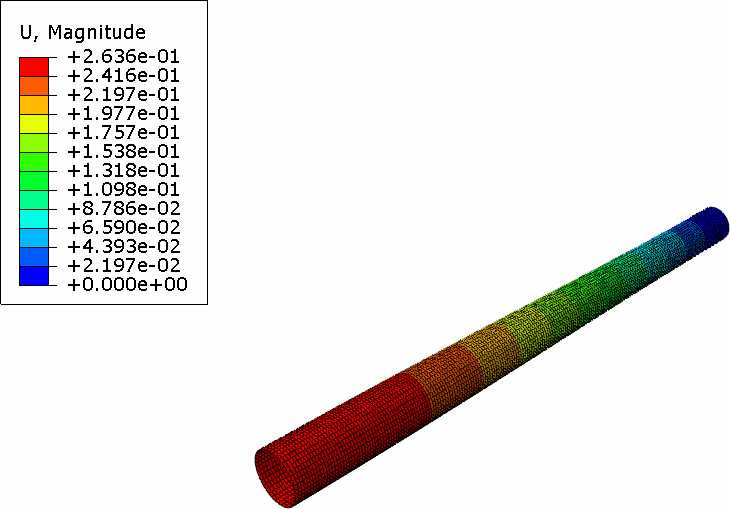
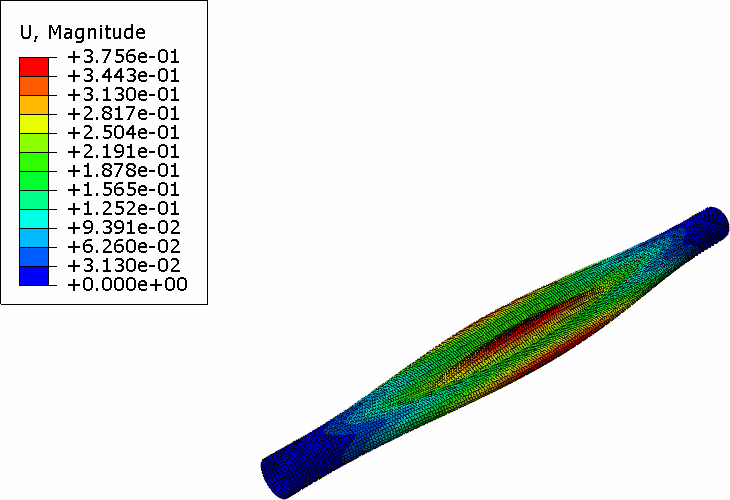
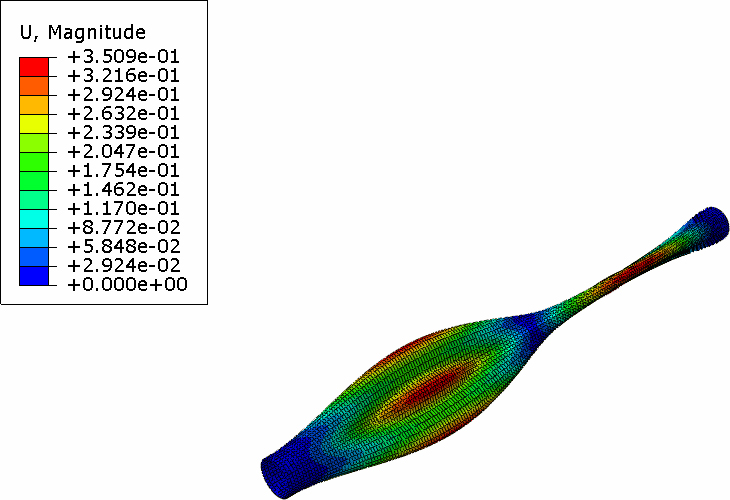
고유치 좌굴해석에서는 구조물의 안정성을 잃기 전에 지지할 수 있는 최대 토크를 찾기 위해 좌굴 이전에는 선형강성행렬이 변하지 않는 것으로 가정한다. 이 해석에서 경계조건은 실제의 운전 조건과 동일하게 하기 위하여 일단은 고정되고 다른 일단은 비틀림만 허용되었다. 구속 조건을 사용하여 양단 끝에서 66 mm까지 스페이서 내면을 중심점과 연계 구속시키고 경계조건과 하중을 이 중심점에 작용하도록 하였다. 단위하중을 작용시킴으로서 해석결과 얻어지는 고유치가 비틀림 좌굴 강도가 된다. 좌굴 비틀림 강도는 스페이서의 칫수와 구성재료의 속성에 의존한다. 임계 좌굴은 재료 파손 보다는 스페이서의 파손 모드이다. 해석 결과는 Fig. 3 ~ Fig. 5와 같다, 첫 번째 비틀림 좌굴 강도는 56 946 N-m이며 좌굴 모드는 Fig. 3과 같다. Fig. 3 ~ Fig. 5는 스페이서의 1차부터 3차까지의 고유치 모드를 보여준다. 스페이서의 단면 대칭때문에 1차와 2차의 고유치가 동일하게 나타난다. 또한 고유치가 음의 숫자로 나타나는 것은 좌굴 토크가 반대 방향으로 작용함을 나타내며 그 크기는 동일하다.
해석 결과를 검증하기 위한 Fig. 6과 같이 해석과 동일한 경계조건으로 최대토크시험을 진행을 하였고 시험결과 Table 3과 같이 해석과 시험결과가 거의 동일한 수준으로 높은 해석 신뢰성을 보였다.
3.5 진동해석(모드 해석)
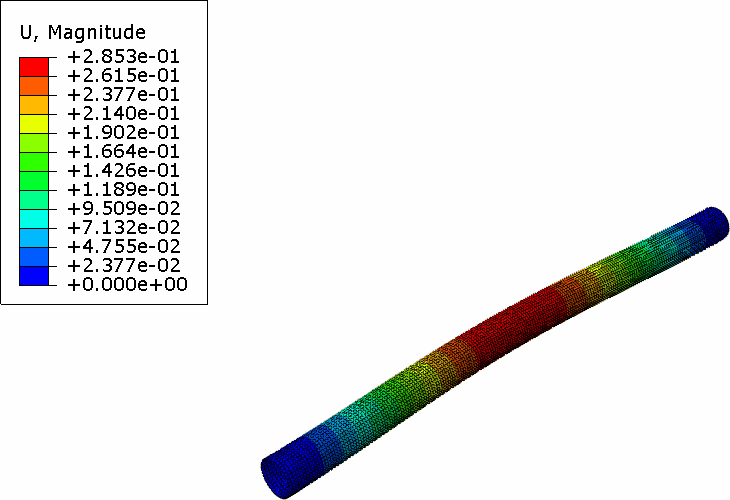
스페이서의 고유주파수와 모드 형상을 결정하기 위해 torsional-fixed 경계조건을 갖는 고유모드 해석을 수행하였다. 모드해석은 스페이서의 최대 허용회전속도를 결정하는데 필요하다. 최대 회전 속도는 구조물의 손상방지를 위해 첫 번째 고유진동수 보다 작아야 한다. 고유주파수는 스페이서의 치수와 비탄성계수(E/ρ)의 함수이다. Fig. 7 ~ Fig. 10에서 알 수 있듯이 1차 고유 진동 모드는 133.86 Hz 주파수에서 스페이서 중앙부를 중심으로 bending mode shape을 나타내며, 3차 고유 진동 모드는 139.76 Hz 주파수에서 타단부로 부터 중앙으로 breathing mode shape을 나타낸다. Breathing mode shape은 4차 고유 진동 모드에서 176.76 Hz와 6차 진동 모드 210.36 Hz 주파수에서 스페이서의 중앙부로부터 타단부 방향으로 mode shape을 가진다.
Fig. 11과 같이 해석 결과 검증을 위한 모달 테스트를 진행하고 해석 결과와 오차를 산출하였다. 실험은 완벽한 구속 조건을 구현하는 것이 현실적으로 불가능함을 감안하여 free-free 경계조건에서 진행하고 이론 값과 free-free 경계조건에서의 해석 값과의 오차를 산출하였다.
Table 4에 나타난 것처럼, 모달테스트 최대 오차는 5차, 6차 모드에서 발생하였으며 각각 6.22 %, 7.81 %의 오차율을 나타냈지만 나머지 1차, 2차, 3차, 4차, 7차 모드에서 모두 0.28 % ~ 3.64 % 수준의 오차범위를 보였다. 따라서 breathing 모드 또는 torsional 모드에서는 오차가 상대적으로 크게 나타나긴 하였지만 일반적인 bending 모드에서는 상당히 낮은 오차를 보였기 때문에 실험을 통하여 해석결과의 신뢰성을 확인할 수 있었다.
4. 결 론
이 연구는 CFRP 제품이 설계요구성능을 만족하는지 예측하는 해석연구와 해석의 신뢰성 향상을 위한 변수인자를 반영하기 위한 연구를 하였다.
회전에 의해 힘이 전달되는 CFRP 스페이서의 비틀림 전단강도, 좌굴강도, 임계속도에 대한 설계한도 설정을 위해 일방향 개별 섬유적층박판과 임의방향을 갖는 개별 섬유적층박판의 응력-변형률 관계식을 각각 정립하였고, 서로 다른 방향으로 적층된 전체 적층 섬유적층박판은 ABD-행렬의 연결 강성 행렬(B-행렬)을 사용하여 횡전단 응력을 구현하는 변수인자을 정립하였다. 그리고 일반적인 CLT 모델로는 횡전단 변형을 반영할 수 없으므로 복합재의 횡전단 변형을 무시할 수 없으면 전단 변형을 고려하는 FSDT를 적용하여 계산 하여야 한다. 해석모델인 스페이서는 길이 4000 mm, 외경 260 mm, 두께 6 mm이며, 섬유적층박판 두께는 0.5 mm, 적층은 (±10)5/(90)2로 진행하였으며 동력전달 축으로서 비틀림 전단강도, 비틀림 좌굴강도, 임계속도에 대한 설계한도 설정을 구조해석과 실험을 통하여 검증하였다.
기 호 설 명
| E : | 일방향 라미나 탄성계수 |
| G : | 일방향 라미나 전단계수 |
| J : | 극관성 모멘트 |
| kx : | x 방향 곡률 |
| ky : | y 방향 곡률 |
| kxy : | xy 평면의 곡률 비틀림 |
| Nx : | x 방향의 수직응력 |
| Ny : | y 방향의 수직응력 |
| Nxy : | xy 평면 전단응력 |
| {n} : | 응력 벡터 |
| Mx : | x축 주변 모멘트 |
| My : | y축 주변 모멘트 |
| Mxy : | xy 평면의 토크 |
| {m} : | 모멘트 벡터 |
| σ : | 응력 |
| ε : | 변형률 |
| εx : | x 방향 변형률 |
| εy : | y 방향 변형률 |
| : | x 방향 초기 변형률 |
| : | y 방향 초기 변형률 |
| ε0 : | 초기변형률 |
| τ : | 전단응력 |
| γ : | 전단변형률 |
| : | xy 평면의 초기 전단변형률 |
| γxy : | xy 평면의 전단 변형률 |
| ν : | 프와송비 |
| η : | 임의방향의 라미나 탄성계수 |
| λ : | 곡률 |
Acknowledgments
이 과제는 부산대학교 기본연구지원사업(2년)에 의하여 연구되었음.
References
-
Kim, C.-J., 2016, Dynamic Analysis of Carbon-fiber-reinforced Plastic for Different Multi-layered Fabric Structure, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 26, No. 4, pp. 375~382.
[https://doi.org/10.5050/KSNVE.2016.26.4.375]

-
Bang, S., Kim, Y. S., Back, J. and Lee, S.-K., 2018, Interior Noise Characteristics Inside of Enclosure of CFRP Composite Plates Made of Different Carbon Fiber Lamination Angles, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 28, No. 5, pp. 617~624.
[https://doi.org/10.5050/KSNVE.2018.28.5.617]

- Ben, G., Sao, S. and Kishitani, N., 2008, Nonlinear Buckling Analysis of CFRP isogrid Cylindrical Shells, Proceedings of the 15th International Congress on Sound and Vibration (ICSV15), pp. 1530~1537.
- Han, E. K., Oh, J. E. and Bang, T. K., 1989, A Study on the Dynamic Characteristics of CFRP PLATE by Modal Analysis Method, Journal of the Korea Society of Automotive Engineers, Vol. 11, No. 1, pp. 44~50.
- Byun, S.-W., Yang, J.-Y., Lee, S.-Y. and Roh, J.-H., 2022, A Study on the Modeling for Boom Structural Behaviors of the Triaxial Woven Fabric Composite, Journal of Aerospace System Engineering, Vol. 16, No. 6, pp. 99~105.
- Kim, H.-S. and Kim, J.-H., 2021, A Study on Simulation of Impact Collapse in Carbon Composite using Stress-based Failure Criterion, Journal of Advanced Engineering and Technology, Vol. 14, No. 1, pp. 9~12.
-
Jung, H. Y., Cho, J. R., Bae, W. B. and Lee, W. H., 2012, Buckling Analysis of Composite Cylindrical Shell using Numerical Analysis Method, Transactions of the Korean Society of Mechanical Engineers A, Vol. 36, No. 1, pp. 51~58.
[https://doi.org/10.3795/KSME-A.2012.36.1.051]


Kyungsun Yoo is currently a mechanical engineering M.S student at Pusan National University, Since 2006, he has been working as a vehicle parts design engineer at Sungwoo Hitech.

Min Park is a research engineer at the R&D Center of JAC Coupling. He holds a M.S. from Pusan University, and a B.S. from Dong-a University.

Byeongyong Lee is an Associate Professor of School of Mechanical Engineering at Pusan National University. He holds a M.S. from Seoul National University and Ph.D. from Georgia Institute of Technology Before joining Pusan National University in 2020, he worked as a postdoctoral fellow at Georgia Institute of Technology and Research Engineer at POSCO.

Seunghun Baek is an Assistant Professor of Mechanical Engineering at Pusan National University. He holds a Ph.D. and M.S. from the University of Michigan and a B.S. from Yonsei University. Before joining Pusan National University in 2020, he worked as a Research Engineer at Ford Motor Company and participated in a program at Sandia National Laboratories.