위상최적화 기법을 활용한 얇은 평판의 굽힘 진동에서 발생하는 특정 모드의 비선형성 수동제어
© The Korean Society for Noise and Vibration Engineering
Abstract
This paper presents the first attempt to optimize the nonlinearity of flexural vibrations in thin plates using topology optimization techniques. Nonlinearity in the flexural vibrations of thin plates is characterized by an increase or decrease in natural frequencies in the frequency domain as the external force or internal energy increases, a phenomenon known as hardening/softening nonlinearity. This study adopts topology optimization techniques to identify the layout of thin plates that either enhance or mitigate this nonlinearity. The nonlinearity of the optimum layout was verified through a nonlinear frequency response curve, obtained using the harmonic balance method.
Keywords:
Topology Optimization, Thin Plate, Geometric Nonlinearity키워드:
위상최적화, 얇은 평판, 기하비선형1. 서 론
모든 구조물은 내재적으로 정적/동적 비선형성을 내포한다. 하지만, 구조물의 일반적인 동적 상태에서 발생하는 비선형성의 영향은 극히 미미하기 때문에 구조물의 동적특성을 파악하는데 고려하지 않는다. 그러나 마이크로 또는 나노 크기의 구조물에서는 선형성만을 고려해서는 정확한 동적특성을 파악하기 어렵게 되어 필히 비선형적 동적 특징들을 고려해야 한다(1). 동적상태에서 고려해야 하는 비선형성 특징들은 구조물의 안전성(2), bifurcation(3), 에너지-주파수 의존성(4), 내부공진 등(5) 다양하다. 일반적으로 비선형성적 동적 특징은 이 영향을 줄이기 위한 극복의 대상으로 여겨져 왔으나, 최근에는 동적 비선형성을 활용한 MEMS 장치를 개발하는 연구도 진행되었다(6). 이 연구는 얇은 평판에서 발생하는 비선형을 강화 또는 저감시키는 평판의 형상을 찾는 것을 목적으로 한다. 얇은 평판이 내재적으로 가지는 동적 비선형성은 경화 비선형으로 내부 에너지 및 외부 힘의 크기에 따라 고유진동수가 증가한다. 경화 비선형은 대표적인 기하비선형성으로 구조물이 대-변형시 중간평면(mid-plane)에서의 신장(stretch)으로 인한 전단응력의 증가로부터 기인한다(7). 얇은 평판에서 발생하는 동적 비선형에 대한 내용은 참조논문에 잘 정리되어 있다(8). 이 논문에서 목적하는 동적 비선형성의 수동 제어를 수행하기 위해 비선형성의 정도를 나타내는 목적함수를 모달영역에서 정의하였다. 설계 변수에 대한 목적함수의 민감도는 보조변수법(adjoint variable method, AVM)으로 구하였다. 만약 특정 모드의 동적 비선형성 중 경화성을 강화시키는 최적설계를 수행한다면 외부 가진력의 크기가 증가함에 따라 초기 형상에 비해 최적 형상에서 공진 주파수의 크기가 증가하는 경향이 커질 것이고, 경화성을 약화시키는 최적설계의 결과 형상은 외부 가진력의 크기의 증가에 따른 고유진동수의 크기 변화가 상대적으로 적을 것이다. 이 연구에서는 최적화 결과를 검증하기 위해 비선형 주파수 응답 선도(nonlinear response curves, NRCs)를 확인한다. 이 선도를 통해 외부 가진력에 따른 공진주파수의 변화를 확인할 수 있다. 비선형 주파수 응답 선도를 구하는 여러 방법론들이 있지만 이 연구에서는 조화 균형 기법(harmonic balance method, HBM)을 활용하였다(9).
2. 얇은 평판의 비선형 유한요소 모델링
이 연구에서는 얇은 평판의 유한요소 모델링을 위해 von Kármán 비선형 변형률-변위 관계식을 식 (1)과 같이 사용하였다.
| (1) |
여기서 와 는 선형 막(membrane) 변형률과 선형 굽힘 변형률이고, 는 기하 비선형 막 변형률이다. u와 v는 각각 x와 y방향의 평면 내(in-plane)변위, w는 z방향의 횡-방향(transverse)변위이다. 얇은 평판의 운동 방정식은 가상일 원리로부터 유도 가능하다.
| (2) |
여기서,
| (3) |
| (4) |
| (5) |
식 (2)에서 U, T, W는 각각 회복력, 관성력, 외력에 의한 가상일이다. 개별 항들에 대한 가상일은 식 (3) ~ (5)에 나타내었다. D와 D‘는 각각 막의 강성과 굽힘 강성 행렬이다. A는 면적이며, ρ와 h는 각각 질량 밀도와 두께이다. N은 형상 함수(shape function) 행렬로 legendre 다항식중에서 rodrigues 형태를 사용하였다, fw는 횡-방향의 외부 힘 벡터이다. 이 연구에서는 횡-방향의 외부 힘만 고려한다. 위첨자 T는 전치 행렬을 나타낸다. 식 (1)을 식 (2)에 대입하고 면내 관성을 무시하면 식 (6)과 같은 운동 방정식이 유도된다.
| (6) |
여기서,
| (7) |
| (8) |
식 (6)에서, M과 r은 각각 질량 행렬과 응답 벡터이며, C는 감쇠 행렬이다. 아래첨자 w는 횡-방향을 나타내고, KL과 KNL은 각각 선형, 비선형 굽힘 강성 행렬이다. 여기서, 비선형 강성 행렬은 횡-방향 변위 벡터 w의 이차 함수로 표현된다. 비선형 강성 행렬의 자세한 형태는 식 (7)에서 나타내었다. 여기서, K2는 rw과 선형적관계인 비선형 강성 행렬이며, K4는 rw과 이차함수관계로 표현되는 비선형 행렬이다. 이들의 자세한 행렬 구성은 식 (8)에 있으며, 여기서 행렬 B와 G는 형상함수(shape function)의 공간에 대한 미분으로 표현되는 것으로 식 (1)과 식 (3)을 통해 유추할 수 있다. 이 행렬들에 대한 자세한 형태는 참조논문(8)에 명기되어 있다. 주목할 점은, 식 (6)에서 확인되듯이 얇은 판에서 ‘면내 관성’ 항을 무시하면 운동 방정식이 횡-방향만으로 표현될 수 있다는 것이다. 이 연구의 목적이 특정 모드의 비선형성을 조절하는 것이므로, 이를 위해 공간영역(spacial domain)의 운동방정식 식 (6)을 모달영역으로 치환한다. 선형 모드이론에 근거하면 식 (6)은 식 (9)와 같이 변환 가능하다.
| (9) |
식 (9)는 p 번째 모드의 운동방정식을 모달 영역에서 표현한 것이다. 여기서 q는 일반좌표이고 하첨자 i, j, k는 개별모드를 나타내는 인덱스이며 벡터 ϕ는 모드형상이다. 는 개별 모드들간의 연성(coupling) 및 해당 모드의 비선형성의 정도를 나타내는 인자로 자세한 형태는 식 (10)과 같다.
| (10) |
만약 개별 모드들이 잘 분리되어 있고(well separated mode), 약한 비선형성(weak nonlinearity)를 가정하면 식 (9)는 식 (11)과 같이 표현 가능하다.
| (11) |
식 (11)은 일반적인 duffing equation의 형태로 3차 비선형성을 포함하고 있다. 이 연구에서는 을 통해 특정모드의 비선형성을 조절하려고 한다.
3. 최적화 문제
3.1 최적화 문제 정의와 설계 민감도
이번 장에서는 얇은 평판의 특정 모드의 비선형성을 수동 제어하기 위한 최적화 문제를 정의한다.
| (12) |
식 (12)에서 c는 목적함수로 +/- 부호는 각각 p 번째 모드의 경화 비선형성의 강화/약화를 유도하고 목적함수의 크기 /는 식 (11)에서 3차 비선형 계수를 해당 모드의 고유주파수로 나눔으로써 경화성의 정도를 나타낸다. ρ는 밀도 기반 위상최적화의 설계변수이다. 이 식에서 보이듯이 이 최적화 과정에서는 체적 구속조건과 관심 모드의 고유진동수에 대한 구속 조건을 정의하였다. 위 식에서 두 번째 구속조건으로 고유진동수의 변화량을 구속한 이유는 최적화 과정에서 모드형상의 급격한 변화를 제한하기 위함이다. 최적화를 수행하기 위해서는 설계 변수에 대한 목적함수의 민감도가 필요하다. 이 연구에서는 보조변수법으로 민감도를 구하였다.
| (13) |
식 (13)은 설계변수에 대한 목적함수의 민감도이다. 여기서 λ과 η는 민감도를 구하기 위해 사용된 보조변수들로 식 (14)의 관계를 만족해야 한다.
| (14) |
3.2 필터링(filtering) 및 매개변수화(parameterization)
이 연구에서는 밀도기반의 위상최적화 문제에서 자주 발생하는 체크보드패턴형상을 제거 또는 저감시키기 위해 밀도기반 필터를 사용하였다.
| (15) |
는 필터링된 i 번째 요소의 밀도이다. w(xj)는 가중치 함수로 자세한 형태는 식 (15)에 명기되어있다, 여기서 r은 사용되는 필터의 반지름이고, 벡터 xj와 xe는 j 번째 요소와 e 번째 요소의 위치벡터들이다. υj는 i 번째 요소의 체적이다. Ne,i는 i 번째 요소 주위에 필터의 반경 r안에 근접하게 위치한 요소들의 집합을 나타낸다. 이 연구에서는 최적화 과정 중 설계변수들이 0, 1이 아닌 불명확한 중간값을 갖는 회색지역을 줄이기 위해 임계값 투영 필터(threshold projection filter)를 사용하였다(10).
| (16) |
는 필터된 설계변수로 물리적 설계변수로 불린다. η는 투영필터에서 정의된는 임계값으로 이 연구에서는 0.5로 설정하였다. β는 투영필터의 과도구간의 기울기를 조절하는 변수로 β→∞이면 식 (16)은 불연속 스텝함수가 된다. 이 연구에서는 최적화 과정 중 이 값을 1부터 시작하여 매 30번의 해석마다 두 배씩 증가시켰고 최대값 βmax로 설정하였다. 밀도 기반 위상최적화는 개별 요소들의 영율(Young’s modulus)과 질량 밀도를 물리적 설계변수를 사용하여 보간한다. 영율과 질량 밀도의 보간식은 식 (17)과 같다.
| (17) |
E와 γ는 영율과 질량밀도를 나타낸다. 하첨자 1과 0은 각각 개별 요소가 고체상태일때와 공극상태를 나타내며, E0=10-9ㆍE1, γ0=10-6ㆍγ1관계가 있다. 이 식에서 상첨자 pk와 pm은 강성과 질량에 작용하는 패널티 계수(penalization factor)로 진동관련 문제에서 지역적 모드형상의 생성을 막기위해 사용된다. 이 연구에서는 pk=3과 pm=1을 사용하였다.
4. 위상최적화 예제
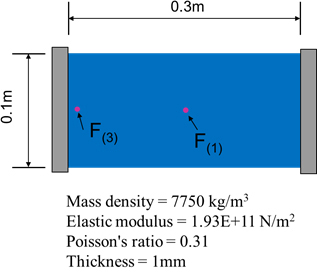
앞서 제시한 정식화의 타당성을 검증하기 위해 Fig. 1에 보이는 양단고정평판을 대상으로 수치예제를 수행한다. 해당 그림안에 사용된 평판의 물성치도 명기되어 있다. 이 수치예제에서는 첫 번째와 세 번째 모드들의 비선형성을 제어하기 위한 최적설계를 진행한다.
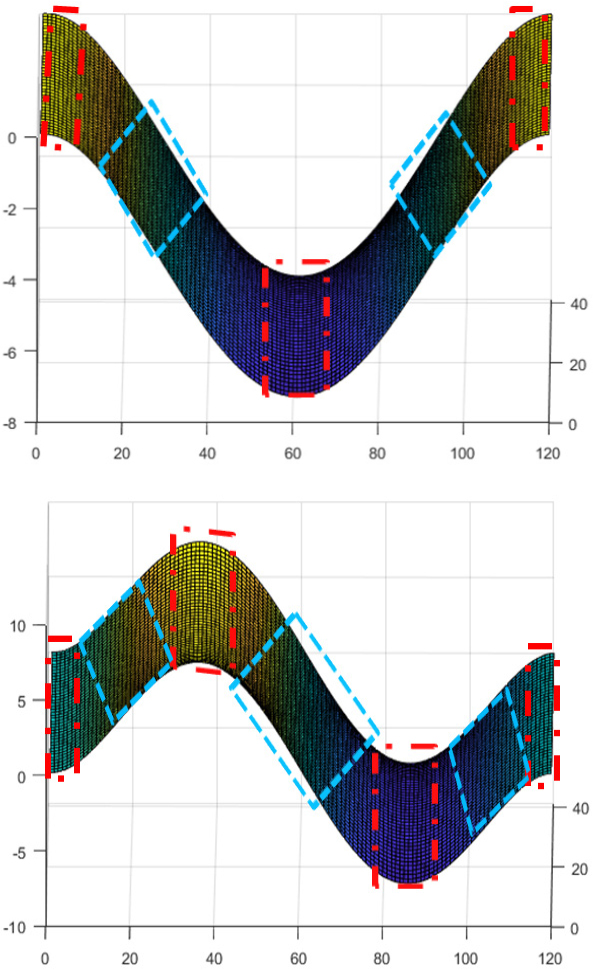
Fig. 2는 첫 번째(위)와 세 번째(아래) 모드의 모드형상이다. 앞에서 언급했듯이 얇은 평판에서 발생하는 비선형성은 구조물이 대-변형시 중간평면(mid-plane)에서의 신장(stretch)으로 인한 전단응력의 증가로부터 기인한다. 이것은 변위가 큰 위치에서 발생하는 것이 아니라 변형률 또는 곡률반경이 작은 위치들에서 전단응력이 증가한다. Fig. 2에 개별 모드들의 변형 형상에서 곡률반경이 작은 위치는 파선-점선 박스로 표기하였고, 변위는 크지만 곡률반경이 아주 큰 위치는 점선 박스로 표기하였다. 이 예제에서는 이 모드들의 비선형성을 ‘저감’시키기 위한 최적설계를 수행하였다, 이것은 식 (12)에서 +부호의 경우 만을 고려한 것이다. 일반적으로 얇은 평판은 내제적으로 경화 비선형성을 가지는데 이 위상최적화를 통해 외부 가진에 따른 증가하는 고유진동수의 변화량 저감을 목적한다. 두 모드들의 예제에서 체적구속 조건은 초기 모델대비 50 %(Vmin)와 80 %(Vmax)로 설정하였고, 해석의 초기 설계변수 ρe=0.8로 설정하였다. 특별히 최적화 과정 중 반복되는 모드(repeated mode)들의 발생을 방지하기 위해 초기설계변수대비 0.1%의 랜덤노이즈를 초기 설계변수에 추가하였다. 최적화 과정중에서 고유진동수의 변화는 초기 모델대비 20 %(ε) 미만으로 설정하였다. 해석에서 얇은 평판은 4800개(40 × 120) 유한요소(finite element)로 모델링되었다. 해석에 사용된 컴퓨터의 CPU는 Intel® 12세대 i9-1290K 3.2 GHz이고 메모리(RAM)는 128 GB이다. 최적화 기법은 일반적인 밀도기반 위상최적화에서 많이 사용하는 MMA(method of moving asymptotes)를 사용하였다(11). 민감도기반 최적설계의 신뢰성을 확인하기 위해 첫 번째 모드를 대상으로 임의의 10개 요소들을 선택하여 식 (13)의 해석적으로 구한 민감도와 유한차분법(FDM)을 통한 수치적으로 구한 민감도의 결과들을 확인해 보았고 이 결과들은 Table 1에 정리하였다. Table 1로부터 얻어진 결과들의 차이가 0.1 % 미만인 것으로 보아 해석상에서 얻어질 결과들의 신뢰성을 예측할 수 있다.
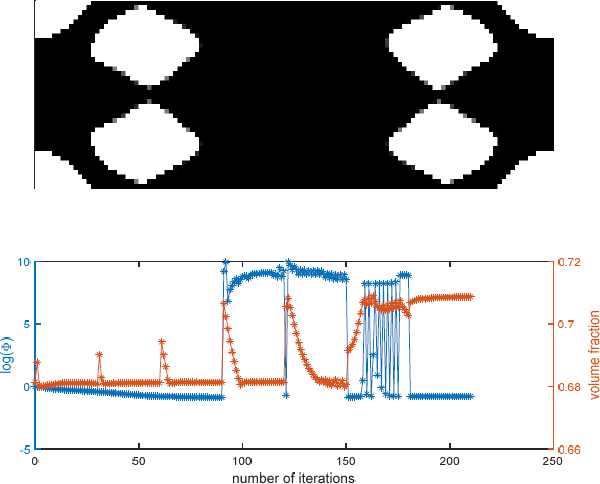
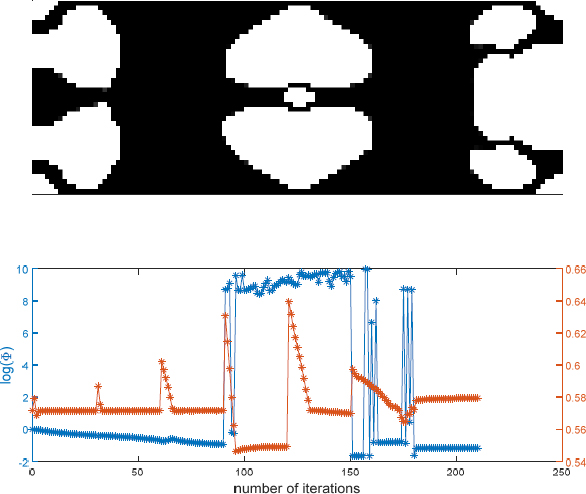
Fig. 3과 Fig. 4는 최적화된 결과 형상 그리고 최적화 과정 동안의 목적함수와 체적 구속조건의 이력선도(history plot)을 나타낸다. Fig. 3은 첫 번째 모드에 대한 것이고 Fig. 4는 세 번째 모드에 대한 것이다. 특이한 점은 두 경우 모두 30번의 해석마다 주기적으로 목적함수와 구속조건이 급격하게 변하는데 이것은 사용된 투영필터의 β가 두배씩 증가하기 때문이다. 이 최적화의 목적은 개별 모드들의 경화 비선형성을 저감하기 위한 것으로 결과 형상들에서 알 수 있듯이 기하비선형을 유발하는 위치들(Fig. 2에서 파선-점선 박스 부분)에서는 매질들을 보강하기 위해 모든 요소들이 채워져있다. 반면에 Fig. 2에서 곡률반경이 아주 큰 위치들(점선 박스 부분)에는 대부분의 공극(void) 요소들이 존재하는 것을 알 수 있다. 만약 비선형성을 증가시키는 최적화를 수행하였다면(식 (12)에서 -부호사용), Fig. 2에서 파선-점선 박스 영역에 공극 요소들이 존재하고 점선 박스 영역은 대부분의 요소들이 채워진 결과가 나왔을 것으로 예상된다. 최적화 과정에서 얻어진 최적형상들에 대한 비선형성 정도를 파악하기 위해 비선형 주파수 선도를 확인하였다.
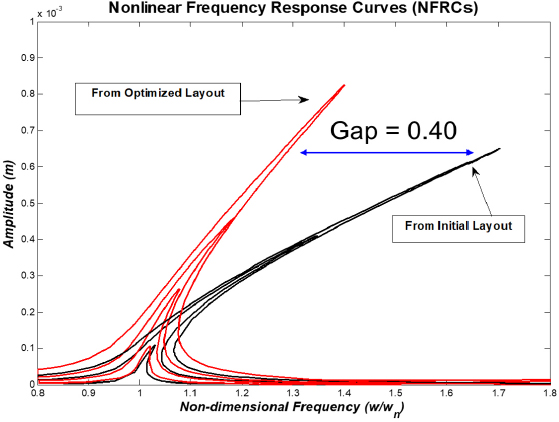
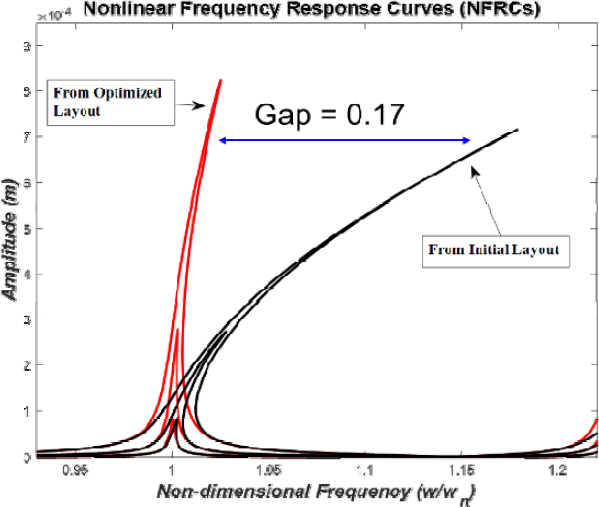
Fig. 5와 Fig. 6은 각각 Fig. 3과 Fig. 4에서 보이는 최적형상들의 비선형성을 확인하기 위해 외력의 크기를 증가시키면서 구한 비선형주파수선도들(NFRCs)이다. 여기서 외력은 첫 번째 모드의 경우 구조의 중심부에 위치시켰고 세 번째 모드는 왼쪽 가장자리 부분에 위치시켰다. 자세한 외력의 위치는 Fig. 1을 참조하기 바란다. 결과선도들에서 보이듯이 초기 형상들에 비해 최적형상에서 공진주파수의 변화가 확연히 줄어든 것을 알 수있다. 주골격(backbone)선도들의 기울기 차이를 두 결과선도들에 표기하였는데 첫 번째 모드에서는 0.4 차이가 보이고 세 번째 모드에서는 0.17 차이가 보이는 것을 알 수 있다. 앞의 이력선도 마지막 해석에서 확인된 목적함수 log(c)는 각각 -0.79(첫 번째 모드)와 -1.164(세 번째 모드)로 세 번째 모드의 최적형상에서 경화비선형성의 정도가 약해진 것을 알 수 있다. 이것은 세 번째 모드(Fig. 6)의 최적형상에대한 비선형주파수선도가 첫 번째 모드(Fig. 5)의 최적형상에서의 결과보다 공진주파수의 증가가 확실히 적은 것으부터 확인된다. 비선형주파수선도 결과들의 비교로부터 제안된 최적화 기법의 실효성을 확인할 수 있다.
5. 결 론
이 연구에서는 얇은 평판에서 발생하는 기하비선형성을 수동으로 제어하기 위해 구조물의 비선형운동방정식을 모달영역으로 치환하였고 여기서 정의되는 상수를 활용하여 최적화의 목적함수로 정의하였다. 최적화를 위한 설계민감도는 보조변수법으로 구하였다. 제안하는 기법을 검증하기 위해 얇은 평판의 첫 번째와 세 번째 모드들의 비선형성을 저감하는 최적설계를 수행하였고 얻어진 결과 형상을 검증하기 위해 비선형 주파수 선도를 통해 공진주파수의 변화량을 분석하였다.
Acknowledgments
This work was supported by the Dong-A University research fund.
References
-
Gourdon, E., Alexander, N. A., Taylor, C. A., Lamarque, C. H. and Pernot, S., 2007, Nonlinear Energy Pumping under Transient Forcing with Strongly Nonlinear Coupling: Theoretical and Experimental Results, Journal of Sound and Vibration, Vol. 300, No. 3-5, pp. 522~551.
[https://doi.org/10.1016/j.jsv.2006.06.074]

-
Villanueva, L. G., Kenig, E., Karabalin, R. B., Matheny, M. H., Lifshitz, R. et al., 2013, Surpassing Fundamental Limits of Oscillators using Nonlinear Resonators, Physical Review Letters, Vol. 110, No. 17, 177208.
[https://doi.org/10.1103/PhysRevLett.110.177208]

-
Raghothama, A. and Narayanan, S., 2000, Bifurcation and Chaos of an Articulated Loading Platform with Piecewise Non-linear Stiffness using the Incremental Harmonic Balance Method, Ocean Engineering, Vol. 27, No. 10, pp. 1087~1107.
[https://doi.org/10.1016/S0029-8018(99)00025-6]

-
Beeby, S. P., Torah, R. N., Tudor, M. J., Glynne-Jones, P., O’Donnell, T. et al., 2007, A Micro Electromagnetic Generator for Vibration Energy Harvesting, Journal of Micromechanics and Microengineering, Vol. 17, No. 7, pp. 1257~1265.
[https://doi.org/10.1088/0960-1317/17/7/007]

-
Vyas, A., Peroulis, D. and Bajaj, A. K., 2009, A Microresonator Design based on Nonlinear 1:2 Internal Resonance in Flexural Structural Modes, Journal of Microelectromechanical Systems, Vol. 18, No. 3, pp. 744~762.
[https://doi.org/10.1109/JMEMS.2009.2017081]

-
Rhoads, J. F., Shaw, S. W. and Turner, K. L., 2010, Nonlinear Dynamics and its Applications in Micro- and Nanoresonators, Journal of Dynamic Systems, Measurement and Control, Vol. 132, No. 3, 034001.
[https://doi.org/10.1115/1.4001333]

-
Chen, S. H., Cheung, Y. K. and Xing, H. X., 2001, Nonlinear Vibration of Plane Structures by Finite Element and Incremental Harmonic Balance Method, Nonlinear Dynamics, Vol. 26, No. 1, pp. 87~104.
[https://doi.org/10.1023/A:1012982009727]

-
Ribeiro, P. and Petyt, M., 1999, Geometrical Non-linear, Steady State, Forced, Periodic Vibration of Plates, Part I: Model and Convergence Studies, Journal of Sound and Vibration, Vol. 226, No. 5, pp. 955~983.
[https://doi.org/10.1006/jsvi.1999.2306]

-
LaBryer, A. and Attar, P. J., 2010, A Harmonic Balance Approach for Large-scale Problems in Nonlinear Structural Dynamics, Computers & Structures, Vol. 88, No. 17-18, pp. 1002~1014.
[https://doi.org/10.1016/j.compstruc.2010.06.003]

-
Lee, J., Detroux, T. and Kerschen, G., 2020, Enforcing a Force-displacement Curve of a Nonlinear Structure using Topology Optimization with Slope Constraints, Applied Science, Vol. 10, No. 8, 2676.
[https://doi.org/10.3390/app10082676]

-
Svanberg, K., 1987, The Method of Moving Asymptotes - A New Method for Structural Optimization, International Journal for Numerical Methods in Engineering, Vol. 24, No. 2, pp. 359~373.
[https://doi.org/10.1002/nme.1620240207]


Jongsuh Lee received the M.S. and Ph.D. degrees from Gwang-ju Institute of Science and Technology (GIST) in 2009 and 2015, respectively. He is currently an Assistant Professor of Department of Mechanical Engineering, Dong-A University, Busan, Korea. His research interests include linear and non-linear vibration analysis via contact phenomenon and topology optimization design for dynamic problems.