자율 주행 버스 좌석에 배치된 개별 HVAC 시스템에서 발생하는 진동 음향 소음의 능동 제어를 위한 공액 기울기 알고리즘
© The Korean Society for Noise and Vibration Engineering
Abstract
The paper presents the conjugate gradient algorithm for the active cancellation of vibroacoustic noise radiated from the compressor installed under each passenger’s seat in an autonomous bus. The sound radiated from the compressor of the HVAC system corresponds to a high-frequency annoyance noise caused by vibroacoustic noise due to the shell vibration of the compressor. The dominant frequency components of the vibroacoustic noise are harmonics of the rotation frequency of the reciprocating compressor. The HVAC system generates vibroacoustic noise dominantly in the frequency range between 300 Hz and 600 Hz. This type of noise is not only distinctly perceptible but also contributes to passenger discomfort and negatively impacts the perceived quality of the vehicle. The aim of this study is to attenuate the vibroacoustic noise of the HVAC system by developing an active noise control(ANC) system. Generally, the widely recognized filtered-X least mean squared(FXLMS) algorithm has been successfully implemented to active noise control of reciprocating compressor. However, its performance was found lacking outside the peak frequency of compressor operation noise. To address this, the conjugate gradient algorithm was employed to enhance ANC performance.
Keywords:
HVAC Noise, Active Noise Control, Conjugate Gradient Algorithm, FXLMS Algorithm키워드:
HVAC 소음, 능동 소음 제어, 공액 기울기 알고리즘, FXLMS 알고리즘1. 서 론
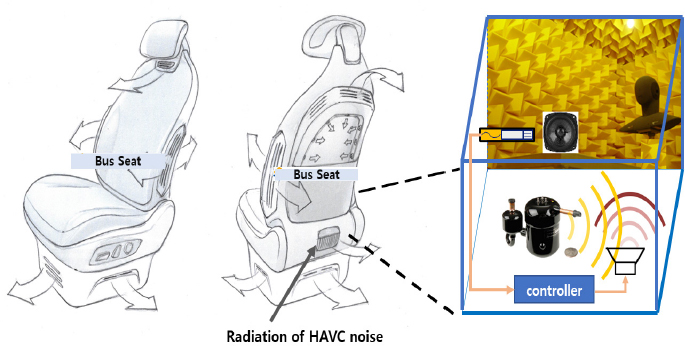
HVAC에서 발생하는 소음은 최근 전기 자동차 내부의 전반적인 소음의 중요한 원인이 되고 있다. 이러한 HVAC 소음은 승객의 승차감에 심각한 영향을 미친다. 결과적으로, 이러한 소음을 분석하고 줄이기 위해 광범위한 연구 노력이 이루어졌다. 연구에 따르면 HVAC에서 공기 흐름 속도는 HVAC 소음에 대한 성가심(annoyance), 라우드니스(loudness) 및 쾌적성(pleasantness)에 중대한 영향을 미친다. 또한, 공기 유량의 증가는 쾌적감 수준의 감소와 관련이 있다(1). 자동차의 HVAC 소음에 대한 주관적인 평가를 반영하여 높은 쾌적성을 갖는 공조 시스템의 성능을 향상하기 위해서 음질지수를 개발하여 사용했다(2). Fig. 1은 이 자율주행 소형버스의 승객 좌석에 적용되는 HVAC 시스템을 보여준다. 좌석 아래 적용되는 HVAC 시스템은 차량 실내공간에 설치됨으로 압축기, 증발기, 응축기 및 팬과 같은 구성 요소에 의해서 실내 소음이 증가한다. 특히 압축기 셸 진동에 기인하는 방사소음은 300 Hz ~ 600 Hz 부근의 소음으로 시트커버에의해서 차음의 효과가 크지 않다.
이 연구에서는 압축기 셸 진동 방사 소음을 저감시키기 위해서 HVAC 시스템에 능동소음제어(active noise control) 장치를 적용하고자 한다. 능동소음제어 기술은 저주파 소음을 억제하는 기술로, 많은 수동적 방식과 달리 추가적인 무게나 공간 소모 없이, 공기 흐름을 방해하지 않고 효과적으로 소음을 감소시킬 수 있다는 장점이 있다(3). 반면, 흡음재와 같은 수동적 방식은 고주파 소음 감소에 더 적합하다(4,5). 능동소음제어 기술은 기본 소음과 진폭은 동일하지만 위상은 반대인 ‘역 노이즈’를 생성하여 작동한다. LMS 알고리즘을 사용하는 적응형(adaptive) 필터링은 시간에 따라 변하는 소음 특성을 해결하기 위한 능동소음제어 시스템의 기본이 된다(6,7). 좌석 아래 장착되는 HVAC 시스템에서 방사되는 압축기 쉘 진동에 기인하는 소음의 주요 주파수 성분은 압축기 회전수의 하모닉(harmonic) 성분이다. 300 Hz 이하의 하모닉 성분은 소형버스 실내 공간에 장착되는 능동소음제어 시스템에 의해서 저감시키고, 600 Hz 이상의 고주파 소음은 시트커버에 흡차음재를 적용하여 소음을 저감 시킨다. 이 연구에서는 300 Hz ~ 600 Hz 사이에 존재하는 주파수 성분을 제어하기 위해서 HVAC 시스템에 부착하는 능동소음제어 시스템을 개발 하고자 한다. 이 주파수 범위는 짧은 파장으로 인해 고주파 입력 신호의 위상을 벗어난 신호를 생성하는 것이 어렵기 때문에 능동소음제어 알고리즘은 빠른 수렴이 필요하다. 능동소음제어 시스템의 성능을 높이기 위해 POCS(projection on convex set) 기술이 구현되었다(8). FxLMS 알고리즘은 계산량이 적고 안정적이므로 능동소음제어에 널리 사용되고 있다. 그러나 고유값 확산(eigenvalue spread)이라는 현상으로 인해 LMS 알고리즘의 수렴 속도가 느리다(9). LMS 알고리즘의 성능은 공액 기울기(conjugate-gradient) 알고리즘을 사용하면 계산 부담은 올라가지만 헤이지안 행렬(Autocorrelation Matrix R)을 사용하는 방법들에 비해서는 거의 증가하지 않으면서도 성능을 향상시킬 수 있다(10). 이 알고리즘은 자동 상관 행렬과 공액 관계인 검색 방향으로 기울기를 업데이트한다. 따라서 공액 기울기 기반 알고리즘은 LMS 알고리즘에 비해 수렴 속도가 빠르고 잔차 오차가 작다. 이 알고리즘은 적응형 필터링 이론의 맥락에서 성공적으로 구현 및 분석되었다(11). 또한, 이 알고리즘을 능동소음제어 시스템에 이론적으로 구현한 연구는 단 하나뿐이다(12). 이 연구에서는 자율주행 버스 좌석용 HVAC 시스템을 위한 공액 기울기 기반 능동소음제어 알고리즘을 개발한다. 능동소음제어 기술에 대한 최적의 참조 신호(reference signal) 를 선택하기 위해 마이크와 참조 신호 역할을 하는 압축기 셸의 진동 간의 상관도(coherence) 분석을 수행한다.
2. LMS(least mean squares) 알고리즘
LMS 알고리즘의 기본 목표는 평균 제곱 오차(error)를 최소화하는 방향으로 적응필터(adaptive filter)를 실시간으로 업데이트(update)한다. 이 최적화는 반복적인 최속하강법(steepest descent method)을 사용하며, 각 반복은 오차 표면(error surface)의 기울기와 반대 방향으로 진행되며 식 (1)과 같이 표현된다(6).
| (1) |
여기서 w(n)은 적응형 필터 이며, ∇는 오차표면의 기울기, 그리고 μ는 알고리즘의 안정성과 정상상태 성능에 중요한 수렴 계수를 나타낸다. 오차신호(error signal) e(n)은 원하는 신호(desired signal) d(n)과 적응형 필터 출력신호(output signal) y(n)의 차이 값이며 식 (2)와 같이 표현된다.
| (2) |
여기서 x(n)은 적응형 필터의 입력신호이며 일반적으로 참조신호(reference)라 불린다. LMS 알고리즘에서 기울기는 확률적 방법으로 계산하여 기울기를 구한다. 따라서 제곱 오차 값의 기울기는 식 (3)과 같이 표현된다.
| (3) |
식 (3)을 식 (1)에 대입하면 식 (4)와 같이 LMS 알고리즘의 최종 형태가 도출된다.
| (4) |
이 알고리즘은 참조 신호의 전력()과 필터 길이(L)에 반비례하도록 계산된 시변 스텝 크기를 사용한다. 이는 식 (5)와 같이 표현된다.
| (5) |
여기서 정규화된 스텝 크기 a는 0 < a < 2 범위 내에 속한다. 기준 신호의 전력은 식 (6)과 같은 공식을 사용하여 추정된다.
| (6) |
불충분한 스펙트럼 여기로 인한 발산 문제를 완화하기 위해 누출(leakage) 메커니즘이 필터 가중치 업데이트 과정에 결합되었다. 따라서 Leaky LMS 알고리즘은 식 (7)과 같이 공식화된다.
| (7) |
이러한 맥락에서 ν는 0 < ν ≤ 1범위 내로 제한된 누출 계수를 나타낸다. 누출 인자 조정에는 견고성과 성능 손실 간의 균형이 필요하다(3). 마이크, 필터, 증폭기 등 전자 부품과 관련된 실제 구현에서 스피커에서 오차 마이크까지의 신호를 2차 경로(secondary path)라고 한다. 이 2차 경로는 능동 소음 제어 시스템의 효율성에 큰 영향을 미친다. Burgess는 시스템 성능을 향상시키기 위해 2차 경로 효과를 보상할 것을 제안했다(13). 이는 2차 경로를 모방하는 필터로 참조 신호를 필터링하여 FxLMS(filtered-x LMS) 알고리즘을 개발함으로써 달성된다. FxLMS 알고리즘의 참조 신호는 식 (8)과 같이 재정의된다.
| (8) |
여기서 s(n)은 2차 경로의 임펄스 응답이고, *는 선형 컨볼루션을 나타낸다. 제곱 오차의 기울기는 식 (9)와 같이 다시 쓸 수 있다.
| (9) |
FxLMS 알고리즘은 식 (10)처럼 최적의 소음 제거를 달성하기 위해 필터 가중치를 반복적으로 업데이트한다.
| (10) |
적응형 필터 출력은 최적 업데이트된 적응형 필터와 참조 신호 간의 선형 컨벌루션을 통해 식 (11)과 같이 계산된다.
| (11) |
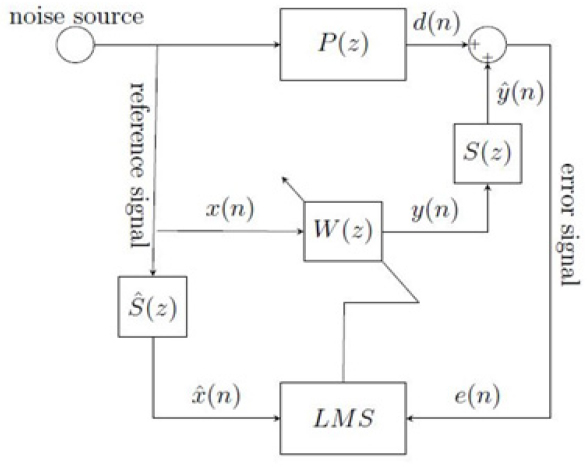
FxLMS 알고리즘의 블록 다이어그램은 Fig. 2에 나와 있다.
이 표현에서 는 2차 경로의 전달 함수를 나타내고, P(z)는 1차 기본경로를 나타내며, W(z)는 적응형 필터를 나타낸다.
3. 공액기울기(conjugate-gradient) 알고리즘
공액기울기 방법은 최속하강법과 뉴턴 방법 사이의 균형을 유지한다. 뉴턴 방법에서 요구되는 헤이지안(Hessian) 행렬의 평가 및 조작과 같은 광범위한 데이터 처리 없이 최속하강법에서 종종 부족한 효율성을 향상시키는 것을 목표로 한다(14). 공액 기울기 알고리즘은 공액 기울기 알고리즘보다 계산 집약적인 RLS(recursive least squares) 알고리즘과 비슷한 성능을 갖는다(11). 반면, LMS 알고리즘은 스텝 크기 μ에 민감하고 입력 신호의 자기상관 행렬과 관련된 고유값 확산으로 인해 수렴이 느리다(9). 최소화해야 할 비용함수(cost function)는 식 (2)의 오차 신호의 제곱이며 식 (12)와 같이 표현된다.
| (12) |
여기서 R은 입력벡터 x(n)의 자기상관 행렬(autocorrelation matrix)이며, p는 원하는 신호 d(n)과 입력 신호 x(n)사이의 상호상관벡터(cross correlation vector)이다. 자기상관 행렬은 식 (13)과 같다.
| (13) |
여기서 식 (14)는 다음과 같다.
| (14) |
상호상관벡터는 식 (15)와 같다.
| (15) |
여기서 식 (16)은 다음과 같으며
| (16) |
최적의 필터계수 w° (n)는 Bernard et al. 최적필터로서 식 (17)과 같다(6).
| (17) |
여기서 w° (n)은 최적의 필터이다. 비용함수의 기울기 g(n)이 되는 음의 잔차(residual) r(n)은 식 (18)과 같다.
| (18) |
LMS 알고리즘은 식 (18)의 기울기를 찾아가는 방법으로 적응필터를 업테이트 하여 식 (9)와 식 (10)을 유도한다. 공액기울기 알고리즘은 업데이트 되는 적응형 필터와 최적필터의 필터의 오차를 구하여 공액기울기를 찾아가면서 필터를 업데이트 한다. 적응형 필터와 최적필터의 오차는 식 (19)와 같다.
| (19) |
필터의 오차를 고려하며 식 (18)의 기울기(음의 잔차)를 다시 표현하면 식 (20)과 같다.
| (20) |
공액기울기 알고리즘은 비용함수를 미분하여 공액기울기를 계산하면 임의점에서 잔차는 오차표면(error surface)과 직교한다. 이때 자기상관행렬 R은 직교성을 만족해야하며 식 (21)과 같이 표현된다(15).
| (21) |
여기서 d(n)은 검색방향(search direction)이며 잔차를 업데이트 하는 방향임으로 식 (22)와 같이 업데이트 한다.
| (22) |
여기서 β(n)은 Gram-Schmidt 계수이며, 식 (23)과 같다.
| (23) |
이 검색 방향을 사용하여 식 (24)와 같이 필터 계수를 업데이트 한다.
| (24) |
여기서 a는 스텝 크기(step size)이며 식 (25)와 같다(15,16).
| (25) |
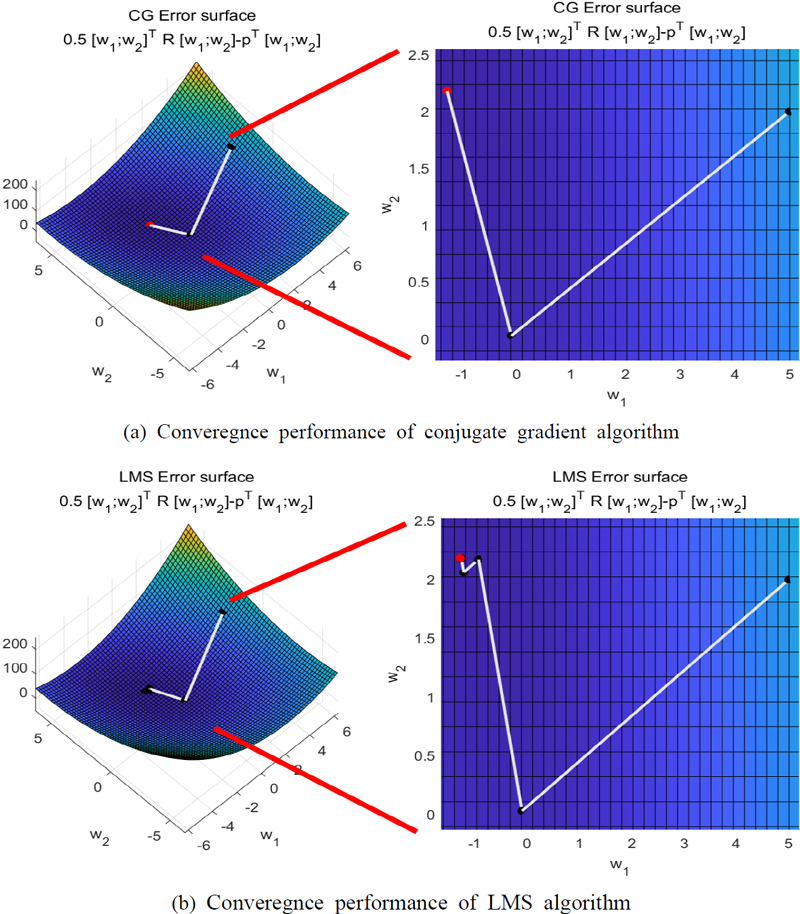
임의의 R, P값에 대한 비용함수를 식 (12)를 통하여 구하고, 비용함수에 대해 LMS 알고리즘과 공액기울기 알고리즘을 적용하여 수렴성능을 계산하였다. 두 알고리즘에 대한 수렴결과를 Fig. 3에 시각화로 나타내었다. 공액기울기 알고리즘은 2번의 반복으로 최적의 필터 계수를 찾는 반면, LMS 알고리즘의 경우 9번의 반복이 필요한다. LMS 필터의 수렴성능이 공액기울기 알고리즘보다 수렴이 느림을 알 수 있다.
4. HVAC 시스템의 진동음향 능동 소음 제어
4.1 알고리즘 흐름도
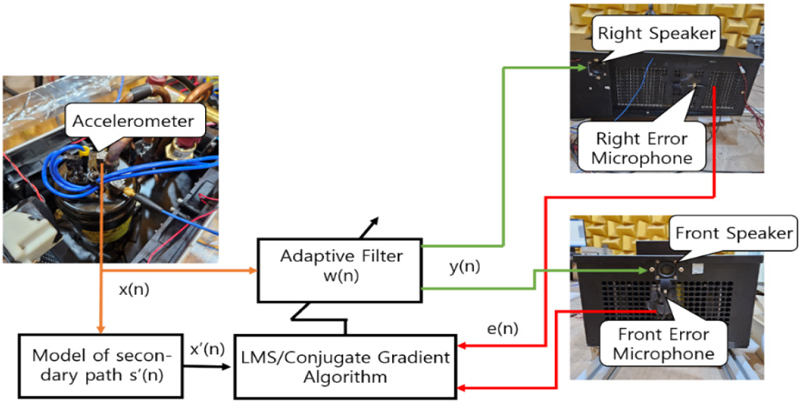
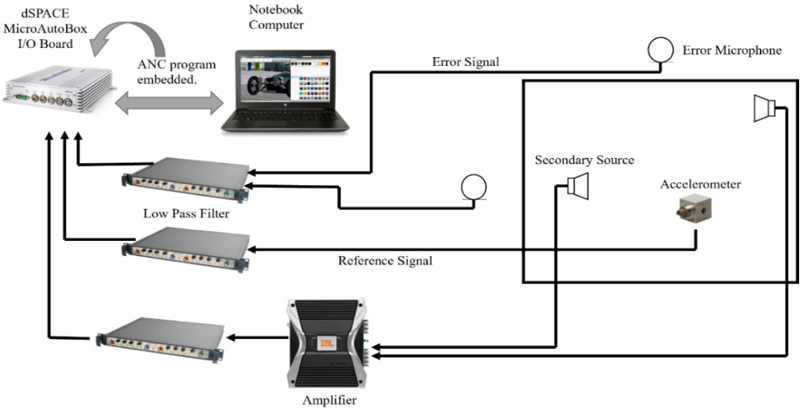
이 연구에 사용된 능동소음제어 시스템은 Fig. 4에 설명된 것처럼 다중입력 다중출력(2 × 2)을 갖는 시스템이다. 시스템은 압축기 쉘 진동을 참조신호로 받기 위해 압축기의 피스톤이 존재하는 압축기 쉘 윗 부분에 가속도계를 설치했다. 압축기의 옆면이나 바닥부분은 가속도계를 부착하고 케이블을 연결하는데 어려움이 있었다. 압축기 쉘에 부착된 가속도계를 통해 참조 신호를 획득한다. HVAC 시스템에는 4개의 스피커가 있었으나 최적화 과정을 통하여 전면과 오른쪽에 위치한 스피커만 활용한다. 최적화 과정은 음향 강도를 기준으로 선택했다. 오차 신호는 HVAC 시스템의 전면과 오른쪽 측면에 배치된 마이크에 의해 측정된다. 참조 신호는 알고리즘에 결합되기 전에 2차 경로 전달함수에 의해 필터링 과정을 거친다. 필터링된 참조 신호는 식 (24)를 이용하여 업데이트 되는 적응필터와 컨벌루션을 거쳐서 목표 소음 신호 d(n)의 안티 노이즈로서 출력 신호 y(n)이 생성된다.
4.2 HVAC 능동 소음 제어 시스템의 실험 설정
능동소음제어 실험에는 Fig. 5와 같이 dSPACE Autobox I/O 보드와 인터페이스된 노트북 컴퓨터가 사용되었다. dSPACE Autobox는 이 설정에서 아날로그에서 디지털로 또는 그 반대로 신호를 변환하는 중요한 역할을 한다. 또한 능동 소음 제어 용으로 지정된 임베디드 MATLAB Simulink 코드를 실행한다.
오차 마이크와 가속도계에서 수집된 신호는 불확실한 주파수 성분으로 인해 필터링이 필요하다. 결과적으로 이러한 신호에 저주파 필터링 과정을 적용하는 것이 필수적이다. 이 단계는 적절한 샘플링 주파수를 결정하는 데 도움이 된다. 저주파 필터는 능동소음제어의 최고 주파수 목표를 약간 초과하는 700 Hz의 차단 주파수로 선택했다. 샘플링 주파수는 2048 Hz로 선택했다. 스피커를 향한 출력 신호 y(n)은 디지털에서 아날로그로의 변환 과정에서 발생할 수 있는 재구성 오차를 수정하기 위해 필터링이 필요하다. 이 재구성 필터의 차단 주파수도 700 Hz로 설정했다. 마지막으로 이 신호는 스피커를 효과적으로 구동하기 위해 증폭기를 사용하여 증폭된다.
4.3 오차 마이크(error microphone) 배치
오차 마이크는의 위치는 압축기로 공기가 흡입되는 부분과 토출 되는 부분에 설치 하였으며 위치는 음향 강도의 측정을 통하여 결정하였다. 음향강도(sound Intensity)는 전파 방향에 수직인 단위 면적을 통과하는 음향 에너지의 양으로 설명할 수 있다(17). 수학적으로 식 (26)과 같이 표현된다.
| (26) |
여기서 p는 음압, u는 입자 속도, T는 시간이다. 강도 측정은 소음원의 위치를 정확히 찾아내고 음향 에너지의 양을 결정하는 데 중요하다(18). 음향강도 측정은 음향강도 마이크(Micro-flown: 독일)을 이용하여 측정되었다(19). 이러한 음향 강도 측정 결과는 Fig. 6 에 나와 있다. Dl 결과에 따라서 능동소음제어를 위한 오차 마이크는 다른 지점보다 상대적으로 사운드 강도가 높은 위치에 전략적으로 배치되었다.
4.4 참조 신호(reference signal) 선택
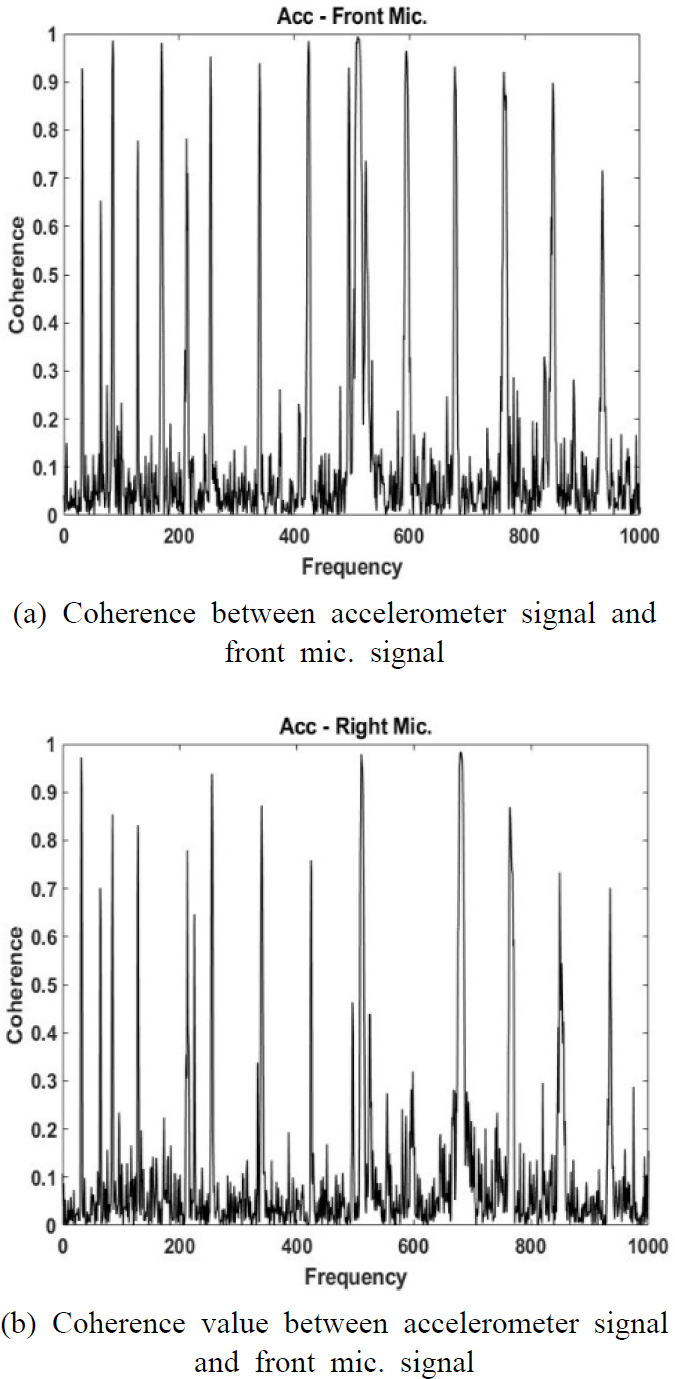
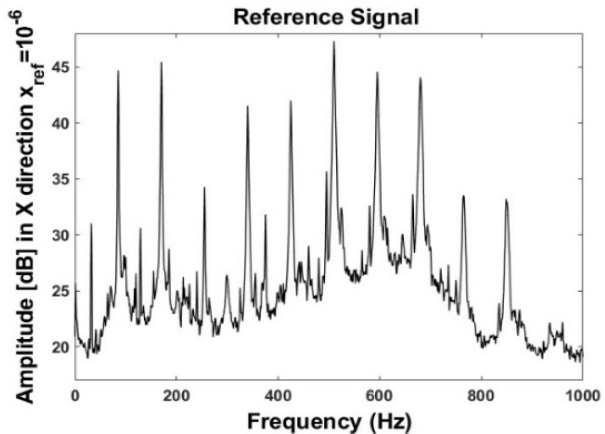
참조 신호는 압축기에 설치된 3축 가속도 값을 이용하였다. 방향은 x, y, z축 방향 중 x축 방향의 가속도 값이 Fig. 7에서 보여주는 바와 같이 2개의 오차 마이크와 상관도가 높음으로 x축 방향으로 결정했다. 이 참조 신호의 푸리에 변환은 Fig. 8에 표시되어 자세한 스펙트럼 표현을 제공한다. 그래프의 피크는 압축기의 작동 주파수와 그 고조파(harmonics)를 나타낸다.
상관도 함수(coherence function)는 입력 및 출력 신호와 같은 두 신호 사이의 선형 상관도를 평가하는 데 사용된다(20). 오차 마이크와 참고신호의 상관도 값은 능동소음제어 시스템의 성능평가에 중요한 매개변수이다(3). 두 개 신호에 대한 상관도 함수는 식 (27) 과 같이 정의된다.
| (27) |
여기서 f는 관심 주파수를 나타내고, Sdx(f)는 교차 전력 스펙트럼, Sdd(f)및 Sxx(f)는 각각 d(n)및 x(n)의 자동 전력 스펙트럼이다. 오차 신호의 자동 전력 스펙트럼의 최소값은 식 (28)과 같이 계산할 수 있다.
| (28) |
식 (28)은 능동소음제어를 성공적으로 적용하려면 참조 신호와 소음 신호 간의 상관도가 높아야 함을 나타낸다. Fig. 7에 표시된 것처럼 가속도계 신호와 전면, 오른쪽 마이크 사이의 상관도 값은 압축기의 작동 주파수와 고조파에서 상관도가 높다. 이는 가속도계 신호를 참조신호로 이용하면 압축기에서 발생하는 소음신호를 효과적으로 능동제어할 수 있음을 시사한다.
4.5 2차 경로 측정
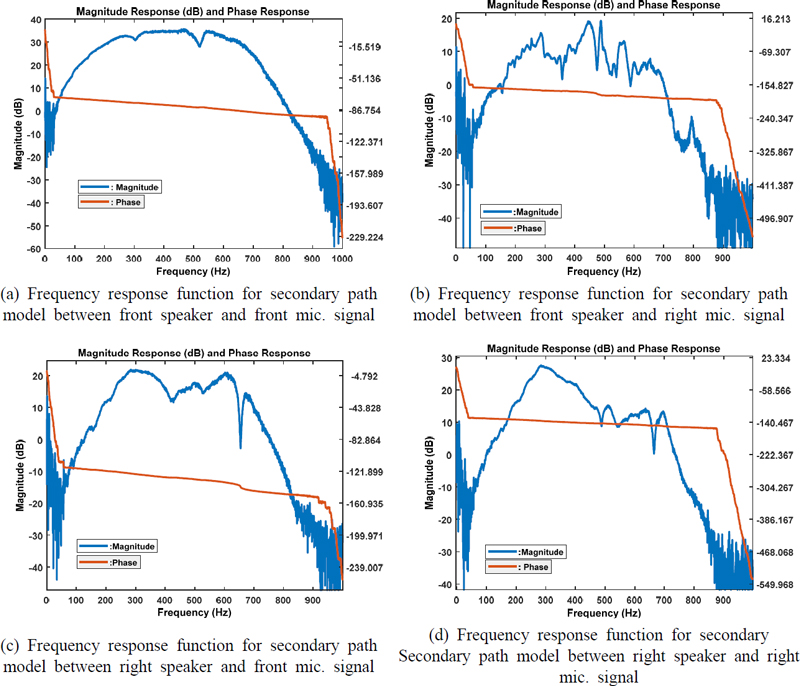
압축기 소음을 제어하기위한 역 위상 음파 발생 스피커와 오차 마이크 사이의 전달 함수인 2차 전달함수는 실험을 통하여 측정 한다. 2차 전달함수는 시불변이라는 가정을 기반으로 한다. 측정 방법은 백색 가진 방법을 사용하여 스피커에 백색 잡음을 발생시켜 오차 마이크로폰에서 소음을 측정하여 전달함수를 측정한다. 실제 제어장치에 대한 특성도 포함되어야함으로 제어장치를 포함하는 2차전달 함수를 측정한다(21). Fig. 9는 2차 전달 함수에 대한 측정결과를 나타낸다. 2차 전달함수를 역 Fourier 변환을 취하여 2차 전달함수에 대한 충격응답함수(impulse response function) s(n)을 구한다. 충격응답함수는 식 (8)에 적용하여 능동제어 알고리즘의 적응필터의 입력 값으로 적용한다.
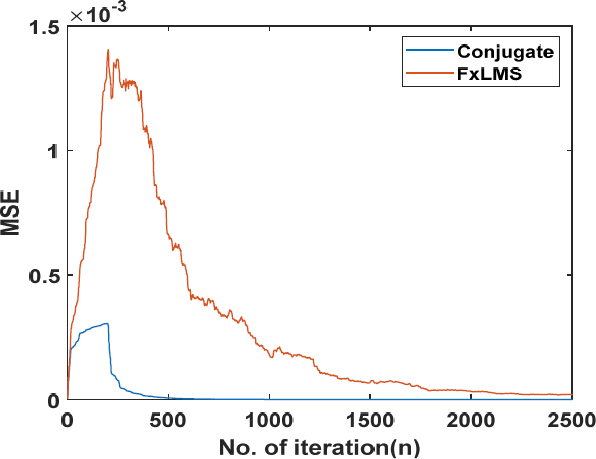
Fig. 9에서 보여주는 2차전달 함수의 위상(phase)은 주파수 함수에 선형적임을 보여주며 이것은 피드포워드(feed forward) 제어방식의 알고리즘에서, 제어에 필요한 시간지연을 고려 할때 순수지연(pure delay) 방식으로 적용함으로 제어 알고리즘 개발이 편리하게 한다. 선형 위상을 가진 2차전달함수를 이용하여 FxLMS 알고리즘과 공액 기울기 알고리즘의 수렴성능을 비교한 결과를 Fig. 10에서 보여준다. 수렴성능 비교에 사용된 오류 신호는 Front 오차 마이크에서 측정된 소음을 Matlab Simulink ANC 모델에 적용하여 비교하였다. 이 결과에 따르면 공액 기울기 알고리즘의 평균 제곱 오차(MSE) 값이 빠르게 수렴되고 잔차 오차의 크기가 더 작아지는 것을 관찰 할 수 있다. 이와 대조적으로 LMS 알고리즘은 수렴 속도가 더 느리고, 잔차 오차 측면에서 공액 기울기 알고리즘과 비교하여 수렴 성능이 더 불리함을 보여준다. 따라서 이 연구에서는 압축기 능동소음제어 알고리즘을 구현 할 때, 공액 기울기 알고리즘을 적용하였다. 동일한 데이터에 대한 필터 업데이터에 필요한 연산량(시간)은 Matlab Simulink 모델에서 제시한 결과는 Table 1과 같다. 이 결과에 의하면 FxLMS 알고리즘이 연산시간은 우수하지만 수렴성능의 한계와 수렴속도의 차이로 실제 ANC 적용결과 공액기울기 알고리즘이 우수하였다.
4.6 능동 소음 제어 결과
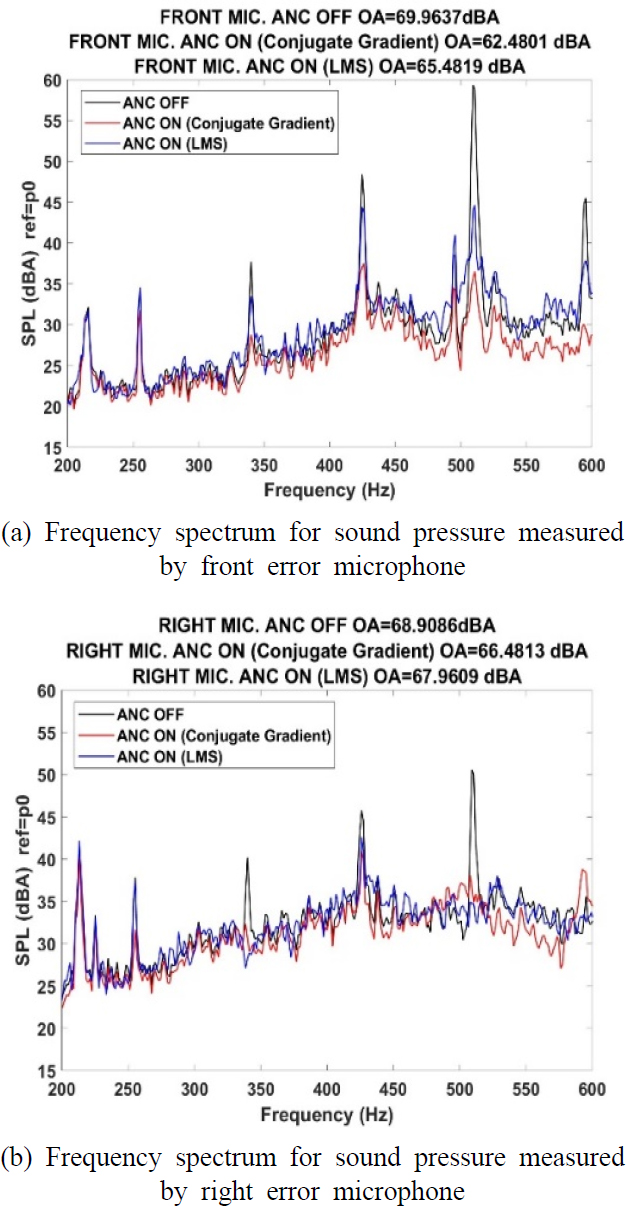
자율주행 버스의 죄석 아래에 배치되는 압축기를 무향실에 Fig. 11과 같이 설치하여 Fig. 4에서 보여주는 바와 같이 2개의 오차 마이크로폰을 설치하고 근접 소음 능동소음제어를 실시하였다. 근접음 제어를 위한 2개의 오차 마이크는 음향강도 측정결과 이용 front와 right에 설치하였다. 공액알고리즘을 적용하여 능동소음제어를 실시하여 근접음 오차 마이크에서 측정된 소음에 대해서 이산 푸리에 변환(DFT)을 적용하면 그 결과는 Fig. 12와 같이 표현된다.
Fig. 12는 샘플링 주파수가 2048 Hz이기 때문에 1000 Hz까지 나타낼 수 있다. 또한 스피커 사이즈로 300 Hz 이하는 ANC가 어렵고, 고주파 파장이 너무 작아서 능동 소음제어 기술로는 고주파 소음제어가 어렵다. 근접 소음 측정 결과에 의하면 300 Hz ~ 600 Hz 사이에 존재하는 압축기의 회전주파수에 대한 고조파(harmonic) 주파수 성분의 피크 소음이 공액 기울기 알고리즘을 적용 할 때, FxLMS 알고리즘을 적용 할 때 보다 크게 감소함을 알 수 있다.
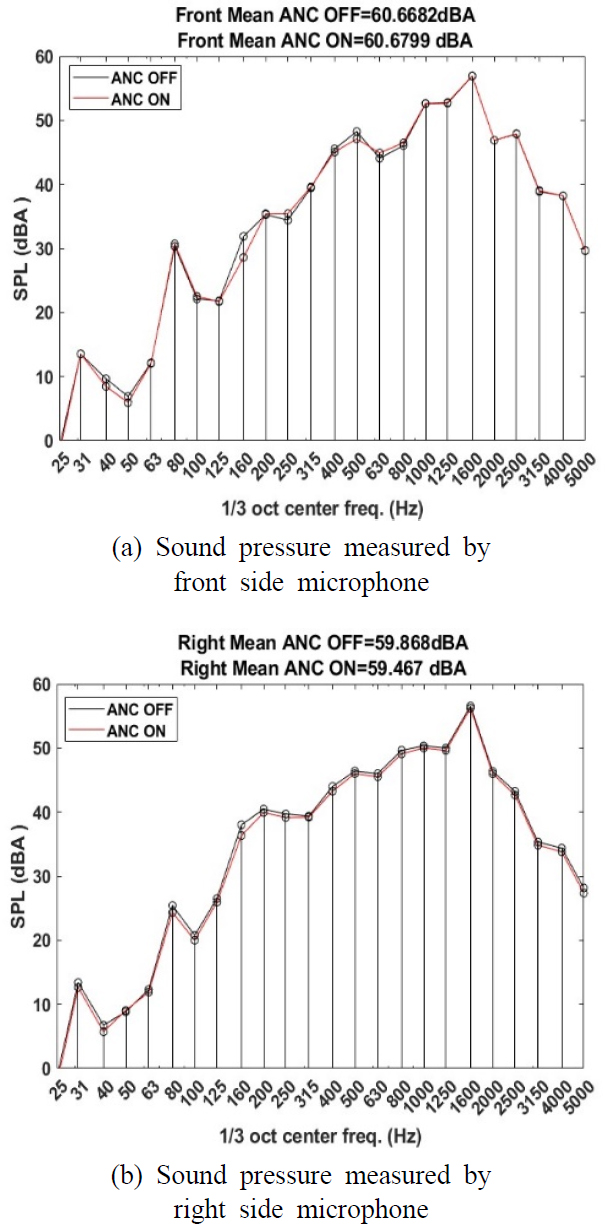
따라서 공액 기울기 알고리즘이 FxLMS 알고리즘 보다 우수한 ANC 성능을 보인다는 것을 알 수 있다. 이 실험에서 ANC 전 후 압축기의 기본소음에 대한 소음 변화를 확인 위해서, 압축기로부터 1 m 거리에 있는 위치에서 소음의 변화를 측정하였다. 1 m에서 측정된 기본 소음의 변화는 ISO 기준에 따라서 1/3 octave 주파수 분석으로 시도하여 Fig. 13에 나타내었다. 압축기로부터 1 m 위치에서 측정된 결과를 보면 중심주파수 500 Hz 부근에서 1 dB 이하의 소음 저감 효과를 나타내었다. 160 Hz에서는 소형 스피커를 적용하였음에도 불구하고 ANC 적용에 기인한 소음저감 효과를 확인 할 수 있다.
5. 결 론
이 연구에서는 압축기에서 방사되는 압축기 셸 진동기인 방사소음 제어를 위한 능동소음제어 기술을 위한 공액 기울기 알고리즘을 개발하였다. HVAC 시스템의 방사소음은 주로 300 Hz ~ 600 Hz 주파수 범위 내에서의 진동음향소음(vibro-acoustic noise)이 중요한 원인이다. 이 소음은 주로 회전 주파수 및 고조파에서 압축기 셸의 진동으로 인해 발생하며, 이로 인해 주파수 응답에서 눈에 띄는 피크가 발생한다. 이러한 파괴적인 소음을 제어하기 위해 능동소음제어 시스템이 개발되었다. 처음에는 음향강도 측정에 따라 오차 마이크가 HVAC 시스템의 전면과 오른쪽 표면에 전략적으로 배치되었다. 능동소음제어 시스템의 참조 신호는 압축기 셸에 부착된 가속도계에서 측정되었다. 가속도계 데이터와 소음 피크 사이의 높은 상관성이 관찰되었으며 이는 능동소음제어 시스템의 잠재적인 효율성을 나타낸다. 2차 경로 전달 함수의 측정에 이어 피드포워드 능동소음제어는 기존 FxLMS 알고리즘과 새로운 공액 기울기 알고리즘을 모두 사용하여 구현비교 하였다. 공액 기울기 알고리즘의 뛰어난 성능은 피크 주파수에만 국한되지 않고, 전면 마이크에서 관찰된 것처럼 이러한 피크 주파수 이외의 주파수 범위까지 확장된다. 압축기의 방사소음을 ANC 한 결과 압축기의 우측에 설치된 오른쪽 마이크의 경우, 주파수 스펙트럼 전체에 걸친 피크 감소 성능은 255 Hz의 피크를 제외하고 FxLMS 알고리즘과 공액 기울기 알고리즘간에 결과는 매우 유사하다. 그러나 공액 기울기 알고리즘은 특히 피크 주파수를 벗어난 주파수 범위에서 향상된 효과를 보여준다. 이 연구에서는 공액 기울기 알고리즘이 HVAC 시스템의 전체 소음 수준을 줄이는 데 FxLMS 알고리즘보다 성능이 우수함을 보여 주었다.
Acknowledgments
이 논문은 2024 년도 정부(산업통상자원부)의 재원으로 한국산업기술평가관리원의 산업기술혁신사업 지원을 받아 수행된 것임(KEIT No. 20018706).
References
-
Massimiliano, M., Yamauchi, K., Dan, M., Cioffi, F. and Maffei, L., 2021, Intercultural Differences in the Perception of HVAC Sound Quality in Car Cabins: From Conventional to Electric Vehicles, Applied Sciences, Vol. 11, No. 23, 11431.
[https://doi.org/10.3390/app112311431]

-
Back, J., Lee, S.-K., Lee, S. M., An, K., Kwon, D.-H. and Park, D.-C., 2021, Design and Implementation of Comfort-quality HVAC Sound Inside a Vehicle Cabin, Applied Acoustics, Vol. 177, 107940.
[https://doi.org/10.1016/j.apacoust.2021.107940]

- Kuo, S. M. and Morgan, D. R., 1996, Active Noise Control Systems: Algorithms and DSP Implementations, Wiley, NY, United States.
- Smith, D. M., Arnold, M. F., Ziegler, E. W., Eghtesadi, K. H. and Brown, M., 1992, A Systems Approach to Appliance Compressor Quieting using Active Noise Control Techniques, Proceedings of the International Compressor Engineering Conference, pp. 317~324.
- Hwang, W., Oh, I., Kim, B., Park, S. and Ryu, K., 2006, A Study on Noise Radiation from Compressor Shell, Proceedings of International Compressor Engineering Conference, C064.
- Bernard, W. and Samuel, D. S., 1985, Adaptive Signal Processing, Prentice-Hall, Englewood Cliffs, NJ, United States.
-
Ku, J. M., Jeong, W. B. and Hong, C., 2019, Active Control of Compressor Noise in the Machinery Room of Refrigerators, Noise Control Engineering Journal, Vol. 67, No. 5, pp. 350~362.
[https://doi.org/10.3397/1/376730]

-
Ku, J.-M., Jeong, W.-B. and Hong, C., 2020, Controller Design for Active Noise Control of Compressor by using the Time Window POCS Technique, Journal of Mechanical Science and Technology, Vol. 34, No. 7, pp. 2693~2700.
[https://doi.org/10.1007/s12206-020-0602-9]

-
Meena, S. R. and Rai, C. S., 2020, Effect of Eigenvalue Spread in Noise Cancellation of Two Sensory Systems using Adaptive Algorithms, Journal of Statistics and Management Systems, Vol. 23, No. 1, pp. 157~169.
[https://doi.org/10.1080/09720510.2020.1721634]

-
Fletcher, R. and Reeves, C. M., 1964, Function Minimization by Conjugate Gradients, The Computer Journal, Vol. 7, No. 2, pp. 149~154.
[https://doi.org/10.1093/comjnl/7.2.149]

-
Boray, G. K. and Srinath, M. D., 1989, Conjugate Gradient Techniques for Adaptive Filtering, Proceedings of IEEE International Symposium on Circuits and Systems (ISCAS), pp. 1752~1757.
[https://doi.org/10.1109/ISCAS.1989.100705]

-
Lu, L., Zhu, G., Yang, X. and Zhou, K., 2022, Conjugate Gradient-based FLANN Algorithms in Nonlinear Active Noise Control, Journal of the Franklin Institute, Vol. 359, No. 9, pp. 4468~4488.
[https://doi.org/10.1016/j.jfranklin.2022.04.002]

-
Burgess, J. C., 1981, Active Adaptive Sound Control in a Duct: A Computer Simulation, The Journal of the Acoustical Society of America, Vol. 70, No. 3, pp. 715~726.
[https://doi.org/10.1121/1.386908]

- Luenberger, D. G., 1984, Linear and Nonlinear Programming, 2nd Edition, Addison-Wesley, MA, United States.
-
Chang, P. S. and Willson, A. N., 2000, Analysis of Conjugate Gradient Algorithms for Adaptive Filtering, IEEE Transactions on Signal Processing, Vol. 48, No. 2, pp. 409~418.
[https://doi.org/10.1109/78.823968]

- Shewchuk, J. R., 1994, An Introduction to the Conjugate Gradient Method without the Agonizing Pain, Carnegie Mellon University, Pittsburgh, PA, United States.
- Kinsler, L. E., Frey, A. R., Coppens, A. B. and Sanders, J. V., 2000, Fundamentals of Acoustics, 4th Edition, John Wiley & Sons, NY, United States.
-
Wang, X., 2010, Vehicle Noise and Vibration Refinement, CRC Press, Boca Raton, FL, United States.
[https://doi.org/10.1533/9781845698041]

- de Bree, H.-E., 2003, The Microflown: An Acoustic Particle Velocity Sensor, Acoustics Australia, Vol. 31, No. 3, pp. 91~94.
- Shin, K. and Hammond, J. K., 2008, Fundamentals of Signal Processing for Sound and Vibration Engineers, John Wiley & Sons, Chichester, England.
-
Kim, H.-W., Park, H.-S., Lee, S.-K. and Shin, K., 2011, Modified-filtered-u LMS Algorithm for Active Noise Control and its Application to a Short Acoustic Duct, Mechanical Systems and Signal Processing, Vol. 25, No. 1, pp. 475~484.
[https://doi.org/10.1016/j.ymssp.2010.09.001]


Orhun Okcu is a Master of Engineering Student of the School of Engineering, Inha University, Incheon, Korea. He received his bachelor’s degree in mechanical engineering from Yildiz Technical University. His research interests include Active Noise Control(ANC).

Seongyeol Kim is a Master of Engineering Student of the School of Engineering, Inha University, Incheon, Korea. He received his bachelor’s degree in mechanical engineering from Inha University. His research interests include Active Noise Control(ANC).

Sang-Kwon Lee studied in the Department of Mechanical Engineering at the Pusan National University, Pusan, Korea for B.S. In 1998, he received a Ph.D. degree in signal processing at the ISVR(Institute of Sound and Vibration Research) of the University of Southampton in U.K. He has continued the sound and vibration research in the department of mechanical engineering Inha University since 1999. He worked in Hyundai Motor Company between 1984 and 1994 and researched Samsung Motor Company on 1998.