진동신호를 이용한 회전기계의 상태감시를 위한 비정상 상태 지수 개발 및 대형 원심압축기에 적용 사례

1. 서 론

회전기계의 운전 중 발생되는 진동 신호를 이용한 상태감시(condition monitoring) 또는 진단(diagnostic) 방법들은 산업체에서 안정적이고 경제적으로 기계를 운영하기 위한 CBM(condition-based maintenance) 시스템 구축을 위한 핵심 요소이다. CBM 시스템에 적용되는 진동신호처리 방법은 크게 시간영역(time domain), 주파수영역(frequency domain) 그리고 시간-주파수영역(time-frequency domain)에서 추출한 특징을 회전기계의 정상운전상태의 특징과 비교하여 상태를 진단 또는 분류하는 것으로 요약될 수 있다^(1~7).

이러한 연구들의 대부분은 추출된 특징의 정확도를 향상시키거나 효과적으로 특징을 추출하는 방법에 중점을 두어 매우 다양한 상태 진단 방법을 제시하고 있다. 그러나 회전기계의 유지보수를 담당하는 현장 엔지니어가 기술적으로 복잡한 신호처리 방법들을 적절히 적용하는 데 어려움이 있다. 따라서 현장에서는 회전기계의 최초설치 또는 오버홀(overhaul) 직후의 정상운전상태에 비하여 현재의 운전상태가 어떤 수준인지를 파악하여 보다 정밀한 점검이 필요한지 또는 전반적인 오버홀이 필요한지를 결정하는, 즉 Son et al.이 제안한⁽⁸⁾ 진단 시스템 프레임의 2단계 중 첫 번째 단계인 CHD(continuous health detection)에 목적을 두는 경우가 많다.

이러한 현실을 고려하여, Shin은 전문지식이 부족한 비전문가도 회전기계의 상태를 손쉽게 파악할 수 있는 4가지의 손상지수를 개발하여 대형 원심압축기에 적용하였고⁽⁹⁾, 개발한 손상지수는 각각 표준편차 손상지수, 비대칭도(skewness) 손상지수, 첨도(kurtosis) 손상지수 그리고 파워스펙트럼 손상지수이다. 이 손상지수들을 계산하기 위해서는, 동일한 사양의 회전기계일지라도 개별 회전기계에 대하여 최초설치 또는 오버홀 직후의 정상운전상태에서 측정한 비교 데이터(reference data)가 반드시 필요하다. 그러나, 실제 현장에서는 CBM 시스템이 제대로 갖추어져 있지 않아서 비교 데이터를 확보하지 못한 경우가 많다. 또한 CBM 시스템을 도입하더라도 경우에 따라서는 오버홀이 수년 간격으로 이루어지기도 하기 때문에, 이미 장시간 운전되고 있는 회전기계에 손상지수를 적용하는 것은 불가능하다.

이 논문에서는 이러한 단점을 극복하기 위해서 현재 운전 중인 회전기계의 진동신호만을 이용하여 기존의 손상지수를 대체할 수 있는 방법을 제시하고자 한다.

이전 논문에서 다루어진 대형 원심압축기의 경우⁽⁹⁾, 오버홀이 이루어진 후 얼마 지나지 않은 경우의 진동신호(Case A)와 최초 설치 후 수년이 지나서 정기적인 오버홀을 앞둔 경우의 진동신호(Case B)를 비교한 결과, 진동신호의 비정상성(non-stationarity) 특징이 Case B에서 두드러지게 나타나는 것이 관찰되었다.

이에, 이 연구에서는 이러한 진동신호의 비정상성 특징을 이용하여 설치 초기에 측정한 정상운전상태의 비교 데이터가 없더라도 회전기계의 상태감시에 이용할 수 있는 비정상 상태지수(non-stationary condition index)를 개발하여 이전 논문에서 사용된 동일한 진동신호에 적용하고, 그 결과를 손상지수를 적용한 이전 논문의 결과와 비교하여 유용성을 검증하였다.

2. 회전기계의 상태감시를 위한 비정상 상태지수

이 논문에서 다루는 회전기계의 경우, 오버홀을 앞둔 경우의 진동신호는 최초설치 또는 오버홀 직후의 진동신호에 비하여 비정상성(non-stationarity)이 상대적으로 크게 나타나는 것이 관찰되었는 데, 다만 새로운 주파수 성분이 나타나는 것과 같은 강한 비정상(strong non-stationary) 특징이 나타나는 것이 아니라, 최초 설치된 동일한 사양의 다른 회전기계와 비교할 때 주요 피크(peak) 성분들의 주파수는 변함이 없고 몇몇 피크 성분의 크기(amplitude)가 시간에 따라 불규칙하게 변하는 특성을 보이고 있다.

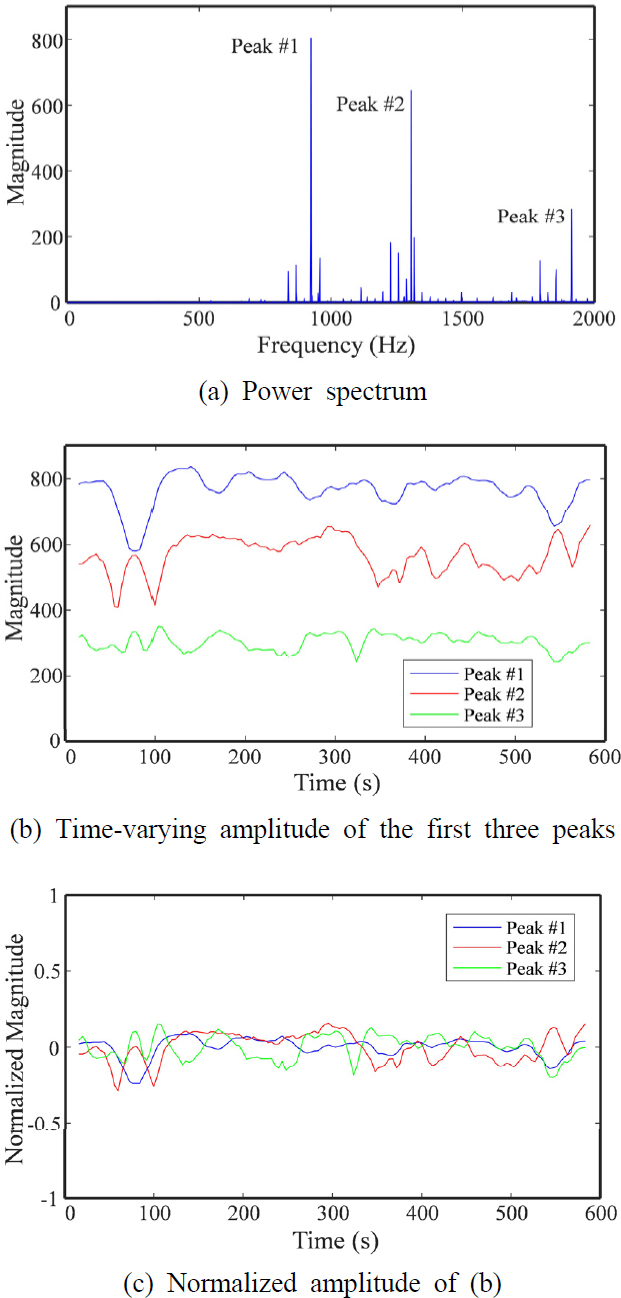
그 예로서, Fig. 1에 나타낸 3차원 스펙트로그램(spectrogram)을 보면, 피크 성분들의 주파수는 시간에 따라 변하지 않고 일정하게 유지되지만, 1300 Hz 부근의 피크 값의 변동성이 매우 크게 나타나는 것을 알 수 있다. 이러한 현상은, 오랜 시간 동안 사용된 대형 원심압축기의 경우, 운전 중 발생할 수 있는 오일의 특성 변화와 공기역학적 변화에 더 민감하게 반응하기 때문인 것으로 추정된다.

Fig. 1

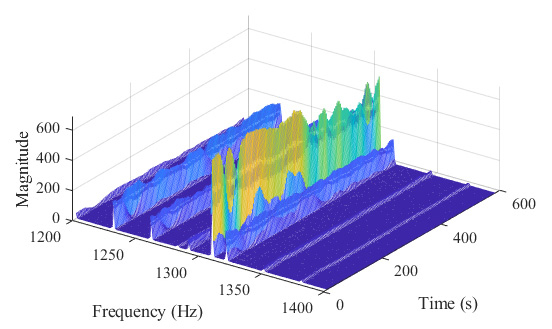
3D spectrogram of the amplitude varying nonstationary vibration signal of a large centrifugal compressor

이 절에서는 이러한 대형 원심압축기의 독특한 시간-주파수 특성 뿐만 아니라 시간 영역에서 통계적 특성의 변화를 나타내는 시변 표준편차(time-varying standard deviation), 시변 비대칭도(time-varying skewness) 그리고 시변 첨도(time-varying kurtosis)를 함께 고려하여 각각에 대한 비정상 상태지수(non-stationary condition index)를 개발하여 이전 연구의 손상지수와 비교하였다.

2.4 파워스펙트럼 비정상 상태지수

비정상 신호의 분석은 시간-주파수 영역에서 웨이블릿 변환(wavelet transform), 단시간 푸리에 변환(short-time Fourier transform) 등을 통하여 주로 이루어지지만, 이 연구에서 다루는 회전기계의 경우 비정상성이 급격히 나타나는 것이 아니라 비교적 천천히 특성이 변하기 때문에 이동창(T_W)의 길이도 크게 설정할 수 있다. 이 경우에는, 일반적인 파워스펙드럼을 계산할 때 많이 사용되는 웰치 방법(Welch’s method)을 이동창 내에서 적용한 웰치 스펙트로그램(Welch spectrogram)을 사용하여 랜덤오차를 줄일 수 있다^(11~13). 예로서, Fig. 1에 나타낸 3차원 스펙트로그램은 웰치 방법을 적용한 것이다.

시간영역의 상태지수들과는 달리, 시간-주파수 영역의 모든 데이터를 이용하여 하나의 상태지수로 나타내는 것은 쉽지 않다. 그러나 이 논문에서 제안하는 비정상 상태지수의 목적은 진동신호의 비정상성을 세밀하게 분석하는 것이 아니라, 문제가 있거나 오랜 기간 운전되어 오버홀을 앞둔 회전기계에서 나타날 수 나타날 수 있는 Fig. 1과 같이 주요 피크 주파수 성분의 크기 비정상성 정도를 파악하여 추가조치의 필요성 여부를 결정하는 데 있다.

따라서 주요 피크주파수(f_peak) 성분의 크기 시변(amplitude time-varying) 특성을 나타내는 ‘시변 파워스펙트럼’ 개념을 새롭게 도입하여 상태지수를 개발하였다. 측정된 전체 시간(T seconds)을 이용하여 구한 i채널 신호의 피크주파수(f_peak) 성분의 파워스펙트럼 값을 $$ {\stackrel{-}{P}}_i\left(f_{\text{peak }}\right)$$라 하고, 길이가 T_W인 이동창 내의 데이터를 이용하여 계산한 시변 파워스펙트럼 값을 P_i(f_peak,t)라고 정의할 때, i채널 신호의 파워스펙트럼 비정상 상태지수, C_P,i를 식 (7) 및 식 (8)과 같이 정의하였다.

$\[ C_{p,i}\left(f_{\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}}\right)=STD\left(\frac{P_i\left(f_{\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}},t\right)}{{\stackrel{-}{P}}_i\left(f_{\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}}\right)}\right)\times 100\left(\%\right) \]$

(7)

$\[ C_{p,i}=\mathrm{M}\mathrm{a}\mathrm{x}\left(C_{P,i}\left(f_{\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}}\right)\right) \]$

(8)

이 연구에서 제시한 시변 파워스펙트럼, P_i(f_peak,t)는 웰치 스펙트로그램 상에서 특정 피크주파수(f_peak)를 따라서 자른 단면으로 볼 수 있으며 시간만의 함수이기 때문에 현장 비전문가들도 물리적인 의미를 쉽게 이해할 수 있는 장점이 있다. 예로서, Fig. 2(a)는 측정된 전체 데이터를 이용하여 구한 파워스펙트럼이며, 3개의 주요 피크주파수 성분의 크기 시변 특성을 나타내는 P_i(f_peak,t)를 Fig. 2(b)에 나타내었는 데 이 피크 성분들은 Fig. 1의 3차원 웰치 스펙트로그램에서 볼 수 있는 것과 같이, 전체 측정시간 동안 주파수 자체의 변화는 없으며 진폭만 변하는 특성을 가지고 있다. 그리고 피크주파수들 간의 상대비교가 가능하도록 P_i(f_peak,t)를 $$ {\stackrel{-}{P}}_i\left(f_{\text{peak }}\right)$$값으로 각각 정규화 하여 Fig. 2(c)에 나타내었다.

Fig. 2

Example of the amplitude varying power spectrum

식 (7)은 표준편차 비정상 상태지수인 식 (1)과 매우 유사한 물리적인 의미를 가지는 데, 식 (1)은 모든 주파수 성분이 포함된 시간영역 데이터를 대상으로 하는 반면, 식 (7)은 진동신호의 특정 주파수 성분만 고려한 것이다. 즉, 시간영역의 상태지수와 마찬가지로, 정상적 신호는 C_P,i(f_peak)값이 0이 되며, 비정상성이 커질수록 C_P,i(f_peak)값이 커지게 된다.

그리고 식 (7)은 모니터링 대상으로 설정한 피크주파수의 개수 만큼 C_P,i(f_peak)값이 계산되어지기 때문에, 하나의 지표로 나타내기 위해서 식 (8)과 같이 시변 특성이 가장 큰 C_P,i(f_peak)값을 파워스펙트럼 비정상 상태지수 C_P,i로 정의하였다. 또한, 다른 상태지수들과 마찬가지로 가중 평균적인 파워스펙트럼 비정상 상태지수, C_P를 식 (9)와 같이 정의하였다.

$\[ C_P=\frac{1}{N}\sum _{i=1}^N w_i{C}_{P,i} \]$

(9)

3. 대형압축기에 적용 사례

이 절에서는 2절에서 제안한 4가지 비정상 상태지수들을 이전 연구에서 다룬 15 000 마력급 대형 원심압축기를 대상으로 측정한 동일한 진동신호에 적용하였다⁽⁹⁾. 또한 이전 연구의 손상지수를 적용한 결과와 비교하여⁽⁹⁾, 정상운전상태에서 측정한 비교 데이터(reference data)가 없는 경우에 이 논문에서 제안한 비정상 상태지수가 손상지수의 대안으로 사용될 수 있음을 보였다.

이 연구에서 제안한 비정상 상태지수는 베어링 손상이나 축 정렬 불량 등과 같은 특정한 이상진동의 원인을 진단하는 것이 아니라, 서론에서 언급한 바와 같이, 오랜 시간 동안 운전 후 나타날 수 있는 회전기계의 전반적인 저하정도를 파악하는 것이 주 목적이다. 즉, 많은 부품들로 구성된 대형압축기의 경우, 장 시간 운전함에 따라 부품들 간의 간극변화와 이물질 축적 등이 발생할 수 있으며 이로 인하여 오일과 압축공기의 변동 등에 따라 진동 특성이 더 민감하게 변할 수 있는데, 이를 감지하여 보다 정밀한 점검 또는 추가적인 오버홀이 필요한 지를 결정하는 지표로 활용하는 것이 목적이다.

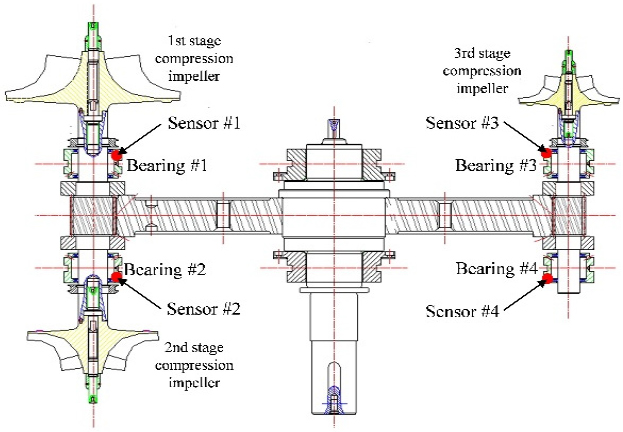
Fig. 3은 원심압축기 핵심 부분의 개략적인 단면도를 나타내고 있으며, 대형 원심압축기의 경우 기어와 압축단 축 그리고 임펠러는 진동 특성에 영향을 미치는 주요 요소들이다. 이 주요 요소들의 동적하중을 직간접적으로 감당하며 중앙 부분에 위치한 베어링 부근에서 진동신호를 측정하는 것이 압축기의 전반적인 저하정도를 파악하기에 가장 적합한 측정 위치로 판단된다.

Fig. 3

Accelerometer locations on the centrifugal compressor

따라서 압축단 축을 지지하고 있는 총 4개의 베어링 부근에, 측정 범위가 0.4 Hz ~ 10 kHz이고 100 mV/g의 감도를 가진 산업용 가속도계(IMI 603C01)를 마그네틱 베이스를 이용하여 부착하고, 안티 에일리어싱 필터(anti-aliasing filter)가 내장된 DAQ 장비(NI USB-4432)를 사용하여 진동신호를 측정하였다.

Case A와 Case B 두 가지 상태의 압축기에 대하여 진동신호를 측정하였는데, Case A는 오버홀이 이루어진 지 얼마 지나지 않았고 Case B는 초기 설치 후 수년이 지나서 정기적인 오버홀을 앞두고 있는 경우이다. 가속도센서 부착위치(BR #1 ~ BR #4) 각각에 대하여 4 kHz의 샘플링 주파수로 측정된 진동신호의 전체 시간(T)은 600초이고, 시간영역의 비정상 상태지수 계산을 위한 이동창의 길이 T_W는 5초로 설정하였으며, 파워스펙트럼 비정상 상태지수 계산을 위한 T_W는 웰치 방법을 적용할 때 충분한 평균(averaging)이 이루어지도록 30초로 설정하였다.

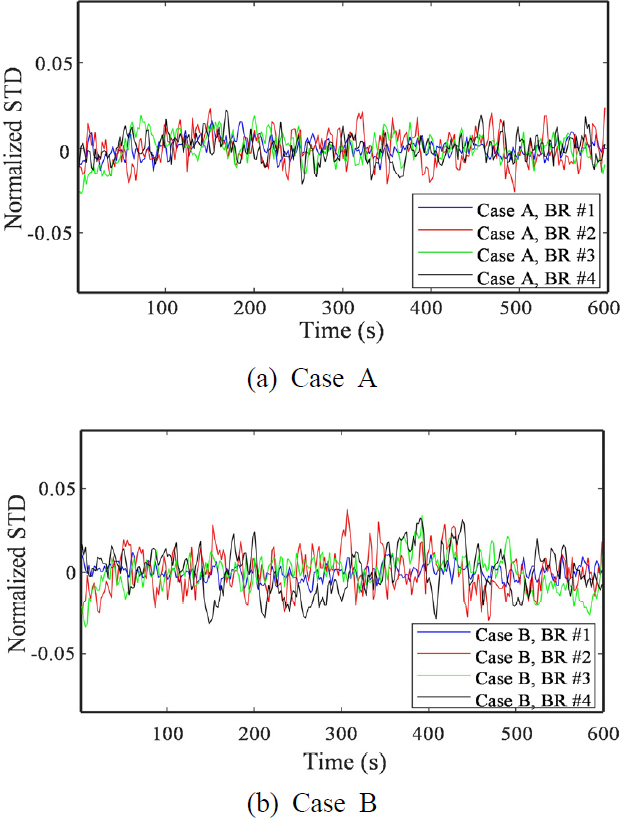
먼저, 표준편차 비정상 상태지수를 계산하기 위하여 Case A와 Case B 각각에 대한 정규화된 시변 표준편차, $$ {\sigma }_i\left(t\right)/\overline{{\sigma }_i}$$를 Fig. 4에 나타내었고 표준편차 비정상 상태지수 값을 Table 1에 나타내었다. Fig. 4와 Table 1을 참고하면, 오버홀이 이루어진 후 얼마 지나지 않은 Case A보다 오버홀이 이루어지지 않은 Case B의 표준편차 비정상성이 전반적으로 크게 나타나는 것을 볼 수 있다. 특히, BR #2와 BR #4에서 Case A와 Case B의 차이가 두드러지게 나타나는 데, 이는 Table 2에 나타낸 표준편차 손상지수의 결과와⁽⁹⁾ 유사한 것을 알 수 있다.

Fig. 4

Time-varying normalized standard deviation on each channel

Table 1

STD non-stationarity indexes(Cσ, i) [%]

Table 2

STD damage indexes(Dσ, i)

비록, 비정상 상태지수가 손상지수 보다는 Case A와 Case B의 차이가 적게 나타나지만 유의미한 차이를 보이고 있기 때문에 상태감시를 위한 지표로서 충분히 사용될 수 있음을 보여준다.

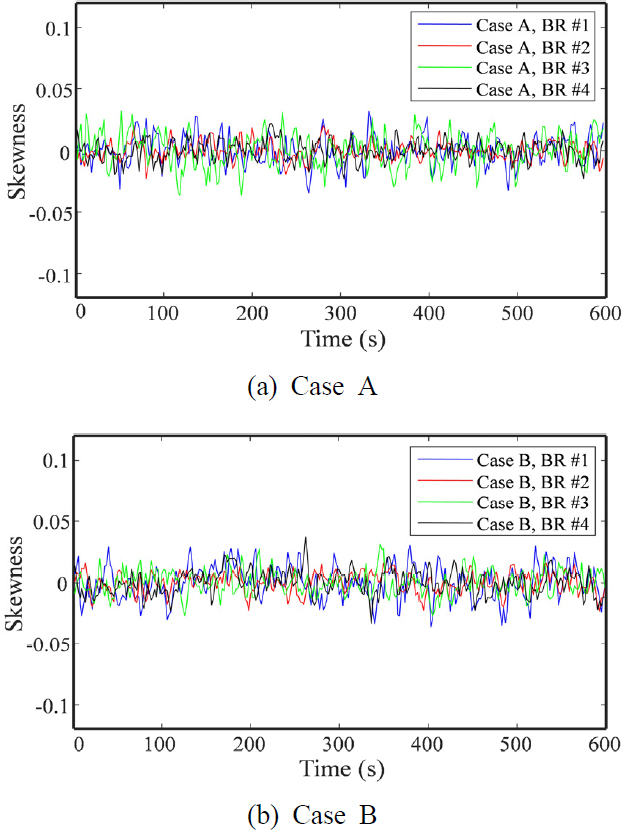
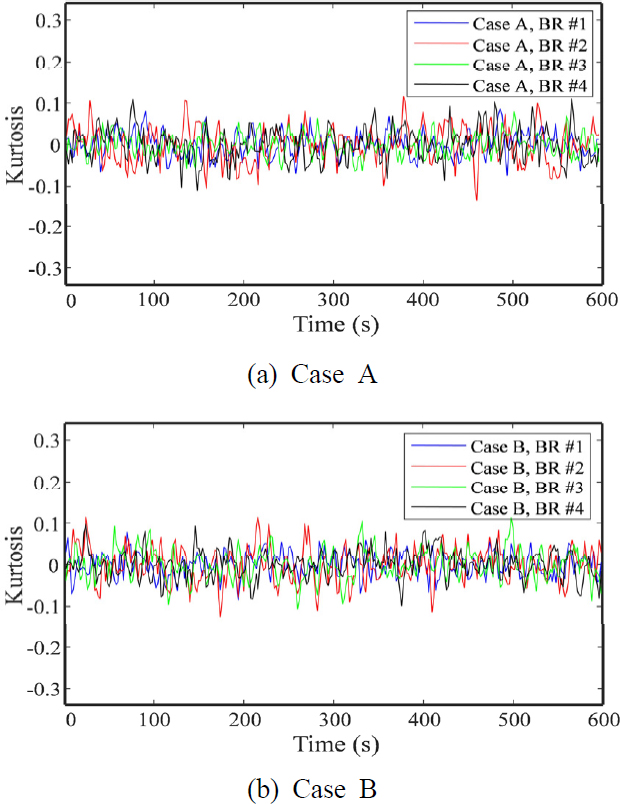
다음으로, Case A와 Case B 각각에 대하여 채널 별 시변 비대칭도와 시변 첨도를 Fig. 5와 Fig. 6에 각각 나타내었으며, 이를 이용하여 계산한 비대칭도 비정상 상태지수와 첨도 비정상 상태지수를 Table 3과 Table 5에 각각 나타내었고, 이전 연구의 결과와⁽⁹⁾ 비교하기 위하여 비대칭도 손상지수와 첨도 손상지수를 Table 4와 Table 6에 각각 나타내었다.

Fig. 5

Time-varying Skewness on each channel

Fig. 6

Time-varying Kurtosis on each channel

Table 3

Skewness non-stationarity condition indexes(Cs, i) [%]

Table 4

Skewness damage indexes(Ds, i)

Table 5

Kurtosis non-stationarity condition indexes(Cr, i) [%]

Table 6

Kurtosis damage indexes(Dr, i)

Fig. 5와 Fig. 6 그리고 Table 3과 Table 5를 보면, 표준편차 비정상 상태지수와는 달리, Case A와 Case B의 비대칭도 및 첨도 비정상 상태지수의 차이는 거의 없음을 알 수 있는데, 이는 Table 3과 Table 5에 나타낸 손상지수의 경우와 유사한데, 이전 연구에서 언급한 바와 같이⁽⁹⁾ 장시간 사용에 따른 전반적인 저하현상 외에 베어링이나 기어의 결함 또는 크랙 등과 같은 회전기계 자체의 특별한 결함은 없기 때문인 것으로 판단된다.

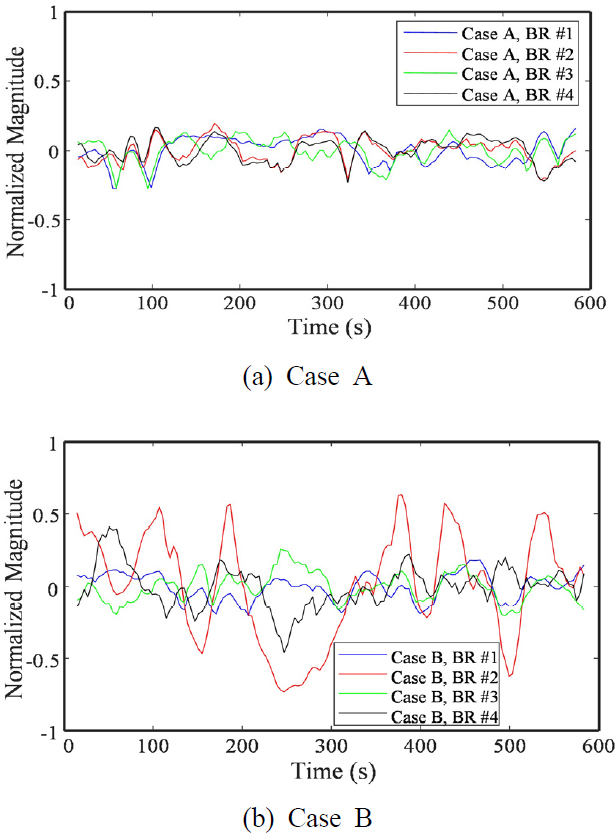
다음으로, Case A와 Case B 각각에 대한 채널 별 피크 주파수 성분의 정규화된 시변 파워스펙트럼 값, $$ P_i\left(f_{\text{peak }},t\right)/\overline{P_i}\left(f_{\text{peak }}\right)$$를 Fig. 7에 나타내었으며, 이를 이용한 파워스펙트럼 비정상 상태지수와 이전 연구 파워스펙트럼 손상지수를⁽⁹⁾Table 7과 Table 8에 각각 나타내었다.

Fig. 7

Time-varying normalized power spectrum value of a peak frequency component on each channel

Table 7

Power spectrum non-stationarity condition indexes(CP, i) [%]

Table 8

Power spectrum damage indexes(DP, i)

Fig. 7과 Table 7을 보면, Case B에서 BR #2와 BR #4의 파워스펙트럼 비정상성이 Case A에 비하여 매우 크게 나타나고 있는 것을 알 수 있다. 특히, BR #2의 비정상 상태지수가 가장 큰 차이를 보이는 데, 이는 Table 7에 나타낸 이전 연구의 파워스펙트럼 손상지수를 적용한 결과와 매우 유사하다.

마지막으로 채널 별(BR #1 ~ BR #4) 비정상 상태지수들을 평균한(가중치는 모두 동일하게 ‘1’로 설정) 평균 비정상 상태지수들을 Table 9에 나타내어 압축기 전체의 상태를 개략적으로 요약하였다.

Table 9

Overall non-stationarity condition indexes with equal weighting values

Table 9는 이 연구에서 다루고 있는 압축기의 특징을 잘 요약하고 있다. 먼저, 비대칭도와 첨도를 이용한 상태지수인 C_s와 C_r는 Case A와 Case B 사이의 차이가 거의 없는 데, 이는 앞에서 언급한 바와 같이 기어나 베어링 등 압축기의 특정한 부품에 이상이 있는 것이 아니기 때문인 것으로 판단된다. 그러나, 주요 피크 주파수 성분들만 이용한 파워스펙트럼 비정상 지수, C_P는 Case A에 비하여 Case B가 약 2배 정도 더 크며 두 압축기의 상태를 잘 구분함을 알 수 있다. 그리고 표준편차 비정상 상태지수, C_σ는 Case A에 비하여 Case B가 약 35 % 정도만 더 크게 나타나고 있는 데, 이는 시간영역 데이터의 특성상 시간에 따른 변동성이 적은 다른 주파수 성분들이 모두 포함된 결과로 판단된다.

이상의 결과들을 종합하면, 이 연구에서 개발된 비정상 상태지수들은 설치 초기에 측정된 정상운전 상태의 비교 데이터가 없는 경우, 이전 연구의 손상지수를 대체하여 사용할 수 있음을 보여준다. 다만, 특정 주파수 성분의 시변 특성을 이용한 파워스펙트럼 비정상 상태지수가 가장 효과적으로 사용될 수 있으며 표준편차 상태지수는 보조적인 용도로 사용할 수 있을 것이다. 그리고, 이 사례의 경우 비대칭도와 첨도를 이용한 상태지수인 C_s와 C_r는 효과성이 없지만, CBM 시스템을 구성할 때는 특정 부품의 이상이 발생할 수 있는 것을 대비하여 함께 사용하는 것이 바람직할 것이다.

4. 결 론

이 논문에서는 회전기계의 초기 정상운전상태에 비하여 장시간 운전에 따른 기계상태의 저하 정도를 나타내는 지표로서 비정상 상태지수들을 제안하였다. 시간영역에서는 시변 표준편차, 시변 비대칭도 그리고 시변 첨도를 이용하여 상태지수를 개발하였으며, 웰치 스펙트로그램 기반의 시간-주파수영역 데이터를 이용하여 파워스펙트럼 비정상 상태지수를 개발하였다.

개발된 비정상 상태지수들을 이전 연구에서 다룬 동일한 대형 원심압축기에서 측정한 진동신호에 적용하고, 그 결과를 이전 연구의 손상지수를 적용한 결과와 비교하였을 때 매우 유사한 결과를 나타냄을 보였다. 따라서, 이 논문에서 제안한 비정상 상태지수들은 회전기계의 설치 초기에 측정한 정상운전 상태의 비교 데이터가 없는 경우 손상지수를 대체하여 유용하게 활용할 수 있다.

비록 이 논문에서 다루어진 한정된 사례의 결과를 일반화할 수 없으나, 회전기계의 유지보수 측면에서 아직까지 TBM(time-based maintenance) 방식을 적용하고 있는 많은 현장에서 CBM 방식으로 전환할 때 비정상 상태지수를 함께 적용하여 효과적으로 CBM 시스템을 구성할 수 있을 것으로 기대된다.

Acknowledgments

이 논문은 국립안동대학교 기본연구지원사업에 의하여 연구되었음.

References

• Jardine, A. K. S., Lin, D. and Banjevic, D., 2006, A Review on Machinery Diagnostics and Prognostics Implementing Condition-based Maintenance, Mechanical Systems and Signal Processing, Vol. 20, No. 7, pp. 1483~1510. [https://doi.org/10.1016/j.ymssp.2005.09.012]
• Jayaswal, P., Wadhwani, A. K. and Mulchandani, K. B., 2008, Machine Fault Signature Analysis, International Journal of Rotating Machinery. [https://doi.org/10.1155/2008/583982]
• Peng, Y., Dong, M. and Zuo, M. J., 2010, Current Status of Machine Prognostics in Conditionbased Maintenance: A Review, The International Journal of Advanced Manufacturing Technology, Vol. 50, No. 1-4, pp. 297~313. [https://doi.org/10.1007/s00170-009-2482-0]
• Ahmad, R. and Kamaruddin, S., 2012, An Overview of Time-based and Condition-based Maintenance in Industrial Application, Computers & Industrial Engineering, Vol. 63, No. 1, pp. 135~149. [https://doi.org/10.1016/j.cie.2012.02.002]
• Hong, S., Zhou, Z., Zio, E. and Hong, K., 2014, Condition Assessment for the Performance Degradation of Bearing based on a Combinatorial Feature Extraction Method, Digital Signal Processing, Vol. 27, pp. 159~166. [https://doi.org/10.1016/j.dsp.2013.12.010]
• Chong, U., Cho, S. and Lee, J., 2006, Fault Diagnosis for Rotating Machine using Feature Extraction and Minimum Detection Error Algorithm, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 16, No. 1, pp. 27~33. [https://doi.org/10.5050/KSNVN.2006.16.1.027]
• ang, M., Lee, J. M., Hwang, Y., Cho, Y. J. and Song, J. B., 2012, Condition Monitoring of Rotating Machine with a Change in Speed using Hidden Markov Model, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 22, No. 5, pp. 413~421. [https://doi.org/10.5050/KSNVE.2012.22.5.413]
• Son, J.-D., Eom, S.-M., Kim, S.-T., Lee, K.-H. and Lee, J.-H., 2015, Vibration Monitoring and Diagnosis System Framework for 3MW Wind Turbine, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 25, No. 8, pp. 553~558. [https://doi.org/10.5050/KSNVE.2015.25.8.553]
• Shin, K., 2017, Development of Damage Indexes for Condition Monitoring of Rotating Machinery using Vibration Signals and its Application to a Large Centrifugal Compressor, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 27, No. 7, pp. 915~923. [https://doi.org/10.5050/KSNVE.2017.27.7.915]
• Shin, K. and Hammond, J. K., 2008, Fundamentals of Signal Processing for Sound and Vibration Engineers, Wiley, Chichester, England.
• Prasad, A. and Sahin, M., 2010, Characterization of Neural Activity Recorded from the Descending Tracts of the Rat Spinal Cord, Frontiers in Neuroscience, Vol. 4. [https://doi.org/10.3389/fnins.2010.00021]
• Vanfretti, L., Dosiek, L., Pierre, J. W., Trudnowski, D., Chow, J. H. et al., 2011, Application of Ambient Analysis Techniques for the Estimation of Electromechanical Oscillations from Measured PMU Data in Four Different Power Systems, European Transactions on Electrical Power, Vol. 21, No. 4, pp. 1640~1656.
• Rusanen, M., Kainulainen, S., Korkalainen, H., Kalevo, L., Myllymaa, K. et al., 2021, Technical Performance of Textile-based Dry Forehead Electrodes Compared with Medical-grade Overnight Home Sleep Recordings, IEEE Access, Vol. 9, pp. 157902~157915.