미시적 교통모형을 이용한 시계열 도로교통소음의 계산 방법
© The Korean Society for Noise and Vibration Engineering
Abstract
Traditional road traffic noise models exhibit the disadvantage of difficulty in interpreting fine temporal distribution that fluctuates moment by moment depending on traffic conditions. In this study, a Microscopic Road Traffic Noise(MTN) model is proposed to solve this limitation. In this model, a microscopic traffic model determines the movement behavior of individual vehicles, and road traffic noise is calculated based on this information. Hence, the MTN model calculates a time series of noise reflecting traffic conditions, allowing for the evaluation of maximum and equivalent noise levels. Comparisons with traditional models confirmed that most receivers’ calculation errors were less than 3 dB(A). Another feature is that the MTN is less sensitive to the heavy vehicles ratio than traditional models. For instance, when the average speed is 100 km/h and the heavy vehicles ratio increases from 0 % to 10 %, the equivalent noise levels of the MTN increase by 1 dB(A), whereas the Leq of RLS90 and NMPB increase by 2.58 dB(A) and 2.30 dB(A), respectively. Although the MTN still requires additional research, it is expected to aid in establishing noise prediction and management that reflect realistic traffic.
Keywords:
Road Traffic Noise, Car-following Model, Moving Noise Source, Noise Prediction키워드:
도로교통소음, 차량추종모형, 이동소음원, 소음예측1. 서 론
현대의 인구가 밀집되고 복잡한 교통체계를 가지는 도시에서는 효과적인 소음의 관리를 위해 소음지도를 활용하고 있다. 이 소음지도의 작성을 위해서 교통량, 차종, 차속 등의 정보를 기반으로 3차원 도로교통소음 모형에 의한 계산 결과를 활용한다(1). 기존에 사용되고 있는 3차원 도로교통소음 모형에서는 선음원(도로)을 기하학적으로 분할하여 분할 소음원에서 전달되는 소음의 총 합을 계산하는 방식을 사용하고 있다. 3차원 도로교통소음 모형은 도로와 건물 사이의 이격거리, 건물의 구조, 높이 등을 고려하여 3차원 공간상의 소음해석을 가능하게 한다. 또한 곡선도로, 종단면 구배가 일정치 않은 도로 등 실제 환경에서의 도로상황에서 발생하는 소음에 대한 예측이 가능하다는 장점이 있다. 대표적인 3차원 도로교통소음 모형은 RLS90, NMPB, CRTN 등이 있고 소음지도 작성에 사용되도록 강제되고 있다(1). 또한 한국도로공사 도로교통연구원에서 고속도로를 대상으로 개발한 소음예측 모형인 KTHN이 많이 사용되고 있다.
다만 기존에 사용되는 도로교통소음 모형들은 소음의 공간상 분포를 확인하는 것이 목적이기 때문에 등가소음도와 같은 대표 소음도를 활용한다. 때문에 도로의 차량 분포에 따른 소음의 미세한 시간적 변화를 알기 어렵다. 또한 유럽을 중심으로 실시간 소음지도의 작성에 대한 요구가 커짐에 따라 기존 접근 방식에는 한계가 있다. 실시간 소음지도의 작성을 위한 접근으로 소음지도와 측정값 사이의 보간법을 사용하는 방식이 주로 이용되어 왔다(2,3). 또는 소음지도의 작성에 필요한 계산 시간을 줄이는 등의 이점이 있는 기계학습 모형 기반의 소음지도 작성방법이 제시되고 있다(4,5). 하지만 이 방법들 역시 매우 미세한 시간 단위의 소음도 계산에는 어려움이 있다. 최근 그에 대한 새로운 대안으로 교통 시뮬레이션을 이용하는 방식이 제안되고 있다(6,7). 미시적 교통시뮬레이션을 이용하는 방식은 높은 컴퓨팅 리소스가 필요하다는 단점이 있지만, 각각의 소음원인 개별 차량으로부터 계산되므로 현실에 가까운 소음 모형 구현이 가능할 것이다. 또한 법적기준에 맞는 등가소음도의 관리도 중요하지만 일시적 최대치에 의한 피해를 검증하는 방법도 필요로 되고 있다.
이 연구에서는 개별차량 이동 교통모형을 활용하여 교통상황에 따라 매 순간 변화하는 도로교통소음을 해석하는 방법을 제안하고 기초적인 검증으로 사용 가능성을 판단하고자 한다. 실시간으로 변하는 소음을 계산하기 위해서는 기존의 선음원 방식으로는 한계가 있기 때문에 개별 차량 한 대를 이동하는 소음원으로 고려한 미시적 접근 방식의 도로교통소음의 계산 방법을 제안하고자 한다. 이를 위해 이 연구에서는 미시적 교통모형 가운데 하나인 차량추종모형(car-following model)을 기반으로 차량을 이동시키며 차량에서 배출, 전달되는 도로교통소음의 시계열 데이터를 생성하는 미시적 도로교통소음(MTN, microscopic road traffic noise) 모형의 계산 방법을 정의했다.
이 연구는 다음과 같이 진행된다. 먼저 개별 차량의 이동 구현을 위해 사용된 차량추종모형에 대해 검토했다. 다음으로 제안하고자 하는 미시적 도로교통소음 모형의 계산 방법에 대해서 소개했다. 마지막으로 미시적 도로교통소음 모형의 계산 결과와 기존에 사용되는 국외 도로교통소음 모형의 계산 결과를 비교했다.
2. 미시적 도로교통소음 모형
2.1 차량추종모형
이 절에서는 차량추종모형에 대하여 간단히 설명하려 한다. 차량추종모형이란 2대 이상의 차량이 존재하는 상황에서 앞차의 종방향 움직임을 따라가는 뒤차 운전자의 행동을 모델링한 것으로 교통류 시뮬레이션에 활용된다. 대표적인 차량 추종 모형에는 Wiedemann, Krauss, IDM(the intelligent driver model) 등이 있다. 그 중 Krauss 모형을 이용했다. Krauss 모형은(8) 안전 속도(vsafe)를 기반으로 차량의 목표 속도(vdes)를 설정하고 현 시점의 차량의 행태를 결정하는 모형이다. 안전속도의 계산은 다음 식 (1) 및 식 (2)와 같다.
| (1) |
| (2) |
여기서 vn-1(t)은 시간 t에서 앞차의 속도, vn(t)은 뒤차의 속도, τk은 운전자의 반응 속도, b는 차량의 최대 감속도, gn(t)는 시간 t에서 앞차와의 간격을 의미한다. 또한 식 (2)의 xn-1(t), xn(t)은 각각 앞뒤차의 위치, s는 최소 간격을 의미한다.
안전 속도는 도로의 제한 속도(vmax)보다 크거나 차량이 도달할 수 있는 속도(vn(t) + a∆t)보다 클 수도 있기 때문에 이 3가지 값 중 최소값을 목표 속도로 한다.
| (3) |
여기서 식 (3)의 a는 가속도, ∆t는 시뮬레이션 타임 스텝을 의미한다.
식 (3)에 의해 결정된 목표 속도를 이용하여 다음 시뮬레이션 타임 스텝에서 차량의 속도는 식 (4)와 같이 결정된다.
| (4) |
여기서 ϵaη은 확률적 오차항이며 ϵ은 속도 변화폭, η은 0에서 1사이의 무작위 수이다.
이렇게 시뮬레이션 타임 스텝별로 결정된 속도에 따라 차량의 행태, 위치가 변화하며 시뮬레이션이 수행된다. 도로의 종방향 이동에 대한 차량 행태의 결정은 위와 같이 결정하지만 차선이 많아지고 차량의 차선변경이 필요한 경우에는 차선변경 모형(lane-change model)이 동시에 적용된다. 다만 이 연구에서는 차선변경모형의 적용에 대해서는 고려하지 않았다.
2.2 미시적 도로교통소음 모형의 계산 방법
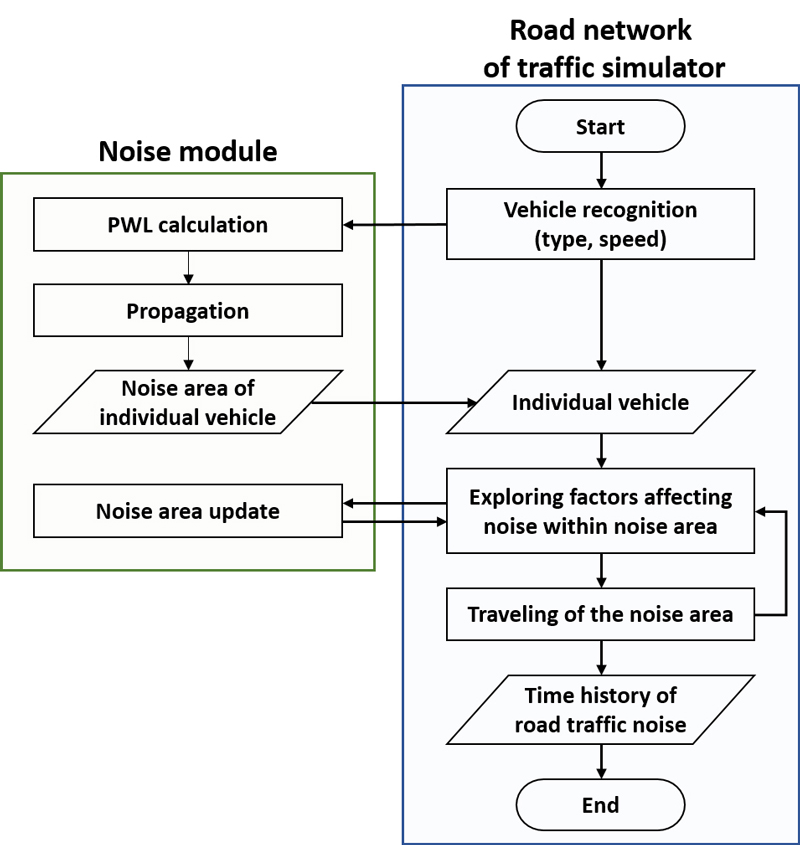
실제 도로에서 차량의 통과 소음을 측정하는 소음계의 역할과 같이 가상으로 구현된 도로 네트워크에서 미시적 교통모형을 기반으로 이동하는 차량이 방출하는 소음을 수음점에서 기록하는 미시적 도로교통소음 모형은 Fig. 1과 같은 과정을 거쳐 수행되도록 설계했다. 먼저 교통 시뮬레이션 상 구현된 도로 네트워크에 차량이 신규로 입력될 때 마다 차량을 인식하여 차종, 속도 정보를 이용해 방출되는 음향파워레벨(sound power level, PWL)을 산정한다. 소음 모듈은 차량의 PWL 방출, 전파되는 영역을 한정하고 격자화한 개별차량 소음영역을 다시 도로 네트워크 상 인식된 차량에 입력한다. 다음으로 도로 네트워크에서 차량 주변의 소음 영향인자를 탐색하고 배경소음도, 회절, 반사 등을 반영하여 1차적으로 소음영역을 갱신한다. 갱신된 소음영역은 차량과 같이 차량추종모형에 따라 도로에서 이동하게 한다. 다음으로 개별차량 소음영역이 차량 행태 정보를 기반으로 갱신하도록 한다. 이동 중 속도, 이동방향, 위치 등의 변화에 따라 PWL을 재산정하여 개별차량 소음영역을 갱신한다. 또한 도로 네트워크에 입력된 차량이 다수인 경우 각 차량의 소음영역 내 개별 격자의 좌표를 탐색하여 격자가 동일 좌표에 존재하는 경우 소음도를 합산하여 갱신한다. 마지막으로 개별차량 소음영역 내 개별 격자가 이동 중 수음점과 동일 좌표로 인식되는 경우에 격자의 소음도를 시뮬레이션 시간 동안 기록한다.
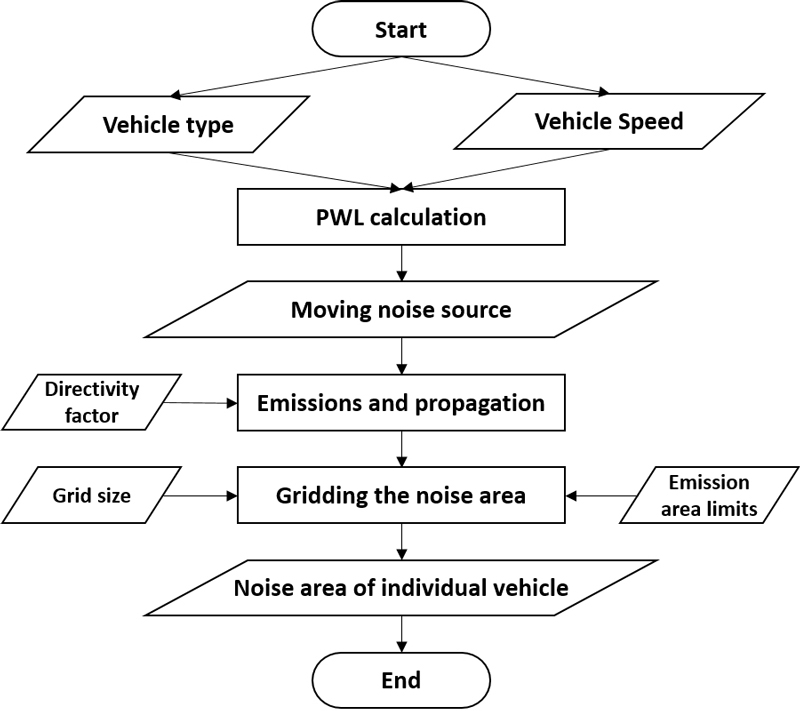
앞서 설명한 전체 계산 과정 중에서 개별 차량의 소음영역을 정의하는 방법은 Fig. 2와 같다. 먼저 도로 네트워크 상 인식된 차량의 차종과 속도 등의 행태 정보를 이용하여 음향파워레벨을 산출한다. 차량 1대의 음향파워레벨 산출은 KHTN을(9,10) 참고하여 식 (5)를 활용하였다.
| (5) |
여기서 A, B는 음향파워계수, V는 차속이다.
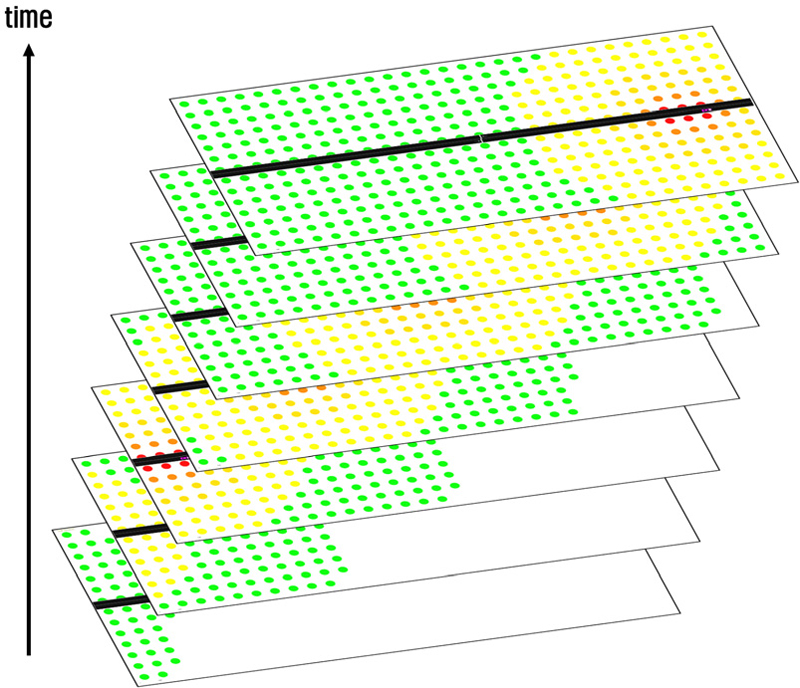
차량 1대의 음향파워레벨을 식 (5)와 같이 산정하는데 A, B는 차종에 따라 다르게 제시되며 KHTN의 경우 5차종 구분에 따라 제시한다(9). 다만 이 연구에서는 국외 도로교통소음 모형과의 비교를 위해 차종을 소형, 대형으로 구분했고 5차종 구분 중 승용차와 소형트력을 소형, 대형버스, 중형트럭, 대형트럭을 대형으로 설정했다. 이에 따라 각 차종별 A, B 계수를 소형과 대형으로 구분하고 평균값으로 재산정해 사용했다. 식 (5)은 인식된 차량에 입력되어 교통 시뮬레이션 상 차량의 속도에 따라 음향파워레벨을 달리 방출하도록 하였으며 이를 개별차량 이동소음원으로 정의하였다. 이동소음원의 음향파워레벨 방출 및 전파에는 거리 감쇠와 공기 흡음의 영향을 고려했다(11). 다음으로 소음의 최대 전달 영역을 설정하고 영역 내를 일정 간격으로 구분하여 x축, y축, z축의 값을 가지는 3차원 격자를 생성했다. 이 연구에서는 최대 전달 영역을 500 m, 각 격자의 크기는 1 m로 설정했다. 각 격자에는 거리감쇠, 공기흡음을 고려하여 산정된 소음도를 입력했다. 또한 지향계수는 고려하지 않았고 차량 중심점을 기준으로 구형으로 전파되도록 했다. 생성된 개별 차량의 소음영역이 도로 네트워크에 입력되어 이동하는 모습은 Fig. 3과 같다.
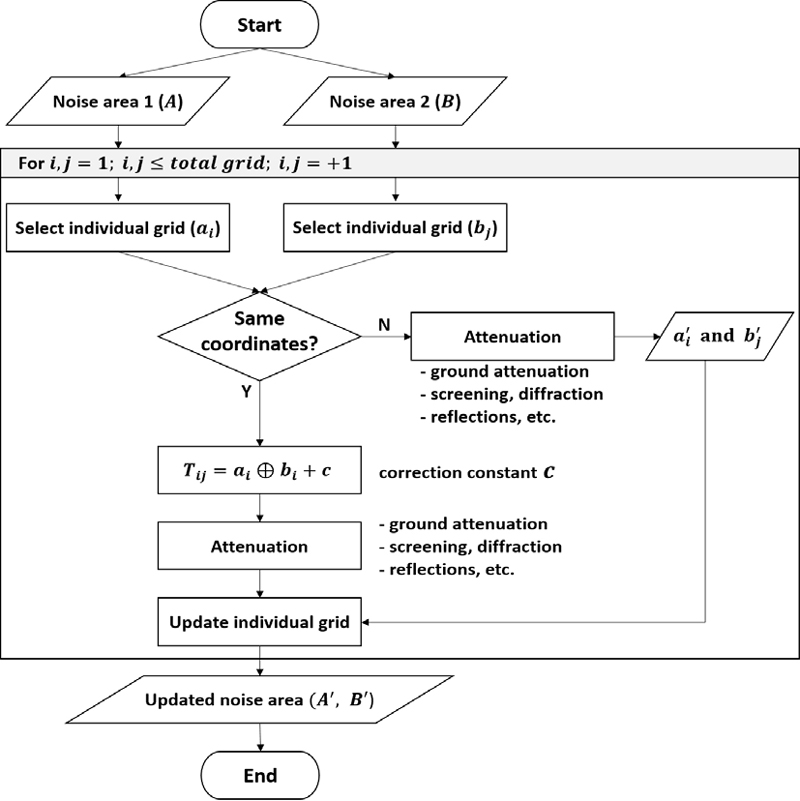
Fig. 2를 통해 생성된 개별차량의 소음영역이 도로 네트워크에 입력된 이후 지형지물 요소에 의한 감쇠와 도로 네트워크 상 다수의 차량이 존재하는 등 상황별 소음영역의 갱신 방법은 Fig. 4와 같다. 먼저 도로 네트워크 상 모든 차량의 소음영역에서 개별 격자 1개씩을 선택한다. 선택된 격자들의 좌표 정보를 비교하여 동일 위치가 아닌 경우에는 각 격자별로 지형지물 요소를 고려한 감쇠치를 적용하여 갱신한다(11). 만일 선택된 격자들이 동일 좌표에 위치하는 경우 각 격자들의 소음도를 합산해 1차 갱신하고 여기에 지형지물 요소를 고려한 감쇠치를 적용한다. 이 과정은 매 시뮬레이션 타임 스텝마다 소음영역 내의 모든 개별 격자에 대해 수행하며 완료시 갱신 소음영역을 출력한다. 갱신 소음영역은 다음 시뮬레이션 스텝에서 다시 갱신에 대한 계산을 수행하는 입력 값으로 이용된다.
2.3 타 모형과의 비교방법
이 연구에서 제안하는 미시적 도로교통소음 모형의 적절성을 알아보기 위하여 기존의 도로교통소음 모형의 계산 결과와 비교하는 실험을 수행했다. 먼저 다른 변수가 개입되지 않은 상태에서 두 모형을 비교하기 위하여 가장 단순한 구조인 토이 도로 네트워크(toy road network)를 시뮬레이션 환경에서 적용했다. 신호가 없는 연속류 도로를 가정하여 평지 지형에 왕복 2차로 도로를 설치했고 총 길이 1 km, 각 도로폭 3.5 m로 설정했다. 노면은 밀입 아스팔트 포장으로 설정하여 식 (5)의 계수를 결정했으며 도로 주변에 건물은 설치하지 않았다. 시계열 도로교통소음을 계산하기 위한 수음점은 도로 500 m 지점의 도로단에서 도로와 수직방향으로 이격거리를 달리하여 위치시켰다. 시뮬레이션을 수행하기 위한 변수의 설정은 Table 1과 같다. 전체 시뮬레이션은 1시간 동안 수행했고 시뮬레이션 타임 스텝은 1초로 설정했다. 차량은 전체 시뮬레이션 시간 동안 설정된 교통량만큼 입력된다. 각 차량이 네트워크에 최초 입력되는 시간은 랜덤하게 설정했다. 평균속도, 교통량 변화와 대형차 혼입률에 따른 소음도 계산 및 결과 비교를 위해 각 변수를 순차적으로 고정하여 시뮬레이션을 수행했다. 먼저 대형차 혼입률을 20 %로 고정한 상태에서 교통량 증가에 따른 도로교통소음의 계산을 수행했다. 다음으로 시간당 교통량을 1000대로 고정하고 대형차 혼입률 변화에 따른 소음도 계산을 수행했다.
위에서 설명한 토이 네트워크의 구성과 시뮬레이션에는 오픈소스 교통 시뮬레이션 프로그램인 SUMO(simulation of urban mobility)를 사용했고(12) 시계열 도로교통소음 계산을 위한 미시적 도로교통소음 모듈은 SUMO에서 제공하는 API 기능인 TraCI를 이용해 구성했다(12). 교통 시뮬레이터 상에서 차량추종모형에 따라 차량의 행태를 결정하는 매개변수는 Table 2와 같다. 차종별 크기, 가감속도, 차간 거리 등은 Krauss 모형의 기본 값을 사용했으며(8) 운전자의 불완전성을 의미하는 σ는 기본 값 0.5보다 낮게 설정하여 운전 숙련도를 높였다(8). 운전자가 앞차의 속도변화를 인지하고 반응하는데 걸리는 시간인 τ는 모형의 기본 값을 사용했다(8). 마지막으로 Table 2에 제시된 시뮬레이션 시간 동안 입력되는 차량의 최고 속도는 Table 1에 제시한 목표속도에 비해 약간 높게 설정했다. 차량추종모형에 의해 도로 네트워크 상 차속이 타임스텝 마다 조정되기 때문에 평균 속도를 목표 속도에 맞추기 위해 최고 속도를 약간 높게 설정한 것이다.
동일한 구조의 토이 네트워크를 SoundPLAN 상에도 구현하고 설정된 교통량과 대형차 혼입률에 따라 RLS90(13)과 NMPM(14)을 이용하여 도로교통소음을 각각 계산했다. 이때 교통 조건은 Table 1과 동일하며 지면흡음은 0으로 설정했다(1). 각 도로교통소음 모형으로 계산된 결과는 시계열 도로교통소음 계산 결과의 1시간 등가소음도와 비교했다.
3. 미시적 도로교통소음 모형의 평가
3.1 시계열 도로교통소음의 계산 결과
미시적 도로교통소음 모형을 통해 전체 시뮬레이션 시간 동안의 도로교통소음과 도로 네트워크의 교통상황은 Fig. 5와 같이 생성된다. Fig. 5는 3600초의 시뮬레이션 시간 동안 1000대의 차량이 통과할 때 계산된 도로교통소음의 예시이다. 이때 평균 차속은 100 km/h이고, 대형차 혼입율은 20 %이다. 도로단에서 도로와 수직 방향으로 10 m와 100 m에 떨어진 공간에 위치한 수음점에서 계산되어 누적되는 소음도와 각 시점별로 도로 네트워크상 입력되어 운행 중인 차량의 수, 네트워크상 모든 차량의 평균 속도를 확인할 수 있다. 동일한 형태의 시계열 소음도는 설정한 모든 수음점에서 계산이 가능하다. 수음점에 누적된 도로교통소음에서는 차량이 수음점 앞을 통과하는 시점을 파악할 수도 있으며 최고소음도, 등가소음도 등의 계산이 가능하다.
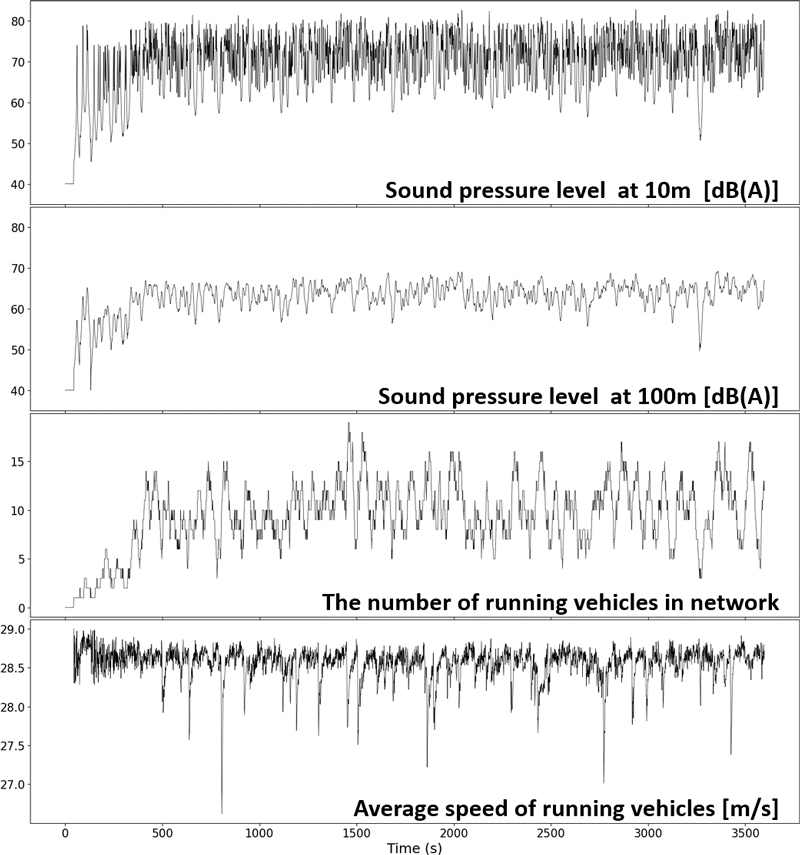
The calculation result of road traffic noise by microscopic road traffic noise model(traffic volume: 1000 vehicles, speed: 100 km/h, heavy vehicle ratio: 20 %)
1시간 동안 도로 네트워크를 통과한 차량 1000대의 평균 속도는 28.2 m/s(101.5 km/s)로 목표 속도 100 km/s보다 약간 높지만 소음도 계산에 있어 큰 오차를 발생시키지 않는 것으로 판단했다. 다만 순간적으로 평균 속도가 급격히 감소하는 순간이 나타나는데 이는 교통 시뮬레이션 상에서 순간 교통량이 많아지거나, 일부 구간에 차량이 밀집되어 정체 현상이 발생하는 경우이다. 교통량의 증감에 따라 교통 정체가 발생하는 경우가 발생하기 때문에 시뮬레이션 시 목표 속도 이하의 결과가 도출될 수도 있다. 기존 도로교통소음 모형을 활용하는 시뮬레이션에서는 신호등이나 정체 구간과 같이 일부 구간에 한정된 속도 변화를 반영하는 것이 쉽지 않다. 하지만 미시적 도로교통소음 모형은 현실성 있는 교통 상황의 반영이 가능하다는 장점이 있다.
3.2 기존 도로교통소음 모형과의 비교
미시적 도로교통소음 모형이 기존 도로교통소음 모형 대비 어느 정도의 오차가 발생하는지 비교했다. 선음원의 기하학적 분할 방식인 독일의 RLS90(13), 프랑스 NMPB를(14) 이용하여 각각 계산한 1시간 등가소음도와 미시적 도로교통소음 모형이 계산한 시계열 소음도의 1시간 등가소음도를 비교했다. 이를 위해 도로 네트워크 내 대형차 혼입율을 20 %로 고정하고 Table 1과 같이 교통량, 속도를 변화시켜 시뮬레이션을 진행했다.
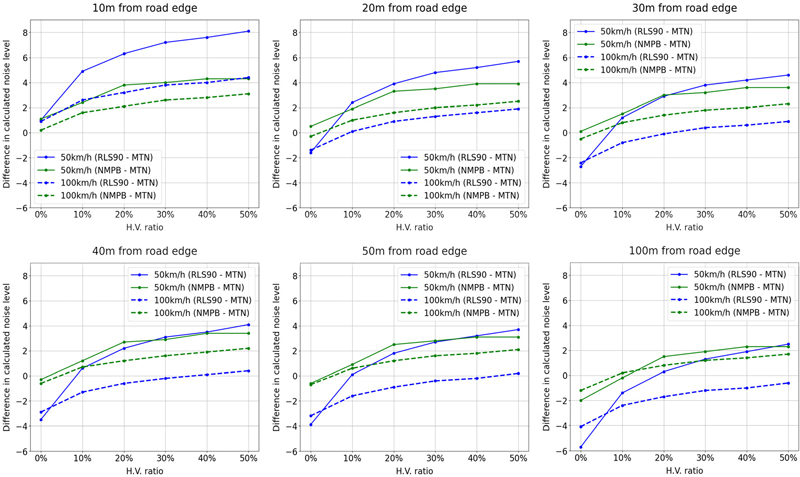
각 속도, 교통량별 시뮬레이션에서 모형별 계산 소음도 차이는 Table 3과 같다. Table 3의 평균 및 표준편차는 각 수음점에서 교통량별로 계산된 소음도의 차이 값을 이용하여 계산했다. 0.06 ~ 0.19의 낮은 표준편차로 확인할 수 있듯이 교통량이 변화해도 모형 별 계산 소음도 차이는 크게 변화하지 않았다. 수음점과 도로 사이의 거리가 10 m인 경우를 제외하고 대부분의 위치에서 기존 모형 대비하여 오차가 3 dB(A) 이내로 나타났다. 미시적 도로교통소음 모형으로 계산한 시계열 도로교통소음의 등가소음도는 대체적으로 다른 모형의 계산 소음도에 비해 낮은 것으로 나타났다. 다만 평균 속도가 100 km/h이고, 도로와 이격거리가 30 m 이상인 경우에는 RLS90 모형으로 계산한 소음도가 미시적 도로교통소음 모형에 비해 낮은 것으로 나타났다.
다음으로 속도와 이격거리에 따라 구분하여 비교하면 다음과 같은 특징을 확인할 수 있었다. 먼저, 속도에 따라 구분하여 비교하면 낮은 속도에서 미시적 도로교통소음 모형과 기존 모형의 계산 소음도 차이가 증가하는 것을 확인할 수 있다. 특히 RLS90의 계산 소음도와 비교하면 속도가 낮아짐에 따라 평균 소음도 차이가 2배 이상으로 증가했다(차이의 절대값 기준). NMPB의 경우에도 속도가 낮아지면 차이가 증가하긴 하지만 상대적으로 변화가 크지 않다. 다음으로 수음점이 도로와 가까울수록 모형별 계산 소음도의 차이가 증가하는 것을 확인할 수 있었다. 특히 도로와 매우 가까운 10 m 위치에서는 계산 소음도의 차이가 큰 것으로 나타났다. RLS90의 등가소음도와 비교할 시 평균적으로 6.37 dB(A), 3.36 dB(A), NMPB와 비교할 경우 3.27 dB(A), 2.23 dB(A)의 차이가 확인되었다. 도로와의 이격거리가 20 m 이상인 지점부터는 계산 오차가 급격히 감소했으며 NMPB의 경우 20 m ~ 100 m 모든 지점에서 계산 오차가 3 dB(A) 이하로 나타났다. NMPB와의 계산오차가 RLS90에 비해 더 적은 이유는 PWL을 계산하는 방식(14)이 유사하기 때문으로 판단되나 이에 대해서는 좀 더 면밀한 연구가 필요하다. 또한 도로와 매우 가까운 곳에서 미시적 모형을 통한 예측의 신뢰성 확보를 위해 미시적 모형에 맞는 PWL에 대한 연구가 더 필요하다.
시간당 교통량은 고정한 상태에서 도로네트워크에 입력되는 대형차 혼입율의 변화에 따른 도로교통소음을 계산하고 기존 모형과 비교했다. 도로 네트워크 상 이동하는 차량의 평균속도는 50 km/h 혹은 100 km/h 이고, 1시간은 교통량은 1000대로 고정한 상태에서 대형차의 비율을 0 %에서 50 %까지 10 %씩 증가시키며 시뮬레이션을 수행하여 소음도를 계산했다.
교통량의 증감과 달리 대형차의 비율 변화는 기존 모형과 미시적 모형의 계산 소음도 차이에 크게 영향을 주는 것으로 판단된다. 이는 대형차량의 비율이 변함에 따라 기존 모형과 미시적 도로교통소음 모형으로 각각 계산한 소음도의 차이를 나타낸 Fig. 6에서 확인할 수 있다. Fig. 6에 나타낸 차이 값은 기존 모형 계산 결과에서 미시적 모형의 계산 결과를 뺀 값이다. 모든 이격거리에서 대형차 비율이 커질수록 기존 모형과 미시적 도로교통소음 모형의 계산 소음도 차이가 증가하는 것을 확인할 수 있다. 특히 도로단에서 10 m 지점인 수음점에서는 평균 속도 50 km/h일 때, RLS90과 미시적 도로교통소음 모형의 계산 소음도 차이가 1.0 dB(A)에서 8.1 dB(A)로 매우 크게 증가했다. 또한 속도가 낮은 경우에 대형차 비율 증가에 따른 계산 소음도 차이의 변화폭이 큰 것을 확인할 수 있다. RLS90과 비교하는 경우 50 km/h일 때, 대형차 비율이 0 %에서 50 %로 증가하는 동안 계산오차의 변화폭은 7.1 dB(A) ~ 7.6 dB(A)인 반면 100 km/h일 때는 3.2 dB(A) ~ 3.7 dB(A)로 나타났다. NMPB와 비교하는 경우엔 50 km/h일 때 계산오차의 변화폭이 3.2 dB(A) ~ 3.7 dB(A), 100 km/h일 때는 2.8 dB(A) ~ 2.9 dB(A)로 나타났다. 또한 대형차 비율이 낮을수록 비율 증가에 민감하게 반응하는데 대형차 비율이 0 %에서 10 %로 증가할 때 가장 변화폭이 큰 것으로 나타났다.
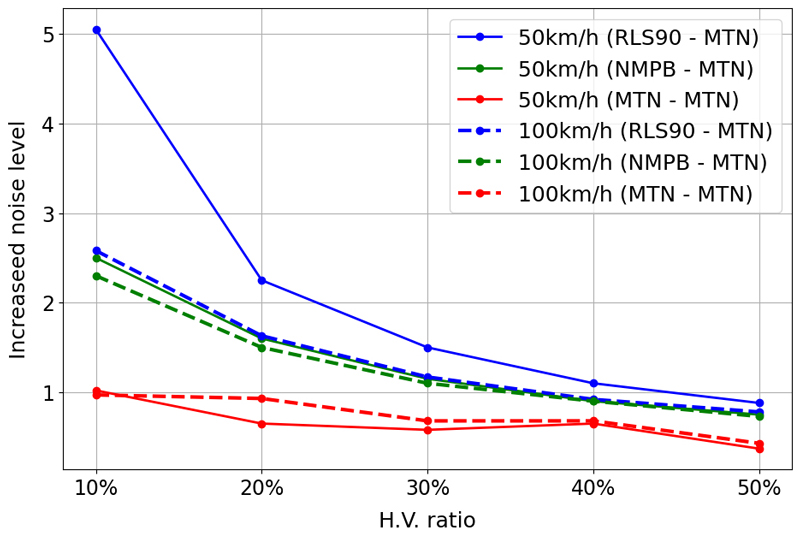
이러한 변화는 대형차량 비율에 따라 각 모형별로 증가하는 소음도가 다르기 때문인 것으로 판단된다. 대형차 비율 증가에 따른 소음도 증가량은 Fig. 7과 같다. Fig. 7에서 확인할 수 있듯이 미시적 도로교통소음 모형의 경우 대형차 비율에 따른 소음도의 증가가 다른 모형에 비해 상대적으로 낮다. 특히 대형차 비율이 낮을 때 소음도 증가량의 차이가 큰데 대형차 비율이 0 %에서 10 %로 증가할 때 미시적 도로교통소음 모형은 1 dB(A) 증가한 반면 RLS90은 속도별로 각각 5.05 dB(A), 2.58 dB(A), NMPB도 2.50 dB(A), 2.30 dB(A)만큼 증가했다. 대형차 비율이 10 %에서 더 증가하면 모형별 소음도 증가량의 편차가 줄어들게 되지만 여전히 미시적 도로교통소음 모형에서의 소음도 증가량이 가장 낮다. 이처럼 미시적 도로교통소음 계산 방법은 대형차 교통량의 변화에 둔감하게 반응하는 것으로 판단된다.
4. 결 론
이 연구에서는 도로의 교통상황에 따른 실시간 도로교통소음을 계산하기 위한 방법으로써 미시적 교통 시뮬레이션을 활용하여 시계열 도로교통소음을 계산하는 방법에 대해서 제안했다(12). 개별 차량에서 방출되는 음향파워레벨의 계산에는 KHTN에서 제시하는 음향파워레벨 산정 방법을 활용했다(9,10). 이 연구에서 제안하는 방식을 이용하여 수음점에서 계산된 도로교통소음의 시계열 데이터로 차량의 통과 이벤트를 모두 확인할 수 있으며 최고소음도, 등가소음도의 평가가 가능하다.
미시적 도로교통소음 모형의 정확도를 평가해보기 위해 계산된 시계열 도로교통소음도에서 등가소음도를 계산하고 이를 기존의 대표적인 국외 도로교통소음 모형인 RLS90과 NMPB의 계산 결과와 비교했다. 비교 결과 첫 번째로 기존 모형대비 계산 오차가 대체적으로 3 dB 이내인 것으로 나타났다. 그리고 미시적 도로교통소음 모형의 등가소음도 계산 결과가 기존 모형에 비해 낮게 계산된다는 것을 확인했다. 이러한 현상은 수음점의 위치가 도로와 가까워질수록 두드러지게 나타났다. 또한 낮은 속도에서 기존 모형과의 계산 오차가 커지는 것을 확인할 수 있었다. 두 번째로 비교 대상으로 삼은 2개의 모형 중에서는 NMPB와 계산 오차가 적은 것으로 나타났다. 거리, 속도 등에 따라 차이는 발생하지만 평균적으로 RLS90과는 2.0(표준편차 1.7) dB(A), NMPB와는 1.8(표준편차 0.7) dB(A)의 계산 오차가 발생했다. 마지막으로 대형차 비율 변화에 대한 소음도의 민감도가 떨어진다. 평균속도가 100 km/h인 경우 대형차 비율이 0 %에서 10 %로 증가할 때 미시적 도로교통소음 모형은 1 dB(A) 증가한 반면 RLS90은 2.58 dB(A), NMPB은 2.30 dB(A) 증가하며 각 모형들의 계산 오차는 원인이 된다.
이 연구는 미시적 도로교통소음 모형을 개발함에 있어 가장 기본이 될 수 있는 계산 방법에 대해서 정의하고 간단한 시뮬레이션으로 가능성을 판단한 기초 연구이다. 미시적 방식을 통한 도로교통소음의 계산은 현실성 있는 예측과 관리방안을 마련하는데 도움을 줄 수 있을 것으로 기대된다. 앞으로 다음과 같은 개발 과정을 통해 미시적 도로교통소음 모형을 완성시키는 것을 목표로 하고 있다. 먼저 실측 도로교통소음을 이용해 계산되는 시계열 도로교통소음의 정확도를 검증하는 과정이 필요하다. 또한 실측 소음도를 기반으로 미시적 도로교통소음의 계산을 위한 음향파워레벨 모형을 정립하는 과정이 필요하다. 다음으로 지형지물 모델링과 지형지물에 의한 회절, 반사 등의 효과를 소음 해석에 적용하는 방안에 대한 연구가 필요하다. 마지막으로 최종적으로 도로 주변에 설치되어 있는 IOT 센서와 연계되어 실시간 교통정보를 반영하는 도로교통소음의 계산과 실시간 소음지도의 출력에 대한 연구를 수행하고자 한다.
Acknowledgments
위 논문은 한국건설기술연구원의 연구비 지원 ‘(24 주요-대1-목적)미래교통 스마트 인프라 핵심기술개발(4/4)’에 의해 수행되었습니다.
References
- Ministry of Environment, 2021, Drawing-up Method of Noise Maps, Ministry of Environment Public Notice No. 2021-54, Ministry of Environment, Sejong-si, Korea.
-
Wei, W., Van Renterghem, T., De Coensel, B. and Botteldooren, D., 2016, Dynamic Noise Mapping: A Map-based Interpolation between Noise Measurements with High Temporal Resolution, Applied Acoustics, Vol. 101, pp. 127~140.
[https://doi.org/10.1016/j.apacoust.2015.08.005]

-
Aumond, P., Can, A., Mallet, V., De Coensel, B., Ribeiro, C. et al., 2018, Kriging-based Spatial Interpolation from Measurements for Sound Level Mapping in Urban Areas, The Journal of the Acoustical Society of America, Vol. 143, No. 5, pp. 2847~2857.
[https://doi.org/10.1121/1.5034799]

-
Kim, P., Ryu, H., Jeon, J. J. and Chang, S. I., 2019, Artificial Neural Network Model Development based on Road-traffic Noise and Urban Form Indicators, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 29, No. 5, pp. 577~583.
[https://doi.org/10.5050/KSNVE.2019.29.5.577]

-
Kim, P., Ryu, H., Jeon, J.-J. and Chang, S. I., 2021, Statistical Road-traffic Noise Mapping based on Elementary Urban Forms in Two Cities of South Korea, Sustainability, Vol. 13, No. 4, p. 2365.
[https://doi.org/10.3390/su13042365]

-
Le Bescond, V., Can, A., Aumond, P. and Gastineau, P., 2021, Open-source Modeling Chain for the Dynamic Assessment of Road Traffic Noise Exposure, Transportation Research Part D: Transport and Environment, Vol. 94, 102793.
[https://doi.org/10.1016/j.trd.2021.102793]

-
Baclet, S., Khoshkhah, K., Pourmoradnasseri, M., Rumpler, R. and Hadachi, A., 2023, Near-real-time Dynamic Noise Mapping and Exposure Assessment using Calibrated Microscopic Traffic Simulations, Transportation Research Part D: Transport and Environment, Vol. 124, 103922.
[https://doi.org/10.1016/j.trd.2023.103922]

- Krauß, S., 1998, Microscopic Modeling of Traffic Flow: Investigation of Collision Free Vehicle Dynamics, Doctoral Disseration, University of Cologne, Köln, Germany.
- Kim, C. H., Chang, T. S., Kang, H. M., Cho, Y. H., Jeung, T. R. et al., 2009, The Highway Traffic Noise Prediction Program, KHTN Model 2007, Proceedings of the KSNVE Annual Autumn Conference, pp. 714~715.
- Kim, C., Kang, H. and Lee, W., 2022, Evaluation Method of Highway Pavement Noise for Environmental Impact Assessment, Korea Expressway Corporation Research Institute, Report No. KECRI-2021-63-534.9607.
- ISO, 2024, Acoustics - Attenuation of Sound During Propagation Outdoors - Part 2: Engineering Method for the Prediction of Sound Pressure Levels Outdoors, International Organization for Standardization, ISO 9613-2:2024.
-
Lopez, P. A., Behrisch, M., Bieker-Walz, L., Erdmann, J., Flötteröd, Y.-P. et al., 2018, Microscopic Traffic Simulation using Sumo, Proceedings of the 21st International Conference on Intelligent Transportation Systems (ITSC), pp. 2575~2582.
[https://doi.org/10.1109/ITSC.2018.8569938]

- Road Construction Department of Germany Ministry of Transport, 1990, Road Noise Abatement Guidelines, Road Construction Department of Germany Ministry of Transport, RLS-90, Stuttgart, Germany.
- Sétra, 2009, Road Noise Prediction: 2 - Noise Propagation Computation Method including Meteorological Effects, Service d’Études sur les Transports, les Routes et leurs Aménagements, NMPB 2008.

Jae Kwan Lee has completed his Ph.D. at dept. of Environmental Engineering in University of Seoul. He is working at Korea Institute of Civil Engineering and Building Technology as a post-doctoral researcher. His research interests is environmental noise control and annoyance of noise. Recently, he is interested in deep learning for classification the noise source and environmental noise change by future mobility.

Hyoungsoo Kim achieved Ph.D. degree in Transportation Engineering program at the University of Maryland in the U.S. He has been a research fellow at Korea Institute Civil Engineering and Building Technology in Korea since 2008. His research interests include advanced transportation and simulation.

Phillip Kim received his B.S. from the School of Environmental Engineering and his Ph.D. from the Department of Energy, Environmental, and System Engineering at the University of Seoul. He previously worked as an associate research fellow at the Daegu Gyeongbuk Institute and is currently a post-doctoral researcher at the Korea Institute of Civil Engineering and Building Technology. His research interests include environmental noise estimation based on deep learning models. Recently, he has been focusing on the prediction and control of environmental noise induced by UAVs and UAM.