단방향 FSI 해석을 이용한 잠수함 항해레이더 안테나장치의 구조건전성 분석

1. 서 론

은밀성을 갖춘 잠수함이라는 플랫폼은 대표적인 비대칭 전력으로서 해군의 주요 전력 중 하나이다. 특히, 우리나라의 경우 최근 세계 8번째로 3천톤급 잠수함을 보유하는 등 잠수함 전력 강화와 주요 장비의 국산화에 매진하고 있다. 항해레이더는 잠수함의 주요 장비로서 함외에 설치되는 안테나장치와 함내에 설치되는 데이터 서버장치 등으로 구성되어 있다.

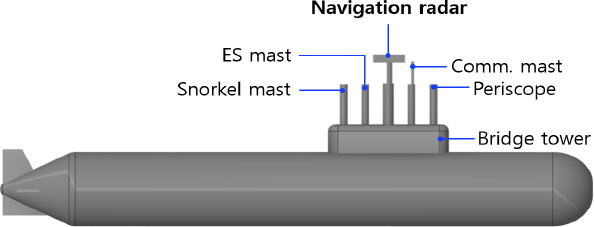
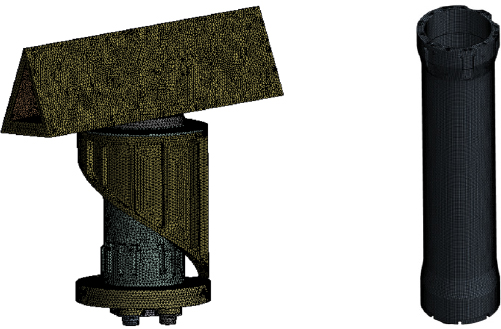
이 장비는 좁은 수로 등 통항량이 많은 구간을 항해하거나 저시정, 악천후 등의 상황에서 함의 안전항해를 책임지고, 전시에는 적함을 탐지 및 추적하여 격침 시키기 위해 필수적이다. 잠수함의 주요 장비들은 함교탑(bridge tower)의 마스트에 설치되며 Fig. 1에서 볼 수 있듯이 일반적으로 항해레이더 외에 잠망경, 스노클 마스트, 통신 마스트, ES(electronic support) 마스트 등으로 구성되어 있다. 이들 장비는 필요에 따라 상승과 하강이 가능하며 하강 시 함교탑 내부에 보관된다.

Fig. 1

Equipments in a submarine bridge tower

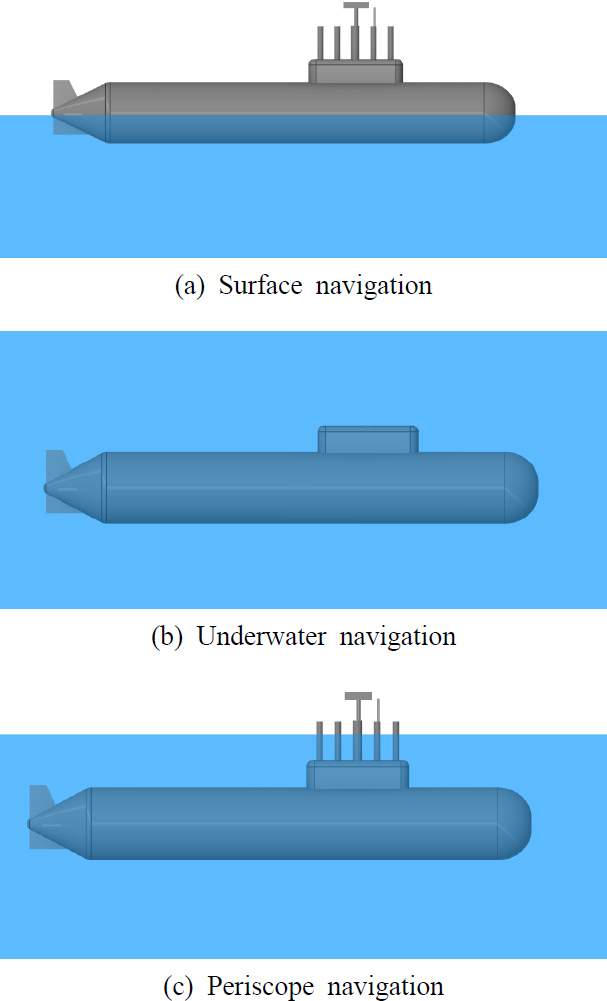
잠수함의 항해상태는 Fig. 2와 같이 수상항해, 수중항해 그리고 선체는 수중에 잠긴 채로 마스트만 상승시켜 항해하는 잠망경항해로 구분된다. 항해레이더는 일반적으로 수상 및 잠망경항해 시에는 상승되어 바람 등의 외력에 노출된 채로 운용되고, 수중항해 시에는 하강되어 함교탑 내부에 보관된다. 하지만 적 항공기의 위협 등 긴급한 상황에는 항해레이더를 비롯한 마스트 장비들을 하강시킬 여유가 없어 일정 수심까지 장비를 상승시킨 채로 잠항하기도 한다⁽¹⁾. 이 경우 항해레이더는 강한 유체저항을 받게 된다. 이처럼 항해레이더는 잠수함의 필수 장비로서 운용 환경에 따라 가해지는 다양한 외력에 대해 구조적 건전성을 갖춰야 한다.

Fig. 2

Submarine navigation

외부 하중에 의한 레이더 장비의 안정성 평가에 관한 연구는 다양하게 수행되었다. 이전 연구에서는 고각 구동 유닛을 포함한 대형 레이더 구조물에 대하여 풍하중에 의한 구조의 응력과 좌굴특성을 분석하고 차량 수송 간 발생 가능한 랜덤 진동에 대한 구조 건전성을 종합적으로 제시하였다⁽²⁾. 또한 풍하중을 고려하여 저속으로 회전하는 대형 레이더의 구동부에 대해 베어링의 변형량을 기준으로 구조 안전성을 확인하는 연구가 수행되었다⁽³⁾. 그리고 함정 마스트에 장착되는 레이더용 회전 안테나에 대해 풍하중에 의한 영향을 FSI 해석을 통해 분석함으로써 형상 설계안을 제시하는 연구도 수행되었다⁽⁴⁾. 이와 같이 여러 가지 형태의 레이더에 대해 플랫폼의 운용환경에 따른 풍하중 등 외력 조건에서의 구조건전성 분석을 수행한 연구가 활발히 진행되었다.

이 연구에서는 잠수함이라는 특수한 플랫폼에 장착되는 항해레이더의 구성품 중 함외에 설치된 안테나장치에 대해 공기중과 수중에서의 외력을 모두 고려하여 구조의 안전성을 분석하는 연구를 수행하였다.이를 위해 안테나장치의 유한 요소 해석 모델을 구축하고 수상 및 수중에서의 주요 외력으로 풍하중과 유체저항을 선정하였다. 풍하중은 미국 국방 표준 규격인 MIL-STD에 명시된 최대 풍속을 적용하였고, 유체저항은 수중에서 항해레이더가 상승된 상태를 가정하여 해석을 수행하였다. 또한 유체-구조 간 상호작용을 정확히 파악하기 위해 단방향 FSI(fluid structure interaction) 해석을 수행하였고 최종적으로 응력 기반 평가를 통해 구조건전성을 분석하였다.

2. 대상모델 및 적용하중

2.1 대상모델

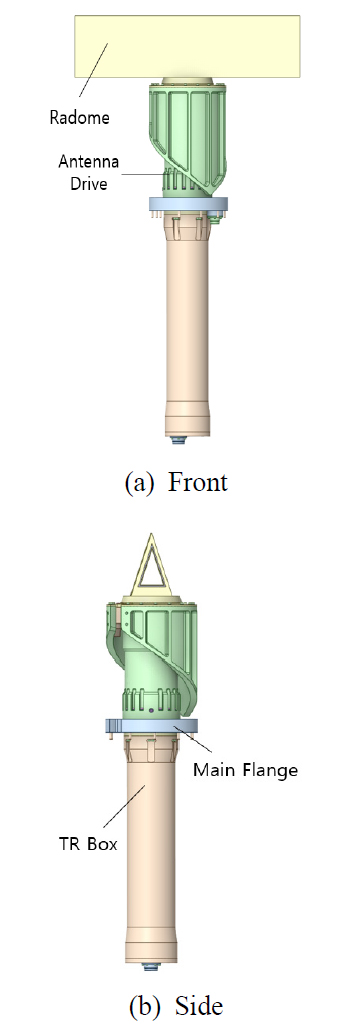
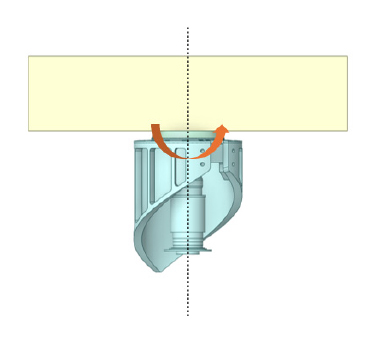
안테나 장치는 항해레이더의 구성품 중 하나로 Fig. 3과 같이 구성되어 있다. 마스트와 직접적으로 연결되는 메인 플랜지를 기준으로 상부에는 레이돔(radome)과 안테나 구동기가 위치하고 있고 하부에는 TR(transmit / receive) box가 있으며, 그 내부는 다양한 전자 부품으로 구성되어 있다. 또한 Fig. 4에서 볼 수 있듯이 레이돔과 안테나 구동기 중 일부구조는 수상 및 잠망경항해 시 24 r/min의 일정한 속도로 회전하며 운용된다.

Fig. 3

Navigation radar antenna device

Fig. 4

Rotating unit

2.2 적용하중

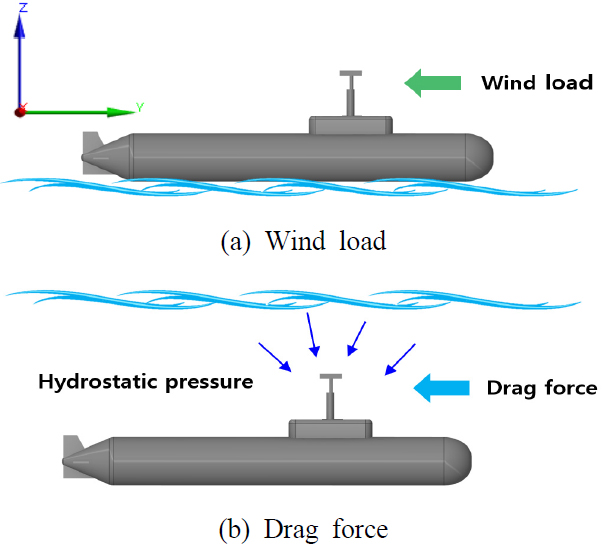
이 연구에서는 항해레이더 안테나 장치의 구조건전성을 분석하기 위하여 잠수함의 수상 및 수중항해 상태에서의 주요 하중을 각각 선정하였다. 먼저 수상상태에서는 풍하중을 선정하였으며, 풍속값은 미군 표준 규격인 MIL-STD-1399-302A에 명시된 최대 돌풍 100 kn을 적용하고⁽⁵⁾ 공기의 밀도는 1.165 kg/m³, 점도는 1.7894 × 10^-5 kg/m·s로 설정하였다. 또한 수중상태에서는 잠수함이 긴급상황에서 항해레이더를 하강시키지 못한 채 잠항한 상황을 가정하였으며, 이때 잠수함의 항해속력에 의해 발생하는 유체저항을 주요 하중으로 선정하였다. 이 경우 수심에 따른 정수압도 고려되어야 한다. 잠수함의 수중속력과 항해레이더를 상승한 채 잠항할 수 있는 최대 수심은 잠수함의 종류와 추진방식 등에 따라 달라지며, 이는 군 보안 사항으로 자세한 내용은 알려져 있지 않다. 따라서 이 논문에서는 연구를 위해 수심은 10 m, 속력은 일반적인 재래식 디젤 추진 잠수함의 수중 최대속력의 범위에 해당되는 20 kn으로 가정하였다⁽⁶⁾. 이때 해수의 밀도는 1025 kg/m³, 점도는 1.003 × 10^-3 kg/m·s로 설정하였다. 적용하중의 종류는 Fig. 5와 같으며, 잠수함은 y축 방향으로 항해하면서 외력을 받는다.

Fig. 5

Types of external forces

3. 해석 방법

3.1 해석절차

유체의 항력(drag force)에 의한 구조물의 영향을 확인하기 위한 방법으로는 먼저 간단한 항력 계산식을 이용하는 방법이 있다. 항력의 계산 방법은 식 (1)과 같다.

$\[ F_D=\frac{1}{2}{C}_{D}A\rho V^2 \]$

(1)

여기서 C_D는 항력계수, A는 물체의 단면적, V는 유체의 속도, ρ는 유체의 밀도를 나타낸다. 이 중 항력계수는 물체의 형상과 크기에 따른 변수이며 보통 단순한 형태의 경우 실험적으로 얻어진 값을 사용하는데, 복잡한 구조의 경우 신뢰성이 낮은 편이다⁽⁷⁾. 다음으로 고려할 수 있는 것은 실험적 방법이다. 풍하중의 경우 풍동실험(wind tunnel test)을 예로 들 수 있는데 이러한 실험의 경우 축소된 모델을 사용하기 때문에 정확성에 한계가 있으며, 실험을 할 수 있는 별도의 시설이 필요하다. 또한 많은 비용과 시간이 필요한 단점이 있다⁽⁸⁾.

따라서 이 논문에서는 위에서 언급한 수식, 실험적 방법이 아닌 수치해석을 통해 유체의 영향을 확인하였다. 수치해석은 구조물을 실제 크기로 모델링 하여 정확성을 높일 수 있고 실험에 비해 시간과 비용이 적게드는 장점이 있다. 또한 참고문헌에 따르면^(9,10) 일반적으로 수치해석으로 도출된 데이터와 실험 결과 간의 오차는 크지 않은 것으로 알려져 있다. 수치해석의 방법으로는 CFD(computational fluid dynamics) 해석이 있으며 이를 통해 유체의 속도, 압력 등의 분포의 확인이 가능하다. 하지만 이는 유체의 작용만 고려하기 때문에 유체의 영향에 의해 구조에 어떤 작용이 발생하는지는 알 수 없다는 한계가 있다. 이러한 한계점은 FSI(fluid structure interaction) 해석을 통해 해결할 수 있다. FSI 해석은 유체, 구조 간의 상호작용을 해석하는 수치해석 방법이다. 유체의 압력은 경계면에서 구조체에 하중으로 작용하며 이 하중에 의해 구조체의 변형이 발생하고, 구조체의 변형은 다시 유동장에 영향을 준다. 유동-구조 간의 결합형태를 수식화한 일반적인 지배방정식은 식 (2), 식 (3)과 같다⁽¹¹⁾.

$\[ \left[M_s\right]\left\{\ddot{U}\right\}+\left[K_s\right]\left\{U\right\}=\left\{F_s\right\}+\left[R\right]\left\{P\right\} \]$

(2)

$\[ \left[M_f\right]\left\{\ddot{P}\right\}+\left[K_f\right]\left\{P\right\}=\left\{F_f\right\}-{\rho }_0{\left[R\right]}^T\left\{U\right\} \]$

(3)

여기서 M_s와 K_s는 구조 요소의 질량행렬과 강성행렬이고, U와 F_s는 노드 변위와 구조의 하중 벡터이다.

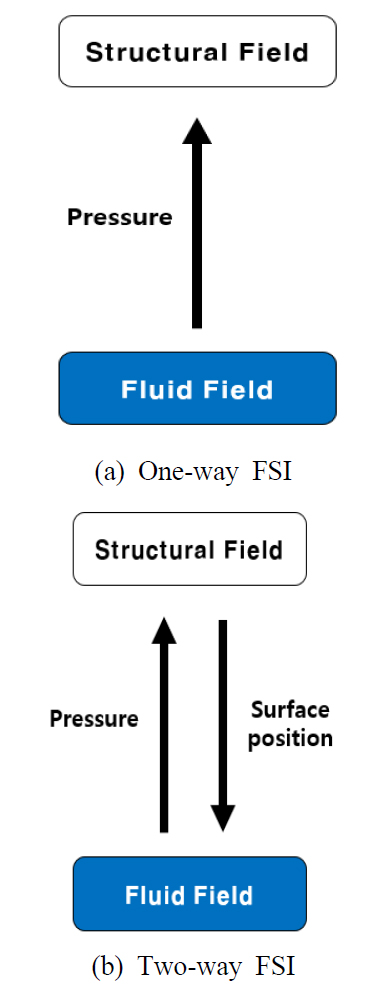
마찬가지로 M_f와 K_f는 유체 요소의 질량행렬과 강성행렬이고 P는 노드 압력, F_f는 유체 하중 벡터이다. R은 경계면에서 유체와 구조의 상호작용을 나타내는 결합행렬(coupling matrix)이다. FSI 해석은 Fig. 6과 같이 해석방식에 따라 두가지 방법으로 나뉜다.

Fig. 6

FSI coupling methods

우선 단방향(one-way) 연성해석은 CFD 해석결과로 계산된 유체의 힘을 구조의 하중 조건으로 적용하여 해석을 수행한다. 이 방법은 유체에 의한 구조의 변형이 크지 않은 경우에 주로 사용한다. 반면 양방향(two-way) 연성해석은 유체의 영향을 받아 변형이 생긴 구조가 다시 유동장에 영향을 미치는 경우에 수행하며 단방향 해석에 비해 정확하고 안정적이나, 해석시간이 길고 매 time step 마다 격자가 변하기 때문에 격자 품질을 일정하게 유지하지 못한다는 단점이 있다⁽¹²⁾. 이 논문의 연구 대상인 항해레이더 안테나 장치의 경우 유체의 영향에 따른 구조의 변형이 크지 않을 것으로 보아 단방향 연성해석을 사용하여 연구를 진행하였다. FSI 해석을 위해 구조영역에 대해서는 상용 소프트웨어인 ANSYS Mechanical 2021 R1를 사용하였고, 유체영역의 해석은 ANSYS Fluent 2021 R1을 사용하였다. Fluent에서 유체에 대한 전산수치해석을 수행하였고 그 결과를 workbench에서 static structural과 연동하여 단방향 연성해석을 수행하였다.

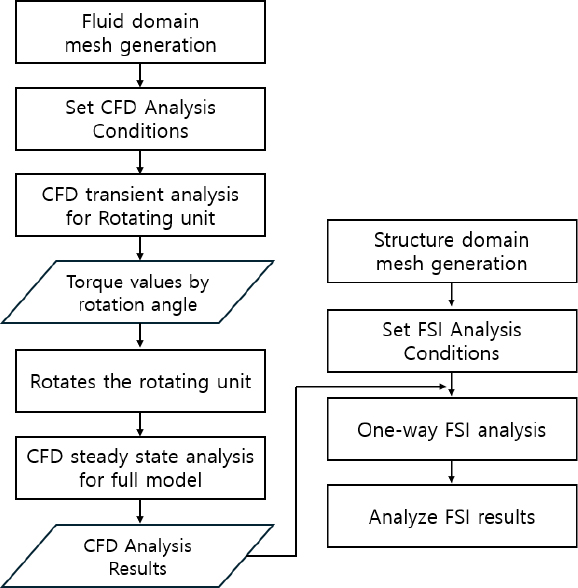
이 연구의 해석절차를 정리하면 Fig. 7과 같다. 먼저 회전부(rotating unit)를 대상으로 CFD 비정상 상태(transient) 해석을 수행하여 회전각도에 따른 회전축 방향 토크 값을 산출하였고 최대토크가 발생하는 회전각도를 확인하였다. 이후 회전부를 해당 각도만큼 회전시킨 채로 전체 안테나장치 모델에 대해 CFD 정상상태(steady-state) 해석을 수행하였고, 유체의 압력분포를 확인하였다. 최종적으로 이 압력 데이터를 구조부에 연동하여 단방향 연성해석을 진행하였으며, 유체의 압력에 의한 구조부의 응력분포를 분석하였다.

Fig. 7

Flow chart of FSI analysis

3.2 유동해석

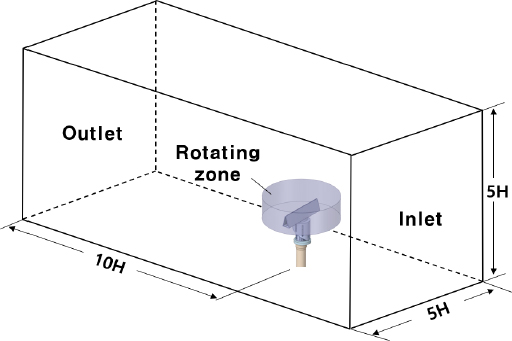
해석을 위한 유동장은 Fig. 8과 같이 형성하였다. 유체가 흐르는 방향을 고려하여 각각 입구측과 출구측을 설정하였고, 레이돔과 안테나 구동기 일부가 포함된 회전부에 대해 별도의 체적(rotating zone)을 형성하였다. 전체 유동장의 크기는 폐쇄율(blockage ratio)을 고려하여 대상 구조의 높이 H에 대해 측면과상부 경계는 5 H, 구조물에서 출구 측까지는 10 H로 설정하였다⁽¹³⁾. 또한 입구 측은 velocity inlet 조건으로 풍속 100 kn, 유속 20 kn을 적용하였고 출구 측은 pressure outlet 조건으로 대기압을 적용하였다. 벽면의 전단 조건(shear condition)은 no slip으로 설정하였다. 유체의 격자는 사면체 요소로 구성하였으며 두 개의 유체영역이 닿는 인터페이스 경계면에 대해서는 격자를 더 조밀하게 형성하였다. 유동장 모델의 절점 수는 6 322 094개, 요소의 수는 4 456 115개이고 격자의 품질은 평균 orthogonal quality 0.77, skewness 0.23으로 양호하게 형성하였다. 안테나의 회전을 해석에 반영하기 위해 fluent의 moving mesh 기능을 활용하여 회전부가 속한 체적에 대해 24 r/min의 속력을 설정하였고, 외부 체적과는 인터페이스 처리하였다. 비정상 상태 CFD 해석의 경우 안테나 장치가 24 r/min으로 1회전(360°) 하는 2.5초 동안의 토크 값을 계산하기 위해 time step size는 0.01초, 개수는 250개로 설정하였다. 유체 해석의 기본 조건은 Table 1과 같다. 특히 해수의 밀도는 압력, 염도, 온도 등 다양한 변수에 영향을 받기 때문에 최대한 정확한 값을 적용하기 위해 수심과 지역별 위도를 고려한 이론적 밀도 모델을 사용하여 계산하였다⁽¹⁴⁾. 또한 난류모델은 벽면 근처에서의 해석 정확성을 높인 SST(shear stress transport) k - ω모델을 사용하였다^(15,16).

Fig. 8

Fluid domain for analysis

Table 1

Design condition of fluid domain

3.3 구조해석

주요 구성품인 레이돔과 안테나구동기, TR box의 형상은 유지하였고 TR box 내부의 전자 부품에 대해서는 집중 질량으로 대체하였다. 해석 결과에 큰 영향을 미치지 않는 선에서 구조 단순화를 통해 요소 수를 감소시켜 해석시간을 단축시켰다. 작성한 유한 요소 해석 모델의 형상은 Fig. 9와 같다. 구축된 해석 모델은 사면체 요소와 육면체 요소로 구성하였고 탄성 영역에서의 선형 해석이 목적이므로 2차 요소가 아닌 1차 요소를 이용하였다. 최종적으로 해석 모델의 절점 수는 185 786개, 요소의 수는 500 389개로 형성하였다. 또한 안테나 장치와 별도의 마스트가 체결되는 부위인 메인플랜지 볼트 체결부에 fixed support 경계 조건을 설정하였다. 또한 수중항해 상태의 경우 유체의 정수압을 고려하기 위해 hydrostatic pressure 기능을 활용하여 수심 10 m의 정수압을 Fig. 10과 같이 구조의 최상단을 기준으로 약 0.1 MPa ~ 0.12 MPa을 적용하였다.

Fig. 9

Finite element model of antenna device

Fig. 10

Hydrostatic pressure

4. 해석 결과

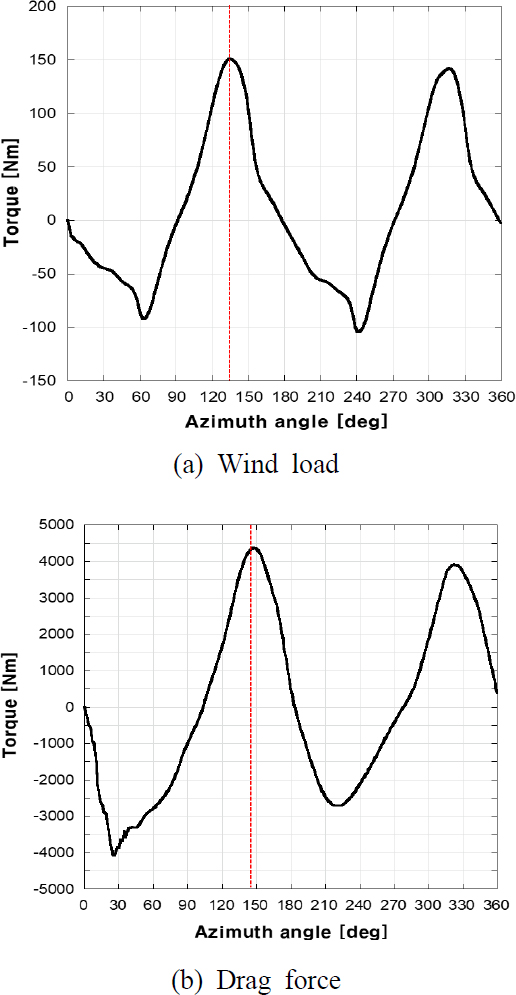
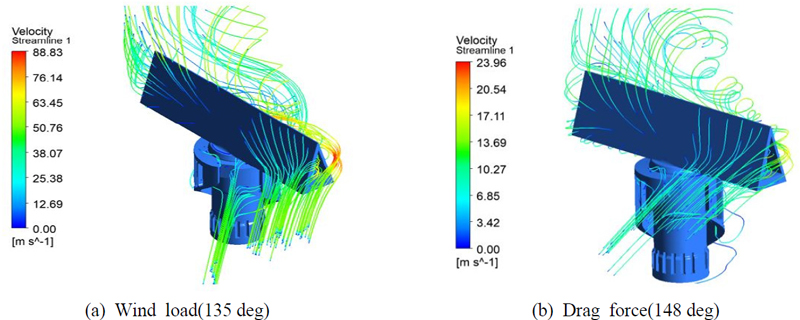
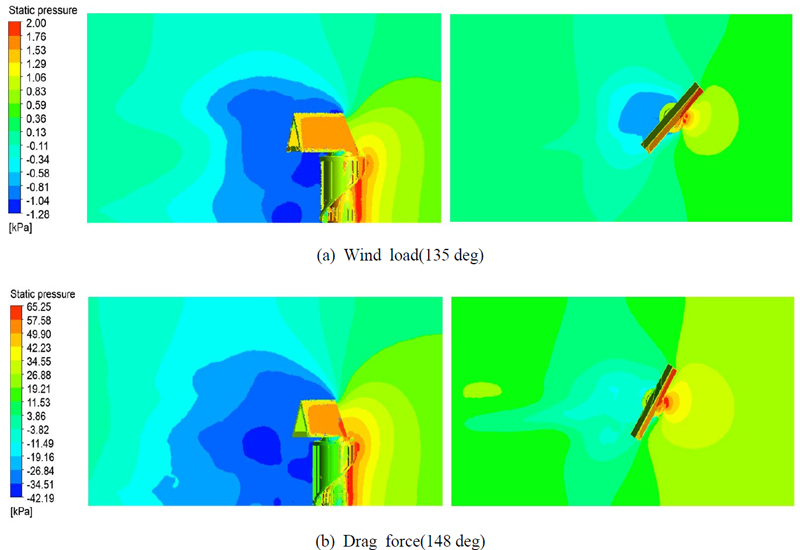
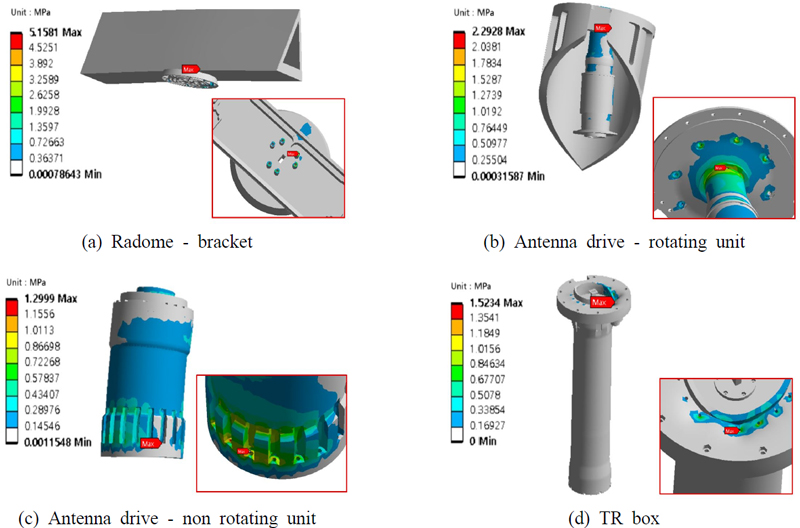
먼저 CFD 비정상 상태 해석 결과 회전축에 대한 최대 토크 값은 Fig. 11과 같이 풍하중의 경우 135°에서 150 Nm, 유체저항은 148°에서 4370 Nm가 발생하였다. 이는 회전부 형상의 특징에 의한 것으로 특히 토크 값에 가장 큰 영향을 미치는 레이돔의 경우 가운데가 비어있는 형상으로 Fig. 12와 같이 유체의 흐름이 레이돔의 빈 공간으로 들어가 강한 힘이 가해진 것으로 판단된다. 이후 안테나장치 회전부 모델에 대해 최대토크 발생 각도인 135°, 148° 만큼 회전시켰고 전체 모델에 대한 CFD 정상 상태 해석을 수행하였다. 해석결과 유체의 최대 압력은 Fig. 13과 같이 풍하중의 경우 약 2 kPa, 유체저항은 65 kPa이 발생하였다. 이러한 압력 데이터를 구조부에 반영하여 단방향 FSI 해석을 수행하였고, 응력기반 평가를 통해 최종적으로 구조건전성 분석을 진행하였다. 평가방법은 안전여유(MOS : margin of safety)를 사용하였는데, 이 값이 0보다 크면 구조건전성을 갖추었다고 볼 수 있다. 안전여유는 안테나 장치의 구성품 별 최대 응력 값을 항복 강도와 비교해 식 (4)와 같이 계산하였고 이때 안전계수(FOS : factors of safety)는 잠수함 장비에 해당되는 1.7을 적용하였다⁽¹⁷⁾.

Fig. 11

Torque for azimuth angle

Fig. 12

Velocity stream line

Fig. 13

Static pressure field contours

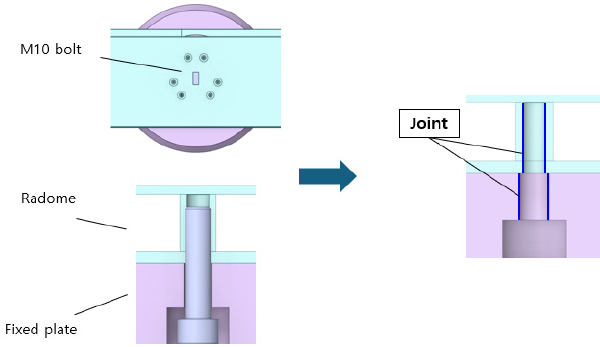
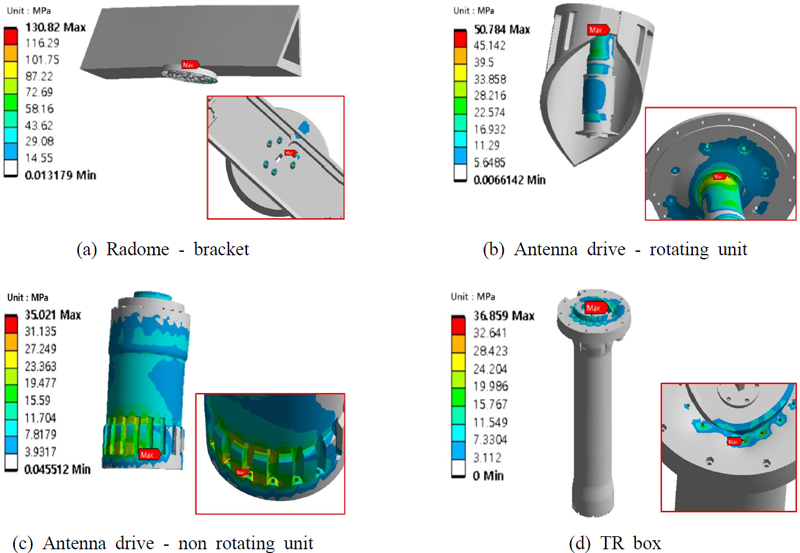
FSI 해석 결과 최대 응력은 레이돔과 그 아래의 고정 플레이트 간 연결부에서 발생하였다. 이 연결부는 6개의 M10 볼트로 체결되어 있는데, 넓은 표면을 가진 레이돔이 유체 하중에 의해 강한 힘을 받으면서 응력 집중이 발생하였다. 볼트의 모델링과 경계조건은 Fig. 14에 나타내었다. 이 해석의 볼트 체결 모사 방법은 볼트의 구조 형상을 삭제하고 Joint로 대체하여 해석을 수행하였다. 안테나장치 4개 구성품의 응력 분포는 풍하중과 유체저항으로 구분하여 각각 Fig. 15, Fig. 16에 나타내었다. 또한 외력에 따른 구성품 별 최대 응력, 안전여유 값은 Table 2, Table 3과 같다. 안테나 구동기 회전부는 상부 플레이트와 연결되는 회전축 연결부에서 최대응력이 발생하였는데 회전부의 경우 중앙에 위치한 회전축이 구조물을 지지하는 형태로 축의 상단 연결부에서 응력집중이 발생하였다. 비 회전부와 TR Box의 경우 메인플랜지와 안테나 구동기가 연결되는 볼트 체결부에서 응력이 최대로 발생하였다. 이 연결부는 16개의 M8 볼트로 체결되어 있는데 안테나 구동기 전체가 받는 하중을 견뎌내는 구조로, 하중의 반대쪽 체결부에서 응력집중이 발생하였다.

Fig. 14

Boundary condition for bolt

Fig. 15

Stress distribution for wind load

Fig. 16

Stress distribution for drag force

Table 2

MOS analysis results for wind load

Table 3

MOS analysis results for drag force

풍하중과 유체저항에 대해 최대 응력 부위인 레이돔 브라켓 연결부에서 안전 여유 값이 각각 30.2와 0.2로 최소값을 보였다. 그 외의 구성품은 2개의 외력에 대해 모두 0보다 큰 안전여유 값을 보였고, 따라서 풍하중과 유체저항에 대해 잠수함 항해레이더 안테나 장치가 구조적인 건전성을 갖추었음을 확인하였다. 이는 항해레이더가 잠수함의 수상항해 및 수중항해 상태에서 모두 구조적으로 안전하다는 것을 의미한다.

5. 결 론

이 연구는 잠수함의 주요장비인 항해레이더 안테나장치를 대상으로 수상, 수중항해 상태에서의 구조건전성 분석을 위해 수행되었다. 먼저 안테나 장치의 유한요소 해석 모델을 구축하고 항해상태별 주요외력으로 풍하중과 유체저항을 선정하였다. 이후 유체인 외력이 구조체인 안테나장치에 어떠한 영향을 미치는지 정확하게 분석하기 위해 단방향 FSI 해석을 수행하였다. 이를 통해 최종적으로 외력에 의한 안테나장치의 최대응력을 산출하였고, 안전여유(MOS) 값을 이용하여 응력 평가를 진행하였다. 풍하중의 경우 최소 안전여유 값이 30.2, 유체저항은 0.2로 두 경우 모두 0보다 큰 값을 가지는 것을 알 수 있었으며 결과적으로 잠수함의 수상 및 수중항해의 주요 외력에 대해 안테나장치가 구조적인 건전성을 갖추었음을 확인하였다.

이 연구 결과를 기반으로 잠수함 항해레이더의 구조 건전성 평가를 유한요소 해석 기법을 통해 예측할 수 있었고, 추후 실험을 통한 해석결과 검증이 필요할 것으로 보인다. 또한 이 연구에서 제시한 잠수함의 수상 및 수중항해 상태의 외력을 모두 고려하여 FSI 해석을 통해 장비의 구조 건전성을 평가하는 방법은 추후 이 논문에서 다룬 장비인 항해레이더 뿐만 아니라 잠수함의 함교탑에 탑재되는 다른 장비에 대한 평가에도 활용이 가능할 것으로 기대된다.

Acknowledgments

이 연구는 LIG Nex1 산학협력과제 지원으로 수행 되었습니다.

References

• Wang, Y., Sun, S. and Yue, Q., 2021, Measurement and Analysis of Drag on a Real Submarine Periscope, International Journal of Offshore and Polar Engineering, Vol. 31, No. 3, pp. 302~308. [https://doi.org/10.17736/ijope.2021.jc802]
• Kim, O., Lim, S., Kim, D., Lee, J.-H., Kim, H.-T. et al., 2024, Structural Safety Analysis of Large Radar Structures with Elevation Drive Units, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 34, No. 3, pp. 339~348. [https://doi.org/10.5050/KSNVE.2024.34.3.339]
• Roh, H. G., Park, Y., Yoo, J., Kim, W., Ra, Y.-E. et al., 2022, Structural Stability of Large Radar Drive System under Wind Load, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 32, No. 5, pp. 438~444. [https://doi.org/10.5050/KSNVE.2022.32.5.438]
• Cho, K. D., Kim, K. W., Kwon, M. S. and Hong, S. I., 2012, Outer Shape Design of Rotating Medium Antenna Installed on Ship Mast, Transactions of the Korean Society of Mechanical Engineers A, Vol. 36, No. 8, pp. 843~850. [https://doi.org/10.3795/KSME-A.2012.36.8.843]
• U.S. Department of Defense, 1988, Interface Standard for Shipboard Systems Weather Environment U.S. Department of Defense, Documentary No. MIL-STD-1399-302A, VA, United States.
• Armo, K. R., 2000, The Relationship between a Submarine’s Maximum Speed and its Evasive Capability, M.S. Thesis, Naval Postgraduate School, Monterey, CA, United States.
• Mohammed, M. G., Messerman, A. F., Mayhan, B. D. and Trauth, K. M., 2016, Theory and Practice of the Hydrodynamic Redesign of Artificial Hellbender Habitat, Herpetological Review, Vol. 47, No. 4, pp. 586~591.
• Yim, S.-R., Kim, H.-J. and Han, S.-E., 2015, The Shape Optimization of Free Form High-rise Buildings under Wind Load Reduction based on the 1-way FSI Analysis - Focused on the Corners Modifications -, Journal of the Architectural Institute of Korea Structure & Construction, Vol. 31, No. 1, pp. 3~10. [https://doi.org/10.5659/JAIK_SC.2015.31.1.3]
• Jeong, S. Y., Lee, K. S. and Han, S. E., 2011, A Numerical Study on Wind Pressure Characteristics of Super-tall Protype Model Considering the Effect of Turbulence Intensity, Journal of Korean Society of Steel Construction, Vol. 23, No. 6, pp. 659~667.
• Kazemian, M. and Hosseini Lavassani, S. H., 2024, One-way FSI Coupling with Steady-state and Transient CFD Analysis for the Umbrella Form of Tensile Membrane Structure, Arabian Journal for Science and Engineering. [https://doi.org/10.1007/s13369-024-09004-7]
• Bang, C. S., Rana, Z. A., Könözsy, L., Marchante Rodriguez, V. and Temple, C., 2022, Numerical Investigation and Fluid-structure Interaction (FSI) Analysis on a Double-element Simplified Formula One(F1) Composite Wing in the Presence of Ground Effect, Fluids, Vol. 7, No. 2, p. 85. [https://doi.org/10.3390/fluids7020085]
• Benra, F.-K., Dohmen, H. J., Pei, J., Schuster, S. and Wan, B., 2011, A Comparison of One-way and Two-way Coupling Methods for Numerical Analysis of Fluid-structure Interactions, Journal of Applied Mathematics. [https://doi.org/10.1155/2011/853560]
• Tominaga, Y., Mochida, A., Yoshie, R., Kataoka, H., Nozu, T. et al., 2008, AIJ Guidelines for Practical Applications of CFD to Pedestrian Wind Environment around Buildings, Journal of Wind Engineering and Industrial Aerodynamics, Vol. 96, No. 10-11, pp. 1749~1761. [https://doi.org/10.1016/j.jweia.2008.02.058]
• Gladkikh, V. and Tenzer, R., 2012, A Mathematical Model of the Global Ocean Saltwater Density Distribution, Pure and Applied Geophysics, Vol. 169, No. 1-2, pp. 249~257. [https://doi.org/10.1007/s00024-011-0275-5]
• Menter, F. R., 1994, Two-equation Eddyviscosity Turbulence Models for Engineering Applications, AIAA Journal, Vol. 32, No. 8, pp. 1598~1605. [https://doi.org/10.2514/3.12149]
• Adanta, D., Fattah, I. M. R. and Muhammad, N. M., 2020, Comparison of Standard k-ε and SST k-ω Turbulence Model for Breastshot Waterwheel Simulation, Journal of Mechanical Science and Engineering, Vol. 7, No. 2, pp. 39~44. [https://doi.org/10.36706/jmse.v7i2.44]
• Korean Register, 2023, Rules and Guidance for the Classification of Underwater Vehicles, Korean Register, Busan, Korea.