비선형 현가 특성을 갖는 하이퍼루프 캡슐차량의 수직방향 반능동 진동제어
© The Korean Society for Noise and Vibration Engineering
Abstract
The hyperloop capsule vehicle employs an Electro-Dynamic Suspension(EDS) magnetic levitation system utilizing non-contact superconducting electromagnets. This system exhibits the characteristics of a nonlinear suspension system, primarily determined by the nature of EDS, which serves as the primary suspension. The nonlinearity of this primary suspension is influenced by the varying distance between the guideway and the vehicle, as well as by the capsule vehicle’s speed. In this study, the effects of semi-active control on the vertical vibrations of a capsule vehicle, operating at speeds ranging from 150 km/h to 1000 km/h in a levitated state, were examined. The capsule vehicle was modeled as a 9-degrees-of-freedom system, incorporating vertical, roll, and pitch motions of the car body, front bogie, and rear bogie, respectively. To achieve vibration reduction, semi-active control was applied by utilizing a magnetorheological damper in the secondary suspension positioned between the bogie and the car body. The vibration mitigation performance across different speeds was then evaluated numerically.
Keywords:
Hyperloop, Capsule Vehicle, Nonlinear Suspension, Nonlinear Subspace Identification, MR Damper키워드:
하이퍼루프, 캡슐차량, 비선형 현가, 비선형 부분공간 식별, MR 댐퍼1. 서 론
최근에 차세대 운송수단으로 각광을 받고 있는 하이퍼루프는 유럽을 중심으로 매우 활발한 연구가 이루어지고 있으며, 한국, 중국, 인도 및 미국 등 전세계적으로도 활발한 연구가 수행되고 있다. 하이퍼루프에 관련된 연구는 차량/가이드웨이의 인터페이스 및 가이드웨이의 동적인 거동, 하이퍼루프 차량의 추진 및 부상시스템 설계, 하이퍼루프 튜브 내에서의 공력특성 등에 대해 제한적으로 이루어져 왔으며, 캡슐차량의 동적 거동에 관한 연구 또한 부분적으로 수행되어 왔다(1,2). 최근 하이퍼루프에 전자기서스펜션(electro-magnetic suspension, EMS) 시스템이 채용된 경우에 대해 캡슐차량의 동적 거동에 대한 연구결과가 시뮬레이션을 통해 발표된 바 있다.(3) 하이퍼루프에 EMS 시스템을 채택할 경우 EMS형 자기부상열차의 경우와 마찬가지로 대차와 가이드웨이 사이의 갭을 약 10 mm 이내로 유지해야 하기 때문에 고속주행 시 수반되는 대차의 수직변위가 문제가 된다. 즉, 고속 주행 시 대차의 수직 변위가 한도를 초과하여 가이드웨이와의 접촉이 발생하기 때문에 EMS형의 하이퍼루프 차량은 기존의 레일형 고속열차보다는 빠르게 주행할 수 있지만 1000 km/h 이상의 고속으로 주행하는 하이퍼튜브 캡슐차량으로 채택하기에는 무리가 있다. 이 연구에서는 그동안 진행되어 왔던 EDS 시스템을 채택한 캡슐차량을 대상으로 부상 상태로 주행하는 150 km/h ~ 1000 km/h의 속도에서 주행 시 대차 및 차체의 진동특성을 알아보고 MR 댐퍼를 이용한 반능동제어를 통해 진동저감 성능을 파악하고자 하였다. 이를 위해 캡슐차량은 차체, 전부대차 및 후부대차 각각 수직방향, 롤방향 및 피치방향 등 3개의 자유도를 고려하여 총 9-자유도 모델로 가정하였으며, 대차와 차체 사이에 있는 2차 현가장치에 MR 댐퍼를 적용하여 시뮬레이션을 수행하였다.
2. 캡슐차량의 수직방향 운동방정식
MR 댐퍼가 적용되지 않은 캡슐차량의 수직방향 운동방정식은 앞서 연구된 바가 있으며(1,2), 이 연구에서는 반능동 제어를 위해 필요한 수식을 다음과 같이 정리하였다.
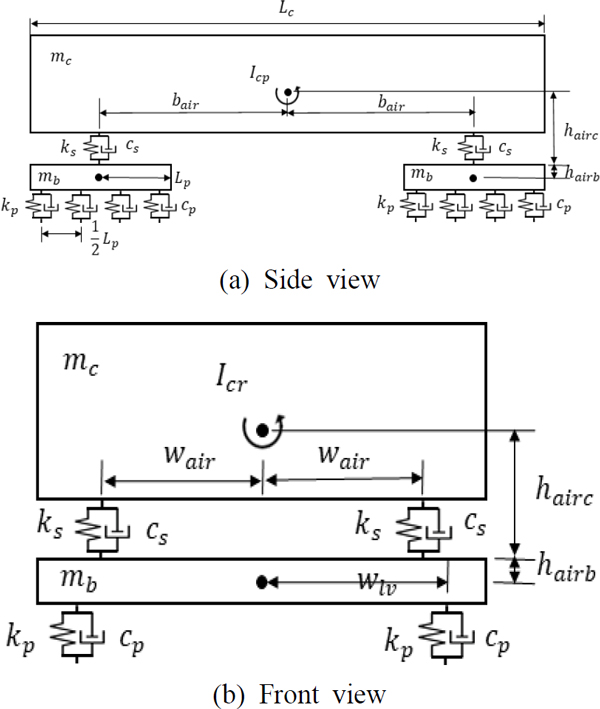
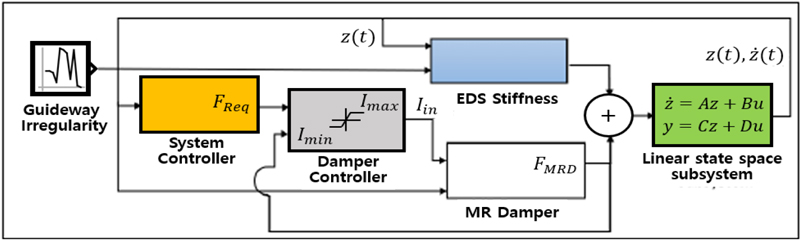
캡슐차량의 수직방향 운동방정식은 Fig. 1과 같이 9-자유도 시스템으로 모델링 할 수 있다. 차체, 전부대차 및 후부대차 각각에 대해 수직방향, 롤방향 및 피치방향의 운동을 고려하였다. 앞서 수행된 연구에서 볼 수 있는 바와 같이 하이퍼루프 캡슐열차에 적용된 자기부상시스템은 대차에 장착된 초전도 전자석과 가이드웨이에 설치된 부상코일 사이에 발생되는 유도 자기장에 의해 부상력을 발생시킨다. 이 부상력은 캡슐차량의 하중을 극복하여 부상상태로 주행하도록 도와주는 역할을 하게 되는데, 이때 가이드웨이 바닥과 캡슐차량 사이의 갭의 수직방향 변화와 부상력과의 관계를 부상강성이라는 용어로 표현하게 된다. 이 부상강성은 Fig. 1에서 보여주고 있는 바와 같이 캡슐차량의 1차 현가장치(kp) 역할을 하게 되는데, 차량의 주행속도와 수직변위의 영향을 받게 되는 비선형 특성을 가지게 되며, 이는 시간에 따라 변화하는 평균치와 맥동치로 식 (1) ~ 식 (3)과 같이 표현할 수 있다.
| (1) |
| (2) |
| (3) |
여기서 v는 캡슐차량의 주행속도이며, z는 수직방향 변위이고, τlv는 대차에 장착된 초전도 전자석의 폴 피치로서 이 연구에서는 대차길이의 1/4이다. 한편 캡슐차량의 수직방향 동특성 분석 및 반능동제어 성능을 해석하기 위한 파라미터는 Table 1과 같다.
앞에서 언급한 바와 같이 캡슐차량은 수직방향의 운동을 고려하여 총 9 자유도 모델로 구성하였다. 캡슐차량의 1차 현가장치가 선형 특성을 가지는 경우 캡슐차량의 동적인 거동에 대한 수학적 모델을 상태방정식으로 표현하면 식 (4)와 같이 간단히 표현되는데, 이때 상태벡터 x와 시스템 행렬 A, 입력 행렬 B 및 출력 행렬 C*는 식 (5), 식 (6)과 같이 표현된다. 식 (5)에서 M은 질량 행렬, C는 댐핑 행렬, K는 강성 행렬을 의미한다.
| (4) |
| (5) |
| (6) |
그러나 EDS 시스템의 특성으로 인하여 캡슐차량의 동적 거동에 대한 수학적 모델은 식 (7)과 같이 비선형 특성이 포함된 방정식으로 표현된다(4).
| (7) |
여기서 Klin과 Keds,i(vx, z, y)는 각각 현가장치의 선형요소와 비선형요소를 나타내는데, 선형요소에는 2차 현가장치와 부상강성의 선형요소가 포함되어 있으며, 비선형요소에는 부상강성의 비선형요소가 포함되어 있다. 또한 μi는 비선형요소의 가중치를 나타내며, Li는 비선형 구성요소의 위치를 나타내는데 그 값은 –1, 0 또는 1이 된다.
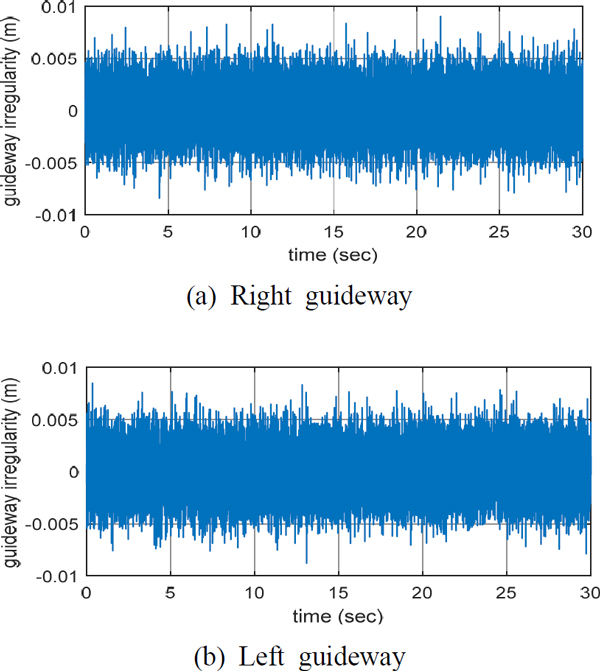
한편, 캡슐차량의 수직방향 운동 특성을 파악하기 위해서는 주행 중인 캡슐차량 시스템의 외란으로 작용하는 가이드웨이의 수직방향 불규칙을 고려해야 한다. 이 연구에서는 대차의 좌측 및 우측에 작용하는 가이드웨이의 불규칙을 Fig. 2와 같은 시간영역 데이터로 가정하였다.
3. MR 댐퍼를 이용한 반능동 진동제어
이 연구에서는 1/4 차량 모델을 이용하여 캡슐차량의 수직방향 진동을 감소시키기 위한 목적으로 개발된 MR 댐퍼의 특성을 활용하여 실물모델 캡슐열차의 수직방향 진동제어 성능을 확인하고자 하였다(5,6). 또한, 1/4 차량 모델에서는 800 km/h 속도에서만의 진동저감 성능에 대해 검토하였으나(7), 이 연구에서는 부상하여 주행하는 150 km/h ~ 1000 km/h 전체 속도에서의 진동저감 성능에 대해 검토하였다.
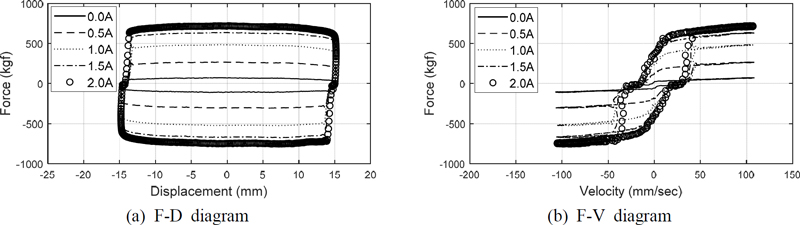
Fig. 3은 이 연구를 위해 사용된 MR 댐퍼를 보여주고 있으며, Fig. 4는 MR 댐퍼의 특성을 보여주고 있다.
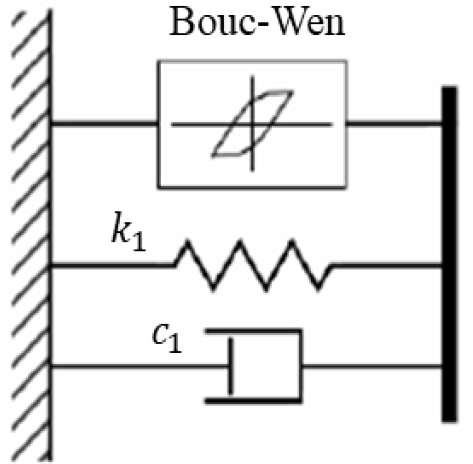
MR 댐퍼를 반능동제어에 사용하기 위해서는 MR 댐퍼 특성에 대한 측정결과를 수학적 모델로 도출해야 한다. MR 댐퍼의 특성을 수학적으로 나타내기 위한 방법으로는, Bingham 플라스틱 모델을 비롯하여 modified Bingham 모델, Bouc-Wen 모델 등 여러 가지가 있으나, 이 연구에서는 Bouc-Wen 모델을 사용하였다. 참고로 Bouc-Wen 모델의 수학적인 표현은 식 (8), 식 (9)와 같으며, 이를 그림으로 표현하면 Fig. 5와 같다(8).
| (8) |
| (9) |
여기서 F는 댐핑력을 나타내며, co, ko, fo, α, δ, β, γ 및 n은 Bouc-Wen 모델의 형상(shape)을 나타내는 파라미터이다.
이 연구에서는 MR 댐퍼를 통해 반능동제어를 위해 생성된 힘을 도출하기 위해 식 (10)으로 표현된 skyhook 제어 알고리즘을 사용했다(8,9). 식 (10)과 같이 skyhook 제어 알고리즘은 차체와 대차의 상대속도에 댐핑계수의 최대값(Cmax)과 최소값(Cmin)을 곱하여 필요한 힘을 계산한다.
| (10) |
비선형 특성이 포함된 식 (7)에서 선형항만을 따로 떼어내면 상태방정식 (4)와 같은 상태로 표현할 수 있다. 이를 MATLAB/Simulink S/W를 이용하여 수치해석 프로그램을 구성하고, EDS 시스템의 비선형 특성으로 나타나는 부분은 별도의 하부 시스템으로 구성하였다. 이는 NSI로 알려진 비선형 부분공간 식별법(nonlinear subspace identification)(4,10)을 적용하기 위함이며, 여기에 진동제어를 위해 MR 댐퍼에서 발생되는 제어력을 스카이훅 제어를 통해 Fig. 6과 같이 입력시켜 시뮬레이션을 수행하였다.
이 연구에 앞서 진행된 연구결과에 의하면 800 km/h의 속도로 주행하는 캡슐차량의 1/4-car 모델에 대한 수직방향 반능동제어 시뮬레이션 결과 차체의 수직방향 변위는 약 36% 정도 감소된 바 있다(7). 이 연구에서는 1/4-car 모델이 아닌 실물모델의 9-자유도 시스템을 고려하였다.
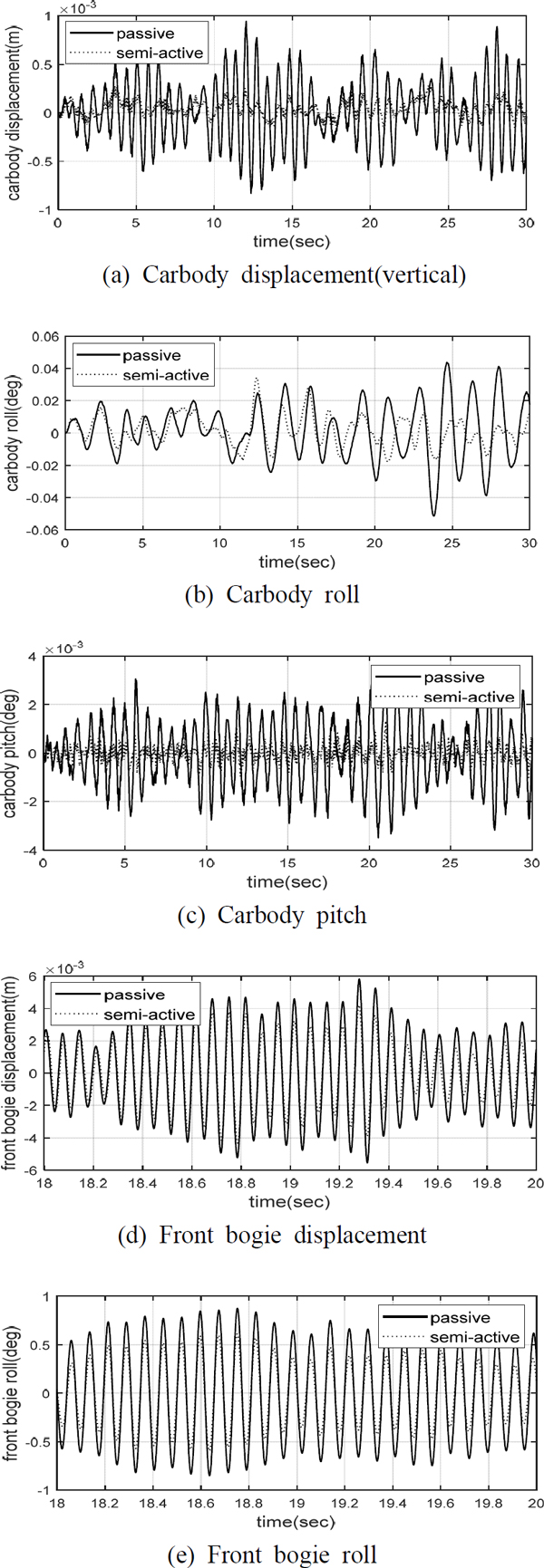
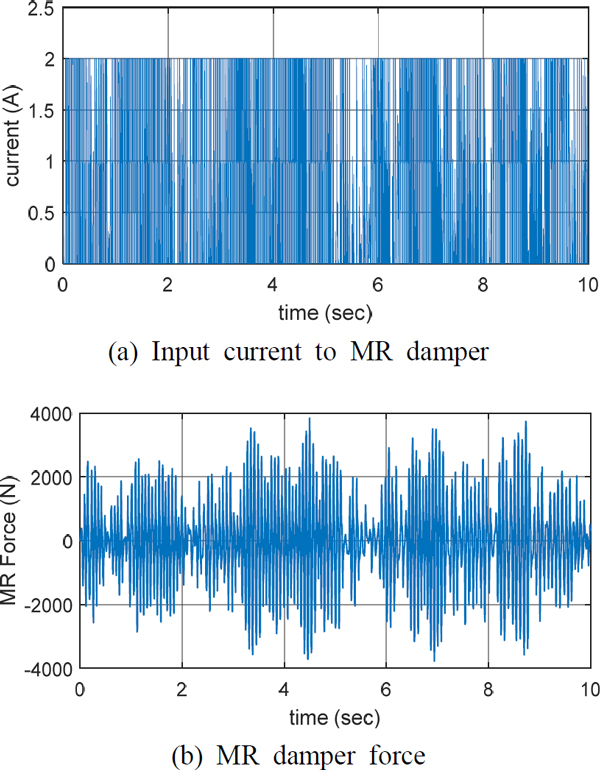
Fig. 7은 대차와 차체 사이에 있는 2차 현가장치에 대차의 좌우로 한 개씩의 MR댐퍼를 적용하여 수직방향으로 총 4개의 MR 댐퍼가 장착되도록 구성한 후 수행된 시뮬레이션 결과의 한 예로서 캡슐차량이 450 km/h로 주행할 때의 MR 댐퍼의 반능동 진동저감 성능을 보여주고 있으며, Fig. 8은 이때 MR 댐퍼에 가해지는 전류와 발생되는 반능동 제어력(댐핑력)을 보여주고 있다.
Fig. 7(a) ~ Fig. 7(c)를 보면 차체의 수직방향 진동변위 및 롤방향 진동 각변위, 피치방향 진동 각변위가 전체 속도대역에서 MR댐퍼에 의해 많이 저감되었음을 알 수 있으며, Fig. 7(d) ~ Fig. 7(e)로부터 대차의 수직방향 진동 변위 및 롤방향 진동 각변위는 차체의 경우에 비해 진동 저감량이 상대적으로 크지는 않지만 상당한 진동 저감효과를 나타내고 있음을 알 수 있다. 이를 RMS 값을 사용하여 표로 나타내면 Table 2와 같다.
Table 2를 보면 MR 댐퍼를 이용한 반능동제어의 결과 매우 좋은 제어 성능을 나타내고 있음을 알 수 있다. 그러나 이는 시뮬레이션 결과이며 MR 댐퍼를 실물에 적용할 경우 반능동 제어 효과는 Table 2 만큼 크게 나타나지 않을 것으로 예상된다.
Fig. 8은 450 km/h의 속도에서 MR 댐퍼에 가해지는 전류와 MR 댐퍼에서 생성되는 힘을 보여준다.
Fig. 8(a)를 보면 MR댐퍼에는 캡슐차량의 진동 저감을 위해 끊임없이 전류가 변동되면서 가해지고 있으며, 이에 따라 Fig. 7(b)와 같이 캡슐차량의 2차 현가장치에 적용된 MR댐퍼에 의한 제어력(또는 댐핑력)이 잘 구현되고 있음을 알 수 있다. 한편 Fig. 7(a)에서 보여주고 있는 전류의 크기가 2A로 제한된 이유는 Fig. 4에서 보여주고 있는 바와 같이 MR 댐퍼의 작동범위를 2A로 제한해 놓았기 때문이다.
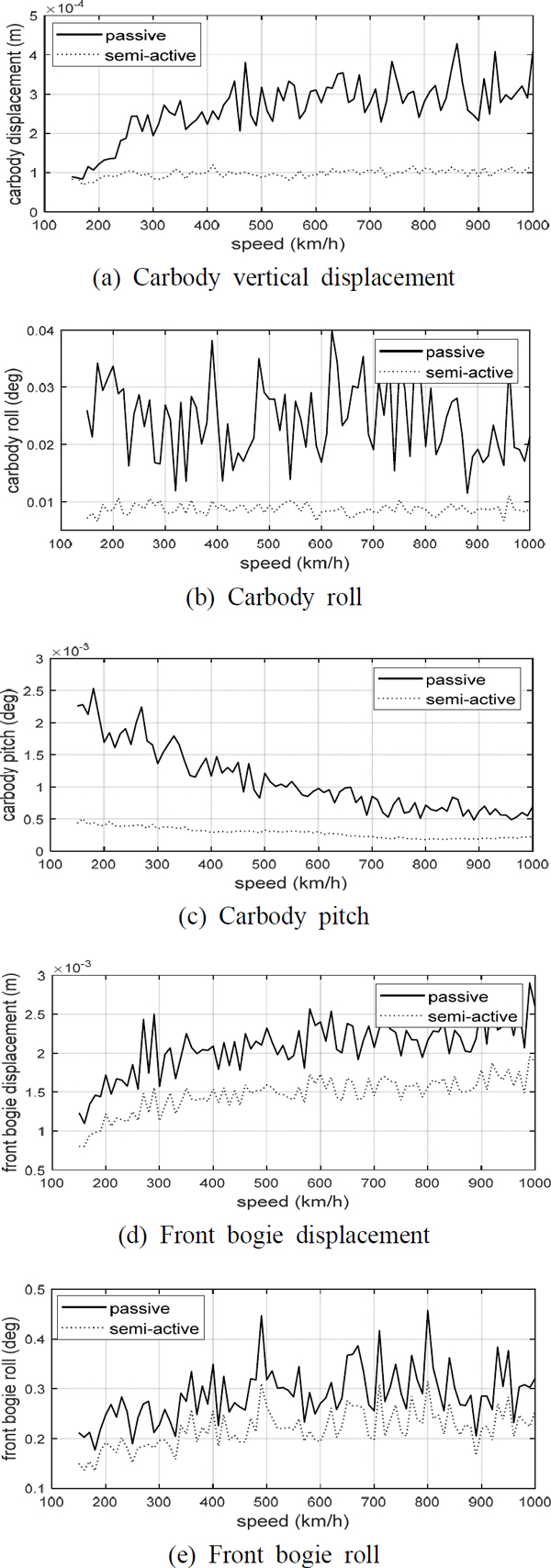
이 연구에서는 캡슐차량이 부상하여 주행하는 150 km/h ~ 1000 km/h 전체 속도에 대해 MR 댐퍼가 충분히 캡슐차량의 진동을 저감할 수 있는지 파악하고자 하였다. 이는 1차 서스펜션에 해당하는 EDS 시스템의 비선형 특성 때문에 MR 댐퍼의 진동제어 성능이 어떤 경향 또는 어떤 특성을 보이는지 확인하기 위함이다. Fig. 9는 150 km/h ~ 1000 km/h의 속도 대역에서 MR 댐퍼의 진동제어 성능을 나타내고 있다.
전반적으로 우수한 진동 저감 성능을 나타내고 있으나 속도의 변화에 따라 진동 저감 성능이 명확한 경향을 보이지 않고 있으며, 캡슐차량의 속도에 무관하게 MR 댐퍼의 진동 저감 성능이 불규칙하게 나타나고 있음을 알 수 있다.
이는 1차 현가장치에 해당하는 EDS 시스템의 비선형성에 영향을 받아 나타나는 현상으로 판단된다.
그러나, 차체의 수직방향 진동 변위를 나타내는 Fig. 9(a)를 보면 230 km/h 이하의 저속에서는 MR 댐퍼의 진동제어 성능이 거의 나타나지 않고 있으며, 약 230 km/h 이상의 속도에서만 진동저감 성능이 우수하게 나타나고 있음을 알 수 있다. 이에 반하여 차체의 피치방향 진동 각변위를 나타내는 Fig. 9(c)를 보면 Fig. 9(a)와는 반대로 저속에서는 우수한 진동 저감 성능을 보이는 반면, 고속에서는 진동 저감 성능이 떨어짐을 알 수 있다. 이로부터 속도에 따른 전체적인 경향을 보면 차체의 수직방향 진동 변위는 속도의 증가에 따라 진동 저감 효과가 증가함을 알 수 있으며, 반대로 차체 피치방향의 경우 속도의 증가에 따라 진동 저감 효과가 떨어짐을 알 수 있다. 즉, 차체의 수직방향 운동과 피치방향 운동이 위상만 반대인 강체운동임을 생각해 보면 의미있는 결과이다.
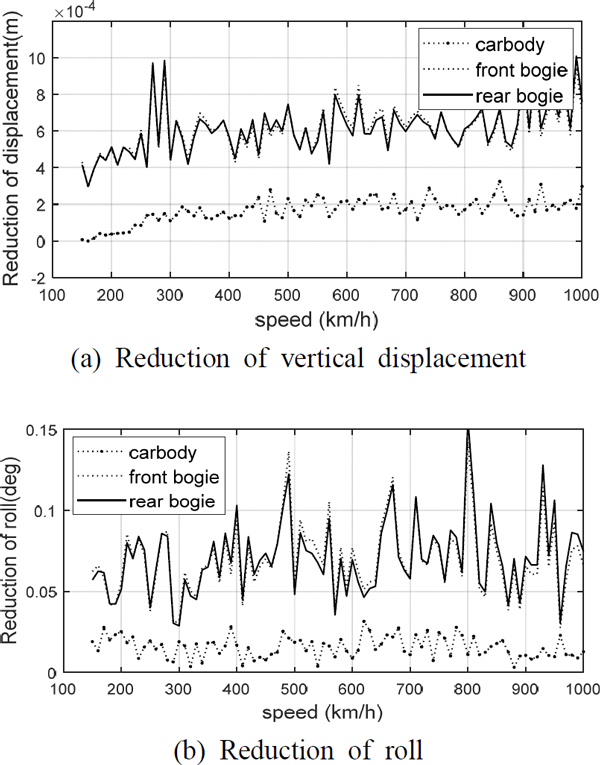
Fig. 10은 150 km/h ~ 1000 km/h의 속도대역에서 MR 댐퍼를 이용한 반능동 제어의 진동저감 효과를 나타낸 그림이다.
MR 댐퍼가 대차의 전후방향 무게중심에 해당하는 위치에 적용되어 있기 때문에 대차의 피치방향 진동은 전혀 저감되지 않을 것이기 때문에 차체와 대차의 진동저감량을 비교하는 것은 의미가 없다. 따라서 여기서는 차체와 대차의 수직방향 진동과 롤방향 진동의 저감 성능만을 비교하여 보고자 하였다. Fig. 10(a), Fig. 10(b)를 보면 전체적으로 차체에 비하여 대차의 진동이 150 km/h ~ 1000 km/h 전체 속도대역에 걸쳐 크게 저감됨을 알 수 있다. 이는 향후 실물 캡슐차량의 제작 및 주행시험을 통해 입증되어야 할 사항이다. 아울러 MR 댐퍼에 의해 대차의 진동변위가 상당히 저감됨으로서 캡슐차량 시스템이 보다 안전해졌으며, 승객의 승차감에 영향을 주는 차체의 진동도 저감됨을 확인할 수 있었다.
4. 결 론
1차 현가장치에 EDS 시스템의 비선형 특성을 갖는 캡슐차량의 9-자유도 수직방향 모델을 도입하고, 진동제어를 위해 제작된 MR 댐퍼의 특성을 이용하여 부상 주행하는 150 km/h ~ 1000 km/h 속도대역에서 반능동제어 시뮬레이션을 수행한 결과 다음과 같은 결과를 얻었다.
(1) 전반적으로 우수한 진동 저감 성능을 나타내고 있으나, 1차 현가장치에 해당하는 EDS 시스템의 비선형성에 영향을 받아 캡슐차량의 속도에 무관하게 MR 댐퍼의 진동 저감 성능이 불규칙하게 나타나고 있다.
(2) 차체의 경우 MR 댐퍼의 진동저감 성능은 저속에서는 수직방향의 진동 저감 성능이 우수한 대신 고속에서는 피치방향의 진동 저감 성능이 우수하게 나타났다.
(3) MR 댐퍼를 이용한 반능동 진동제어 결과 차체에 비하여 대차의 진동변위가 크게 감소되었으며, 승객의 승차감에 직접 영향을 주는 차체의 진동도 많이 감소되었다.
기 호 설 명
| co, ko, fo, α, δ, β, γ, n : | Bouc-Wen 파라미터 |
| Klin, Keds : | 부상강성의 선형 및 비선형항 |
| klv : | 부상강성 |
| τlv : | 초전도 전자석의 폴 피치 |
| v : | 캡슐차량의 속도 |
Acknowledgments
이 연구는 한국철도기술연구원 기본사업의 일환으로 수행된 ‘아음속 캡슐트레인 핵심기술개발(PK2401A1)’ 과제의 연구결과임.
References
-
Yoon, R., You, W., Lee, J., Lee, C. and Lee, K., 2019, Study on Dynamic Characteristics of Superconducting Capsule Train, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 29, No. 4, pp. 453~461.
[https://doi.org/10.5050/KSNVE.2019.29.4.453]

-
Yoon, R., You, W., Lee, J., Lee, C. and Lee, K., 2019, Dynamic Analysis of Capsule Train with 9-DoF according to Speed, Journal of the Korean Society for Railway, Vol. 22, No. 2, pp. 109~117.
[https://doi.org/10.7782/JKSR.2019.22.2.109]

-
Nøland, J. K., 2021, Prospects and Challenges of the Hyperloop Transportation System: A Systematic Technology Review, IEEE Access, Vol. 9, pp. 28439~28458.
[https://doi.org/10.1109/ACCESS.2021.3057788]

-
You, W.-H. and Lee, J.-H., 2024, Study on the Appropriate DoF of Rigid Body Motion of Carbody Considering Capsule Vehicle Nolinear Characteristics, Journal of the Korea Academia-Industrial Cooperation Society, Vol. 25, No. 8, pp. 332~340.
[https://doi.org/10.5762/KAIS.2024.25.8.332]

-
Yoon, R., Negash, B. A., You, W., Lee, J., Lee, C. and Lee, K., 2023, Bi-exponential Model and Inverse Model of Magnetorheological Damper for the Semi-active Suspension of a Capsule Vehicle, Measurement and Control, Vol. 56, No. 3-4, pp. 558~570.
[https://doi.org/10.1177/00202940221101675]

-
Negash, B. A., You, W., Lee, J. and Lee, K., 2020, Parameter Identification of Bouc-Wen Model for Magnetorheological(MR) Fluid Damper by a Novel Genetic Algorithm, Advances in Mechanical Engineering, Vol. 12, No. 8.
[https://doi.org/10.1177/1687814020950546]

-
Negash, B. A., You, W., Lee, J., Lee, C. and Lee, K., 2021, Semi-active Control of a Nonlinear Quarter-car Model of Hyperloop Capsule Vehicle with Skyhook and Mixed Skyhook-acceleration Driven Damper Controller, Advances in Mechanical Engineering, Vol. 13, No. 2, doi: 10.1177/1687814021999528.
[https://doi.org/10.1177/1687814021999528]

-
Guglielmino, E., Sireteanu, T., Stammers, C. W., Ghita, G. and Giuclea, M., 2008, Semi-active Suspension Control: Improved Vehicle Ride and Road Friendliness, Springer-Verlag, London, UK.
[https://doi.org/10.3397/1.3110986]

-
Karnopp, D., Crosby, M. J. and Harwood, R. A., 1974, Vibration Control using Semi-active Force Generators, Journal of Engineering for Industry, Vol. 96, No. 2, pp. 619~626.
[https://doi.org/10.1115/1.3438373]

-
Marchesiello, S. and Garibaldi, L., 2008, A Time Domain Approach for Identifying Nonlinear Vibrating Structures by Subspace Methods, Mechanical Systems and Signal Processing, Vol. 22, No. 1, pp. 81~101.
[https://doi.org/10.1016/j.ymssp.2007.04.002]


Wonhee You received the Ph.D. from Department of Mechanical Engineering at Yonsei University. He is currently a Executive Researcher in New Transportation Innovative Research Center at Korea Railroad Research Institute. His research interests are in the area of railway vehicle dynamics and control, and railway noise and vibration.

Jinho Lee received the Ph.D. from Department of Mechanical and Aerospace Engineering at University of Florida. He is currently a Principal Researcher in New Transportation Innovative Research Center at Korea Railroad Research Institute. His research interests are in the area of vibration control, vehicle dynamics, and advanced actuator.