유전알고리즘에 의한 Johnson-Champoux-Allard 모델의 비음향학적 파라미터 추정
© The Korean Society for Noise and Vibration Engineering
Abstract
In this paper, an advanced method is proposed for estimating the non-acoustic parameters of porous materials. The parameters targeted for estimation include flow resistivity, porosity, tortuosity, and the thermal and viscous characteristic lengths within the Johnson-Champoux-Allard model. A genetic algorithm was employed as an optimal design technique to perform the estimation. To compute the objective function, the sound absorption coefficient and surface impedance were calculated within the 1/3 octave band, with Delany-Bazley’s law providing supplementary support. The results demonstrate that estimation accuracy improves for materials exhibiting relatively higher porosity and lower tortuosity.
Keywords:
Porous Materials, Equivalent Fluid Model, Genetic Algorithm, Non-acoustic Parameters, Noise키워드:
다공성 물질, 등가유체 모델, 유전알고리즘, 비음향학적 파라미터, 소음1. 서 론
다공성 물질에서 파동 전파에 관한 다양한 이론이 존재하며, 가장 널리 사용되는 이론 중 하나로 Johnson-Champoux-Allard(JCA) 모델을 들 수 있다(1,2). 이 모델은 점성 효과(viscous effect)에 관한 Johnson 모델(1)과 열 효과(thermal effect)에 관한 Champoux-Allard 모델(2)을 병합한 것으로, 이를 통해 다공성 물질의 유효 밀도(effective density)와 유효 벌크 계수(effective bulk modulus)를 계산할 수 있다. 물질의 일반적 물성에 더해 유동저항(flow resistivity), 공극률(porosity), 뒤틀림도(tortuosity), 점성특성길이(viscous characteristic length)가 유효 밀도 계산에 추가 요구되며, 열특성길이(thermal characteristic length)가 유효 벌크 계수 계산에 추가 요구되는 것이 특징이다.
유동저항은 다공성 물질에서 주어진 자극에 대한 응답 즉, 인가 압력(induced pressure)과 유속에 관한 유체역학적 특성을, 그리고 공극률, 뒤틀림도, 열 및 점성특성길이는 다공성 물질 내 기공(pore)의 크기, 형상, 상호 연결 관계와 같은 순수 기하학적 특성을 나타낸다. 이들은 음향학 외 학문분야에서 정의됐거나 순수 기하학적 특성에 관한 것으로 통상 비음향학적 파라미터(non-acoustic parameter)라고 부른다. 이들 비음향학적 파라미터는 일반적인 실험 설비로 쉽게 측정될 수 없거나 측정에 고가의 전용 장비가 요구된다. 이는 JCA 모델의 활용성을 저해하는 요소로써 작용한다고 할 수 있다(1,2).
비음향학적 파라미터가 갖는 측정 상 문제점을 해결하기 위해 최적화 기법을 활용한 추정 관련 연구가 다수 수행된 바 있다. Atalla et al.은 차분 진화(differential evolution) 알고리즘을 활용하여 뒤틀림도와 특성길이를 추정한 바 있으며 목적함수 계산에 임피던스 튜브에서 측정한 표면 임피던스(surface impedance)를 활용하였다(3). Lee et al.은 유전알고리즘(genetic algorithm)과 실험계획법을 복합 활용하여 5가지 비음향학적 파라미터를 추정한 바 있으며(4) Biot 이론과(5,6) JCA 모델을(1,2) 복합한 모델로 추정한 흡음계수를 목적함수 계산에 활용하였다. 이때, 프레임 물질의 밀도, 진공상태에서 영률(in-vacuo Young’s modulus), 손실계수(loss factor) 등이 사전에 정의되어야 한다.
Hentati et al.은 최적해 탐색 절차를 다단(multi-level)화한 뒤 넬더-미드 방법(Nelder-Mead method)을 활용하여 비음향학적 파라미터들을 흡음계수에 대한 기여 순으로 순차 추정한 바 있다(7). 하지만, 이들 기법은 일부 비음향학적 파라미터만을 추정 대상으로 하거나, 목적함수 계산에 비교적 제한적인 정보를 표현하는 흡음계수만을 활용하는 등에 기인한 것으로 보이는 추정 결과와 실제 값 간 비교적 큰 오차는 해결되어야 할 문제라 할 수 있다.
따라서, 이 논문에서는 임피던스 튜브에서 얻을 수 있는 1/3 옥타브 밴드대역 흡음계수와 주파수 변화에 대한 증감 특성이 비교적 두드러지는 표면 임피던스를 복합 활용하여 JCA 모델에 대한 비음향학적 파라미터를 유전알고리즘에 의해 추정하는 방법을 제안하고자 한다(1,2). Delany-Balzey의 법칙을 추가 활용하여 다공성 물질의 음향학적 성능에 가장 지배적인 영향을 미치는 유동저항과 공극률이 개별적으로 탐색되도록 하였다(8). 이 논문에서 제안한 알고리즘의 추정 정확성 및 속도를 임의 정의한 4가지 비음향학적 파라미터 조합에 대해 검증하였다.
2. 다공성 물질에서 음파 전달 해석
2.1 Johnson-Champoux-Allard 모델
다공성 물질에서 음파의 에너지 소산은 점성과 열의 관점에서 해석될 수 있다. 고체 프레임을 갖고 유체로 포화된 일반적인 다공성 물질에서 음파가 진행할 때 고체와 유체 간 상대운동이 발생될 수 있다. 이때, 고체와 유체간 큰 밀도차에 근거하여 고체를 강체로 취급할 수 있다. 결과적으로 음향학적 관점에서 음파 진행에 대한 다공성 물질의 응답은 물질을 구성하는 유체의 조화 유동으로 이해될 수 있다. Johnson et al.은 프레임과 유체의 경계에서 점성에 의해 음파의 에너지가 소산되며(1), 다공성 물질 중 유체에서 전파되는 음파의 속도는 이 유체가 단일매질일 때의 속도보다 느리다는 실험 결과 등을 활용하여(9) 동적 뒤틀림도(dynamic tortuosity)를 식 (1)과 같이 유도하였다.
| (1) |
여기서, ν는 동점성계수(kinematic viscosity), ϕ는 공극률, η는 점성계수, α∞는 뒤틀림도, σ는 유동저항, ω는 각주파수, 그리고 Λ는 점성특성길이다. 식 (1)을 활용하여 강성 프레임을 갖는 다공성 물질의 유효밀도를 식 (2)와 같이 계산할 수 있다(10).
| (2) |
여기서, ρ0는 공기 밀도이다. 점성과 유사하게, 다공성 물질에서 음파가 전파될 때 고체와 기체가 서로 인접한 영역 즉, 열 경계층(thermal boundary layer)에서 서로 상이한 열전도율에 의해 열에너지 이동이 발생될 수 있다. 열전도율은 일반적으로 프레임 물질이 공기보다 비교적 매우 크므로 열에너지 이동은 주로 공기에서 프레임으로 발생하게 된다. 이러한 물리적 현상에 근거하여 Champoux et al.은 식 (3)과 같이 동적 열 뒤틀림도(dynamic thermal tortuosity)를 유도하였다(2).
| (3) |
여기서, Λ'은 열특성길이, Pr은 프란틀 수(Prandtl number)이다. 식 (3)을 활용하여 강성 프레임을 갖는 다공성 물질의 유효 벌크 계수를 식 (4)와 같이 계산할 수 있다(10).
| (4) |
여기서, P0는 대기압, γ는 비열비이다. 식 (2)와 식 (4)를 결합하여 식 (5a), 식 (5b)와 같이 다공성 물질의 특성 임피던스(characteristic impedance) 및 파수(wave number)를 정의할 수 있다.
| (5a) |
| (5b) |
이를 강성 프레임을 갖는 다공성 물질에서의 음파전달에 관한 등가유체모델 즉, JCA 모델이라 한다(1,2).
보다 정교한 이론으로 Biot 이론에 기반한(5,6) 다공성 물질 내 음파전달 이론을 들 수 있다. 이 모델은 프레임을 강체로 취급하지 않고 각 상(phase)의 관점에서 음파 전파에 의한 프레임-유체간 상호작용을 고려하는 것이 특징이며 식 (6a), 식 (6b)와 같은 파동방정식으로 정의된다.
| (6a) |
| (6b) |
여기서, b는 소산 계수, e와 ϵ는 각각 프레임과 유체의 변형률, ρ11 = (1 - ϕ)ρs - ρ12, ρ22 = ϕρ0 - ρ12, ρ12 는 프레임과 유체간 상호작용에 의한 부가질량(5,6), ρs는 프레임 물질의 밀도, G는 점성에 대한 주파수 보정함수로 식 (7)과 같이 정의된다(1).
| (7) |
P, R은 각각 프레임과 유체의 탄성계수, Q는 프레임과 유체의 탄성에너지 교환에 관한 연성계수로 식 (8a) ~ 식 (8c)와 같이 정의된다(5,6,10).
| (8a) |
| (8b) |
| (8c) |
여기서, N은 전단 탄성계수, Kf는 식 (4)의 Keff와 같으며, Kb는 식 (9)와 같이 정의된다.
| (9) |
Biot 이론은(5,6) JCA 모델에(1,2) 비해 다공성 물질에서 음파전달 현상을 보다 정교하게 모사한다. 하지만, 식 (6)에 대한 파동방정식 해의 도출 과정 및 형태가 상대적으로 복잡하고, 해 계산에 프레임 물질의 물성이 추가적으로 요구된다. 이 절의 서두에서 언급한 바와 같이 프레임 물질의 밀도가 유체에 비해 매우 큰 다공성 물질의 경우 Biot 이론이 가지는 복잡성과 프레임 물질의 물성에 관한 정보를 배제하고(5,6) JCA 모델을 활용하여(1,2) 비교적 높은 정확도로 음파전달 특성을 추정할 수 있다.
2.2 Delany-Bazley의 법칙
Delany et al.은 다수의 섬유질 다공성 물질에 대해 파수와 특성 임피던스를 측정하고, 그 결과를 주파수와 유동저항으로써 정의된 새로운 변수에 대해 도시하였다(8). 이때의 결과가 가지는 선형적 경향성에 착안해 식 (10a), 식 (10b)와 같은 경험식을 도출하였다.
| (10a) |
| (10b) |
여기서, Zc는 특성 임피던스, k는 파수, c0는 공기 중 음속, 그리고 X = ρ0f/σ. 식 (10)은 0.01 < X < 1.0 구간에서 유효한 것으로 알려져 있다(8).
주파수 유효구간에 더해, Delany-Bazley의 법칙은 공극률이 높고 뒤틀림도가 낮은 물질에 대해 유효한 것으로 알려져 있다(8). 이상과 같은 여러 제한사항에도 불구하고 유동저항만으로 파동 전파특성을 지배하는 특성 임피던스와 파수를 비교적 손쉽게 계산할 수 있다는 장점이 있다.
2.3 흡음계수
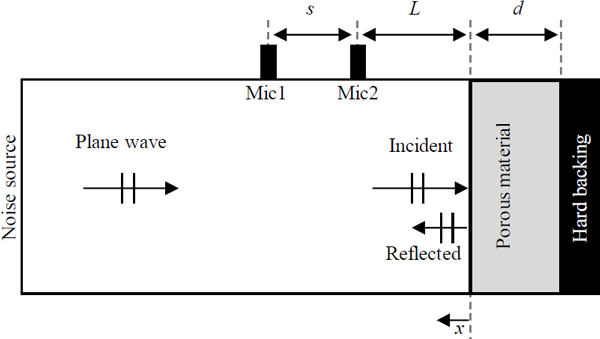
임피던스 전달관계에 의해 Fig. 1에 도시된 임피던스 튜브에서와 같이 단단한 면으로 지지되며, 음파가 두께 d인 물질 표면에 수직으로 입사하는 경우 표면에서의 임피던스는 식 (11)과 같이 계산 가능하다.
| (11) |
식 (7)을 활용하여 Rc = (Zs - Z0) / (Zs + Z0)와 같이 입사 표면에서 반사계수를 정의할 수 있다. 이때, 물질의 특성 임피던스는 Delany-Balzey의 법칙(8) 또는 JCA 모델에(1,2) 의해 계산 가능하다. 흡음계수는 α = 1-|Rc|2과 같이 정의할 수 있다.
추가로, 전달함수법(transfer function method)을 활용하여 흡음계수를 실험적으로 정의할 수 있다(11). Fig. 1을 기준으로, 마이크로폰 1과 마이크로폰 2 사이 전달 함수 H12는 각 지점에서 측정된 음압(acoustic pressure)을 식 (12)에 적용하여 정의할 수 있다.
| (12) |
여기서, 하첨자 ‘1’과 ‘2’는 각 마이크로폰을 의미하고 하첨자 ‘I‘과 ‘R‘은 각각 입사파와 반사파를 의미한다. 반사계수의 정의에 따라 식 (12)은 식 (13)과 같이 전달 함수와 파수, 그리고 각 마이크로폰의 위치에 대한 함수로써 정의될 수 있으며, 이를 통해 수직입사 조건에 대한 반사계수를 실험적으로 정의할 수 있다.
| (13) |
3. 비음향학적 파라미터 추정
3.1 문제 정식화
최적화 문제로 정식화를 위해 제어변수는 JCA 모델(1,2)의 활용에 필요한 유동저항, 공극률, 뒤틀림도, 열 및 점성특성길이 총 5가지 비음향학적 파라미터로 정의하였다. 각 제어변수에 대한 상한(upper bound) 및 하한(lower bound) 등 구속조건은 Table 1과 같이 정의하였다(3,4,8).
최적해를 추정하기 위해 임피던스튜브를 활용하여 비교적 쉽게 얻을 수 있는 수직 입사에 대한 100 Hz ~ 16 kHz 대역 1/3 옥타브 밴드 주파수 대역 흡음계수 및 표면 임피던스를 추정 기준으로 하여 목적함수(objective)를 식 (14)와 같은 오차함수(error function) 형태로 정의하였다.
| (14) |
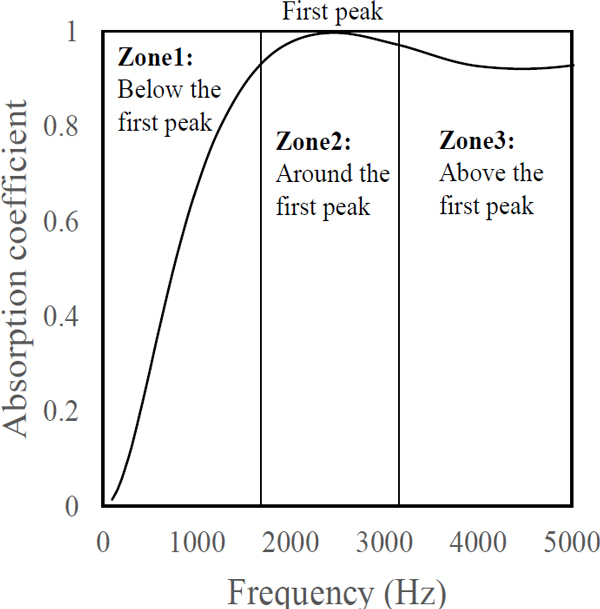
여기서, Φ는 흡음계수 또는 임피던스, f는 주파수, v = [σ, φ, α∞, Λ', Λ], 하첨자 ‘ana’는 등가유체모델에 의한 계산결과, 하첨자 ‘ref’는 임피던스튜브에서 측정 결과이다. 이 논문에서 다루는 최적화 문제에 대한 제어변수 즉, 비음향학적 파라미터들이 지배적인 영향을 미치는 주파수 대역은, Fig. 2를 기준으로, 유동저항과 공극률이 Zone 1에, 뒤틀림도와 열 및 점성특성길이가 Zone 2와 Zone 3에 해당한다고 알려져 있다(3). 식 (14)는 제어변수의 목적함수에 대한 주파수별 기여를 고려할 수 없다는 문제가 있다. 하지만, Atalla et al.에 의하면(3), 목적함수가 식 (14)와 같은 형태로 정의될 때, 계산에 활용되는 주파수 대역이 적어도 Zone 1과 Zone 2를 적절히 포함할 경우, Zone 1에서 유동저항과 공극률의 목적함수에 대한 가중치가 매우 큼에도 불구하고, 이 목적함수를 활용한 최적화 문제는 이론적으로 정확한 해에 수렴한다.
흡음계수의 최초 피크(first peak)가 형성되는 주파수대역이 다공성 물질의 두께에 의해 결정되고, 다공성 물질의 두께가 7 mm 일 때 최초 피크가 약 12.5 kHz 대역 부근에서 형성되므로 식 (14)의 목적함수는 두께 약 10 mm 이상의 다공성 물질에 대해서만 유효하다. 목적함수 계산을 위한 추정 기준값은 앞선 장에서 언급한 바와 같이 임피던스 튜브를 활용하여 측정 가능하고, 다공성 물질의 시편 두께는 비교적 쉽게 제어할 수 있는 요소이므로 식 (14)와 같이 목적함수를 설정하는 것은 공학적으로 타당하다 판단된다.
이상의 내용을 종합하여 다공성 물질의 비음향학적 파라미터 추정 문제를 다음과 같이 최적화 문제로 정식화하였다.
- · Find : v = [σ, ϕ, α∞, Λ', Λ]
- · Minimize : F(v)
3.2 비음향학적 파라미터 추정 알고리즘
다공성 물질의 흡음 성능에 지배적인 영향을 미치는 요소는 유동저항과 공극률이라 할 수 있다. 하지만 이들 각각의 정확한 기여율과 주로 영향을 미치는 주파수 대역 등을 명확히 정의할 수 없으므로 최적해 탐색 과정이 특정 제어변수에 편향되지 않도록 모든 제어변수가 동시에 또는 병렬적으로 탐색되어야 한다. 또한, Table 1에 제시된 바와 같이 각 제어변수의 탐색 공간의 넓이가 큰 편차를 가지는 문제, 국소 수렴 탈출 장치가 적절히 다뤄져야 한다.
Holland에 의해 정립된 것으로 평가받는 유전알고리즘은(12) 해집단을 구성하는 개체들 간 유전적 진화과정을 통해 개체의 적합도(fitness)를 점진적으로 향상시키는 기법으로 민감도 해석 등의 최적화 기법에 비해 다변수 최적화 문제를 비교적 용이하게 다룰 수 있다. 해 탐색 공간의 넓이에 대한 제약이 없고, 기울기 정보가 요구되지 않아 비교적 복잡한 최적화 문제를 다루는데 적합하다. 변이 연산(mutation operation)을 통해 국소수렴 문제를 적절히 다룰 수 있다는 특징이 있다. 이상을 종합하여 검토해볼 때 이 논문에서 다루는 문제에 대해 유전알고리즘이 적정한 최적화 기법이라 할 수 있다.
유전알고리즘에 의한 비음향학적 파라미터의 효과적인 추정을 위해 앞선 절에서 언급한 유효 밀도 계산에 지배적인 영향을 미치는 유동저항, 공극률이 상호 곱해진 형태로 계산에 참여하여 각각의 최적값이 아닌 조합의 최적값으로 수렴하는 문제가 해결되어야 한다. 이를 위해 최적해 탐색 알고리즘을 유동저항 단독 추정, 공극률 단독 추정, 그리고 모든 제어변수 동시 추정 순으로 구분하였다.
적정한 해집단 크기(population size) 선정에 대한 여러 방법이 존재한다. Alander에 의하면 유전알고리즘을 적용함에 있어 최적 해집단 크기 Np은 식 (15)와 같이 정의될 수 있다(13).
| (15) |
여기서 ng은 유전자(gene) 개수이다. 이 논문에서 다루는 모든 제어변수의 상한을 이진수로 변환하여 합한 결과가 55 bit 이므로 해집단 크기를 110개체로 정의할 수 있다. 해집단 크기가 증가할수록 연산 시간은 증가하지만, 추정의 정확도 또한 상승함을 감안하여 앞서 도출된 해집단 크기의 약 2배에 해당하는 200개체를 해집단 크기로 정의하였다.
추정 알고리즘 시작 직후 제어변수별 해집단 크기에 해당하는 개체를 Table 1을 만족하는 조건 내에서 중복을 허용하지 않고 무작위로 선택하여 초기 해집단을 정의하였다. Delany-Bazley의 법칙에 의한 흡음계수를 활용하여 다공성 물질의 흡음계수에 가장 큰 영향을 미친다고 알려진 유동저항을 우선 추정하였다(8). 해집단을 구성하는 모든 개체가 특정 값으로 수렴하여 다양성을 저해하는 것을 방지하기 위해 상기 유동저항 단독 추정 과정을 해집단 크기의 1.5배에 해당하는 300세대만큼 수행하도록 임의 정의하였다.
이후, 현재까지 계산된 유동저항 중 적합도(fitness)가 가장 우수한 즉, 목적함수가 가장 낮은 개체를 활용하여 Delany-Bazley의 법칙에 의해(8) 계산된 유효밀도의 허수부를 유동저항, 공극률, 그리고 유효밀도간의 관계(14)에 관한 식 (16)에 대입하여 전체 주파수 대역에서 유동저항을 추정한다.
| (16) |
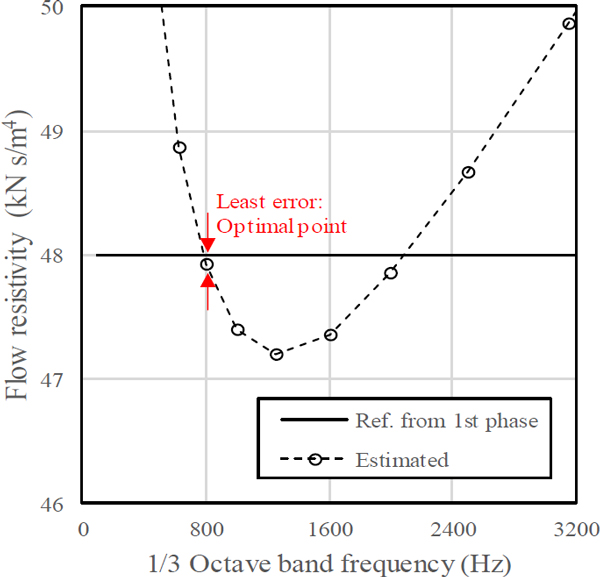
공극률을 단일 제어변수로 하여 Fig. 3에 도시한 바와 같이 기준값 즉, 이전 단계에서 얻어진 유동저항과의 오차가 최소가 되는 공극률을 탐색한다. 이 과정을 유동저항 추정 이후부터 300세대만큼을 수행하도록 정의하였으며, 세대 제한 근거는 앞선 과정에서 제시한 바와 동일하다.
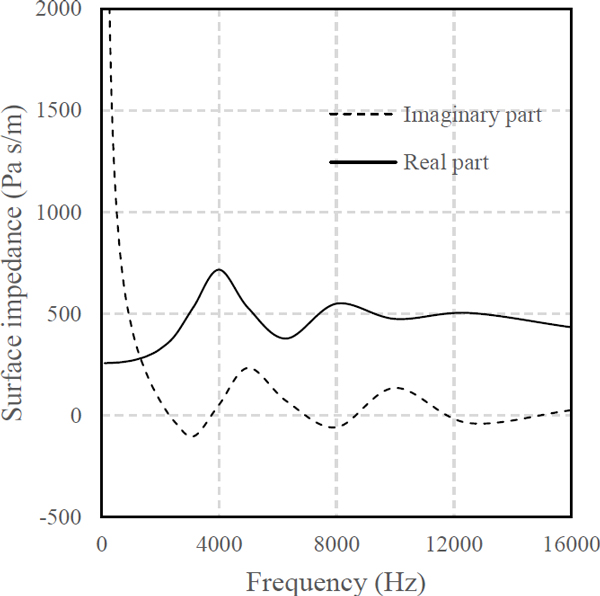
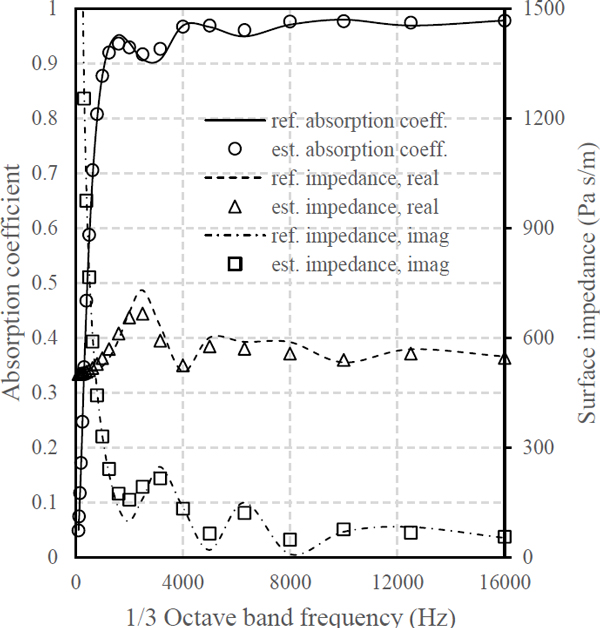
유동저항과 공극률 단독 추정 이후, 모든 제어변수를 동시 탐색하도록 정의하였다. 목적함수 계산에 JCA 모델에 의한 입사 표면에서 임피던스를 활용하였다(1,2). 이때, 표면 임피던스는 Fig. 4에 도시한 바와 같이 실수부와 허수부 모두 주파수 변화에 대한 증감 특성이 흡음계수에 비해 두드러지나, 허수부는 낮은 주파수 대역에서 공기의 특성 임피던스에 비해 매우 큰 값을 가져 식 (14)를 활용한 목적함수 계산 시 비교적 높은 주파수 대역에서의 오차가 적절히 반영되지 못할 수 있다. 이러한 사실에 착안하여 표면 임피던스의 실수부만을 목적함수 계산에 활용하였다. 이를 유동저항 또는 공극률 단독 추정 시 세대수의 세배에 해당하는 900세대 동안 수행하도록 정의하였다.
전술한 바를 종합하여 유전알고리즘에 의한 최적해 추정 과정을 Fig. 5와 같이 도시하였다. Fig. 5에서 ‘breeding operation’에 해당하는 선택 연산(selection operation), 교차 연산(crossover operation), 그리고 변이 연산(mutation operation)은 알고리즘의 성능에 핵심적인 영향을 미치는 요소로, 연산 시간, 적용의 용이성 등을 고려하여 선정 및 활용하였다.
선택 연산으로 토너먼트 선택(tournament selecti- on)을 활용하였다. 토너먼트 선택은 비례 룰렛 휠(ratio roulette wheel selection) 등에 비해 연산속도가 빠르고, 선택 압력 제어가 용이하다고 알려져 있다(15,16). 이 논문에서는 하나의 부모해 선택을위해 해집단에서 23개체를 선택하여 토너먼트에 참가시켰다. 이때, 중복 선택은 허용하지 않았다. 각 대진에서 우성 개체가 승리할 확률은 70 %로 정의 하였다.
교차 연산으로 simulated binary crossover(SBX)를 활용하였다. Deb에 의해 제안된 SBX는 이진(binary) 표현에 의한 교차 연산을 실수 영역에서 통계적으로 모사한다(17). 식 (17)과 같이 정의되는 SBX는 유전연산을 위해 각 개체를 2진수나 16진수로 변환하는 부호화(encoding) 과정이 필요치 않아 연산 속도가 빠르고 비교적 손쉽게 적용할 수 있다는 등의 장점을 가진다.
| (17) |
여기서, c는 자식해, p는 부모해, 하첨자 ‘f’, ‘m’은 부모해를 의미하며 β는 식 (18)과 같이 정의된다.
| (18) |
여기서, η는 부모해에 대한 자식해의 분포를 결정하는 분포 지표(distribution index)이다. 모든 제어변수를 탐색하는 3단계에서 교차 연산은 2개 이상의 제어변수를 가변적으로 선택하도록 정의하였다.
변이 연산으로 polynomial mutation을 활용하였다(18). 식 (19)와 같이 정의되는 polynomial mutation은 실수 영역에서 제어변수를 직접 변이시키는 것이 특징으로 SBX와 동일한 장점을 가진다. 이 논문에서 변이 확률은 10 %로 정의하였다.
| (19) |
여기서, 하첨자 ‘o’는 자식해를 의미하고, 상첨자 ‘u’, ‘l’은 Table 1에 제시된 각 제어변수의 상한, 하한을 의미하며, δ는 식 (20)과 같이 정의된다.
| (20) |
여기서, r은 변이 연산이 수행될 때 무작위로 정해지는 상수로 (0,1) 범위에서 정의되며, ηm은 변이 분포에 관한 분포 지표(mutation distribution index)이다.
다음 세대를 구성하기 위한 대치 연산(replace operation)은 엘리트주의(elitism)에 기반해 정의하였다. 전술한 선택, 교차, 그리고 변이 연산을 통해 부모 해집단(parents solution group)과 동일한 크기의 자식 해집단(offspring solution group)을 생성하고 서로 병합하여 임시 해집단을 구성한다. 이를 목적함수에 대한 오름차순으로 정렬한 뒤 첫 번째 해부터 해집단 크기만큼의 해를 다음 세대로 활용하고 나머지는 버리도록 정의하였다.
3.3 비음향학적 파라미터 추정 결과
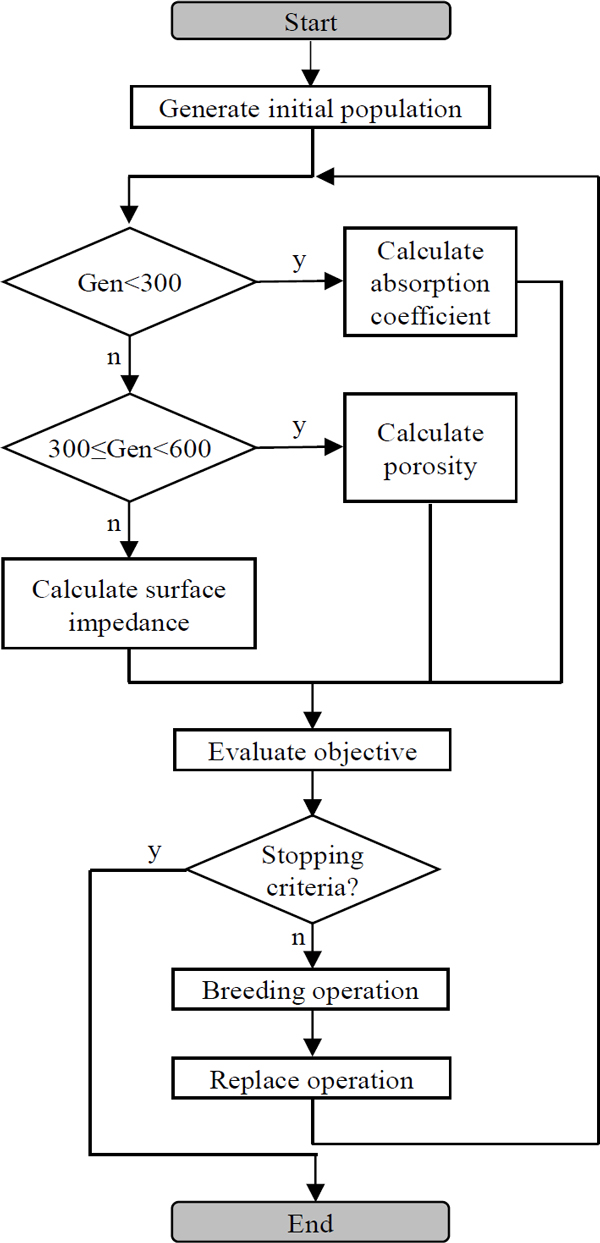
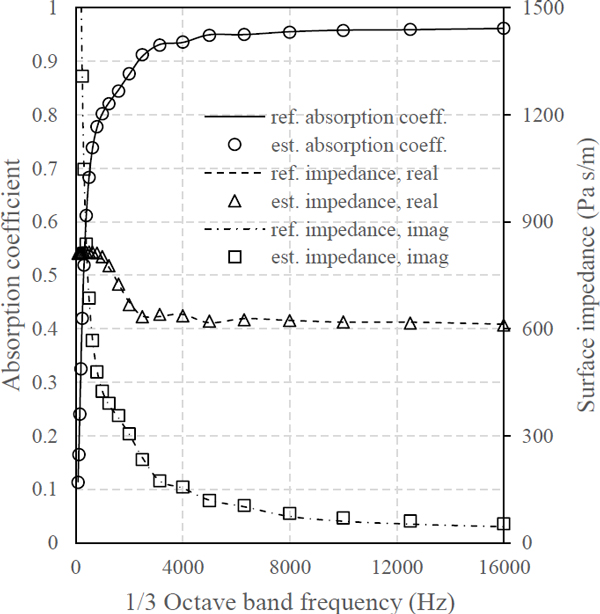
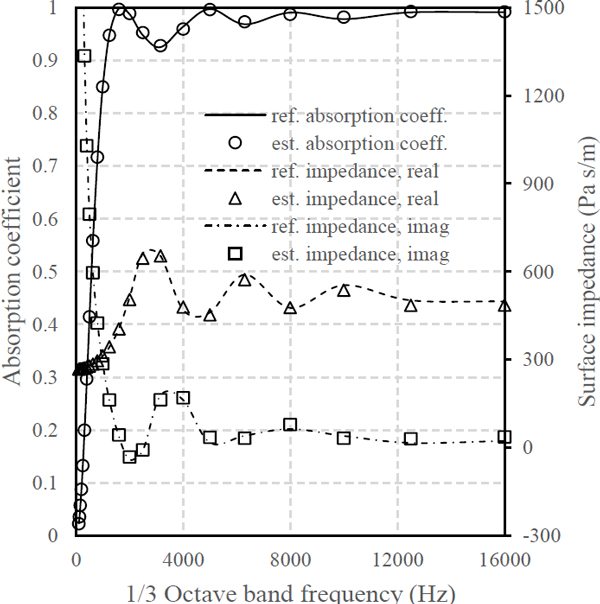
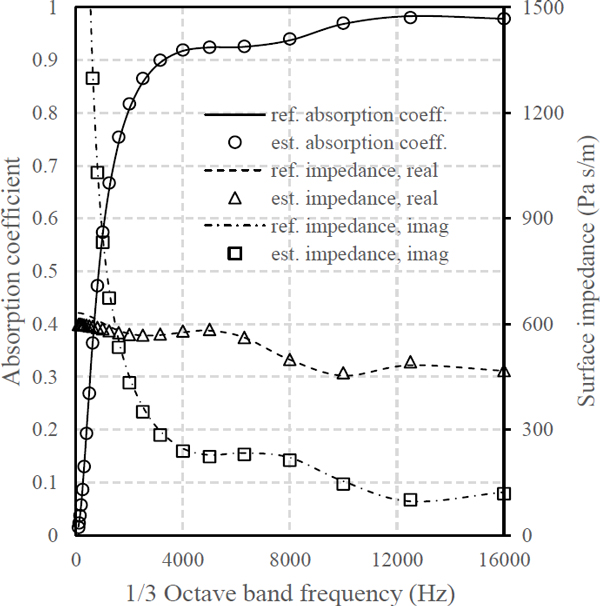
임의로 정의한 4가지 비음향학적 파라미터 조합을 전술한 알고리즘을 활용하여 추정하였다. 확률에 기반하여 최적해를 탐색하는 유전알고리즘의 특성상 매 시행마다 다른 결과가 얻어질 수 있다. 이를 감안하여 추정 과정을 10회 반복한 뒤 얻어진 결과를 산술평균하여 최종 결과로써 정의하였다. 각 케이스별 기준값과 추정 결과는 Table 2에 나타낸 바와 같다. 추정 결과 상대오차가 유동저항은 최저 0.63 %, 최대 7.19 %, 공극률은 최저 1.01 %, 최대 3.16 % 그리고 뒤틀림도는 최저 2.35 %, 최대 11.67 % 수준으로 확인되었다. 열 및 점성특성길이 추정 결과는 상대오차 최저 4.5 %, 최대 28.51 %로 다른 파라미터에 비해 비교적 큰 상대오차를 갖는 것으로 확인되었다.
이 논문에서 개발한 추정 방법의 성능 추정 정확도와 연산 시간의 관점에서 Lee et al.의 방법과 비교검토 하였다(4). Intel i7-7700 CPU, 8GB RAM 환경에서 1회 추정에 이 논문의 방법은 약 42초를, Lee et al.의 방법은 약 282초를 기록하였다(4). 추정 결과를 활용하여 JCA 모델(1,2)을 통해 계산한 흡음계수와 표면 임피던스는 Fig. 6 ~ Fig. 9에 도시한 바와 같다.
4. 결 론
이 논문에서 다공성 물질의 JCA 모델에 대한 비음향학적 파라미터를 유전알고리즘을 통해 추정하였다(1,2). 유동저항과 공극률이 동적 뒤틀림도 계산에 곱해진 형태로 활용되어 최적해가 각각의 최적값이 아닌 상호 곱의 최적값으로 수렴하는 문제를 회피하기 위해 Delany-Balzey의 법칙을 활용하여 유동저항과 공극률을 개별 추정한 후, 모든 비음향학적 파라미터를 동시 탐색 하도록 알고리즘을 구성하였다(8).
이 논문에서 개발한 추정 방법을 임의로 정의한 4가지 비음향학적 파라미터 조합에 대해 검토하였다. 유동저항의 최대 상대오차가 7 %를 초과하는 비교적 큰 수준이나 이를 활용해 계산한 흡음계수와 표면 임피던스가 기준값과 상당 부분 일치하는 것으로 확인되어 이러한 오차가 공학적으로 유용한 범위 이내인 것으로 판단된다.
하지만, 고주파수 대역 파라미터에 해당하는 점성 및 열 특성길이의 최대 상대오차가 28.51 %로 비교적 높고 매 시행 별 상대오차의 편차 또한 비교적 높다는 점은 개선되어야할 부분이라 판단된다. 식 (14)와 같은 목적함수의 활용이 이론적으로 타당하다 할지라도 각 비음향학적 파라미터가 흡음 성능에 주로 기여하는 주파수 대역에서 적절한 가중치를 가져야 할 것으로 보이며, 이를 위한 목적함수 개선에 관한 연구가 추가적으로 수행되어야 할 것으로 판단된다.
추가로, 이 논문과 Lee et al.의 추정 방법을(4) 상호 비교검토 하였다. JCA 모델에 기반한(1,2) 이 논문의 추정 방법이 Biot 이론에 기반한(5,6) Lee et al.의 추정 방법에 비해 프레임 물질의 물성 정보 등이 요구되지 않고 유전 연산을 위한 개체의 이진 부호화, 복호화(decoding) 과정을 거치지 않아 결과적으로 적은 정보로 비교적 빠른 시간 내에 유사한 결과를 도출할 수 있는 것으로 평가된다(4).
Acknowledgments
이 논문은 2023년 ~ 2024년도 창원대학교 자율연구과제 연구비 지원으로 수행된 연구결과임.
References
-
Johnson, D. L., Koplik, J. and Dashen, R., 1987, Theory of Dynamic Permeability and Tortuosity in Fluid-saturated Porous Media, Journal of Fluid Mechanics, Vol. 176, pp. 379~402.
[https://doi.org/10.1017/S0022112087000727]

-
Champoux, Y. and Allard, J.-F., 1991, Dynamic Tortuosity and Bulk Modulus in Air-saturated Porous Media, Journal of Applied Physics, Vol. 70, No. 4, pp. 1975~1979.
[https://doi.org/10.1063/1.349482]

- Atalla, Y. and Panneton, R., 2005, Inverse Acoustical Characterization of Open Cell Porous Media using Impedance Tube Measurements, Canadian Acoustics, Vol. 33, No. 1, pp. 11~24.
-
Lee, I.-S. and Park, Y.-H., 2022, Non-acoustic Parameter Estimation for Multilayer System with Porous Material by Genetic Algorithm, International Journal of Naval Architecture and Ocean Engineering, Vol. 14, 100469.
[https://doi.org/10.1016/j.ijnaoe.2022.100469]

-
Biot, M. A., 1956, Theory of Propagation of Elastic Waves in a Fluid-saturated Porous Solid I. Low-frequency Range, Journal of the Acoustical Society of America, Vol. 28, No. 2, pp. 168~178.
[https://doi.org/10.1121/1.1908239]

-
Biot, M. A., 1956, Theory of Propagation of Elastic Waves in a Fluid-saturated Porous Solid II. Higher Frequency Range, Journal of the Acoustical Society of America, Vol. 28, No. 2, pp. 179~191.
[https://doi.org/10.1121/1.1908241]

-
Hentati, T., Bouazizi, L., Taktak, M., Trabelsi, H. and Haddar, M., 2016, Multi-levels Inverse Identification of Physical Parameters of Porous Materials, Applied Acoustics, Vol. 108, pp. 26~30.
[https://doi.org/10.1016/j.apacoust.2015.09.013]

-
Delany, M. E. and Bazley, E. N., 1970, Acoustical Properties of Fibrous Absorbent Materials, Applied Acoustics, Vol. 3, No. 2, pp. 105~116.
[https://doi.org/10.1016/0003-682X(70)90031-9]

-
Plona, T. J., 1980, Observation of a Second Bulk Compressional Wave in a Porous Medium at Ultrasonic Frequencies, Applied Physics Letters, Vol. 36, No. 4, pp. 259~261.
[https://doi.org/10.1063/1.91445]

-
Allard, J. F. and Atalla, N., 2009, Propagation of Sound in Porous Media: Modelling Sound Absorbing Materials, 2nd Edition, Wiley, Chichester, UK.
[https://doi.org/10.1002/9780470747339]

- ISO(International Organization for Standardization), 2023, Acoustics — Determination of Acoustic Properties in Impedance Tubes — Part 2: Two-microphone Technique for Normal Sound Absorption Coefficient and Normal Surface Impedance, ISO 10534-2:2023.
-
Holland, J. H., 1992, Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control and Artificial Intelligence, The MIT Press, Cambridge, United Kingdom.
[https://doi.org/10.7551/mitpress/1090.001.0001]

-
Alander, J. T., 1992, On Optimal Population Size of Genetic Algorithms, Proceedings of CompEuro, pp. 65~70.
[https://doi.org/10.1109/CMPEUR.1992.218485]

-
Panneton, R. and Olny, X., 2006, Acoustical Determination of the Parameters Governing Viscous Dissipation in Porous Media, Journal of the Acoustical Society of America, Vol. 119, No. 4, pp. 2027~2040.
[https://doi.org/10.1121/1.2169923]

- Miller, B. L. and Goldberg, D. E., 1995, Genetic Algorithms, Tournament Selection and the Effects of Noise, Complex Systems, Vol. 9, No. 3, pp. 193~212.
-
Shukla, A., Pandey, H. M. and Mehrotra, D., 2015, Comparative Review of Selection Techniques in Genetic Algorithm, Proceedings of International Conference on Futuristic Trends on Computational Analysis and Knowledge Management(ABLAZE), pp. 515~519.
[https://doi.org/10.1109/ABLAZE.2015.7154916]

- Deb, K. and Agrawal, R. B., 1995, Simulated Binary Crossover for Continuous Search Space, Complex Systems, Vol. 9, No. 2, pp. 115~148.
-
Deb, K. and Deb, D., 2014, Analysing Mutation Schemes for Real-parameter Genetic Algorithms, International Journal of Artificial Intelligence and Soft Computing, Vol. 4, No. 1, pp. 1~28.
[https://doi.org/10.1504/IJAISC.2014.059280]


In-Seok Lee received his M.S. degree in Naval Architecture and Marine Engineering at Changwon National University. He is currently working at Korea Marine Equipment Research Institute as a senior researcher.

Tae-Heum Yoon received his M.S. degree in Naval Architecture and Marine Engineering at Changwon National University. He is currently working at Korea Marine Equipment Research Institute as a researcher.

Young-Ho Park received his Ph.D. degrees in Naval Architecture and Ocean Engineering at Seoul National University. He currently works as a professor in the Dept. of Smart Ocean Mobility Engineering at Changwon National University.