오목 멤브레인의 저차 고유치 미 추출 문제 극복을 위한 분할 영역법 기반 무차원동영향함수법 개발: 제2부(예제 연구 및 고찰)
© The Korean Society for Noise and Vibration Engineering
Abstract
The first part of this paper proposed a theoretical formulation of an improved NDIF method designed to overcome the issue of non-extraction of low-order eigenvalues in the NDIF method when applied to the sub-domain method. The validity of the proposed formulation was confirmed using membranes of simple geometries. In this second part of the paper, example studies are conducted on concave membranes with various shapes, including V-shaped, L-shaped, and concave circular membranes, in order to verify the validity and accuracy of the NDIF method theory presented in Part 1.
Keywords:
NDIF Method, Concave Membrane, Eigenvalue, Free Vibration, Determinant Curve, Sub-domain Method키워드:
무차원동영향함수법, 오목 멤브레인, 고유치, 자유 진동, 판별식 곡선, 영역 분할법1. 서 론
이 논문의 1부에서는 엄밀해가 존재하는 사각 멤브레인과 오목 홈을 가진 사각 멤브레인에 영역 분할법 기반 무차원동영향함수법을 적용하여, 절점 수가 증가했을 때 저차의 고유치들이 구해지지 않는 원인을 먼저 규명하였다. 이를 바탕으로 절점 수와 무관하게 저차의 고유치가 정확하게 추출되게 하는 ‘새로운 분할 영역법 기반 무차원동영향함수법’이 제안되었다.
이 논문(2부)에서는 논문 1부에서 제안된 방법의 정확성과 타당성을 검증하기위해 V형상 멤브레인, L 형상 멤브레인, 오목 원형 멤브레인에 대한 다양한 예제 연구가 수행되었다.
2. 논문 1부에서 제안된 이론 결과 식
분할 영역법 기반 무차원동영향함수법은 오목 멤브레인의 고유치를 구하기 위해 개발되었다(1). 이때 시스템 행렬의 판별식을 구하기 위해 식 (1)이 사용된다.
| (1) |
여기서 SM(Λ)는 축약된 시스템 행렬, S는 시스템 행렬의 크기, γk(Λ)는 시스템 행렬에 대한 대수 고유치 문제에서의 k번째 고유치를 의미한다(2). 참고로 SM(Λ)은 식 (2)와 같다(1).
| (2) |
식 (1)은 절점 수가 증가했을 때 저차 고유치가 구해지지 않는 문제점을 가진다. 이를 극복하기 위해 논문의 1부에서는 볼록 멤브레인 고유치 해석에서 이용되는 식 (3)이 먼저 사용되었다(2).
| (3) |
여기서 R(Λ)는 시스템 행렬의 랭크이다. 그러나 식 (3) 또한 오목 멤브레인 고유치를 구하기위해 사용되는 분할영역법 기반 무차원동영향함수법에서는 유효하지 않음이 확인되었다. 그래서 이 논문의 1부에서는 축약 기법을 사용하지 않고 시스템 행렬을 구한 후 이 비축약 시스템 행렬을 식 (3)에 적용해서 판별식을 계산하는 식 (4)가 제안되었다.
| (4) |
여기서 RT(Λ)는 비축약 시스템 행렬 TM의 랭크, τk(Λ)는 시스템 행렬 TM에 대한 대수 고유치 문제에서의 k번째 고유치를 의미한다. 참고로 TM은 식 (5)와 같이 주어지며 보다 자세한 내용은 이 논문의 1부에서 확인 가능하다.
| (5) |
3. 예제 연구
3.1 V 형상 오목 멤브레인
이 논문의 1부에서 제안된 판별식 계산식 식 (4)의 타당성을 검증하기 위해 Fig. 1과 같은 V 형상 오목 멤브레인이 먼저 고려된다. 이 오목 멤브레인의 가로와 세로 길이는 각각 1.2 m와 세로 0.9 m이며, V 홈의 깊이는 0.4 m이다. 두 영역분할법을 적용하기 위해 멤브레인의 영역은 두개의 볼록 영역으로 먼저 분할한 후 각 영역의 경계와 두영역의 접경을 절점으로 이산화 하였다.
Fig. 1(a)와 같이 27개의 절점을 사용하여 이산화한 멤브레인의 판별식 곡선을 기존 무차원동영향함수법 식인 식 (1) 또는 식 (3)을 이용하여 그려 보면 Fig. 2의 실선과 같이 된다. 이 실선 판별식 곡선에서 극소값에 해당되는 주파수 파라미터 값들이 고유치에 해당되며, 이 고유치들은 Table 1의 두 번째 열에 요약되었다. 이 고유치들을 1290개의 절점을 사용한 FEM 고유치들과 비교해보면 약간의 오차가 있음을 알 수 있다. 특히, 6차와 8차 고차 고유치가 오차가 큼을 확인할 수 있으며, 7차 고유치가 고차 고유치임에도 오차가 적은 이유는 모드 형상과 관련 있는 것으로 이전 연구 결과(2)에 근거하여 추정된다. 이들 오차를 줄이기 위해 Fig. 1(b)와 같이 절점의 수를 27개에서 36개로 증가시킨 후 판별식 곡선을 그리면 Fig. 2의 점선 곡선이 된다. 이 점선 판별식 곡선을 살펴 보면, 저주파수 영역에서 시스템 행렬이 발산하여 1차, 2차 저차 고유치들은 추출되지 않고 3차 ~ 8차 고차 고유치들만 추출되는 문제점이 확인된다. 추출된 고차 고유치들은 Table 1의 세 번째 열에 요약되었으며 이 고차 고유치들은 27개 절점을 사용한 경우보다 FEM 고유치에 더 근접했음이 확인된다.
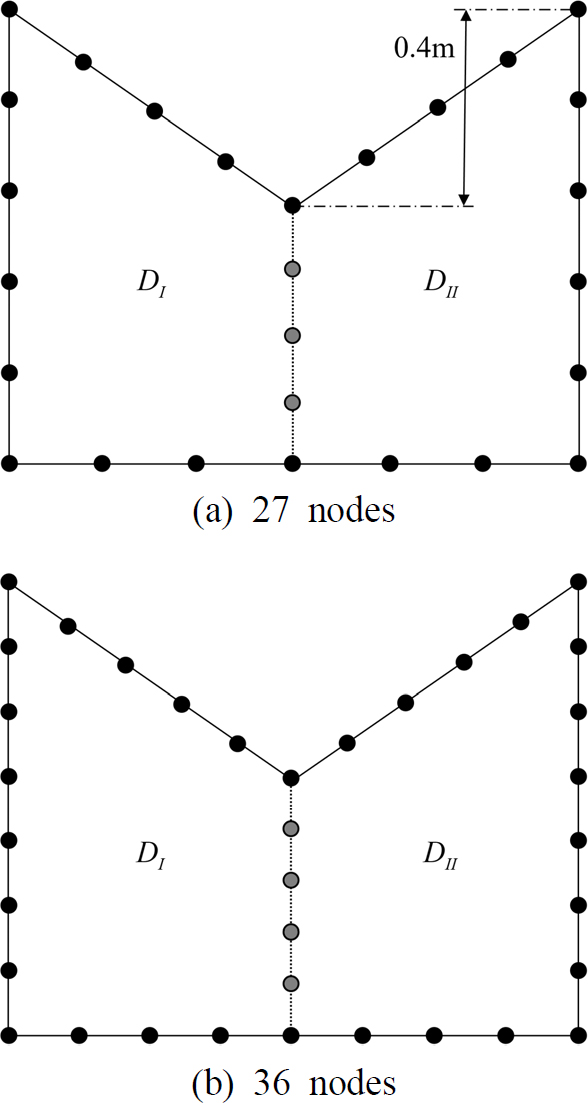
V-shaped concave membranes divided into two domains and discretized with 27 and 36 nodes, respectively
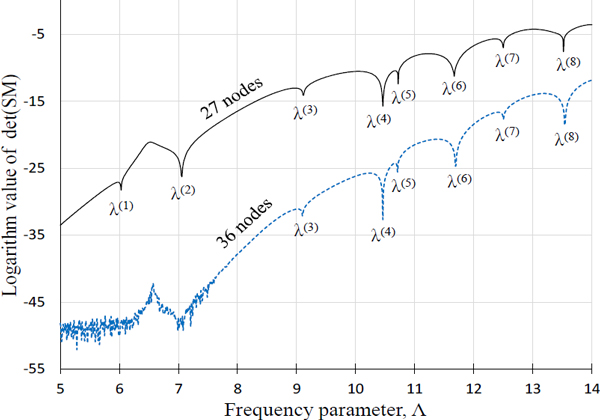
Determinant curves of the V-shaped concave membrane for 27 and 36 nodes plotted by the previous NDIF method using Eq. (1) or Eq. (3)

Eigenvalues of the V-shaped concave membrane obtained by the previous NDIF method using Eq. (1) or Eq. (3), FEM(ANSYS) and the proposed method using Eq. (5)
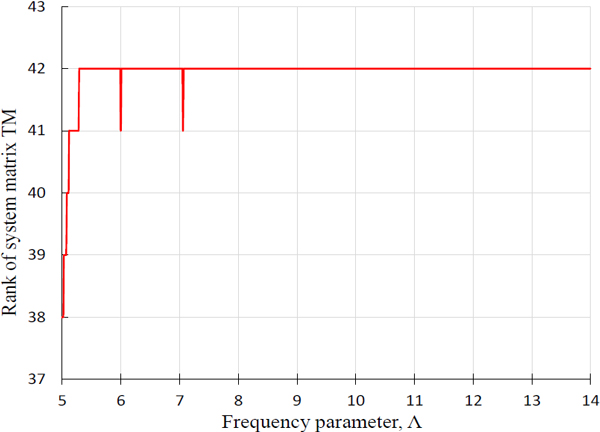
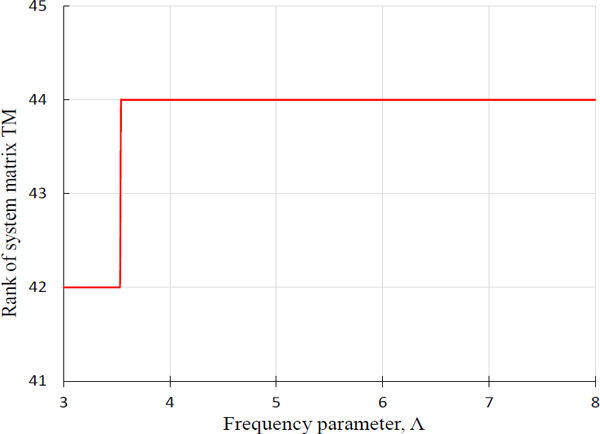
상기와 같이 저차 고유치가 구해지지 않는 문제점을 해결하기 위해 제안된 식 (4)를 이용하여 판별식 곡선을 그리면 Fig. 3과 같다. 이 판별식 곡선을 살펴 보면 저주파수 영역에서 발산 현상이 사라졌음이 확인되며, 동시에 저차 고유치를 포함한 전 주파수 영역 고유치가 모두 추출되었음도 확인된다. 추출된 고유치들은 Table 1의 마지막 열에 요약되었으며, 이들 고유치가 FEM 고유치와 거의 근접한 결과를 보이므로 이 논문의 1부에서 제안된 식 (4)는 타당하고 정확한 결과를 제공한다고 결론 지을 수 있다. Fig. 4는 식 (4)를 계산할 때 RT(Λ)값으로 사용되어진 시스템 행렬의 랭크 곡선이며 저주파 수 영역에서 풀 랭크(full rank)가 아님이 보여진다.
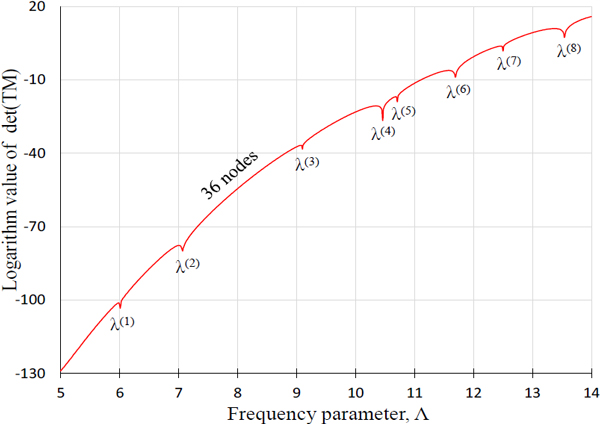
Determinant curve of the V-shaped concave membrane for 36 nodes plotted by the proposed method using Eq. (5)
3.2 L 형상 오목 멤브레인
두 번째 예제로 Fig. 5와 같은 L 형상 오목 멤브레인이 고려된다. 멤브레인의 오목 영역을 두 개의 볼록 영역으로 먼저 이산화한 후 경계와 두 영역 접경을 이산화 하였다. Fig. 5(a)와 Fig. 5(b)는 각각 28개와 45개의 절점으로 이산화한 경우를 각각 보여 준다. 먼저 28개로 이산화한 경우에 대해, 이전 연구에서 개발한 식 (1) 또는 식 (3)을 이용하여 판별식 곡선을 그려보았다. 그 결과는 Fig. 6의 실선과 같으며 여기서 극소값에 해당하는 고유치들을 추출하여 요약하면 Table 2의 두 번째 열과 같이 된다. 이 고유치들을 1281개의 절점을 사용한 FEM 결과와 비교해보면 오차가 약간 있음을 확인할 수 있다. 특히 1차, 5차, 7차 고유치가 오차가 상대적으로 큰 것이 확인되는데 이는 이전 연구의 경험에(2) 비추어 모드 형상의 영향일 것으로 추정된다. 부연 설명하면, 무차원동영향함수법에서는 절점의 위치가 모드의 노달 라인에 근접하면 적은 절점 수로도 정확한 고유치가 추출되는 경향이 있다.
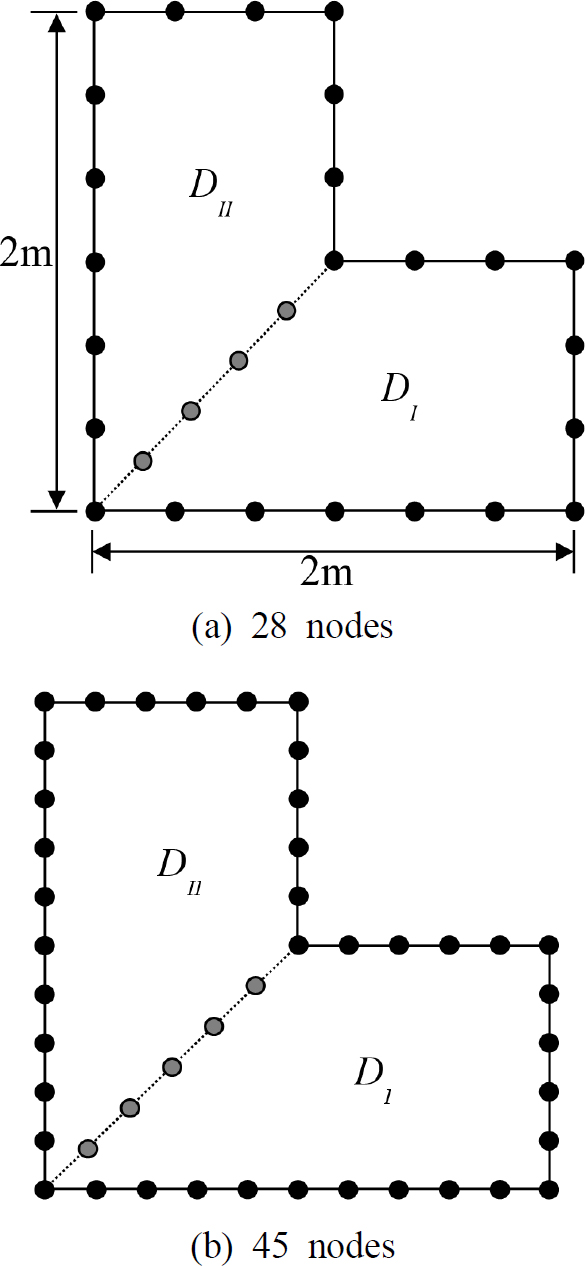
L-shaped concave membranes divided into two domains and discretized with 28 and 45 nodes, respectively
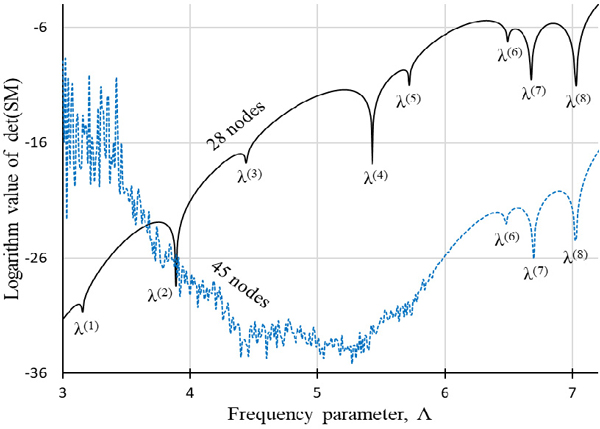
Determinant curves of the L-shaped concave membrane for 28 and 45 nodes plotted by the previous NDIF method using Eq. (1) or Eq. (3)

Eigenvalues of the L-shaped concave membrane obtained by the previous NDIF method using Eq. (1) or Eq. (3), FEM(ANSYS) and the proposed method using Eq. (4)
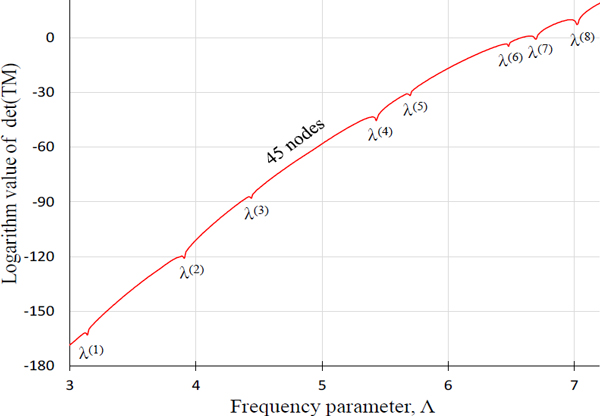
상기의 고유치 오차의 줄이기 위해 Fig. 5(b)와 같이 절점의 개수를 45개로 증가시킨 후 판별식 곡선을 그려보았다. 그 결과는 Fig. 6의 점선과 같으며 절점 개수 증가의 영향으로 저주파수 영역에서 시스템 행렬이 발산하고 있음이 보여 진다. 단지 6차 ~ 8차 고차 고유치 만이 추출되었으며 이들은 Table 2의 3열에 요약되었다. 비록 1차 ~ 5차 고유치는 추출되지 않았지만 28개의 절점을 사용했을 때 오차가 컸던 7차 고유치의 오차가 줄어들었음이 확인된다. 한편 8차 고유치는 28개를 절점을 사용했을 때 보다 45개를 사용한 경우에 오차가 0.02에서 0.03으로 커진 것으로 확인된다. 그 이유는 1281개의 절점을 사용한 FEM 8차 고유치가 아직 수렴을 하지 않아 그 수렴값(일종의 엄밀해)은 7.05보다 더 작은 값(예를 들어 7.01)을 가지기 때문이다. 한편, 8차 고유치의 수렴값이 7.01이라면, 45개의 절점울 사용한 무차원동영향함수법이 FEM 보다 더 정확한 결과를 제공한다고 말할 수 있다. 참고로, 무차원동영향함수법이 FEM 보다 더 정확한 결과를 제공함이 엄밀해를 가지는 사각 멤브레인을 다룬 이 논문의 1부에서 검증되었다.
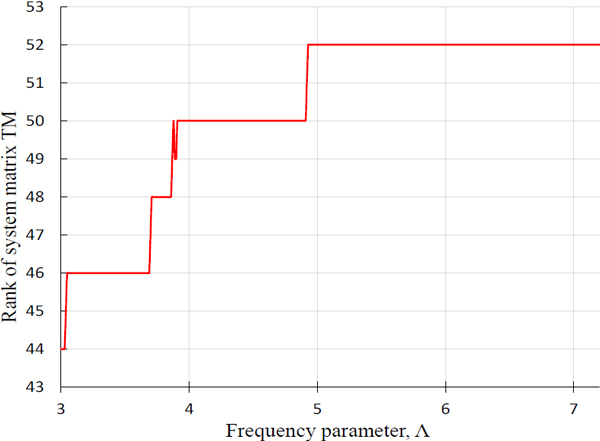
Fig. 7은 식 (4)를 계산하여 Fig. 8의 판별식 곡선을 그릴 때 사용되어진 시스템 행렬의 랭크를 보여준다. 이 랭크 곡선에서 주파수 파라미터가 5보다 작은 영역에선 풀 랭크(full rank)가 아님을 확인할 수 있다.
3.3 오목 원형 멤브레인
앞서 다룬 두가지 예제는 직선 경계로만 이루어진 오목 다각형 형상인 반면에 3.3절에서는 Fig. 9와 같이 곡선과 직선 경계로 이루어진 오목 원형 멤브레인이 고려된다. 두 영역 분할법을 사용하기 위해 오목 영역을 두개의 볼록 영역으로 분할한 후 경계와 접경을 20개, 29개, 38개의 절점으로 Fig. 9(a) ~ Fig. 9(c)와 같이 각각 이산화 하였다.
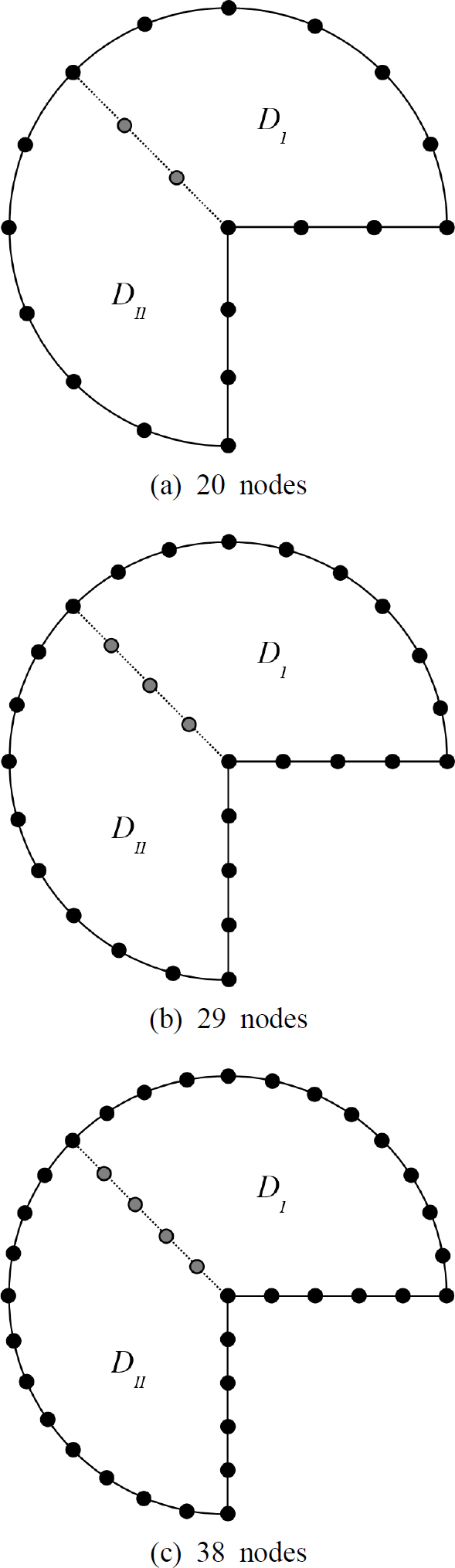
Concave circular membranes of unit radius divided into two domains and discretized with 20, 29 and 38 nodes, respectively
먼저 20개 절점으로 이산화한 경우에 대해 이전 무차원동영향함수법에서 개발한 식 (1) 또는 식 (3)을 적용하여 판별식 곡선을 그렸다. 그 결과는 Fig. 10의 실선에 해당되며 여기서 극소값에 해당되는 고유치를 추출하여 Table 3의 두 번째 열에 요약하였다. 이 결과를 1830개 절점을 사용한 FEM 결과와 비교해보면, 약간의 오차가 있음을 확인할 수 있다. 특히, 5차 고유치가 오차가 상대적으로 큰데, 이는 모드 형상과 관련된 것으로 추정된다. 참고로 오목 원형 멤브레인은 엄밀해가 존재하지 않기 때문에 두 결과 중 어느 것이 더 정확한 결과라고 말 할 수 없다.
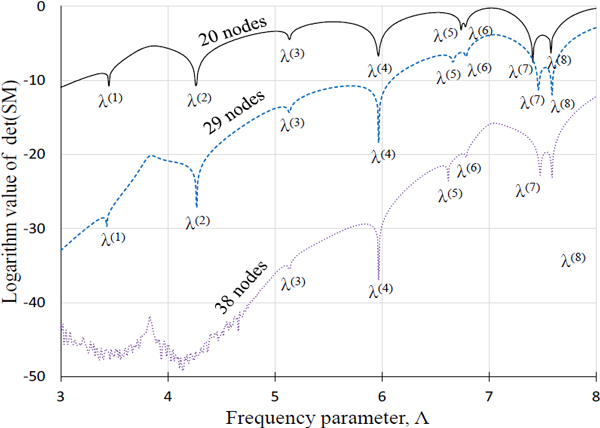
Determinant curves of the concave circular membrane for 20, 29 and 38 nodes plotted by the previous NDIF method using Eq. (1) or Eq. (3)

Eigenvalues of the concave circular membrane obtained by the previous NDIF method using Eq. (1) or Eq. (3), FEM (ANSYS) and the proposed method using Eq. (4)
상기의 오차를 줄이기 위해 절점의 개수를 Fig. 9(b)와 같이 29개까지 증가시킨 후 판별식 곡선을 그린 결과는 Fig. 10의 긴 점선과 같다. 이 판별식 곡선으로부터 추출한 고유치들은 Table 3의 세 번째 열에 정리하였다. 이들 고유치들은 20개 절점을 사용한 경우보다 FEM 고유치에 더 근접했음이 확인된다. 특히, 5차 고유치의 오차가 많이 개선되었음을 알 수 있다.
오차를 더 줄이기 위해 Fig. 9(c)와 같이 38개의 절점을 사용하여 판별식 곡선을 그리면 Fig. 10의 짧은 점선과 같다. 앞의 두 절에서 설명한 바와 같이 절점 수가 증가하여 1차, 2차 저차 고유치가 추출되지 않고 3차 ~ 8차 고차 고유치만 추출되는 것이 확인된다. Table 3의 네 번째 열에 요약된 고차 고유치들은 FEM 고유치들과의 오차가 더 줄어들었다. 하지만 1차 ~ 2차 고유치가 추출되지 않는 문제점을 발생하였으며, 이를 개선하기 위해 이 논문에서 제안된 식 (4)를 사용하여 Fig. 11의 판별식 곡선을 그렸다. 이때 사용되어진 시스템 행렬 TM의 랭크는 Fig. 12와 같이 구해졌다. 이 판별식 곡선을 살펴보면 저차와 고차 고유치가 모두 추출됨이 확인되며, 이들 고유치들은 Table 3의 마지막 열에 정리되었다. 제안된 방법에 의해 구해진 이들 고유치들이 1830개의 많은 절점을 사용한 FEM 고유치들과 거의 오차가 없는 것으로 확인되며, 이러한 사실로부터 제안된 방법의 타당성과 정확성은 입증된다고 말할 수 있다.
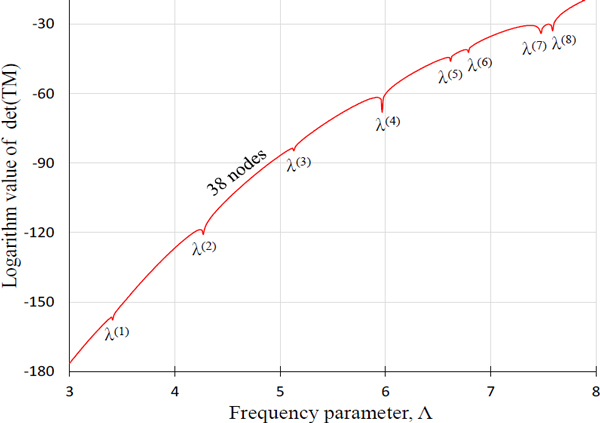
Determinant curve of the concave circular membrane for 38 nodes plotted by the proposed method using Eq. (4)
4. 결 론
이 논문의 1부에서는 분할영역법을 사용하는 무차원동영향함수법에서 저주파수 영역에서 시스템 행렬이 발산하여 저차 고유치가 추출되지 않는 문제점을 극복한 새로운 무차원동영향함수법을 제안하였다. 논문 2부에서는 논문 1부에서 제안된 이론의 타당성과 정확성을 검증하기 위해 다양한 형상의 오목 멤브레인에 대한 예제 연구가 수행되었다. 향후 연구에서는 오목 멤브레인을 3개 이상의 영역으로 분할하는 다 영역 분할법(multi-domain method)에 근거한 무차원동영향함수법에서 발생하는 시스템 행렬 발산 문제를 극복하는 연구가 진행될 예정이다.
Acknowledgments
이 연구는 한성대학교 교내학술연구비 지원 과제임.
References
-
Kang, S. W. and Lee, J. M., 2000, Application of Free Vibration Analysis of Membranes using the Non-dimensional Dynamic Influence Function, Journal of Sound and Vibration, Vol. 234, No. 3, pp. 455~470.
[https://doi.org/10.1006/jsvi.1999.2872]

-
Kang, S. W., 2022, Improvement of Eigenvalue Extraction Method in the NDIF Method for Free Vibration Analysis of Arbitrarily Shaped Membranes, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 32, No. 1, pp. 97~104.
[https://doi.org/10.5050/KSNVE.2022.32.1.097]


Sang Wook Kang received a B.S., M.S. and Ph.D. degrees in Dept. of Mechanical Design Engineering from Seoul National University. He is working in Hansung University.