질량 관성모멘트 측정 장치의 제작과 구동 모터에의 응용

1. 서 론

동역학 해석에서 질량 관성모멘트는 중요한 부분 중 하나이다. 이는 물체의 회전 운동 및 안정성을 이해하고 제어하기 위해 필수적인 정보를 제공하며, 다양한 응용 분야에서의 공학적 설계 및 분석에 핵심적인 역할을 한다.

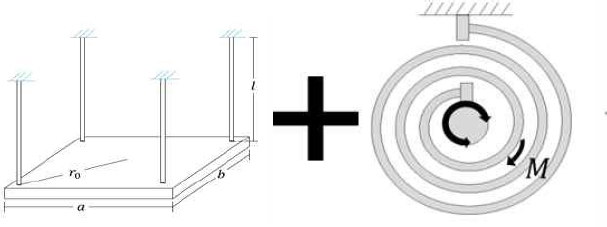
질량 관성 모멘트의 측정은 대상 물체의 크기나 질량 및 측정 비용에 따라 다양하게 행해지고 있다. 이들 방법을 크게 나누어 보면, 토오크 및 각가속도 측정, 가속도 측정과 신호처리에 의한 방법에 의한 방법, 진자 시스템을 구성하는 방법이 있다. 토오크 및 각가속도 측정에 의한 방법은 대부분 특정 제품에 대한 전용장비로서 물체에 가해지는 제어 가능한 회전구동부와 각가속도 측정시스템으로 구성되어 있고^(1,2), 센서의 정밀도에 따라서 정밀한 측정이 가능하나 높은 비용을 요구한다는 특징이 있다. 가속도 측정에 의한 방법은 대상물체를 자유단 조건에서 얻은 주파수응답함수를 이용하여 강체 정보를 추정하는 방법으로 간단한 장비로 빠르게 측정할 수 있으나 자유단 조건의 구현이 어려울 수 있고 추정과정에서의 오차가 큰 경우도 있다는 제한점이 있다^(3~5). 진자 시스템을 이용하는 경우는 제작이 비교적 쉬워서 사용된 예가 많지만^(6~9), Fig. 1과 같이 보다 정확한 주기를 측정을 위해 주기를 느리게 만들기 위해서는 많은 공간이 필요하거나 줄길이에 따라서 측정오차가 상당히 영향을 받는다는 제한점이 있다⁽⁸⁾.

Fig. 1

Pendulum systems for the measurement of moment of inertia

이 연구에서는 이러한 제약들을 극복하기 위해 Fig. 2와 같이 스파이럴 스프링을 활용한 질량 관성 모멘트 측정 장치를 제작하고자 하였다. 스파이럴 스프링의 유연하면서도 강한 탄성 특성을 활용하여 물체의 회전 운동 방향 강성을 부가하고 이의 주기를 간편하게 측정할 수 있는 이 장치는 공간적 제약을 최소화하면서 비용 측면에서 저렴하다는 장점이 있다. 제작된 질량 관성 모멘트 측정 장치는 공간에 줄을 이용해서 매달지 않고 테이블에 올려놓으면 되기 때문에 실험 공간에 대한 부담을 줄일 수 있으며, 단순한 구조로 인해 측정 준비가 간편하다는 장점을 지니고 있다. 이러한 특성들은 연구 및 실험 환경에서의 효율성을 향상시키고, 측정에 필요한 비용과 시간을 절감할 수 있게 함으로써 새로운 방법을 제시한다. 이 연구에서는 스파이럴 스프링을 이용한 간편한 질량 관성 모멘트 측정 장치의 제작 및 검증 과정과 자동차 모터부품의 측정 결과를 제시하고, 이를 통해 기존의 측정 방법들과의 측정결과를 비교하여 장치의 정확성을 확인한다.

Fig. 2

The concept of inertia measurement system

2. 측정장치의 제작 및 검증

2.1 관성 모멘트 측정장치의 제작

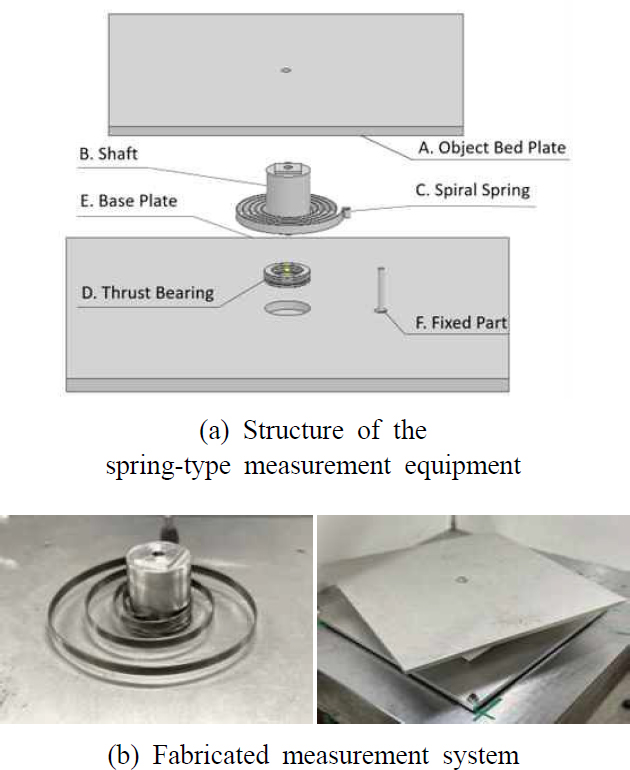
측정 장치는 Fig. 3(a)에서 보는 바와 같이 회전축, 스파이럴 스프링, 기저부(base plate), 상판(object bed plate), 쓰러스트 베어링으로 구성되어 있다.

Fig. 3

Spiral spring-type measurement system

회전축의 아랫부분은 베어링의 크기에 맞게 가공하였고, 윗부분은 상판의 사각 홈에 맞게 가공하였다. 축과 스파이럴 스프링의 연결부위는 회전 시 발생하는 유격으로 인한 움직임을 방지하기 위해 금속 접착제를 사용하여 연결 뒤 접착제로 고정하였다. 제작된 측정장치를 Fig. 3(b)에서 볼 수 있다.

질량 관성모멘트를 측정은 대상물체를 상판에 고정한 후 1자유도계 회전운동의 주기를 측정하면 식 (1), 식 (2)와 같이 구할 수 있다.

$\[ T=\frac{2\pi }{{\omega }_n},{\omega }_n=\sqrt{\frac{K}{J}} \]$

(1)

$\[ J=J_M+J_0=K{\left(\frac{T}{2\pi }\right)}^2 \]$

(2)

식 (1), 식 (2)에서 T는 1자유도 회전시스템의 회전운동 주기, K는 회전 탄성 스프링 계수이고, J_M과 J₀는 각각 측정대상물체와 상판의 질량 관성 모멘트다.

질량 관성 모멘트를 측정하기 위해서는 측정장치를 구성하는 스파이럴 스프링의 회전 강성계수를 알아야 하는데 이는 측정장치의 상판에 측정 구조물을 올리지 않고 일정한 초기 회전 변위를 주었을 때 나타나는 회전운동의 주기를 측정하여 구하였다. 이때 사용된 상판과 회전축의 질량 관성 모멘트 값은 측정한 질량을 질량 관성 모멘트 관계식, $$ J=\frac{1}{12}M\left(A^2+B^2\right),J=\frac{1}{2}M{R}^2$$을 사용하여 계산되었고, 유도된 강성식인 $$ K=J{\left(\frac{2\pi }{T}\right)}^2$$을 통해 스파이럴 스프링의 회전 강성계수를 도출하였다.

측정 방법으로는 초기각도 30°, 35°, 40°, 45°, 50°, 55°로 회전 후 측정 30° 미만에서는 마찰로 인해 회전력이 부족하였고, 55° 초과시 스프링과 축 고정부분 파손이 발생할 수 있어 측정을 진행하지 않았다. 주기 측정은 스마트폰 내장 카메라를 이용하여 스톱워치와 측정 장치를 영상 촬영하여 측정하였다. 측정은 각 초기 각 변위에 대해서 10번씩 수행하였다. Table 1에 그 측정값을 표시하였다. 관성 모멘트 측정장치의 회전 스프링상수는 Table 2에 측정데이터에서 30° ~ 45° 구간의 주기 평균값(3.65 s)을 기준으로 스프링 상수를 도출하여 K=3.347 N·m/rad로 계산하였다.

Table 1

Measured periods of unloaded case

Table 2

Specification of the measurement equipment

2.2 측정장치의 검증

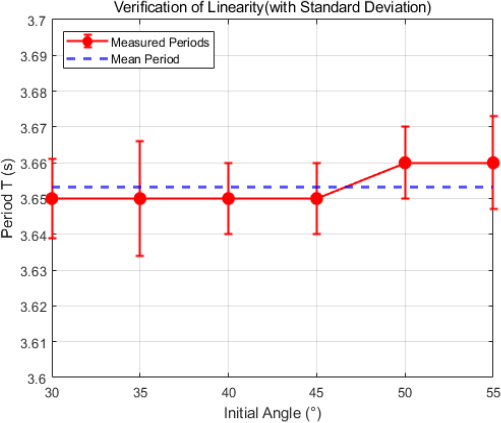
이 장치는 선형성 범위와 밀접하게 연관되어 있으며, 이를 확인하기 위해 주기의 변동성을 Fig. 4와 같이 확인하였다. 그림을 보면 초기 각도가 증가해도 주기의 변동성이 크지 않으며, 평균 주기와의 편차가 일정하게 유지됨을 확인할 수 있다. 이는 스프링의 강성이 일정하게 유지되며, 시스템이 선형성을 갖고 있음을 의미한다.

Fig. 4

Variation of measured periods with initial angles

Fig. 5와 Table 3과 같이 관성 모멘트 측정장치의 정확도를 검증하기 위해 모양이 일정하고 질량 관성 모멘트의 이론 값을 알고 있는 바벨 원판을 이용하였다. 이론 값은 판의 경우와 같이 질량 측정을 통해 모델 수정 후 계산 값을 사용하였다. 측정에 사용된 바벨의 경우 단순 도형 및 균일 밀도로 가정하였으며, 질량 중심을 판별하기 위해서 실험 과정에서 여러 시행을 반복하며 주기를 측정하였고, 주기가 가장 작은 상태에서 고정함으로써 질량 중심이 판별되도록 하였다.

Fig. 5

Measurement of moment of inertia for the barbells

Table 3

Property of the barbell

측정은 바벨을 1개부터 4개까지 순차적으로 상판에 고정하고 주기를 측정하는 방법을 수행하였다. 수기로 초기각도를 설정하다 보니 정확한 각도 설정에 제한이 있었다. 이에 오차를 최소화하기 위해 중간 각도로서 35°와 40°를 기준으로 채택했다. 다양한 각도에서의 측정 오차를 비교한 결과, 35°에서 40°보다 오차가 상대적으로 일정한 경향을 확인할 수 있었다. 따라서 질량 관성모멘트를 알 수 없는 구조물을 측정할 때는 초기각도를 35°로 설정하여 측정을 실시했다. 측정결과를 Table 4에 정리하였다.

Table 4

Measured results for the barbell

측정 장치의 오차를 확인한 결과, 최대 3.64 %의 차이가 나타났다. 이는 질량 관성 모멘트 관계식을 통해 얻은 질량 관성모멘트와 실제 바벨 원판의 질량 관성모멘트 간의 불확실성 및 주기측정에서의 오차로 추정된다. 또한, 오차의 일정함을 고려할 때, 최소값과 최대값 간의 차이가 0.88 %로 1 % 이내의 안정성을 보이고 있어 질량 관성모멘트가 증가하더라도 일정한 측정 값을 얻을 수 있다는 점을 확인할 수 있었다.

3. 구동모터의 관성 모멘트 측정에의 응용

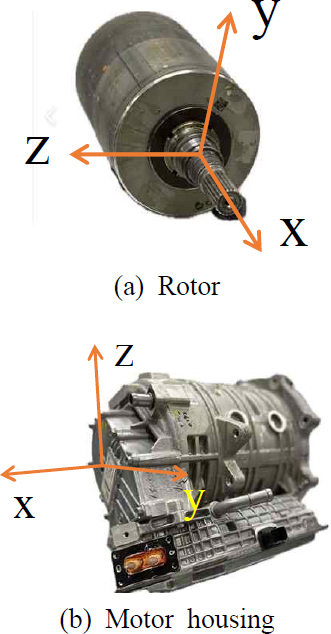
제작 및 검증을 완료한 관성 모멘트 측정장치를 이용하여 전기자동차 구동모터의 질량 관성 모멘트를 측정하였다. 구동모터는 로터와 모터하우징로 나눌 수 있다.

Fig. 6은 측정에 사용된 구동 모터의 로터와 모터 하우징을 나타낸다. 로터와 모터 하우징은 복잡한 권선과 여러 부품으로 이루어져 있어 기하학적 모델링을 통한 질량 관성 모멘트의 정밀한 산출이 어렵다. 이에 따라, 보다 정확한 값을 확보하기 위해 관성 모멘트 측정 장치를 이용하여 실험적으로 질량 관성 모멘트를 측정하고자 한다. 로터와 모터하우징에 대하여 2장에서 수행한 방법과 동일하게 대상 부품을 관성 모멘트 측정장치의 상판 위에 고정하고 초기 각변위를 인가하는 방식으로 회전 자유진동을 일으켰을 때 발생하는 진동의 주기를 측정하고, 2장에서 도출한 회전 스프링 강성계수를 이용하여 대상부품의 질량 관성 모멘트 값을 추정하였다. 질량 관성 모멘트는 Fig. 6에 표시한 각 부품의 주축에 대하여 측정을 반복하였다. Fig. 7에는 각 주축방향으로 대상부품을 측정하는 상태를 보여주고 있다. 관성 모멘트 측정장치의 상판에 대상부품을 고정하기 위한 지그는 스티로폼이나 골판지, 고무 등으로 제작하여 추정 값에 미치는 영향을 최소화하였다.

Fig. 6

Power motor for electric vehicle

Fig. 7

Measurement setup for power motor components with spiral spring-type system

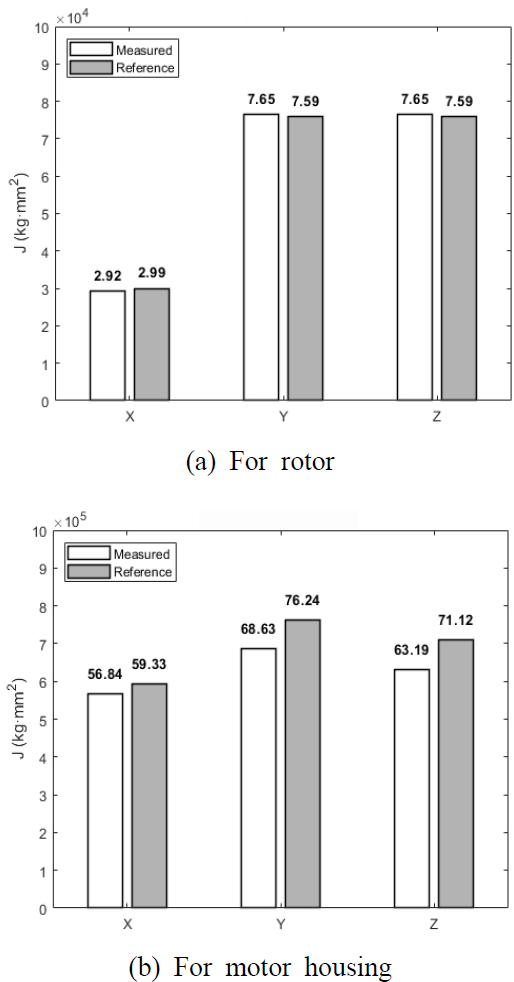
측정결과는 Table 5과 Fig. 8에 나타내었다. 측정값의 비교를 위해서 Fig. 9에서 보인 바와 같이 현을 사용한 시스템을 통해 도출한 관성 모멘트 값을 Table 6에 정리하였고 이 값을 기준으로 한 측정값의 비율을 백분율로 나타내어 표와 결과에 나타내었다. 참고 값은 동일한 대상부품에 대하여 4개의 철선과 받침대로 구성된 회전진자를 이용하여 측정한 결과이다.

Table 5

Measured results of power motor components by spiral spring-type system

Fig. 8

Measured results plot for power motor components

Fig. 9

Measurement setup for power motor components with cable-type system

Table 6

Mass properties of power motor by cable-type measurement system

Fig. 8을 통해 결과를 비교하면, 로터의 경우 모든 축에 대해서 3 % 이내로 유사한 측정값이 도출되었다. 이는 내부 권선 등의 복잡합이 있지만 주축을 중심으로는 대칭적인 형상을 가지고 있어 중심축 정렬의 불확실성이 크지 않았기 때문이라고 판단되며, 동시에 제작한 관성 모멘트 측정장치의 유효성을 잘 나타내고 있다. 반면 모터 하우징의 경우 X축에 대한 질량 관성 모멘트는 단순한 형태이고 대칭에 가깝고 정확한 회전축의 위치가 존재하여 두 장치 간의 추정 값의 차이가 크지 않았으나, Y축과 Z축에 대한 값은 비교적 복잡한 형태이어서 회전중심을 정확히 일치시키기 어려운 불확실성 등의 영향으로 참고 값과 비교했을 때 각각 9.98 %와 11.15 %의 차이를 보인 것으로 판단된다.

이 연구에서 제작한 관성측정장치가 현을 이용한 진자형 장치보다 안정적으로 측정대상물체를 상판에 고정시킬 수 있었으며, 회전축을 유지하기 더 용이하였고 공간적 측면에서도 장점을 보였다.

4. 결 론

이 연구에서는 스파이럴 스프링을 활용하여 질량관성 모멘트를 측정하는 장치를 제작하고, 해당 장치의 성능을 이론 값을 추정가능한 물체의 측정을 통해서 검증하였다. 관성 모멘트 측정장치의 검증 시 대상물체의 질량, 초기 인가각도 등의 다양한 조건에서 측정 장치의 성능을 평가한 결과 관심 질량 범위내에서 1 % 이내의 정확도로 질량 관성 모멘트를 측정할 수 있었다. 이를 바탕으로 전기차 구동모터의 로터와 모터 하우징에 대하여 질량 관성 모멘트 값을 추정하였고, 이전 연구에서 진행한 현을 이용한 진자 시스템의 결과와 비교를 통해서 그 신뢰성을 확인하였다. 제작/검증한 관성 모멘트 측정장치는 현의 이용한 진자 시스템과 유사한 신뢰성으로 질량 관성 모멘트 값을 추정할 수 있음을 보였다.

이 연구에서 제안하는 관성 측정 장치는 기존의 현을 이용한 진자형 장치보다 측정 대상물을 더욱 안정적으로 고정할 수 있으며, 자유 운동을 용이하게 관측할 수 있도록 설계되었다. 현 기반 시스템에서는 측정 대상물의 회전축을 유지하기 어럽거나 비대칭 운동이 발생할 가능성이 있다. 반면, 이 연구에서 개발한 장치는 스프링을 활용하여 회전축을 명확하게 정의하고, 안정적인 1축 회전을 유지할 수 있도록 설계되었다. 따라서 측정 대상물의 불필요한 자유도가 제거되어 보다 정밀하고 재현성 높은 측정을 시행할 수 있으며 보다 작은 규모의 공간에서도 안정적인 회전 운동을 구현할 수 있어 실험 환경의 제약이 현저히 줄어든다. 결론적으로, 이 연구에서 제안하는 관성 측정 장치는 기존 장치의 한계를 보완하면서, 측정 신뢰성과 공간 효율성을 동시에 향상시킬 수 있었다.

향후 연구로 제작된 질량 관성 모멘트 장비의 구동부를 개선하여 편심에도 강건하게 측정이 가능하도록 할 예정이며, 장주기 측정이 원활할 수 있도록 베어링의 마찰을 감소시킬 수 있는 구동부의 설계와 감쇠를 고려한 측정장치 설계를 계획하고 있다.

Acknowledgments

이 연구는 한국연구재단의 지원을 받아 수행된 연구이며(NRF-2022R1A2C1006938), 이에 감사드립니다.

References

• Park, J., Kim, D., Lee, J., Hong, W., Kim, D.-H. and Ahn, J., 2022, A Study on Measurement of Mass Moment of Inertia of Rigid Bodies using Load Cell, Proceedings of the KSAS Spring Conference, pp. 569~571.
• Kim, K. R., Kang, H. W. and Shul, C. W., 2018, The Confidence Estimation of MOI Measurement Equipment using Uncertainty Analysis, Journal of Aerospace System Engineering, Vol. 12, No. 3, pp. 53~57.
• Won, G.-M., 2001, An Apparatus for Measure a Specification of Power Train a Vehicle, KR20010061158A, Korean Intellectual Property Office, Dajeon, Korea.
• Seo, K., Cho, S., Lee, H., Oh, J. and Kim, I., 2013, A Study on COG, MOI of Experimental Methods and CAD Model Methods, Proceedings of the KSNVE Annual Autumn Conference, pp. 785~786.
• Song, K.-S. and Choi, Y.-S., 2013, Field Measurement of the Center of Gravity and the Moment of Inertia of Railway Vehicles using Vibration, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 23, No. 10, pp. 878~884. [https://doi.org/10.5050/KSNVE.2013.23.10.878]
• Park, H. J., Joh, J. S. and Kim, K. U., 1998, Measurement of Mass Moment of Inertia of Rigid Bodies by Suspension Method, Proceedings of the Korean Society for Agricultural Machinery Summer Conference, pp. 7~13.
• Lee, J. J., Koo, S. O., Kim, J. U. and Lee, J. W., 2000, Measurement of Mass Moments of Inertia for Unmanned Target Drone, Proceedings of the KSAS Spring Conference, pp. 81~84.
• Lee, J. J., 2013, Experimental Determination of Mass Moments of Inertia for Tilt Rotor UAV(unmanned aerial vehicle), Proceedings of the KSAS Spring Conference, pp. 1005~1008.
• Chung, J. E. and Lee, S., 2016, Measurement of Inertia of Turbocharger Rotor in a Passenger Vehicle, Transactions of KSAE, Vol. 24, No. 1, pp. 33~38. [https://doi.org/10.7467/KSAE.2016.24.1.033]