축-굽힘 커플링을 고려한 균열보의 모드진동수 예측
© The Korean Society for Noise and Vibration Engineering
Abstract
This paper presents a frequency equation to predict the modal frequencies of a cracked beam considering axial-bending coupling. The effects of axial-bending coupling are considered for the compatibilities of axial displacement and rotational angle at the crack location. Neglecting all incident evanescent wave motions results in a unified closed-form frequency equation for any support types of a beam. The validity of the proposed frequency equation is demonstrated through the comparison to the numerical results from the finite element analysis and experimental data. The effects of axial-bending coupling become significant with respect to crack depth ratio when a bending modal frequency is in the vicinity of an axial modal frequency.
Keywords:
Beam, Crack, Modal Frequency, Axial-bending Coupling, Frequency Equation키워드:
보, 균열, 모드진동수, 축-굽힘 커플링, 진동수 방정식1. 서 론
구조물 건전성 감시(structural health monitoring)에서 균열이 보의 진동 특성에 미치는 영향에 대한 연구는 매우 활발히 진행되어 왔다(1~3). 보의 손상진단을 쉽고 저렴하게 할 수 있기 때문에 균열보의 모드진동수의 예측은 가장 많이 연구되어 온 주제 중 하나이다(2). 보에 발생한 균열은 질량을 변화시키지 않고 강성만 감소시키기 때문에 균열보의 모드진동수는 손상이 없는 보와 비교하여 작은 것으로 알려져 있다(1). 신뢰할 수 있는 균열 진단을 위해 균열보의 모드진동수를 정확하게 예측하는 것이 중요하다.
지금까지 균열보의 모드진동수를 예측하기 위해 많은 해석적 연구들이 수행되어 왔다(4~8). 대부분의 연구들은 1차 모드를 포함한 소수의 저차 굽힘모드에 대응되는 진동수를 예측하는 데 집중되어 있다. 일부 연구에서 횡방향 균열을 갖는 외팔보의 축-굽힘 커플링이 보의 진동특성에 미치는 영향을 다루었다(9~11). 여기서 균열은 파괴 역학에 기초하여 유도된 2×2 유연도 행렬(flexibility matrix)을 통해 모사된다. 유연도 행렬에서 두 개의 대각항은 각각 축과 굽힘 거동을 나타낸다. 나머지 두 개의 비대각항은 균열에 의해 유발되는 축-굽힘 커플링 거동을 나타낸다(9). 진동수 방정식은 균열보의 고유행렬의 행렬식으로 표현된다. 이 경우 보의 지점 조건에 따라 고유행렬의 행렬식이 달라지게 된다. 또한, 행렬식이 매우 복잡한 음함수 형태로 표현되므로 식의 동역학적 의미 이해가 매우 어렵다(12).
이 논문은 임의 지점을 가진 균열보의 진동수 방정식을 하나의 닫힌형태식으로 정식화한다. 입사 소멸파를 무시할 수 있는 경우, 제안된 진동수 방정식은 지점 조건에 대한 매개변수화를 통해 임의 지점에 대해 적용 가능하다(13). 축-굽힘 커플링은 균열에서 축방향 변위와 처짐각의 적합조건으로 나타낼 수 있다(14). 제안된 진동수 방정식의 타당성은 유한요소 해석과 실험 데이터의 결과와의 비교를 통해 나타내었다.
2. 정식화
2.1 스펙트럴 해와 기본 가정
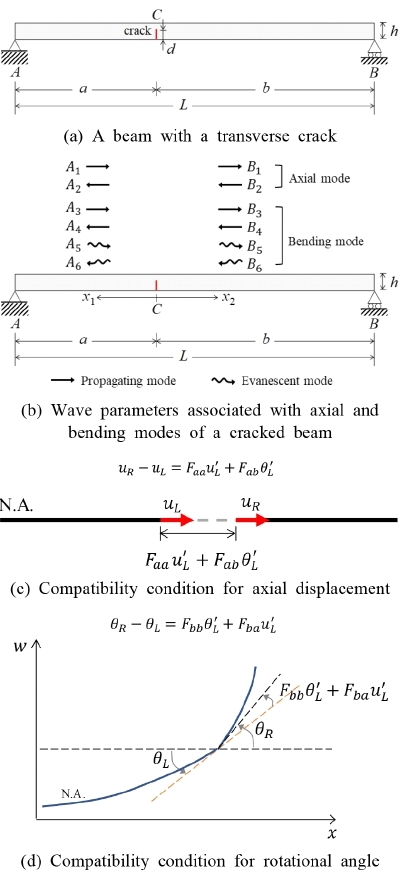
설명의 편의상 Fig. 1(a)는 임의 지점을 가진 균열보의 예로 단순 지지보를 나타낸다. 균열의 좌우측의 축방향 스펙트럴 변위는 각각 식 (1)과 같이 나타낼 수 있다(15).
| (1) |
여기서 uL, uR 그리고 k는 각각 균열의 좌우측에서 축방향 변위 그리고 보의 축방향 거동과 관련된 파수(wave number)이다. A1, A2, B1 그리고 B2는 축방향모드의 진행파를 나타낸다. 균열보의 횡방향 변위 또한 각각 다음과 같이 스펙트럴 해로 표현된다.
| (2) |
여기서 wL, wR 그리고 는 각각 균열의 좌우측에서 횡방향 변위 그리고 보의 굽힘방향 거동과 관련된 파수이다. A3, A4, B3, B4, A5, A6, B5 그리고 B6은 굽힘모드의 진행파와 소멸파를 나타낸다.
균열의 동적 거동을 모사하기 위해 국부 유연도를 모사할 수 있는 스프링을 사용한다. 두 개의 적합 조건식은 균열에 의해 생긴 축-굽힘 커플링을 모델링하는데 사용된다(14).
| (3a) |
| (3b) |
여기서 θL, θR 그리고 ′는 각각 균열의 왼쪽과 오른쪽에서의 처짐각 그리고 공간 미분 연산자이다.
| (4a) |
| (4b) |
| (4c) |
| (4d) |
여기서 ν는 푸아송비이고 식(3)의 유연도 계수인 Faa, Fab, Fbb 그리고 Fba는 Levy and Rice에 의해 제안된 축-굽힘 커플링 매개변수 att, abb 그리고 atb를 통해 나타낼 수 있다(14).
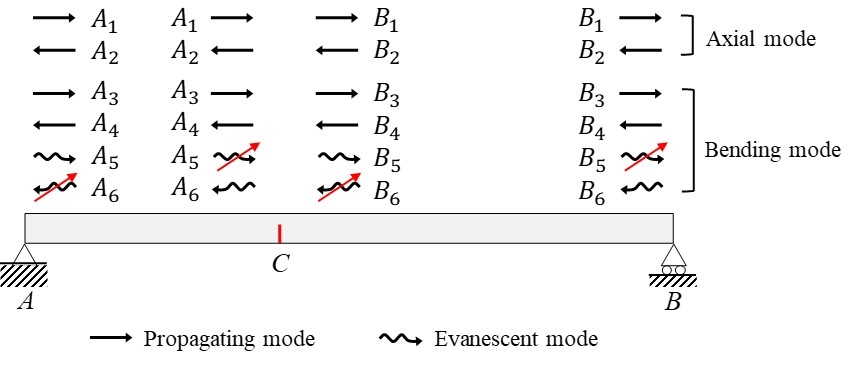
Fig. 2는 제안하려고 하는 진동수 방정식에서 균열보의 동적 거동을 근사화하는 방법을 나타낸다(13). 고주파수 대역의 경우 소멸파가 균열 또는 지점에 발생되는 즉시 소멸되기 때문에 다른 지점 또는 균열로 전파되지 않는다. 예를 들어 Fig. 2에서 지점 A에서 발생한 굽힘 소멸파 A5는 발생되는 즉시 소멸되기 때문에 균열 C로 입사되지 않는다. 따라서, 균열 또는 지점에서 모든 입사 소멸파는 무시할 수 있다. Fig. 2에서 입사 소멸파를 무시하면 지점 A에서 A6, 균열 C의 좌측에서 A5, 균열 C의 우측에서 B6, 지점 B에서 B5를 무시할 수 있다(13).
2.2 진동수 방정식 유도
식 (1)에는 4개, 식 (2)에는 8개의 미지수가 있다. 미지수가 총 12개이기 때문에 균열에서의 3개의 평형방정식과 3개의 적합방정식, 보의 양단 지점 조건 6개를 통해 진동수 방정식을 유도할 수 있다.
- (i) C에서의 축방향변위 적합조건식
| (5) |
여기서 오일러-베르누이보 이론에 기초하여 θ = w′이다. 미분연산자 ′는 균열의 왼쪽과 오른쪽에서 각각 와 를 의미하며 로 나타낸다. 식 (5)에서 소멸파 A5는 균열에 도달하기 전에 소멸되기 때문에 무시한다. 이 외의 조건식에도 동일한 절차를 적용한다.
- (ii) C에서의 횡방향변위 적합조건식
| (6) |
- (iii) C에서의 처짐각 적합조건식
| (7) |
- (iv) C에서의 축방향 평형방정식
| (8) |
여기서 E와 A는 탄성계수와 보의 단면적이다.
- (v) C에서의 횡방향 평형방정식
| (9) |
- (vi) C에서의 모멘트 평형방정식
| (10) |
여기서 I는 보의 이차 관성 모멘트이다.
- (vii) A에서의 축방향 지점조건
| (11) |
- (viii) A에서의 횡방향 지점조건
| (12) |
- (ix) A에서의 모멘트 지점조건
| (13) |
- (x) B에서의 축력 지점조건
| (14) |
- (xi) B에서의 횡방향변위 지점조건
| (15) |
- (xii) B에서의 모멘트 지점조건
| (16) |
식 (5) ~ 식 (16)을 이용하여 다음과 같이 진동수 방정식을 유도할 수 있다. 자세한 유도절차는 Kang의 논문에 나와 있으므로 여기서는 지면관계상 생략한다(12).
| (17) |
여기서,
| (18a) |
| (18b) |
| (18c) |
| (18d) |
| (18e) |
그리고, 이며 이다.
2.3 임의 지점 조건의 진동수 방정식
지점에서 발생하는 파 반사에 의한 축방향과 굽힘방향 전달파의 위상 변이에 따라 다음과 같이 를 매개변수화함으로써 식 (17)을 임의 지점 조건에 대한 진동수 방정식으로 적용 가능하다.
| (19a) |
| (19b) |
| (19c) |
| (19d) |
여기서 그리고 는 지점 조건에 따라 Table 1에 나타냈다. 파동 관점에서 매개변수화의 물리적인 의미에 관한 내용은 저자의 기존 연구에 자세히 기술되어 있다(13).
3. 제안된 진동수 방정식 검증
3.1 실험 구성
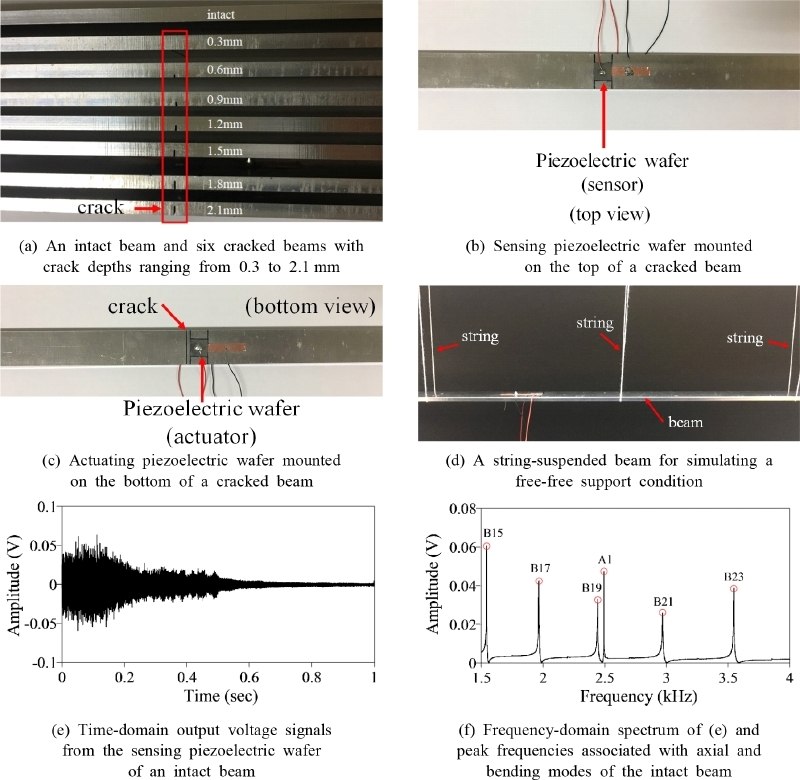
축-굽힘방향 커플링이 고려된 제안된 균열보의 진동수 방정식은 유한요소 해석 결과와 실험 데이터의 비교를 통해 검증한다. Fig. 3은 양단이 모두 자유단인 균열보의 형상을 나타낸다. 균열은 보의 중심에 위치하며 균열비는 0 ~ 0.7까지 0.1 간격으로 설정한다. 탄성계수, 푸아송비 그리고 밀도는 각각 71 GPa, 0.33 그리고 2700 kg/m3이다.
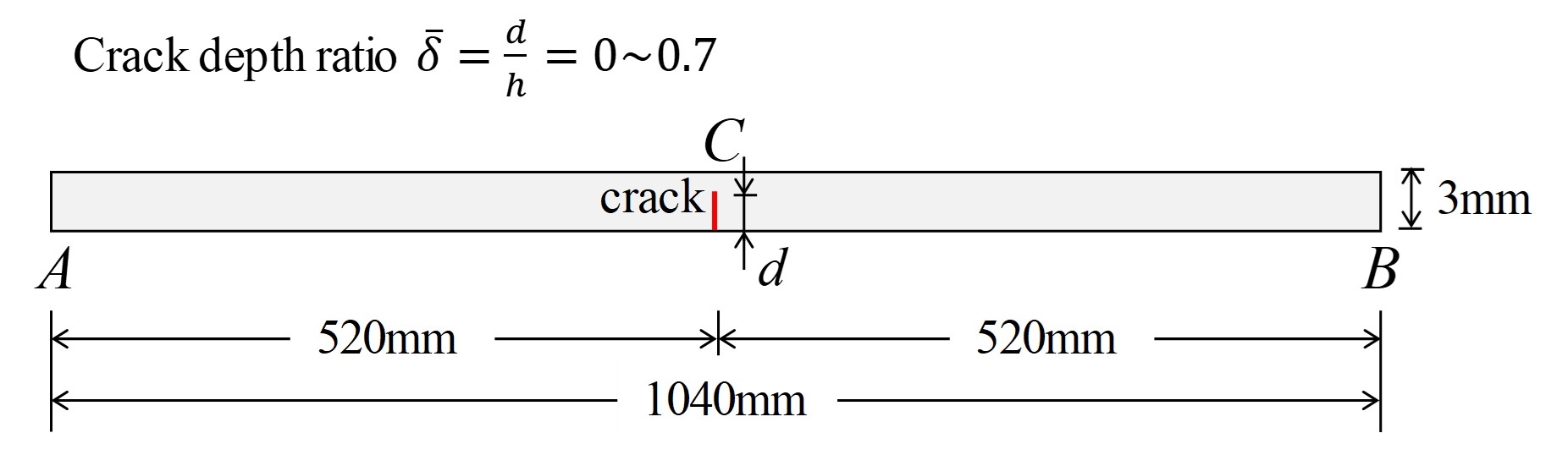
Geometry for a cracked aluminum beam with free-free support conditions (width: 20 mm / not to scale)
유한요소 해석은 KISTI 수퍼컴퓨팅 센터 신바람 시스템의 ABAQUS 6.14/standard에서 수행한다(16). 균열에 의한 모드진동수의 변화를 정확하게 계산하기 위해 충분히 유한요소망을 세분화한다. 개별요소 크기가 가로 세로 모두 50 μm로 총 1 248 000개의 8절점 2차원 고체 요소를 사용한다. 균열의 역학적 거동은 자유경계면인 균열면에 이중 노드를 생성함으로써 모사한다(13).
Fig. 4는 제안된 방법을 검증하기 위한 실험 구성이다. 1개의 그룹은 손상이 없는 보와 균열비가 0.1 ~ 0.7인 보 7개를 포함하는 8개의 보로 구성된다(Fig. 4(a)). 보의 중심에 있는 균열은 각각 원하는 깊이까지 0.3 mm 너비의 노치(notch)를 제작하여 모사한다. 각 보에 2개의 압전소자(Piezo Systems사의 PSI-5A4E L10 mm × T0.191 mm × W10 mm)(17)를 부착하고 피치-캐치(pitch-catch) 방법을 이용하여 보의 동적 응답을 수집한다. 신호감지 압전소자는 보의 상단 중심에 부착한다(Fig. 4(b)). 신호구동 압전소자는 보의 하단의 중심 균열로부터 8 mm 떨어진 곳에 부착한다(Fig. 4(c)). 양단 자유 지점 조건을 모사하기 위해 보를 실로 매단다(Fig. 4(d)). 구동 주파수 범위가 1 kHz ~ 20 kHz인 첩(chrip) 전압 입력 신호를 16 bit 임의 파형 발생기(NI PXI-5422)을 사용하여 압전소자에 가한다. 첩 전압 입력 신호의 지속시간과 진폭은 각각 0.5초와 6 V이다. 출력 전압 신호는 14 bit 고속 디지타이저(NI PXle-5122)로 측정한다. 샘플링 속도와 주파수 분해능은 각각 5 MHz와 1 Hz이다. 주파수 분해능을 결정하는 측정 시간은 주파수 관심대역의 보의 동적 거동이 감쇠하기에 충분하도록 1초로 설정한다. LabviewTM을 통해 자동으로 10번 반복 측정하여 신호감지 압전소자의 출력 전압 신호의 평균값을 구한다. 손상이 없는 보에 대한 평균 출력 전압신호의 예를 Fig. 4(e)에 나타냈다. 각 보의 주파수 응답 스펙트럼은 입력 및 출력 전압신호를 고속 푸리에 변환시킴으로써 구할 수 있다. 피크진동수는 주파수 스펙트럼을 통해 추출한다. 추출된 피크진동수와 관련된 모드들은 유한요소 해석을 통해 계산된 모드진동수와 비교하여 확인 가능하다(Fig. 4(f)).
3.2 비교 결과
Fig. 5는 축-굽힘 커플링을 고려하지 않은 진동수 방정식과 유한요소 해석 및 실험결과를 균열비에 대한 모드진동수로 비교한다. 진동수 방정식에서 균열비를 0.01씩 증가시키면서 모드진동수를 계산한다. 진동수 방정식이 비선형이므로 뉴턴랩슨법을 이용하여 진동수 방정식의 해를 구한다. Fig. 5(a)는 1차 축방향모드와 15차 ~ 23차 굽힘모드 9개중 홀수차 모드 5개를 포함하는 1.4 kHz ~ 3.6 kHz 범위에서 모드진동수를 보여준다. 여기서 실선과 점선은 각각 진동수 방정식을 통해 구한 축방향모드와 굽힘모드의 진동수를 나타낸다. 네모와 동그라미는 각각 유한요소 해석을 통해 계산된 축방향모드와 굽힘모드의 진동수를 의미한다. 엑스와 십자표시는 각각 실험을 통해 획득된 축방향모드와 굽힘모드의 진동수를 나타낸다. Fig. 5(b)에서 1차 축방향모드와 19차 굽힘모드를 포함하는 2.1 kHz ~ 2.7 kHz 범위로 좁혀서 모드진동수를 나타낸다. Fig. 5(b)의 모든 모드진동수는 균열비 0.4이하에서 유한요소 해석 및 실험결과와 비교할 때 최대 상대오차가 각각 0.7 %와 1.15 %가 발생한다. 균열비가 0.4보다 커짐에 따라 1차 축방향모드와 19차 굽힘모드에 대응되는 진동수는 유한요소 해석 및 실험결과와 비교할 때 차이가 크게 발생한다. 이 현상은 실험결과와의 비교에서도 명확하게 확인할 수 있다. 균열비가 0.7일 때 1차 축방향모드와 19차 굽힘모드에서의 최대상대오차는 유한요소 해석 결과와 비교할 때 각각 3.7 %와 3.0 %이고 실험결과와 비교할 때 각각 4.3 %와 2.7 %이다. 1차 축방향모드의 진동수는 손상이 없는 보의 19차 굽힘모드의 진동수보다 약간 크다. 균열비가 증가할수록 1차 축방향모드의 진동수는 19차 굽힘모드의 진동수보다 더 빨리 감소한다. 균열비에 대한 모드진동수의 감소율의 차이로 인하여 Fig. 5(b)에서 균열비 0.6 인근에서 1차 축방향모드와 19차 굽힘모드의 진동수가 서로 교차한다.
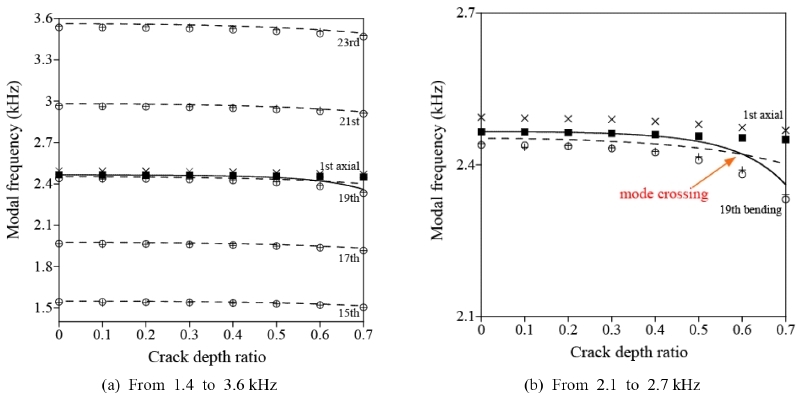
Modal frequencies from frequency equation without axial-bending coupling with respect to crack depth ratios(― : axial mode, ‒ ‒ – : bending mode, ■ : axial mode from FE analysis, ○ : bending mode from FE analysis, × : axial mode from experiment, + : bending mode from experiment)
Fig. 6에서 축-굽힘 커플링을 고려한 진동수 방정식과 유한요소 해석 결과를 균열비에 대한 모드진동수로 비교한다. 식 (17)은 모든 관심대역 모드에 대하여 유한요소 해석에서 계산된 진동수와 잘 일치한다. 1차 축방향모드의 진동수는 19차 굽힘모드의 진동수보다 균열비에 대해 천천히 감소하기 때문에 Fig. 5(b)와는 다르게 Fig. 6(b)에서는 진동수가 교차되는 현상이 발생하지 않는다. 균열비가 0.7일 때 1차 축방향모드와 19차 굽힘모드의 최대상대오차는 유한요소 해석결과와 비교하면 각각 0.3 %와 0.6 %로, 실험결과와 비교하면 0.4 %로 크게 감소한다. 이것은 굽힘모드의 진동수가 축방향모드의 진동수에 근접해 있을 때 균열비 증가에 따른 축-굽힘 커플링 효과가 모드진동수에 명백하게 나타남을 의미한다.
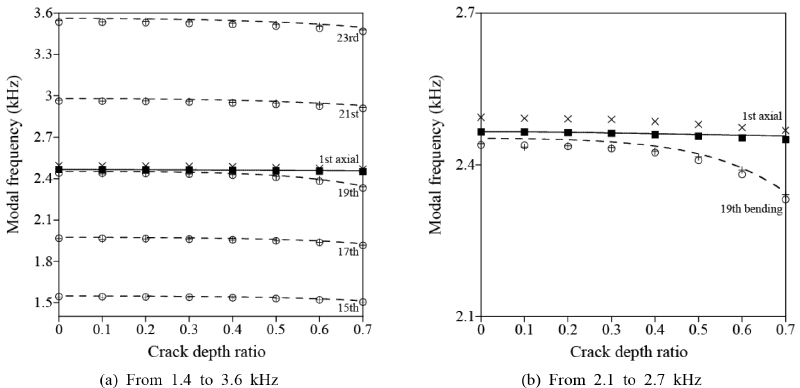
Modal frequencies from frequency equation with axial-bending coupling with respect to crack depth ratios(― : axial mode from Eq. (17), ‒ ‒ – : bending mode from Eq. (17), ■ : axial mode from FE analysis, ○ : bending mode from FE analysis, × : axial mode from experiment, + : bending mode from experiment)
Fig. 7은 축-굽힘 커플링을 고려한 경우와 그렇지 않은 경우의 1차 축방향모드와 15차~23차 굽힘모드 중 홀수차에 해당하는 정규화된 모드진동수를 유한요소 해석 및 실험과 비교한 결과이다. 여기서 정규화된 모드진동수는 균열이 있는 보의 모드진동수를 손상이 없는 보의 모드진동수로 나눈 값이다. 실선, 동그라미 그리고 엑스표시는 각각 식 (17)에서 얻은 정규화된 모드진동수, 유한요소 해석, 그리고 실험결과를 나타낸다. 점선은 축-굽힘 커플링을 고려하지 않은 순수 축방향모드와 굽힘모드의 정규화된 모드진동수를 나타낸다. 유한요소 해석 및 실험결과와 비교하였을 때 정규화된 모드진동수를 정확히 예측하기 위해 축-굽힘 커플링이 중요한 것을 확인할 수 있다. 균열비가 0.3일 때 정규화된 모드진동수에 대한 축-굽힘 커플링의 효과가 나타나기 시작한다. 균열비가 증가함에 따라 커플링 효과는 더욱 두드러진다. 1차 축방향모드보다 낮은 진동수를 가지는 15, 17, 19차 굽힘모드로 가면서 축-굽힘 커플링 효과가 증가함을 알 수 있다. 1차 축방향모드보다 큰 진동수를 가지는 21, 23차 굽힘모드에서는 축-굽힘 커플링 효과가 상대적으로 작게 나타난다.
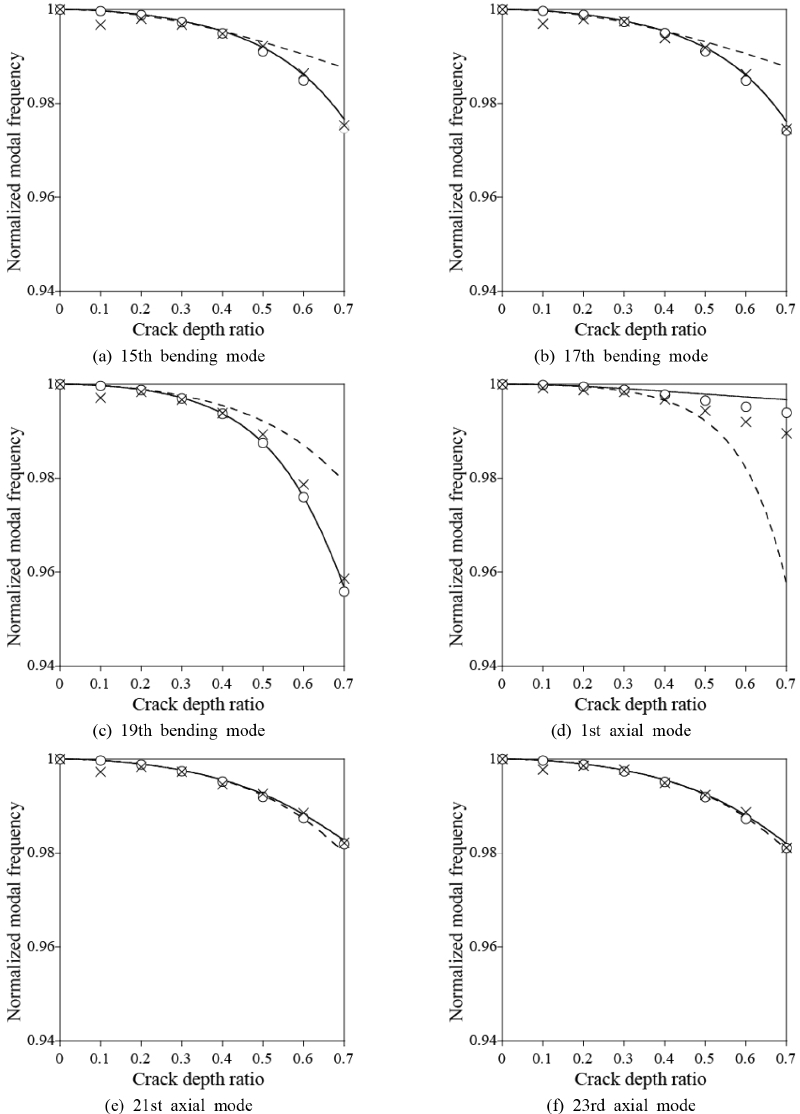
Normalized modal frequencies with respect to crack depth ratios(― : with axial-bending coupling, ‒ ‒ – : without axial-bending coupling, ○ : FE analysis, × : experiment)
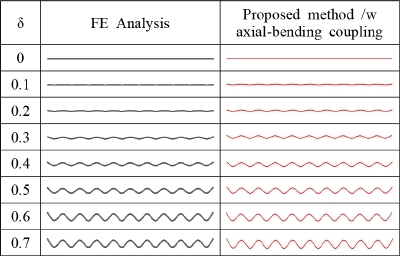
Fig. 8은 제안된 방법과 유한요소 해석에서의 균열비에 대한 1차 축방향모드의 형상을 비교한 것이다. 제안된 식 (17)을 통해 계산된 1차 축방향모드 진동수를 사용하여 2차원 모드 형상을 계산한다. 모드 형상은 모드형상벡터의 2-norm값이 1이 되도록 정규화한다. 모드 형상을 가독성을 높이기 위해 적절한 환산 계수를 사용해 크기가 조정된 모드 형태로 나타낸다. 제안된 방법은 유한요소 해석과 비교할 때 균열비에 대한 모드 형상의 변화를 정확하게 예측하고 있다. 균열비가 0.1보다 작은 경우, 모드형상에서 축 방향 거동이 지배적이다. 균열비가 0.2가 되면 굽힘 거동이 매우 작지만 모드 형상에 영향을 주기 시작한다. 균열비가 0.4보다 커지면 굽힘 거동이 1차 축모드 형상에서 지배적으로 나타난다. 축-굽힘 커플링의 효과를 균열비에 대한 1차 축 모드의 굽힘 거동의 변화를 통해 분명하게 관찰된다.
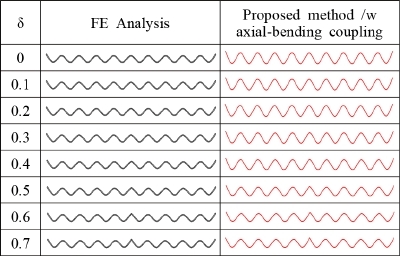
Fig. 9는 제안된 방법과 유한요소 해석에서의 균열비에 대한 19차 굽힘모드의 형상을 비교한 것이다. Fig. 8과 유사하게 모드 형상을 적절한 환산 계수를 사용해 크기가 조정된 모드 형태로 나타낸다. 제안된 방법은 유한요소 해석의 결과와 비교하여 균열비에 대한 모드 형상의 변화를 정확하게 예측한다. 균열비가 0.4보다 작은 경우, 모드 형상에서 규칙적인 굽힘 거동이 지배적이다. 반대로 균열비가 0.4보다 커질 경우, 균열 위치에서 꺾인 지점이 발생하기 시작하고 균열비가 0.7일 때 분명하게 나타난다.
4. 결 론
이 논문은 축-굽힘 커플링을 고려하여 임의 지점을 가진 균열보의 진동수 방정식을 하나의 닫힌형태식으로 제안하였다. 입사 소멸파를 무시할 수 있는 경우, 제안된 식 (17)은 지점 조건에 대한 매개변수화를 통해 임의 지점에 대해 적용 가능하다. 제안된 진동수 방정식은 균열이 중심에 있는 양단이 모두 자유단인 보를 사용하여 유한요소 해석 및 실험 데이터 결과와 비교하여 검증하였다. 진동수에 대해 비선형 방정식이기 때문에 진동수 방정식을 풀기 위해 뉴턴랩슨법을 사용하였다. 균열깊이가 증가함에 따라 축방향모드와 인접한 굽힘모드가 서로 간섭이 일어나는 경우에 모드진동수에 대한 축-굽힘 커플링 효과가 두드러지게 나타났다. 서로 인접한 축방향모드와 굽힘모드 사이의 축-굽힘 커플링 현상에 관해서 제안된 진동수 방정식에 의한 해석결과는 유한요소 해석 및 실험 결과와 잘 일치하였다. 축방향모드와 굽힘모드사이의 커플링은 세장비가 작은 경우 더 두드러지는 경향이 있다는 보고가 있다(10,11). 향후 고차보 이론인 티모센코 보 이론을 이용한 고주파 대역에서 축-굽힘 커플링 효과에 대한 추가 연구가 필요하다.
Acknowledgments
2장의 주요 내용은 제 1저자의 연구(12)를 기초로 작성되었음. 이 논문은 정부(교육과학기술부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업입니다(NRF-2016R1D1A1B03933260).
References
-
Dimarogonas, A. D., (1996), Vibration of Cracked Structures: A State of the Art Review, Engineering Fracture Mechanics, 55(5), p831-857.
[https://doi.org/10.1016/0013-7944(94)00175-8]

-
Salawu, O. S., (1997), Detection of Structural Damage through Changes in Frequency: A Review, Engineering Structures, 19(9), p718-723.
[https://doi.org/10.1016/s0141-0296(96)00149-6]

- Fan, W., and Qiao, P., (2011), Vibration-based Damage Identification Methods: A Review and Comparative Study, Structural Health Monitoring – An International Journal, 10(1), p83-111.
-
Morassi, A., 1993, Crack-induced Changes in Eigenparameters of Beam Structures, Journal of Engineering Mechanics, Vol. 119, No. 9, pp., (1993), Crack-induced Changes in Eigenparameters of Beam Structures, Journal of Engineering Mechanics, 119(9), p1798-1803.
[https://doi.org/10.1061/(asce)0733-9399(1993)119:9(1798)]

-
Ostachowicz, W. M., and Krawczuk, M., (1991), Analysis of the Effect of Cracks on the Natural Frequencies of A Cantilever Beam, Journal of Sound and Vibration, 150(2), p191-201.
[https://doi.org/10.1016/0022-460x(91)90615-q]

-
Liang, R. Y., Hu, J., and Choy, F., (1992), Theoretical Study of Crack-induced Eigenfrequency Changes on Beam Structures, Journal of Engineering Mechanics, 118(2), p384-396.
[https://doi.org/10.1061/(asce)0733-9399(1992)118:2(384)]

-
Shifrin, E. I., and Ruotolo, R., (1999), Natural Frequencies of a Beam with an Arbitrary Number of Cracks, Journal of Sound and Vibration, 222(3), p409-423.
[https://doi.org/10.1006/jsvi.1998.2083]

-
Kasper, D. G., Swanson, D. C., and Reichard, K. M., (2008), Higher-frequency Wavenumber Shift and Frequency Shift in a Cracked, Vibrating Beam, Journal of Sound and Vibration, 312(1), p1-18.
[https://doi.org/10.1016/j.jsv.2007.07.092]

-
Papadopoulos, C. A., and Dimarogonas, A. D., (1987), Coupled Longitudinal and Bending Vibrations of a Rotating Shaft with an Open Crack, Journal of Sound Vibration, 117(1), p81-93.
[https://doi.org/10.1016/0022-460x(87)90437-8]

- Papadopoulos, C. A., and Dimarogonas, A. D., (1988), Coupled Longitudinal and Bending Vibrations of a Cracked Shaft, Journal of Vibration, Acoustics, Stress, and Reliability in Design, 110(1), p1-8.
-
Dado, M. H. F., and Abuzeid, O., (2003), Coupled Transverse and Axial Vibratory Behaviour of Cracked Beam with End Mass and Rotary Inertia, Journal of Sound and Vibration, 261(4), p675-696.
[https://doi.org/10.1016/s0022-460x(02)01004-0]

- Kang, J. K., (2016), Predicting the Natural Frequencies of a Cracked Beam Considering Axial-bending Coupling from Wave Propagation Perspective, M.S. thesis, Dong-A University, Busan, Korea.
-
Park, H. W., (2017), A Simplified Frequency Equation and Its Approximate Solution of a Beam with an Incipient Crack from a Wave Perspective, Wave Motion, 75, p1-12.
[https://doi.org/10.1016/j.wavemoti.2017.08.001]

-
Levy, N., and Rice, J., (1972), The Part-through Surface Crack in an Elastic Plate, Journal of Applied Mechanics, 39(1), p185-194.
[https://doi.org/10.1115/1.3422609]

-
Doyle, J. F., (1989), Wave Propagation in Structures, New York, NY, Springer.
[https://doi.org/10.1007/978-1-4684-0344-2_6]

- S/W Resources, (2018), http://www.nisn.re.kr/eng/action.do?menuId=50007. (accessed January 6, 2018).
- PSI-5A4E PIEZOCERAMIC SHEETS and Their Properties, (2018), http://www.piezo.com/prodsheet1sq5A.html (accessed January 6, 2018).

Ji-Kang Kang received his B.S and M.S. degrees from Dept. of Civil Engineering at Dong-A University in 2015 and 2017, respectively. The title of his master thesis is “Predicting the natural frequencies of a cracked beam considering axial-bending coupling from wave propagation perspective.” He is working at Construction SW Business Department in MIDAS IT Co., Ltd.

Tae-Jeong Lim is a graduate student at Dept. of Civil Engineering at Dong-A University. Her recent research work is investigating the axial-bending coupling of a cracked beam in the high-frequency range through analytical approach and experimental work using surface-mounted piezoelectric wafers.

Hyun-Woo Park, His recent research interest is analytical and numerical investigation of electromechanical admittance of piezoelectric transducers mounted on a beam from wave propagation perspective. He is interested in investigating the change of vibration characteristics due to crack in a beam from a wave perspective as well.