그래핀 나노판 보강 다공 코어 샌드위치판의 진동 특성
© The Korean Society for Noise and Vibration Engineering
Abstract
This study investigates the free vibration characteristics of sandwich plates, which are composed of two isotropic faces and a porous core, using the analytical method based on the third order shear deformation theory. The core is reinforced uniformly by graphene nanoplatelet and composed of open or closed-cell foam with functionally graded pore distribution through the thickness direction. Four different porosity distributions are considered: a uniform and three functionally graded types. Comparison of the analytical results with the existing solutions in open literature and with those of finite element analysis (FEA) based on the shell element are made to verify the reliability of the presented analytical method. Characteristics of the open and closed-cell foams were investigated. Some numerical results are presented to check the influences of the weight fraction, geometry of the graphene nanoplatelet, porosity distribution, and porosity coefficient.
Keywords:
Graphene Nanoplatelet, Porosity Distribution, Functionally Grade Material, Free Vibration키워드:
그래핀 나노판, 기공 분포, 경사기능재료, 자유 진동1. 서 론
샌드위치 구조는 자동차, 항공/우주, 해양/조선 등의 많은 분야에 널리 이용되고 있다. 특히 하니컴 코어, 금속 폼 등과 같은 경량 코어를 갖는 샌드위치 구조는 기존의 전통적인 금속 구조에 비해 무게를 줄일 수 있다는 사실 때문에 많은 관심을 받아 왔다(1). 그러나 폼과 같은 다공성 물질의 코어에서 기공의 존재는 코어의 강성을 감소시킨다. 따라서 무게의 증가없이 다공 구조의 강성을 증가시키는 것은 매우 중요한 과제이다. 그래핀은 금속재료에 비해 높은 전기 전도도, 높은 열전도도, 저밀도 및 고강도 등과 같은 우수한 전기적, 열적 및 기계적 특성 때문에 지난 십 수년 전부터 탄소 나노 튜브와 더불어 차세대 나노 필러로 많은 관심을 받고 있다. 특히 그래핀 나노판(graphene nanoplatelet, GNP)은 넓은 표면적, 고강도, 저밀도 때문에 큰 보강 효과를 얻을 수 있어 판, 셸 등의 복합재료 경량 구조물 개발에 많은 기회를 제공한다. GNP 보강 다공성 재료를 샌드위치 구조의 코어로 사용함으로써 높은 굽힘강성을 갖는 고성능 경량 스마트 구조 요소로 이용할 수 있다. 또한 기공을 두께방향으로 연속적으로 변하도록 분포시킴으로써 두께방향으로 응력의 불연속이 없는 구조를 만들 수 있으며 강성을 조절할 수 있다. 이와 같은 다공성 경사 기능 구조물에 대한 정적/동적 해석을 통해 구조물의 특성을 향상시키기 위한 많은 연구가 진행되고 있다. Kitipornchai 등(2)은 외피가 없는 다공성 보에 대해 선형 진동 및 탄성 좌굴 특성을 연구하였으며, Setoodeh 등(3)은 다공 코어, 경사 기능 탄소 나노 튜브로 보강된 외피 및 압전층을 갖는 2중 곡면 스마트 샌드위치 패널에 대해 자유진동을 연구하였다. Adhikari 등(4)은 불균일 내평면 압축력에 의한 사각판의 좌굴특성을 연구하였다. Srikarun 등(5)은 3차 전단변형이론을 적용하여 샌드위치 보에 대해 선형/비선형 굽힘해석을 수행하였다. 한편 GNP로 보강된 다공판에 대해 Yang 등(6)은 사각판에 대한 좌굴 및 진동해석을, Ansari 등(7)은 후좌굴된 임의 형상의 판에 대한 진동특성을 연구하였다. GNP 보강 다공성 재료를 코어로 사용한 샌드위치 구조에 대해서도 일부 연구가 진행되고 있다. Tao 등(8)은 횡하중에 의한 원통형 패널의 후좌굴 거동을 분석하였다.
샌드위치판은 두께가 비교적 두꺼운 구조로 횡전단변형에 대한 특성을 얻기 위해 고전 판이론이나 1차 전단변형이론을 적용할 경우 3차원 평형방정식으로부터 추가적인 작업을 수행하여야 하는 번거로움이 있다. 그러나 고차 전단변형이론을 적용할 경우 추가 작업없이 횡전단 변형 특성을 얻을 수 있다. 다공성 폼에는 공기가 머무는 셀이 열려있는 개방형과 닫혀있는 폐쇄형이 있어 이전 연구들은 다공성 폼에 대해 개방형 또는 폐쇄형만을 한정적으로 다루었으며, 이들을 동시에 취급한 연구는 찾아볼 수 없다. 따라서 이 연구에서는 GNP 보강 다공 코어를 갖는 샌드위치판에 대해 3차 전단변형이론을 적용하여 진동 특성에 대해 연구하였다. 또한 다공 셀 폼에 대해 개방형 및 폐쇄형을 모두 고려하여 그에 따른 결과를 비교하였다. 해석에서 GNP는 모든 방향에 대해 균일하게 분포한다고 가정하였으며, 기공은 두께 방향으로만 연속적으로 변한다고 가정하였다. 또한 제안된 이론해석의 타당성을 검증하기 위해 ANSYS를 이용한 유한요소해석을 수행하여 그 결과를 비교/검토하였다. GNP의 무게비 및 형상비, 기공의 양 및 기공의 두께 방향 분포 형태 등이 진동 특성에 미치는 영향도 검토하였다.
2. GNP 보강 다공성 코어 샌드위치판의 수식화
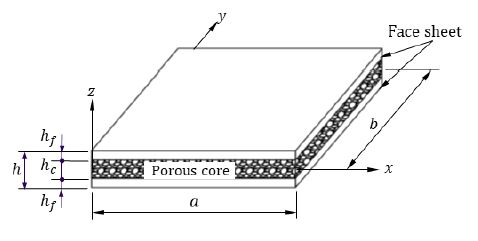
이 연구에서는 길이가 a, 폭이 b인 샌드위치 사각판을 고려하였다. 샌드위치판의 코어 두께는 hc, 각 외피의 두께는 hf로 총 두께는 h이다(Fig. 1). 외피는 등방성 재료로 구성되며, 코어는 외피와 같은 재료에 나노 크기의 GNP로 보강된 복합 재료이며 기공을 갖는 구조이다. GNP 보강 코어는 제조상의 이유로 적층 복합재료이다. 따라서 GNP 보강 다공성 코어의 각 층의 두께는 동일하며 각층에서의 기공은 균일하게 분포되기 때문에 각 층의 재료물성은 각 층의 중앙면에서의 물성으로 취할 수 있다.
각 층에서 GNP는 모든 방향에 대해 균일하게 분포되며, 무작위로 위치하게 된다. 기공이 없는 GNP 보강 복합재료의 유효 탄성계수(E1)는 Halpin-Tsai 모델을 근거로 Raffee 등(9)이 처음 제시하였으며, Kitipornchai 등(2)이 다음과 수정하였다.
| (1) |
| (2) |
여기서 Em, EG은 기저 및 GNP의 탄성계수이다. GNP의 기하계수 ξL, ξT는 식 (3)과 같다.
| (3) |
식에서 aG, bG 및 tG은 GNP의 길이, 폭 및 두께이다. 코어에 보강되는 GNP의 부피 비는 식 (4)와 같다.
| (4) |
여기서 wG은 GNP의 무게 비, ρG 및 ρm는 GNP 및 기저 재료의 질량 밀도이다.
GNP 보강 복합재료의 푸아송 비 및 밀도는 혼합법칙에 따라 식 (5), (6)과 같다.
| (5) |
| (6) |
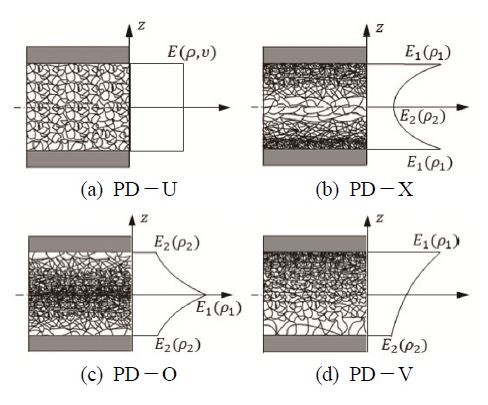
다공성 코어의 기공은 두께 방향으로 연속적으로 변한다. 이 연구에서 고려한 기공분포 형상은 총 4가지로 기공 분포가 균일한 것(PD-U)과 중앙면을 기준으로 대칭 분포된 것(PD-X, PD-O), 비대칭으로 분포된 것(PD-V) 등이다(2,5). 여기서 PD-X는 중앙면을 기준으로 기공이 작아지며, PD-O는 기공이 커지는 분포 패턴을 갖는다. PD-V는 기공이 상단 면으로 갈수록 작아진다(Fig. 2(2,5)). 두께방향으로의 기공 분포는 식 (7)에 따라 결정된다.
| (7) |
PD-U에 대한 분포함수 α는 개방형 및 폐쇄형 셀 폼에 따라 달라진다. 개방형 셀 폼에 대한 계수 α는 식 (8)과 같이 정의된다(10).
| (8) |
폐쇄형 셀 폼에 대해서는 식 (9)와 같이 된다(11).
| (9) |
여기서 Mt는 코어의 총 질량으로 모든 기공 분포에 대해 동일하며 식 (10)과 같이 계산된다.
| (10) |
유효 탄성계수는 개방형 및 폐쇄형 폼에 대해 다음과 같이 같은 형태를 갖는다(6,11).
| (11) |
여기서 e0은 다공성 계수로 다공성 코어의 최대/최소 탄성계수 (E1, E2)의 함수이다.
| (12) |
다공성 재료의 밀도는 개방형과 폐쇄형 폼에 따라 달라진다. 개방형 폼이 균일 분포된 경우에 대해서는 다음과 같다(10).
| (13) |
기타 다른 개방형 및 폐쇄형 폼의 기공 분포에 대해서는 다음과 같다(6,11).
| (14) |
여기서 em(z)은 질량 밀도 계수로 개방형 폼은 다음과 같이 다공성 코어의 최대/최소 밀도(ρ1, ρ2)의 함수로 두께 방향에 대해 일정하다.
| (15) |
그러나 폐쇄형 폼인 경우에는 다음과 같이 된다(12).
| (16) |
여기서 p(z)는 다음과 같이 정의된다.
| (17) |
한편 푸아송 비는 개방형 폼의 경우에는 식 (18)과 같이 두께 방향에 대해 일정하다(10).
| (18) |
그러나 폐쇄형 폼에 대한 푸아송 비는 두께 방향에 따라 식 (19)와 같이 변한다(12).
| (19) |
사각 샌드위치판에 대한 해석에서 횡전단변형과 회전 관성을 고려하기 위해 Reddy의 3차 전단변형이론을 적용하였다(13). 3차 전단 변형 이론으로부터 변위장(u, v 및 w는 x, y 및 z 방향 변위)을 다음과 같이 쓸 수 있다.
| (20) |
여기서 u0, υ0 및 w0는 중립면에서의 각 방향 변위이며, ϕx, ϕy는 y 및 x 축에 대한 회전을 나타낸다. 식에서 (,)는 다음에 나타나는 첨자에 대한 미분을 의미하며, c1=4/(3h2)이다.
사각판의 변형률은 내평면 변형률(ϵxx, ϵyy, ϵxy) 및 횡전단 변형률(γyz, γzx)로 구성된다.
| (21) |
샌드위치판의 k번째 층의 응력(σ)과 변형률(ϵ) 관계는 다음과 같다.
| (22) |
여기서 Q(k)는 축약 강성도이다.
판의 중립면에 대한 변위식을 다음과 같이 2중 급수로 표현할 수 있다.
| (23) |
식에서 Umn, Vmn, Wmn, Xmn, Ymn는 미지수로 결정해야 할 계수이며, wmn은 고유모드(m, n)에서의 고유 각진동수이다. 함수 Ψi(ξ), ζi(ξ)는 판의 경계조건을 만족하여야 한다. 이 연구에서는 모든 단이 식 (24)와 같은 조건을 갖는 고정 경계조건을 갖는다.
| (24) |
식 (23)에서의 변위함수는 다음과 같다.
| (25) |
| (26) |
여기서 i=m, n이며 ζ=x, y이다. 그리고 ai=βi/L(여기서 L은 판의 폭 또는 길이), βi는 파수(wave number)와 관계된 수, σi은 경계조건을 만족하는 계수이다.
판에 저장되는 총 에너지는 다음과 같다.
| (27) |
여기서 U는 샌드위치판의 변형에너지, T는 운동에너지로 각각 다음과 같다.
| (28) |
| (29) |
가정된 변위식 (23)을 총 에너지식 (27)에 대입한 후 Rayleigh-Ritz 정리에 적용하면 다음과 같은 고유치 문제가 된다.
| (30) |
여기서 K, M은 강성 및 질량행렬이며, d는 구하여야 할 계수행렬로 모드형상을 결정한다.
3. 수치해석 결과 및 토의
이 연구에서 고려한 샌드위치판의 외피는 구리, 코어는 구리를 그래핀 나노판으로 보강한 다공성 적층복합재료이다. 구리의 재료 물성은 Em = 130 GPa, υm= 0.34, ρm = 8960 kg/m3이며, GNP는 EG = 1.01 TPa, υG = 0.186, ρG = 1062.5 kg/m3이다. GNP의 크기는 aG = 2.5 μm, bG = 1.5 μm, tG = 1.5 nm이다(6). 판의 고유진동수는 다음과 같이 무차원화하여 수치결과를 제시하였다.
| (31) |
제안된 해석방법의 타당성을 검증하기 위해 외피가 없는 개방형 폼으로 구성된 다공성 판에 대한 기본 진동수를 참고문헌의 결과(6)와 함께 Table 1에 제시하였다. 표에 나타난 것처럼 참고문헌과 매우 잘 일치하고 있으며, 최대 차이는 1 % 미만이다.
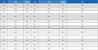
Dimensionless fundamental natural frequencies of GNP-reinforced porous open cell plate (a/b = 1, a/h = 20, hf = 0, wG = 1.0 %, e0 = 0.5).
또한 샌드위치판에 대해서는 ANSYS를 이용한 유한요소해석 결과를 이론해와 비교하였다. 이론 및 유한요소해석에서 샌드위치판에 대해 등방성재료인 외피의 적층수는 각 1개, 코어의 적층수는 수렴성 검토를 통해 39개로 하여 판의 총 적층수를 41로 하였다. 유한요소해석에서 적층 복합재료 판을 모델링하기 위해 1차 전단변형이론을 기초로 한 SHELL281 요소가 이용되었다. 이 요소는 8절점으로 구성되며, 절점 당 6개의 자유도(3개의 각 방향 병진운동 및 3축에 대한 회전운동)를 갖는다. 고려된 샌드위치판의 크기는 a⁄b = 1, hc = 0.8h, a/h = 20이며, 특별한 언급이 없는 한 이 기하 자료가 다음 수치 예에서 사용된다.
개방형 및 폐쇄형 폼 코어 샌드위치판에 대해 1차에서 5차까지의 무차원 고유진동수를 Table 2에 제시하였다. 표에 나타난 것처럼 고려된 모든 기공 분포에 대해 유한요소해석 및 이론해석 결과의 차이는 최대 1.6 % 미만으로 매우 잘 일치하고 있다. 한편 같은 다공성 계수를 갖는 조건에서 코어가 개방형 폼인 경우 폐쇄형 폼인 샌드위치판보다 약간 큰 고유 진동수를 갖지만 그 차이는 매우 작다. 따라서 고유 진동해석에서 다공성 코어를 개방형이나 폐쇄형 폼으로 가정해도 큰 차이는 없다고 할 수 있다. 기공분포 형태에 따른 기본 진동수의 크기를 보면 PD-X, PD-V, PD-U, PD-O의 순으로 나타난다. PD-X에서 가장 큰 기본 진동수를 보이는 것은 PD-X의 경우 판의 중립면으로부터 멀수록 재료가 많이 분포하게(기공은 적게) 되어 굽힘강성이 다른 분포형태보다 더 많이 증가하기 때문이다. 반대 현상으로 PD-O가 가장 작은 기본 진동수를 보인다.

Dimensionless natural frequencies of sandwich plate with GNP-reinforced porous core (wG = 0.5 %, e0 = 0.6).
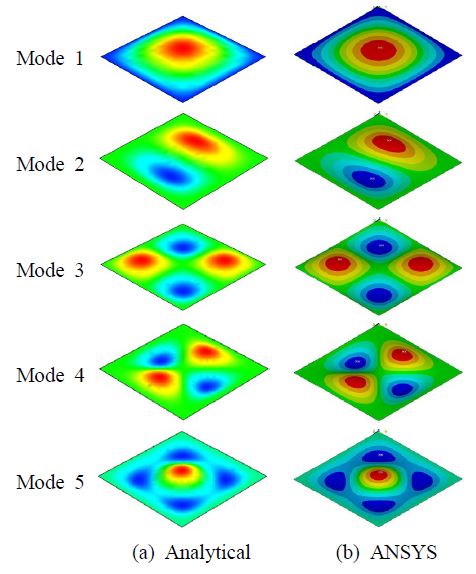
Fig. 3은 Table 2에서 고려한 폐쇄형 폼을 갖는 PD-U 샌드위치판에 대해 모드형상 및 무차원 기본 진동수를 유한요소 결과와 비교하였다. 그림에 나타난 것처럼 유한요소 및 이론 해석에서 얻은 모드형상도 매우 잘 일치하는 것을 볼 수 있다.
앞으로 제시되는 모든 수치예는 폐쇄형 코어를 갖는 샌드위치판에 대한 결과이다.
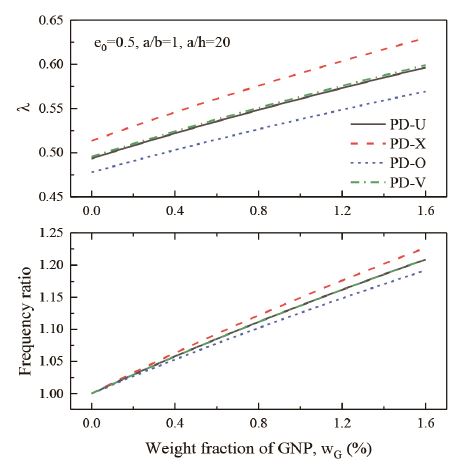
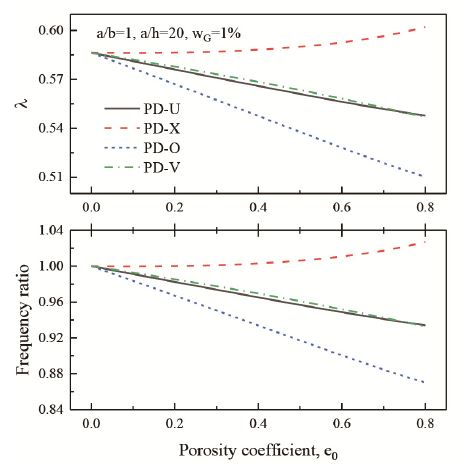
GNP의 무게비 wg가 기본 진동수에 미치는 영향을 알아보기 위해 Fig. 4가 제시되었다. 그림에서 진동수 비는 GNP 보강 판의 기본 진동수를 GNP가 없는 판의 기본 진동수로 나눈 값이다. 기본 진동수는 GNP양이 증가함에 따라 거의 선형적으로 증가한다. Table 2에서처럼 PD-X에서 가장 큰 GNP보강효과를 보이고 있으며, PD-O에서 가장 작은 보강효과를 보인다. 이는 GNP 증가에 따른 굽힘강성의 증가 때문에 나타나는 현상이다.
Fig. 5에서는 GNP 보강 샌드위치판에 대해 다공성 계수가 기본 진동수에 미치는 영향을 보여준다. 그림에서 진동수 비는 다공성 판의 기본 진동수를 기공이 없는 판의 기본 진동수로 나눈 값이다. 그림에서처럼 다공성 계수가 증가함에 따라 기본 진동수는 전반적으로 감소를 하지만 PD-X판은 오히려 증가한다. 다공성 계수가 커짐에 따라 다공성 판의 강성 및 질량은 모두 감소한다. 이때 기공분포 형태에 관계없이 질량 감소는 동일하지만 강성 감소는 그렇지 않다. PD-X를 제외한 다른 기공분포에서 굽힘강성 감소가 질량감소가 보다 크기 때문에 고유 진동수가 감소하는 경향을 보이며, PD-X의 경우에는 반대로 굽힘강성이 질량보다 적게 감소하여 고유 진동수는 증가하는 거동을 하게 된다.
PD-X 판에 대한 보다 자세한 거동을 보기 위해 여러 가지 외피 두께를 고려하여 다공성 계수에 따른 기본 진동수 변화를 Fig. 6에 제시하였다. 그림에서처럼 샌드위치판의 외피가 없거나 외피의 두께가 얇은 경우에는 다공성 계수 증가에 따라 기본 진동수가 감소를 하다가 계수의 어느 특정 값 이후에는 증가를 한다. 그러나 두께가 두꺼워지면 기본 진동수는 처음부터 증가한다. 이와 같은 현상은 외피의 두께가 얇아 질수록 코어의 두께는 증가하여 기공량의 증가에 따라 샌드위치판의 강성감소가 질량감소보다 크기 때문에 기본 진동수는 감소를 한다. 그러나 샌드위치판의 외피가 두꺼워지면 코어의 두께가 얇아져 다공성 계수 증가에 따라 강성감소보다 질량감소효과가 커지면서 반대로 기본 진동수는 증가를 한다. 또한 동일한 판 두께에 대해 외피의 두께가 두꺼워질수록 기본 진동수는 감소를 한다. 이와 같은 현상은 외피의 두께에 따른 강성 증가보다는 질량증가효과가 크기 때문에 나타난다. Figs. 5 ~ 6의 진동수 비에서 나타난 것처럼 다공성 계수에 따라 기본 진동수가 PD-O의 경우 최대 13 %정도 감소하지만 다른 기공 분포의 경우 약 4 %정도로 그다지 크지 않다. 이와 같이 코어에 기공을 주어 큰 기본 진동수의 변화없이 구조물의 질량을 줄일 수 있는 효과가 있다는 것이 주목할 만하다.
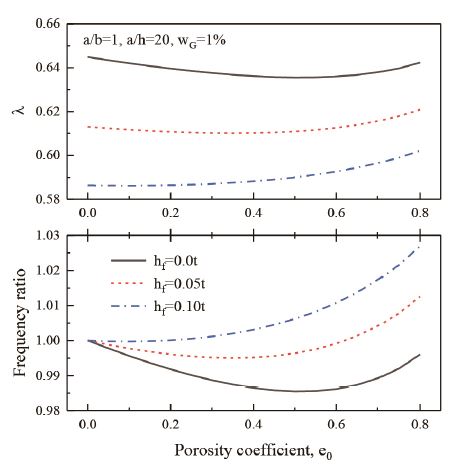
Effect of porosity coefficient e0 on fundamental frequency for sandwich plate with PD-X distribution
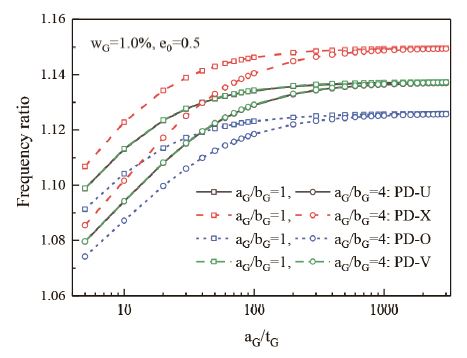
Fig. 7은 GNP의 두께 비(aG⁄tG)가 기본 진동수에 미치는 영향을 알아보기 위해 진동수비를 제시한 것이다. 여기서 진동수비는 GNP보강 판의 기본 진동수를 GNP가 없는 비보강 판의 기본 진동수로 나눈 값이다. 고려된 GNP의 두께 tG는 일정하다. 그림에서처럼 두께 비(aG⁄tG)가 커질수록 (GNP의 길이가 길수록, 또는 접촉면적이 클수록) 기본 진동수는 증가를 하며 어느 값 이상이 되면 기본 진동수는 거의 일정해 진다. 또한 GNP의 형상비(aG⁄bG)가 작을수록(GNP가 정사각형일 경우 직사각형보다 접촉면적이 커짐) 보다 큰 기본 진동수를 갖으며, 형상비가 클수록 두께비의 영향은 커져 진동수가 급격히 증가를 한다.
4. 결 론
이 연구에서는 그래핀 나노판으로 보강된 다공성 코어를 갖는 샌드위치판에 대해 진동 특성을 연구하였다. 해석을 통해 다음과 같은 결론을 얻었다.
(1) 동일한 다공성 계수를 갖는 조건에서 코어가 개방형 폼인 경우 폐쇄형 폼인 샌드위치판보다 약간 큰 고유 진동수를 갖으나 그 차이는 매우 작다.
(2) 같은 양의 재료를 이용할 때 기공을 판의 중앙면 쪽으로 많이 분포시킬수록 보다 큰 고유 진동수를 얻을 수 있다.
(3) 다공성 계수가 커질수록 기본 진동수는 전반적으로 감소를 하지만, PD-X 기공 분포의 경우 어느 계수이상에서는 기본 진동수가 증가한다. 이와 같은 현상은 외피의 두께가 두꺼울수록 명확히 나타난다.
(4) GNP양이 많아질수록 기본 진동수는 증가한다.
(5) 같은 양의 GNP로 보강할 때 기저재료와의 접촉면적이 큰 GNP를 적게 사용할 경우 접촉면적이 적은 GNP를 많이 사용할 때보다 기본 진동수는 커진다.
References
-
Park, H. S., Hwang, D. H. and Han, J. H., 2019, Experimental and Analytical Study on Shock Wave Transfer Characteristic of Honeycomb Sandwich Panel Insert, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 29, No. 3, pp. 389~395.
[https://doi.org/10.5050/KSNVE.2019.29.3.389]

-
Kitipornchai, S., Chen, D. and Yang, J., 2017, Free Vibration and Elastic Buckling of Functionally Graded Porous Beams Reinforced by Graphene Platelets, Materials and Design, Vol. 116, pp. 656~665.
[https://doi.org/10.1016/j.matdes.2016.12.061]

-
Setoodeh, A. R., Shojaee, M. and Malekzadeh, P., 2019, Vibrational Behavior of Doubly Curved Smart Sandwich Shells with FG-CNTRC Face Sheets and FG Porous Core, Composites Part B: Engineering, Vol. 165, pp. 798~822.
[https://doi.org/10.1016/j.compositesb.2019.01.022]

-
Adhikari, B., Dash, P. and Singh, B. N., 2020, Buckling Analysis of Porous FGM Sandwich Plates under Various Types Nonuniform Edge Compression Based on Higher Order Shear Deformation Theory, Composite Structures, Vol. 251, p. 112597.
[https://doi.org/10.1016/j.compstruct.2020.112597]

-
Srikarun, B., Songsuwan, W. and Wattanasakulpong, N., 2021, Linear and Nonlinear Static Bending of Sandwich Beams with Functionally Graded Porous Core under Different Distributed Loads, Composite Structures, Vol. 276, p. 114538.
[https://doi.org/10.1016/j.compstruct.2021.114538]

-
Yang, J., Chen, D. and Kitipornchai, S., 2018, Buckling and Free Vibration Analyses of Functionally Graded Graphene Reinforced Porous Nanocomposite Plates Based on Chebyshev-Ritz Method, Composite Structures, Vol. 193, pp. 281~294.
[https://doi.org/10.1016/j.compstruct.2018.03.090]

-
Ansari, R., Hassani, R., Gholami, R. and Rouhi, H., 2021, Free Vibration Analysis of Postbuckled Arbitrary-shaped FG-GNP-reinforced Porous Nanocomposite Plates, Thin-Walled Structures, Vol. 163, p. 107701.
[https://doi.org/10.1016/j.tws.2021.107701]

-
Tao, C. and Dai, T., 2021, Isogeometric Analysis for Postbuckling of Sandwich Cylindrical Shell Panels with Graphene Platelet Reinforced Functionally Graded Porous Core, Composite Structures, Vol. 260, p. 113258.
[https://doi.org/10.1016/j.compstruct.2020.113258]

-
Rafiee, M. A., Rafiee, J., Wang, Z., Song, H., Yu, Z. Z. and Koratkar, N., 2009, Enhanced Mechanical Properties of Nanocomposites at Low Graphene Content, ACS Nano, Vol. 3, No. 12, pp. 3884~3890.
[https://doi.org/10.1021/nn9010472]

-
Ashby, M. F., Evans, A., Fleck, N. A., Hutchinson, J. W., Wadley, H. and Gibson, L. J., 2000, Metal Foams: A Design Guide, Butterworth-Heinemann, Boston, MA.
[https://doi.org/10.1115/1.1421119]

-
Roberts, A. P. and Garboczi, E. J., 2001, Elastic Moduli of Model Random Three-dimensional Closed-cell Cellular Solids, Acta Materialia, Vol. 49, No. 2, pp. 189~197.
[https://doi.org/10.1016/S1359-6454(00)00314-1]

- Roberts, A. P. and Garboczi, E. J., 2002, Computation of the Linear Elastic Properties of Random Porous Materials with a Wide Variety of Microstructure, Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, pp. 189~197.
-
Reddy, J. N., 1990, A General Non-linear Third-order Theory of Plates with Moderate Thickness, International Journal of Non-.inear Mechanics, Vol. 25, No. 6, pp. 677~686.
[https://doi.org/10.1016/0020-7462(90)90006-U]


Young-Wann Kim received his Ph.D. degree from Chungnam National University in 1997. He is a professor of department of mechanical design engineering, Chonnam National University. His research interest includes the structural vibration & dynamics, and smart materials.