도로 수송에서의 컨테이너 화물 방진장치 연구

2.1 도로 수송에서 컨테이너 진동 PSD 측정

컨테이너 화물의 진동 특성을 파악하기 위해서 컨테이너 트럭을 천안-의왕 구간의 일반국도와 고속도로에서 운행하면서 진동을 측정하였다. 화물의 운송 시 발생하는 진동의 크기는 진동 PSD(power spectral density)로 나타내는 것이 일반적이며, 화물의 진동 충격 특성에 대한 시험 규격들에서도 대부분 해당 값을 이용하고 있다^(6,9). 컨테이너 내부 진동은 내부 바닥의 2개소의 3축 방향(길이, 횡, 수직 방향)으로 가속도센서를 부착하여 진동 이력을 측정하였다. 센서 및 데이터 저장장치는 Lansmont사의 Saver 9 × 30이었다.

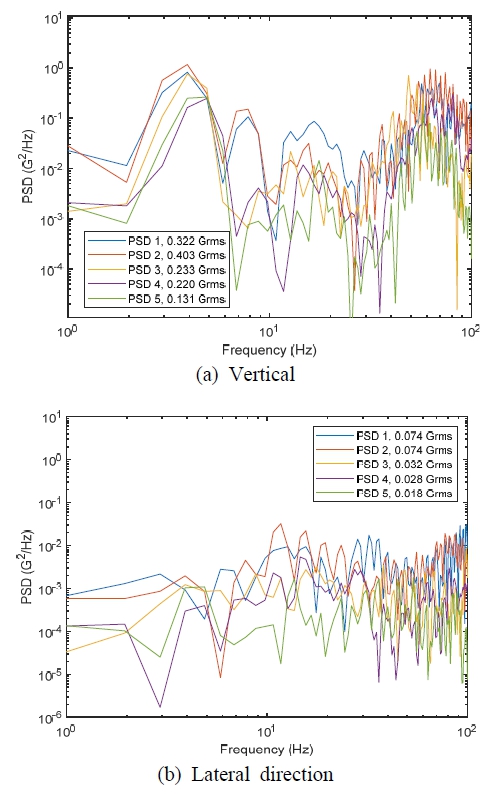
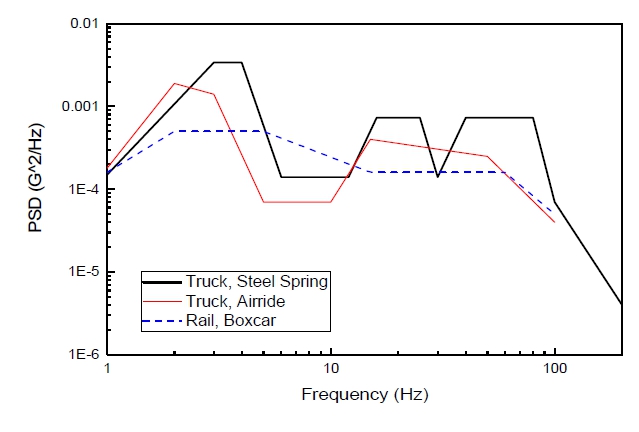
운송 구간에서 측정된 수직 및 횡 방향 PSD 중 큰 값을 가지는 것을 Fig. 1에 보였다. 리프 스프링으로 구성된 현가장치 위의 컨테이너 바닥 진동값이며, 차량 주행속도는 약 70 km/h ~ 80 km/h의 정상 운전 상황이었고 화물 무게는 0톤, 1톤, 5톤으로 각각 운행하였다. 수직 방향의 경우 대략 3개의 주파수 밴드(4 Hz, 15 Hz, 60 Hz 부근)로 나타나는 공진 현상이 관찰되는데, Fig. 2에 나타낸 ISTA(international safe transit association)가 제시하는 현장 측정값에서 볼 수 있는 것과 유사하다⁽¹⁰⁾. 이들은 저주파수 대역부터 순서대로 현가장치, 타이어, 차체 구조 공진으로 이미 알려져 있다⁽⁶⁾. 횡 방향의 경우는 수직 방향보다는 뚜렷한 공진 주파수를 보이지 않으며 그 크기도 작다. 여기에 보이지 않았으나 길이 방향의 경우는 횡 방향과 그 크기와 경향이 유사하였다.

Fig. 1

Measured PSD

Fig. 2

Field measurement levels presented by ISTA

Fig. 2의 ISTA 트럭 진동 프로파일(truck, steel spring)과 비교하면, 횡 방향 및 길이 방향 진동 측정 이력은 크기가 유사하지만 수직 진동은 전체적으로 크기가 더 크다. 이는 국가마다, 운송 경로마다 도로 건설 및 유지보수 상황 등이 다르기 때문으로 여겨진다⁽¹⁰⁾.

특히, Fig. 2에서 에어스프링이 적용된 저진동 트럭(truck, airride)은 총합 레벨로 0.136 Grms이며, 일반적인 강철 스프링이 적용된 트럭(truck, steel spring)의 0.242 Grms으로써, 저진동 트럭 진동이 대략 50 % 작다고 알려진 것과 같다.

한편, 천안-의왕 측정 구간에서 수직 진동의 최대 변위는 약 70 mm이었다. 이상의 측정된 PSD를 3절의 방진장치 설계 및 해석에서 입력값으로 이용하였다.

3.1 컨테이너 방진장치 설계 및 해석

도로 운송 시 측정된 수직 방향의 진동 데이터를 보면 충격성의 진동으로 주요 주파수는 약 4 Hz의 저주파수임을 알 수 있다. 일반적인 1-자유도 시스템의 진동 전달율 T_d는 식 (1)과 같다⁽²⁾.

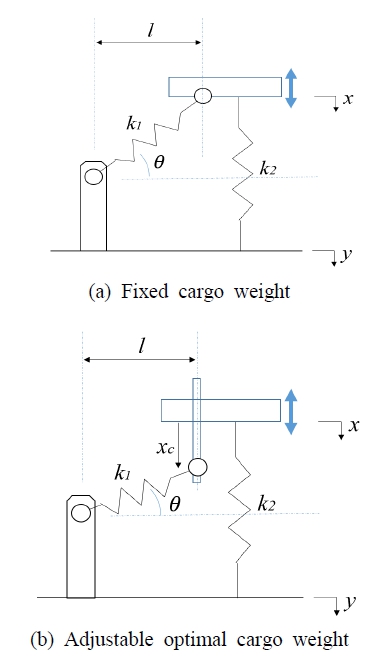
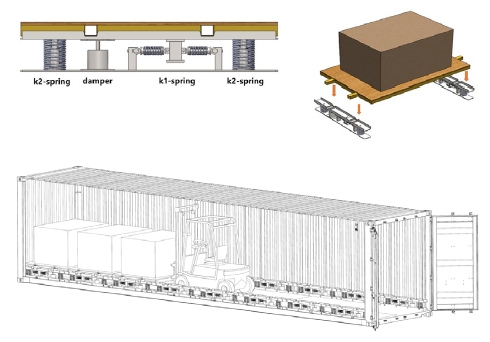
여기서 r은 주파수와 고유진동수의 비, ζ는 감쇠율이다. 따라서 방진 시스템의 강성을 작게 하고 감쇠(damping)를 크게 하는 설계가 필요하지만, 큰 중량의 화물에 대한 하중 지지를 위해 강성이 충분해야 하는 상황과 대치된다. 예를 들어 화물 무게 2톤, 강성 10 N/mm, 댐핑 2 E + 7 Ns/mm일 때, 4 Hz에서 진동 전달률 0.32이지만 화물 무게에 따른 처짐량은 980 mm로 과다하며, 실제 컨테이너에 적용하기 어렵다. 기존의 저진동 트럭에서는 일반적인 코일 또는 고무 스프링을 적용하지 않고 에어 스프링을 이용하되 공기압을 조정하여 이러한 문제를 해결하였으며, 화물 적재함에 에어 스프링을 적용하고자 한 사례도 있다^(3,4). 그러나 에어 스프링에서는 공기압력을 전기 또는 엔진 동력으로부터 에어 컴프레서를 작동하여 발생시키며, 공기압력을 조절하여 지지 하중을 조정할 수 있다. 반면에 공기가 누설될 수 있어서 압력이 일정 이하로 떨어지면 컴프레서가 작동하여 보충하여야 한다. 즉, 에어 스프링에서는 외부 동력이 필요하며 컴프레서, 어큐뮬레이터, 에어밸브 블록 등 추가적인 부품들로 인하여 구조가 복잡하고 정비가 어렵다. 또한 제작 비용이 높고 에어호스, 벨로즈 고무 등의 노화로 인한 내구성이 비교적 좋지 않다. 또한 밀폐형 에어 스프링의 경우에도 주기적인 공기 주입과 유지보수가 필요하다. 이러한 사항은 도로 이외의 철도, 해운의 장거리, 장기간 수송하는 화물에 적용하기 어려우며 물류비 상승을 초래하기도 한다. 따라서 이 논문에서는 Fig. 3에서와 같이 에어 스프링 없이 코일 스프링의 최적 배치로 화물 하중을 지지하면서 저주파수 대역의 진동을 저감하기 위한 장치를 제안하였다. 이하 해당 장치를 MSNS(multi-spring nonlinear suspension)라고 칭하기로 한다.

Fig. 3

Schematic of MSNS devices

Fig. 3(a)에서 x와 y는 각각 화물과 컨테이너 바닥의 변위를 나타낸다. 또한 강성 k₁과 k₂인 스프링이 각도 θ와 수직으로 배치되며, 하중이 0일 때 θ와 x변위를 θ₀와 x₀라고 표시하고, θ=0으로 k₁스프링이 수평일 때 x=0이라고 한다. 스프링들에 의하여 화물에 작용하는 수직 방향 힘 F_v는 식 (2)와 같다⁽²⁾.

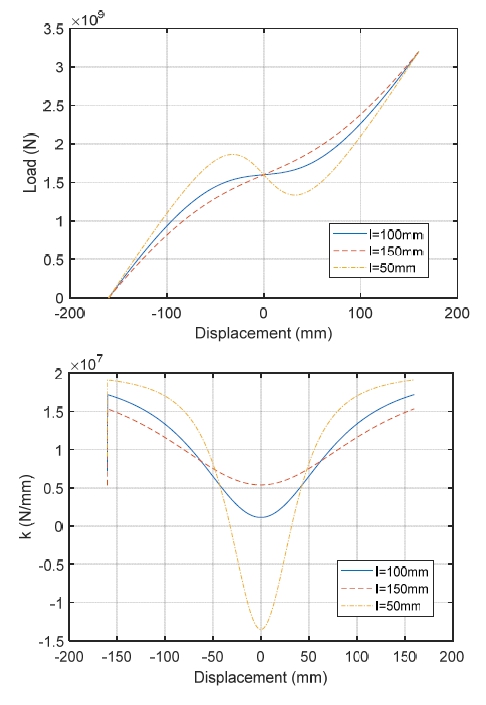
여기서, z는 x-y로 화물 상판과 컨테이너 바닥의 상대 변위이고, l₀는 k₁스프링의 초기 길이로서 $$ \sqrt{\left(x_0^2+l^2\right)}$$에 해당한다. 식 (2)를 이용하여 x₀가 -160 mm, l이 100 mm, 150 mm, 50 mm, k₁과 k₂가 모두 1E + 7 N/mm일 때의 하중-변위 및 강성-변위 그래프를 나타내면 Fig. 4와 같다. l이 100 mm인 경우 초기 변위에서는 강성이 크다가 변위가 증가할수록 강성이 작아지며 x=0 지점을 지나면 다시 강성이 커짐을 볼 수 있다. 이러한 특성은 에어 스프링의 하중-변위 곡선과 유사하다. 즉, x=0 부근의 변위를 작동 범위로 하여 고유진동수를 작게 하고 저주파수 대역의 방진 성능을 높이면서 비교적 큰 하중을 지지하는 것이 가능함을 알 수 있다.

Fig. 4

Calculated load & stiffness values varying the displacement x

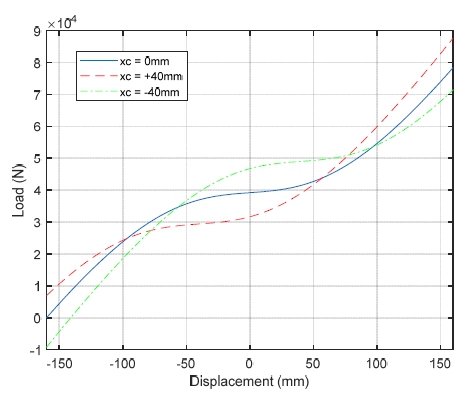
반면에 l이 50 mm인 경우 음의 강성(negative stiffness) 값을 가지고 불안정해지는 영역이 있으며, l이 150 mm인 경우 최소 강성이 l이 100 mm인 경우보다 더 커짐을 알 수 있다. 이러한 방진장치는 최적의 방진 성능이 발휘되는 하중의 크기가 고정되는 단점이 있다. 예를 들어 l이 100 mm인 경우 최적 성능을 내는 하중은 약 1.6 E + 9 N이다. 따라서 Fig. 3(b)와 같이 k₁스프링의 피봇 높이(x_c)를 수동 조절하여 화물 무게에 따라서 최적 하중을 조정할 수 있도록 하였다⁽¹¹⁾. 수직 방향 힘 F_v는 식 (3)과 같이 나타낼 수 있다.

여기서 x₀는 하중이 0이며 x_c가 0일 때 화물 상판의 변위임이 주의 된다. 식 (2)와 식 (3)의 마지막 항을 비교하면 화물 무게 변화에 따라서 피봇 높이(x_c)를 조정하여 정적 평형 상태를 k₁스프링이 수평인 상태(θ=0)로 맞출 수 있음을 확인할 수 있다. Fig. 5에 x_c가 변경될 때 하중과 변위 곡선을 나타내었으며, 여기서는 k₁과 k₂는 각각 325 N/mm와 245 N/mm이다. x_c가 +40 mm, 0 mm, -40 mm이면 강성 및 고유진동수가 최소가 되는 최적 하중은 각각 약 30 kN, 40 kN, 50 kN로 조정됨을 볼 수 있다. 식 (2)와 식 (3)에서 볼 수 있듯이 비선형 스프링 힘 때문에 진동 전달률의 이론 해를 직접 구하기 어려우며, 선형 시스템에서의 중첩 원리(superposition principle)도 적용되지 않는다. 그러나 시스템 특성에 대한 이해를 위해 비선형 힘 성분을 테일러 시리즈(Taylor series)를 이용하여 식 (4)와 같이 세제곱 함수로 근사하고 근사 해(approximate solution)를 구해볼 수 있다⁽⁸⁾.

Fig. 5

Calculated load-displacement values varying xc

여기서, x_c=0일 때이고, f₀=k₂x₀는 정적 항이며, K₁=k₂-k₁(l₀/l-1)와 K₃=k₁l₀/2l³이다. 실제로는 운송 중의 진동은 광대역 랜덤 가진으로 주어지지만, 문제를 간단히 하기 위하여 컨테이너 바닥에 Ycosωt로 조화 가진(harmonic excitation) 된다고 가정하면 운동방정식은 식 (5)와 같다.

여기서, m은 화물 질량이며, c는 k₂스프링과 같이 수직으로 설치되는 감쇠기의 감쇠상수이다. 또한 화물 무게 (mg)와 f₀가 같아서 정적 항들이 제외된다고 가정하고 동적인 성분들만 나타내었다. 식 (5)를 무차원화 시키면 식 (6)과 같다.

여기서, $$ \widehat{z}=z/Y$$, $$ {\omega }_0^2=k_2/m$$, ζ=c/2mω₀, r=ω/ω₀, τ=ω₀t, (ㆍ)’=d(ㆍ)/dτ이고, α=K₁/k₂, γ=K₃/k₂이다. ω₀는 k₂만의 고유진동수이다. 식 (6)은 더핑 식(Duffing equation) 또는 더핑 진동자(Duffing oscillator)로 알려져 있다. 조화균형법(harmonic balance method)을 적용하여 해를 $$ \widehat{z}=\widehat{Z}\mathrm{c}\mathrm{o}\mathrm{s}\left(r\tau +\varphi \right)$$로 가정하고 cos(3rτ)를 포함한 항을 무시하면, 식 (7)과 같이 r²에 대한 2차 방정식을 얻을 수 있고, 결국 r과 $$ \widehat{Z}$$의 관계를 나타내는 해를 구할 수 있다^(8,12). 또한 진동 전달률 T_d는 식 (8)로 구할 수 있다⁽⁸⁾.

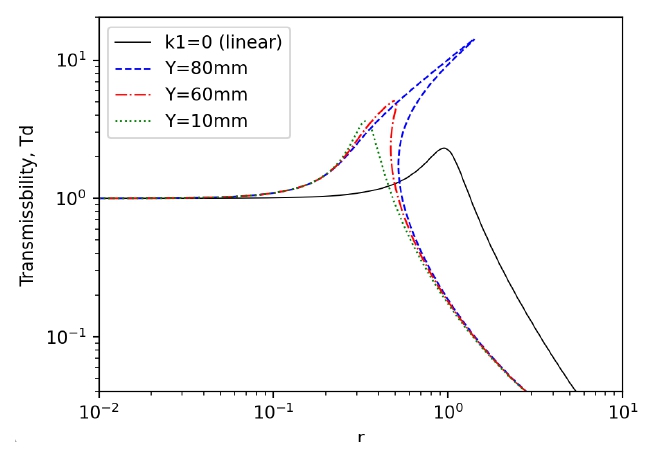
Fig. 6에 컨테이너 바닥 진동 진폭의 변화에 따른 T_d 계산 결과를 나타내었다. k₁과 k₂는 각각 162.3 N/mm과 122.5 N/mm이며, l은 120 mm, l₀는 200 mm, m은 2 t, ζ=0.05이다. 또한 식 (1)에 보인 k₁스프링이 없는 상태(k₁=0)의 선형 방진장치 경우를 함께 나타내었다.

Fig. 6

Transmissibility for different amplitudes of excitation Y and for ζ = 0.05

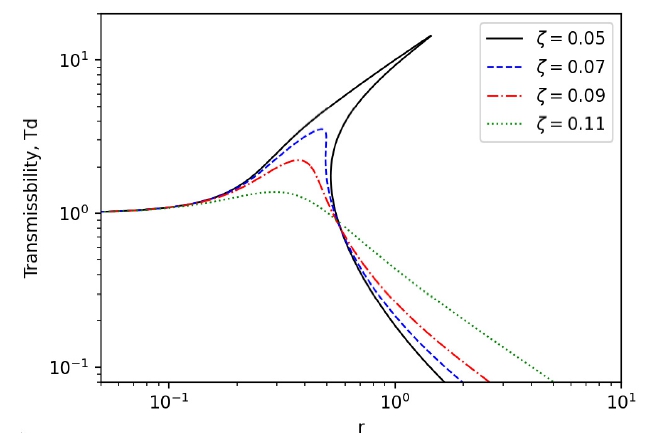
선형 식과 달리 비선형 식에서는 바닥 진동 진폭 Y의 크기에 따라서 서로 다른 전달률이 나타나는 것을 볼 수 있다. MSNS의 경우에 전달률이 1보다 작아지는 주파수가 선형 장치(k₁=0)에 비하여 더 낮아짐을 볼 수 있다. 그러나 진폭이 약 60 mm 이상으로 큰 경우에는 점프업(jump-up) 및 점프다운(jump-down) 주파수가 존재하는 것을 알 수 있으며, 진폭 Y = 80 mm의 경우에 r이 각각 0.5와 1.3일 때에 해당한다. 이것은 더핑 식의 특징으로 알려져 있다⁽¹⁰⁾, 바닥 진폭 80 mm로 동일한 상태에서 감쇠비 ζ가 변화될 때의 전달률을 Fig. 7에 나타내었다. 감쇠비가 증가하면 점프업 및 점프다운 주파수가 나타나지 않으며 r = 0.3 ~ 0.4 부근에서 전달률이 1로 근접하게 되지만 그보다 더 큰 주파수 영역에서 전달률이 다소 증가하는 것을 볼 수 있다. 따라서 이 컨테이너 방진장치에서 점프업 및 점프다운이 발생하지 않으면서 저주파수 대역의 전달률 증폭을 막기 위해서 적절한 감쇠비를 가지는 감쇠기의 설치가 필요함을 알 수 있다. 반면에 외부 가진 주파수가 점프다운 주파수보다 더 큰 범위에만 있는 방진장치의 설계에서는 감쇠기가 필요하지 않을 수 있다.

Fig. 7

Transmissibility for various values of damping ratio ζ and for Y = 80 mm

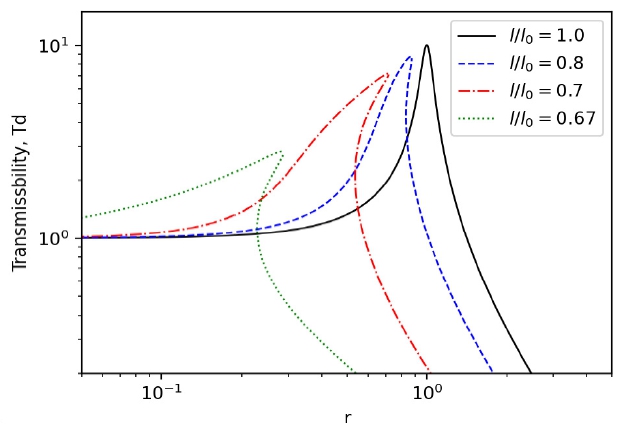
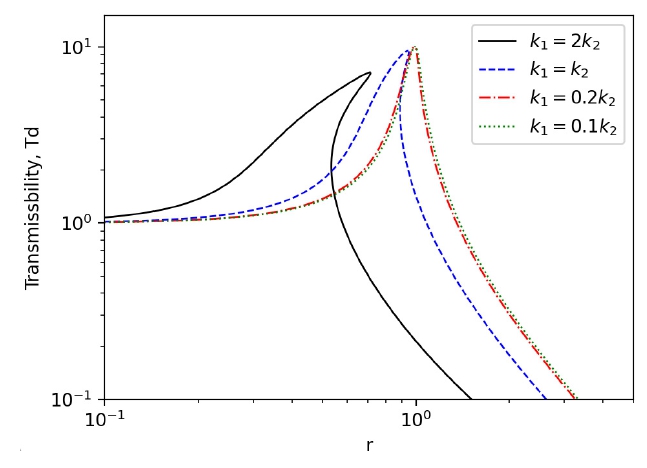
다른 파라미터를 고정하고 k₁스프링의 자유 길이 대비 수평 위치에서의 길이의 비 l/l₀를 변화하였을 때의 전달률을 Fig. 8에 나타내었다. l/l₀가 1에 가까워질수록 r=1(k₂스프링에 의한 고유진동수)에서 공진 특성이 나타나며 r>1에서 전달률이 커짐을 알 수 있다. k₁스프링의 강성 변화에 대한 비교 결과인 Fig. 9에서는 k₁이 커질수록 전달률이 1이하인 방진 주파수 영역이 커지는 것을 볼 수 있다. 그러나 비선형 특성이 커지므로 점프업 및 점프다운이 발생하게 되는 것을 볼 수 있다. 결국, l/l₀를 작게 하고 k₁을 크게 하여 방진 주파수 영역을 확보하되 적절한 감쇠비를 가지도록 하여야 한다.

Fig. 8

Transmissibility for various ratios of l/l0 and for k1 = 2k2, Y = 80 mm, ξ = 0.05

Fig. 9

Transmissibility for various ratios of k1/k2 and for l/l0 = 0.7, Y = 80 mm, ξ = 0.05

이상과 같이 MSNS 시스템을 더핑 식으로 근사화하고 이론 해를 살펴본 사항들은 중첩 원리가 적용되지 않기 때문에 실제 도로 운송 중의 다양한 주파수 성분들이 동시에 가진되는 상황에서 다소 다른 결과가 나올 수 있음이 주의된다. 그러나 방진 시스템의 특성을 이해하고 파라미터의 의미를 파악하는데 도움이 될 수 있다.

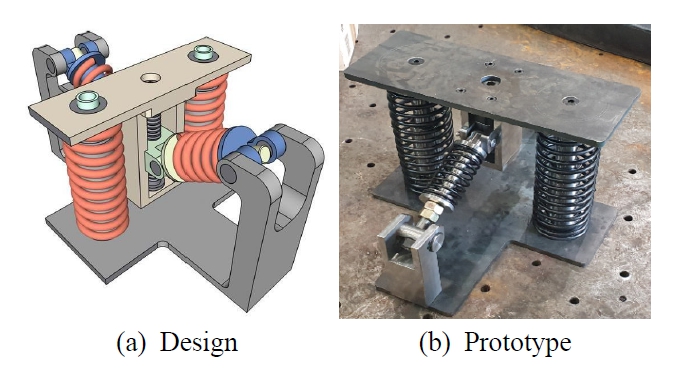
MSNS 개념을 기반으로 방진 마운트를 설계하고 초기 시험품을 제작한 사항을 Fig. 10에 나타내었다. 방진 마운트는 상부프레임, 하부프레임, 그리고 이 둘을 연결하는 코일 스프링들로 구성된다. k₁스프링부는 상부프레임의 중앙 블록에 상부링크, 하부프레임의 측면블록에 하부링크가 연결된 구조이다. 프레임과 연결은 피봇으로 체결되어 있다. 상부링크와 하부링크는 슬라이더(slider) 방식으로 연결되며 그 사이에 k₁ 스프링이 위치한다. 한편, 상부프레임 상판과 하부프레임 하판 사이에는 슬라이더 방식의 봉에 k₂스프링이 수직으로 위치한다. k₁스프링이 연결된 중앙 블록은 상부프레임에 스크류를 이용하여 위아래로 위치가 조절될 수 있으며, 화물 무게에 맞추어 스크류 상부의 무두볼트를 돌려서 k₁스프링이 수평이 되도록 조정하게 된다. 한편, Fig. 1에서 본 바와 같이 횡 방향 및 길이 방향의 진동은 수직 방향의 진동보다 매우 작으며 고주파수 성분이 주요하고, 또한 수직 방향과 달리 화물 하중이 수평으로 걸리지 않는다⁽²⁾. 따라서 수평 방향의 방진은 수직 방향과 비교하여 수월한 편으로서, 이 논문에서는 상부프레임과 화물 상판의 결합부에 고무 부싱을 설치하여 해당 방향 진동 저감이 되도록 하였다.

Fig. 10

Design and prototype of MSNS mount

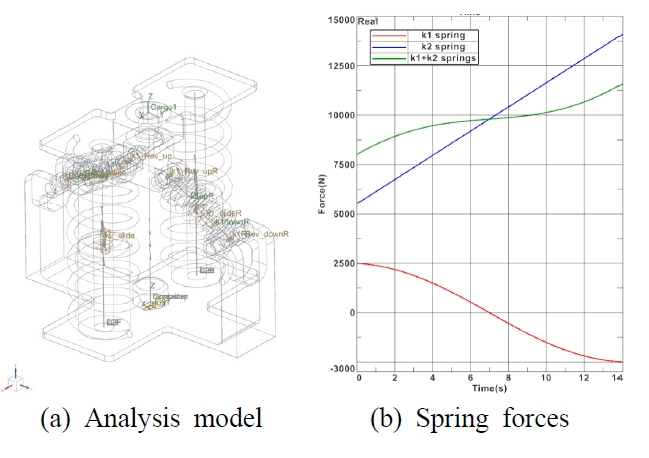
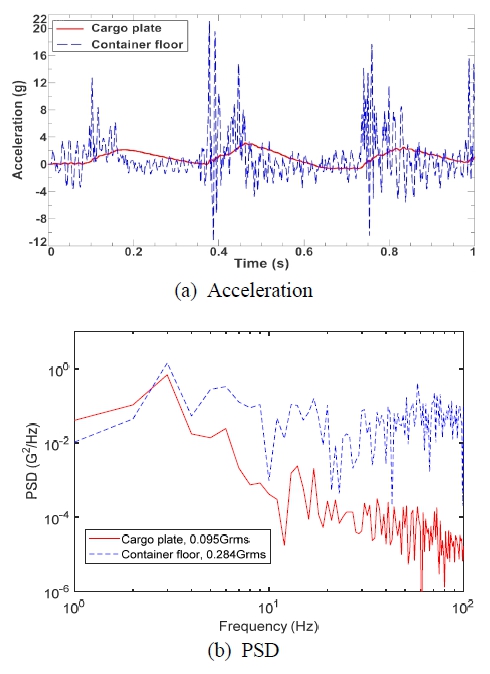
설계된 MSNS 마운트의 치수들을 이용하여 시간 적분을 통한 비선형 수치해석을 수행하였다. Simens사의 Simcenter3D Motion(multi-body dynamics) 해석 프로그램을 이용하였으며, k₁과 k₂는 각각 162.3 N/mm과 122.5 N/mm, l은 120 mm, 감쇠기 상수는 20 Ns/mm이다. Fig. 11에 해석 모델과 각 스프링의 힘 성분을 나타내었다. Fig. 11(b)에서 시간 0 s ~ 14 s 동안 상판을 x = -70 mm에서 x = 70 mm까지 10 mm/s의 동일 속도로 이동할 때, 각 스프링의 수직방향 성분을 나타낸 것이다. x = 0 지점에 해당하는 7 s 지점에서 합력이 9800 N을 나타낸다. 각 스프링이 한 쌍씩이므로 총 최적 화물 무게는 2톤에 해당한다. 마운트의 하부프레임에 2절에서 측정된 도로 수송 시의 큰 진동 이력을 입력하였으며 상부프레임의 진동 응답을 수치 모사하였다. 가속도 시간 응답과 그 결과를 FFT한 PSD를 Fig. 12에 나타내었다. 가속도의 최대값은 약 1/8 크기로 줄었으며 고주파수 변동이 크게 줄었음을 볼 수 있다. PSD에서도 3 Hz이상의 대역에서 감소하였으며 PSD의 총합은 0.284에서 0.095 Grms로 저감되었다.

Fig. 11

Dynamic analysis model of MSNS mount and its force components at the deformation

Fig. 12

Calculated vertical vibration response of MSNS mount

3.2 컨테이너 방진장치 시험

이 논문의 방진장치를 기존 컨테이너 내부 바닥에 설치하여 실제 도로 수송 시의 방진 성능을 시험하였다. 일반적으로 화물 상하차 시간과 노력을 저감하고 물류비 절감을 위하여 컨테이너에 화물을 빠르게 싣고 내리기 위한 지게차의 진입이 원활하여야 한다⁽²⁾. 이러한 사항을 고려하여 컨테이너에 방진장치를 설치하는 방식은 Fig. 13과 같이 각 스프링 구성품을 일렬로 배치하고 화물 상판을 분리 설치할 수 있도록 하였다. 방진 마운트는 컨테이너 바닥 양측 모서리 부근에 설치되며 화물과 함께 상판을 지게차로 상하차할 때 통행에 방해가 되지 않게 하였다. Fig. 14에는 40피트 하이큐브 컨테이너에 방진 마운트를 설치하고 화물 무게를 모사하는 무게추를 싣고 시험한 모습을 나타내었다. Fig. 13(b)의 방진 모듈을 길이 방향으로 8세트 일렬로 설치하였으며 각 모듈에 화물을 모사하기 위한 50 kg의 무게추(10 kg × 5개)를 설치하여, 컨테이너 내부에 총 400 kg을 설치하였다. 또한 진동이 가장 큰 컨테이너 후방에 컨테이너 바닥과 화물 상판, 각각에 가속도 센서(Lansmont사 Saver 3 × 90 및 9 × 30)를 설치하였다. 큰 충격성 진동이 발생하였을 때 측정된 가속도 시간 이력을 Fig. 15에 나타내었다. 이러한 충격은 도로-도로 간 이음매 구간이나 도로-교량 간 이음매 구간을 통과할 때 주로 발생하였다. 컨테이너 후방에서 계측된 값이며, 그림에 표기된 x,y,z 방향은 각각 길이 방향, 횡 방향, 수직 방향을 나타낸다. 컨테이너 바닥의 세 방향 가속도 최대값은 각각 1.296 G, 4.574 G, 12.937 G이었으며, MSNS 마운트를 거친 바로 위 지점의 화물 상판에서는 각각 0.368 G, 0.292 G, 1.513 G이었다.

Fig. 13

Conceptual diagram of the installation of MSNS mounts in a cargo container

Fig. 14

Vibration measurement situations of MSNS mounts in road transport

Fig. 15

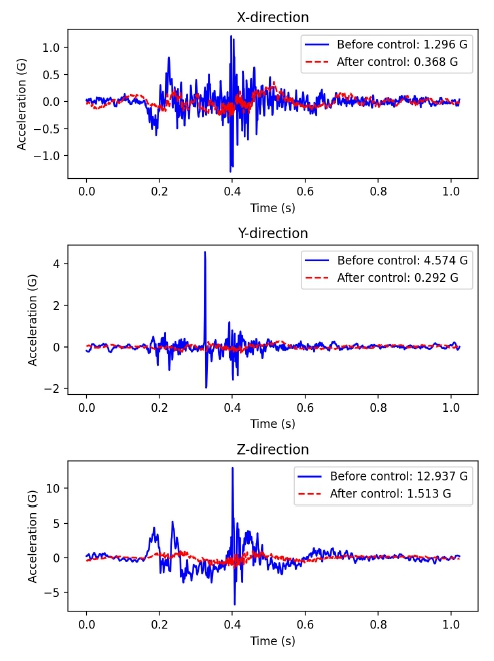
Measured time history of accelerations in three directions at the container floor and the cargo plate with MSNS mounts

결국, 세 방향 모두에서 그 크기가 감소하였으며, 세 방향의 합성인 가속도 크기는 12.94 G에서 1.51 G로 약 88.3 %가 감소하였음을 알 수 있다.

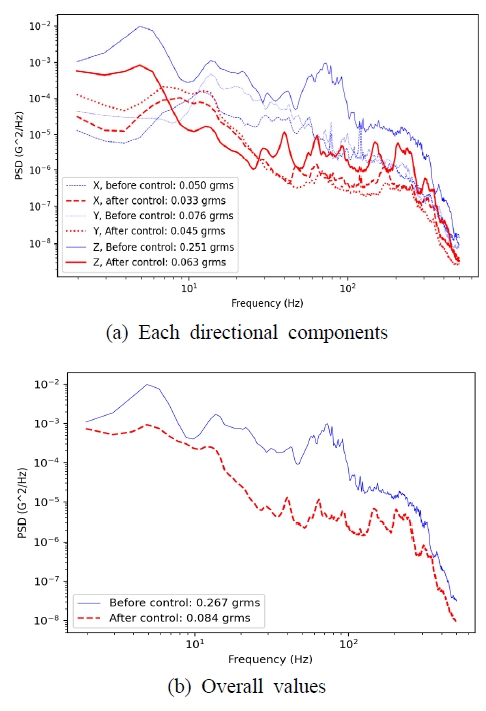
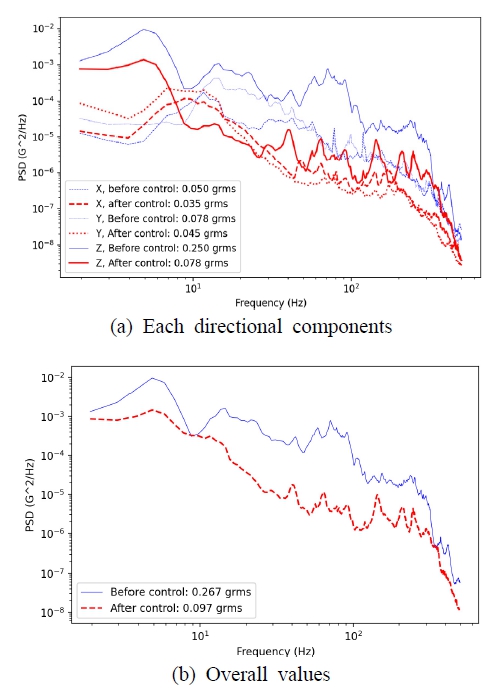
Fig. 16과 Fig. 17에 운송 구간 동안 0.5 G 이상의 모든 진동 입력에 대해 에너지 평균(0.5 G-triggered average)으로 통계 처리한 PSD 값을 나타내었다. Fig. 16은 천안에서 의왕까지, Fig. 17은 의왕에서 천안까지 운송한 경우의 측정값이다. Fig. 16(a)에서 컨테이너 바닥과 방진 장치 상판의 3축 가속도 성분들을 볼 수 있는데, 수직 방향(Z) 컨테이너 바닥에서 Fig. 1(a)에서와 같은 트럭의 3개의 공진 밴드들이 관찰된다. 방진 장치의 효과로 그래프에 표시한 모든 주파수(2 Hz ~ 500 Hz)에서 PSD 값이 더 작아짐을 알 수 있다. 반면에 길이 방향(X)과 횡 방향(Y)에서는 약 10 Hz 이상에서는 방진 효과가 관찰되지만 약 10 Hz 이하에서는 방진 장치 상판에서 더 큰 PSD 값이 관찰된다. 또한 길이 방향과 횡 방향 모두 최대인 주파수 대역이 약 10 Hz ~ 20 Hz 범위에 있어서, 총합 레벨은 길이 방향에서 0.050 Grms에서 0.033 Grms로 감소하였으며 횡 방향에서 0.076 Grms에서 0.045 Grms로 다소 감소하였음을 알 수 있다. Fig. 16(b)에는 3축 성분들을 합산한(RMS) 가속도 크기의 PSD를 나타내었는데, 길이 방향과 횡 방향의 진동이 수직 방향보다 훨씬 작으므로 수직 방향과 유사한 형태를 보이며 역시 전체 주파수에서 진동의 크기가 감소함이 관찰된다. 총합 레벨은 0.267 Grms에서 0.084 Grms로 감소하였다. Fig. 17의 역방향 운송 구간에서는 Fig. 16과 유사한 경향을 볼 수 있으며, Fig. 17(b)의 총합 레벨은 0.267 Grms에서 0.097 Grms로 감소하였음을 알 수 있다.

Fig. 16

Measured PSD of acceleration magnitude. 1.0 G-triggered average. Cheonan to Uiwang

Fig. 17

Measured PSD of acceleration magnitude. 0.5 G-triggered average. Uiwang to Cheonan