[ Article ]

Transactions of the Korean Society for Noise and Vibration Engineering - Vol. 34, No. 4, pp.424-431

ISSN: 1598-2785 (Print) 2287-5476 (Online)

Print publication date 20 Aug 2024

Received 09 Apr 2024 Revised 29 May 2024 Accepted 30 May 2024

DOI: https://doi.org/10.5050/KSNVE.2024.34.4.424

섭동법을 이용한 양변위 되먹임 제어 시스템의 수렴성 해석

김대웅^* ; 곽문규^†

Convergence Analysis of Positive Position Feedback Control using Perturbation Methods

Dae Woong Kim^* ; Moon Kyu Kwak^†

*Member, Department of Mechanical Engineering, Dongguk University, Student

Correspondence to: ^†Member, Department of Mechanical, Robotics and Energy Engineering, Dongguk University, Professor E-mail : kwakm@dgu.ac.kr # A part of this paper was presented at the KSNVE 2023 Annual Autumn Conference‡ Recommended by Editor Seunghun Baek

Abstract

This study presents a comprehensive analysis of the convergence properties of a positive position feedback (PPF) control system applied to a single-degree-of-freedom system, utilizing perturbation techniques. Through the application of the multiple-scale perturbation method, approximate solutions for the system dynamics are derived, revealing insights into amplitude reduction and convergence behavior under PPF control. The findings demonstrate the efficacy of the perturbation approach in accurately predicting the exponential decay of controlled responses.

Keywords:

Perturbation Methods, Multiple-scale Analysis, Vibration Control, Positive Position Feedback Control

키워드:

섭동법, 다중 척도 해석, 진동 제어, 양변위 되먹임 제어

1. 서 론

압전 액츄에이터와 압전 센서를 이용한 지능구조물의 진동제어를 위해 제안된 수많은 알고리즘 중 단순하면서도 효율적으로 사용된 제어알고리즘으로는 Fanson and Caughey가⁽¹⁾ 제안한 양변위 되먹임(positive position feedback, PPF) 제어 알고리즘이 있다. Baz et al.은^(2~4) 1자유도계 이론을 확장하여 다자유도계의 진동 억제를 위한 PPF 제어기를 조사해 각 모드를 제어하는 모달 양변위 되먹임(modal positive position feedback) 제어기법을 제안하였다^(5,6). Denoyer and Kwak은⁽⁷⁾ 연성된 PPF 제어기를 제안했다. Friswell and Inman은⁽⁸⁾ PPF 제어기와 출력 되먹임(output feedback) 제어기의 관계를 연구했다. Kwak et al.은⁽⁹⁾ PPF 제어기의 안정성, 제어 성능 및 설계 방법을 연구했다. 최근에는 비선형 진동의 억제를 위한 PPF 제어기 연구가 진행되었다^(10~15).

PPF 제어기는 특정 고유진동모드에 대해 90도의 위상차를 가지는 제어력을 적용하는데 그 결과 감쇠가 증가된 효과가 얻어진다. 그렇기 때문에 PPF 제어기를 적용하면 폐루프 응답은 일반적으로 진동하면서 그 진폭은 시간에 따라 지수적으로 감소하게 된다. 응답이 지수적으로 어떻게 줄어드는가를 계산하는 것은 폐루프 제어 시스의 특성을 이해하는데 큰 도움이 된다. 섭동법을 적용한 연구들을 살펴보면 다음과 같다. Saeed et al.은⁽¹⁶⁾ 다중 척도 섭동법을 적용해 진동 억제를 위한 제어기를 비교했다. El-Ganaini et al.은⁽¹⁷⁾ 복합재로 구성된 유연한 보의 진동을 억제하기 위해 비선형항을 고려했고, 다중 척도 섭동법을 사용해 근사해를 유도했다. 이 연구에서는 PPF 제어기의 특성을 확인하는 방법으로 섭동법을 이용해 제어기의 수렴 특성과 자유진동응답을 포위하는 선을 구하는 방법을 연구했다.

섭동법은 정확한 해를 구할 수 없는 비선형 문제의 해를 근사적으로 구할 수 있는 중요한 수학적 도구이다. 특히 다중 척도 방법(method of multiple scales)은 주기적인 운동을 하는 구조물에 최소한 두 가지의 시간 척도가 존재한다고 보고, 영속항(secular term) 혹은 공진항(resonance term)이라고 불리는 항이 없어지도록 하는 조건을 순차적으로 적용하며 근사해를 구한다. 일반적으로 상수 계수의 비제차 미분 방정식의 특수해가 제차 미분 방정식의 해와 같을 때 시간과 삼각함수의 곱으로 주어지는 항이 항상 나타난다. 이 항으로 인해 시간이 무한대로 감에 따라 진동의 진폭이 무한대로 커지게 된다. 이러한 항을 영속항이라고 한다. 다중 척도 방법을 사용하면 시스템의 동적 거동을 보다 정확하게 이해할 수 있다.

이 연구에서는 일자유도 진동계와 PPF 제어기가 연성된 시스템에 섭동법을 적용해 PPF 제어기의 수렴 특성 해석과 진폭이 줄어드는 수렴도를 구했다. 수치해석 결과는 다중 척도 섭동법의 적용을 통해 폐루프 시스템의 실제 거동을 정확히 예측할 수 있음을 보여준다.

2. 다중 척도 섭동법을 이용한 연성 진동제어계의 섭동해석

PPF 제어기와 연결된 일자유도 진동계에 대한 방정식은 식 (1a), 식 (1b)와 같이 표현할 수 있다.

x ¨ + 2 ε ζ ω n x ˙ + ω n 2 x = ε g ω n 2 u + ε ω n 2 d

(1a)

u ¨ + 2 ε ζ f ω n u ˙ + ω n 2 u = ε g ω n 2 x

(1b)

여기서 u는 PPF 제어기의 제어력을 나타낸다. d는 외부 교란을 나타내며 g는 이득을 나타낸다. ㆍ는 시간에 대한 미분을 나타내는데 식 (2)와 같다.

∙ = d d t

(2)

그리고 ε는 작은 섭동 파라미터(small perturbation parameter)이다. 이는 PPF 제어기와 연결된 일자유도 진동계의 운동에 대한 대략적인 해를 결정할 때 섭동 파라미터로 사용될 수 있음을 나타낸다. 더 나아가서 시간 t는 시스템의 고유 진동수의 역수를 사용하여 무차원으로 만들 수 있고, 무차원화 변수로 τ=ω_nt를 도입했다. 그러면 시간에 대한 일차와 이차 도함수가 식 (3a), 식 (3b)와 같이 표현된다.

d d t = ω n d d τ

(3a)

d 2 d t 2 = ω n 2 d 2 d τ 2

(3b)

식 (3)을 식 (1)에 대입하면 고유진동수가 제거된 식 (4a), 식 (4b)를 유도할 수 있다.

x'' + 2 ε ζ ω n x' + x = ε g u + ε d

(4a)

u'' + 2 ε ζ f ω n u' + u = ε g x

(4b)

여기서 ′ 은 τ에 대한 미분을 나타내는데 식 (5)와 같다.

' = d d τ

(5)

가진력이 없는 자유진동 문제의 경우 d = 0가 되어 식 (6a), 식 (6b)와 같이 표현할 수 있다.

x'' + 2 ε ζ ω n x' + x = ε g u

(6a)

u'' + 2 ε ζ f u' + u = ε g x

(6b)

식 (6)에 대해 다중 척도 방법(method of multiple scales)을 적용해 보자. 진동 문제의 해의 형태가 단일 변수 t에 대한 함수가 아니라 여러 시간 척도(scale)을 포함한다는 아이디어로 일반해를 구하는 방법을 다중 척도 방법이라고 하는데, 이를 위해 빠른 시간과 늦게 변하는 시간을 식 (7a), 식 (7b)와 같이 쓸 수 있다.

T 0 = τ

(7a)

T 1 = ε τ

(7b)

이렇게 정의하면 τ가 증가함에 따라 T₀는 같은 비율로 증가하고, T₁은 ε이 작기 때문에 천천히 증가하게 된다. 따라서 T₀는 빠르게 진동하는 빠른 시간 척도를 나타내며, 주기 운동(periodic motion) 자체에 관한 시간 척도를 나타낸다. 그리고 T₁은 그보다는 조금 느리게 변하는 시간 척도를 나타내며, 진폭의 이동(amplitude drift)에 관한 시간 척도를 나타낸다. 즉, 다중 척도 방법은 별도의 독립 변수를 각각 연관시켜서 이 두 시간 척도를 구별하는 것이다. 따라서 진동계의 변위와 제어력을 식 (8a), 식 (8b)와 같은 형태와 같다고 가정할 수 있다.

x τ; ε = x T 0, T 1; ε

(8a)

u τ; ε = u T 0, T 1; ε

(8b)

Chain rule을 사용하면 일차와 이차의 미분을 식 (9a), 식 (9b)와 같이 유도할 수 있다.

d d τ = ∂ ∂ T 0 ∂ T 0 ∂ τ + ∂ ∂ T 1 ∂ T 1 ∂ τ = ∂ ∂ T 0 + ε ∂ ∂ T 1

(9a)

d 2 d τ 2 = ∂ 2 ∂ T 02 + 2 ε ∂ 2 ∂ T 0 ∂ T 1

(9b)

식 (9a)와 식 (9b)를 이용해 식 (6)을 다시 정리하면 식 (10a), 식 (10b)와 같이 쓸 수 있다.

∂ 2 x ∂ T 02 + 2 ε ∂ 2 x ∂ T 0 ∂ T 1 + 2 ε ξ ∂ x ∂ T 0 + ε ∂ x ∂ T 1 + x = ε g u

(10a)

∂ 2 u ∂ T 02 + 2 ε ∂ 2 u ∂ T 0 ∂ T 1 + 2 ε ζ f ∂ u ∂ T 0 + ε ∂ u ∂ T 1 + u = ε g x

(10b)

그리고 식 (6)의 근사해를 구하기 위해 x와 u는 다시 점근적 근사(asymptotic approximation)에 의해 식 (11a), 식 (11b)과 같이 쓸 수 있다.

x T 0, T 1; ε = x 0 T 0, T 1 + ε x 1 T 0, T 1

(11a)

u T 0, T 1; ε = u 0 T 0, T 1 + ε u 1 T 0, T 1

(11b)

식 (11)을 식 (10)에 대입하면 식 (12a), 식 (12b)가 유도된다.

∂ 2 x 0 ∂ T 02 + ε ∂ 2 x 1 ∂ T 02 + 2 ε ∂ 2 x 0 ∂ T 0 ∂ T 1 + 2 ε ζ ∂ x 0 ∂ T 0 + ε ∂ x 0 ∂ T 1 + x 0 + ε x 1 = ε g u 0

(12a)

∂ 2 u 0 ∂ T 02 + ε ∂ 2 u 1 ∂ T 02 + 2 ε ∂ 2 u 0 ∂ T 0 ∂ T 1 + 2 ε ζ f ∂ u 0 ∂ T 0 + ε ∂ u 0 ∂ T 1 + u 0 + ε u 1 = ε g x 0

(12b)

이를 다시 ε의 각각의 거듭제곱의 차수별로 정리하면 식 (13), 식 (14)가 유도된다.

O(ε⁰):

∂ 2 x 0 ∂ T 02 + x 0 = 0

(13a)

∂ 2 u 0 ∂ T 02 + u 0 = 0

(13b)

O(ε¹):

∂ 2 x 1 ∂ T 02 + x 1 = - 2 ∂ 2 x 0 ∂ T 0 ∂ T 1 - 2 ζ ∂ x 0 ∂ T 0 + g u 0

(14a)

∂ 2 u 1 ∂ T 02 + u 1 = - 2 ∂ 2 u 0 ∂ T 0 ∂ T 1 - 2 ζ f ∂ u 0 ∂ T 0 + g x 0

(14b)

O(ε⁰), O(ε¹)는 각각 ε이 0이될 때 ε⁰, ε¹의 유한 상수배보다 크지 않은 양을 나타낸다. 그리고 ε의 0차에 대한 미분방정식은 비감쇠 운동방정식으로 유도된다. 따라서 식 (13)의 일반해는 식 (15a), 식 (15b)와 같이 표현된다.

x 0 = A 0 T 1 c o s ⁡ T 0 + B 0 T 1 s i n ⁡ T 0

(15a)

u 0 = C 0 T 1 c o s ⁡ T 0 + D 0 T 1 s i n ⁡ T 0

(15b)

그리고 식 (14)의 secular 항이 0이 되기 위해서는 식 (16a), 식 (16b)를 만족해야 한다.

∂ 2 x 0 ∂ T 0 ∂ T 1 = - ζ ∂ x 0 ∂ T 0 + g 2 u 0

(16a)

∂ 2 u 0 ∂ T 0 ∂ T 1 = - ζ f ∂ u 0 ∂ T 0 + g 2 x 0

(16b)

식 (14)를 이용하면 식 (16)의 각 편미분항이 식 (17a) ~ 식 (17d)와 같이 계산된다.

∂ x 0 ∂ T 0 = - A 0 s i n ⁡ T 0 + B 0 c o s ⁡ T 0

(17a)

∂ u 0 ∂ T 0 = - C 0 s i n ⁡ T 0 + D 0 c o s ⁡ T 0

(17b)

∂ 2 x 0 ∂ T 1 ∂ T 0 = - d A 0 d T 1 s i n ⁡ T 0 + d B 0 d T 1 c o s ⁡ T 0

(17c)

∂ 2 u 0 ∂ T 1 ∂ T 0 = - d C 0 d T 1 s i n ⁡ T 0 + d D 0 d T 1 c o s ⁡ T 0

(17d)

그리고 식 (17)을 식 (16)에 대입하면 식 (18a), 식 (18b)가 유도된다.

- d A 0 d T 1 s i n T 0 + d B 0 d T 1 c o s T 0 = - ζ - A 0 s i n T 0 + B 0 c o s T 0 + g 2 C 0 c o s T 0 + D 0 s i n T 0

(18a)

- d C 0 d T 1 s i n T 0 + d D 0 d T 1 c o s T 0 = - ζ f - C 0 s i n ⁡ T 0 + D 0 c o s T 0 + g 2 A 0 c o s T 0 + B 0 s i n T 0

(18b)

sinT₀와 cosT₀항에 대해 각각 풀어내면 식 (19a) ~ 식 (19d)가 유도된다.

d A 0 d T 1 = - ζ A 0 - g 2 D 0

(19a)

d D 0 d T 1 = g 2 A 0 - ζ f D 0

(19b)

d B 0 d T 1 = - ζ B 0 + g 2 C 0

(19c)

d C 0 d T 1 = - g 2 B 0 - ζ f C 0

(19d)

식 (19)를 행렬식으로 정리하면 식 (20a), 식 (20b)와 같이 쓸 수 있다.

d A 0 d T 1 d D 0 d T 1 = - ζ - g 2 g 2 - ζ f A 0 D 0

(20a)

d B 0 d T 1 d C 0 d T 1 = - ζ g 2 - g 2 - ζ f B 0 C 0

(20b)

식 (20)은 간단하게 다시 식 (21a), 식 (21b)와 같이 간단한 일차의 행렬미분식으로 표현할 수 있다.

z ˙ 1 = A s 1 z 1

(21a)

z ˙ 2 = A s 2 z 2

(21b)

여기서 z₁(T₁)=[A₀(T₁)D₀(T₁)]^T, z₂(T₁)=[B₀(T₁)C₀(T₁)]^T이며, A_s₁는 식 (22)와 같다.

A s 1 = - ζ - g 2 g 2 - ζ f

(22)

식 (21a)의 해는 식 (23)과 같이 표현할 수 있다.

z T 1 = e A s 1 T 1 z 0

(23)

여기서

e A s 1 T 1 = L - 1 s I - A s 1 - 1

(24)

식 (23)에서 알 수 있듯이 행렬 A_s가 0차의 응답에 영향을 주는 것을 알 수 있다. 행렬 A_s의 특성은 고유치에 의해 결정되는데 특히 고유치의 실수부의 값에 의해 좌우된다. 행렬 A_s의 고유치는 식 (25)와 같이 유도된다.

λ 1,2 = - ζ + ζ f ± ζ - ζ f 2 - g 2 2

(25)

따라서 고유치의 실수부 최대값은 이득값, g에 의해 식 (26)과 같이 결정됨을 알 수 있다.

Re ⁡ λ m a x - ζ + ζ f + ζ - ζ f 2 - g 2 2, g < ζ f - ζ - ζ + ζ f 2, ≥ ζ f - ζ

(26)

3. 수치 계산

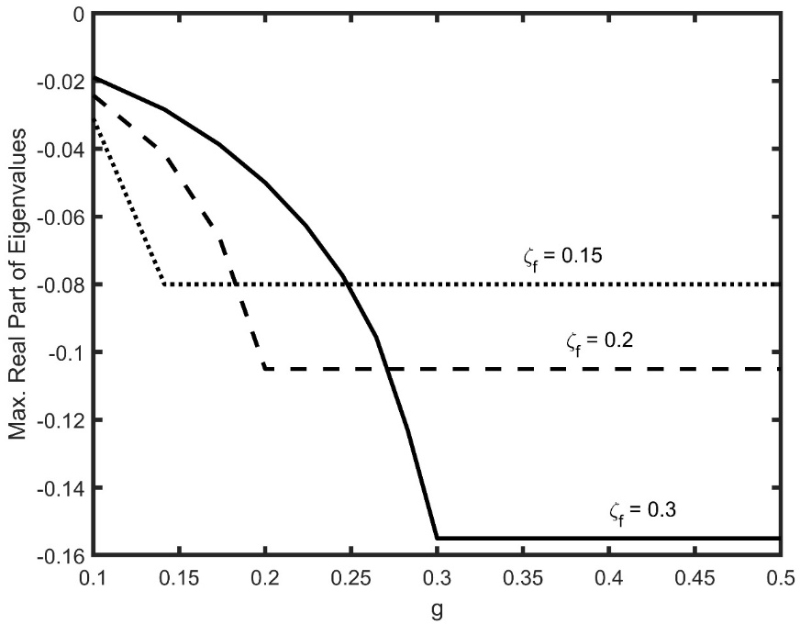
먼저 PPF 제어기의 적용에 의한 수렴 특성을 조사했다. 구조물의 감쇠비는 ξ=0.01로 하고 식 (26)을 사용해 Kwak 등의⁽⁹⁾ 연구를 참고하여 ξ_f가 0.15, 0.2, 0.3인 경우에 대해 수치계산을 수행했다. 이득값 변화에 따른 고유치의 실수부의 최대값을 구해보면 Fig. 1과 같다.

Fig. 1

Maximum real part of eigenvalues vs. g(approximate solution)

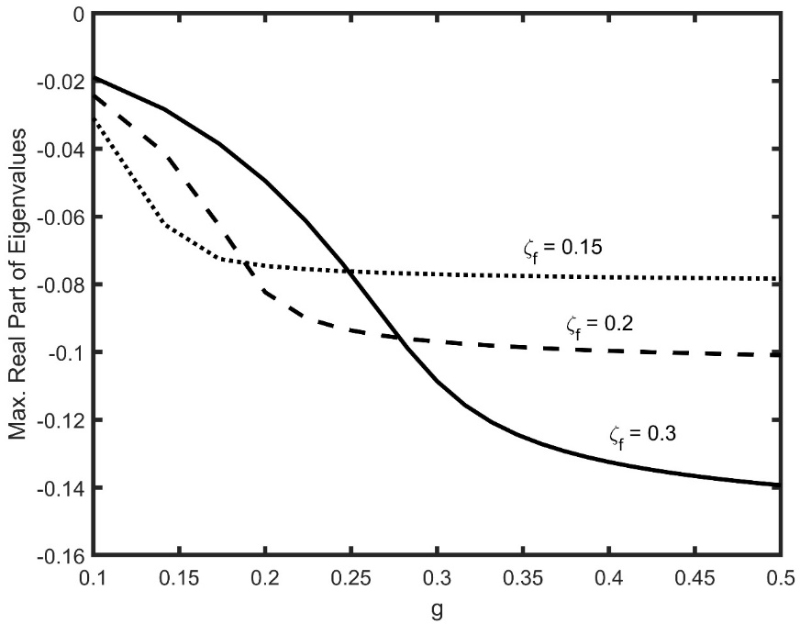
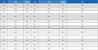
섭동법에 근거한 근사값 계산식을 사용하지 않고 제어기가 연성된 식 (6)을 사용해 고유치의 엄밀해를 계산하면 Fig. 2와 같이 나타난다. ξ_f가 0.3인 경우, 이득값의 변화에 따른 고유값의 최대 실수부값이 Table 1에 정리되어 있다. Fig. 1과 Fig. 2 그리고 Table 1로부터 특정 ξ_f에 대해서 이득값을 올려도 수렴 특성이 더 이상 향상될 수 없음을 알 수 있다. 따라서 섭동법에 근거한 Fig. 1을 수렴 특성을 판단하기 위한 근사값으로 사용할 수 있음을 알 수 있다.

Fig. 2

Maximum real part of eigenvalues vs. g(exact solution)

Table 1

Comparison of convergence for various gains(ξf=0.3)

식 (6)의 자유진동 문제에 대한 초기조건을 식 (27a) ~ 식 (27d)와 같이 간단하게 고려했다.

x 0 = 1

(27a)

x' 0 = 0

(27b)

u 0 = 0

(27c)

u' 0 = 0

(27d)

식 (9a)를 이용하면 식 (27)의 초기조건이 식 (28a), 식 (28b)와 같이 유도된다.

x = 1, ∂ x ∂ T 0 + ε ∂ x ∂ T 1 = 0, for T 0 = T 1 = 0

(28a)

u = 0, ∂ u ∂ T 0 + ε ∂ u ∂ T 1 = 0, for T 0 = T 1 = 0

(28b)

식 (28)에 식 (11)을 대입하면 식 (28)을 식 (29a), 식 (29b)와 같이 쓸 수 있다.

x 0 + ε x 1 = 1, ∂ x 0 ∂ T 0 + ε ∂ x 1 ∂ T 0 + ∂ x 0 ∂ T 1 = 0, f o r T 0 = T 1 = 0

(29a)

u 0 + ε u 1 = 0 ∂ u 0 ∂ T 0 + ε ∂ u 1 ∂ T 0 + ∂ u 0 ∂ T 1 = 1, f o r T 0 = T 1 = 0

(29b)

그러므로 0차의 항에 대한 초기조건을 식 (30a), 식 (30b)와 같이 쓸 수 있다.

x 0 = 1, ∂ x 0 ∂ T 0 = 0, f o r T 0 = T 1 = 0

(30a)

u 0 = 0, ∂ u 0 ∂ T 0 = 0, f o r T 0 = T 1 = 0

(30b)

초기조건 식 (30)을 사용하면 x₀와 u₀의 상수들이 식 (31)과 같이 유도된다.

A 0 0 = 1, B 0 0 = 0, C 0 0 = 0, D 0 0 = 0

(31)

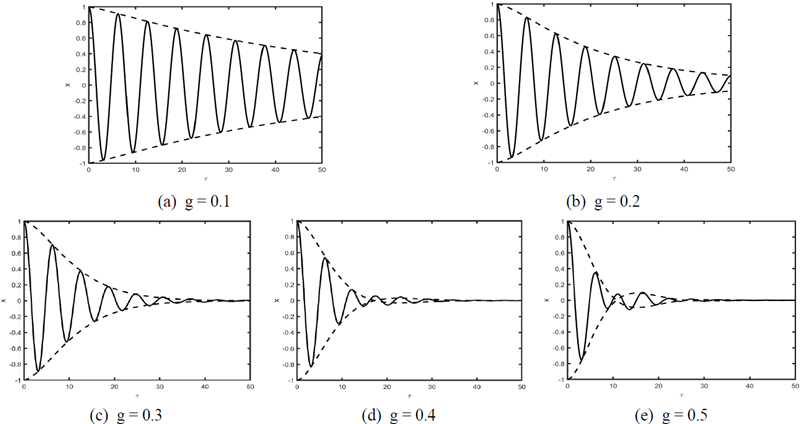
초기조건 식 (27b), 식 (27c)로 인해 자연적으로 B₀(T₁)=C₀(T₁)=0이 된다. 초기조건 식 (31)과 ξ=0.01, ξ_f=0.3에 대해 1차 미분방정식 식 (21)의 해를 구해보면 이득값에 따라 응답 곡선이 Fig. 3과 같이 변화함을 알 수 있다. ξ_f를 작게 하면 가장 큰 감쇠 효과를 얻을 수 있지만, 최적의 필터 주파수를 사용하지 않으면 오히려 ξ_f가 큰 값일 때보다 제어 성능이 좋지 않아진다. 따라서 Kwak 등의⁽⁹⁾ 연구에서 추천하는 값인 ξ_f=0.3을 사용하였다. Fig. 3에서 실선은 식 (6)을 사용해 계산한 응답곡선이고 점선은 식 (21)을 이용해 구한 0차의 수렴 곡선을 나타낸다. Fig. 3(d), Fig. 3(e)에서 이득이 커진 경우, 특정 구간에서의 약간의 불일치를 제외하고 응답 곡선과 수렴곡선이 거의 완벽하게 일치한다. 그림으로부터 이 연구에서 섭동법을 이용해 유도한 수렴 곡선 계산식이 유효함을 알 수 있다.

Fig. 3

Exact time response and the convergence envelope

4. 결 론

이 연구에서는 일자유도 진동계와 PPF 제어기가 연성된 시스템에 섭동법을 적용해 PPF 제어기의 수렴 특성 해석과 응답진폭이 줄어드는 수렴도를 구했다. 일자유도 진동계 방정식과 연성된 PPF 제어기식에 대해 다중 척도 방법을 사용해 시스템의 근사해를 유도했다. 그 결과 고유진동수로 진동하는 0차해와 지수적으로 감소하는 1차해를 구할 수 있었다. 0차의 미분 방정식은 비감쇠 운동방정식으로 유도되는데, 형태는 2차의 선형 미분 방정식으로 나타난다. 그리고 그 해는 삼각함수 형태로 쉽게 구할 수 있다. 즉 0차의 해는 비감쇠 운동을 보여준다. 1차의 미분방정식은 secular 항을 포함하면 안 된다는 조건을 사용하면 삼각함수의 계수에 대한 미분방정식이 1차의 선형 미분 방정식으로 표현되어 그 해가 지수함수로 표현되게 된다. 따라서 1차의 해는 지수적으로 감소하는 형태를 보이게 된다.

이 연구에서 유도한 식을 사용하면 시스템의 실제수렴 거동을 예측할 수 있음을 확인했다. 수치 시뮬레이션 결과는 섭동법을 이용해 구한 1차의 근사해가 지수적으로 감소하는 제어 응답을 정확하게 예측함을 보여준다. 특히 PPF 제어기는 이득을 크게 하면 정적 불안정이 발생할 수 있는데, 이 경우의 과도 응답도 정확하게 예측함을 확인할 수 있다. 더 높은 차수의 근사해로도 수렴도 해석이 가능하지만, 너무 많은 대수 방정식을 풀어야 하는 번거로움이 있다. 이 연구에서는 섭동법을 이용해 구한 1차의 근사해의 모든 예측이 수치 시뮬레이션과 잘 일치함을 확인했다.

References

Fanson, J. L. and Caughey, T. K., 1990, Positive Position Feedback Control for Large Space Structures, AIAA Journal, Vol. 28, No. 4, pp. 717~724. [https://doi.org/10.2514/3.10451]
Poh, S. and Baz, A., 1990, Active Control of a Flexible Structure using a Modal Positive Position Feedback Controller, Journal of Intelligent Material Systems and Structures, Vol. 1, No. 3, pp. 273~288. [https://doi.org/10.1177/1045389X9000100302]
Baz, A., Poh, S. and Fedor J., 1992, Independent Modal Space Control with Positive Position Feedback, Journal of Dynamic Systems, Measurement and Control, Vol. 114, No. 1, pp. 96~103. [https://doi.org/10.1115/1.2896512]
Baz, A. and Hong, J.-T., 1997, Adaptive Control of Flexible Structures using Modal Positive Position Feedback, International Journal of Adaptive Control and Signal Processing, Vol. 11, No. 3, pp. 231~253. [https://doi.org/10.1002/(SICI)1099-1115(199705)11:3<231::AID-ACS435>3.0.CO;2-8]
Meirovitch, L. and Baruh, H., 1982, Control of Self-adjoint Distributed-parameter Systems, Journal of Guidance, Control, and Dynamics, Vol. 5, No. 1, pp. 60~66. [https://doi.org/10.2514/3.56140]
Meirovitch, L. and Baruh, H., 1983, Robustness of the Independent Modal-space Control Method, Journal of Guidance, Control, and Dynamics, Vol. 6, No. 1, pp. 20~25. [https://doi.org/10.2514/3.19797]
Denoyer, K. K. and Kwak, M. K., 1996, Dynamic Modelling and Vibration Suppression of a Swelling Structure Utilizing Piezoelectric Sensors and Actuators, Journal of KSNVE, Vol. 189, No. 1, pp. 13~31. [https://doi.org/10.1006/jsvi.1996.0003]
Friswell, M. I. and Inman, D. J., 1999, The Relationship between Positive Position Feedback and Output Feedback Controllers, Smart Materials and Structures, Vol. 8, No. 3, pp. 285~291. [https://doi.org/10.1088/0964-1726/8/3/301]
Kwak, M.-K., Han, S.-B. and Heo, S., 2004, The Stability Conditions, Performance and Design Methodology for the Positive Position Feedback Controller, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 14, No. 3, pp. 208~213. [https://doi.org/10.5050/KSNVN.2004.14.3.208]
Warminski, J., Bochenski, M., Jarzyna, W., Filipek, P. and Augustyniak, M., 2011, Active Suppression of Nonlinear Composite Beam Vibrations by Selected Control Algorithms, Communications in Nonlinear Science and Numerical Simulation, Vol. 16, No. 5, pp. 2237~2248. [https://doi.org/10.1016/j.cnsns.2010.04.055]
Wang, K., Xiong, S. and Zhang, J., 2011, Active Vibration Control of a Flexible Cantilever Beam using Piezoelectric Actuators, Energy Procedia, No. 13, pp. 4367~4374. [https://doi.org/10.1016/j.egypro.2011.12.028]
Omidi, E. and Mahmoodi, S. N., 2015, Nonlinear Vibration Suppression of Flexible Structures using Nonlinear Modified Positive Position Feedback Approach, Nonlinear Dynamics, Vol. 79, No. 2, pp. 835~849. [https://doi.org/10.1007/s11071-014-1706-5]
Marinangeli, L., Alijani, F. and HosseinNia, S. H., 2018, Fractional-order Positive Position Feedback Compensator for Active Vibration Control of a Smart Composite Plate, Journal of KSNVE, Vol. 412, pp. 1~16. [https://doi.org/10.1016/j.jsv.2017.09.009]
Dhobale, S. M. and Chatterjee, S., 2023, A General Class of Optimal Nonlinear Resonant Controllers of Fractional Order with Time-delay for Active Vibration Control - Theory and Experiment, Mechanical Systems and Signal Processing, Vol. 182, 109580. [https://doi.org/10.1016/j.ymssp.2022.109580]
Balasubramanian, P., Ferrari, G., Hameury, C., Silva, T. M. P., Buabdulla, A. and Amabili, M., 2023, An Experimental Method to Estimate the Electro-mechanical Coupling for Active Vibration Control of a Non-collocated Free-edge Sandwich Plate, Mechanical Systems and Signal Processing, Vol. 188, 110043. [https://doi.org/10.1016/j.ymssp.2022.110043]
Saeed, N. A., Awwad, E. M., Abdelhamid, T., El-Meligy, M. A. and Sharaf, M., 2021, Adaptive Versus Conventional Positive Position Feedback Controller to Suppress a Nonlinear System Vibrations, Symmetry, Vol. 13, No. 2, p. 255. [https://doi.org/10.3390/sym13020255]
El-Ganaini, W. A., Saeed, N. A. and Eissa, M., 2013, Positive Position Feedback(PPF) Controller for Suppression of Nonlinear System Vibration, Nonlinear Dynamics, Vol. 72, No. 3, pp. 517~537. [https://doi.org/10.1007/s11071-012-0731-5]
Nayfeh, A. H., 1973, Perturbation Methods, John Wiley & Sons, New York, United States.
Kevorkian, J. and Cole, J. D., 2013, Perturbation Methods in Applied Mathematics, Springer, New York, United States.
Bender, C. M. and Orszag, S. A., 1978, Advanced Mathematical Methods for Scientists and Engineers, McGraw‐Hill, New York, United States.
Nayfeh, A. H. and Mook, D. T., 2008, Nonlinear Oscillations, John Wiley & Sons, New York, United States.
Weinan, E., 2011, Principles of Multiscale Modeling, Cambridge University Press, Cambridge, UK.
Bensoussan, A., Lions, J.-L. and Papanicolaou, G., 2011, Asymptotic Analysis for Periodic Structures, AMS Chelsea Publishing, Rhode Island, United States. [https://doi.org/10.1090/chel/374]
Chatterjee A., 2009, A Brief Introduction to Nonlinear Vibrations, Mechanical Engineering, Indian Institute of Science, Bangalore, India.
Salih, A., 2014, The Method of Multiple Scales. Department of aerospace engineering, Indian Institute of Space Science and Technology, Kerala, India.

Dae Woong Kim received B.S. in Mechanical Engineering from Dongguk University in 2022. He is currently a graduate student in the Dept. of Mechanical Engineering in Dongguk University.

Moon Kyu Kwak received B.S. and M.S. degrees in Naval Architecture from Seoul National University in 1981 and 1983. He then received his Ph.D. degree from the Dept. of Engineering Science and Mechanics of Virginia Tech in 1989. He is currently a Professor at the Department of Mechanical, Robotics and Energy Engineering of Dongguk University in Seoul, Korea. His research interests are dynamics and control of flexible multibody system and active vibration control of smart structure.

g	Exact solution e^-ατ	Approximate solution e^-βτ
0.1	-0.0189	-0.0189
0.2	-0.0495	-0.0500
0.3	-0.1086	-1.5500
0.4	-0.1325	-1.5500
0.5	-0.1393	-1.5500