부가질량과 Nonhomogeneous 베어링 지지 조건이 고려된 로터 킷의 진동해석 모델
ⓒ The Korean Society for Noise and Vibration Engineering
초록
In this study, a refined structural model of a complex rotating shaft system with nonuniform cross-section, disks, and supported by several bearings are established via Hamilton’s variational principle. Timoshenko beam theory is adopted to incorporate transverse shear and the rotary inertia effect. It is assumed that the shaft spins with a constant speed about its spin axis and is subjected to a conservative axial force. Elastic coupling between vertical and lateral bending motion is caused by Coriolis acceleration. The implications of the gyroscopic effect, additional masses, axial force, and nonhomogeneous boundary conditions (reflecting bearing stiffness and damping) are revealed and analytical results are compared with those obtained from the ANSYS finite element analysis. The prediction model established in this study could be used for the preliminary design of a complicated rotating system.
Keywords:
Rotating Shaft System, Additional Mass, Non-homogeneous Boundary Conditions, Coriolis Acceleration, Rotor Kit키워드:
회전축계, 부가질량, non-homogeneous 경계조건, 코리올리 가속도, 로터 킷1. 서론
단순한 형상을 가진 회전축계에 대해서는 보 이론에 기초하여 구조 모델을 정립하고 그 동특성을 규명하여 기초설계 자료로서 활용하여 왔다.
그러나 회전축 중간 중간에 집중질량(디스크)들이 부가되고 축의 단면 형상 및 치수가 연속/불연속적으로 변화하며 한정된 강성과 감쇠 성능을 갖는 다수의 베어링으로 지지된 경우에는 이론적 모델링과 그 모델에 대한 해석이 일반적으로 쉽지 않다. 따라서 복잡한 형상 및 구조를 가진 경우에는 대표적으로 유한요소법을 이용하여 동특성을 분석하나 이 경우 변수 변화에 따른 다양한 동특성변화를 구명하는데 많은 시간과 노력이 필요하다.
디스크와 같은 집중질량을 갖는 회전축계 진동 연구는 Park(1)과 Yang(2)에 의해 티모센코 보 이론을 적용한 연구가 진행되었다. 또한 양단 단순 지지되고 축에 부가질량이 존재하는 경우의 회전축계 모델에 대해 자이로스코프 행렬의 2차 고유치 문제를 1차로 변환하여 해석하는 연구가 진행되었다(3).
1997년 Jun(4)은 토크와 회전관성, 전단변형을 고려한 다단 회전축계의 고유진동 특성 연구를 수행하였다. 2006년 Multi-stage rotor-blade system의 모델링작업을 위해 합성, 다중 프레임 및 혼합 방식을 도입하여 선형 커플링에서 축의 비틀림 및 블레이드의 진동에 대한 연구가 진행되었다(5). 다단 불균일 단면 복합재료 회전축의 정적 불안정과 동적 불안정 특성, 보존력과 자이로스코프 힘, 섬유각 변수에 대한 동특성 변화 연구가 이루어졌다(6,7). 또한 터보 압축기 다단 회전축계에 대하여 축하중의 크기, 베어링의 강성, 그리고 코리올리 가속도를 변수로 하는 수치해석 모델을 정립하여 동특성 해를 구하였다(8).
이 연구에서는 회전축 중간에 집중질량 디스크들이 부가되고, 축의 단면 형상 및 치수가 연속/불연속적으로 변화하고, 회전축방향으로 축하중이 작용하며, 유한한 강성 및 감쇠를 갖는 베어링으로 지지된, 즉 non-homogeneous 경계조건을 갖는 복잡 회전축계에 대하여 티모센코 보 이론과 해밀턴 원리를 적용하여 이론적 모델링 작업을 수행하였다(9).
그리고 이 구조 모델에 대하여 정확하고 효과적인 수치해석법인 EGM(extened Galerkin’s method)를 사용하여 다양한 변수 변화에 따른 동특성 변화 경향을 도출하고 이를 유한요소 해석(ANSYS) 결과와 비교 분석하여 이론 모델의 타당성에 대한 검증을 수행한다. 검증된 구조 모델은 유한요소법보다 빠르고 손쉽게 다양한 변수에 대한 동특성 변화경향을 제공할 수 있다. 따라서 이 연구에서 제시된 복잡 회전축계 이론 모델은 복잡한 형상과 구조를 가진 회전축계의 기초설계에 유용하게 사용될 수 있을 것으로 기대된다.
2. 이론적 구조 모델링
2.1 베어링지지 회전축계
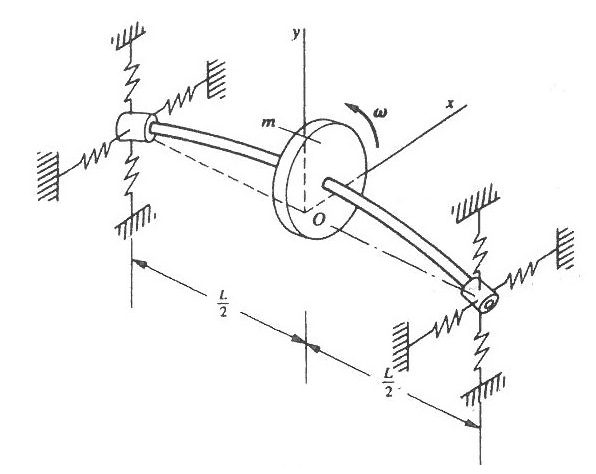
Fig. 1은 각속도로 회전하고 있는 회전축에 질량 m인 디스크가 부착되어 있고 유한한 강성을 갖는 베어링에 의해 양단이 탄성적으로 지지되어 있는 단순한 회전축계 모델을 나타내고 있다(10).
이 연구에서는 관성좌표계인 OXYZ와 회전체 축의 중심에 고정된 회전좌표계 Oxyz를 사용하였으며, 두 좌표계의 공통원점 O는 회전축 단면의 중심에 위치해 있다.
회전축은 길이가 L이고, 단면형상이 연속적, 또는 불연속적으로 변화하는 불균일 단면을 가지며, z축 방향의 회전속도 Ω가 일정하고, 축 방향으로 양단에 압축하중 P가 작용하며, 전단변형과 회전관성 효과가 고려된 티모센코 보로 Fig. 2와 같이 모델링하였다.
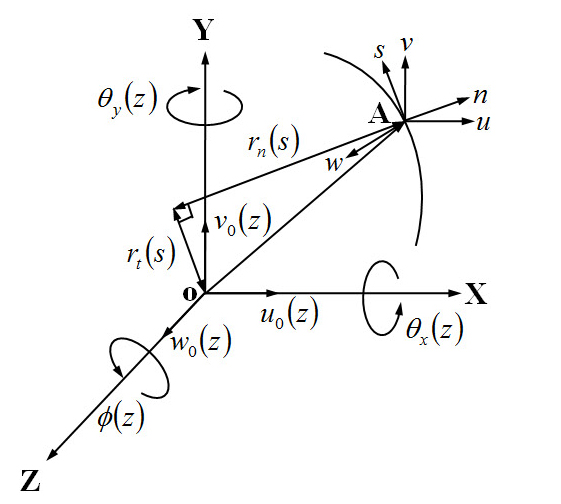
3차원 변위를 1차원 변위변수로 표현하기 위해 회전축 단면 내의 임의의 한 점 A에서의 3D 변위 u, v, w와 1D 변위변수 u0, v0, θx, θy와의 관계를 Fig. 3에 나타내었다.
| (1) |
여기서θx (z;t) = γyz(z;t) - v0´(z;t)
θy (z;t) = γxz(z;t) - v0´(z;t)
u0, v0와 θx, θy는 각각 x, y축 방향의 병진변위와 x, y축 중심의 회전각을 나타낸다. θy의 방향이 θx의 방향과 반대인 것은 1상한에서의 변위 w가 양이 되도록 θx, θy의 방향을 선택한 결과이다.
한 점 A(x,y,z)에서의 위치, 속도, 가속도벡터는 다음과 같다.
| (2) |
식 (2)에서 는 Coriolis(gyroscopic) 가속도, -Ω2(x+u), -Ω2(y+v)는 회전중심을 향하는 구심(centripetal) 가속도를 나타낸다.
2.2 운동방정식과 경계조건
식 (3)과 같은 Hamilton 원리를 사용하여 운동방정식과 경계조건을 동시에 유도하였다(11).
| (3) |
여기서
- 회전축 및 베어링에 저장되는 탄성에너지
| (4) |
- 회전축 및 부가질량(디스크)의 운동에너지
| (5) |
- 압축하중 P에 의한 일
| (6) |
- 베어링의 Rayleigh’s dissipation function
| (7) |
위 식에서 부가질량 및 베어링의 위치를 dirac delta 함수를 이용하여 나타내었다.
식 (4) ~ (7)의 변분을 취하고 그 결과를 식 (3)에 대입하여 정리하면 다음 식 (8) ~ (14)의 운동방정식과 경계조건을 얻을 수 있다.
식 (8) ~ (14)에서 양단 베어링 (i=1, N)은 경계조건으로, 축 중간에 위치한 부가질량 및 베어링 ()은 경계조건이 아닌 운동방정식 안에 포함되어 나타나는 것을 알 수 있다. 회전축 단면의 형상과 크기, 재료가 임의로 변화하는 경우를 고려하였으므로 회전축의 강성 및 관성이 모두 축방향 좌표 z의 함수로서 k2GA(z), EI(z), m(z), J(z)와 같이 나타나 있다. 회전축의 전단변형 (k2GA(z))과 회전관성 (), 그리고 회전축의 축방향으로 작용하는 압축하중 P에 의한 효과가 고려되었다.
- ∙ 운동방정식
| (8) |
| (9) |
| (10) |
| (11) |
- ∙ 경계조건
이상적인 clamped-clamped, free-free 경계조건은 식 (12), (13)과 같이 homogeneous하나, 실제 경계조건은 non-homogeneous하며 식 (14)와 같다.
| (12) |
| (13) |
| (14) |
3. 수치해석 및 유한요소 해석
3.1 해석 대상 및 시험함수
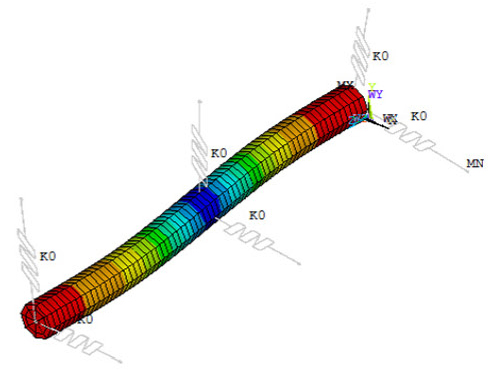
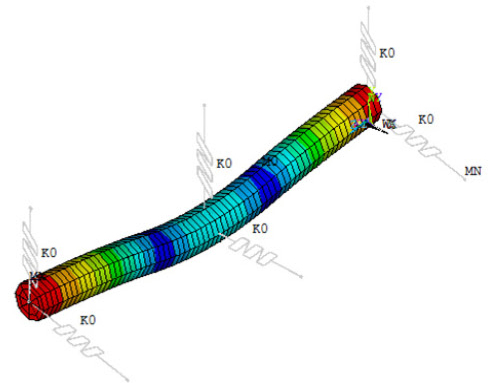
이론 및 유한요소 해석을 수행할 대상은 Fig. 4의 양단 베어링 지지 로터 킷과 Fig. 5의 중간지지 베어링이 추가되어 있는 로터 킷이다. 로터 킷의 물성과 치수를 조사 측정하고 베어링의 스펙을 조사하여 해석 모델에 적용하였다.
Fig. 6에 보인 회전축계의 사양을 Table 1에 나타내었다.
C-C, F-F, spring-spring의 3가지 경계조건들을 만족시키는 시험함수는 기 연구된 다단 회전축계 진동 이론을 참고하여 Table 2와 같이 선정하였다(12).
3.2 이론 해석
자유진동의 동기운동(synchronous motion)을 가정하면 변위는 다음과 같이 표현된다.
| (15) |
식 (15)를 식 (8) ~ (14)에 대입하고 extended Galerkin’s method를 적용하면 식 (16)이 유도되며 이에 대한 특성방정식과 복소고유치를 식 (17)에서 구한다.
| (16) |
| (17) |
- [M]=질량행렬, [C]=감쇠행렬, [G] Gyroscopic 행렬, [K]=강성행렬 (부록 참조)
3.3 유한요소 해석
이 연구에서는 ANSYS를 사용하여 유한요소 해석을 수행하였으며, 회전축은 3차원 beam 요소(beam188), 원판 디스크는 부가질량 요소(mass 21), 베어링은 spring-damper 요소(combin 14)를 사용하였고 회전축과 디스크의 재질 특성은 Table 3과 같다.
3.4 결과 분석
이 연구에서는 양단이 베어링으로 지지되어 있는 회전체 시스템의 경계조건을 C-C, F-F, spring-spring 3가지로 구분하여 TBM(Timoshenko beam model)을 기반으로 하는 이론해석과 ANSYS S/W를 이용한 유한요소 해석을 수행하였다.
Table 4는 C-C 경계조건의 부가질량이 없는 회전축의 고유진동수를 비교한 결과이며, Table 5는 집중질량 2개가 부가된 경우의 고유진동수를 비교한 결과이다. Table 6은 F-F 경계조건의 부가질량이 없는 회전축의 고유진동수를 비교한 결과이며, Table 7은 집중질량 2개가 부가된 경우의 고유진동수를 비교한 결과이다.
C-C 경계조건에서 회전축에 집중질량이 부가되지 않은 경우, 고유진동수의 차이는 1차 1.522 %, 2차 3.991 %, 3차 5.213 %이었으며, 집중질량이 부가되었을 때는 1차 2.657 %, 2차 1.271 %, 3차 3.017 %의 차이를 보였다.
F-F 경계조건에서는 회전축에 집중질량이 부가되지 않은 경우, 고유진동수의 차이는 1차 0.07 %, 2차 0.26 %, 3차 0.4 %를 보였으며, 집중질량이 부가된 경우에는 1차 1.32 %, 2차 6.13 %, 3차 2.02 %의 차이를 보이며 매우 유사한 결과를 도출하였다.
Tables 4, 6에서 집중질량이 부가되지 않은 회전축의 경우에는 C-C와 F-F 경우의 고유진동수가 거의 비슷하게 나타났으나 Tables 5, 7과 같이 집중질량 (디스크)이 부가된 경우에는 부가질량의 영향으로 고유진동수가 감소함을 확인할 수 있었다. 또한, F-F 경우보다 C-C인 경우의 고유진동수가 더 낮아지는 것을 확인할 수 있으며 이는 C-C인 경우에 회전축의 굽힘운동이 F-F인 경우보다 더 부가질량에 의한 효과가 크다는 것을 확인할 수 있다.
Table 8은 Fig. 4와 같이 집중질량이 부가되고 양단 spring-spring 지지 조건의 고유진동수를 비교한 것이다. Table 9는 Fig. 5와 같이 양단이 spring-spring 지지 조건이고, 회전축의 중간지점에 베어링이 추가 배치된 경우의 고유진동수 비교를 나타낸다.
Tables 8, 9에서 양단에만 베어링으로 지지된 경우(2 bearings)에 두 방법(TBM, Ansys) 사이의 고유진동수 차이는 1차 3.53 %, 2차 5.35 %, 3차 4.85 %를 보였고, 축의 중간 지점에 베어링이 추가된 경우(3 bearings)에는 1차 1.48 %, 2차 6.10 %, 3차 0.37 % 의 차이를 보였다. 따라서 모든 경우에 이론식의 결과가 유한요소 결과와 매우 유사한 결과를 보여 이론식의 정확성을 검증할 수 있었다. 또한, 회전축의 중간에 베어링이 추가된 경우(3 bearings)의 고유진동수 변화를 살펴보면, 2차, 3차 고유진동수에서는 거의 차이가 없으나 1차 고유진동수는 약 2배 정도의 차이가 발생하여 1차 모드가 중간 베어링의 영향을 가장 많이 받는 것을 확인할 수 있었다.
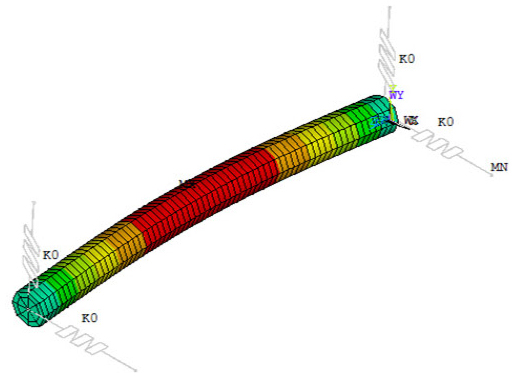
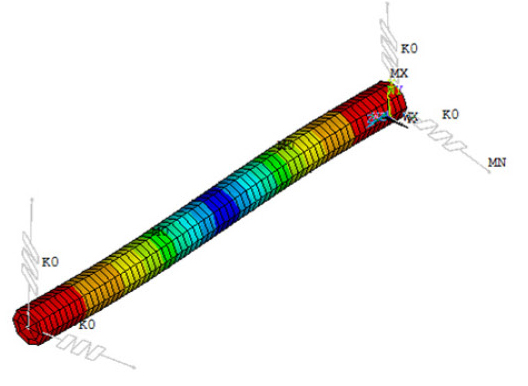
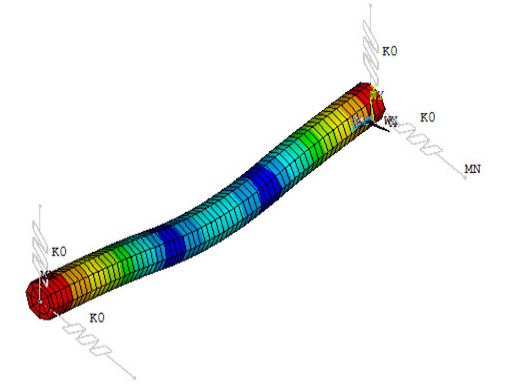
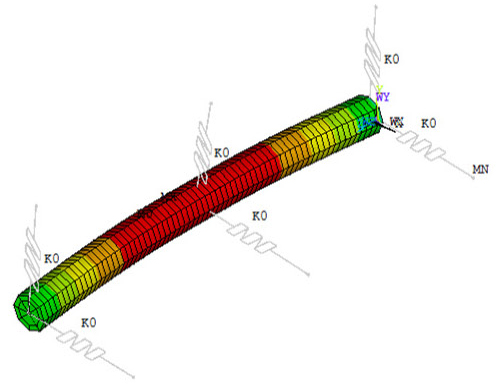
Tables 10, 11, 12는 Fig. 4와 같이 2개의 집중질량(디스크)이 부가되고 회전축의 양단이 베어링으로 지지되고 있는 경우에 대하여 1차, 2차, 3차 모드의 모드형상을 각각 나타낸다.
Tables 13, 14, 15는 Fig. 5와 같이 2개의 집중질량 (디스크)이 부가된 회전축의 양단과 중간 지점에 베어링이 추가되어 지지되고 있는 경우에 대한 1차, 2차, 3차 모드의 모드형상을 각각 나타낸다.
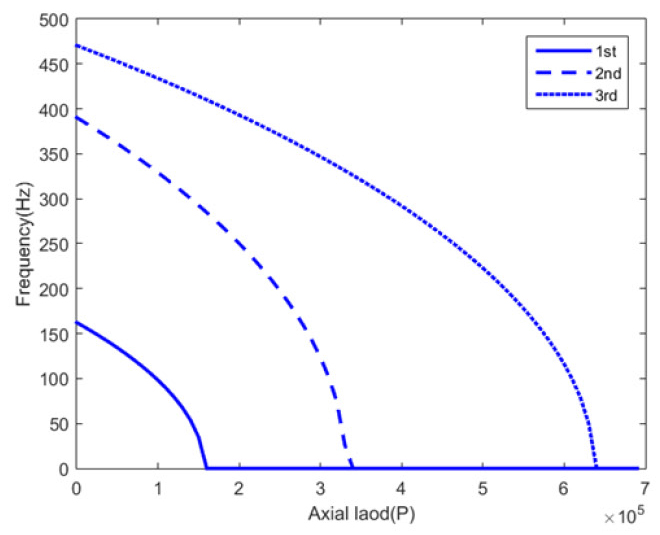
Fig. 7은 압축기(compressor) 회전축의 경우, 축 방향으로 압축하중을 받는 경우, 압축하중과 고유진동수와의 관계를 나타내었다. 압축하중 P는 강성행렬 [K]에서 음의 값으로 나타나므로(부록 참조), P가 증가하면 강성이 감소하여 고유진동수 감소를 초래한다. 특정 P값에서 고유진동수가 0이 되는데, 이를 임계하중 Pcr(critical load)이라 하며 이때 좌굴현상이 발생한다.
4. 결론
이 연구에서 회전축 단면의 형상 및 크기가 임의로 변화하며, 회전축 상에 여러 개의 집중질량이 부가되고, 회전축 임의의 위치에서 여러 개의 베어링으로 지지되어 있으며, 축방향으로 압축하중을 받는 복잡한 회전축계에 대하여 전단변형과 회전관성을 고려한 티모센코 보 이론을 기초로 구조모델링 작업을 수행하였다. 회전축의 전단변형에너지, 회전관성 에너지, 베어링의 탄성에너지와 감쇠 성능, 부가질량의 운동에너지가 고려되었다.
유한요소 해석을 통하여 복잡한 구조물에 대한 해석을 수행함에 있어 모델링과 메시 작업 등에 많은 시간과 노력이 소요되며 변수가 바뀌면 다시 작업을 해야 하는 반면에 이 연구에서 정립된 구조 모델을 사용할 경우에 수치 입력만으로 다양한 변수 변화에 대한 동특성 결과를 빠르고 정확하게 구할 수 있다.
실제 회전축계 시스템의 변수는 그 값을 정확하게 알기 힘들다. 이 연구에서 도출된 구조모델을 활용하면 실험 또는 해석으로 도출된 고유진동수를 가지고 역으로 해당 시스템 변수 및 non-homogeneous 경계조건(즉, 베어링 강성 및 감쇠)을 추정할 수 있다. 또한 다양한 운전 조건에서 좌굴 불안정 현상이 일어나는 압축하중 P값을 예측하여 회전축계의 안전설계에 기여할 수 있을 것으로 기대된다.
Acknowledgments
이 연구는 충남대학교 학술연구비에 의해 지원되었음.
References
- Park, J. H., and Yu, H. H., (1998), Flapwise Bending Vibration of Rotating Timpshenko Beams with Concentrated Mass and Mass Moment of Inertia, Journal of the Korean Society for Noise and Vibration Engineering, 8(2), p353-360.
- Yang, J. S., and Yu, H. H., (1998), Vibration Analysis of Rotating Cantilever Plates with a Concentrated Mass, Transactions of the Korean Society for Noise and Vibration Engineering, 8(6), p1130-1136.
-
Ganguly, S., Neogy, S., and Nandi, A., (2016), On Lumping of Gyroscopic Matrix in Finite Element Analysis of Rotors, Procedia Engineering, 114, p398-405.
[https://doi.org/10.1016/j.proeng.2016.05.149]

- Jun, O. S., Kim, H. G., and Jin, O. K., (1997), Natural Vibration Characteristics of Multi-step Rotating Shaft, Proceedings of the Korean Society of Manufacturing Technology Engineers Annual Autumn Conference, p114-119.
- Turhan, Ö., and Bulut, G., (2006), Linearly Coupled Shaft-torsional and Blade-bending Vibrations in Multi-stage Rotor-blade Systems, Journal of Sound and Vibration, 296(1-2), p292-318.
- Song, O. S., Park, S. Y., Kang, S. H., and Seo, J. S., (2014), Vibration Analysis of a Multi-stage Nonuniform Shaft, Transactions of the Korean Society for Noise and Vibration Engineering, 24(8), p506-508.
- Song, O. S., Park, S. Y., Kang, S. H., Seo, J. S., and Kim, S. H., (2013), Vibration Analysis of a Multi-stage Rotating Shaft Shape, Proceedings of the KSNVE Annual Spring Conference, p730-735.
-
Seo, J. S., Kang, S. H., Park, S. Y., An, C. G., and Song, O. S., (2014), Vibration and Stability Analysis of a Multi-stepped Shaft System of Turbo Compressor, Transactions of the Korean Society for Noise and Vibration Engineering, 24(8), p583-591.
[https://doi.org/10.5050/KSNVE.2014.24.8.583]

- Chen, W. J., and Gunter, E. J., (2007), Introduction to Dynamics of Rotor-bearing Systems, Trafford Publishing, Bloomington.
-
Lee, C. H., (1993), Vibration Analysis of Rotors: Solid Mechanics and Its Applications, Kluwer Academic Publishers, Dordrecht.
[https://doi.org/10.1007/978-94-015-8173-8]

- Librescu, L., and Song, O. S., (2006), Thin-walled Composite Beams: Theory and Application, Springer, Dordrecht.
- Seo, J. S., (2014), Vibration Analysis of Spinning High Power Turbo Compressor Shaft, Chungnam National University Press, Daejeon.
부 록
식 (20) 행렬의 요소

JongTak Jeong received his B.S. and M.S. degree in Mechanical Engineering from Chungnam National University. His research interest is vibration of rotating machinery.

JungSeok Seo received his B.S. and M.S. degree in Mechanical Engineering from Chungnam National University. His research interests encompass vibration control of rotating shaft system.

Ohseop Song received his Ph.D. degree from Virginia Polytechnic Institute & State Univ. He is a professor in Chungnam National University. His research interests include vibration of composite structures and rotor-dynamics.