섭동법에 의한 캡슐열차용 대차의 상하방향 불안정성 연구

2.1 측벽 EDS 시스템의 특성

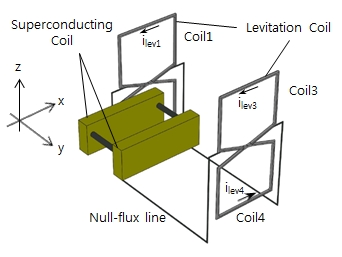
측벽 EDS 부상 캡슐열차의 대차는 Fig. 1에서 보는 바와 같이⁽¹⁾측벽에 설치된 8자 코일에 의해 그 부상특성이 영향을 받으며, 이로 인해 나타나는 부상스프링의 상하방향 강성은 식 (1)에서 보는 바와 같이 선형 성분과 3차 비선형 성분으로 표현된다⁽¹⁾.

Fig. 1

Side wall electrodynamic suspension

여기서 K_avez= k₁z－ k₂z³, K_ascz= k_o1z－ k_o2z³이며 z는 초전도전자석이 장착된 대차의 상하 변위를 나타낸다. K_asc는 측벽 부상코일과 초전도 전자석에 의한 상하방향 부상강성의 주기적인 변동성분의 크기를 나타내며, K_ave는 평균값을 나타낸다. k₁, k₂, k_o1및 k_o2은 각각 K_ave의 선형 성분과 3차 비선형 성분 및 K_osc의 선형 성분과 비선형 성분을 나타내는데, 이들은 모두 z와는 무관하고 차량의 주행속도에 따라 변하는 특며, k₁, k₂, k_o1및 k_o2사이에는 k₁k_o2≈ k₂k_o1인 관계가 있다. 또한, f_lv는 대차가 측벽의 전자석 코일을 지나감에 따라 주기적으로 발생되는 전자기부상력의 주파수이다.

Fig. 1에서 보는 바와 같이 초전도자석이 장착된 자기부상차량의 주행 동특성은 이와 같은 부상특성을 고려하여 검토되어야 하지만 대부분의 경우 계산의 용이성을 위하여 부상스프링을 비선형 성분을 제외하고 변위에 선형적으로 비례하는 선형스프링으로만 가정하여 검토하고 있다^(2~4).

2.2 1-D EDS 부상 대차의 비선형 방정식

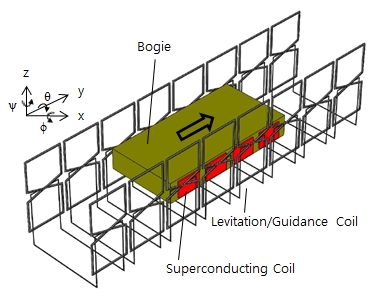
이 연구에서는 이와 같은 선형스프링의 특성보다는 비선형 스프링의 특성에 초점을 두고 측벽 EDS 대차의 주행 중 상하 방향의 비선형 동특성을 파악하고자 하였다. 이 때 주행속도는 임의의 속도로 일정하다고 가정하였으며, 초전도 전자석이 장착된 캡슐열차용 대차는 1자유도 수송체로 가정하였다. 또한, 대차와 궤도 사이에는 전자기력의 특성에 따라 매우 약한 댐핑과 선형 및 3차 비선형 특성을 갖는 스프링이 있다고 가정하였다. 이를 그림으로 표현하면 Fig. 2와 같다⁽⁵⁾.

Fig. 2

Bogie system for capsule train

Fig. 2에 보여주고 있는 캡슐열차용 대차의 상하방향 운동방정식은 대차의 질량 M, 부상댐핑 C_lv및 부상스프링 K_lv를 이용하여 식 (2)와 같이 표현할 수 있다.

식 (2)에 식 (1)을 적용하여 정리하면

와 같이 된다. 계산의 용이성을 위하여 다음과 같은 무차원 파라미터를 도입한다.

즉, δ는 평균 부상스프링의 1차항에 대한 것이고, ε은 평균 부상스프링의 주기 항에 대한 것이며, γ는 평균 부상스프링의 1차 및 3차 항의 비에 관한 것을 나타낸다.

아울러 k₁, k₂, k_o1및 k_o2사이에는 k₁k_o2≈ k₂k_o1인 관계가 있으므로⁽¹⁾ 식 (3)은 다음과 같이 표현될 수 있다.

매우 작은 감쇠를 가지는 자기부상스프링의 특성을 고려하여 식 (5)에서 감쇠항을 제외하면 최종적으로 다음 식 (6)을 얻을 수 있다.

3.1 3차항을 제외한 표준 Mathieu 식

식 (6)에서 3차항을 제외하면 다음 식 (7)과 같은 표준 Mathieu 식이 된다⁽⁶⁾.

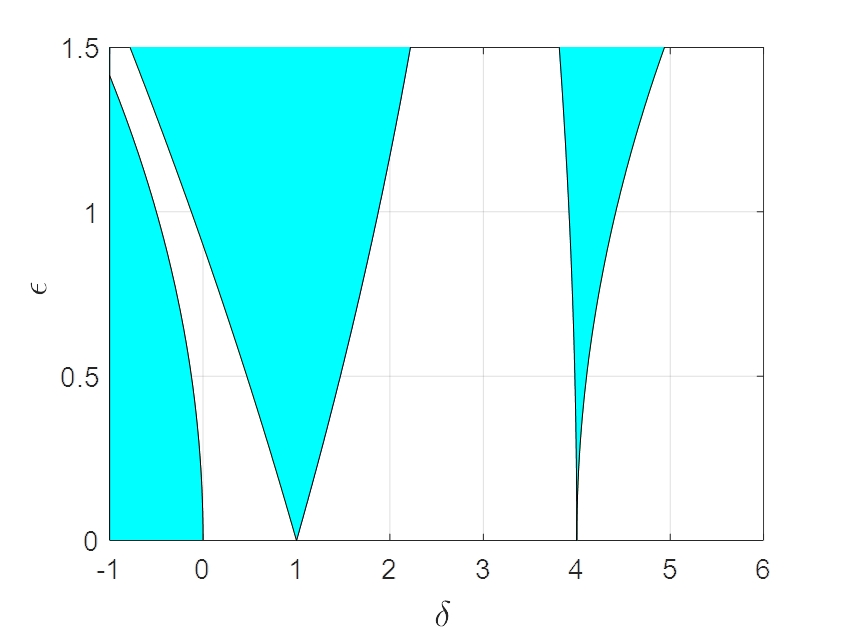
표준 Mathieu 식에 대한 동특성은 여러 자료에서 볼 수 있으며, 대체로 다음과 Fig. 3과 같은 특성을 가진다. 이 그림에서⁽⁷⁾그늘진 영역이 불안정 영역을 나타낸다. 이 그림에서 볼 수 있는 변이곡선(transient curve)의 식은 ε³이상의 고차항을 제외하면 식 (8)과 같이 표현된다^(7,8).

Fig. 3

Unstable zone of Standard Mathieu Equation

3.2 3차항을 포함한 Mathieu 식

이 절에서는 식 (6)에 대하여 섭동법을 이용하여 변이곡선을 찾고자 한다. 일반적으로 고차 비선형항을 가지는 미분방정식의 경우 공진주파수 부근의 전달함수의 모양이 한 쪽으로 기울어지는 현상을 나타내며, 위상 또한 선형 미분방정식과는 약간 다르게 나타난다^(6,7). 또한 고차 비선형항에 의해 Mathieu 식의 불안정성을 그림으로 나타내고 있는 Fig. 2의 변이곡선의 형태가 바뀔 것으로 예상된다.

고차 비선형항이 있는 경우 식 (6)으로부터 변이곡선을 도출하기 위하여 다음 식 (9)와 같이 가정한다^(6,7).

식 (9)를 식 (6)에 대입하여 ϵ에 대해 정리하면 다음과 같다. 여기서는 ϵ³까지만 고려하고, 고차항은 제외한다.

식 (10)의 해는 다음과 같다.

표준 Mathieu식을 만족하는 해의 주기는 2πn(n= 0, 1, 2, …)이므로 식 (13)으로부터 $$ \sqrt{{\delta }_0}$$는 다음과 같이 구해진다.

식 (14)에서 보는 바와 같이 Mathieu 식을 만족하는 해는 매우 많다. 그러나 비선형 시스템의 불안정성을 해석하는 경우 n값이 작을 때 그 특성이 잘 나타나므로 이 연구에서는 n= 0, 1, 2인 경우를 위주로 해석하였다.

(3) n= 2인 경우

n= 2인 경우 식 (14)로부터 δ₁= 4가 되고 이를 식 (10)에 대입하여 초기조건 (10)을 적용하면 다음을 얻을 수 있다.

$\[ \begin{array}{cc}{u}_0 = a \mathrm{c}\mathrm{o}\mathrm{s}\left(2\tau \right),\hfill & b \mathrm{s}\mathrm{i}\mathrm{n}\left(2\tau \right)\hfill \end{array} \]$

(32)

따라서 u₀= acos(2τ)와 u₀= bsin(2τ) 각각에 대하여 다음과 같이 해를 구한다.

(i) u₀= acos(2τ)인 경우

u₀= acos(2τ)를 식 (11)에 대입하여 정리하면

$\[ \ddot{u_1}+4u_1=-a-a {\delta }_1 \mathrm{c}\mathrm{o}\mathrm{s}\left(2\tau \right)-a \mathrm{c}\mathrm{o}\mathrm{s}\left(4\tau \right) \]$

(33)

을 얻게 되고, u₁에 영년항이 존재하지 않으려면 δ₀= 1이 되어야 한다. 그러면 식 (33)은

$\[ \ddot{u_1}+4u_1=-a-a \mathrm{c}\mathrm{o}\mathrm{s}\left(4\tau \right) \]$

(34)

가 되며 u₁의 해는 $$ u_1=-\frac{1}{4}a+\frac{1}{12}a\cos \left(4\tau \right)$$가 된다.

이를 식 (12)에 대입하여 정리하면 다음과 같은 식을 얻는다.

$\[ \begin{array}{c}\ddot{u_2}+4u_2 = a\frac{1}{12}\left(5-36 a^2\gamma -12{\delta }_2\right) \mathrm{c}\mathrm{o}\mathrm{s}\left(2\tau \right)\hfill \\ -a\frac{1}{12}\left(1+12a^2\gamma \right) \mathrm{c}\mathrm{o}\mathrm{s}\left(6\tau \right)\hfill \end{array} \]$

(35)

u₂에 영년항이 없으려면 $$ {\delta }_2=\frac{5}{12}-3a^2\gamma $$가 되어야 하며, 이에 따라 최종해와 변이곡선을 다음과 같이 얻을 수 있다.

$\[ u=\epsilon a \mathrm{c}\mathrm{o}\mathrm{s}\left(2\tau \right)-\frac{1}{12}{\epsilon }^{2}a\left(3- \mathrm{c}\mathrm{o}\mathrm{s}\left(4 \tau \right)\right)+O\left({\epsilon }^3\right) \]$

(36)

$\[ \delta =4+{\epsilon }^2\left(\frac{5}{12}-3 a^2\gamma \right)+O\left({\epsilon }^3\right) \]$

(37)

(ii) u₀= asin(2τ)인 경우

u₀= asin(2τ)를 식 (11)에 대입하여 정리하면

$\[ \ddot{u_1}+4u_1=-b {\delta }_1 \mathrm{s}\mathrm{i}\mathrm{n}\left(2\tau \right)+b \mathrm{s}\mathrm{i}\mathrm{n}\left(4\tau \right) \]$

(38)

을 얻게 되고, u₁에 영년항이 존재하지 않으려면 δ₁= 0이 되어야 한다. 그러면 식 (38)은

$\[ \ddot{u_1}+4 u_1=-b \mathrm{s}\mathrm{i}\mathrm{n}\left(4\tau \right) \]$

(39)

가 되며 u₁의 해는 $$ u_1=\frac{1}{12}b\sin \left(4\tau \right)$$가 된다.

이를 식 (12)에 대입하여 정리하면 다음과 같은 식을 얻는다.

$\[ \begin{array}{c}\ddot{u_2}+u_2 = -b\frac{1}{12}\left(1+36 b^2\gamma +12{\delta }_2\right) \mathrm{s}\mathrm{i}\mathrm{n}\left(2\tau \right)\hfill \\ -b\frac{1}{12}\left(1-12b^2\gamma \right) \mathrm{s}\mathrm{i}\mathrm{n}\left(6\tau \right)\hfill \end{array} \]$

(40)

u₂에 영년항이 없으려면 $$ {\delta }_2=-\left(\frac{1}{12}+3b^2\gamma \right)$$가 되어야 한다. 따라서 최종해와 변이곡선을 다음과 같이 얻을 수 있다.

$\[ u=\epsilon b \mathrm{s}\mathrm{i}\mathrm{n}\left(2\tau \right)-\frac{1}{12}{\epsilon }^2 b \mathrm{s}\mathrm{i}\mathrm{n}\left(4\tau \right)+O\left({\epsilon }^3\right) \]$

(41)

$\[ \delta =4-{\epsilon }^2\left(\frac{1}{12}+3 b^2\gamma \right)+O\left({\epsilon }^3\right) \]$

(42)

이상에서 해석한 바와 같이 δ와 ε사이의 관계를 ε³이상의 고차항을 제외하고 정리하면 최종적으로 다음과 같이 표현된다.

$\[ \begin{array}{c}\delta =-\frac{1}{2}{\epsilon }^2\hfill \\ \delta =1-\epsilon -\frac{1}{8}\left(1+6 a^2\gamma \right){\epsilon }^2\hfill \\ \delta =1+\epsilon -\frac{1}{8}\left(1+6 b^2\gamma \right){\epsilon }^2\hfill \\ \delta =4+\left(\frac{5}{12}-3 a^2\gamma \right) {\epsilon }^2\hfill \\ \delta =4-\left(\frac{1}{12}+3 b^2\gamma \right) {\epsilon }^2\hfill \end{array} \]$

(43)

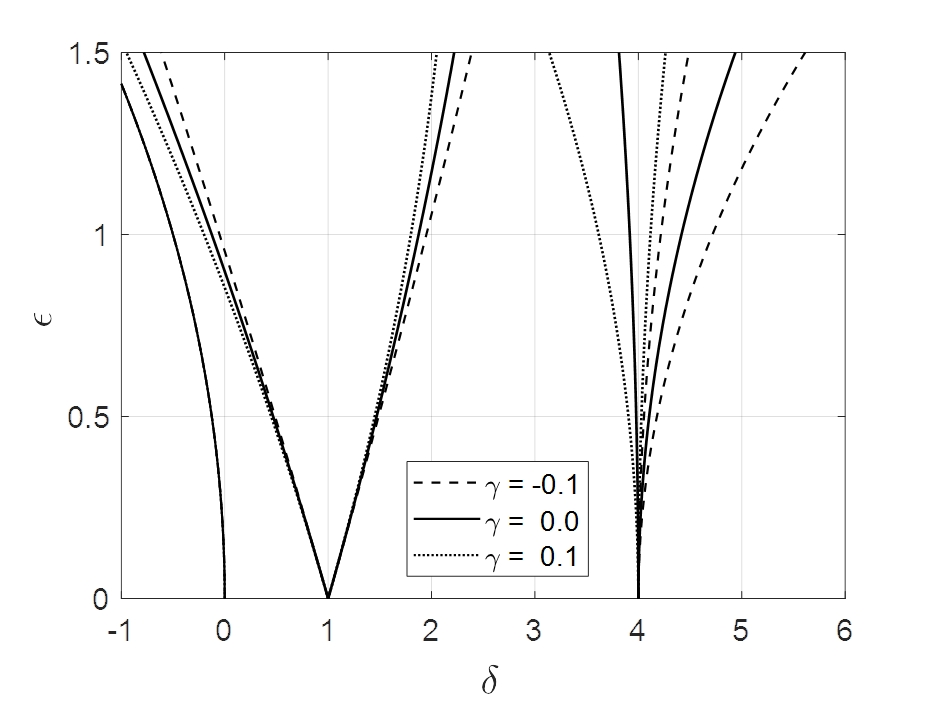
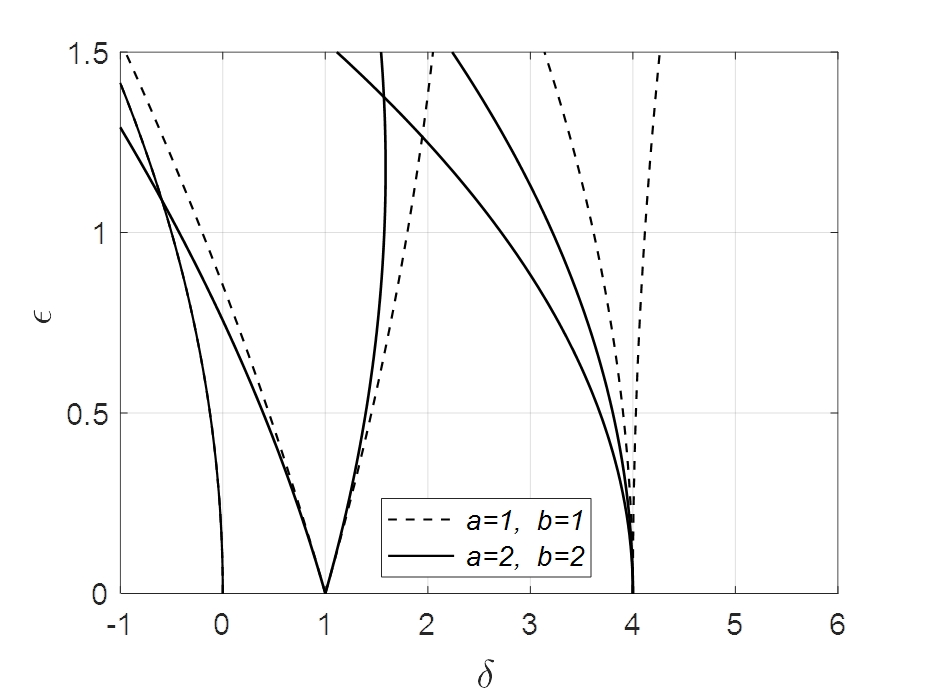
식 (8)과 식 (43)을 비교해 보면 첫 번째 곡선은 $$ \delta =-\frac{1}{2}{ϵ}^2$$로서 동일한 곡선을 나타내고 있으며, 그 외의 곡선은 ε²항에서 a와 b및 γ에 따라 다르게 나타남을 알 수 있다. a와 b는 초기조건과 관계가 있으며, γ는 평균 부상스프링의 1차 및 3차 항의 비에 관한 것이므로 이들의 변화에 따른 불안정 영역과 안정영역 사이의 변이곡선을 Fig. 3및 Fig. 4와 같이 나타낼 수 있다.

Fig. 4

Unstable zone (a= 1, b= 1)

Fig. 4는 a= 1, b= 1인 경우를 나타낸다. γ값이 0인 경우는 Fig. 3에서 보는 바와 같이 표준 Mathieu 식의 경우와 동일하게 나타남을 볼 수 있으며, γ값이 0보다 작은 경우에는 변이곡선이 오른쪽으로 기울어지고, 0보다 큰 경우에는 왼쪽으로 기울어짐을 알 수 있다.

Fig. 5는 γ= 0.1인 경우를 나타내고 있다. 초기조건과 관계가 있는 a와 b에 대하여 a= 2, b= 2인 경우 a= 1, b= 1인 경우보다는 변이곡선이 왼쪽으로 기울어짐을 알 수 있다. 즉, 초기조건에 따라 불안정 영역이 달라짐을 알 수 있다.

Fig. 5

Unstable zone (γ= 0.1)

따라서, 초전도전자석-부상코일 설계 시 부상스프링에 의한 대차의 비선형 불안정성을 반드시 고려해야 하며, 특히 초기조건과 평균 부상스프링의 1차 및 3차항의 비에 유의하여야 함을 알 수 있다.

3.3 안정성에 영향을 주는 요소에 대한 검토

앞 절에서 언급한 바와 같이 EDS 자기부상 대차의 비선형 불안정성을 해소하기 위해서는 초기조건과 평균 부상스프링의 1차 및 3차 항의 비에 유의하여 설계를 수행해야 한다.

자기부상열차가 저속에서 바퀴를 이용하여 주행하다가 정해진 주행속도에서 부상을 하게 되는데, 이때 열차의 무게중심의 변화가 이 연구의 초기조건과 관계가 있다. 즉, 바퀴 주행 시의 무게중심과 부상 주행 시의 무게중심의 변화가 급격히 이루어지지 않도록 설계하거나 혹은 그 변화가 최소화되도록 하는 것이 중요하다. 이는 캡슐열차에 탑재되는 초전도 전자석의 위치와 주행 바퀴의 접는 메커니즘 및 부상코일, 추진코일의 배치와 관계가 있다.

한편, 평균 부상스프링의 1차 항과 3차 항의 비 또한 중요한 사항인데, 이는 평균 부상스프링의 특성으로부터 결정된다. 부상스프링의 특성을 결정하는 가장 중요한 요소는 초전도 전자석의 성능 즉, 초전도 전자석을 이루는 금속의 조성과 매우 큰 관계가 있다. 초전도 전자석의 성능 및 경제성을 동시에 판단하여 고려해야 할 사항이다. 초전도 전자석의 성능과 함께 부상스프링의 특성을 결정짓는 중요한 요소는 측벽 부상코일의 배치에 관한 것이다. 즉, 초전도 전자석과 부상코일의 거리에 따라 부상스프링의 특성이 변하게 된다. 아울러 부상코일에 흐르는 전류 또한 부상 스프링의 특성을 변화시키는 요소이다. 이 외에도 여러 가지 많은 요소가 부상스프링의 특성을 변화시킬 수 있는데, 가능한 한 이러한 요소들을 최대로 반영하여 대차의 비선형 불안정성을 검토해야 할 것으로 보인다.