병진 및 회전 운동을 하는 내향 외팔보의 모델링 및 진동해석

1. 서 론

자동차에 여러가지 편의 기능들이 연구되고 적용되면서 주요 부품인 타이어도 지능형 구성요소로 발전하고 있다. 자동차는 운전자에게 여러 정보를 제공하는데, 그 중 주행 중 타이어 상태를 알려주는 TPMS(타이어 압력 감지 시스템) 장착이 의무화되어 있다. 현재 TPMS는 소형 배터리를 사용하고 있어 주기적인 교체를 필요로 한다. 이것은 사용자에게 비용의 증가와 번거로움을 야기시키므로 배터리를 대신하거나 수명을 연장시킬 수 있는 에너지 공급 장치에 대한 관심이 증대되고 있으며 이와 관련한 연구가 활발하게 이루어지고 있다.

이 연구는 운동에너지를 이용하는 압전 에너지 하베스팅 장치와 같이 자동차 타이어에의 적용을 목적으로 하는 발전시스템을 위한 기초적인 연구로, 회전과 병진운동을 하는 내향 외팔보를 모델링하고 진동 특성을 파악하였다. 이 연구와 유사한 주제의 연구들은 그 동안 여러 연구자들에 의해 수행되어 왔다. Mostaghel et al.⁽¹⁾는 회전하는 내향 외팔보의 진⁽²⁾는 Mostaghel et al.의 연구 결과를 발전시켜서 장착각을 고려하여 내향 외팔보의 진동특성 변화에 관한 연구를 수행하였다. Naguleswaran⁽³⁾은 내향 외팔보의 경계조건 변화에 따른 진동 특성을 연구하였다. Turhan et al.⁽⁴⁾은 장착각을 가진 내향 외팔보의 각속도 변화에 따른 안정성 해석을 수행하였다. Lee et al.⁽⁵⁾는 집중질량과 초기 비틀림각을 고려한 내향 외팔보의 진동특성을 연구하였다. Oh et al.⁽⁶⁾은 장착각과 집중질량을 고려하여서 내향 외팔보의 진동특성을 연구하였다. 이 같은 기존의 연구들은 회전운동 효과만을 고려하여 연구가 수행되었고 자동차 바퀴의 운동과 같이 병진과 회전 운동이 동시에 발생하는 운동으로 인한 내향 외팔보의 진동해석은 수행되지 않았다. 또한 이제까지 이전 어느 논문에서도 병진운동과 회전운동의 연성 현상으로 인해 발생하는 가진주파수 변화가 연구되지 않았다.

이 논문에서는 병진 및 회전운동을 동시에 하는 내향 외팔보의 모델링을 수행하고, 그의 진동특성을 조사하였다. 이 시스템의 운동방정식⁽⁷⁾은 복합변형변수 모델링과 Kane의 방법을 이용하여 유도하였고, 상용 프로그램인 ANSYS와 Recurdyn을 통해 얻은 결과와 비교해 제안된 모델의 정확성을 검증하였다. 또한 병진 및 회전운동이 연성됨으로써 가진주파수 분기현상이 발생하고 이 주파수에서 공진현상이 발생하는 것을 규명하였다.

2. 시스템의 형태

2.1 시스템 소개

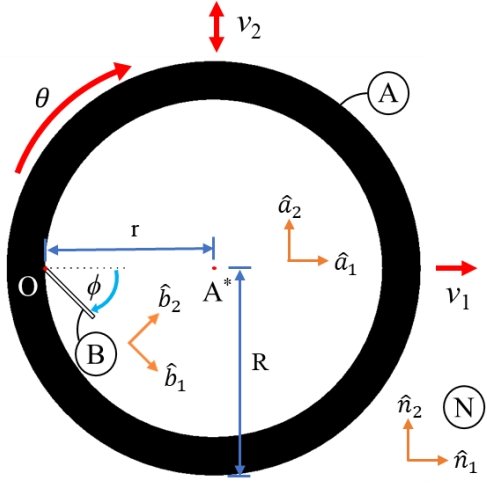
Fig. 1은 제안된 시스템의 모습을 보여주고 있다. Fig. 1에는 세 좌표계가 나타나 있는데 $$ \left({\widehat{n}}_1,{\widehat{n}}_2,{\widehat{n}}_3\right)$$는 절대기준틀의 좌표계, $$ \left({\widehat{a}}_1,{\widehat{a}}_2,{\widehat{a}}_3\right)$$는 타이어 림을 나타내는 기준틀 A의 좌표계, 그리고 $$ \left({\widehat{b}}_1,{\widehat{b}}_2,{\widehat{b}}_3\right)$$는 기준틀 A의 중심점인 A^*에서 r만큼 떨어진 O점에 장착각 ϕ의 기울기로 설치된 외팔보 고정단 단면 기준틀 B에 고정된 좌표계이다.

Fig. 1

Configuration of an inward cantilever beam mounted on reference frame A with a setting angle ϕ

2.3 운동방정식

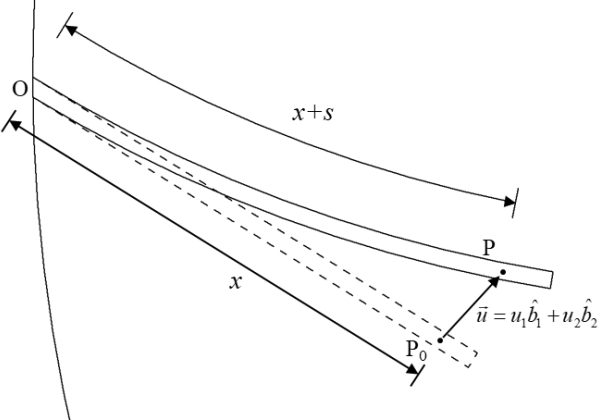
Fig. 2는 Fig. 1의 강체 A에 부착된 외팔보 변형 시 형상을 함께 보여주고 있다. x는 외팔보와 고정점 O로부터 변형 전 중립 축 상의 임의의 점까지의 거리, s는 중립 축 상의 임의의 점에서 보가 인장된 길이를 나타낸다. 비틀림 변형은 매우 작아 무시할 수 있다 가정하였다. P₀는 변형 후 x+s의 길이를 갖는 P의 위치로 이동한다. s와 u는 Rayleigh-Ritz 근사화 방법을 통해 다음과 같이 나타낼 수 있다.

Fig. 2

Undeformed and deformed shapes of the inward cantilever beam

$\[ s\left(x,t\right)=\sum _{j=1}^{{\mu }_1}{\varphi }_{1j}\left(x\right)q_{1j}\left(t\right) \]$

(4)

$\[ u_2\left(x,t\right)=\sum _{j=1}^{{\mu }_2}{\varphi }_{2j}\left(x\right)q_{2j}\left(t\right) \]$

(5)

여기서 ϕ_1j, ϕ_2j는 보의 j번째 모드함수, q_1j, q_2j는 j번째 일반좌표, 그리고 μ₁, μ₂는 각각의 일반좌표의 수이다.

P의 속도 $$ {\overrightarrow{v}}^P$$는 다음과 같이 나타낼 수 있다.

$\[ \begin{array}{c}{\overrightarrow{v}}^P={\left[\begin{array}{c}{\dot{u}}_1+\omega u_2+\mathrm{c}\mathrm{o}\mathrm{s}\varphi \left(v_1\mathrm{c}\mathrm{o}\mathrm{s}\theta -v_2\mathrm{s}\mathrm{i}\mathrm{n}\theta \right)\hfill \\ -\mathrm{s}\mathrm{i}\mathrm{n}\varphi \left(v_1\mathrm{s}\mathrm{i}\mathrm{n}\theta +v_2\mathrm{c}\mathrm{o}\mathrm{s}\theta +\omega r\right)\hfill \end{array}\right]}^{{\hat{b}}_1}\hfill \\ +{\left[\begin{array}{c}{\dot{u}}_2-\omega \left(x+u_1\right)+\mathrm{s}\mathrm{i}\mathrm{n}\varphi \left(v_1\mathrm{c}\mathrm{o}\mathrm{s}\theta -v_2\mathrm{s}\mathrm{i}\mathrm{n}\theta \right)\hfill \\ +\mathrm{c}\mathrm{o}\mathrm{s}\varphi \left(v_1\mathrm{s}\mathrm{i}\mathrm{n}\theta +v_2\mathrm{c}\mathrm{o}\mathrm{s}\theta +\omega r\right)\hfill \end{array}\right]}^{{\hat{b}}_2}\hfill \end{array} \]$

(6)

위 식을 시간에 대해 미분하여 P의 가속도 $$ {\overrightarrow{a}}^P$$를 구하면 다음과 같다.

$\[ \begin{array}{c}{\overrightarrow{a}}^P={\left[\begin{array}{c}{\ddot{u}}_1+\dot{\omega }{u}_2+2\omega {\dot{u}}_2+\mathrm{c}\mathrm{o}\mathrm{s}\varphi {\omega }^{2}r-{\omega }^2\left(x+u_1\right)\hfill \\ +\mathrm{c}\mathrm{o}\mathrm{s}\varphi \left({\dot{v}}_1\mathrm{c}\mathrm{o}\mathrm{s}\theta -{\dot{v}}_2\mathrm{s}\mathrm{i}\mathrm{n}\theta \right)\hfill \\ -\mathrm{s}\mathrm{i}\mathrm{n}\varphi \left({\dot{v}}_1\mathrm{s}\mathrm{i}\mathrm{n}\theta +{\dot{v}}_2\mathrm{c}\mathrm{o}\mathrm{s}\theta +\dot{\omega }r\right)\hfill \end{array}\right]}^{{\hat{b}}_1}\hfill \\ +{\left[\begin{array}{c}{\ddot{u}}_2-\dot{\omega }\left(x+u_1\right)-2\omega {\dot{u}}_1+\mathrm{s}\mathrm{i}\mathrm{n}\varphi {\omega }^{2}r-{\omega }^2{u}_2\hfill \\ +\mathrm{s}\mathrm{i}\mathrm{n}\varphi \left({\dot{v}}_1\mathrm{c}\mathrm{o}\mathrm{s}\theta -{\dot{v}}_2\mathrm{s}\mathrm{i}\mathrm{n}\theta \right)\hfill \\ +\mathrm{c}\mathrm{o}\mathrm{s}\varphi \left({\dot{v}}_1\mathrm{s}\mathrm{i}\mathrm{n}\theta +{\dot{v}}_2\mathrm{c}\mathrm{o}\mathrm{s}\theta +\dot{\omega }r\right)\hfill \end{array}\right]}^{{\hat{b}}_2}\hfill \end{array} \]$

(7)

식 (6)과 (7)에서 u₁은 근사화를 위해 s와 u₂로 나타내야 하며, 다음의 관계식이 유도되어⁽⁸⁾사용된다.

$\[ s=u_1+\frac{1}{2}{\int }_0^x{\left(\frac{\partial u_2}{\partial \sigma }\right)}^{2}d\sigma \]$

(8)

외팔보의 Kane에 의한 운동방정식⁽⁸⁾은 다음과 같이 표현된다.

$\[ \begin{array}{cc}{F_i}^{*}+F_i=0& \left(i=1,\cdots ,\mu \right)\end{array} \]$

(9)

여기서

$\[ {F_i}^{*}=-{\int }_0^L\left(\frac{\partial {\overrightarrow{v}}^P}{\partial {\dot{q}}_i}\right)\cdot \rho {\overrightarrow{a}}^{P}dx \]$

(10)

$\[ F_i=-\frac{\partial U}{\partial q_i} \]$

(11)

여기서 U는 탄성에너지를 나타내며 다음과 같다.

$\[ \begin{array}{c}U=\frac{1}{2}{\int }_0^{L}EA{\left(\frac{ds}{dx}\right)}^{2}dx\hfill \\ +\frac{1}{2}{\int }_0^{L}EI{\left(\frac{d^2{u}_2}{{dx}^2}\right)}^{2}dx\hfill \end{array} \]$

(12)

여기서 E는 탄성계수, A는 단면적, I는 면적 2차 모멘트를 나타낸다.

이제 속도, 가속도, 그리고 탄성에너지를 식 (10)과 (11)에 대입하여 식 (9)를 정리하면 다음과 같은 운동방정식을 얻을 수 있다.

$\[ \begin{array}{c}\sum _{j=1}^{{\mu }_1}{K}_{ij}^S{q}_{1j}-{\omega }^2\sum _{i=1}^{{\mu }_1}{M}_{ij}^{11}{q}_{1j}+\sum _{j=1}^{{\mu }_1}{M}_{ij}^{11}{\ddot{q}}_{1j}\hfill \\ +\dot{\omega }\sum _{j=1}^{{\mu }_2}{M}_{ij}^{12}{q}_{2j}+2\omega \sum _{j=1}^{{\mu }_2}{M}_{ij}^{12}{\dot{q}}_{2j}-{\omega }^2{Q}_{1i}\hfill \\ +{\left[\begin{array}{c}cos\varphi {\omega }^{2}r+cos\varphi \left({\dot{v}}_1\mathrm{c}\mathrm{o}\mathrm{s}\theta -{\dot{v}}_2\mathrm{s}\mathrm{i}\mathrm{n}\theta \right)\hfill \\ -sin\varphi \left({\dot{v}}_1\mathrm{s}\mathrm{i}\mathrm{n}\theta +{\dot{v}}_2\mathrm{c}\mathrm{o}\mathrm{s}\theta +\dot{\omega }r\right)\hfill \end{array}\right]}^{P_{1i}}\hfill \\ =0\hfill \\ \left(i=1,\cdots ,{\mu }_1\right)\hfill \end{array} \]$

(13)

$\[ \begin{array}{c}{\omega }^2\sum _{j=1}^{{\mu }_2}{K}_{ij}^{GB}{q}_{2j}+\sum _{j=1}^{{\mu }_2}{K}_{ij}^B{q}_{2j}\hfill \\ +\sum _{j=1}^{{\mu }_2}{M}_{ij}^{22}{\ddot{q}}_{2j}-{\omega }^2\sum _{i=1}^{{\mu }_2}{M}_{ij}^{22}{q}_{2j}\hfill \\ -{\left[\begin{array}{c}cos\varphi {\omega }^{2}r+cos\varphi ({\dot{v}}_{1}cos\theta -\underset{\_}{{\dot{v}}_2\mathrm{s}\mathrm{i}\mathrm{n}\theta })\hfill \\ -sin\varphi ({\dot{v}}_{1}sin\theta +{\dot{v}}_{2}cos\theta +\dot{\omega }r)\hfill \end{array}\right]}^{\sum _{j=1}^{{\mu }_2}{K}_{ij}^{GA}{q}_{2j}}\hfill \\ -\dot{\omega }\sum _{j=1}^{{\mu }_1}{M}_{ij}^{21}{q}_{1j}-2\omega \sum _{j=1}^{{\mu }_1}{M}_{ij}^{21}{\dot{q}}_{1j}-\dot{\omega }{Q}_{2i}\hfill \\ +{\left[\begin{array}{c}sin\varphi {\omega }^{2}r+sin\varphi ({\dot{v}}_{1}cos\theta -\underset{\_}{{\dot{v}}_2\mathrm{s}\mathrm{i}\mathrm{n}\theta })\hfill \\ +cos\varphi ({\dot{v}}_{1}sin\theta +{\dot{v}}_{2}cos\theta +\dot{\omega }r)\hfill \end{array}\right]}^{P_{2i}}\hfill \\ =0\hfill \\ (i=1,\cdots ,{\mu }_2)\hfill \end{array} \]$

(14)

식 (13)은 s방향, 식 (14)는 u₂방향 운동방정식이다. 여기서

$\[ M_{ij}^{ab}\equiv {\int }_0^L\rho {\varphi }_{ai}{\varphi }_{bi}dx \]$

(15)

$\[ K_{ij}^S\equiv {\int }_0^{L}EA{\varphi }_{1i,x}{\varphi }_{1j,x}dx \]$

(16)

$\[ K_{ij}^B\equiv {\int }_0^{L}EI{\varphi }_{2i,xx}{\varphi }_{2j,xx}dx \]$

(17)

$\[ K_{ij}^{GA}\equiv {\int }_0^L\rho \left(L-x\right){\varphi }_{2i,x}{\varphi }_{2j,x}dx{q}_{2j} \]$

(18)

$\[ K_{ij}^{GB}\equiv \frac{1}{2}{\int }_0^L\rho \left(L^2-x^2\right){\varphi }_{2i,x}{\varphi }_{2j,x}dx{q}_{2j} \]$

(19)

$\[ Q_{ai}\equiv {\int }_0^L\rho x{\varphi }_{ai}dx \]$

(20)

$\[ P_{ai}\equiv {\int }_0^L\rho {\varphi }_{ai}dx \]$

(21)

3. 수치 해석

3.1 유도된 방정식의 검증

앞장에 유도된 운동방정식의 정확성을 검증하기 위해 수치 예제를 통해 진동 및 과도 해석을 수행하여 얻은 결과를 상용 프로그램을 이용하여 구한 결과와 비교하였다.

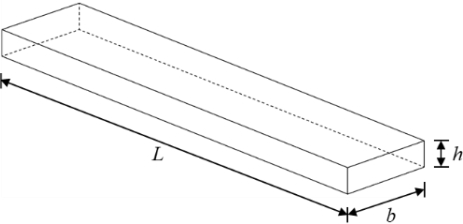
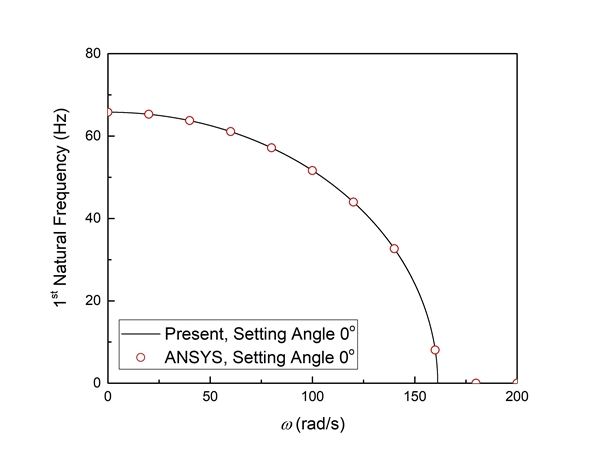
진동해석은 ANSYS Mechanical APDL v19.1을 사용하였으며, 유한요소 모델은 beam 188 요소들을 사용하였다. Fig. 3과 Table 1은 해석에 사용된 파라미터와 물성치들을 보여준다. 해당 예제에 사용된 재료의 물성은 steel의 물성을 사용하였다. 먼저 장착각 ϕ가 0°인 경우 각속도에 따른 고유진동해석을 수행하였다. 제안된 해석 모델과 ANSYS를 사용해 얻은 결과는 Fig. 4와 Table 2에 보여주고 있으며, 상대오차 0.002% 미만의 일치도를 보여준다.

Fig. 3

Configuration of cantilever beam

Table 1

The properties used in the analysis

Fig. 4

Comparison of the first natural frequency obtained with proposed model and ANSYS

Table 2

Comparison of the 1st Natural frequencies

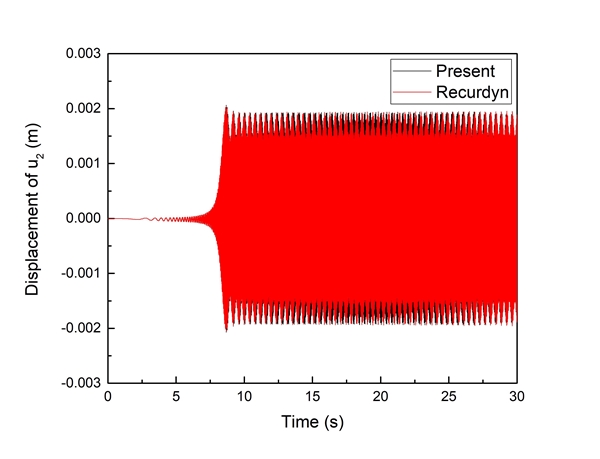
과도 해석은 Recurdyn V9R1을 사용한 결과들과 비교하였으며, 그 유한요소 모델은 Force의 Beam(G) 요소들을 사용하였다. 이 해석에 사용된 물성치들은 진동해석의 경우와 같다. 과도해석에서 속도의 경우, 0초 ~ 10초는 가속을 하며 10초 ~ 30초는 일정한 속도가 유지되는 spin-up motion을 적용하였다. Fig. 5는 모델 장착각이 0°이고 정상상태 시의 각속도가 55 rad/s에 다다르는 spin-up 운동을 하는 0초 ~ 30초 동안 제안된 모델과 Recurdyn을 사용하여 구한 결과를 비교하여 나타낸 그림이다. Table 3은 과도해석 결과에서 20초 ~ 30초 구간에서 제안된 모델과 Recurdyn 해석 결과의 최대 진폭 상대오차를 나타낸 것으로, 1.03 % 정도의 미세한 차이만을 보여주고 있다. 이상의 진동해석과 과도해석 결과 비교를 통해 제시된 모델링 방법의 정확성과 신뢰성을 파악할 수 있었다.

Fig. 5

Comparison of transient analysis results obtained with proposed model and Recurdyn

Table 3

Comparison of the transient analysis results

3.2 가진주파수 분기현상

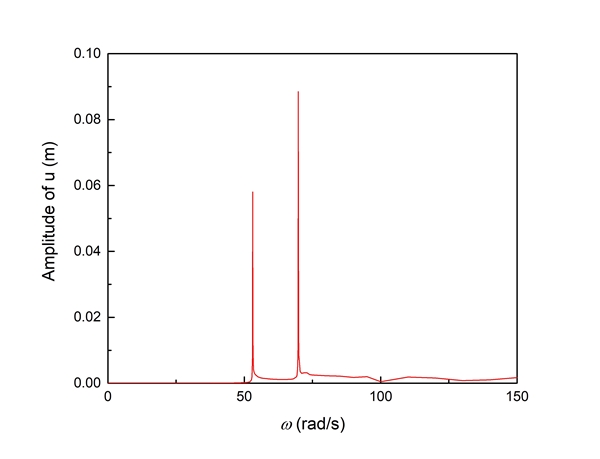
이 장에서는 제안된 모델의 장착각이 0°일 때 각속도 별 과도해석을 수행하고, 해석결과 중 20 ~ 30초 구간에서 최대 진폭을 계산하여 Fig. 6에 나타냈다. 이를 통해 0 rad/s ~ 150 rad/s 범위에서 진폭이 크게 나오는 2개의 구간이 존재함을 확인할 수 있다. 이와 같은 현상은 식 (14)의 밑줄로 표시된 두 항에 의해 발생하는 것으로서 병진방향 성분과 회전방향 성분의 곱은 삼각함수 곱셈 공식에 의해 2개의 삼각함수 성분으로 나뉘게 되어 다음과 같이 나타낼 수 있다.

Fig. 6

Transient Analysis result by angular velocity

$\[ \begin{array}{c}{\dot{v}}_2\mathrm{s}\mathrm{i}\mathrm{n}\theta =C \overline{\omega }\mathrm{c}\mathrm{o}\mathrm{s}\left(\overline{\omega }t\right)\cdot \mathrm{s}\mathrm{i}\mathrm{n}\omega t\hfill \\ =\frac{C \overline{\omega }}{2}\left[\mathrm{s}\mathrm{i}\mathrm{n}\left(\overline{\omega }+\omega \right)t-\mathrm{s}\mathrm{i}\mathrm{n}\left(\overline{\omega }-\omega \right)t\right]\hfill \end{array} \]$

(22)

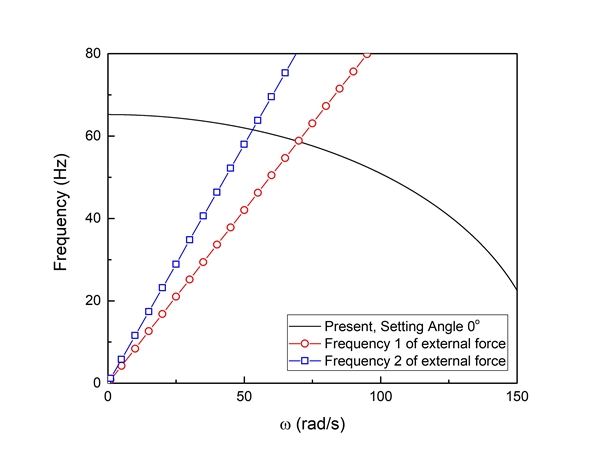
따라서 병진운동과 회전운동의 연성으로 가진력은 2개의 주파수를 갖게 되고, Fig. 7에서 보듯 제안된 모델의 1차 고유진동수와 가진주파수가 만나게 되는 2개의 지점이 생기는데 이 지점들의 각속도들로 운동을 하면 공진이 발생하게 되며 Fig. 6이 보여주는 결과처럼 큰 진폭이 발생하는 구간이 2개 생기게 된다.

Fig. 7

The first natural frequency locus and two excitation frequencies generated by coupled motion

3.3 장착각 별 고유진동수의 변화 추이

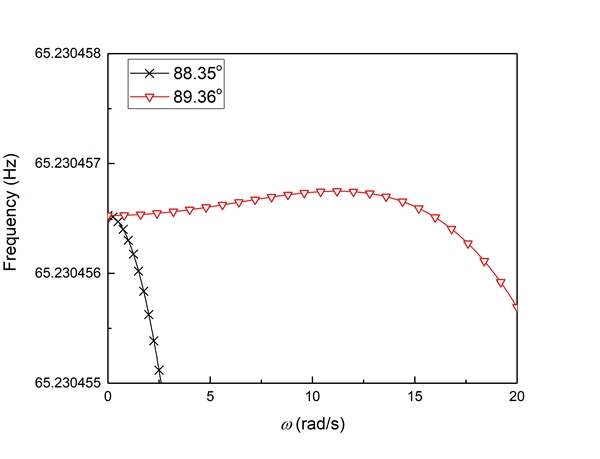
앞장에서는 임의 장착각을 갖는 내향 외팔보의 운동방정식을 유도하였다. 내향 외팔보의 경우에는 장착각별로 회전각속도에 따른 고유진동수의 변화 추이가 다르게 나타난다. 변화 추이는 크게 3가지로 구분할 수 있다. 첫 번째는, 장착각이 0° ~ 88.35°의 범위에서는 회전 각속도가 증가함에 따라서 고유진동수가 단순 감소하는 경향을 보여준다.

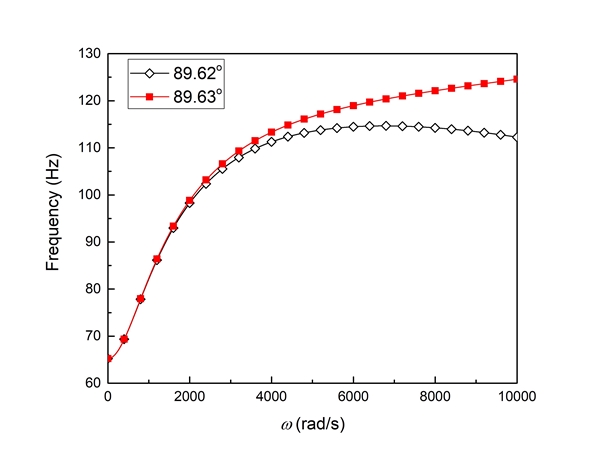
두 번째는, 장착각이 88.36° ~ 89.62° 범위인 경우로 회전각속도가 증가함에 따라 고유진동수가 증가하다가 감소하는 경향을 보여준다. 세 번째는, 장착각 89.63° 이상인 경우로 회전각속도가 증가함에 따라 고유진동수가 단순 증가하는 경향을 보여준다. Fig. 8과 Fig. 9는 각 경향 별 경계 장착각들에서의 고유진동수 변화를 보여주고 있다.

Fig. 8

The first setting angle range of the first natural frequency characteristic change

Fig. 9

The second setting angle range of the first natural frequency characteristic change

4. 결 론

이 연구에서는 회전 및 병진운동을 하는 시스템의 가진주파수 분기현상을 규명하고 이를 이용해 공진현상을 유도하여 에너지 하베스팅 시스템에 적용할 수 있음을 보였다. 가진주파수 분기현상에 의해 회전운동 주파수와 병진운동 주파수는 서로 가감되어 두 개의 주파수 항으로 나타나게 되며 이는 에너지 하베스팅 장치를 설계하기 위해 공진주파수를 결정할 때 고려해야 할 핵심적인 사항이다. 에너지 하베스팅을 목적으로 큰 떨림이 요구되는 경우 공진의 발생을 필요로 한다. 그런데 자동차 바퀴 같이 낮은 회전각속도로 움직이는 시스템의 경우 시스템 고유진동수가 높으면 공진을 유도하기 어렵다. 그렇기 때문에 회전각속도 증가에 따라 고유진동수의 감소 폭이 큰 장착각이 0°인 모델을 사용할 수가 있다. 그러나 만일 동작 조건 내에서 고유진동수가 0에 도달하면 동적 좌굴 현상이 일어나 설계 시에 목표했던 시스템 거동과 다른 경향이 나타날 수 있다. 그러므로 주파수 분기 현상과 장착각 변화에 따른 고유진동수 변화 추이를 동시에 고려하여 외팔보 구조형태를 갖는 에너지 하베스팅 기구를 설계하는 것이 필요할 것이다.

Acknowledgments

A part of this paper was presented and selected as one of best papers at the KSNVE 2018 Annual Autumn Conference

이 연구는 산업통상자원부(MOTIE)와 한국에너지기술평가원(KETEP)의 지원을 받아서 수행한 연구 과제입니다(No. 2018201010636A).

References

• Mostaghel, N., and Tadjbakhsh, I., (1973), Buckling of Rotating Rods and Plates, International Journal of Mechanical Sciences, 15(6), p429-434. [https://doi.org/10.1016/0020-7403(73)90026-x]
• Fox, C. H. J., and J. S. Burdess, (1979), The Natural Frequencies of a Thin Rotating Cantilever with Offset Root, Journal of Sound Vibration, 65(2), p151-158. [https://doi.org/10.1016/0022-460x(79)90509-1]
• Naguleswaran, S., (1997), Out-of-plane Vibration of a Uniform Euler-Bernoulli Beam Attached to the Inside of a Rotating Rim, Journal of Sound Vibration, 200(1), p63-81. [https://doi.org/10.1006/jsvi.1996.0667]
• Turhan, Ö., and Bulut, G., (2005), Dynamic Stability of Rotating Blades (Beams) Eccentrically Clamped to a Shaft with Fluctuating Speed, Journal of Sound and Vibration, 208, p945-964.
• Lee, G. H., and Yoo, H. H., (2015), Vibration Analysis of Rotating Pre-twisted Inward Beams with a Concentrated Mass, Transactions of the Korean Society for Noise and Vibration Engineering, 25(6), p384-390. [https://doi.org/10.5050/ksnve.2015.25.6.384]
• Oh, Y. T., and Yoo, H. H., (2016), Vibration Analysis of Rotating Cantilever Beams Orienting Inward, Journal of Mechanical Science and Technology, 30(9), p4177-4184. [https://doi.org/10.1007/s12206-016-0829-7]
• Yoo, H. H., Ryan, R. R., and Scott, R. A., (1995), Dynamics of Flexible Beams Undergoing Overall Motions, Journal of Sound and Vibration, 181(2), p261-278. [https://doi.org/10.1006/jsvi.1995.0139]
• Kane, T. R., and David, A. L., (1985), Dynamics: Theory and Applications, McGraw Hill, New York.