응답의존 모달 데이터를 이용한 고층건물의 FE모델 향상
© The Korean Society for Noise and Vibration Engineering
Abstract
This work updates the FE models for 25- and 42-story tall buildings having walls or a shear core as a major lateral force-resisting system, utilizing modal parameters such as natural frequencies, and mode shapes identified from measured vibration records in a previous study. Automated FE model updating adopting optimization theory includes a series of procedures that estimate sensitivity matrices, unknown parameters (based on a Bayesian technique), and correlation coefficients. A simplified FE model, considering 3 stiffnesses and 3 masses at each story as structural parameters, was derived from the analysis results of a more detailed 3D-FE model normally used in design practice, and was employed as the starting model for the update process. Although the test and analysis values of the natural frequency and mode shape for the lower three modes currently considered were in excellent agreement, many stories in both buildings exhibited a significant increase in stiffness, approximately 100 %, and decrease in mass, approximately 50 %. However, given that the natural frequencies from a 3D-FE analysis were found to be approximately 1.5 times as small as than the measured frequencies, at least for the three lower modes in both of them, this is unsurprising. Furthermore, the detailed 3D-FE model developed in the design office could be subject to a number of practical uncertainties/inaccuracies. This supports the conclusion is that the contemporary domestic design practice for FE analysis remains very conservative. It is shown that the proposed FE model updating technique using output-only modal data can be effectively applied to determine uncertain structural behavior or parameters and employed in the damage detection or structural health monitoring fields.
Keywords:
Dynamic Properties, Experimental Modal Analysis, Finite Element Analysis, FE Model Updating, Natural Vibration, Operational Modal Analysis, System Identification, Tall Buildings키워드:
동적특성치, 실험 모달해석, 유한요소해석, 유한요소해석 모델향상, 자연진동, 응답의존 모달해석, 시스템판별, 고층건물1. 서 론
구조설계 실무의 관점에서 보면, 이미 건설된 고층건물에 대하여 동적계측실험을 수행하는 데는 여러 가지 중요한 이유가 존재한다. 가령, 지진발생 빈도가 높은 지역에 위치한 건물의 건물주가 기존 구조체가 현행 내진설계기준에서 요구하는 조건들을 잘 만족하고 있는지 알아보기를 원할 때 등이다. 만약 규모가 큰 지진이 발생하였을 때 구조물이 위험에 노출되어 있다면 구조적 처방 혹은 보강을 해당 구조요소 혹은 전체구조에 적절하게 수행하여야 한다. 이에 구조기술자는 안정성 및 사용성 조건을 만족하는 경제적인 보강방법을 제시하여야 하는데, 구조물의 동적성능을 포함한 실제 건물의 상태를 평가할 수 있는 수단뿐만 아니라, 여러 보강의 효과를 정량적으로 산정하기 위한 유한요소해석(finite element analysis) 모델의 개발이 필요하다. 이러한 상황에서 대형 구조물의 동적성능을 경제적 및 효율적으로 결정할 수 있는 실험방법 및 구조물의 물리적 거동을 실질적으로 묘사할 수 있는 신뢰성이 높은 유한요소해석모델의 확보는 매우 바람직하다.
여러 진동계측 방법 중에서 바람, 교통 등에 의하여 발생하는 구조물의 상시 미세진동을 측정하는 자연진동(natural excitation) 실험은 건축/토목 구조물과 같은 대형구조물에 매우 적합한 경제적인 비파괴 실험방법이다. 자연진동원을 고려하므로 인공으로 혹은 특별히 제작된 가진기를 설치할 필요가 없으며, 단지 감도가 높은 적절한 수의 센서 및 데이터 수집 장치만 있으면 손쉽게 진동기록을 확보할 수 있다. 이외에도 실험하는 동안 구조물의 사용을 제한할 필요가 없으며, 또한 실제 경계조건하에서 구조물의 진동기록을 확보할 수 있다.
하지만, 입력 및 출력진동 기록 모두를 사용하는 전통적인 모달실험(experimental modal testing)(7,9) 기법과는 달리 응답만을 기록하여 구조물의 동적성능을 추출하여야 하므로 보다 복잡한 시스템판별법이 요구된다. 이러한 이유로 지난 수십 년 동안 응답기록만(output-only or operational)을 사용하는 시스템판별법에 대한 연구가 상당히 진행되어 왔으며, 현재는 어느 정도 성숙단계를 맞이하고 있다(12). 하지만, 응답의존 시스템 혹은 모달판별법의 단점 중의 하나는 측정된 모드형태에 대한 절대적인 스케일링이 불가능하다는 점이다.
한편, 최근 들어 진동기록을 사용하여 구조물의 손상을 감지하거나(damage detection), 건강상태를 지속적으로 감시하는 모니터링 기술(structural health monitoring)에 대한 관심이 더욱 높아지고 있다(5,13). 자연/고유진동수(f), 모드형태(ψ) 및 감쇠율(ξ)등 모달계수의 변화로부터 강성, 감쇠율 혹은 질량 등과 같은 구조물의 물리적 성능변화를 추적하는 이러한 기술 또한 효율적인 실험방법 및 신뢰성이 높은 유한요소해석모델의 개발이 필수적이다.
따라서 진동계측 및 시스템판별기법에 의하여 산정된 구조물의 동적성능치는 구조물의 동적거동을 이해하고, 바람 및 지진하중에 대하여 구조물의 안전성을 확보하는데 있어 매우 중요하다. 더 나아가서 측정된 모달계수에 근거한 유한요소해석 모델향상(FE model updating)은 미확정 구조변수(uncertain structural parameters)를 결정하거나, 구조물의 손상감지 및 건강상태를 모니터링하는 분야에 매우 유용한 수단이다(2,8).
이 연구의 목적은 초고층건물과 같은 대형건축/토목구조물의 신뢰성 있는 유한요소해석모델을 확보하기 위하여 어떻게 효과적으로 응답의존 시스템판별 및 유한요소해석 모델향상 기법이 적용될 수 있는지를 구현하는데 있다. 이를 위하여 이미 수차례에 걸쳐 동적계측실험을 수행하여 진동기록 및 시스템판별결과를 확보하고 있는 25층 및 42층 콘크리트 건물을 대상으로 이 연구에서 개발한 일련의 자동모델향상 절차를 적용하였다(1).
2. 모달데이터를 이용한 모델향상
동적/정적이던 주어진 조건하에서 구조물의 거동을 이해하기 위하여 구조기술자는 실제상황을 모사할 수 있는 수치해석모델에 종종 의존한다. 유한요소해석은 다양성 및 확장성 때문에 현재로서는 가장 널리 사용되는 수치해석법 중의 하나이다. 해석법의 성격상 해석기술자는 자유도의 수 및 사용되는 요소의 유도방법 등을 통하여 해석모델의 정확도를 상당히 조정할 수 있으나, 보다 정확한 모델을 구축하기에는 아직도 실제상황에 근사한 모사에 불과하다. 따라서 단순하면서도 구조물의 실제상황을 정확히 모사할 수 있는 근사 해석모델의 개발은 구조기술자에게는 또 하나의 도전이다.
해석모델과정에서 해석자는 기하학적 조건, 재료성능 혹은 경계조건에 포함되어 있는 불확실성을 고려하여야 하며, 일반적으로 모델의 부정확도는 근사화에 기인한다. 하지만, 매우 정확한 유한요소해석 모델을 구축하였더라도 실험결과에 의하여 검증되기 전까지는 정확도를 판단하기 힘들다. 모델향상의 목적은 설계변수의 변화가 어떻게 전체 시스템의 응답에 영향을 미치는지 혹은 해석과 실험결과의 차이를 정의하는 오차함수(error function)가 어떻게 최소화될 수 있는지를 알아보는 것이다(8,11). 이는 정적 및 동적 실험데이터를 사용하여 질량, 강성 및 감쇠율에 대한 모사를 연속적으로 향상시킴으로 달성할 수 있다.
2.1 변수산정법(Parameter Estimation)
모달계수와 구조변수와의 관계는 1차 항만을 포함한 Taylor급수에 의하여 아래와 같이 표시한다(11).
| (1) |
여기서 {Re} = 기준 혹은 실험 데이터를 포함하는 응답벡터, {Ra} = 초기치 {Po}를 갖는 구조변수의 변화에 의하여 예측된 시스템응답 벡터, {Pu} = 향상된 변수 값을 포함하는 벡터, {Po} = 초기변수 값을 포함하는 벡터 및 [S] = 민감도행렬이다.
식 (1)은 일반적으로 변수의 수가 방정식의 수보다 작은 overdetermined형식을 나타내며, pseudo-inverse (혹은 least squares), 가중치를 부여한 최소 자승치(weighted least squares) 혹은 Bayesian기법에 의하여 해를 산정한다. Taylor급수에 고차 항이 포함되어 있지 않으므로, 특히 {ΔR}이 클 경우에는 여러 번의 반복계산이 요구된다.
방정식의 수가 미지수의 수와 같을 경우에는 민감도의 역행렬을 산정하여 간단히 해를 구할 수 있지만, 대개는 방정식의 수가 미지수의 수보다 크므로 민감도의 pseudo-inverse행렬을 산정하여 변수의 증분을 아래와 같이 표현할 수 있다.
| (2) |
Least squares는 식 (2)로부터 산정한 잉여치를 최소화한다. 또한, 미지수의 수가 방정식의 수보다 큰 경우에는 민감도의 pseudo-inverse행렬은 아래와 같다.
| (3) |
| (4) |
Bayesian 변수산정법은 변수 및 응답에 가중치를 고려한다. 초기모델예측과 실험결과의 차이는 가중치가 고려된 오차 E(식 (6))를 최소화함으로서 해를 산정하며, 여기서 [G]는 Gain행렬이다.
| (5) |
| (6) |
| (7) |
미지수의 수가 방정식의 수보다 많은 경우에는,
| (8) |
식 (7)에서 [Cp]는 모델변수의 신뢰도(confidence)를 나타내는 대각선 가중치행렬(diagonal weighting matrix)이며, [CR]은 실험결과의 신뢰도를 나타내는 대각선 가중치행렬이다. 이들 값은 실제 구조물의 특성, 실험방법 및 모델링 과정에 의존하며 역행렬은 각각 변수와 응답의 상호변동행렬(covariance matrix)이다. 유용한 통계적 절차에 의하지 않는다면, 이 값은 해석자 및 실험수행자의 판단에 의존하여 결정하여야 한다. 다음은 신뢰도행렬의 대각선 항을 나타낸다.
| (9) |
| (10) |
여기서 Ri = 응답치 i, Pj = 변수 j의 초기치, C’R = 응답치 Ri의 신뢰도, C’p = 초기 변수치 Pj의 신뢰도를 각각 나타낸다. 식 (7) 및 (8)에서 민감도가 규정화되면(normalized) 식 (9) 및 (10)에서 Ri및 Pj는 1.0이 된다. 및 각각 응답 및 변수에 대하여 산정된 상대적 변동치를 나타낸다.
[Cp] = 0이면 식 (7)은 가중치를 갖는 최소 자승치 변수산정법이 되며 아래 식으로 표현할 수 있다. 이는 변수치에 대한 오차가 산정되지 않았을 때를 의미한다. 하지만 [CR] = 0이면 실험치에 대한 신뢰도가 매우 낮아 모델향상에 사용할 수 없음을 의미한다. 따라서 [Cp] = 0이면,
| (11) |
이외에도 최적이론에 기반을 둔 변수산정법은 수치해석상의 불안정성 문제를 향상시키기 위한 여러 다양한 방법이 존재한다(3,16,20). 특히, 최근에 소개된 시간영역의 일치를 위한 변수산정법에 특히 주목할 필요가 있다(10).
2.2 민감도해석(Sensitivity Analysis)
민감도해석은 모델향상 절차에 있어서 필수단계이다. 민감도계수는 고려하는 응답량(R)의 변화와 해석모델변수(P)의 변화 비율이다(3,15). 미분식혹은 유한차분법(finite difference)에 의하여 유도할 수 있으며, 절대, 상대 혹은 규정화된 상대 값 등의 다양한 형태로 표시할 수 있다.
상대민감도 및 응답치에 대하여 규정화한 상대민감도는 각각 아래와 같다.
| (12) |
| (13) |
또한, 자연진동수 및 모드형태에 대하여 미분식으로 표시된 민감도계수는 각각 아래와 같다.
| (14) |
| (15) |
여기서 [K] 및 [M] = 각각 강성 및 질량행렬이다.
2.3 상관도해석(Correlation Analysis)
이상적으로는 FE해석과 모달실험으로부터 획득한 모달계수는 서로 일치하여야 하지만, 실제상황에서는 여러 가지 이유로 큰 차이가 발생한다. 상관도 해석은 실험 및 해석으로부터 획득한 모달계수가 얼마나 혹은 어떻게 차이가 나는지를 정량 및 정성적으로 조사하는 기법이다.
자연진동수, 모달변위 등과 같은 모달계수를 개별응답으로 취급하거나 혹은 MAC(modal assurance criterion)값을 산정하고 전체응답으로 취급하여 다양한 상관계수(correlation coefficient)를 정의할 수 있다. 또한 고려하고자 하는 응답의 종류에 따라 예상되는 상대오차를 적용하여 가중치()를 부여할 수 있으며, 그 결과 표준 목적함수에 사용되는 상관계수는 아래와 같다.
N개의 자연진동수에 대하여 weighted relative difference(CCMEAN) 혹은 weighted absolute relative difference(CCABS), 모드형태에 대하여 average MAC (MACMEAN 혹은 CCMAC) 등으로 정의한다.
| (16) |
| (17) |
여기서
| (18) |
여기서 K1= 가중치이다.
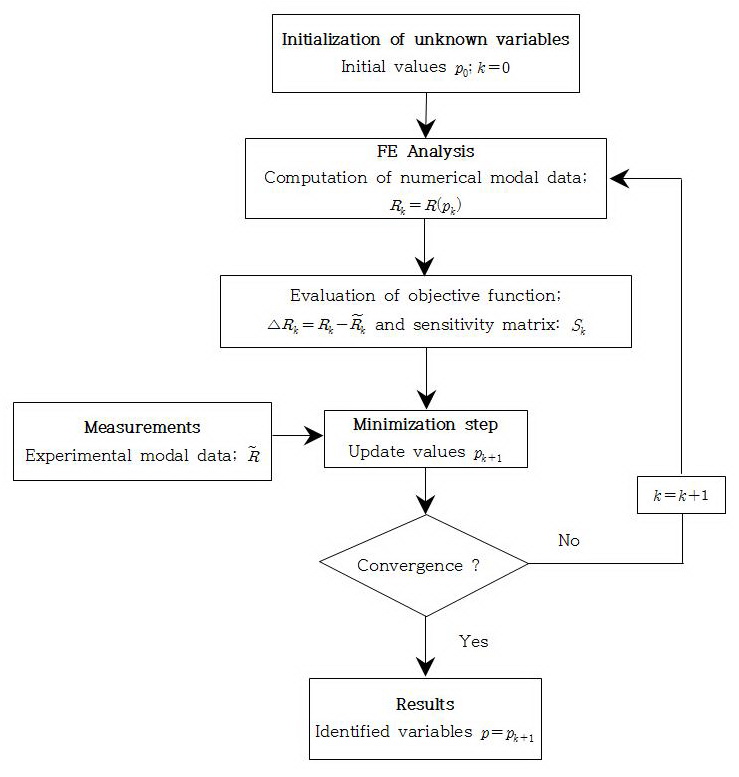
전술한 해석모델향상의 전체과정을 흐름도로 표시하면Fig. 1과 같으며, 이 연구는 상용패키지인 MATLAB(18) 및 FEMtools(6)에서 제공하는 모듈을 이용하여 coding하였다.
3. 실제적용
기존연구(17,19,21)에 의하면 건물에 대한 FE해석모델의 동적응답에 영향을 미치는 주요 구조변수는 보, 기둥, 벽체, 슬래브 등의 영계수(E), 밀도(ρ), 단면2차모멘트(I), 보-기둥 접합부의 강성 및 비구조체의 강성 혹은 외피재의 두께(H) 등을 열거할 수 있다. 하지만, 이러한 변수들을 충실하게 고려하기 위하여서는 매우 정교한 FE모델 사용과 그에 따른 문제규모(problem size)의 거대화 혹은 비실용성, 실무로부터 관련 정보취득의 어려움이 존재한다. 피해감지보다는 자동 모델향상을 위한 일련의 절차를 개발하는 것이 이 연구의 주요 목적임을 감안할 때, 보다 단순화된 모델구축의 필요성이 제기되었다.
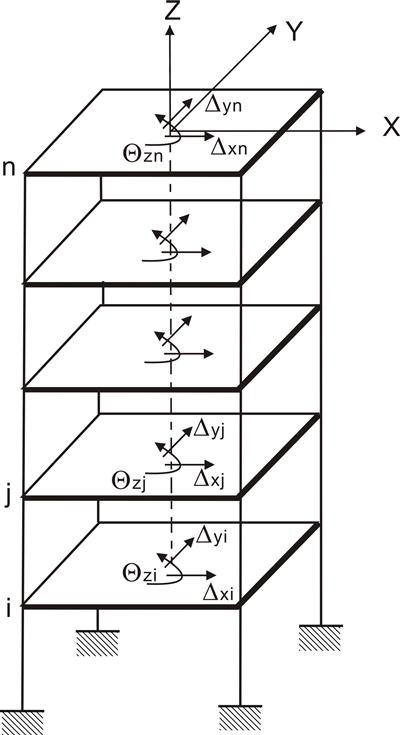
이에 이 연구는 매 층마다 2개의 수평방향강성(Kxi,Kyi)과 1개의 회전방향강성(Kθi) 및 이에 해당하는 질량(mxi, myi, mθi)을 주요변수로 하는 단순해석모델을 채택하고, Bayesian 변수산정 기법을 사용하여 자연진동수 및 모드형태의 일치를 시도하였다(Fig. 2). 이는 슬래브 격막작용 및 해당 층에 포함된 모든 구조요소의 강성을 하나의 값으로 축약하는 것을 의미한다. 3D 보-기둥요소를 사용하였으며 지하층 및 지반과의 상호작용은 무시하였다. 변수에 대한 초기치는 구조계산 시 구축한 상세 3D-FE모델의 해석결과로부터 산정한 층강성(story stiffness) 및 층질량을 사용하였다. 이렇게 하여 산정한 층강성은 구조물 형태 혹은 구성요소의 배치 및 하중분포에 따라 다소 다른 값을 나타낼 수 있으나, 모델향상을 위한 초기치로 채택하기에는 충분한 것으로 판단하였다(14).
3.1 해석 예1
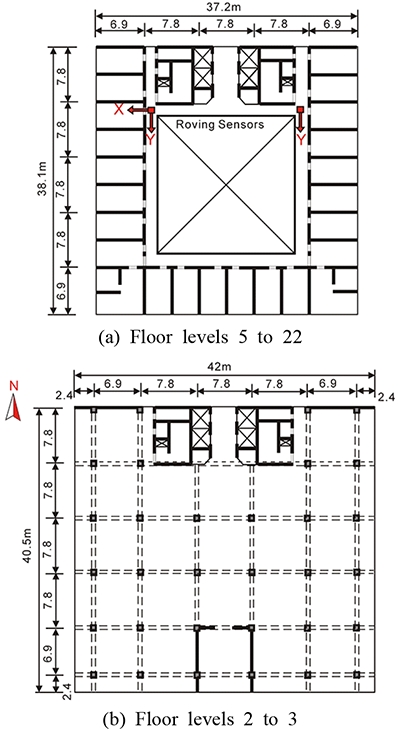
광주, 상무지역에 위치한 Dawoo Diovelle 25층, 철근콘크리트, 오피스텔 건물(DWD)은 37.2 m × 38.1 m 크기의 타워부분에 주거공간이 배치되어 있고, 4층 바닥이하는 42 m × 40.5 m의 약간 확장된 바닥면적에 상업시설을 포함하고 있다(Figs. 3, 4).
3층과 4층 사이에는 층고 3 m의 추가층이 존재하며(3+층), 2.0 m × 1.8 m의 전이보가 타워부분 외곽부에 설치되어 있다. 주차시설을 위하여 54 m × 51.3 m의 지하 5층을 포함하고 있으며, 지상 1층 바닥에서부터 전체건물의 높이는 104 m이다. 기초바닥판은 거의 정사각형에 가까운 형태를 지니고 있으나, 3+층에서부터 지붕층까지 평면의 중앙부분이 개방된 속이 빈 단면형태(hollow section)를 취하고 있다. 외곽부의 길이 및 단변방향에서 건물이 차지하는 부분의 두께는 6.9 m 혹은 7.8 m이며, 사용된 콘크리트의 강도는 24 MPa ~ 30 MPa이다. 구조대칭성은 단지 남북방향(NS)에서만 유지되고 있으며, 기초는 토질의 지내력(fe = 0.6 MPa)에 직접 지지되는 매트형으로서 두께가 1.0 m ~ 1.8 m이다. 2006년도에 건물이 완성되었으며, 측정은 시공단계에서 입주직전에 이르기까지 수차례에 걸쳐 수행되었다. 자연진동실험, 모달계수 추출 및 수동모델향상에 관한 자세한 설명은 참고문헌(1)을 참조하라.
75개의 자유도, 150개의 구조변수, 25개의 일치점에 대하여 실험으로부터 추출한 모달계수를 기준으로 FE모델 향상을 시도한 결과는 Table 1과 같다. 실험모달계수(EMA)는 주파수영역의 FDD(frequency domain decomposition) 시스템판별법에 의하여 추출된 값을 사용하였다(4). 또한, 모델향상을 위하여 단순화한 FE모델의 타당성을 검증하기 위하여 구조설계 시 사용한 상세한 3D-FE모델에 의하여 예측된 자연진동수 값도 포함하였다. 고차모드에 대한 측정은 신뢰도가 낮은 점을 감안할 때, 현재는 3차 모드까지만 고려하였다.
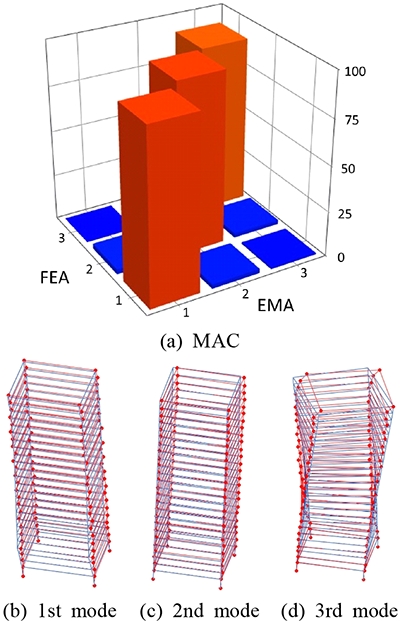
단순모델은 3D모델의 해석결과로부터 층강성 및 층질량을 유도하였으므로, 3D 해석결과와 비교하여 허용할만한 자연진동수 값을 보여주고 있다. 최종으로 19번의 반복계산 이후 향상된 FE 모델에 의하여 예측된 자연진동수 및 모드 형태는 Table 1 및 Fig. 5에서 보는 바와 같이 실험치와 잘 일치하고 있다.
대부분의 변수변화는 초기 1회 ~ 2회 반복계산에서 발생하였으며, 이후에는 단지 작은 변화만을 나타내고있다.
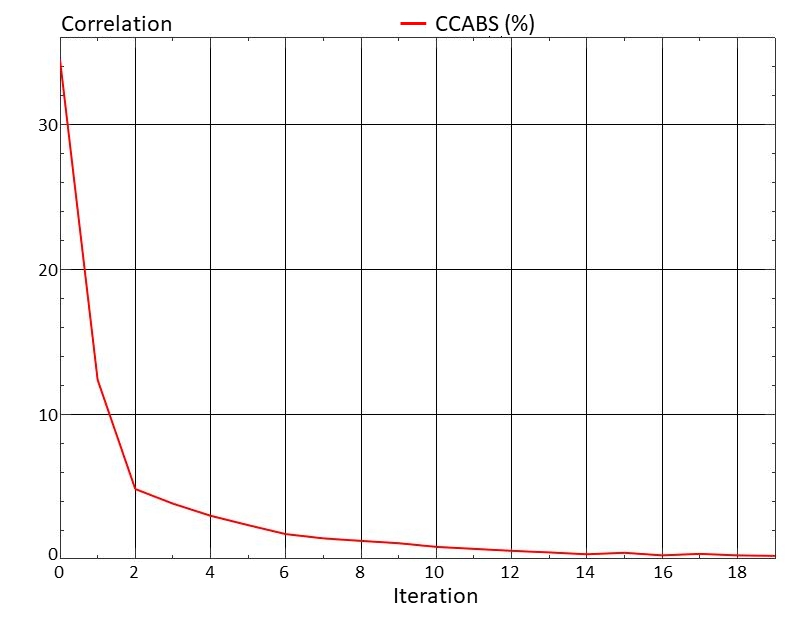
Fig. 6은 자연진동수에 대하여 산정한 CCABS(절대 상대차이 상관계수)와 반복계산 수의 관계를 도식하고 있는데, 안정적으로 해에 수렴하고 있음을 알 수 있다.
3.2 해석 예2
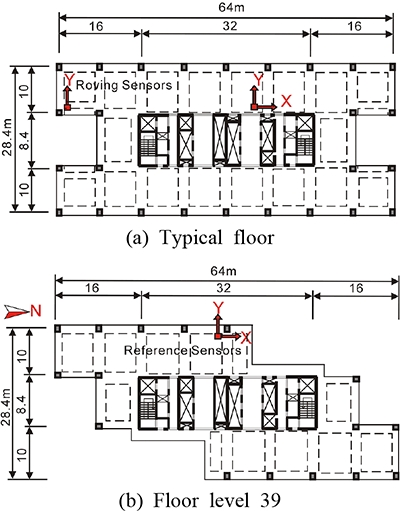
또 다른 42층 철근콘크리트 건물은 Daelim Acroville이라 불리는 주상복합건물(DLA)로서 평촌에 위치하고 있으며, Fig. 7에서 보는 바와 같이 120.8 m × 82.2 m 크기의 확장된 저층부와 1쌍의 타워를 갖고 있다. 5층 바닥을 기준으로 주용도는 주거 및 상업용이다. 타워부분의 바닥면적은 64 m × 28.4 m이며, 지상1층 바닥으로부터 전체 건물높이는 162 m이다. 2개의 타워를 묶는 공동지역에 지하5층의 주차시설이 설치되어 있으며, 7층과 8층 사이에는 관련 기계시설을 집중적으로 수용하기 위하여 층고 1.8 m의 추가층이 배치되어 있다. 사용된 콘크리트의 강도는 30 MPa ~ 42 MPa이다. 각 타워는 중앙부 코아, 외곽부 골조 및 이를 연결하는 outrigger보로 구성되어 있으나, 25층에서 41층 바닥까지 건물의 남북면이 서로 마주보면서 계단형태로 setback이 되어있으므로 고층부에는 반대칭 형태(anti-symmetrical)의 구조배치를 나타낸다(Fig. 8). 기초형식은 지반토질에 의하여 직접 지지되는 매트형이며(fe = 1.5MPa), 두께는 대략 1.8 m이다. 이 건물의 공사는 2007년도에 완료되었으며, 측정은 시공단계에서 최종 내부공사가 진행될 때까지 서너 번에 걸쳐 수행하였다. 자연진동실험, 모달계수 추출 및 수동모델향상에 관한 자세한 설명은 참고문헌(1)을 참조하라.
126개의 자유도, 252개의 구조변수, 42개의 일치점에 대하여 실험에서 추출한 모달계수를 기준으로 FE모델 향상을 시도한 결과는 Table 2와 같다. 실험 모달계수(EMA)는 주파수영역의 FDD(frequency domain decomposition) 시스템판별법에 의하여 추출된 값을 사용하였다(4). 구조설계사무소에서 구축한 3D-FE모델에 의하여 예측된 자연진동수를 포함하고 있으며, 3차 모드까지만 고려하였다.
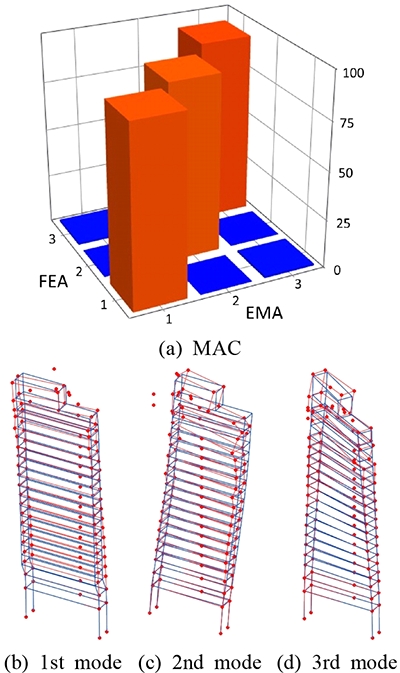
최종으로 18번의 반복계산 이후 향상된 FE 모델에 의하여 예측된 자연진동수 및 모드형태는 Table 2 및 Fig. 9에서 보는 바와 같이 실험치와 잘 일치하고 있다.
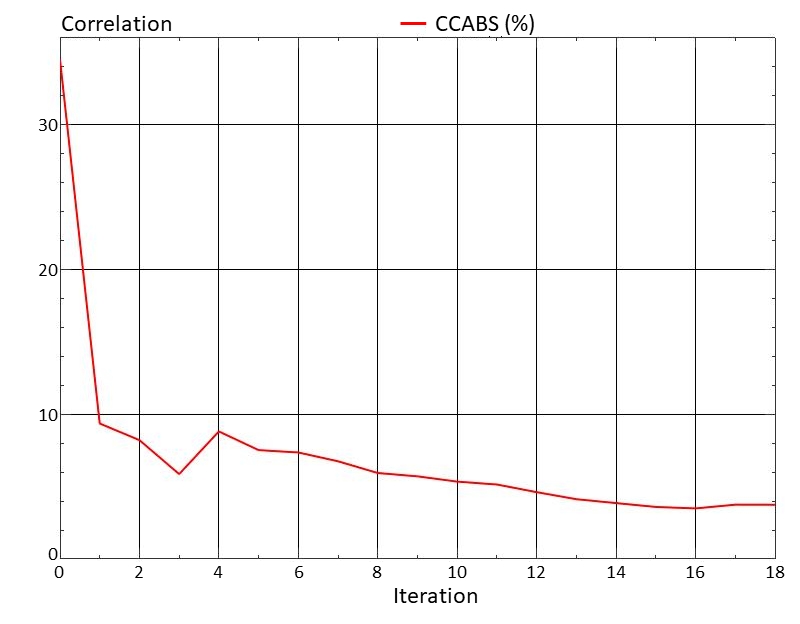
대부분의 변수변화는 초기 1회 ~ 2회 반복계산에서 발생하였으며, Fig. 10은 CCABS와 반복계산 회수의 관계이다. 초기에 불연속적으로 수렴하는 과정을 나타내고 있으나, 이후에는 안정적임을 보여주고 있다.
4. 토 의
두 건물 모두에 대하여 모델향상 시 사용한 구속조건은 각각 –100 % ≤ K≤ 100 %, –50 % ≤ m≤ 50 %이다. DWD 건물의 경우 최종 FE모델에서 고려한 실제변수의 변화는 Kx는 9층 ∼ 12층까지, Ky은 2층 ∼ 4층까지, Kθ는 6층 ∼ 16층까지 100 %에 근접하였다. 또한 mx는 15층 ∼ 25층까지, my는 2층 ∼ 25층까지, mθ는 15층 ∼ 25층까지 –50 %에 가까운 변화를 나타내었다. 한편, DLA 건물의 경우에도 최종 FE모델에서 고려한 실제변수의 Ky는 4층, 7층 ∼ 8층, 10층 ∼ 25층 및 27층 ∼ 29층까지, Kθ는 2층 ∼ 7층 및 9층 ∼35층까지 100 %에 근접하였다. 또한 mx는 19층 ∼ 40층까지, my는 20층 ∼ 40층까지, mθ는 18층 ∼ 40층까지 –50 %에 가까운 변화를 나타내었다. 이는 초기 해석모델에서 층강성은 상당히 과소평가된 반면에 층질량은 상당히 과대평가되었음을 의미한다.
초기 해석모델은 구조계산을 위하여 실무자가 설계사무소에서 작성한 자세한 3D-FE모델을 의미한다. 이에 의하여 예측된 자연진동수의 값을 진동기록으로부터 추출한 실험치와 비교하여 보면 적어도 저차 3개 모드에서 1.5배 정도의 차이가 나는 사실을 고려해 볼 때, 그렇게 놀라운 사실은 아니다(1). 모델향상에 사용한 단순해석모델도 3D모델로부터 유도되었기 때문에 처음부터 3D모델 자체가 정확히 작성되지 않았다고 판단할 수 있다.
일반적으로 실무에서 작성하는 FE모델은 슬래브 기여 및 지진발생 시를 고려하여 비구조체에 대한 기여를 배제하고, 주로 횡방향 지지요소만을 포함하여 모델링한다. 이렇게 할 경우 실험치와의 자연진동수 차이는 최대 15 % ∼ 30 % 정도이다. 그럼에도 불구하고, 국내에서 구축한 자세한 3D-FE모델에 의한 예측은 200 % 정도의 자연진동수 차이를 나타내고 있는데, 구조실무자 접촉 및 현장방문 등과 같이 관련자료 습득에 심각한 어려움이 발생하여 현재로서는 그 이유를 단지 다음과 같이 추정만 할 수 있을 뿐이다.
대개 실무에서 FE해석은 초급기술자에 의하여 수행되므로 복잡한 구조물인 경우 해석모델링의 부정확성이 존재할 수 있으며, 초기 해석모델의 구축 후 많은 설계변경이 이루어지고 있는데 반하여, 이에 맞게 최종 FE모델이 수정되었는지 여부, 국내 시공현장에서 보다 강한 재료의 사용이 일반적으로 허용되는 점, 설계기준에서 제시하는 질량이 다른 여러 가지 이유로 과다하게 설정된 점, 슬래브 및 칸막이벽, 외피 및 창문틀과 같은 비구조체의 기여가 고려되지 않은 점 등을 들 수 있다. 결론적으로 현재의 국내 구조설계 실무는 상당히 보수적으로 수행되고 있음을 알 수 있다.
하지만, 보수적인 설계가 항상 유리한 것은 아니다. 지진하중에 대한 연성설계 시 어느 정도 강도에 도달하면 항복거동을 나타내어 그 이후에는 큰 변형능력이 요구되는데, 현재의 구조설계는 이러한 설계철학을 만족시키기에는 무리가 있는 것으로 판단된다. 이 부분에 대해서는 추후 지속적인 연구가 필요하다.
5. 결 론
이 연구의 주요 목적은 초고층건물과 같은 대형건축/토목구조물을 대상으로 자연진동계측 실험으로부터 추출한 모달계수를 이용하여 초기에 구축한 유한요소해석모델을 보다 실제적이며 정확한 거동을 예측할 수 있는 모델로 향상시키기 위한 자동화 기법을 개발하는 것이다. 이렇게 실험결과에 근거하여 조정된(tuning) FE모델은 구조물의 거동을 보다 신뢰성 있게 예측, 조사할 수 있어 초기에 사용한 여러 구조가정의 오류 여부를 판단할 수 있다. 더 나아가서는 동일기법에 의하여 구조물의 피해여부, 위치 및 정도 등을 예측할 수 있다.
이를 위하여 이미 진동계측 실험 및 시스템판별이 수행된 바 있는 25층 및 45층 고층건물에 대하여 최적이론에 근거한 자동 FE모델향상이 수행되었다. 그 결과, 이 논문의 결론은 아래와 같다.
- (1) 초고층건물과 같은 대형건축/토목구조물에 대하여 응답의존 모달계수(자연진동수 및 모드형태)를 이용하여 성공적으로 FE모델 향상을 수행할 수 있다. 현재는 3차모드까지만 고려하였으나, 필요시 고차모드까지 고려가 가능하다. 하지만 이를 위해서는 보다 정확한 실험결과 및 강력한(robust) 수치해석기법이 요구된다.
- (2) 자세한 3D-FE해석결과를 이용하여 유도된 단순 FE모델은 변수의 변화 등을 추적하고자 하는 목적의 모델향상에 사용하기에 충분한 것으로 판단된다. 피해감지 등과 같은 목적의 모델향상에는 보다 정교한 모델이 요구되나, 문제규모의 거대화로 수치해석상의 불안정, 메모리문제, 비효율성 등이 대두된다.
- (3) 자동모델향상 기법은 실험과 해석결과의 일치를 위하여 어떤 변수가 얼마나 수정되어야 하는지를 손쉽게 효과적으로 결정할 수 있다. 하지만, 최종으로 향상된 FE모델의 수정된 구조변수를 허용하느냐, 아니면 거절하느냐는 전적으로 구조해석자의 책임이며 이전 경험 및 합리적인 공학적 판단에 의거하여야 한다.
- (4) 고유진동수와 모드형태가 가장 일치하는 FE모델 향상의 결과 DWD 및 DLA의 경우 상당한 층강성의 증가(최대 100 %)와 층질량(최대 50 %)의 감소를 요구하였다. 이는 구조계산목적의 자세한 3D-FE모델에 의하여 예측된 자연진동수가 진동기록으로부터 추출한 실험치와 적어도 저차 3개 모드에서 1.5배 정도의 차이가 나는 사실을 고려해 볼 때, 허용할 만하다. 이러한 점에 비추어 볼 때 현재의 국내 구조설계사무소에서 사용하는 FE모델은 상당히 보수적(작은 강성 및 큰 질량)으로 구축된 것으로 판단된다.
Acknowledgments
이 연구는 2015년도 광주대학교 대학연구비의 지원을 받아 수행되었다. 한국학술진흥재단(KRF-2006-013-D00328) 및 광주대학교의 연구년 지원으로 2007년 저자가 1년간 벨기에, 루벤대학, 토목공학과, 구조그룹에서 수행한 연구내용이 기초가 되었다.
References
- Cho, S.-H., (2008), Output-only System Identification and Model Updating for Performance Evaluation of Tall Buildings, Journal of the Earthquake Engineering Society of Korea, 12(4), p19-33.
-
Hwang, I. H., Jeon, J. Y., and Kim, J. Y., (2013), FE Model Calibration of Myeong-dong Cathedral Using Vibration Measurement Data, Transactions of the Korean Society for Noise and Vibration Engineering, 23(11), p1598-2785.
[https://doi.org/10.5050/ksnve.2013.23.11.987]

-
Bakir, P. G., Reynders, E., and De Roeck, G., (2007), Sensitivity-based Finite Element Model Updating Using Constrained Optimization with a Trust Region Algorithm, J. Sound Vib., 305(1~2), p211-225.
[https://doi.org/10.1016/j.jsv.2007.03.044]

- Brinker, R., Zhang, L., and Anderson, P., (2000), Modal Identification from Ambient Responses Using Frequency Domain Decomposition, Proc., 18th Int. Modal Analysis Conf., Texas, USA, p625-630.
- Brownjohn, J. M. W., Xia, P. Q., Hao, H., and Xia, Y., (2001), Civil Structure Condition Assessment by FE Model Updating: Methodology and Case Studies, Finite Elements in Analy. and Desig., 37(10), p761-775.
- Dynamic Design Solutions, (2010), FEMtools Users’ Guide Version 3.5, Leuven, Belgium.
- Ewins, D. J., (2000), Modal Testing: Theory, Practice and Application, Research Studies Press, Baldock, Hertfordshire, UK.
-
Friswell, M. I., and Mottershead, (1995), Finite Element Model Updating in Structural Dynamics, Kluwer Academic Publishers, Dordrecht, The Netherlans.
[https://doi.org/10.1007/978-94-015-8508-8]

- Heylen, W., Lammens, S., and Sas, P., (1995), Modal Analysis Theory and Testing, Dept. of Mech. Engrg., Katholieke Univ., Leuven, Heverlee, Belgium.
-
Link, M., and Weiland, M., (2009), Damage Identification by Multi-model Updating in the Modal and in the Time Domain, Mech. Syst. Signal Process., 23(6), p1734-1746.
[https://doi.org/10.1016/j.ymssp.2008.11.009]

- Nocedal, J., and Wright, J., (1999), Numerical Optimization, Springer, New York, USA.
-
Peeters, B., and De Roeck, G., (2001), Stochastic System Identification for Operational Modal Analysis: A Review, J. Dyn. Syst., Meas. and Control, ASME, 123(12), p659-667.
[https://doi.org/10.1115/1.1410370]

- Peeters, B., (2000), System Identification and Damage Detection in Civil Engineering, Ph.D. Thesis, Dept. of Civil Engrg., Katholieke Univ., Leuven, Heverlee, Belgium.
- Schulz, A. E., (1992), Approximating Lateral Stiffness of Stories in Elastic Frames, J. Struct. Engrg., ASCE, 118(1), p243-263.
- Teughels, A., (2003), Inverse Modeling of Civil Engineering Structures Based on Operational Modal Data, Ph.D. Thesis, Dept. of Civil Engrg., Katholieke Univ., Leuven, Heverlee, Belgium.
-
Teughels, A., De Roeck, G., and Suykens, J. A. K., (2003), Global Optimization by Coupled Local Minimizers and its Application to FE Model Updating, Comp. & Struct., 81(25), p2337-2351.
[https://doi.org/10.1016/s0045-7949(03)00313-4]

-
Teughels, A., Maeck, J., and De Roeck, G., (2002), Damage Assessment by FE Model Updating Using Damage Function, Comp. & Struct., 80(25), p1869-1879.
[https://doi.org/10.1016/s0045-7949(02)00217-1]

- The Mathworks, (2005), Using MATLAB, Version 7.0.4, Natick, MA, USA.
- Turek, M., Ventura, C. E., and Guerrero, S., (2007), Ambient Vibration Testing and Model Updating of a 44-Storey Building in Vancouver, Canada, Proc., 25th Int. Modal Analysis Conf., Orlando, Florida, USA.
-
Weber, B., Paultre, P., and Proulx, J., (2009), Consistent Regularization of Nonlinear Model Updating for Damage Identification, Mech. Syst. Signal Process., 23(6), p1965-1985.
[https://doi.org/10.1016/j.ymssp.2008.04.011]

-
Wu, J. R., and Li, Q. S., (2004), Finite Element Model Updating for a High-rise Structure Based on Ambient Vibration Measurements, Engrg. Struct., 26(7), p979-990.
[https://doi.org/10.1016/j.engstruct.2004.03.002]


Soon Ho Cho is a professor of Architectural Engineering at Gwangju Univ., Gwangju, Korea. He obtained his engineering degrees from Hanyang Univ. for M.S. in Architectural Engineering and from McGill Univ. for Ph.D. in Civil Engineering and Applied Mechanics. His research interests include analytical and experimental evaluations of steel-concrete composite members in shear critical regions, and currently dynamic measurements and vibration analysis for tall buildings.