간섭계를 이용한 지진 센서 감도의 절대 측정
© The Korean Society for Noise and Vibration Engineering
Abstract
The absolute measurement of seismic sensor sensitivity is conducted through the application of interferometry to a primary method of accelerometer calibration. Recently, several methods for seismometer calibration were published as ISO standards. These standards are limited to utilization of the comparison and in-situ methods; therefore, it is essential that there is a reference sensitivity available that is based on absolute calibration. This reference will be inherently useful for the calibration of accelerometers because seismic sensors are also used as transducers in measuring vibration for this purpose. The sensitivity of a seismic accelerometer and two different broadband seismometers are measured using the sine-approximation method and it is observed that this method can be applied to the absolute calibration of seismometers for the frequency range that is of interest to seismology. Moreover, the effects of sensor direction misalignment and imbalance are observed in the actual measurements.
Keywords:
Seismic Sensor, Absolute Calibration, Interferometer키워드:
지진센서, 절대교정, 간섭계1. 서 론
지진관측에 사용되는 지진 센서는 기본적으로 진동의 크기를 계측한다는 점에서 진동분야 측정 표준과 소급성(traceability)을 가져야 한다. 측정의 소급성이란 연속적인 교정을 통해 측정 결과를 단위의 정의에 해당하는 기준까지 연결할 수 있는 특성을 의미하며, 측정값을 신뢰할 수 있는 근거가 된다(1). 그러나 관측하는 대역이나 신호의 크기가 일반적인 진동 센서들과는 크게 차이가 있다는 점 때문에, 교정과 검증 과정이 국제 표준 체계와 괴리된 채 운영되어 왔다(2).
그렇지만 최근에 들어서 포괄적 핵실험 금지조약기구(Comprehensive Nuclear Test Ban Treaty Organization, CTBTO)가 국제 모니터링 체계(International Monitoring System, IMS)에 활용되는 관측 장비 들에 대한 소급성 확보 및 국제 측정 표준 시스템과의 연결 필요성을 제기한바 있으며, 국제도량형국 음향진동초음파 분야 자문위원회에서도 이 부분에 대한 검토가 진행되고 있다.
근래에 들어서 코일을 이용한 방법이나 중력을 이용한 방법과 같은 전통적인 지진 센서의 평가 방법들도 ISO 표준이 제정되어 국제표준화가 이루어졌다(3~5). 이들 표준에도 공통적으로 정현 가진에 기반한 기준과 비교하여 센서의 특성을 결정하도록 정하고 있기 때문에, 일반적인 비교 교정 과정으로 볼 수 있다. 그러므로 소급성 확보를 위해서는 절대 교정에서 소급 받은 기준기를 활용하거나 지진계 자체에 대한 절대 교정이 필요하다.
지진계의 절대 감도 측정을 위해서는 기본적으로 가속도계의 절대 교정 방법(6)을 활용하는 것이 가능하다. 이 연구에서는 가속도계의 절대 교정에 적용되는 간섭계 기반 방법을 지진계의 감도 평가에 적용하고, 그 특성을 검토한다. 이러한 간섭계를 이용한 교정 방법은 정밀하고 안정적일 뿐만 아니라, 레이저의 파장에서 직접 소급을 받기 때문에 변위를 절대적으로 측정하는 것이 가능하다. 이 때문에 진동 측정의 일차표준으로 적용되어 왔다(6). 그러나 이러한 간섭계를 정점으로 한 진동 측정의 소급체계는 지진 관측분야에는 적용되지 않았다.
이는 기본적으로 지진 센서를 개발하는 회사 자체가 매우 한정적이며, 이를 운용하는 곳도 제한되어 있었기 때문에 업계 내부적인 경험에 의존하는 경향이 강했기 때문으로 볼 수 있다. 또한, 기존의 지진분야 측정은 일반적인 산업응용 진동 측정등과 주파수 대역에서 큰 차이가 있었으며, 극단적으로 높은 민감도를 요구하였기 때문에, 과거의 진동 계측 분야의 범위와 상이한 문제도 존재하였다.
실제로 10 Hz 이하의 낮은 주파수 대역에 대해서는 2017년에 최초의 국제 비교 결과가 공개되었기 때문에(7), 그 이전에는 지진계의 주요 주파수 대역에 대한 측정 표준이 확립되지 않았던 점도 중요한 원인으로 볼 수 있다.
이 연구에서는 지진센서들의 절대 감도 평가에 대한 측정표준 소급성을 위해 ISO 16063-11(6)에 기반한 절대감도 측정을 적용하고 그 특성을 살펴보았다.
2. 진동센서의 절대 감도 측정
진동을 표현하는 물리량으로는 일반적으로 가속도(m/s2) 또는 속도(m/s)를 사용하며, 이는 기본단위 길이(m)와 시간(s)에서 소급된다. 진동 센서의 감도를 측정하는 방법은 정현파 가진기를 이용하여 센서를 가진하고, 가진 되는 양과 센서의 출력을 비교하여 센서의 특성을 결정하게 된다. 이 때, 시간에 따른 변위를 측정함으로써 가속도 값을 알게 되며, 간섭계를 이용하여 절대적인 변위를 측정한다.
진동센서(가속도계)에 대한 절대 교정을 수행하기 위한 방법은 ISO 16063-11(6)에 기술되어 있다. 측정 시스템은 크게 센서를 정현파로 가진 하는 가진부와 센서의 변위를 측정하는 광 간섭계로 구성된다.
상기 표준에서는 3가지의 간섭계 구성 및 신호처리 방법을 제시하고 있으며, 이 연구에서는 정현파 근사법을 적용하였다. 정현파 근사법의 기본적인 구성은 Fig. 1과 같다(6). 광원으로는 안정화된 He:Ne 레이저를 이용하며, 광원에서 출력된 빔은 편광자를 통과하여 정렬되고 1/4 파장판을 통과하여 원편광 빔이 된다. 이 빔은 빔 스플리터로 5:5로 분할되어 한 빔은 정지된 기준 거울에서, 다른 빔은 진동면에서 반사되어 다시 모이며, 편광 빔스플리터를 통과한 후 광 검출기로 입사한다. 각 광 검출기에서 얻어진 출력신호는 식 (1)과 같이 표현 할 수 있다.
| (1a) |
| (1b) |
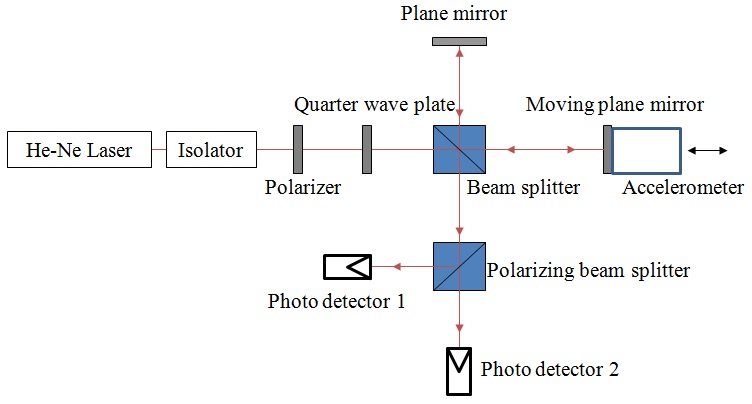
Conceptual configuration of the primary calibration system based on the sine approximation method for accelerometer
이 때, 과 는 광 검출기의 출력이며, 는 광신호의 초기 위상, 는 피스톤 운동의 초기위상을 의미하며, 은 변조 위상의 진폭으로 다음과 같이 주어진다(8).
| (2) |
위 식에서 는 가속도계 변위의 진폭, λ는 레이저의 파장이다. 변조 위상은 식 (3)과 같이 주어지며, 광 검출기 신호로 구할 수 있다(8).
| (3) |
이 때, m은 불연속점이 없도록 위상 신호를 펴기 위한 (unwarpping) 정수이다. 식 (3)의 관계식을 측정결과를 대입하여 풀면, 을 얻을 수 있으며, 이를 이용하여 가속도계의 진폭은 다음과 같이 구할 수 있다(7).
| (4) |
그러므로 위 가속도에 대한 가속도계 출력의 비를 구함으로써 가속도계의 감도를 측정 할 수 있다.
저주파수 대역에서 왜곡이 없는 정현파 출력을 얻기 위해서는 가진기의 변위를 크게 할 필요가 있다. 이를 위하여 최대변위 450 mm의 대변위 가진기(long-stroke exciter, SPEKTRA APS-600)를 이용하였다.
측정 시스템의 확장 불확도는 진동 표준용 기준 가속계를 측정할 경우, 0.4 Hz 이하에서 1 %, 0.5 Hz ~ 0.8 Hz 에서 0.75 %, 그 이상부터 40 Hz 까지는 0.5 % 수준이다. 측정은 가속도계는 0.1 Hz ~ 40 Hz 범위, 광대역 속도 지진계는 0.1 Hz ~ 20 Hz 범위에서 수행하였다. 주파수 범위는 시스템이 안정적으로 가진이 가능한 범위로, 0.1 Hz 이하에서는 정현파로 가진 하는 것이 어렵고, 상기 대역 이상에서는 가진 축 방향 이외의 횡방향 성분이 발생하기 시작하여, 이 영향을 무시할 수 있는 주파수 대역으로 한정 하였다. 측정은 5회 반복하여 평균하였다.
3. 지진센서 감도 교정
3.1 가속도지진센서의 감도 측정
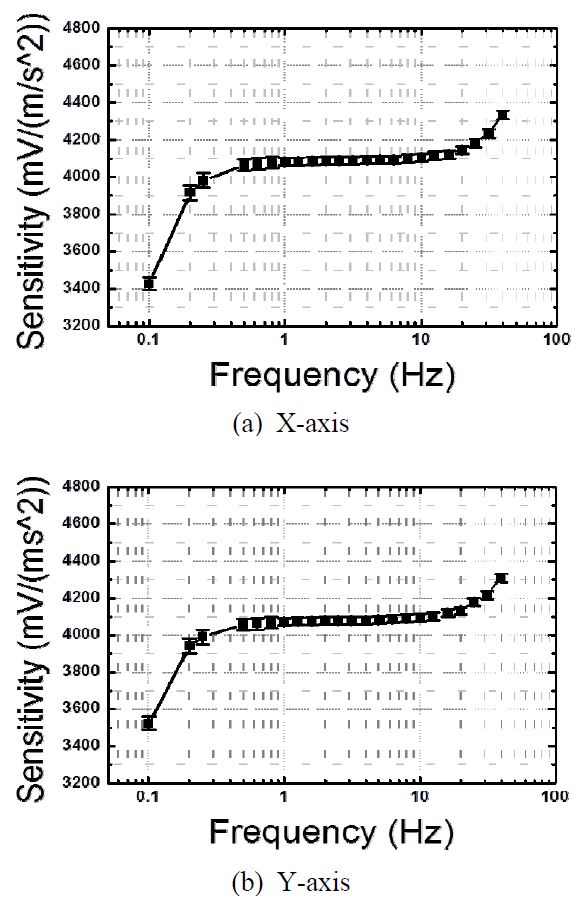
앞에서 제안한 방법을 이용하여 지진 가속도계의 감도 측정을 수행하였다. 대상 센서는 Kinematrics ES-T로 직경은 133 mm, 높이는 62 mm이며, 무게는 1.8 kg이다. 지진계는 일반적인 계측용 가속도계에 비하여 크기가 크고 무겁기 때문에, 이를 고정하기 위한 지그를 별도로 제작할 필요가 있다. 지진계는 많은 경우 X, Y, Z의 3축에 대한 출력을 제공하므로 각 축에 대하여 개별적으로 교정이 될 필요가 있다. 그러나 현재 보유하고 있는 가진 시스템은 수평 가진만을 지원하는 관계로 평면상의 축인 X, Y 두 축에 대해서만 측정을 수행하였다. Fig. 2(a)는 지진 가속도계 Kinematrics ES-T를 가진기에 고정하기 위하여 제작한 지그이며, Fig. 2(b)와 같이 설치되어 수평방향으로 가진 되게 된다. 가진시 가속도계가 불안정하게 흔들리는 것을 방지하기 위하여, 가진 테이블에 완전히 접촉되도록 제작하였다.
측정된 가속도계의 감도는 Fig. 3과 같다. 에러바(error bar)는 측정값의 확장 불확도(9)로, 2장에 기술된 측정 시스템이 갖는 불확도와 5회 반복시의 측정편차에서 도출된 불확도를 합성하고 포함인자 2를 적용하였다. 기본적으로 1 Hz ~ 10Hz 범위에서 상대적으로 평탄한 응답을 보여주고 있으며, 고주파수 대역으로 가면 공진에 가까워지는 영향으로 인하여 감도가 증가하며, 1 Hz 이하 저주파수 대역에서는 주파수가 낮아짐에 따라 감도가 감소하는 경향을 보이고 있다.
3.2 광대역 속도 지진계의 교정
광대역 지진계는 지진 관측에서 가장 정밀한 측정에 적용되는 센서로 가장 넓은 측정 주파수 대역과 동적 범위를 갖는다. 진동 측정 분야에서는 일반적으로 가속도에 대한 감도를 평가하고 있으나 광대역 지진계의 경우 속도를 측정 물리량으로 하고 있기 때문에 속도에 대한 감도를 평가한다.
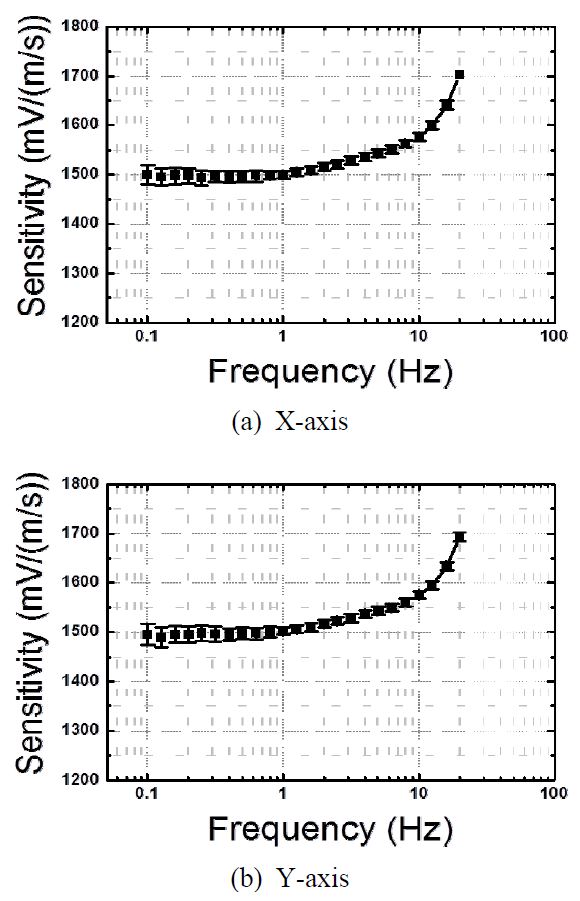
측정 예제로 Streckeisen STS-2 및 Streckeisen STS-2.5 두 종류의 광대역 속도 센서에 대하여 감도평가를 진행하였다. 해당 모델은 지진 관측망에서 가장 널리 사용되고 있는 모델로, STS-2.5는 STS-2의 특성을 개선한 것으로 알려져 있는데 이 실험을 통하여 특성 변화를 확인해 보았다. STS-2는 직경 235 mm, 높이 250 mm에 무게는 13 kg이다. STS-2.5는 STS-2와 동일한 크기이며, 무게는 12 kg이다.
Fig. 4(a)는 대상 센서를 고정하기 위한 치구를 보여주고 있으며, Fig. 4(b)와 같이 가진 테이블로 가진하게 된다. STS-2와 STS-2.5는 기본적으로 동일한 외형적 구조를 가지고 있기 때문에, 실험 장치의 구성은 동일하게 적용하였다.
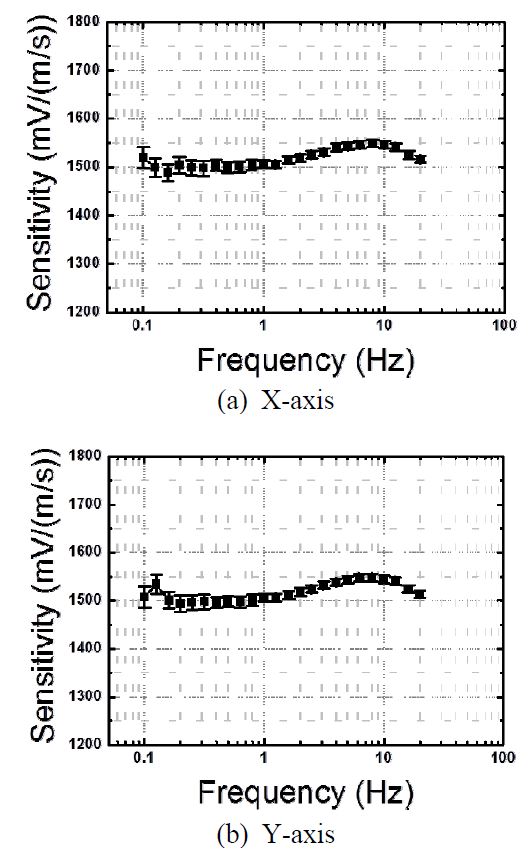
측정된 광대역 센서 STS-2의 주파수에 따른 감도 변화는 Fig. 5와 같다. 고주파수 대역으로 갈수록 감도가 증가하는 경향을 보이고 있으며 이는 공진점에 가까워지기 때문으로 볼 수 있다. STS-2.5의 경우 공진 점에서의 감도 증가 경향이 상대적으로 작게 나타나고 있음을 알 수 있다(Fig. 6). 따라서 공진에 의한 영향이 기존 모델에 비하여 크게 줄어들었음을 확인할 수 있다.
STS-2.5의 경우 0.2 Hz 이하 주파수에서 값의 변동이 상대적으로 크게 나타나는 것을 알 수 있다. 기본적으로 속도 센서의 경우 감도가 매우 크게 설계되어 있기 때문에 작은 변위로도 계측기 범위를 초과하는 출력이 나오기 때문에 변위를 작게 설정하여야 한다.
그러나 작은 변위를 느리게 움직이는 경우 매끄러운 정현파 가진이 어렵기 때문에, 저주파수 대역으로 갈수록 파형의 왜곡이 발생할 수 있다. 그러므로 반복측정시의 편차가 증가하고, 결과적으로 높은 불확도 범위를 갖게 된다.
위의 실측 결과에서 보면, 센서 종류 및 모델에 따라서 주파수에 따른 감도 특성이 다르게 나타남을 알 수 있다. 그러나 일반적인 지진계의 경우에는 감도의 공칭값과 측정 범위만을 제시하기 때문에 이러한 특성을 확인하기 어렵다. 지진계의 교정 방법으로 제시되어 있는 중력기반 방법(3)의 경우도 정적 감도만을 측정하기 때문에 주파수 특성을 알 수 없고, 교정 코일을 이용하는 방법(5)은 소급성을 확보하기 위한 기준 응답이 필요하다. 그러므로 이 시험에서 적용한 간섭계 기반 절대 교정이 지진계의 정확한 특성 확인을 위하여 필요함을 알 수 있다.
3.3 현장 설치 시 주요 불확도 인자 영향 평가
기본적인 불확도 인자는 일반적인 가속도계의 절대 교정에서 고려되는 인자들을 포함한다. 추가적으로 고려되어야 하는 인자로는 센서의 정렬 오차에 의한 영향이 있다. 기본적으로 지진센서는 수평을 맞추어 설치되는 것을 원칙으로 하며, 방향을 맞추어 설치되어야 한다. 그러나 일반적인 지진계는 실험실 환경이 아닌 옥외 관측소에 설치되기 때문에, 설치시 정밀한 정렬에 한계가 있다. 이러한 정렬상의 오차에 의한 영향을 검토하기 위하여, 설치 각도 및 수평 오차에 의한 영향을 검토하였다.
Fig. 7은 각도를 조절하기 위한 치구를 보여주고 있다. X축에 맞추어 정렬된 상태에서 2.5° 및 5°만큼 돌린 상태에서 감도를 측정하고 정렬된 상태 감도와 비교하였으며, 그 결과는 Fig. 8과 같다. 이론적으로 각도 변화에 의한 편차는 2.5°일 때 0.1 %, 5°일 때 0.4 %이며, 실측 결과는 불확도 범위를 고려할 때, 유사한 경향을 보이고 있다고 할 수 있다. 그러므로 설치시의 예상 각도 오차 범위를 이용하여 현장 측정의 불확도 기여를 산정할 수 있다.
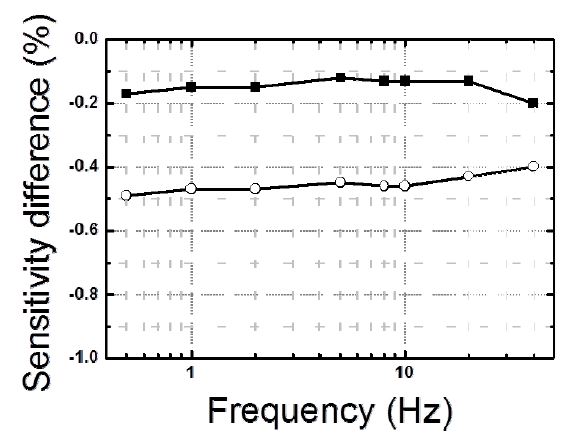
Sensitivity difference of the accelerometer according to direction misalignment (black square: 2.5°, white circle: 5°).
설치시 수평을 맞출 때에는 센서에 설치되어 있는 수준기를 이용한다. Fig. 9는 가속도계 센서에 부착되어 있는 수준기를 보여주고 있다. 일반적으로 기준원 안쪽에 지시용 버블이 들어가는 범위에서 설치하게 된다.
수평 오차의 영향을 검토하기 위하여 지시용 버블이 기준원에 접하는 경우(touched)와 기준원 위에 위치하는 경우(on the line)에 대해서 측정을 수행하고 완전히 수평을 맞춘 경우(centered)와 측정 감도의 편차를 비교하였다. Fig. 10의 결과에서 보면, 낮은 주파수에서는 크게 영향을 받지 않으나, 10 Hz 이상의 주파수부터 영향이 급격하게 증가하는 것을 관찰 할 수 있다. 이는 구조적인 불안정성이 증가하기 때문으로 볼 수 있으며, 현장 설치시의 상황을 고려하여 현장 측정값의 불확도에 반영하여야 한다.
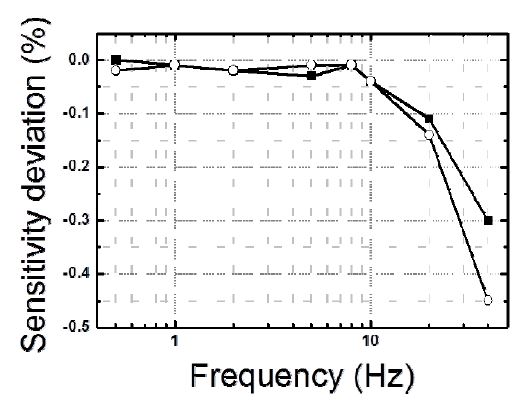
Sensitivity difference of the accelerometer according to horizontal misalignment (black square: touching the reference circle, white circle: on the reference circle)
예를 들어 2장에 기술되어 있는 실험실 등에서 정밀한 정렬이 가능한 경우의 불확도 값에 추가적으로 정렬오차에 의한 불확도 성분의 합성 불확도(9)값을 이용하여야 한다.
4. 결 론
연구에서는 가속도계의 절대 교정에 적용되는 간섭계 기반 방법을 지진계 감도의 절대 측정에 적용하였다. 센서의 무게 및 크기를 고려하여, 지진가속도계 1종에 대하여 0.1 Hz ~ 40 Hz, 광대역 속도 지진계 2종에 대하여 0.1 Hz ~ 20 Hz 영역에서 측정을 수행하였으며, 해당 범위에서는 각 센서의 감도 특성을 안정적으로 평가 할 수 있음을 확인하였다.
추가적으로 설치시에 발생할 수 있는 정렬 및 수평 오차의 영향을 정량적으로 평가하고 현장 측정 결과에 반영할 수 있도록 하였다. 이러한 절대 교정 방법을 통하여 지진 분야에 직접적으로 소급성을 제공하는 것이 가능하다.
Acknowledgments
이 연구는 기상청 기상·지진See-At기술개발연구/지진화산기술사업 (KMI2017-9100)의 지원으로 수행되었습니다.
References
- ISO/IEC, 2007, International Vocabulary of Metrology - Basic and General Concepts and Associated Terms (VIM), Guide 99.
-
Hutt, C. R., Evans, J. R., Followill, F., Nigbor, R. L. and Wielandt, E., 2009, Guidelines for Standardized Testing of Broadband Seismometers and Accelerometers, USGS Open-File Report 2009-1295.
[https://doi.org/10.3133/ofr20091295]

- International Organization for Standardization, 2014, Methods for the Calibration of Vibration and Shock Transducers - Part 42: Calibration of Seismometers with High Accuracy using Acceleration of Gravity, ISO 16063-42.
- International Organization for Standardization, 2015, Methods for the Calibration of Vibration and Shock Transducers - Part 43: Calibration of Accelerometers by Model-based Parameter Identification, ISO 16063-43.
- International Organization for Standardization, 2017, Methods for the Calibration of Vibration and Shock Transducers - Part 45: In-situ calibration of Transducers with Built in Calibration Coil, ISO 16063-45.
- International Organization for Standardization, 1999, Methods for the Calibration of Vibration and Shock Transducers - Part 11: Primary Vibration Calibration by Laser Interferometry, ISO 16063-11.
-
Sun, Q., Yang, L., Bartoli, C., Veldman, I., Ripper, G. P., Bruns, T., and Dickinson, L., 2016, Final Report of CCAUV.V-K3: Key Comparison in the Field of Acceleration on the Complex Charge Sensitivity, Metrologia, Vol. 54, No. 09001.
[https://doi.org/10.1088/0026-1394/54/1A/09001]

-
Dobosz, M., Usuda, T. and Kurosawa, T., 1998, Methods for the Calibration of Vibration Pick-ups by Laser Interferometry: I. Theoretical Analysis, Measurement Science and Technology, Vol. 9, No. 2, pp. 232~239.
[https://doi.org/10.1088/0957-0233/9/2/010]

- ISO/IEC, 1995, Uncertainty of Measurement – Part 3: Guide to the Expression of Uncertainty in Measurement, Guide 98-3.

Yong-Bong Lee received M.S. and Ph.D. degree in Mechanical Engineering at KAIST. He is currently working at Korea Research Institute of Standards and Science as a senior researcher. His research interests are standards for vibration measurement and seismology.

Wan-Ho Cho received M.S. and Ph.D. degree in Mechanical Engineering at KAIST. He is currently working at Korea Research Institute of Standards and Science as a senior researcher. His research interests are in the area of acoustic metrology, sound field control, and acoustical array system. He also interest in the product sound quality (PSQ) and noise control.