발사장치를 포함한 소형 초음속 제트 소음 예측 및 검증

1. 서 론

초음속 제트 소음은 로켓 엔진으로부터 생성되는 높은 압력이 주변 대기로 분사되며 생성된다. 생성된 초음속 제트 소음은 크게 지향성(directivity)을 갖는 난류인 large scale structure(LSS)와 지향성이 거의 없는 fine scale structure(FSS) 성분으로 구분할 수 있다. 초음속 제트 소음은 엔진노즐 출구로부터 초기 혼합 영역(initial mixing region), 전환 영역(transition region), 완전 발달 영역(fully-developed region) 순으로 전개된다. 이 때 초음속 제트 출구로부터 마하수가 1이 유지되는 구간을 포텐셜 코어(potential core), 대기압과 혼합되며 마하 코어(mach core)가 생성되고 붕괴되는 구간을 초음속 코어(supersonic core)라고 지칭한다. 포텐셜 코어부터 후류 구간에서는 전단 흐름을 갖는 난류가 생된다. 이러한 초음속 제트 소음특성을 변화시켜 비행체 구조물에 작용하는 음향 하중을 감소시키고자 다양한 발사장치가 고안되었다.

NASA SP-8072⁽¹⁾에서는 실제 발사된 우주발사체 및 초음속 발사체의 실험 결과 등을 이용하여 초음속 제트의 원거리 소음을 예측하기 위한 준 경험식이 제공되었으며 이를 최소화 하고자 평판, 경사판 및 발사장치 등이 이용되었다. 또한 최대 복사 각도(maximum radiation angle)는 엔진 출구의 음속에 비례하여 증가한다고 제시하였다. Eldred, K. M.⁽¹⁾는 소음의 원점(source)을 분산시킨 후 거리에 대한 원거리 소음을 예측하였으며, 이는 Varnier, J.⁽²⁾에 의해 개선되었다. Haynes, J. et al.⁽³⁾는 Reynolds averaged Navier-Stokes(RANS) 기반 전산유체해석을 통하여 Varnier, J.에 의해 제시된 분산 소음 기법(distributed source method, DSM)이 더 적절하다고 밝혔다. 그러나, RANS기반전산유체해석은 광범위한 주파수 특성을 가진 제트소음 예측에 부정확하므로, large eddy simulation(LES)를 이용한 초음속 제트 소음 예측이 연구되어 왔다. Bodony, D. J. et al.^(4,5)은 공간/시간 차분 차수, 경계조건 및 원거리 소음 예측 기법 등이 LES기법을 이용한 초음속 제트 소음 예측에 중요한 요인임을 제시하였다. 하지만 LES기법으로는 벽면으로부터 생성되는 난류를 예측하기 위해서 과도한 격자가 필요하게 되므로, 자유 분사 제트 소음 (free-jet noise) 예측에서만 주로 이용되었다. 또한 높은 Reynolds수의 제트 소음 특성을 예측하기에는 과도한 해석 자원이 필요하다⁽⁶⁾. 이러한 벽면에 의한 난류 특성이 지배적인 특성 또는 현상을 해석고자 detached eddy simulation(DES) 기법이 개발되었다. DES기법은 벽면 난류가 생성되는 지역에는 RANS기법이 적용되고, 계산된 소용돌이(eddy)를 LES영역 내로 전달하므로 효율적인 해석이 가능하다. 하지만 DES기법 내 사용되는 격자는 일반적인 크기에 비해 작아서 소음 예측 시, 실제 현상에 비해 감소된 난류 응력을 예측한다⁽⁷⁾. 이를 해결하기 위해 보호 함수(shielding function)를 도입한 delayed DES(DDES) 기법으로 확장되었다. 다양한 현상에 대해 DDES기법이 적용되었고, LES기법에 비해 비교적 복잡한 형상이 포함된 초음속 제트소음 예측 연구가 진행되었다⁽⁸⁾. 최근 Arian 5, Epsilon 등 우주발사체의 소음 저감을 위해 축소 형상을 이용한 연구가 활발하다. Gely, D. et al.⁽⁹⁾은 1/47 목업 (mock-up) 형상을 이용, 물 분사(water-injection) 및 발사장치 길이를 연장함으로써 5 dB이상의 소음 저감 결과를 제시하였다. Tsutsumi, S. et al.^(10~12)는 화염발사장치(Flame launch system, FD) 및 다양한 발사장치 형상을 적용하여 1/42 축소 실험 및 실제 크기 형상에 대한 수치 해석 결과를 비교하였다. 초음속 로켓 엔진 출구로부터 지면과의 높이를 로켓엔진 출구 지름 (D_e)으로 무차원화 후 높이에 따른 소음 저감 결과를 제시하였다. 하지만 소음저감 발사장치를 포함한 초음속 제트 소음 연구는 실험 또는 수치 해석 연구가 개별적으로 수행되었으며, 복잡한 발사장치 형상에 대한 정확한 정보가 공개되어 있지 않다.

이 연구에서는 기존 Tsutsumi, S. et al.⁽¹²⁾에 의해 제시된 발사장치를 모사한 형상을 이용하여, 발사장치에 의해 변화된 소형 초음속 제트 소음 생성과 저감 특성을 연구하고자 한다. 첫째, 출구 마하수 1.8 (M_e=1.8)을 갖는 소형 로켓 노즐에 대한 자유분사 제트 소음에 대한 수치 해석 및 실험을 수행하였다. 둘째, 개발된 수치 해석 기법을 이용하여 발사장치를 포함하는 소형 초음속 제트 소음을 예측하였으며, 실험을 통해 비교 및 검증하였다. 셋째, 3개의 다른 추가 발사장치 형상을 실험에 적용하여 추가적인 소음 저감 효과를 제시하고자 한다.

2. 출구 마하수 1.8 소형 초음속 자유분사 제트 소음 예측 기법 및 실험

2.1 자유분사 제트 소음 예측

(1) 출구 마하수 1.8 소형 노즐 형상

초음속 자유분사 제트 소음을 생성시키기 위하여, 이 연구에서는 출구 마하수가 1.8인 소형 노즐을 설계하였다. 등 엔트로피 과정(isentropic process)을 가정한 로켓 노즐의 출구 마하수 및 면적 비 관계는 식 (1)과 같다.

$\[ \frac{A}{A^{\mathrm{*}}}=\frac{1}{M_e}{\left(\frac{1+\frac{\gamma -1}{2}{M}_e^2}{1+\frac{\gamma -1}{2}}\right)}^{\frac{\gamma +1}{2\left(\gamma -1\right)}} \]$

(1)

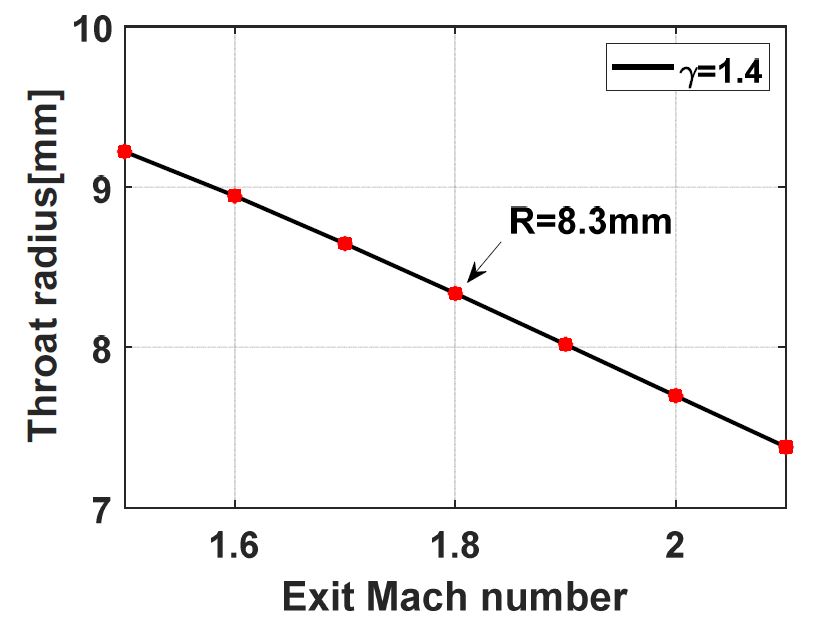
식 (1)에서 A 는 출구 단면적, A ^*는 노즐 목 단면적, M_e는 출구 마하수, γ는 기체 상수를 나타낸다. 비가열 로켓 노즐 (unheated rocket nozzle)일 경우, 기체 상수는 1.4이므로 출구 마하수는 노즐 목과 출구의 단면적 비에 의해 결정되는 것을 알 수 있다. 이 연구에서는 소형 로켓 노즐의 출구 지름을 20 mm로 설정하였으며, 출구 마하수 변화에 대한 노즐 목 반지름은 Fig. 1과 같다.

Fig. 1

Correlation between the exit Mach number and radius at nozzle throat

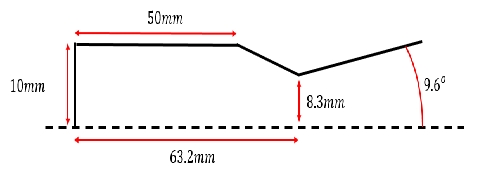
Fig. 2는 노즐 목 반지름 8.3 mm를 갖는 소형 로켓 노즐에 대한 축 대칭 형상 정보이다.

Fig. 2

Sketch of small rocket nozzle

(2) 유동/음향 단방향 연계 해석 기법

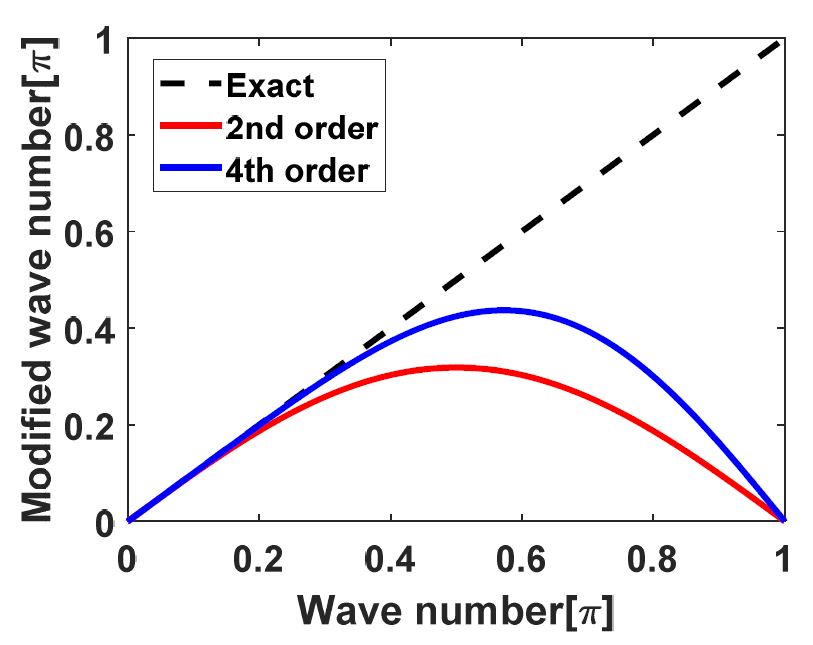
출구 마하수 1.8을 갖는 소형 초음속 자유 분사 제트 소음을 예측하기 위해서 유동/음향 단방향 연계해석 기법을 적용하였다. DDES기법을 이용한 유동해석은 초음속 자유 분사 제트의 소음 생성 과정과 소음원의 위치를 예측하고, 음향 해석에서 사용될 압력 등의 시간/공간에 관한 변수를 제공한다. 이 때, 유동해석 내 공간 차분 차수에 따라 파장을 예측하기 위한 최대 격자 크기가 결정된다⁽¹³⁾. Fig. 3은 공간 차분 기법 차수에 따라 파수의 정해 및 수치적 신뢰 파동수(wave number)가 다름을 나타낸다. 높은 차수의 공간 차분 기법일수록 정해를 예측하기 위한 파동수가 높으며 이는 파동수를 예측하기 위한 최소 격자 개수를 뜻한다. Table 1은 파동수의 정해를 예측하기 위한 파장 당 최소 격자 개수를 나타낸다.

Fig. 3

Resolved wave number according to the discretization scheme order

Table 1

Resolution for capturing acoustic propagation according to the different discretization scheme

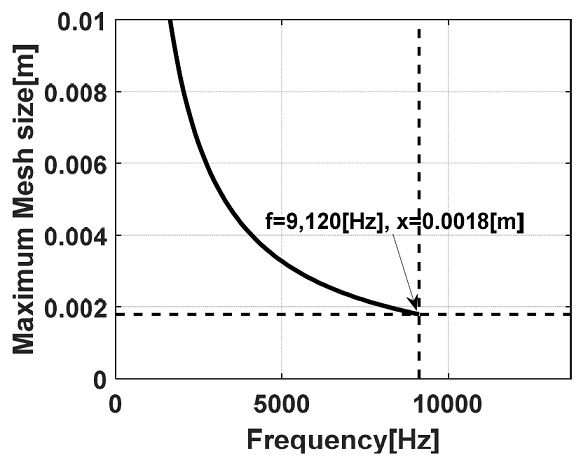
이 연구에서는 유동해석을 위해 ANSYS FLUENT를 이용, 2차 기법 차수를 사용하였으며, Fig. 4와 같이 최대 신뢰주파수 9600 Hz를 예측하기 위해서 최대 격자 크기 0.0018 m을 사용하였다.

Fig. 4

Maximum mesh size according to the frequency

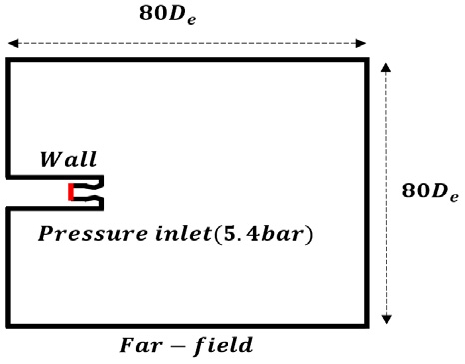
하지만 유동해석만으로 원거리장에서 높은 주파수 특성을 갖는 소음을 예측하기 위해서는 과다한 격자 개수가 요구된다. 이를 방지하고자 유동/음향 단방향 연계 해석 기법을 적용하였다. 비선형성이 지배적인 소음원 영역인 초음속 자유분사 제트 후류 영역은 유동해석을 통하여 소음의 생성을 예측하며 선형적인 영역에 Kirchhoff 평면을 삽입, Helmholtz- Kirchhoff(H-K) 적분식을 이용하여 원거리장에서의 소음특성을 예측한다. 우선 유동해석에서는 후류가 긴 초음속 자유 분사 제트를 모사하기 위해 Fig. 5와 같이 충분히 넓은 영역을 정의한다. 선형적인 영역에 Kirchhoff 평면을 삽입하기 위하여 시간에 따른 정압 섭동이 1 % 이내인 곳을 기준으로 하였다. Fig. 5의 해석 영역을 이용하여 2차원 축대칭 영역을 설정할 수 있으며 비정상 RANS(unsteady RANS)를 수행하였다.

Fig. 5

Computational domain for supersonic free-jet analysis

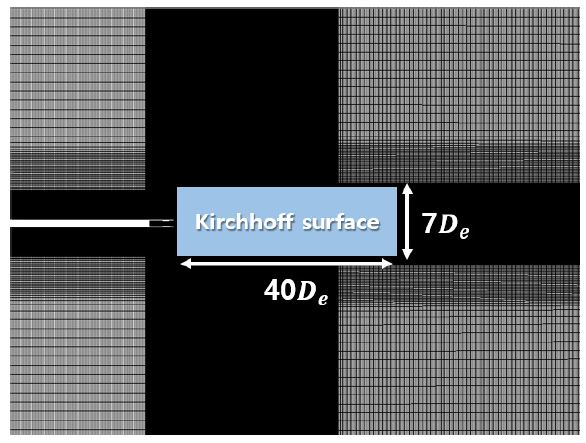
Fig. 6은 0.02초에서의 정압 분포 및 정압 섭동이 1%이내인 곳에 삽입된 Kirchhoff 평면을 나타낸다. 삽입된 Kirchhoff 평면의 위치는 노즐 축 방향으로 0 - 40D_e , 반경방향으로 7D_e의 원통면으로 설정하였다.

Fig. 6

Static pressure contour of the axisymmetric URANS with Kirchhoff surface

Fig. 7과 같이 Kirchhoff surface 영역 안으로는 조밀한 격자를 생성한 후 3차원 DDES해석을 진행하였다. 시간 전진은 1 × 10^{- 6}[s]를 사용하였으며, 이는 CFL < 1을 만족한다. Table 2는 DDES해석 내의 해석 기법 정보를 나타낸다.

Fig. 7

Cross section of the present grid on the z=0 plane with Kirchhoff surface

Table 2

Information of DDES analysis

Kirchhoff 평면으로부터 얻어진 유동해석 결과는 음향해석기법 내의 입력값으로 원거리 음장을 예측을 위해 사용되었다. H-K 적분법을 이용할 경우, 임의의 위치에서의 음압을 예측하기 위해서는 음향 전파 영역의 경계 조건만 필요하므로 유동해석 결과를 경계조건으로 대체하였다. 유동해석 내 압력 변수들은 Kirchhoff평면에서 공간 및 시간에 대해 Δx = 0.005[m], Δt = 2 × 10^{- 5} [s]간격으로 저장하였다.

$\[ p\left(Q,t\right)=\frac{1}{4\pi }\int \left\{\begin{array}{c}-\frac{1}{s}\left[\frac{\partial p}{\partial n}\right]\\ +\frac{\partial }{\partial n}\left(\frac{1}{s}\right)\left[p\right]\\ -\frac{1}{c_{0}s}\frac{\partial s}{\partial n}\left[\frac{\partial p}{\partial t}\right]\end{array}\right\}dS \]$

(2)

식 (2)에서 p는 음압, n은 수직 벡터, c₀ 는 음속, t는 시간이다. 유동해석결과를 이용하여 ∂p/∂n, p∂p/∂t을 계산한 후, 식 (2)에 대입하여 원하는 임의의 위치 및 원거리장의 음압을 예측한다.

2.2 자유분사 제트 소음 실험

(1) 소형 초음속 자유분사 제트 소음 측정 실험

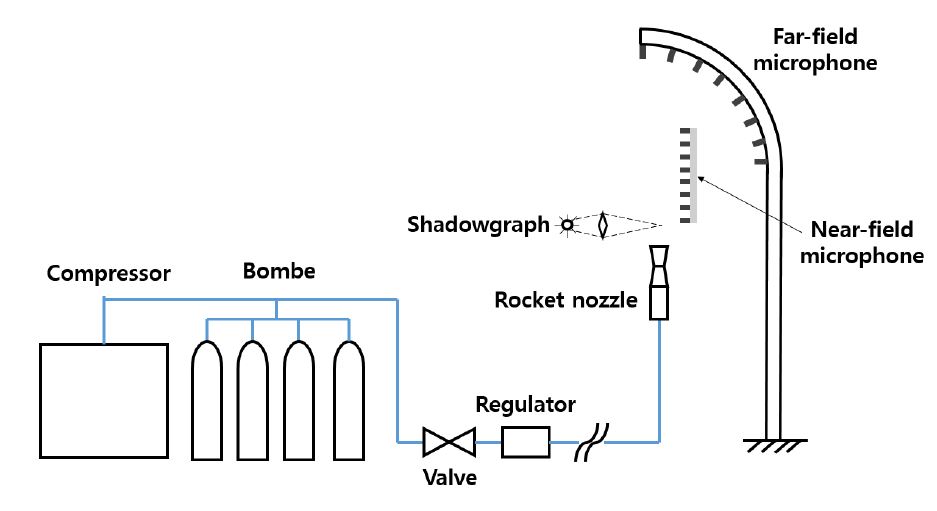
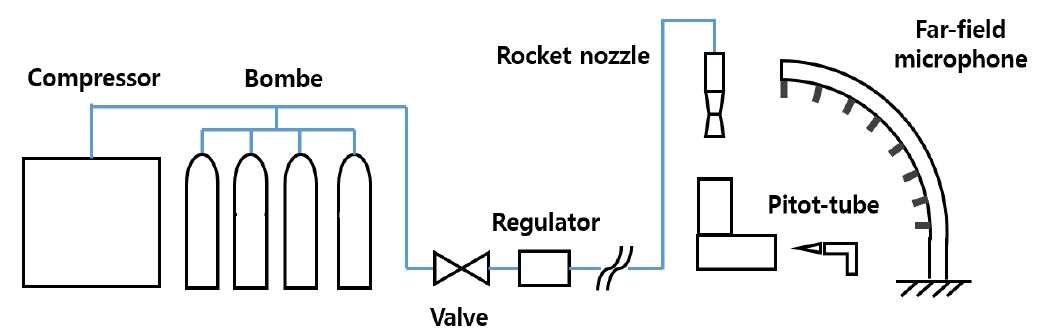
위에서 언급된 출구 마하수 1.8을 갖는 소형 초음속 자유분사 제트 소음을 측정하기 위하여 Fig. 8과 같이 실험 장비를 구성하였다.

Fig. 8

Conceptual sketch of experimental setup for supersonic free-jet

고압 조건을 만족시키기 위하여 총 6개의 봄베를 사용하였으며, 수 차례 분사 이후 봄베 압력이 낮아질 경우 충전하기 위하여 압축기를 사용하였다. 밸브와 레귤레이터를 이용하여 초음속 로켓 노즐 입구의 압력을 5.4 bar로 구성하였다. 초음속 로켓 노즐은 지상 상방으로 설치하여 제트 소음의 지면에 대한 반사 효과를 최소화 하고자 하였다. 로켓 노즐로부터 분사되는 초음속 제트 소음을 측정하고자 섀도 그래프, 근거리장 및 원거리장 마이크로폰을 설치하였다. 1 회 실험 수행 시, 3 초가량 분사하였으며 이 연구에 사용한 실험 결과는 측정된 압력이 비교적 정상 상태인 1초~ 2초 구간의 결과를 사용하였다. 또한 3회 분사 시, 최대 0.8 dB의 오차를 보였으므로 실험의 재현성을 확보하였다.

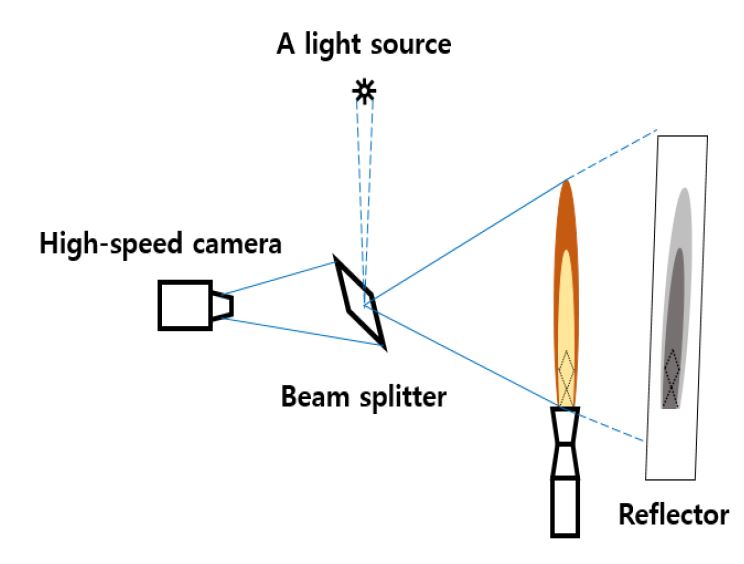
첫째, 소형 로켓 노즐 출구로부터 생성되는 마하수 특성을 측정하고자 역반사 섀도 그래프 기법(retroreflective shadowgraph technique)을 적용하였다. Fig. 9는 역반사 섀도 그래프 기법에 대한 개략도를 나타낸다. 빛이 없는 암막 및 고휘도 반사지를 이용하여 실험 환경을 조성한 후 초고속 카메라, 광원 및 빔 스플리터를 이용하여 반사면에 맺힌 그림자를 사진으로 저장한다. 저장된 사진들의 평균값 및 배경제거 기법을 통하여 노즐 출구에 생성되는 마하충격파를 촬영하였다.

Fig. 9

Conceptual sketch of retroreflective shadowgraph technique

둘째, 근거리장 소음 특성을 측정하기 위하여 총 16개의 마이크로폰을 이용하여 근거리장 음압 측정장치를 구성하였다. 노즐 출구 중심으로부터 반경방향으로 7D_e떨어진 지점에 2.5D_e간격으로 각각의 마이크로폰을 설치하였다.

셋째, 원거리장 소음 특성을 측정하기 위하여 총 15개의 마이크로폰을 이용하여 원거리장 음압 측정 장치를 구성하였다. 노즐 출구 중심으로부터 축방향으로 17D_e떨어진 지점을 원점으로, 반지름 100D_e을 갖는 환형 배열의 장치를 구성하였다. 근거리장 및 원거리장 측정 창지에 사용된 마이크로폰 특성은 Table 3과 같다.

Table 3

Specification for two types of microphone

2.3 자유분사 제트 소음 결과 비교

(1) 초음속 자유분사 제트 소음 해석 및 검증

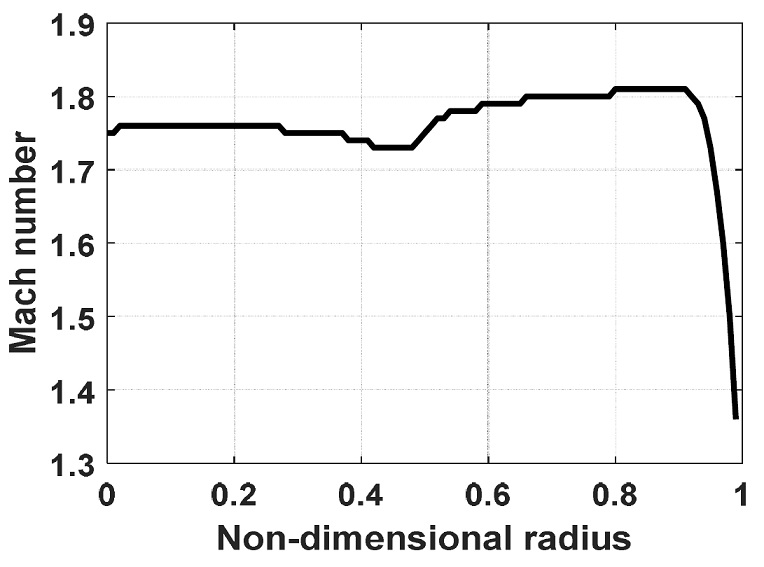
출구 마하수 1.8을 갖는 소형 초음속 자유분사 제트 소음 해석/실험결과의 비교 및 검증 절차는 아래와 같다. 우선, 제작된 로켓 노즐 형상이 출구 마하수 1.8 특성을 갖는지에 대해 해석 결과와 비교하였다. Fig. 10은 URANS 해석 결과로서, 노즐 출구 중심부터 벽까지에 대한 마하수를 나타낸다. 노즐 출구 마하수 해석 결과는 1.76 ~ 1.8 로, 설계하였던 출구 마하수 1.8과 유사한 것을 확인할 수 있다.

Fig. 10

Mach number according to the non-dimensional radius

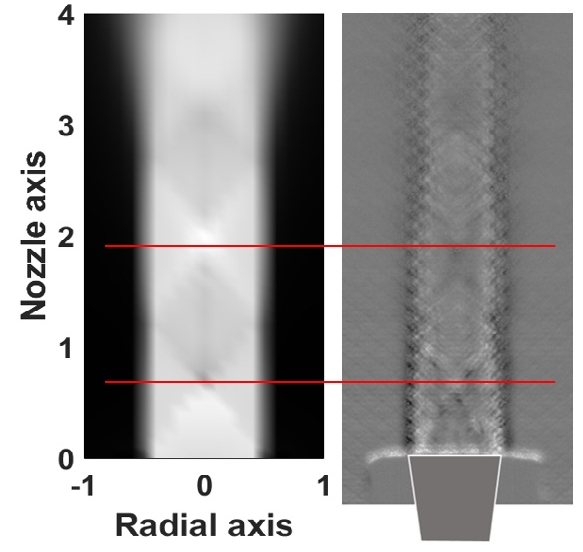
또한 유동해석 밀도 결과 및 역반사 섀도 그래프기법을 이용한 마하충격파 특성은 Fig. 11과 같다.

Fig. 11

Shock cell length comparison (left: DDES analysis, right: shadowgraph technique)

초음속 특성에 의해 충격파이 발생하며 충격파간의 거리(shock cell length, L _sc)는 해석 결과 및 측정 결과 모두 1.45D_e임을 확인하였다.

근거리장의 소음특성을 비교하기 위하여 Kirchhoff평면 영역 내 존재하는 유동해석 압력결과 및 근거리장 음압 측정 장치 결과를 비교하였다. Fig. 12는 근거리장 음압 측정 장치 및 16개의 마이크로폰 배열을 나타낸다.

Fig. 12

Photograph of near-field measurement for supersonic free-jet

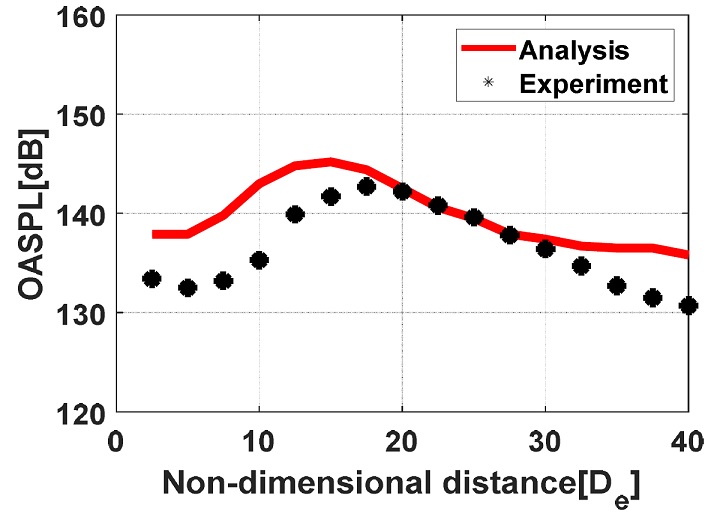
Fig. 13 및 Table 4는 근거리장 음압 비교 위치 및 해석/실험 결과를 나타낸다. 총 16개의 위치에서 실험결과와 해석 결과는 평균 3.24 dB 차이가 있음을 확인할 수 있다. 특히 지향성⁽¹⁴⁾이 있는 large scale structure(LSS영역, 17.5 - 22.5D_e , θ_LSS ≅ 35^o)에서는 평균 1 dB 이내의 차이가 있으며, 나머지 영역에서는 해석 결과의 음압이 실험 측정 결과에 비해 크게 예측되었다. 이는 유동해석에서 사용된 2차 기법을 이용할 경우, 지향성이 있는 영역에서는 소음 특성을 예측할 수 있으며 나머지 영역에서도 해석결과가 실험결과에 비해 과도하게 예측하지만 경향은 잘 모사하는 것을 알 수 있다.

Fig. 13

Comparison of the sound pressure level at near-field for supersonic free-jet

Table 4

Sound pressure level at near-field for supersonic free-jet

Kirchhoff 평면 및 유동해석 결과를 H-K적분식에 대입하여 원거리장 16개의 임의의 위치에 분포하는 음압을 예측하였다. 또한, Fig. 14와 같이 16개의 마이크로폰을 환형배열에 구성하여 해석 결과와 비교하였다.

Fig. 14

Photograph of far-field measurement for supersonic free-jet

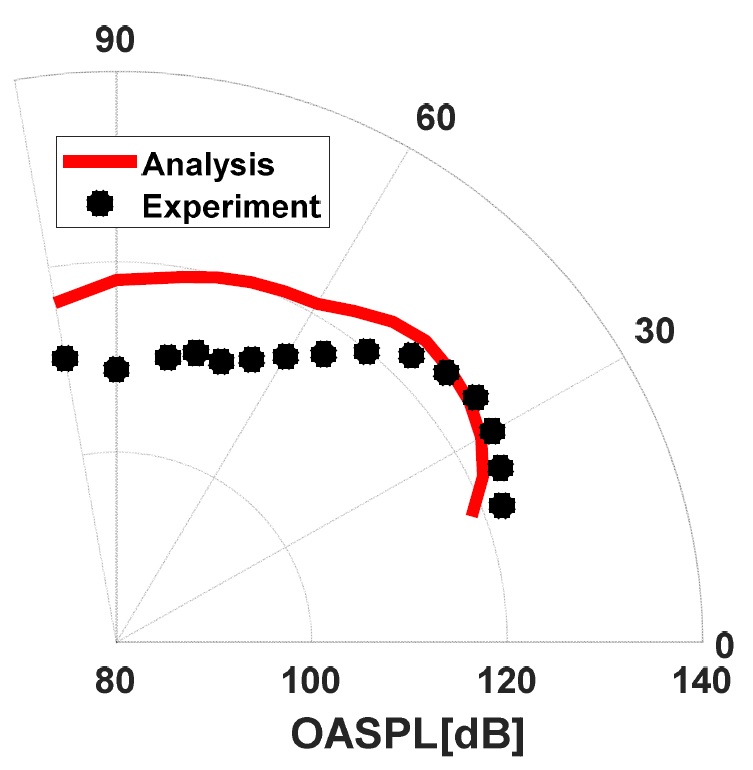
Fig. 15 및 Table 5는 원거리장 음압 비교 각도 및 해석/실험 결과를 나타낸다. 총 15개의 위치에서 해석 및 실험 결과는 평균 4.7 dB 차이가 있음을 확인 할 수 있다. 근거리장의 경향과 유사하게, LSS영역에서 해석결과 및 실험결과가 매우 유사함을 확인하였다. 하지만 50° 이상의 높은 각도에서는 해석결과가 실험결과에 비해 과도하게 예측하는 것을 알 수 있다.

Fig. 15

Comparison of the sound pressure level at far-field for supersonic free-jet

Table 5

Sound pressure level at far-field for supersonic free-jet

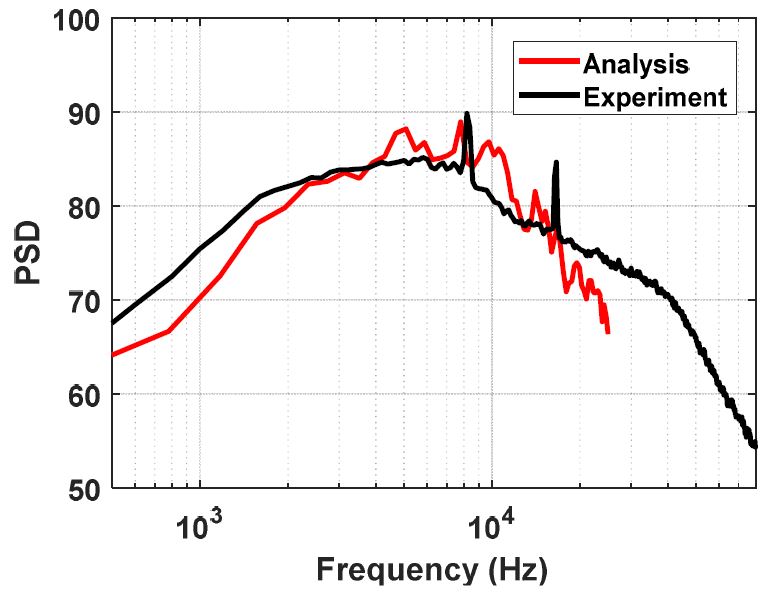
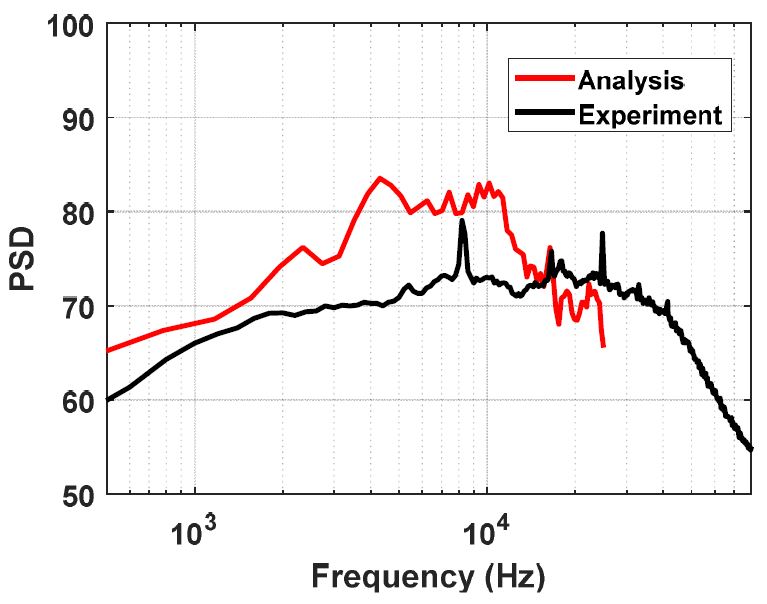
Figs. 16, 17은 원거리장 45°와 75°에서의 파워스펙트럼밀도(power spectrum density, PSD)이다. 원거리장 45°에서는 예측한 주파수 범위 내에서 실험결과와 비교적 일치하며 75°에서는 해석 결과가 실험결과에 비해 과대하게 예측함을 확인하였다. 따라서 이 연구에서 적용한 소음 예측 기법은 근거리/원거리장에서 음압 경향은 지향성이 있는 LSS영역에서는 매우 정확한 예측을 하나 나머지 영역에서는 해석 결과가 과대하게 예측하는 것을 확인하였다.

Fig. 16

Comparison of the power spectrum density at far-field (45°) for supersonic free-jet

Fig. 17

Comparison of the power spectrum density at far-field (75°) for supersonic free-jet

3. 발사장치를 포함한 소형 초음속 제트 소음 예측 기법 및 실험

비행체 구조물에 작용하는 음향하중을 저감시키기 위하여 Tsutsumi, S. et al.⁽¹²⁾에 보고된 발사장치를 Fig. 18과 같이 모사 및 제작하여 해석/실험에 각각 적용하였다.

Fig. 18

Configuration of present launch system

앞서 사용된 출구 마하수 1.8 을 갖는 소형 로켓노즐과 발사장치 하단과의 거리는 11D_e 로 두었으며 이는 Ishii, T. et al.⁽¹⁵⁾에 의해 모든 주파수 대역에서 가장 낮은 음향하중을 갖는 거리이다.

3.1 발사장치를 포함한 제트 소음 예측

(1) 발사장치를 포함한 유동/음향 단방향 연계 해석 기법

발사장치를 포함한 제트 소음을 예측하기 위해서 앞서 언급된 유동/음향 단방향 연계 해석 기법과 동일한 절차를 적용하였다. 유동해석에서 DDES기법을 이용하기 전 Kirchhoff 평면의 위치를 결정하기 위하여 URANS 해석을 진행하였다. 발사장치가 포함될 경우, 초음속 자유분사 제트에 비해 후류가 길게 형성되지 않으므로 해석 영역은 Fig. 19와 같이 설정하였다. URANS 유동해석 결과를 이용하여 정압 분포 및 정압 섭동이 1 %이내인 곳에 Kirchhoff 평면을 삽입하였다. Fig. 20은 DDES해석 내 발사장치 출구로부터 축 방향으로 0 - 40D_e , 반경방향으로 7D_e 의 반원통면의 Kirchhoff 평면을 나타낸다.

Fig. 19

Computational domain for impinging jetanalysis with a launch system

Fig. 20

Static pressure contour of the URANS with Kirchhoff surface

발사장치를 포함한 초음속 제트 소음 해석은 자유분사 제트 해석에 비해 과도한 격자가 요구되므로, 최대 신뢰주파수를 7600 Hz을 만족하는 격자를 사용하였다. 유동 해석에는 Table 2에서 제공된 기법을 동일하게 사용하였으며 시간전진도 동일하게 적용하였다. 소형 로켓 노즐로부터 전파되는 유동 현상이 정상(steady) 상태가 된 후로부터 Kirchhoff 평면 위 압력 변수들을 저장하였다. 변수들은 Kirchhoff 평면 위에서 자유 분사 제트 해석과 동일한 공간 및 시간 조건으로 저장하였다. 이를 식 (2)에 대입함으로써 임의의 위치 및 원거리장의 음압을 예측하였다.

3.2 발사장치를 포함한 제트 소음 실험

(1) 발사장치를 포함한 제트 소음 측정 실험

기존 자유 분사 제트 실험 장비를 개선하여 발사장치가 포함된 실험을 진행하였으며 이는 Fig. 21과 같다. 초음속 로켓 노즐의 입구 압력은 5.4 bar로 동일하게 구성하였으며, 실제 발사 환경을 모사하기 위하여 지상 하방으로 분사하였다. 발사장치 출구 주변은 높은 압력이 지배적이므로 마이크로폰 대신 피토튜브를 이용하여 압력 및 마하수를 비교하고자 하였다. 원거리장 환형 배열의 중심은 초음속 로켓 노즐 출구로부터 발사장치 하방에 수직인 위치로 설정하였으며 반지름은 100D_e으로 구성하였다.

Fig. 21

Conceptual sketch of experimental setup for impinging jet with launch system

첫째, 발사장치 출구로부터 전파되는 정압 및 전압을 2개의 피토 튜브로 측정한 후, 식 (3)과 같은 등 엔트로피 방정식을 이용하여 마하수로 변환한다. 사용한 피토 튜브는 전압을 측정하기 위하여 PSA-C01, 정압을 측정하기 위하여 PSA-01 피토 튜브를 사용하였다. 변환된 마하수는 유동해석에서 예측된 마하수와 비교하였다. 피토 튜브의 측정 위치는 URANS 유동해석 층류(streamline) 분포 결과를 이용하였다.

$\[ \frac{P_{total}}{P_{static}}={\left(1+\frac{\gamma -1}{2}{M}^2\right)}^{\frac{\gamma }{\left(\gamma -1\right)}} \]$

(3)

둘째, 원거리장 환형 배열에 16 개의 마이크로폰을 구성한 후, 압력을 측정하였다. 측정된 압력은 유동/음향 단방향 해석 결과와 측정된 위치에서 비교 검증하였다.

3.3 발사장치를 포함하는 제트 소음 결과 비교

(1) 발사장치를 포함하는 제트 소음 해석 및 검증

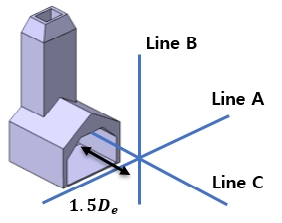
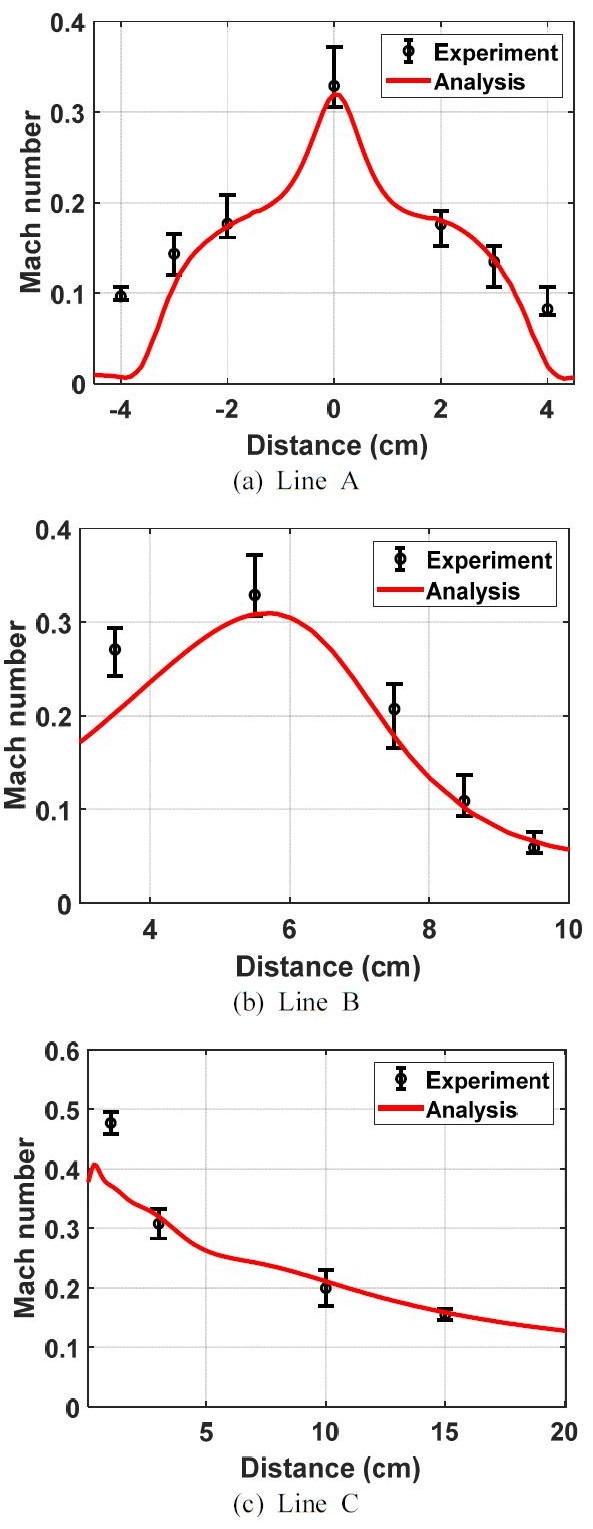
발사장치 출구 근거리에 존재하는 마하수 분포는 Fig. 22와 같이 총 3 개의 선, 16 개의 위치에서 비교하였다. 발사장치 출구로부터 나오는 유동 특성이 대칭성이 있는지 확인하기 위하여 출구로부터 1.5D_e거리에 Line A를 선정하였으며, Line B와 Line C는 수직/수평의 유동 특성을 확인하기 위하여 선정하였다.

Fig. 22

Schematic diagram for near-field pressure measurement

Fig. 23은 각 위치에서의 마하수 해석 결과와 실험에서 측정된 압력을 마하수로 변환하여 비교한 결과이다. 발사장치 출구로부터 대칭적인 마하수 분포 특성이 있음을 확인하였다. 지면 수직방향으로 발사장치 출구로부터 또한, 일정 거리에서 비교적 높은 마하수가 분포된다. 발사장치 출구로부터 멀어질수록 유동의 속도는 감소됨을 확인하였다.

Fig. 23

Mach distribution

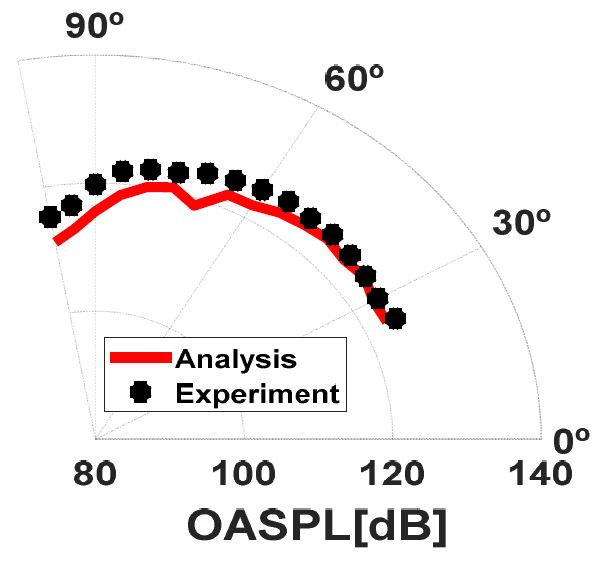
발사장치를 이용한 유동/음향 단방향 해석 결합 기법을 검증하기 위하여 원거리장의 해석 및 실험 음압을 비교하였다. Fig. 24 및 Table 6은 발사장치를 포함한 제트 원거리장 음압 비교 각도 및 해석/실험 결과를 나타낸다. 총 16개의 위치에서 평균 2.43 dB 차이가 있음을 확인하였다.

Fig. 24

Comparison of the sound pressure level at far-field for impinging jet with launch system

Table 6

Sound pressure level at far-field for impinging jet with launch system

이 연구에서 사용한 유동/음향 단방향 해석 기법은 초음속 자유 분사 제트에 비해 발사장치가 포함된 제트 소음을 더 정확히 예측함을 확인하였다. 초음속자유 분사 제트 소음 특성은 지향성이 강한 특성에 대해 2차 차수 기법이 적용될 경우, 방사(radiation)에 의한 에너지 소산(dissipation)이 실제 현상에 비해 높게 예측한 것으로 추측된다.

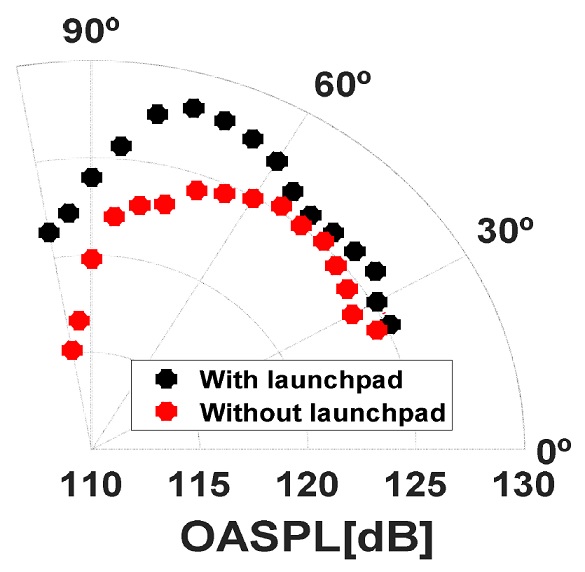
발사장치를 적용하여 비행체 구조물에 작용하는 음압 저감 효과를 확인하기 위하여, 발사장치 없이 로켓노즐을 바닥으로 분사시키는 충돌제트(impinging jet) 실험을 진행하였다. Fig. 25은 발사장치가 포함될 경우, 모든 각도에서 원거리장 음압이 감소함을 나타낸다. 특히 수직 각도(θ=90°)에 작용하는 음압은 4.2 dB감소하였으며 이는 발사장치를 통한 소음 저감 효과가 있음을 확인하였다.

Fig. 25

Comparison of the sound pressure level at far-field for impinging jet with/without launch system

3.4 추가 발사장치 형상들을 이용한 실험

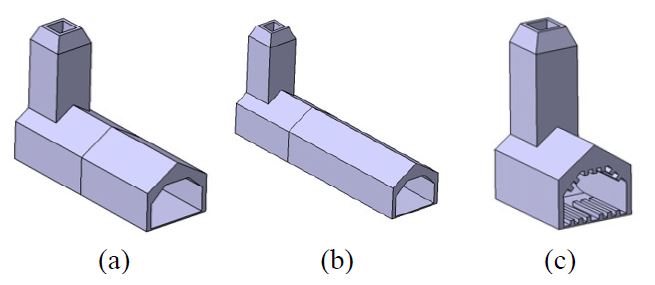
Tsutsumi, S. et al.⁽¹²⁾에 의해 제시된 발사장치 형상을 기준으로 길이를 연장한 2 개의 발사장치와 출구 위아래에 추가구조물을 추가한 1 개의 발사장치 형상에 대해 Fig. 26과 같이 제작하였다.

Fig. 26

Three different configurations of the present launch system

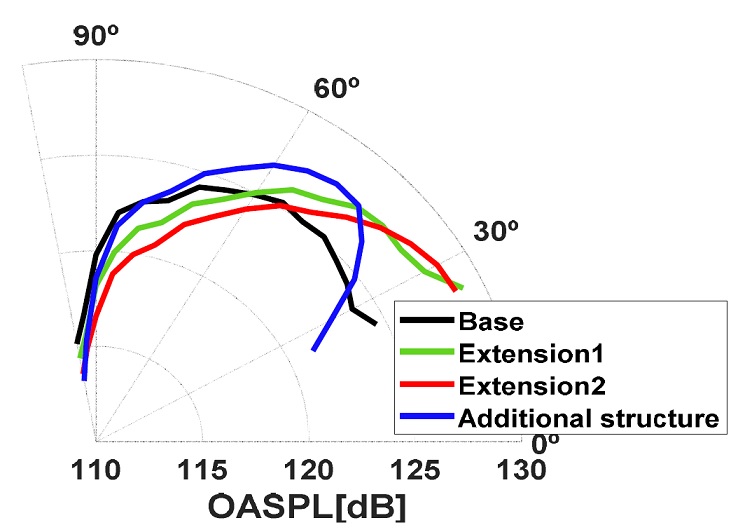
Fig. 27은 총 4개의 다른 발사장치 형상에 대한 음압분포를 나타낸다. 기존 형상은 base, Fig. 26(a) 형상은 extension1, Fig. 26(b) 형상은 extension2, Fig. 26(c)형상은 additional structure로 명명하였다. 비행체 구조물에 작용하는 음압은 기존 형상에 비해 3개의 추가 발사장치에서 감소됨을 확인하였다. 이는 기존 NASA SP-8072에서 보고된 실험결과에 부합한다. 발사장치의 길이를 연장할수록 내부 소음원으로부터 비행체 구조물까지의 거리가 멀어지므로 음압이 감소하는 것으로 판단된다. 또한 발사장치 출구에 추가구조물을 추가한 형상 또한 비행체 구조물에 작용하는 음압이 추가적으로 2 dB ~ 3 dB 감소함을 확인하였다. 그러나 추가구조물을 포함한 발사장치의 경우 기존의 발사장치 형상에 비해 5 dB이상의 음압이 증가하였다. 추가구조물을 포함한 발사장치를 적용할 경우 내부에 생성되는 소음원에 대한 추가 연구가 필요하다.

Fig. 27

Comparison of the sound pressure level at far-field for different configurations of launch system

4. 결 론

이 연구에서는 초음속 자유분사 제트 및 발사장치를 포함한 충돌 제트 소음을 예측하기 위한 해석 기법·절차 개발 및 검증을 위한 실험을 수행하였다. 출구 마하수 1.8을 갖는 소형 로켓노즐을 설계하고 초음속 자유분사제트에 대해 유동·음향 단방향 연계 해석 기법을 적용하여 출구 마하수, 출구 부근의 충격파 특성, 근거리·원거리장의 음압을 예측하였다. 이를 검증하고자 역반사 섀도 그래프, 근거리·원거리장 배열 및 마이크로폰을 이용하였다. 마하충격파 특성 길이는 1.45D_e 로 유사함을 확인하였으며 근거리·원거리장 음압은 해석·실험결과가 서로 3.24 dB, 4.7 dB의 오차가 있음을 확인하였다. 또한 발사장치를 포함하는 충돌 제트 소음에 대해 동일한 유동·음향 단방향 연계 해석 기법을 적용하였다. 이를 검증하고자 동일한 조건에서의 실험을 진행하였다. 발사장치의 형상은 소음 저감 효과가 검증된 형상을 적용하였다. 발사장치 출구 주변의 마하수는 2개의 피토 튜브에서 측정된 압력을 치환하여 해석 결과와 비교하였다. 원거리장의 음압은 해석·실험 결과 평균 2.43 dB의 오차를 보였다. 따라서 이 연구에서 적용한 유동·음향단방향 해석 기법은 초음속 자유분사·충돌 제트 소음을 비교적 정확히 예측할 수 있음을 검증하였다. 발사장치의 소음 저감 효과를 확인하기 위하여, 발사장치 유무에 따른 음압을 비교하였으며 비행체 구조물에 작용하는 음압이 최대 4.2 dB 감소하는 것을 확인하였다. 3개의 추가 발사장치 형상들을 실험에 적용하여 추가 소음 저감 효과를 확인하였다. 하지만 다양한 발사장치 형상에 대한 음압 분포는 상이하였으며, 이는 추후 유동·음향 단방향 연계 해석 기법을 적용하여 추가 연구를 모색하고자 한다.

Acknowledgments

이 연구는 방위사업청과 국방과학연구소의 지원으로 한국과학기술원 초고속비행체특화센터에서 수행되었습니다(과제번호: Contract UD170018CD).

References

• Eldred, K. M., 1971, Acoustic Loads Generated by the Propulsion System, NASA SP-8072.
• Varnier, J., 1998, Noise Radiated from Free and Impinging Hot Supersonic Jets, Proceedings of the 4th AIAA/CEAS Aeroacoustics Conference, No. AIAA 98-2206. [https://doi.org/10.2514/6.1998-2206]
• Haynes, J. and Kenny, R. J., 2009, Modifications to the NASA SP-8072 Distributed Source Method II for Area I Lift-off Environment Predictions, Proceedings of the AIAA 30th Aeroacoustics Conference, No. AIAA 2009-3160. [https://doi.org/10.2514/6.2009-3160]
• Bodony, D. J. and Lele, S. K., 2006, 433 Review of the Current Status of Jet Noise Predictions Using Large-eddy Simulation, Proceedings of the AIAA 44th Aerospace Sciences Meeting and Exhibit, No. AIAA 2006-486. [https://doi.org/10.2514/6.2006-486]
• Bodony, D. J. and Lele, S. K., 2008, Current Status of Jet Noise Predictions Using Large-eddy Simulation, AIAA Journal, Vol. 46, No. 2, pp. 364~380. [https://doi.org/10.2514/1.24475]
• Choi, H. and Moin, P., 2012, Grid-point Requirements for Large Eddy Simulation: Chapman’s Estimates Revisited, Physics of Fluid, Vol. 24, No. 1, p. 011702. [https://doi.org/10.1063/1.3676783]
• Caruelle, B. and Ducros, F., 2003, Detached-eddy Simulations of Attached and Detached Boundary Layers, International Journal of Computational Fluid Dynamics, Vol. 17, No. 6, pp. 433~451. [https://doi.org/10.1080/10618560310001598880]
• Housman, J. A., Stich, G.-D., Kiris, C. C. and Bridges, J., 2017, Jet Noise Prediction Using Hybrid RANS/LES with Structured Overset Grids, Proceedings of the 23th AIAA/CEAS Aeroacoustics Conference, Denver, Colorado. [https://doi.org/10.2514/6.2017-3213]
• Gely, D., Elias, G., Bresson, C., Foulon, H. and Radulovic, S., 2000, Reduction of Supersonic Jet Noise - Application to the Ariane 5 Launch Vehicle, Proceedings of the 6th AIAA/CEAS Aeroacoustics Conference, Lahaina, Hawaii, No. AIAA 2000-2026. [https://doi.org/10.2514/6.2000-2026]
• Tsutsumi, S., Kato, S., Fukuda, K., Takaki, R. and Ui, K., 2009, Effect of Launch System Shape on Acoustic Field of Launch Vehicle at Lift-off, Proceedings of the 47th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, Florida, No. AIAA 2009-328. [https://doi.org/10.2514/6.2009-328]
• Tsutsumi, S., Ishii, T., Ui, K., Tokudome, S. and Wada, K., 2015, Study on Acoustic Prediction and Reduction of Epsilon Launch Vehicle at Liftoff, Journal of Spacecraft and Rockets, Vol. 52, No. 2, pp. 350~361. [https://doi.org/10.2514/1.A33010]
• Tsutsumi, S., Ishii, T., Ui, K. and Tokudome, S., 2015, Assessing Prediction and Reduction Technique of Lift-off Acoustics Using Epsilon Flight Data, Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, Florida, No. AIAA 2015-1007. [https://doi.org/10.2514/6.2015-1007]
• Tam, C. K. W., 2012, Spatial Discretization in Wave Number Space, Computational Aeroacoustics: A Wave Number Approach, Cambridge University Press, New York, pp. 21~37. [https://doi.org/10.1017/CBO9780511802065.003]
• Greska, B. J., Krothapalli, A., Horne, W. C. and Burnside, N., 2008, Proceedings of the 14th AIAA/CEAS Aeroacoustics Conference, Vancouver, Canada. No. AIAA 2008-3026.
• Ishii, T., Tsutsumi, S., Ui, K., Tokudome, S., Ishii, Y., Wada, K. and Nakamura, S., 2012, Acoustic Measurement of 1:42 Scale Booster and Launch Pad, Proceedings of the Meetings on Acoustics, Vol. 18, No. 1, p. 040009.