호모토피법을 이용한 압축센싱 기반 음원위치추정 알고리듬의 개선

1. 서 론

음향지도(acoustic map)를 이용하여 음원의 위치를 특정하고 가시화하는 기법은 기계진단을 포함한 다양한 분야에서 효과적으로 활용되고 있다^(1~3). 청음센서 배열을 통해 비교적 빠른 속도로 구현 가능한 빔형성(beamforming) 기법을 고려할 수 있으나, 낮은 공간해상도, 허상음원(ghost source) 출현 등의 제한 사항이 있으며^(4,5), 이를 보완할 수 있는 여러 기법이 활발히 개발 중에 있다.

최근 음원위치추정 분야에서 주목받는 압축센싱(compressive sensing)⁽⁶⁾ 기법은, 역문제 y=Ax에서 만약 해 x가 희소벡터(sparse vector)이고 선형변환행렬 A가 제한등방성(restricted isometry property, RIP)⁽⁷⁾이라는 기준을 만족하면, 최적화 기법을 통해 관측치 y로부터 x를 구할 수 있는 방법이다. 종래의 빔형성 기법보다 소수의 청음센서만으로 고해상도의 음원위치추정 결과를 얻을 수 있는 장점이 있으며, 초음파 영상⁽⁸⁾, 레이더 탐지⁽⁹⁾ 등 다양한 분야에서 활용되고 있다.

압축센싱 기반 음원위치추정 알고리듬은 크게 3가지로 구분할 수 있다. 첫 번째는 선형계획법 또는 이차계획법 등을 통해 다항시간(polynomial time) 내에 해를 구할 수 있는 기저추적(basis pursuit)⁽¹⁰⁾이다. 볼록 최적화(convex optimization) 기법을 이용하기 때문에 해가 국소적으로 수렴하지 않고 항상 전역해(global solution)를 찾는 장점이 있지만, 계산속도가 상대적으로 느린 단점이 있다.

두 번째는 탐욕 알고리듬(greedy algorithm)이며, 각 단계별 임기응변적인 최적해를 선택함으로써 결국에는 전역 최적해에 이르기 기대하는 방법을 사용하기에 ‘탐욕’이라는 용어가 사용된다. 대표적으로는 orthogonal matching pursuit (OMP)나 호모토피법(homotopy method) 등이 있다⁽¹¹⁾. 역행렬 계산을 포함하므로 계산비용이 큰 단점이 있지만, 잔차상관(residual correlation)의 값이 가장 큰 요소부터 순차적으로 최적화하기에 반복계산 횟수가 적은 장점이 있다.

세 번째는 threshoding based method (TBM)이다. TBM은 고정점 반복법(fixed point iteration)을 기반으로 해를 근사하며, 대표적인 알고리듬으로는 iterative hard threshoding (IHT)⁽¹²⁾이 있다. 사전 설정한 종료조건을 만족할 때까지 x의 지지집합(support set)을 반복 갱신하여 해를 추정하는 점에서 탐욕 알고리듬과 유사하나, 역행렬과 같이 복잡한 계산과정이 없어 상대적으로 계산비용이 낮다. 그러나 많은 반복계산을 요구하는 단점이 존재하며, 알고리듬의 수렴성을 결정짓는 스텝크기(step size)에 그 원인이 있다. 이를 해결하고자 스텝크기를 자동 결정하는 선행연구⁽¹³⁾가 있었으나, 여전히 많은 반복계산 횟수를 요구하였다.

이 연구에서는 비교적 구현이 간편하며 계산량 측면에서도 이득이 있는 IHT를 음원추정의 기본 알고리듬으로 사용하되, 스텝크기 결정과 관련한 기존의 문제점을 호모토피법으로부터 착안하여 개선하고자 하였다. 언급한 바와 같이 탐욕 알고리듬의 일종인 호모토피법⁽¹⁴⁾은 l₁-norm 최소화 문제에 라그랑주 승수법(lagrange multiplier method)⁽¹⁵⁾을 적용한 목적함수를 통해 해를 추정한다. 라그랑주 승수가 0으로 수렴하면 이에 대응하는 해가 l₁-norm 최소화 문제의 해와 같아지는 점이 핵심이며, 호모토피법은 보장된 수렴성을 바탕으로 스텝크기를 자동 결정하는 장점을 가지고 있다. 이를 기존 IHT 알고리듬에 적용한 결과 계산시간을 24 % 가량 저감할 수 있었고, 이후 내용을 통해 상술하도록 한다.

이 연구는 총 4장으로 구성되어 있다. 2장에서는 압축센싱 및 제안 알고리듬에 대해 설명하였고, 3장에서는 모사 및 실제 실험을 통해 제안 알고리듬을 검증하였다. 마지막으로 4장에서는 결론을 맺는다.

2. 관련 이론

2.1 압축센싱

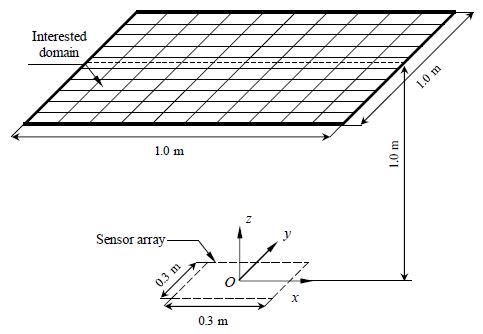
압축센싱의 정식화는 단극음원을 기반으로 한 등가음원법(equivalent source method)으로부터 출발한다. 즉, 음장(sound field)을 여러 개의 단극음원에서 방사되는 파(wave)의 조합으로 근사한다. Fig. 1과 같이, 어떤 관심공간 내 음장이 N개의 등가음원으로 구성되어 있다고 가정하자. 이때 m(=1, 2, ..., M)번째 센서에서 계측되는 음압값 y_m은 그린 함수(green function)⁽¹⁶⁾를 통해 주파수 영역에서 식 (1)과 같이 나타낼 수 있다.

$\[ y_m=\sum _{n=1}^N\frac{e^{-jk{r}_{mn}}}{4\pi r_{mn}}{x}_n \]$

(1)

Fig. 1

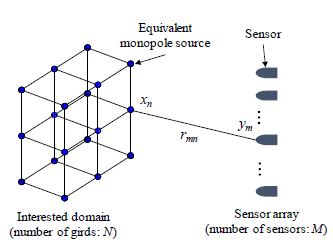
Distribution of N equivalent monopole sources in the interested domain. n-th equivalent source with strength xn is located at each grid point. m-th sensor in the array receives the signal ym

여기서 x_n [Pa⋅m]은 n번째 등가 음원의 강도를 나타내고, r_mn [m]은 n번째 등가 음원과 m번째 센서 사이의 거리이며, k(=2πf/c) [1/m]는 주파수 f [Hz]에 해당하는 파수를 나타낸다. 단, c=343 [m/s]는 음속을 의미한다. 식 (1)을 M개의 배열 센서에 대하여 확장하면, 관측벡터(measurement vector) y∈ℂ^M은 식 (2)와 같이 나타낼 수 있다.

$\[ \begin{array}{l}\mathbf{y}\mathbf{ }=\mathbf{ }\mathbf{A}\mathbf{x}\\ \begin{array}{ccc}\mathbf{y}=\left[\begin{array}{c}{y}_1\\ ⋮\\ y_M\end{array}\right],& \mathbf{A}=\frac{1}{4\pi }\left[\begin{array}{ccc}\frac{e^{-jk{r}_{11}}}{r_{11}}& \cdots & \frac{e^{-jk{r}_{1N}}}{r_{1N}}\\ ⋮& \ddots & ⋮\\ \frac{e^{-jk{r}_{M1}}}{r_{M1}}& \cdots & \frac{e^{-jk{r}_{MN}}}{r_{MN}}\end{array}\right],& \mathbf{x}=\left[\begin{array}{c}{x}_1\\ ⋮\\ x_N\end{array}\right]\end{array}\end{array} \]$

(2)

여기서 A∈ℂ^M×N은 관측행렬(measurement matrix)이라고 한다.

그러나 실제 환경에서의 계측은 다양한 원인으로 유발된 잡음의 영향을 포함하기 때문에, 식 (2)를 일반화하면 식 (3)과 같다.

$\[ \mathbf{y}\mathbf{ }=\mathbf{ }\mathbf{A}\mathbf{x}\mathbf{ }+\mathbf{ }\mathbf{e} \]$

(3)

여기서 e=[e₁, ..., e_n]^T∈ℂ^M은 서로 상관관계가 없는 요소로 구성된 가우시안(gaussian) 잡음벡터이며, 위 첨자 T는 전치(transpose)를 의미한다.

일반적으로 관심 공간 내 등가 음원의 개수 N은 배열 센서의 개수 M보다 크기(M < N) 때문에. 식 (3)의 관측행렬 A는 미지수의 개수(N)가 식의 개수(M)보다 많은 부족결정 시스템(underdetermined system)을 구성하게 된다. 따라서 무한가지 경우의 해를 가지게 되나, 만약 실 음원의 개수 s가 등가 음원의 개수 N보다 매우 작다면(s ≪ N), 해 x∈ℂ^N는 대부분의 요소가 0 또는 0에 가까운 값을 가지는 희소벡터(sparse vector)로 볼 수 있으며, 식 (4)와 같은 l₀-norm 최소화 문제를 통해 해를 구할 수 있다.

$\[ \begin{array}{cc}\mathrm{m}\mathrm{i}\mathrm{n}{‖\mathbf{x}‖}_0& \mathrm{s}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{ }\mathrm{t}\mathrm{o}{‖\mathbf{A}\mathbf{x}\mathbf{ }-\mathbf{ }\mathbf{y}‖}_2\le \mathbf{\epsilon }\end{array} \]$

(4)

여기서 l₀-norm ‖x‖₀은 0이 아닌 요소의 개수를 나타내며, l₂-norm은 ‖x‖₂=(∑x_n²)^1/2이고, ε은 잡음벡터 e의 l₂-norm을 나타낸다.

그러나 식 (4)의 최소화 문제는 NP-hard(Non-deterministic Polynomial-time hard) 문제에 해당하기에 사실상 계산이 불가능함이 알려져 있다⁽¹⁷⁾. 따라서 서론에서 언급한 바와 같이 볼록완화(convex relaxation)를 이용한 l₁-norm 최소화 문제(또는 기저추적이라고도 한다.)로 식 (4)를 근사하거나, OMP나 IHT 등을 통해 x의 지지집합을 반복 갱신하여 해를 추정하게 된다.

2.2 알고리듬

(1) Iterative Hard Thresholding

탐욕 알고리듬과 달리 IHT는 역행렬 계산이 불필요하여 상대적으로 적은 계산비용으로 해를 구할 수 있는 알고리듬으로, x^[0]=0에서 시작하여 식 (5)와 같은 갱신 과정을 통해 해를 구한다.

$\[ {\mathbf{x}}^{\left[i+1\right]}=H_s\left({\mathbf{x}}^{\left[i\right]}+\mu {\mathbf{A}}^T\left(\mathbf{y}-\mathbf{A}{\mathbf{x}}^{\left[i\right]}\right)\right) \]$

(5)

여기서 H_s는 hard thresholding operator로, 요소의 절대값이 가장 큰 s개의 요소를 제외한 나머지를 0으로 치환하는 연산자, x^[i]는 i번째 반복(혹은 갱신)에서 얻은 해, 그리고 μ는 스텝크기를 나타낸다.

식 (5)의 갱신은 종료조건을 만족할 때까지 반복되며, 식 (3)과 같이 잡음이 포함된 환경에서는 일반적으로 ‖Ax-y‖₂≦ε(ε>0)을 사용한다.

이때 μ는 통상적으로 사용자가 직접 설정하나, 적절한 값이 지정되지 않을 경우 해가 발산하거나, 혹은 수렴을 위한 반복 횟수가 급격히 증가할 수 있다. 이를 해결하고자 Blumensath, T. et al.⁽¹³⁾은 식 (6)과 같이 해가 발산하지 않는 μ의 자동 결정법을 제안하였으나, 여전히 많은 반복계산 횟수가 필요하였다. 이 연구에서는 식 (6)을 사용하는 IHT를 기존 알고리듬으로써 고려하기로 한다.

$\[ \mu =\frac{{\mathbf{c}}_S^T{\mathbf{c}}_S}{{\mathbf{c}}_S^T{\mathbf{A}}_S^T{\mathbf{A}}_S{\mathbf{c}}_S} \]$

(6)

여기서 c(=A^T(y-Ax))는 잔차상관이며, 아래 첨자 S는 지지집합을 나타낸다.

(2) 호모토피법을 이용한 스텝크기 μ의 결정

호모토피법⁽¹⁵⁾은 l₁-norm 최소화 문제에 라그랑주 승수법을 적용한 목적함수를 이용하며, 목적함수의 미분항을 반복 갱신함으로써 해를 추정한다. 호모토피법의 갱신 과정은 크게 방향벡터의 계산, 스텝크기의 결정, 지지집합의 갱신, 해 벡터의 갱신 및 종료조건 확인의 4가지 단계로 구분할 수 있으며, 알고리듬의 자세한 구조는 Qi, C. et al.⁽¹⁴⁾을 참조하기 바란다.

이 연구에서 제안하는 알고리듬은 IHT 및 호모토피법의 갱신 과정이 경사 하강법(gradient descent)과 같은 전형적인 최적화 기법의 방법과 유사한 점을 미루어, 식 (7)을 이용하여 IHT 알고리듬의 스텝크기 μ를 자동으로 결정하고자 하였다.

$\[ \mu =\min \left\{\gamma {\mathbf{d}}^{\left[i\right]}\otimes {\mathbf{A}}^T\left(\mathbf{y}-\mathbf{A}{\mathbf{x}}^{\left[i\right]}\right)\right\} \]$

(7)

여기서 ⊗은 요소별 나눗셈(Hadamard division)⁽¹⁸⁾을 수행하는 연산자이다. 또한, γ와 d는 각각 호모토피법에서의 스텝크기와 방향 벡터를 나타내며, 부록에 그 산출법을 다루었다.

기존 IHT⁽¹³⁾와 제안 알고리듬의 반복계산 횟수를 비교하기 위해 M=3, N=6의 관측행렬 A와 s=2의 해 벡터 x=[1, -1, 0, 0, 0, 0]^T을 예로 고려하자. A의 요소는 가우시안 정규분포(gaussian distribution)를 통해 생성하였고, 종료조건의 ε은 잡음벡터 e의 l₂-norm을 고려하여 10^-6으로 설정하였다.

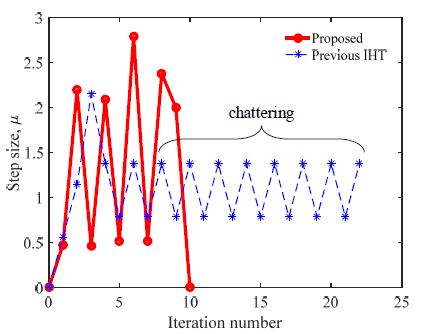
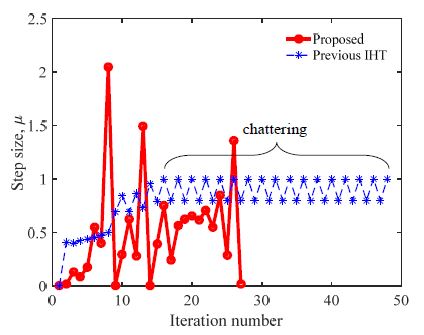
Fig. 2에는 반복에 따른 알고리듬별 스텝크기를 비교하였다. 기존 IHT는 해가 수렴할 때까지, 다시 말해서 종료조건을 만족할 때까지 22회의 반복계산 횟수가 필요하였고, 제안 알고리듬은 10회 만에 수렴한 것을 알 수 있다. 구체적으로, 기존 IHT의 경우(점선) 일정한 스텝크기의 증감이 반복되는 채터링(chattering) 현상이 나타난 반면, 제안 알고리듬(실선)에서는 비교적 큰 폭의 스텝크기 변화가 나타났으며 채터링 현상이 발생하지 않음을 볼 수 있다.

Fig. 2

Comparison of the step size between the proposed- and previous algorithm in simulation

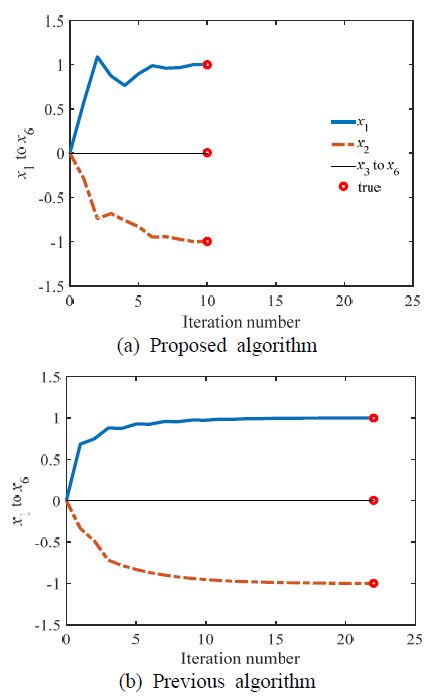
Fig. 3에는 추정된 해의 경로(solution path)를 도시하였고, 좌측에는 제안 알고리듬, 우측에는 기존 알고리듬의 결과를 나타내었다. 앞서의 이유로 기존 알고리듬의 경우 수렴이 더딘 편이나, 제안 알고리듬의 해는 상대적으로 크게 변화하여 빠르게 수렴하였음을 알 수 있다.

Fig. 3

Solution path of the algorithm

기존 IHT 알고리듬에서 발생하는 채터링의 제거를 통해 해의 수렴성을 촉진함을 강조할 수 있으며, 더 나아가 계산시간의 저감이 가능함을 기대할 수 있다. 단, IHT에서의 채터링 발생 원인 규명에 대해서는 추가 연구를 수행하고 있다.

3. 모사 및 실제 실험

3.1 모사실험 환경 및 결과

음원의 형태는 크게 3가지로 구분할 수 있으며, 모든 방향으로 균일한 음을 방사하는 점음원(point source), 무한개의 점음원이 직선의 형태로 분포하는 선음원(line source), 그리고 2차원 평면의 형태를 가지는 면음원(surface source) 등이 있다. 이 연구에서는 하나의 음원을 관심공간 내 하나의 격자점으로 표현 가능한 점음원에 대해서만 고려하기로 한다.

Fig. 4에는 제안 알고리듬의 검증을 위한 모사실험의 조건을 나타내었다. 센서 배열의 중심을 좌표계의 원점으로 설정하였고, 원점에서 z-축 방향으로 1.0 m 떨어진 1.0×1.0 m²의 영역을 5 mm 간격의 441개 격자로 분할하여 관심공간으로 지정하였다. 센서 배열에는 Fig. 5(a)와 같이 24개의 센서를 사용하여 랜덤한 배열을 구성하였고, 이로부터 M=24, N=441인 관측행렬 A를 생성하였다. 관측행렬 A의 RIP 조건 부합⁽⁷⁾에 대한 분석을 0 kHz ~ 12 kHz 주파수 대역에 사전 수행하였고, 분석 결과로부터 candes criteria⁽⁷⁾를 만족하는 주파수 대역은 5 kHz ~ 12 kHz로 나타났다. 이는 생성된 관측행렬 A, 다시 말해 현 실험조건에서 추정 가능한 음원의 주파수 대역이 5 kHz ~ 12 kHz임을 의미하며, 음원의 하나 또는 여러 주파수 성분이 해당 대역에 속하면 제안 알고리듬을 주파수 별로 반복 적용함으로써 음원위치추정이 가능함을 나타낸다. 여기서는 8 kHz의 순음(pure tone)을 음원의 주파수로 선정하였다.

Fig. 4

Schematic drawing for the arrangement of interested domain and the sensor array

Fig. 5

The random sensor array used in anti-aliasing low pass filter

Table 1에는 기존 IHT와 제안 알고리듬의 성능 비교를 위한 실험조건을 나타내었다. 음원 개수 s를 1에서 8까지 증가시키며 위치추정을 1000회씩 반복 수행하였으며, 이때 음원 위치는 각 시행마다 무작위로 지정하였고, 음원의 강도는 모든 시행에 걸쳐 동일하게 유지하였다.

Table 1

Conditions of simulation

Fig. 6에는 모사실험 결과를 나타내었다. 각 그림의 x-축은 음원 개수 s를 센서 개수 M으로 정규화화한 상대 음원수를 뜻하며, 제안 알고리듬(실선)과 기존 IHT⁽¹³⁾(점선)의 결과를 동시에 비교하였다. 신호 대 잡음비(signal-to-noise ratio, SNR)가 10 dB로 비교적 높은 환경(Fig. 6(a))과 0 dB로 낮은 환경(Fig. 6(b))에 대해, 그림의 좌측에는 반복계산 횟수의 평균을, 우측에는 복구 오차율 ψ의 평균을 도시하였다. 단, 복구 오차율 ψ는 식 (8)과 같다.

$\[ \psi =\sqrt{\left(\frac{{‖{\mathbf{x}}_t-{\mathbf{x}}_e‖}_2^2}{4{‖{\mathbf{x}}_t‖}_2^2}\right)} \]$

(8)

Fig. 6

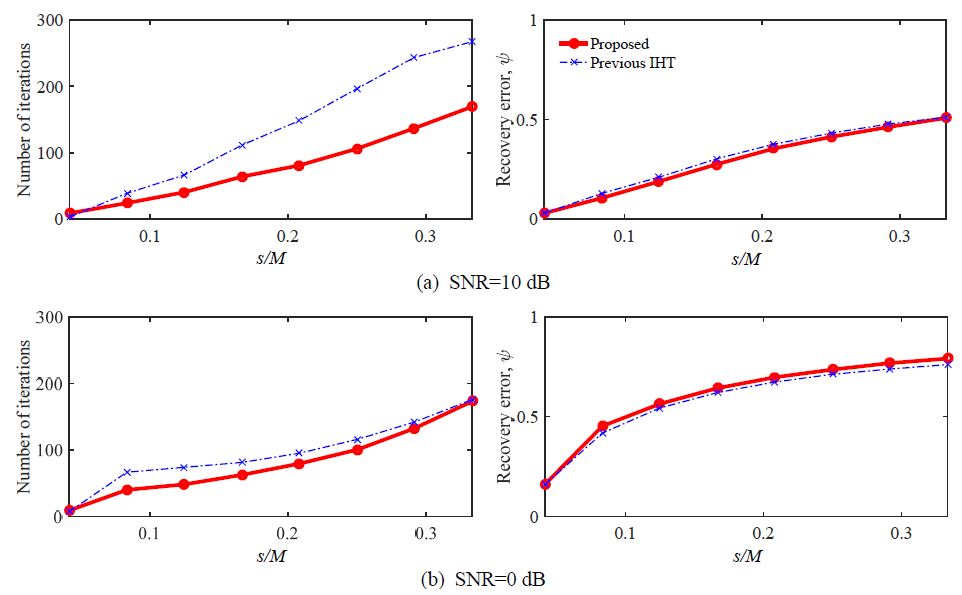
Comparison of the number of iterations (left) and recovery error (right) between the proposed- and previous algorithm

여기서 아래 첨자 t와 e는 각각 참값과 추정치를 의미한다.

제안 및 기존 알고리듬의 반복계산 횟수와 복구 오차율 ψ는 음원 개수 s가 증가할수록 비례하는 경향을 띠었다. 이는 음원이 많아질수록 음원위치추정에 필요한 반복계산 횟수, 즉 계산시간(혹은 계산비용)이 증가하며 해가 수렴하였어도 실제와는 다른 위치를 추정했을 가능성이 큼을 의미한다. 그러나 제안 알고리듬의 결과(실선)는 높은 SNR 환경(Fig. 6(a))에서 반복계산 횟수가 기존 IHT(점선) 대비 약 50 % 감소한 것을 알 수 있다. SNR과 무관하게 복구 오차율 ψ가 유사한 점을 미루어 동일 환경에서 제안 알고리듬은 기존보다 2배 빠르게 수렴한다고 볼 수 있으며, IHT 알고리듬의 계산시간 단축이 가능함을 다시 확인하였다. SNR이 상대적으로 열악한 환경(Fig. 6(b))에서는 알고리듬의 개선 효과가 반감되기는 하나, 여전히 기존 대비 성능 우위에 있음을 알 수 있다.

3.2 실제실험 환경 및 결과

알고리듬 개선 효과는 상대 음원수(s/M)가 0.2 이상에서 급격하게 확대됨을 모사실험을 통해 볼 수 있었다. 이를 실제실험을 통해 검증하기 위해, 3(=s)개의 스피커 (SONY SRS-XB10)를 음원으로 사용하였고, 9(=M)개의 마이크로폰 유닛으로 구성된 센서 배열(Fig. 5(b))을 구성하였다. 각 유닛은 MEMS 마이크로폰(Knowles SPU0414HR5H-SB)과 고주파 잡음의 영향 억제를 위한 아날로그 안티 에일리어싱 필터(analogue anti-aliasing filter)의 조합으로 구성되어 있다(Fig. 5(c)).

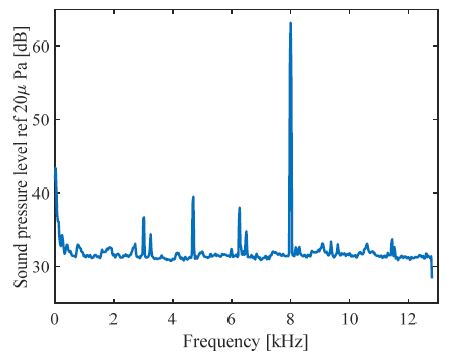
모사실험의 경우와 마찬가지로 관측행렬 A의 RIP 조건에 대한 만족 여부를 사전 검토하였으며, candes criteria를 만족하는 주파수 대역 7 kHz ~ 12 kHz 중 8 kHz의 순음을 음원의 주파수로 선정하였다. Fig. 7에는 스피커 3개를 배치했을 때 각 배열 센서에서 계측된 신호의 평균 파워 스펙트럼을 도시하였고, 주파수 분해능 25 Hz, 해닝 창문함수(hanning window function), 75 %의 오버랩(overlapping)을 적용하여 계산하였다. 안티 에일리어싱 필터를 통해 고조파(harmonic) 성분이 어느 정도 억제된 것을 알 수 있으며, 8 kHz 부근에서 약 63 dB의 피크가 나타났다.

Fig. 7

Averaged power spectrum of measurement signal

Table 2에는 실제실험의 조건을 나타내었다. 스피커의 음량을 조절하여 음원의 강도를 가급적 동일하게 유지하였으며, 모든 실험에 대해 샘플링 주파수 25.6 kHz로 신호를 수집하였다. 음원의 개수가 2개, 그리고 3개인 경우로 나누어 각각 30회씩 위치 추정을 반복하였으며, 이때 음원의 위치는 각 시행마다 임의로 배치하였다.

Table 2

Conditions of experiment

종료조건과 관련한 ε은 정규화 요소(regularization parameter)의 역할을 하며 그 값에 따라 추정결과가 크게 달라질 수 있다. 잡음의 l₂-norm으로부터 적절한 값을 선정함이 바람직하나, 모사실험과 달리 실제 환경에서는 잡음의 특성을 알 수 없다. 여기서는 시행착오적으로 여러 ε값을 시도한 결과 10^-6으로 결정하였다. 참고로, 제시된 값에서 상당 정도의 변화가 있더라도 추정결과에는 큰 변화가 없었다.

Table 3에는 음원 개수별로 두 성능지표에 대한 결과를 정리하였다. 제안 알고리듬의 평균 반복계산 횟수와 평균 계산시간은 기존 IHT 대비 음원의 개수가 2개일 때 각각 35.8 %, 24.7 %, 음원의 개수가 3개일 때 각각 27.6 %, 23.3 % 감소하였고, 모사실험의 결과로부터 예상할 수 있었듯 호모토피법의 스텝크기 결정방식을 이용한 제안법을 통해 IHT 알고리듬의 성능이 향상되었음을 알 수 있었다. 이때 평균 반복계산 횟수와 평균 계산시간의 감소율이 동일하지 않은 이유는 알고리듬이 한 번 반복될 때 소요되는 시간이 다르기 때문으로 추측된다.

Table 3

Comparison of the number of iterations and computing time between the proposed- and previous algorithm

Fig. 8에는 스피커 3개를 배치한 경우의 계측 신호를 바탕으로 계산된 반복계산 횟수의 비교 예시를 나타내었다. Fig. 2와 같이, 제안 알고리듬은 스텝크기를 큰 폭으로 변화시켜 해의 수렴을 촉진하는 반면, 기존 알고리듬에서는 도중부터 발생한 채터링 현상으로 해가 더디게 수렴함을 알 수 있다. 이를 통해 채터링 현상의 제거가 계산시간 저감에 직접적인 영향을 미쳤음을 확인할 수 있었다.

Fig. 8

Comparison of the step size between the proposed- and previous algorithm in experiment

Fig. 9에는 Fig. 8에서의 위치추정결과를 나타내었다. 제안(Fig. 9(a)) 및 기존(Fig. 9(b)) 알고리듬 모두 음원의 위치, 다시 말해서 스피커의 위치를 잘 추정한 것을 알 수 있다. 음원의 추정 강도는 제안 알고리듬이 기존 대비 최대 2 dB 정도의 차이를 보였는데, 스피커의 음량을 가급적 동일하게 설정하였음을 고려하면 제안 알고리듬의 강도 추정 정확도가 상대적으로 뛰어나다고 할 수 있다.

Fig. 9

Acoustic source map for algorithm

4. 결 론

이 연구에서는 압축센싱 기반 IHT 알고리듬의 계산시감 저감을 위한 수정 알고리듬을 제안하였고, 모사 및 실제 실험을 통해 검증하였다. 보장된 수렴성을 바탕으로 스텝크기를 자동 결정하는 호모토피법을 적용함으로써 기존 IHT 알고리듬에 발생하던 채터링 현상을 제거하였고, 이를 통해 반복계산 횟수를 줄여 알고리듬의 계산 소요시간을 저감할 수 있었다. 제안 알고리듬은 기존 IHT 대비 반복계산 횟수가 32 %, 계산시간이 24 % 가량 감소하였으며, 동일한 복구율을 가졌다.

호모토피법과 IHT 알고리듬의 결합을 시도한 측면에서, 아울러 계산속도 저감을 통해 압축센싱 기반 위치추정 알고리듬의 실시간 구현 가능성을 높인 측면에서도 이 연구의 의미를 찾을 수 있다. 현재 단계에서 원인을 규명하지 못한 현상(예: IHT의 채터링 현상) 등을 향후 연구의 주제로 남겨두며, 또한 실시간 구현과 관련한 여러 문제를 다루어 연구의 완성도를 높이고자 한다.

Acknowledgments

이 논문은 2018년도 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(2018R1A5A6075959).

References

• Cabada, E. C., Leclear, Q., Antoni, J. and Hamzaoui, N., 2017, Fault Detection in Rotating Machines with Beamforming: Spatial Visualization of Diagnosis Features, Mechanical Systems and Signal Processing. Vol. 97, No. 1, pp. 33~43. [https://doi.org/10.1016/j.ymssp.2017.04.018]
• Foeth, E. J. and Bosschers, J., 2016, Localization and Source-strength Estimation of Propeller Cavitation Noise Using Hull-mounted Pressure Transducers, 31st Symposium on Naval Hydrodynamics, Monterey, California, USA.
• Lee, G. S., Shin, S. H., Cheong, C. and Jung, S. S., 2009, Localization of Acoustic Sources on Wind Turbine by Using Beam-forming Techniques, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 19, No. 8, pp. 809~815. [https://doi.org/10.5050/KSNVN.2009.19.8.809]
• Haddad, K. and Hald, J., 2008, 3D Localization of Acoustic Sources with a Spherical Array, Journal of the Acoustical Society of America, Vol. 123, No. 5, p. 3311. [https://doi.org/10.1121/1.2933754]
• Cigada, A., Lurati, M., Ripamonti, F. and Vanail, M., 2008, Moving Microphone Arrays to Reduce Spatial Aliasing in the Beamforming Technique: Theoretical Background and Numerical Investigation, Journal of the Acoustical Society of America, Vol. 124, No. 6, pp. 3648~3658. [https://doi.org/10.1121/1.2998778]
• Donoho, D. L., 2006, Compressed Sensing, Institute of Electrical and Electronics Engineers Transactions on Information Theory, Vol. 52, No. 4, pp. 1289~1306. [https://doi.org/10.1109/TIT.2006.871582]
• Lee, J. H., Kim, Y. H. and Shin, Y. H., 2019, Optimal Sensor Arrangement in Random Array for Compressive-sensing Based Sound Source Identification, Mechanical Systems and Signal Processing, Vol. 133, No. 1, p. 106296. [https://doi.org/10.1016/j.ymssp.2019.106296]
• Wagner, N., Eldar, Y. C. and Friedman, Z., 2012, Compressed Beamforming in Ultrasound Imaging, IEEE Transactions on Signal Processing, Vol. 60, No. 9, pp. 4643~4657. [https://doi.org/10.1109/TSP.2012.2200891]
• Ender, J. H., 2010, On Compressive Sensing Applied to Radar, Signal Processing, Vol. 90, No. 5, pp. 1402~1414. [https://doi.org/10.1016/j.sigpro.2009.11.009]
• Chen, S. S., Donoho, D. L. and Saunders, M. A., 2001, Atomic Decomposition by Basis Pursuit, SIAM Journal on Scientific Computing, Vol. 20, No. 1, pp. 33~61. [https://doi.org/10.1137/S1064827596304010]
• Foucart, S. and Rauhut, H., 2013, A Mathematical Introduction to Compressive Sensing, Springer, New York. [https://doi.org/10.1007/978-0-8176-4948-7]
• Blumensath, T. and Davies, M. E., 2009, Iterative Hard Thresholding for Compressed Sensing, Applied and Computational Harmonic Analysis, Vol. 27, No. 3, pp. 265~274. [https://doi.org/10.1016/j.acha.2009.04.002]
• Blumensath, T. and Davies, M. E., 2010, Normalized Iterative Hard Thresholding: Guaranteed Stability and Performance, IEEE Journal of Selected Topics in Signal Processing, Vol. 298, No. 2, pp. 298~309. [https://doi.org/10.1109/JSTSP.2010.2042411]
• Qi, C., Wnag, X. and Wu, L., 2011, Underwater Acoustic Channel Estimation Based on Sparse Recovery Algorithms, IET Signal Processing, Vol. 5, No. 8, pp. 739~747. [https://doi.org/10.1049/iet-spr.2010.0347]
• Strang, G., 2006, Linear Algebra and Its Applications, 4th Ed., Thomson Brooks/Cole, Belmont, CA.
• Pierce, A. D., 2019, Acoustics: An Introduction to Its Physical Principles and Applications, 3rd Ed., Springer, New York. [https://doi.org/10.1007/978-3-030-11214-1]
• Donoho, D. L., 2006, For Most Large Underdetermined Systems of Linear Equations the Minimal l1-norm Solution is also the Sparsest Solution, Communications on Pure and Applied Mathematics, Vol. 59, No. 6, pp. 797~829. [https://doi.org/10.1002/cpa.20132]
• Cyganek, B., 2013, Object Detection and Recognition in Digital Images: Theory and Practice, John Wiley & Sons, New York.