구조물 진동의 시각적 확대를 통한 인지성 향상

2.1 공간 영역 기반 영상처리 방법

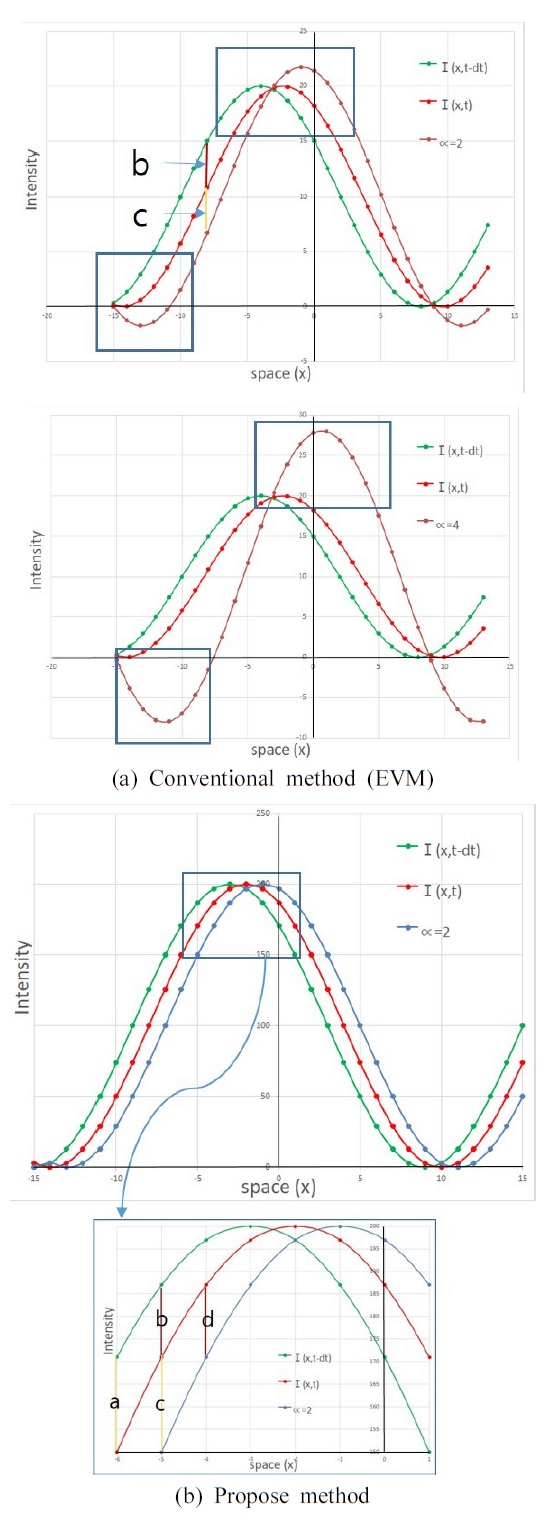
기존 EVM방법은 공간영역에서 영상의 밝기 변화를 확대하는 방법이다. Fig. 1(a)에서 보는 바와 같이 확장계수 α값을 밝기 변화값에 곱하여 증폭시키면 어두운 쪽은 더 어둡게 밝은 쪽은 더 밝아지게 된다. 따라서 Fig. 1(a)에서 보는 바와 같이 α값을 크게 하면 할수록 실제 형태가 왜곡되는 문제점이 발생한다. 따라서 노이즈에 취약하고 미소진동을 확대할 경우 영상품질이 좋지 않은 단점이 있다.

Fig. 1

Pixel intensity of one-dimensional image

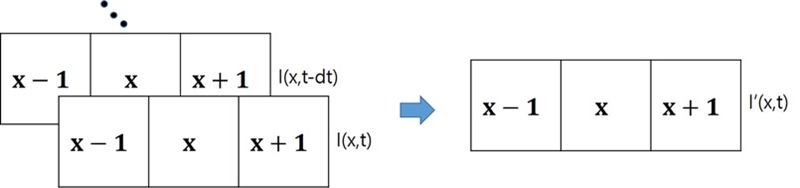
Fig. 1(b)는 기존 방법의 문제점인 왜곡 현상을 해결하기 위하여 α 확장계수 값에 따라 동일한 형태를 유지하면서 변위 발생 방향으로 α배수로 변위를 확장하는 방법이다. 기존 방법에서 α=2일 때, b≈c라고 가정하였으나 이상적인 경우 b=d, a=c라고 할 수 있다. 카메라를 통하여 빠르게 취득한 영상에서 물체의 이동량은 매우 적게 나타난다. I(x,t)는 시간 t에서 1차원 영상 데이터의 픽셀값으로 정의한다. Fig. 2에서 I(x,t)의 입장에서 볼 때, 어느 한 픽셀값은 이전 영상의 주변 값으로부터 이동했다고 볼 수 있다. 따라서 I(x,t)는 I(x-1,t-dt), I(x,t-dt), I(x+1,t-dt) 중 하나로부터 이동했다고 볼 수 있다. 시간 t에서의 취득한 영상을 I(x,t), 이전 영상을 I(x,t-dt), 각 픽셀에서의 변화량을 D(x,t)라 하면 식 (1)과 같이 나타낼 수 있다.

Fig. 2

One-dimensional image data

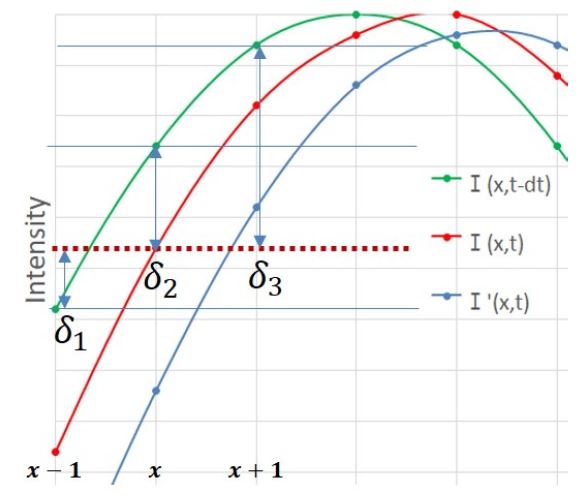
Fig. 3에서 현재 영상I(x,t)와 이전 영상의 주변값의 차이값을 각각 식 (2)와 같이 나타낼 수 있다. δ₁은 현재 영상 x픽셀값과 이전영상 x-1픽셀값의 차이, δ₂는 현재 영상 x픽셀값과 이전 영상 x픽셀값과의 차이 그리고 δ₃는 현재 영상 x픽셀값과 이전 영상 x+1픽셀값과의 차이를 나타낸다. 식 (2)의 δ₁, δ₂, δ₃에서 가장 작은 값을 찾아서 현재 영상의 I(x,t)값이 이전 영상의 주변 픽셀 중 어느 픽셀로부터 이동했는지를 결정한다.

Fig. 3

Select the shifted pixel in the reference image

식 (3)에서 δ₁이 가장 작으면 현재 영상 x값이 이전 영상 x-1의 위치에서 이동, δ₂가 가장 작으면 현재 영상 x값이 이전 영상 x의 위치에서 이동 그리고 δ₃가 가장 작으면 현재 영상 x값이 이전 영상 x+1의 위치에서 이동된 경우이다. 이와 같이 결정된 픽셀 위치에서의 현재 영상 픽셀값과 이전 영상 픽셀값과의 차이를 현재 영상 I(x,t)픽셀에 더해 줌으로써 실제 진동 변화량을 확대 변화시킨 결과 영상 I^′(x,t)를 구할 수 있다.

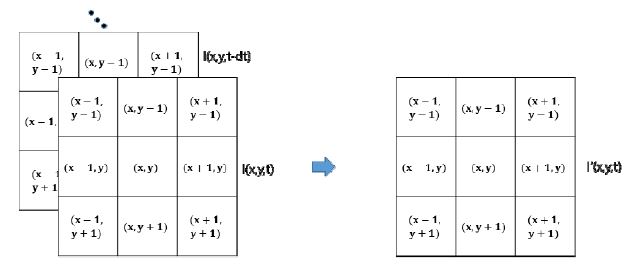
영상에 적용하기 위해서는 Fig. 4와 같이 2차원 영역에서 픽셀의 움직임이 고려되어야 한다.

Fig. 4

Two-dimensional image data

1차원에서 식 (1) ~ (3)을 이용하여 진동 변화량을 확장하여 I^′(x,t)를 구하는 방법과 같이 2차원 영역에서 식 (4) ~ (6)을 이용하면 2차원 공간에서 움직임 확대 결과 영상 I^′(x,y,t)를 구할 수 있다.

2.2 진동변위 확대 처리과정

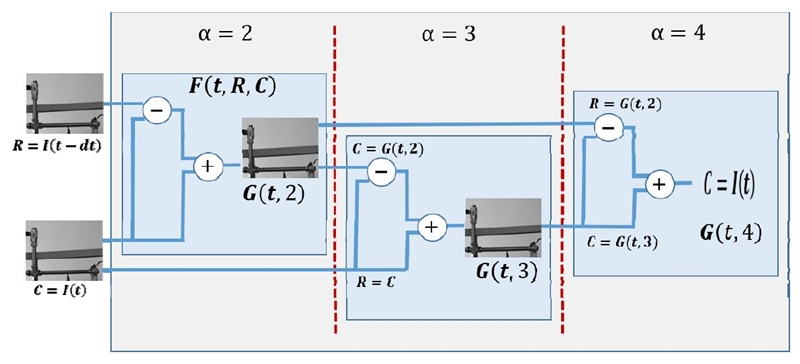
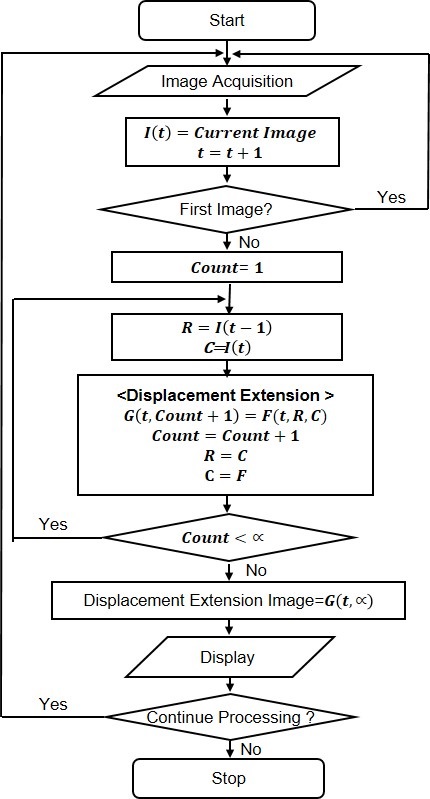
α배수의 진동변위 확대 처리 과정을 Fig. 5에서 보여준다. 현재시간 t에서 이전 영상을 R, 현재 영상을 C라 할 때 진동 변위량 2배 확대 함수를 F(t,R,C)라 하고 α배수 확대 결과 영상을 G(t,α)라 하면, Fig. 5와 같이 처리 과정을 반복 수행함으로써 α배수 확대 영상을 구현할 수 있다. ⊖는 시간 t에서의 변화량을 산출하는 것을 나타내고, ⊕는 시간 t에서의 영상에 변화량을 더해주는 것을 나타낸다. Fig. 6은 진동 변위를 확대하는 전체적인 처리 과정을 보여준다. 연속적인 영상을 취득하여 이전 영상 R과 현재 영상 C를 이용하여 픽셀의 변화량을 산출하고 현재 영상에 픽셀의 변화량을 더해주어 2배수 변위를 확장한다. 이 과정을 α 확장계수만큼 반복 수행을 함으로써 최종적 변위 확장 영상인G(t,α)를 만들면 시각적 변위 확장된 영상을 보여줄 수 있다.

Fig. 5

Process for vibration extension

Fig. 6

Diagram of the proposed method

3.1 실험실 진동확장 실험

Fig. 7과 같이 가진기를 이용하여 외팔보를 5 Hz로 가진하는 실험 장치를 구성하였다. 제안한 모션확장 기법을 확인하기 위한 실험이다.

Fig. 7

Experimental setup for motion extention

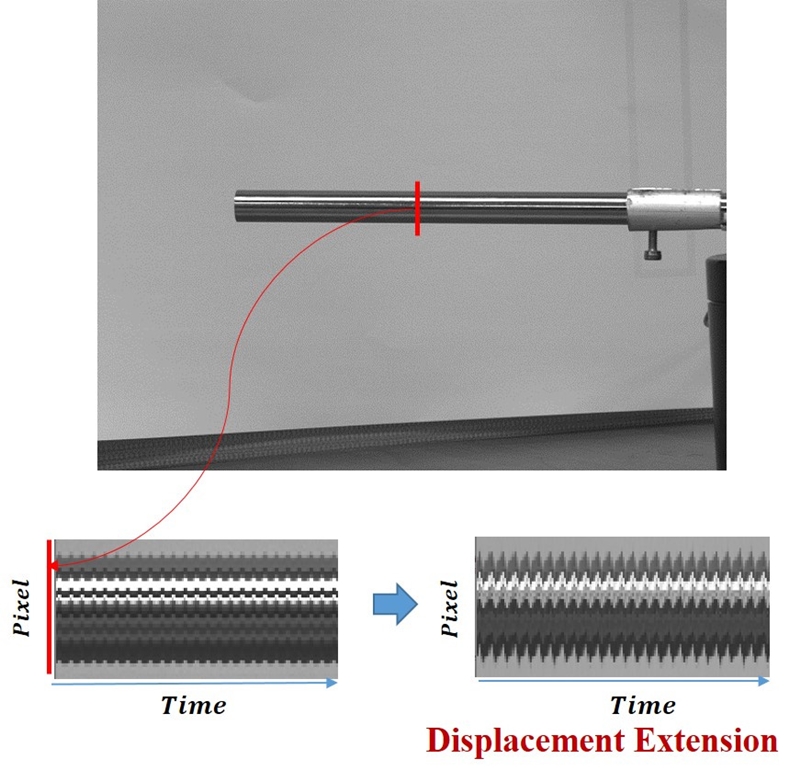
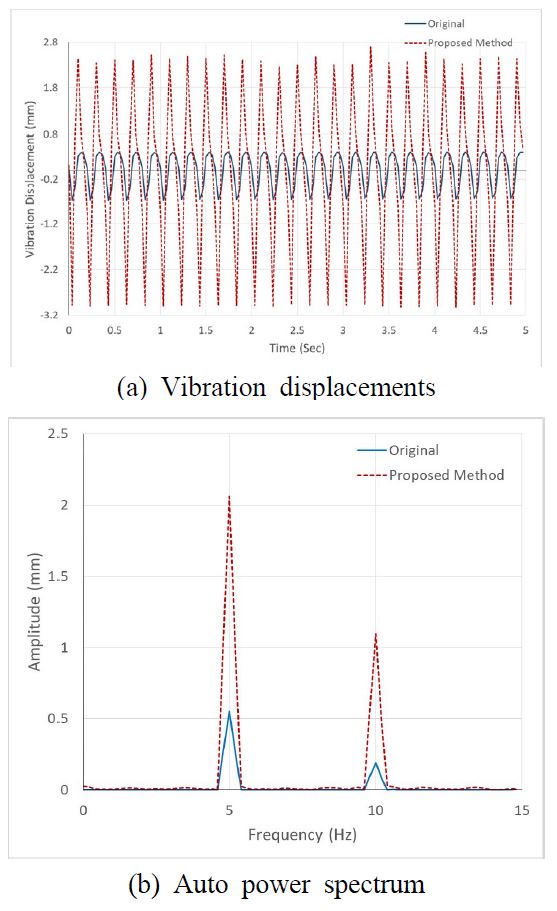
성능평가를 위하여 실험에 사용된 카메라 영상은 640×480, 30 frame/s 연속영상을 취득하면서 α=5를 적용한 진동확장 알고리듬을 처리하였다. Fig. 8은 카메라를 이용하여 5 Hz로 가진되어지는 외팔보의 영상을 취득하여 시간에 따라서 진동 확장하는 결과를 보여준다. Fig. 9에서 진동 확장의 정확성을 확인하기 위하여 영상을 이용한 진동변위 측정방법을 사용하여 검증을 하였다⁽³⁾. Fig. 9는 진동확장을 위한 제안방법의 사용전과 후의 진동 변위와 주파수를 보여준다. 결과를 통하여 진동 변위가 확장되어 시각적으로 확인하기 어려운 미세한 진동을 확인할 수 있다.

Fig. 8

Vibration extension result of vibrator

Fig. 9

Extension result of propose method

Fig. 10은 2차원 영상에서 모션확장 결과이다. 카메라를 이용하여 실시간으로 미세한 진동을 시각적으로 확인하기 위해서 변위 확장 결과의 일부분을 캡쳐한 영상이다. Fig. 10(a)는 이전영상, Fig. 10(b)는 현재 영상을 보여준다. 이전 영상과 현재 영상을 확인하면 미세하게 외팔보가 상승하는 것을 알 수 있다. 제안 방법인 모션확장 기법을 적용하면 Fig. 10(c)에서와 같이 Fig. 10(b)인 현재 영상보다 상승폭이 확장되는 결과를 확인할 수 있다. 또한, 현장에서 실시간으로 영상을 취득과 동시에 미세진동이 확장된 결과를 얻기 위해서는 1 frame 당 평균 처리시간이 중요하다. 제안된 방법을 사용하여 α=5를 적용한 1 frame 당 처리시간을 측정한 결과(영상 입출력 포함) 0.023초를 보였다. 따라서 현장에서 영상취득과 동시에 바로 진동확장 결과를 확인할 수 있는 성능을 보여준다.

Fig. 10

Vibration extension result of 2D image

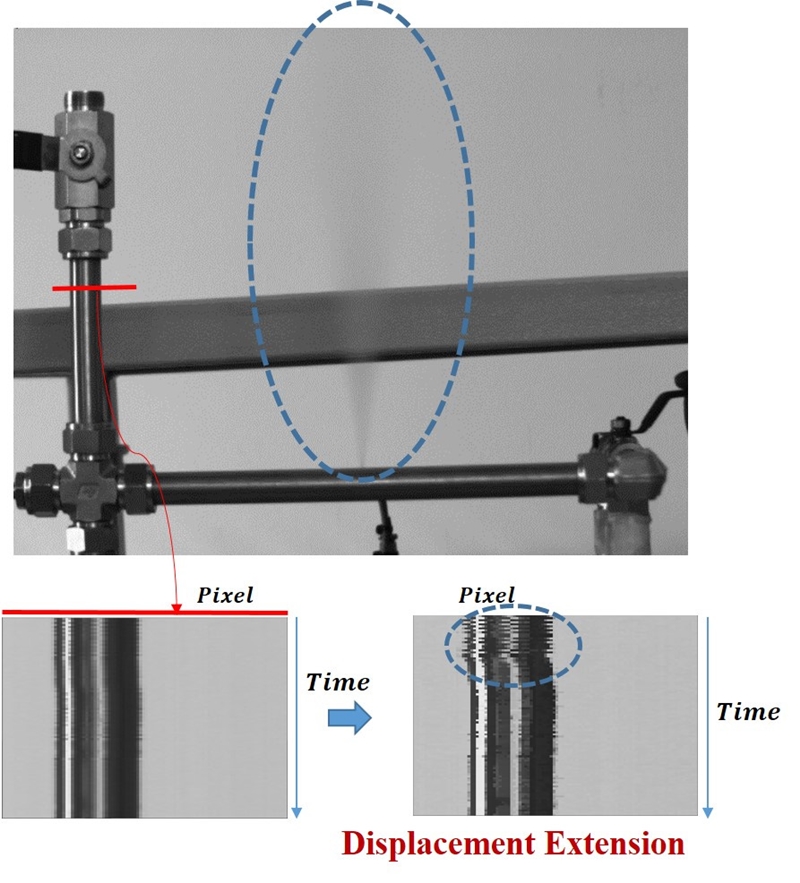
노이즈 문제점이 있는 기존 EVM 방법과 노이즈에 강하지만 많은 연산을 해야 하는 PBM 방법의 문제를 개선한 제안한 방법을 검증하였다. 기존 EVM 방법⁽⁴⁾에서 공개한 eulerian motion magnification C++ 소스와 제안한 방법을 비주얼 C++ 프로그램을 사용하여 같은 영상에 적용한 결과를 Fig. 11에서 보여준다. EVM 방법에서 특정 성분을 증폭하는 bandpass filtering은 제안한 방법과 동일한 실험 조건을 위하여 설정하지 않았다. Fig. 11(b)와 Fig. 11(c)는 Fig. 11(a) 원영상을 각각 EVM 방법과 제안한 방법으로 처리한 결과이다. 640×480 영상을 30 frame/s 연속영상을 취득하면서 α=5로 확장한 결과 제안 방법이 기존의 EVM 방법 보다 노이즈에 강한 것을 알 수 있다. 그리고 연산처리 속도 측정결과(영상 입출력 포함) EVM 방법보다 제안한 방법이 0.013초 빠르게 나왔다. 640×480 영상에서 제안 방법의 α 확장계수 1회 반복 연산 수행시간은 0.0025초로 측정된다. 또한 영상 입출력 수행시간은 0.01초이다. 따라서 α=8일 때 영상 입출력 포함한 전체 수행시간은 0.03초이므로 30 frame/s 연속 영상을 실시간으로 8배까지 확장 수행할 수 있는 결과를 보여준다. 노이즈에 강하지만 연산처리속도가 문제인 기존 PBM 방법⁽⁵⁾을 향상시킨 참조논문의 개선된 PBM 방법⁽⁶⁾의 실험결과를 참조하면 EVM 방법이 가장 빠른 연산속도를 보여준다. 따라서 제안한 방법이 노이즈에 강한 PBM 방법과 연산처리속도가 빠른 EVM 방법의 장점을 모두 적용하고 있는 것을 알 수 있다. Fig. 12는 제안된 방법을 검증하기 위하여 고온 고압 누설 실험 장치를 이용한 실험을 하였다. 순간 누설을 발생할 수 있는 장치로서 누설 발생시 배관 진동을 확인하는 실험이다. 실험에 사용된 카메라 영상은 640×480, 30 frame/s 연속영상을 취득하면서 α=5를 적용한 진동확장 알고리듬을 처리하였다. Fig. 12는 누설이 발생하는 순간 진동이 확연히 차이나는 것을 보여준다. 누설이 순간적으로 발생할 때 생기는 배관의 이상 진동을 확인할 수 있다.

Fig. 11

Experimental results of EVM and propose method

Fig. 12

Vibration extension result of high temperature and high pressure pipe

3.2 회전체 미세 진동확장 실험

회전체 실험 장비를 이용한 미세 진동이 있는 회전체 진동확장 실험을 진행하였다. 3.1 실험실 진동확장 실험과 동일하게 카메라 영상 640×480, 30 frame/s을 취득하면서 α=5 진동확장 알고리듬을 처리하였다. Fig. 13에서의 결과와 같이 시각으로는 인지할 수 없는 미세진동을 시각적으로 확인 가능하도록 변화된 영상을 보여주고 있다.

Fig. 13

Fine vibration extension result of rotor

3.3 현장 배관 구조물 진동확장 실험

실험실에서 적용한 모션확장 기법을 현장에 적용 실험하여 검증하였다. Fig. 14의 영상은 기존에 진동변위 측정을 위하여 발전소에서 영상 640×480, 100 frame/s로 촬영되어진 고온 고압 현장 배관이다. 촬영 영상은 시각적으로 진동 변화를 판별하기는 어렵다. 그러나 제안한 알고리듬에 α=5를 적용함으로써 시각적으로 진동의 움직임을 인지할 수 있는 결과를 잘 보여주었다.

Fig. 14

Vibration extension result of field pipeline

3.4 현장 전동기 구조물 진동확장 실험

제안된 방법을 현장 검증하기 위하여 Fig. 15와 같이 카메라를 설치하여 현장에서 환기시스템 전동기 진동 촬영을 진행하였다. 영상 데이터를 공간영역에서 처리하여 모션 확장하는 방법을 적용함으로써 현장에서 촬영과 동시에 실시간으로 구조물의 진동을 시각적으로 확인 할 수 있었다.

Fig. 15

Experimental setup for vibration extension of field motor

카메라 영상 640×480, 30 frame/s을 취득하면서 α=5 진동확장 알고리듬을 처리하였다. Fig. 16에서의 결과와 같이 진동 변위를 확장함으로써 시각적으로는 쉽게 진동을 인지할 수 있는 결과를 보여준다.

Fig. 16

Vibration extension result of field motor