와이어로프 타입 마운트의 가속도-주파수 의존 동강성 및 감쇠 추정
‡ Recommended by Editor Won Ju Jeon
© The Korean Society for Noise and Vibration Engineering
Abstract
The wire mount, which is made of metal and is suitable for harsh environments, has a rubber-like nonlinear hysteresis (for example, stiffness and damping). To estimate the nonlinear property according to the excitation acceleration, the transmissibility and phase were measured through a single-axis sine sweep test. The measured transmissibility and phase were applied to a one-degree-of-freedom system to estimate the stiffness and viscous damping coefficient. As a result of the estimation, the damping and stiffness differ according to the excitation acceleration level and frequency, and tend to decrease as the excitation acceleration level increases. As a vibration isolator, the wire-mount three-axis seismic test was conducted to confirm the performance, and the results were compared with the single-axis test and discussed.
Keywords:
Wire Mount, Frequency-acceleration Dependant, Dynamic Stiffness, Seismic Testing키워드:
와이어마운트, 주파수-가속도 의존, 동강성, 내진시험1. 서 론
경주, 포항 지진 이후 재난 시 필수적인 건물에 설치되는 기계, 전기 장비에 대한 내진검증이 필수화되고, 원자력 발전소의 설계 기준이 되는 내진가속도 조건이 강화되고 있다. 그에 따른 기계 전기 장비의 내진 설계 보강이 진행되고 있으나, 내진 조건이 높을수록 강성을 키우는 방향의 설계는 한계가 있어 점차 면진장치 설치 필요성이 부각되고 있다.
산업계에서 흔히 사용되는 면진장치로는 고무 소재의 마운트가 주로 사용되는데, 원자력 발전소에서는 방사선이나, 열, 진동 등에 의한 경화가 발생하므로 재료의 수명이 제한적이며 물성이 변경될 수 있고, 유지 관리 등의 문제가 발생한다. 따라서 금속 소재만으로 구성된 마운트의 경우 이러한 문제를 피할 수 있다.
금속 소재의 마운트 중 와이어로프 타입 마운트는 스테인리스 선을 꼬아서 만든 스트랜드를 다시 꼬아서 나선형 형태로 만든 금속 재질 마운트로, 고온, 방사선, 내 화학 특성이 좋아 내구성이 높다. 따라서 원전 환경에서 관리, 내구성에 강한 강점을 지니고 있다. 또한 변형 시 소선의 마찰 및 방향에 따른 반발력 차이와 히스테리시스 현상으로 인한 감쇠 효과를 가지고 있어 충격 진동을 흡수하는 능력 또한 우수하다.
국내에서도 와이어 소재의 마운트 개발에 관련된 연구가 진행된 바 있으며, 고유진동수 및 강성 확인을 위해 가진기를 사용하거나(1), 충격 시험(impact test)(2), 만능 재료 시험기(universal testing machine)를 이용한 정적실험 등을 수행하여 강성을 추출한 바 있다(2). 이 밖에도 일반 마운트의 동특성을 살펴보기 위한 동적 실험 연구(3), 주파수에 대한 강성 및 감쇠를 실험적으로 구하려는 연구가 수행된바 있다(4).
또한 히스테리 특성을 가지는 고무 소재 물질의 경우 노출 가속도 및 주파수별로 실험을 하여 저장탄성률과, 손실 탄성률을 추정하고 노출 가속도 및 주파수에 따른 모델이 제시된 바 있는데(5), 와이어마운트의 경우 점탄성 물질과 동일한 유사한 특성을 보이고 있어 다양한 노출 가속도 및 주파수에 대한 동강성, 감쇠에 대한 시험적 확인이 필요한 실정이다.
이 연구에서는 비금속을 사용하지 않는 면진 장치로 와이어로프 타입 마운트의 활용 가능성을 3축 내진시험을 통해 확인하고자 한다. 또한 점탄성 물질과 유사한 시험을 통해 마운트가 가진 특성을 파악하여 내진 성능과 연관성을 찾기 위해 노출 가속도 및 주파수에 따른 와이어로프 타입 방진 마운트의 성능을 파악 하고자 한다. 이를 위해 강성 및 감쇠 도출을 위한 간단한 1 자유도계 계산식을 제시하고 시험별 강성 및 감쇠 변화 추이를 살펴보고자 한다.
2. 동강성 감쇠 추출 실험
2.1 실험 방법
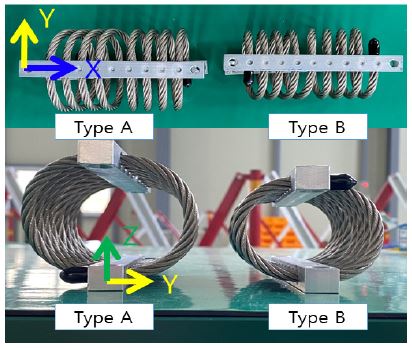
와이어로프 타입 마운트는 Fig. 1과 같이 스테인리스 스틸 소재의 와이어로프가 용수철 형태로 구부려져 알루미늄 가이드 보에 고정되어있는 형상이다. 체결은 알루미늄 가이드 보를 볼트 체결하며, 시험품은 Type A, Type B로 제작하였다. 시편의 높이는 각 70 mm, 60 mm 폭은 84 mm, 73 mm 와이어의 직경은 6.4 mm로 동일하다. 가이드 보의 높이 폭 길이 치수는 12×15×146 mm3로 동일하다.
시험은 164 kg의 직육면체 질량(높이×폭×길이 160×600×600 mm3)을 지지할 수 있도록 4개의 마운트를 설치하였고, 6개의 시편에서 2개씩을 골라 1, 2, 3그룹으로 나누고, 1-2그룹, 2-3그룹, 1-3그룹에 해당하는 시편을 교대로 설치하여 축 당 3케이스로 시험을 진행하였다. 시편의 좌표계는 길이방향을 X, 횡방향을 Y, 지면에 수직한 방향을 Z축으로 설정하였다.
전달률을 구하기 위해 사인 스윕 시험을 진행하였고, 가진주파수가 5 Hz에서 50 Hz로 올라가서 5 Hz로 다시 내려오는 왕복 스윕 시험을 2번 연속 수행하였다. 스윕 속도(sweep rate)는 1 oct/min, 질량과 하단부 간섭으로 인해 Z축의 시험 변위는 10 mm로 제한하였다. 전달함수는 스윕 가속도를 0.2 G부터 0.2 G씩 증가하며 1.2 G까지 6종류 크기의 가속도에 대한 전달률과 위상을 계측하였다. 여기서 기술한 시험 조건은 Table 1에 명시되어 있다.
마운트가 받는 가속도 즉 외부 하중 변화에 따른 전달 특성을 보기 위해 스윕 가속도를 달리하였다. 시험에 사용된 장비는 전자식 단축진동 시험기(famtech)이다.
Fig. 2는 수평축 단축시험 시험 사진이다. 시험 시 기초에 부착된 Ch. 1 가속도 센서를 사용하여 단축진동시험기를 제어하였고, Ch. 2 가속도 센서에서 계측되는 상부 질량의 가속도 신호를 사용하여 전달률을 구하였다. 전달률 계산에는 스윕 시 센서에서 검출되는 가속도를 변화하는 스윕 주파수를 중심으로 5 Hz의 밴드를 사용하여 스윕 주파수 주변부를 제외한 신호는 필터링하여 구해진 진폭과 위상을 사용하였다.
시편은 바닥 테이블의 직선 운동을 이용하여, 가진하고 축이 변경될 때마다 시편이 고정된 나사를 풀어 축을 변경하고 시험을 진행하였다.
2.2 전달률 시험 결과
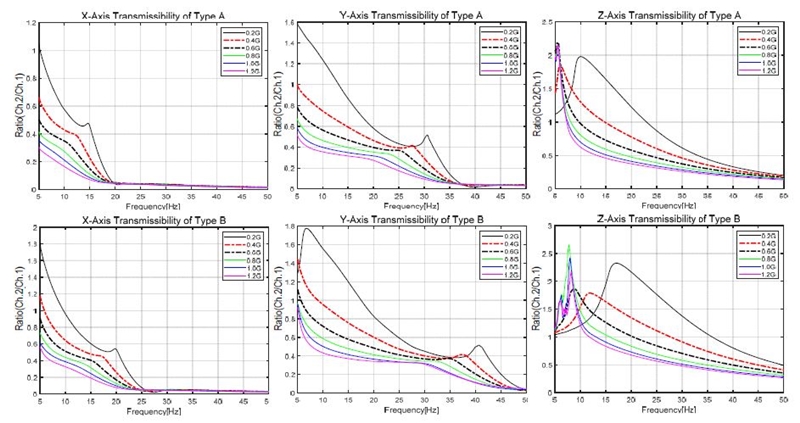
전달률 실험 결과, 와이어 마운트의 비선형 특성과 일반적인 특성들이 실험 결과로 도출되었다. 비선형적 특성은 바닥 가진 가속도가 증가함에 따라 전달률이 감소하고 Z축의 경우 우향 스윕, 좌향 스윕 별로 다른 전달 특성을 보이는 시험 케이스가 존재하였다. Fig. 3에서 나타낸 전달률은 각 스윕시험의 평균을 취한 것이다. 전달률의 경우 X-Y-Z 축 순으로 전달 특성이 작았으며, 주파수가 증가함에 따라 전달률이 감소하는 1자유도계의 특성이 있고, 0.2 G 가진의 경우 감소 후 소폭 상승하는 현상이 관찰된다.
Type B 전달률 시험 결과 Type A와 동일한 비선형 및 일반특성을 지니고 있었고 X, Y, Z축 모두 Type A보다 최대 전달률이 높았으며 이는 와이어가 금속 바에 감긴 반경 차이 즉 마운트 강성이 Type A보다 크기 때문에 전달률이 상대적으로 높다. Fig. 3의 Type A와 Type B 전달률을 비교해 보면 강성에 따른 차이로 전달률의 크기가 차이가 나지만 각 바닥 가속도에 따른 전달률의 변동 양상은 모든 축에서 동일한 것을 알 수 있다.
2.3 강성 및 감쇠 추정
가속도 신호만을 사용하여 강성 및 감쇠를 추정하기 위해 1자유도 기초 조화운동 방정식을 이용하였다. 전달률은 식 (1)과 같다. 여기서 m은 정육면체의 질량, c는 점성감쇠계수, k는 강성을 의미한다.
| (1) |
여기서, x(t)는 상부질량의 변위, y(t)는 기초의 변위를 의미한다. 정현파 가진 시 각 변위는 식 (2)와 같다.
| (2) |
여기서 X는 상부질량의 변위 진폭, Y는 기초의 변위 진폭을 의미한다. ϕ는 기초 변위와 상부질량 변위의 위상차이며, 정현파 스윕을 통해 각 변위와 위상차를 구할 수 있다. 각 신호가 식 (2)와 같이 정현파라면 가속도 항에서 구한 위상 ϕ도 변위에서 구한 결과와 동일하므로 가속도계를 통해 구한 위상 ϕ를 강성 추정에 사용한다.
식 (2)에서 x(t)와 y(t)의 차이를 z(t)라 두고 정현파라 가정하면 식 (3)과 같다.
| (3) |
여기서 Z는 상대좌표의 변위 진폭, θ는 기초변위 y(t)와 상대변위 z(t)의 위상차를 의미한다.
식 (2)를 식 (3)에 대입하여 시간 항을 소거하여 정리하면 식 (4)와 같다.
| (4) |
상대좌표 z(t)를 사용하여 1자유도 기초 조화운동 방정식 식 (1)을 정리하고, 시간항을 소거하여 정리하면 식 (5)와 같다.
| (5) |
여기서 오일러 정리를 사용하여 e-iθ를 실수부와 허수부를 분리하여 행렬로 정리한뒤 강성 k 및 점성감쇠 항 cω를 구하면 식(6), (7)과 같다.
| (6) |
| (7) |
따라서 스윕시험을 통해 구한 가속도 진폭을 정현파라 가정한 후 변위 진폭을 계산하여 X, Y에 대입하고 시험에서 구한 위상 ϕ를 식 (4)에 대입하면 상대변위 진폭과 위상 Z, θ를 구할 수 있고 이를 식 (6), (7)에 대입하면 주파수별 강성과 점성감쇠 항을 구할 수 있다.
3. 단축 시험 결과 분석
3.1 강성 및 감쇠 추정 결과
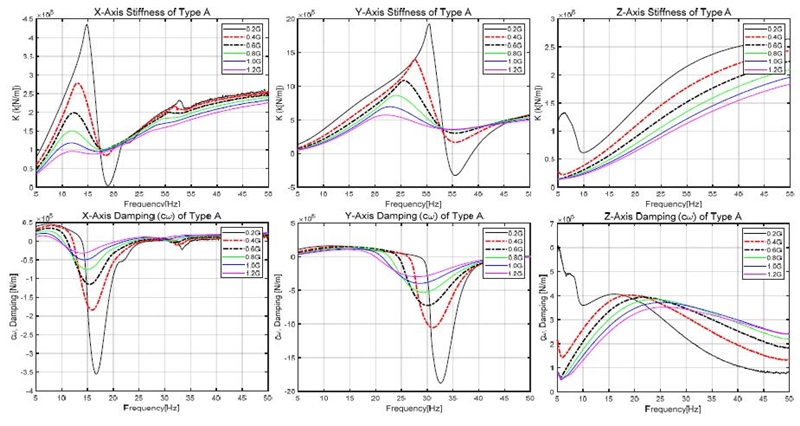
2.2절에서 구한 식 (3), (4)를 사용하고, 1자유도계에 대해 검증된 코드를 사용하여 시스템의 강성과 점성감쇠 항을 구하였다. 바닥가속도가 증가함에 따라 전체적으로 강성은 감소한다. 바닥 가속도가 낮은 가속도일 경우 강성의 변화가 급격히 나타났고 높은 가속도의 경우 비교적 완만한 곡선의 모양을 보였다. 주파수가 높아질수록 강성이 증가하는 모습을 보여주지만, 바닥가속도가 큰 경우 강성의 변화 폭이 크지 않다. Type B의 경우도 비슷한 특성을 지니고 있고 전달률 변화 경향과 유사하므로 이 논문에는 기술 하지 않았다.
점성감쇠 항의 경우도 바닥가속도가 증가함에 따라 그 변화의 폭이 줄어드는 경향을 볼 수 있다. 크기의 경향은 주파수마다 다르나, 연속적인 형태로 변화한다. 따라서 Fig. 4의 그래프를 3차원으로 표현하면 곡면의 형태를 띠게 되고, 각 특성이 주파수와 외력의 크기와 연관되어 있다. 이는 점탄성 물질의 저장탄성계수와 손실탄성계수가 주파수와 진폭에 의존적인 것과 유사하며, 와이어로프 마운트의 히스테리시스 및 비선형 특성에 기인한 것으로 보인다.
각 수평축 실험 결과에서 강성 및 점성감쇠 항은 음의 값이 도출되는데, 수평으로 시험할 경우 바닥 테이블이 운동하면 질량의 중심축을 기준으로 회전력이 발생되고, 그에 따라 회전운동 가속도가 도출된다. 이는 Fig. 3에서 X, Y축 전달률이 떨어지다가 살짝 커지는 현상을 통해 간접적으로 확인 할 수 있고, 시편의 끝단부에 센서를 붙여 신호를 받아 확인하였다. 상부질량이 회전하면 상단부의 센서에서도 질량중심점과의 거리로 인해 운동이 발생되는 현상으로 추정되며, 1-DoF 모델 사용에 따른 한계점으로 보인다.
이 논문에서 제시하는 강성과 점성감쇠 항은 4개의 마운트를 1자유도 단일 마운트로 두고 계산된 값이다. 다만 회전 영향까지도 모두 고려한 이유는 1자유도계로 모델링된 값을 실제 해석에 적용하기 위해서는 각 마운트점을 강체로 연결하여 1개의 질점에 실험에서 구한 강성과 감쇠를 대입하는 것이 실험과 매칭 되며, 각축의 강성과 감쇠를 회전에 따른 운동을 반영하여 구하는 것이 현실과 가깝기 때문이다.
동강성, 점성감쇠 항 k[w], ωc[ω]항의 주파수 관계는 특정 주파수 구간별로 1 ~ 2차 방정식 형태로 근사될 수 있는 형태이다.
4. 다축 내진시험
4.1 다축 내진시험 방법
Fig. 5는 내진시험 시편 및 센서 설치 사진이다. 3축 내진 시험은 164 kg 직육면체 질량체를 4개의 마운트로 지지하고 바닥치구와 질량체 상단 중앙에 3축 가속도계를 설치하여 진행하였다. 마운트 시험 결과 Type A의 면진 성능이 상대적으로 우수하였기 때문에 내진시험용 마운트로 Type A를 사용하였다.
시간 영역의 지진파형은 최대 가속도 1.0 g 수준의 1 Hz ~ 50 Hz 주파수 범위를 갖는 요구응답스펙트럼(require response spectrum)을 통해 각각 주요 가속도 성분이 수평을 기준으로 6 Hz, 11 Hz, 16 Hz인 내진시험파형을 만들어 3축 동시가진으로 6자유도 내진시험기(MTS)를 사용하여 시험을 수행하였다.
4.2 다축 시험 결과
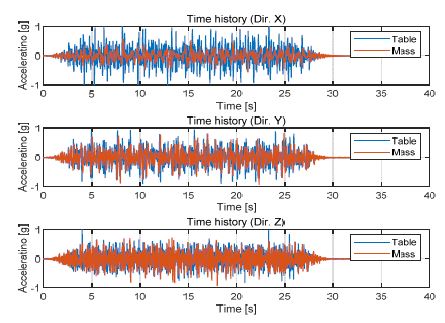
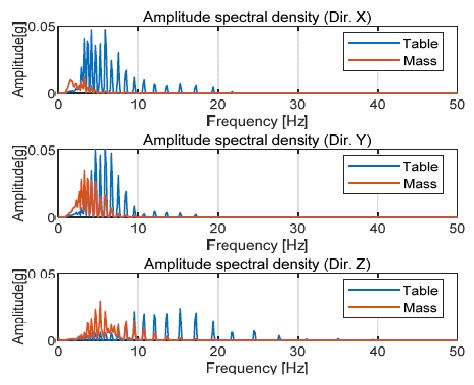
Fig. 6는 주요 가진 주파수가 6 Hz인 시험 파형으로 면진 효과가 가장 적은 시간파형이며, 단축 시험 결과와 같이 X, Y, Z 축 순으로 진동 차단 효과가 있음을 알 수 있다. 다만 Fig. 3의 Type A의 전달률은 6 Hz에서 각각 X축 0.3, Y축 0.5, Z축 2의 크기를 가지지만 Fig. 8의 Y, Z 축은 가속도 크기가 비슷한데, 이는 Z축의 경우 주요 가속도 성분이 Y축보다 높고 보다 넓은 범위에서 분포하고 있기 때문이다. 이는 Fig. 7에서 Z축 가속도 신호의 주파수 성분을 통해 확인 할 수 있다.
Fig. 7은 Fig. 6의 시간 파형의 주파수 분석을 위해 ASD(amplitude spectral density)를 구한 것이다. 저주파수에서 가속도 증폭이 상대적으로 많이 발생하고, 그 증폭의 정도는 Z가 가장 크며 그다음 Y, X 순으로 크다. 4.6 Hz에서 각 가속도 정도를 비교해 보면, X축은 6 %, Y축은 51 % 정도로 절감되고 Z축은 431 %로 증폭된다. 이는 1.2 G의 단축 시험 결과가 5 Hz에서 약 X축 30 %, Y축 50 %, Z축 200 %로 도출되는 것과 유사하며, 생성된 지진파의 최대 가속도 크기가 1.0 G인 것을 볼 때 전달률의 특성은 지진파의 최대가속도와 상관관계가 있었다.
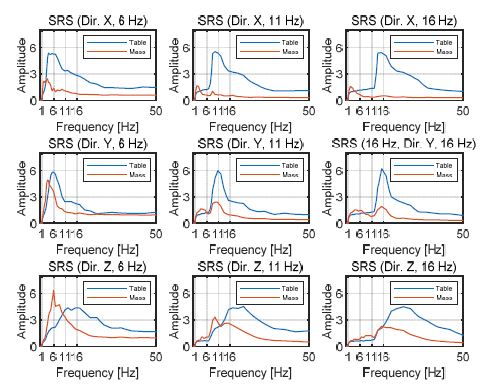
Fig. 8은 주요 가속도 성분이 6 Hz, 11 Hz, 16 Hz인 내진시험을 수행한 결과 바닥 및 상부가속도의 SRS(shock response spectrum)를 구해본 결과이다. 바닥 가속도의 주요 주파수 대역이 6 Hz 근처에 있을 때 상부 가속도의 6 Hz 이하의 주파수 성분이 Y, Z 축에서는 증폭되는 것을 확인 할 수 있다. 이는 각 축별 마운트의 공진에 따른 결과이다. 단축 전달률 특성 시험에서 5 Hz 이하의 결과를 볼 수 없었지만 이 시험에서는 수평 공진이 약 1 Hz, 2.5 Hz, 수직은 단축 시험 결과와 일치하는 약 5 Hz인 것을 알 수 있다. 따라서 주요 주파수 성분이 Type A의 공진주파수인 5 Hz 보다 높을수록 면진 효과는 우수하다 예측할 수 있고 시험 결과는 16 Hz, 11 Hz, 6 Hz 순으로 우수하였다. 따라서 특정 위치에서 지진파형의 주요 주파수 성분보다 면진장치의 고유진동수가 낮게 설계되어야 한다.
5. 결 론
이 논문에서는 와이어로프 타입 마운트의 주파수별 강성과 감쇠를 추출하였다. 추출 결과 마운트가 노출되는 가속도 및 주파수 별로 다른 강성 및 감쇠 특성을 보유하고 있었다. X, Y, Z 축 순으로 전달률 특성이 우수하였고, 가진 가속도가 커지면 주파수 전영역에서 전달률이 줄어들고, 전달률로 계산된 강성도 감소한다. 이는 와이어 마운트가 가지는 비선형적 특성으로 히스테리시스 효과에 기인하는 것으로 추측된다. 따라서 마운트 설치 시 노출 가속도를 사전에 고려하여야 하며 면진 장치로 활용하기 위해서는 바닥 가속도의 주요 주파수 성분이 와이어 마운트의 절연 효과가 발생하는 주파수 이상이어야 한다.
이 논문에서 시험 된 와이어 마운트의 주파수와 동강성, 점성감쇠 항 k[ω], ωc[ω]의 관계는 부드러운 곡선형태로 각 가속도 별로 1차 ~ 2차 방정식으로 근사화 가능하다. 또한 단축시험기를 사용하고, 지진바닥가속도의 최대값보다 큰 가속도를 사용하여 마운트의 축별 전달률을 구하면 3축 내진시험의 특성과 유사하므로 단축진동시험기를 통해 사전시험을 수행한다면 연구 개발 비용을 절감할 수 있을 것으로 기대된다.
Acknowledgments
이 논문은 한국기계연구원의 2020년도 주요사업(과제번호: NK228C)의 지원을 통해 수행되었음을 밝힙니다.
References
-
Shin, Y. H., Lee, J. H., Jung, B. C. and Moon, S. J., 2020, Design of Passive Vibration Isolation Element by Wire Mesh Material for Developing a Hybrid Mount, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 30, No. 1, pp. 75~81.
[https://doi.org/10.5050/KSNVE.2020.30.1.075]

-
Kim, T. Y., Shin, Y. H., Moon, S. J., Jung, B. C. and Lee, T. J., 2016, Elastic Modulus Extraction of Wire Mesh for Vibration Mount Development, Transactions of the Korean Society for Noise and Vibration Engineering. Vol. 26, No. 7, pp. 806~813.
[https://doi.org/10.5050/KSNVE.2016.26.7.806]

-
Moon, S. J., Shin, Y. H., Chung, J. H. and Song, C. K., 2014, Experimental Review on Dynamic Characteristics of the Commercial Mounts for Vibration Reduction, Transactions of the Korean Society for Noise and Vibration Engineering. Vol. 24, No. 9, pp. 687~694.
[https://doi.org/10.5050/KSNVE.2014.24.9.687]

-
Moon, S. J., Kim, H. S., Chung, T. Y., Lee, D. H. and Hwang, J. Y., 2010, A Study on the Experimental Dynamic Identification of Cylindrical Oil Dampers in the Wide Frequency Range, Transactions of the Korean Society for Noise and Vibration Engineering. Vol. 20, No. 6, pp. 528~536.
[https://doi.org/10.5050/KSNVE.2010.20.6.528]

-
Höfer, P. and Lion, A., 2009. Modelling of Frequency-and Amplitude-dependent Material Properties of Filler-reinforced Rubber, Journal of the Mechanics and Physics of Solids, Vol. 57 No. 3, pp. 500~520.
[https://doi.org/10.1016/j.jmps.2008.11.004]


Seunghoon Bae received B.S., M.S. and Ph.D. degrees from Sch. of Mech. Eng. at Pusan National University in 2009, 2011 and 2016 respectively. He is currently working at the KIMM Busan Machinery Research Center from 2016. His research interests include vibration damping, vibration& seismic testing and FEM.