CNN을 활용한 카오스 신호 분류 검증
© The Korean Society for Noise and Vibration Engineering
Abstract
The aim of the study was to classify the chaotic time-series data with the nonlinear problem using the convolutional neural network (CNN), and to determine and verify the chaotic characteristics from a deterministic system. The classical nonlinear differential equation established by the Rossler model was used, and the chaotic characteristics were determined by the Lyapunov exponent. The chaotic properties was visualized using an unthresholded recurrence plot through the proposed procedure. A simple CNN model was developed to learn the extracted image using the proposed feature-visualization technique. As a result, the chaotic characteristics were classified with an accuracy of 99 % or more.
Keywords:
Convolutional Neural Network, Lyapunov Exponent, Recurrence Plot, Chaos키워드:
합성곱 신경망, 리아푸노브 지수, 리커런스 플롯, 카오스1. 서 론
카오스 신호 문제는 동역학계에서 오랫동안 연구되어져 왔다(1~5). 결정론적 카오스는 동역학계에서 파라미터 및 초기조건에 의한 비 주기적인 해가 불안정 하지만 일정한 범위내의 제한을 갖는다. 이는 많이 알려져 있는 Lorenz, Rossler 방정식 등에 잘 소개되어 있다. 다이나믹 특성을 분석하기 위한 방법은 주로 시계열 분석 방법과 위상공간내 해의 움직임(trajectory)을 표현한 분석을 이용하였다. 그러나 카오스를 수반하는 고차 비선형 시스템을 분석하기에는 한계가 있다. 카오스 현상을 포함하는 많은 비선형 동역학 이론 연구는 발전을 통해 HOSA(higher order spectrum analysis), logistic map, Lyapunov exponent 등을 통해 카오스를 정량화하였다(6~8). Lyapunov exponent는 시스템 파라미터 변화에 대한 카오스를 정량화하기 위한 가장 잘 알려진 방법으로 사용되며, 특히 Wolf, A. et al.(9)에 의해 제안된 Largest Lyapunov exponent는 카오스를 정량적으로 표현할 수 있다.
기계진동 분야에서 신호 분석은 시스템 고유의 다이나믹 특성 및 불안정 신호 검출 등에서 사용된다. 선형 시스템 또는 특성이 명확한 신호 분석은 일반적으로 FFT와 spectrum을 통해 실험적 신호 분석으로 규명되어진다(10~14). 그러나 선형 신호 외에도 고차 비선형을 포함하는 신호 분석 방법 또한 위와 같은 방법으로 수행되기 때문에 특성을 판단하기 난해한 경우가 많다. 특히, 마찰, 충격이 포함되는 신호는 고장진단 등에서 분석되지만 고차 비선형 특성인 카오스를 포함하는 신호는 주파수가 매우 모호하다(15,16). Kang, J.(15)은 2 자유도 모델을 구성하여 마찰에서 발생할 수 있는 카오스 진동현상에 대해 이론적으로 접근하였다. 진동 시스템에서 카오스를 만들어내는 이론적 파라미터를 규명하고 마찰 곡선에 의해 고차 비선형성인 카오스가 발현됨을 보여주었다. 또한 Serwet, W. et al.(17)은 충격 접촉 모델을 Hertz’s와 Newton’s 접촉 모델에 대해 Muller’s 방법으로 불연속 시스템에서 Lyapunov exponent를 구하고 카오스 특성을 연구하였다.
이론적인 접근법 외에도 진동 신호 분석은 신호의 가시화 방법을 이용하여 많은 연구가 진행되었다. 앞서 언급했던 FFT와 Spectrum외에도 recurrence plot, Gauss wavelets(18) 등 많은 연구가 진행되었지만 이중 다이나믹 시스템의 recurrence 특성을 반영하는 recurrence plot이 가장 활발하게 연구되고 있다. Marwan, N. et al.(19)은 복잡한 시스템에서 발생하는 진동특성에 대해 다양한 recurrence plot 방법을 이용하여 분석하였다. 그러나 이러한 방법은 엔지니어의 주관적인 판단이 지배적이고, 카오스와 같은 복잡한 신호를 분석하는데 한계가 있다.
최근 딥러닝을 이용한 인공신경망은 비약적인 발전을 이루고 있다. 특히 이미지 분류는 2015년 발표된 ResNet(20)을 기점으로 인간의 분류능력을 초월하였다. 각 분야에서는 CNN을 활용하기 위한 많은 모델들이 구성되었고, loss 함수의 최적화를 위한 방법들이 소개되었다(21).
따라서 이 논문은 다이나믹 시스템에서 발생되는 가장 복잡한 현상인 카오스 신호를 Rossler 식을 이용하여 구현하고, 이론적 접근을 통해 카오스 신호를 분석하고자 한다. 또한 복잡한 신호를 제안된 방법을 통해 이미지화 시키고 CNN을 이용하여 카오스 신호를 분류하고자 하였다. 이 결과를 Lyapunov exponent를 이용하여 검증하였다.
2. 본 론
2.1 이론적 접근법
이 논문의 목적은 딥러닝을 활용한 카오스 신호의 분류 및 검증이다. 때문에 운동방정식은 카오스 신호를 만들어 내는 대표적인 Rossler 방정식을 이용하였다. Rossler 방정식은 식 (1)과 같다.
| (1) |
여기서 a, b, c는 시스템 파라미터다. 결정론적 카오스는 Lyapunov exponent를 통해 결정할 수 있으며, 운동방정식은 벡터 형식을 갖는 상태공간 방정식으로 식 (2)와 같이 변형될 수 있다.
| (2) |
여기서 x=[x1, ..., xn]=T는 상태 벡터이고, f=[f1, ..., fn]=T은 미분가능한 연속적 벡터 공간이다. 또한 t0는 다이나믹 시스템의 초기 조건이다. 미소 초기조건 변화에 대한 다이나믹 시스템의 해 변화를 살펴보기 위해 perturbed solution을 y=x+δx로 가정하였다. 이후 시스템의 거동(trajectory) 및 초기조건은 다음과 같다.
| (3) |
여기서 y(t0)는 perturbed solution의 초기조건이며, x(t)에서 Taylor 시리즈를 취하면 선형화된 perturbed 방정식을 얻을 수 있다.
| (4) |
여기서 δx=[Φt(x0)]δx0를 선형화된 perturbed 방정식에 대입하면, 다음과 같이 변동 방정식(variational equation) 및 초기조건을 기술할 수 있다.
| (5) |
| (6) |
여기서 [Dxf], [I], [Φt(z0)]은 각각 자코비안 행렬,단위행렬, state transition matrix이다. 방정식 (5), (6)은 time-varying 선형 미분 방정식이며, 변동방정식의 해는 자코비안 행렬과 비선형 미분방정식을 동시에 풀면 얻을 수 있다. Lyapunov exponent는 식 (7)과 같이 정의된다.
| (7) |
여기서 mi는 i번째 변동방정식(variational equation)의 고유값이며, λi는 i번째 Lyapunov exponent를 의미한다. 단 정의에서 보듯이 위의 식은 연속적인 수치적분을 통해 직접적으로 계산되기 불가능하다. 따라서 iterative 접근법을 통해 수치적분을 수행할 수 있으며, 이때 perturbation δx는 수정된 gram-schmidt 직교 정규화를 기반으로 계산된다. 이를 통해 결정론적 카오스를 정량적으로 표현할 수 있다.
실제 진동 시스템에 대한 분석은 FFT나 spectrum과 같이 이미지 차원에서 주관적으로 분석되고 있다. 다이나믹 시스템에서 이미지 차원의 분석은 오랫동안 연구되었다. Recurrence는 다이나믹 시스템의 가장 큰 특징으로 recurrence plot를 통해 가시화가 가능하다. 이산화된 시계열 데이터는 식 (8)과 같이 정의된다.
| (8) |
여기서 △t는 샘플링 시간이다. 카오스와 같이 복잡한 시스템은 시스템 차원에서 해의 움직임(trajectory)이 자기교차(self-crossing) 될 수 있다. 따라서 재구성된 위상공간이 필요하며, time-delay 방법을 통해 재구성된 위상 공간을 표현할 수 있다.
| (9) |
여기서 m은 embedding dimension이고, τ는 time delay, ej는 j번째 직교좌표계의 단위벡터를 의미한다. 적절하게 선택된 embedding dimension과 time delay를 통해 위상공간을 재구성시킬 수 있다. embedding dimension은 기하학적 문제이며, time delay는 다이나믹 문제이다. 이 논문은 기하학적 측면에서 카오스를 분류하고 물리적 차원의 효율성을 위해 FNN(false nearest neighbor)을 이용하여 기하학적 차원을 재구성하였다(22).
식 (9)로부터 d차원에서 xr은 x의 r번째 가장 가까운 이웃이 된다. 이때 두 벡터 사이의 유클리드 거리의 제곱은 식 (10)과 같이 표현될 수 있다.
| (10) |
Time delay embedding 의해 d + 1차원으로 확장될 경우 d + 1 차원에 대한 r번째 이웃사이의 유클리드 거리는 식 (11)과 같다.
| (11) |
확장된 공간 사이의 유클리드 거리의 변화는 매우 크다. 따라서 두 사이거리의 변화율을 통해 최소 확장공간을 추정할 수 있다. 변화율로 정의된 유클리드 거리는 식 (12)와 같이 다시 작성될 수 있다.
| (12) |
여기서 Rtol은 임계값이며, 연구결과에서 Rtol>10일 때 자기교차(self-crossing)가 제거되었다(22).
재구성된 위상공간으로부터 threshold recurrence plot는 식 (13)과 같이 정의된다.
| (13) |
여기서 H는 Heaviside 함수, ε는 임계값,|| ⋅ ||는 L2-노름, N은 측정된 포인트의 수, 는 재구성된 시스템 해의 궤적(trajectory) 벡터이다. 이 논문은 주관적인 값을 최대한 배제하기 위해 오직 재구성된 솔루션 벡터 차의 노름을 통해 recurrence plot를 구성하였으며, 이는unthresholded recurrence plot()이라 정의된다.
2.2 CNN model
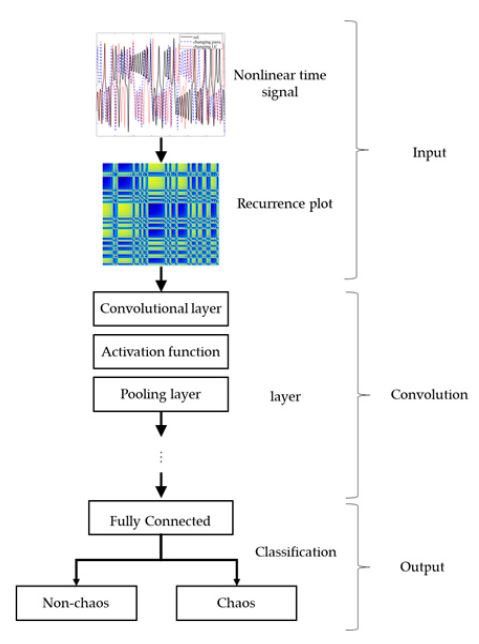
이론적 접근법을 통해 표현된 unthresholded recurrence plot을 CNN 모델을 활용하여 분류하고자 CNN 모델을 구성하였다. 먼저, 파라미터를 포함하는 비선형 시계열 데이터를 수치적분을 이용하여 해석을 수행하였다. 이후 얻어진 시계열 데이터를 FNN 알고리즘을 이용하여 최소차원의 embedding dimension을 결정하고 재구성된 위상공간을 구성하였다. 마지막으로 파라미터 변화에 대한 Lyapunov exponent를 계산하고 그에 상응하는 unthresholded recurrence plot을 추출하였다. 이를 기준으로 labeling을 정의하였으며, CNN 기반의 분류를 수행하였다. 요약된 분류절차는 Fig. 1에서 보여준다.
최근 CNN을 활용한 이미지 분류는 인간의 인지능력을 초월하는 정교한 모델들이 개발되었다. 이 연구의 목적은 고차원적의 비선형 신호를 CNN을 활용하여 분류가 가능하다는 것을 보여주는 것에 있다. 따라서 CNN 모델을 2단계의 구조로 단순하게 구성하였고, 각 단계에서는 convolution, 활성화 및 풀링 레이어가 포함된다. 제안된 모델은 각 단계에서 32-3×3 필터, 64-3×3 필터가 있는 2개의 convolution 레이어로 구성되었다. 또한 풀링 크기는 2×2의 2개의 최대 풀링 레이어가 사용되었다. 두 개의 convolution 레이어를 거쳐 특성 맵은 열벡터로 평평해지고 이미지의 지배적인 특징을 구분하여 2가지 유형의 신호에 대해 완전 연결 레이어로 분류되었다. 출력 값의 활성 함수는 softmax가 사용되었다.
다이나믹 시스템의 반복 특성을 표현하기 위해 200×200 픽셀의 이미지를 사용하였다. 사용된 CNN 모델은 Table 1에서 보여준다.
Convolutional 레이어의 활성함수는 ReLU함수를 사용하였으며, 앞서 언급했듯이 반복특성이 매우 짧은 구간에서 발생할 수 있기 때문에 필터 사이즈를 작게 설정하였고, stride도 1로 설정하였다. 최적화 방법은 빠른 수렴을 위해 경사 하강법 기반의 Adam optimizer를 사용하였다. 초기 가중치의 설정은 매우 중요한 문제 중 하나이다. 초기 가중치 설정은 많은 방법이 있지만 ReLU함수에 가장 잘 대응되는 He 가우시안 초기화 방법을 사용하였다(23~25).
2.3 결과
Rossler 시스템에서 파라미터나 초기 조건의 미소변화는 system의 상태변화를 야기한다. 카오스 분류를 위해 사용된 기준 파라미터는 a = 0.3, b = 0.3, c = 7이다.
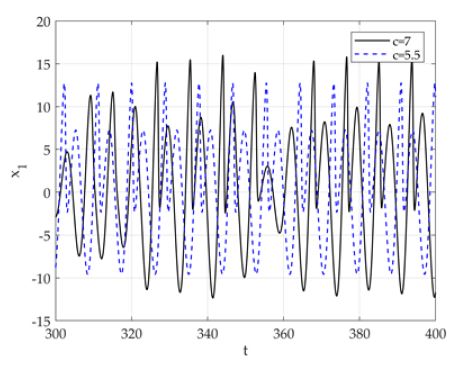
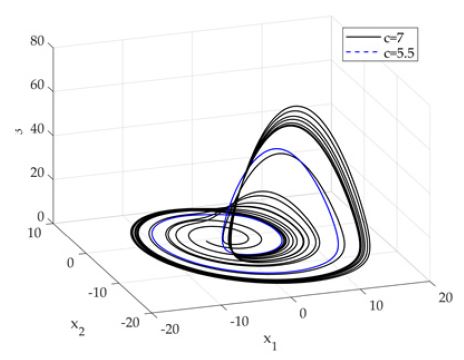
Fig. 2는 기준모델과 c = 5.5에 대한 Rossler 시스템의 시계열데이터를 보여주며, 미소한 파라미터의 변화로 시계열 데이터의 상태가 크게 변화되었다. 따라서 더 큰 파라미터의 변화는 시스템의 상태를 완전히 변화시킬 수 있음을 암시한다. 즉, 카오스와 비카오스 신호는 파라미터 변화에 의해 발현될 수 있다. Fig. 2에 상응하는 해의 궤적은 Fig. 3에서 보듯이 위상공간에서 표현될 수 있다.
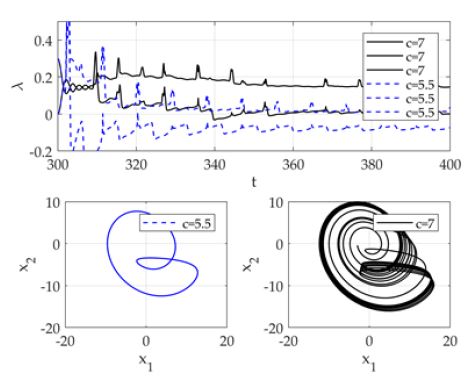
기준 모델은 Rossler 시스템의 대표적인 카오스 형태이며, c = 5.5는 period 1을 나타낸다. 각 파라미터에 해당하는 Lyapunov 지수를 수학적으로 정량화하기 위해 식 (7)의 iterative 접근법을 통해 정량화하였다. 또한 시스템의 위상공간을 2차원에서 표현하여 period 차원을 보기 쉽게 가시화하였다. 결과는 Fig. 4에서 보여준다.
Fig. 4에서 보듯이 c = 5.5일 때, Lyapunov exponent는 (λ1,λ2,λ3) = (0,−,−)으로 계산된다. 이는 stable limit cycle을 의미하며, 해의 궤적에서 2차원 위상공간에 period 1 limit cycle로 형성된다.
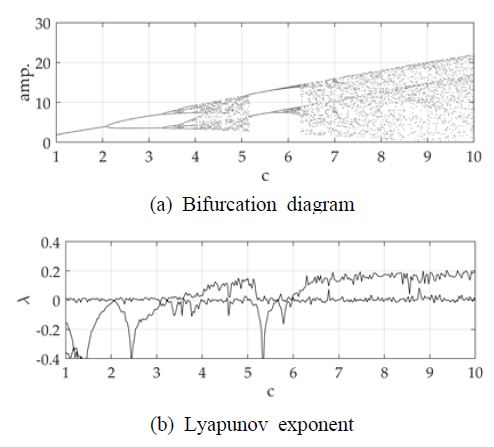
반면에 c = 7일 때, Lyapunov exponent는 (λ1,λ2,λ3) = (+,0,−)으로 계산된다. 이는 strange attractor를 나타내며, 2차원 위상공간에서 비 주기적이지만 일정의 제한을 갖는 해의 움직임으로 표현된다. 미소한 파라미터의 차이는 카오스를 발현시키며, 이를 정량적으로 나타내기 위해 파라미터 c 에 대해 Largest Lyapunov exponent를 계산하였다. 또한 해의 움직임을 보다 가시적으로 표현하기 위해 bifurcation diagram을 표현하였다. 결과는 Fig. 5에서 보여준다.
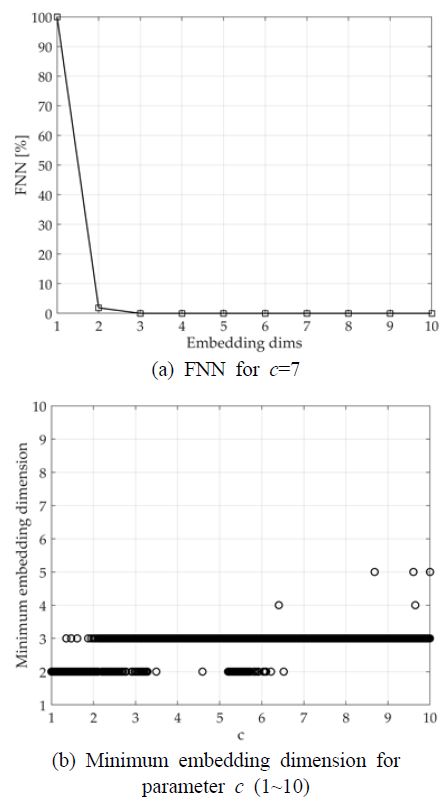
3차원 위상 공간에서 attractor는 4가지 타입으로 존재한다. Stable fixed point, stable limit cycle, stable 2-torus, 카오스(strange attractor)로 각각의 동적인 특성이 존재한다. 그러나 이 연구에서는 오직 카오스와 카오스를 만들어 내지 않는 신호만 분류하기 때문에 카오스를 제외한 나머지 타입의 특성은 고려하지 않고 구성하였다. 이론적으로 정량화된 각 파라미터에 대한 다이나믹 특성의 가시화를 위해 시계열 데이터에 대해 식 (9), (12)를 이용하여 최소 embedding dimension으로 확장하였다. 즉, 각 파라미터에 대한 자기교차를 판별하였다. 각 파라미터에서 결정된 최소 embedding dimension은 Fig. 6에서 보여준다. Fig. 6(a)는 c = 7에서 FNN을 보여주며, Fig. 6(b)는 파라미터 c 의 변화에 대한 최소 embedding dimension을 보여준다.
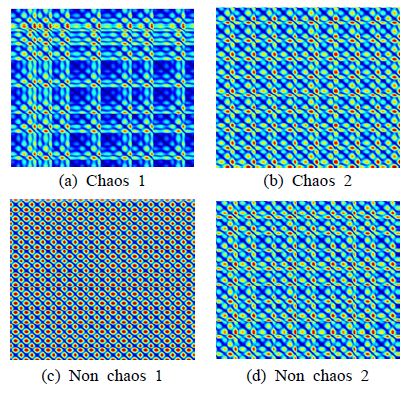
최소 embedding dimension은 각 구간의 기울기를 구하여 최소 기울기를 나타내는 최초의 차원으로 정의하였다. 각 파라미터에 상응하는 최소 차원을 결정하여 식 (9)를 통해 시스템의 해는 재구성되었다. 식 (13)의 재구성된 해의 노름만을 통해 unthresholded recurrence plot을 표현하였다. Fig. 7은 표현된 recurrence plot의 대표적인 이미지를 나타냈다.
unthresholded recurrence plot의 (a)와 (b)는 카오스이며, (c)와 (d)는 카오스를 만들어 내지 않는 신호이다. (a)와 (c)의 경우 사람이 특징을 인지하여 구분 지을 수 있지만, b와 d는 사람의 인지능력을 통해 분류하기 난해하다. 따라서 파라미터에 대한 unthresholded recurrence plot를 표현하고 데이터셋을 구성하였다.
데이터셋은 80 %의 학습(training)데이터와 20 %의 실험(test)데이터로 구분하고 학습데이터 내에서 20 %의 검증(validation)데이터를 다시 분할하였다. 학습에 사용된 분할 데이터 샘플은 Table 2에 정리하였다. 여기서 실험데이터는 학습에 사용하지 않은 데이터셋이다. 또한 각 Lyapunov exponent 증가에 따라 데이터가 생성되기 때문에 데이터셋이 순차적으로 생성된다. 따라서 데이터셋 셔플을 통해 일률적 데이터에 의한 오류를 제거하였다.
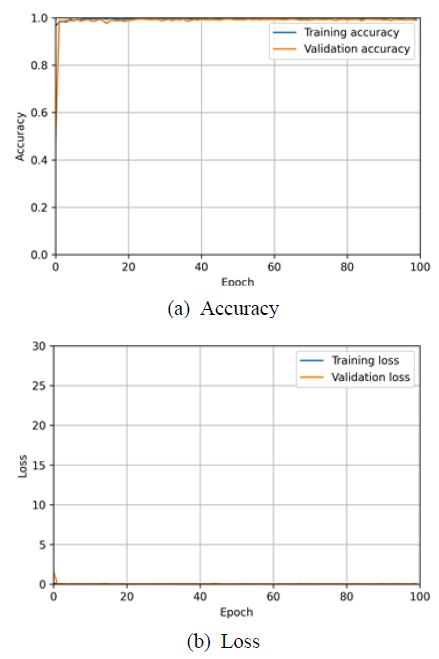
카오스 신호의 분류는 제안된 CNN 모델을 이용하여 학습이 수행되었다. 2560개에 대한 학습 데이터 샘플에서 카오스의 특성을 찾고 동시에 각 에폭에서 640개의 데이터 샘플을 통해 검증되었다. 그 이후 훈련된 CNN 모델에 800개의 샘플데이터에 대해 테스트를 수행하였다. 결과는 Fig. 8에서 보여준다. 배치 사이즈는 10으로 설정하였으며, 최적화 함수의 learning rate는 0.0001로 설정하였다. Fig. 8(a), (b)에서 보면 초기부터 정확도 및 loss가 안정화되고 학습된 모델은 100 에폭에서 약 99 % 정확성을 얻었다. 이후 학습에 사용되지 않은 800개의 실험 샘플에 대해 99.7 %의 정확성을 가지고 분류하였다.
Fig. 9는 초기 가중치에 의해 설정된 첫 번째 convolution 레이어의 필터 맵을 보여준다. 각 이미지는 필터 맵과 convolution을 거쳐 이미지의 특성을 추출한다. 추출된 첫 번째 convolution 레이어의 특징 맵은 Fig. 10에 표현하였다. 공백과 같이 표현된 맵은 해당 필터에서 이미지의 특성이 추출되지 않음을 의미한다. 카오스 이미지의 특성 맵을 보면 unthresholded recurrence plot의 카오스 특성은 CNN을 통해 높은 정확도로 추정이 가능한 것으로 예측된다.
3. 결 론
이 논문은 Lyapunov exponent를 이용하여 결정론적 역학계에서 카오스 신호를 결정하고, 반복 특성을 기반으로 가시화하는 방법론을 제안하였다. 또한 제안된 간단한 CNN 모델을 이용하여 카오스 특성을 분류하였다. 이를 통해 다음과 같은 결론에 도달하였다.
(1) 시스템 파라미터의 미소 변화에 의해 카오스현상은 나타날 수 있고, 이론적 반복 특성을 고려하여 카오스 특성의 이미지 가시화가 가능하다.
(2) 제안된 카오스 이미지는 사람의 인지능력으로 정확하게 분류하기 어렵고, 이론적 방법을 통한 분류는 매우 긴 연산 시간을 필요로 한다.
(3) 반면에 CNN 모델을 활용한 방법론은 비교적 단순한 모델임에도 99 %이상의 높은 수준으로 카오스 특성을 분류하였으며, 학습된 모델에 800개의 이미지에서 수초 이내의 빠른 분류가 가능하다.
향후 추가적인 불확실성 등을 고려한 다이나믹 모델을 개발하여 다양한 조건에서 진동 및 고장 신호 분류에 대해 연구할 예정이다.
Acknowledgments
이 논문은 2020년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업 임.(NRF-2019R1I1A2A03056014)
References
-
Barrio, R., Blesa, F. and Serrano, S., 2009, Qualitative Analysis of the Rössler Equations: Bifurcations of Limit Cycles and Chaotic Attractors, Physica D: Nonlinear Phenomena, Vol. 238, No. 13, pp. 1087~1100.
[https://doi.org/10.1016/j.physd.2009.03.010]

-
de Sousa Vieira, M., 1995, Chaos in a Simple Spring-block System, Physics Letters A, Vol. 198, No. 5-6, pp. 407~414.
[https://doi.org/10.1016/0375-9601(95)00076-F]

-
Oberst, S. and Lai, J. C. S., 2011, Chaos in Brake Squeal Noise, Journal of Sound and Vibration, Vol. 330, No. 5, pp. 955~975.
[https://doi.org/10.1016/j.jsv.2010.09.009]

-
Popp, K. and Stelter, P., 1990, Stick-slip Vibrations and Chaos, Philosophical Transactions: Physical Sciences and Engineering, Vol. 332, No. 1624, pp. 89~105.
[https://doi.org/10.1098/rsta.1990.0102]

-
Wei, D., Ruan, J., Zhu, W. and Kang, Z., 2016, Properties of Stability, Bifurcation, and Chaos of the Tangential Motion Disk Brake, Journal of Sound and Vibration, Vol. 375, pp. 353~365.
[https://doi.org/10.1016/j.jsv.2016.04.022]

-
Nikias, C. L. and Mendel, J. M., 1993, Signal Processing with Higher-order Spectra, IEEE Signal Processing Magazine, Vol. 10, No. 3, pp. 10~37.
[https://doi.org/10.1109/79.221324]

-
Wu, G. C. and Baleanu, D., 2014, Discrete Fractional Logistic Map and Its Chaos, Nonlinear Dynamics, Vol. 75, No. 1-2, pp. 283~287.
[https://doi.org/10.1007/s11071-013-1065-7]

-
Sun, K. and Sprott, J. C., 2009, Dynamics of a Simplified Lorenz System, International Journal of Bifurcation and Chaos, Vol. 19, No. 04, pp. 1357~1366.
[https://doi.org/10.1142/S0218127409023688]

-
Wolf, A., Swift, J. B., Swinney, H. L. and Vastano, J. A., 1985, Determining Lyapunov Exponents from a Time Series, Physica D: Nonlinear Phenomena, Vol. 16, No. 3, pp. 285~317.
[https://doi.org/10.1016/0167-2789(85)90011-9]

-
Baek, J., Nam, J., Do, H. and Kang, J., 2016, Finite Element Analysis for Friction Noise with Respect to the Friction Curve of several Materials, Transactions of the Korean Society of Mechanical Engineers A, Vol. 40, No. 5, pp. 449~455.
[https://doi.org/10.3795/KSME-A.2016.40.5.449]

-
Nam, J., Do, H. and Kang, J., 2017, Effect of Groove Surface on Friction Noise and its Mechanism, International Journal of Precision Engineering and Manufacturing, Vol. 18, No. 8, pp. 1165~1172.
[https://doi.org/10.1007/s12541-017-0136-y]

-
Nam, J. and Kang, J., 2020, Friction-induced Vibration by Dust Effect, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 30, No. 2, pp. 201~210.
[https://doi.org/10.5050/KSNVE.2020.30.2.201]

-
Han, Y., 2019, Performance Investigation of Wall-wetting Reduction in Vehicle Engines Utilizing Piezoelectric Ultrasonic Vibrator, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 29, No. 6, pp. 794~800.
[https://doi.org/10.5050/KSNVE.2019.29.6.794]

-
Bae, S., Kim, K. and Kang, J., 2019, An Experimental Study on the Friction Noise of Interior and External Automotive Materials by Endurance Test, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 29, No. 3, pp. 347~354.
[https://doi.org/10.5050/KSNVE.2019.29.3.347]

-
Kang, J., 2018, Lyapunov Exponent of Friction-induced Vibration Under Smooth Friction Curve, Journal of Mechanical Science and Technology, Vol. 32, No. 8, pp. 3563~3567.
[https://doi.org/10.1007/s12206-018-0707-6]

-
Kang, J., 2018, Calculation of Lyapunov Exponents in Impacted Beam on Distributed Contact, Journal of Sound and Vibration, Vol. 431, pp. 295~303.
[https://doi.org/10.1016/j.jsv.2018.06.023]

-
Serweta, W., Okolewski, A., Blazejczyk-Okolewska, B., Czolczynski, K. and Kapitaniak, T., 2014, Lyapunov Exponents of Impact Oscillators with Hertz׳s and Newton׳s Contact Models, International Journal of Mechanical Sciences, Vol. 89, pp. 194~206.
[https://doi.org/10.1016/j.ijmecsci.2014.09.007]

-
Astaf'eva, N., 1996, Wavelet Analysis: Basic Theory and Some Applications, Physics-uspekhi, Vol. 39, No. 11, p. 1085.
[https://doi.org/10.1070/PU1996v039n11ABEH000177]

-
Marwan, N., Romano, M. C., Thiel, M. and Kurths, J., 2007, Recurrence Plots for the Analysis of Complex Systems, Physics Reports, Vol. 438, No. 5-6, pp. 237~329.
[https://doi.org/10.1016/j.physrep.2006.11.001]

-
He, K., Zhang, X., Ren, S. and Sun, J., 2016, Deep Residual Learning for Image Recognition, Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 770~778.
[https://doi.org/10.1109/CVPR.2016.90]

- Lim, H. K., Kim, J. B., Kwon, D. H. and Han, Y. H., 2017, Comparison Analysis of TensorFlow's Optimizer Based on MNIST's CNN Model, Journal of Advanced Technology Research, Vol. 2, No. 1, pp. 6~14.
-
Kennel, M. B., Brown, R. and Abarbanel, H. D., 1992, Determining Embedding Dimension for Phase-space Reconstruction using a Geometrical Construction, Physical Review A, Vol. 45, No. 6, p. 3403.
[https://doi.org/10.1103/PhysRevA.45.3403]

- Glorot, X. and Bengio, Y., 2010, Understanding the Difficulty of Training Deep Feedforward Neural Networks, Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, pp. 249~256.
-
He, K., Zhang, X., Ren, S. and Sun, J., 2015, Delving Deep into Rectifiers: Surpassing Human-level Performance on Imagenet Classification, Proceedings of the IEEE International Conference on Computer Vision, pp. 1026~1034.
[https://doi.org/10.1109/ICCV.2015.123]

-
LeCun, Y. A., Bottou, L., Orr, G. B. and Müller, K., 2012, Efficient Backprop, Neural Networks: Tricks of the Trade. Springer, Berlin, Heidelberg, pp. 9~48.
[https://doi.org/10.1007/978-3-642-35289-8_3]


Jaeyoung Kang is a Professor in the Department of Mechanical Engineering, Inha University. He received his Ph.D. degree in Mechanical Engineering from Purdue University in 2008. His research interests include friction noise, structural vibration and nonlinear dynamics.