다중 사이클릭 헬리콥터 진동 제어

1. 서 론

헬리콥터 진동 저감을 위한 능동 로터 제어 시스템에 대한 여러 가지 수치 해석 및 실험 연구가 진행되어 왔고, 그 중에서 Higher harmonic control(HHC) 기법이 진동과 소음 저감에 성공적으로 적용되었다⁽¹⁾. HHC는 진동과 소음 저감 능력을 보여주었지만, 다른 능동 제어 기법이 계속해서 연구되었다. HHC의 주요 단점은 작동 가능한 주파수의 제약과 소음과 진동이 동시에 줄어들지 않을 수 있다는 사실이다⁽²⁾. HHC의 가장 유망한 대안은 individual blade control(IBC)⁽³⁾이다. 현재까지 능동 피치 로드⁽⁴⁾, 능동 뒷전 플랩^(5,6), 능동 비틀림^(7~9), 능동 탭⁽¹⁰⁾, 능동 거니 플랩⁽¹¹⁾ 등의 여러 가지 개념의 IBC 작동기가 설계되고 테스트 되었다. 그 중에서 능동 뒷전 플랩이 광범위하게 연구되었고 비행시험에 이르기까지 성공적으로 시연되었다. Dieterich 등은⁽⁶⁾ 능동 플랩과 시간 영역 제어 알고리즘을 적용한 BK117 항공기에서 최대 80 % 진동 저감 성능을 보여주었다. 그러나 블레이드에 뒷전 플랩 작동기를 구현하기 위해서는 기계적 부품이 추가로 필요하며, 블레이드 회전에 의한 원심력 환경에서 원활한 작동을 보장하기 위한 여러 가지 조치가 필요하다. 반면에 표면 변형에 의해 유발되는 비틀림을 이용하는 능동 비틀림 제어 로터는 기계적 부품이 필요하지 않다.

압전 재료를 이용한 active fiber composite(AFC) 또는 macro fiber composite(MFC)가 축소 능동 비틀림 로터에서 표면 변형을 유발시키기 위한 작동기로 활용되어 왔다. 블레이드 표면에 부착된 작동기에 전기장이 부가되면 작동기의 변형이 발생되고 이를 활용하여 블레이드의 비틀림 변형을 생성한다. AFC를 기반으로한 ATR(active twist rotor) 연구에서는 NASA langley transonic dynamics tunnel(TDT)의 풍동시험을 통해 고정부 진동하중을 60 % ~ 95 % 감소시켰다⁽⁷⁾. 개-루프 제어 방법이 적용되었고 작동 주파수는 단일 하모닉이었다. 여러 가지 제어 진폭으로 3P (3/rev), 4P 및 5P 작동 주파수에 대해 제어 위상 스윕이 수행되었으며, 그 결과를 통해 최상의 작동 주파수, 진폭 및 제어 위상을 식별 할 수 있었다.

독일 DLR(german aerospace center)에서는 1995년부터 MFC 작동기를 이용한 능동 비틀림 로터에 대한 연구 활동을 수행해 오고 있다⁽¹²⁾. 2009년부터 국제 공동연구인 STAR(smart twisting active rotor) 프로그램으로 확장하여 진행 중, 예비 시험 과정에서 MFC 작동기의 피로 문제가 발생하여 초기 풍동시험이 중단된 바 있다⁽⁹⁾. 이에 대한 원인 분석을⁽¹³⁾ 통해 작동기 및 블레이드 설계 개선이 수행되었다⁽¹⁴⁾. 현재 새로운 블레이드 제작 및 풍동시험을 추진 중이다.

진동 저감을 위한 비틀림 작동에 있어서 가장 널리 사용되는 방식은 하모닉(harmonic) 작동을 기반으로 한다. 단일 하모닉 제어의 경우 진폭 및 위상 스윕을 여러 가지 가진 주파수에 대해서 수행한다. 그런 다음 진동 저감 성능이 가장 우수한 제어 입력 주파수, 진폭 및 위상을 식별할 수 있다. 이 방법은 다중 하모닉 제어 방식으로 확장할 수 있다. 다중 하모닉을 이용한 능동 비틀림 작동은 성능 향상, 진동 및 소음 저감 시뮬레이션 연구에 적용된 바 있다^(15,16). 다중 하모닉 제어 입력에 단일 하모닉 제어와 같은 진폭, 위상 스윕 방법을 적용할 경우 고려해야할 경우의 수가 매우 크게 증가한다. 또 다른 접근 방법은 비 하모닉(non-harmonic) 형태의 비틀림 작동이다. Fogarty 등은⁽¹⁷⁾ 시작 방위각 위치, 지속시간 및 진폭으로 특정 형상의 계단 파형 입력을 소음 저감에 적용한 바 있다. Jain 등은⁽¹⁸⁾ 전진면 영역에서만 2P 하모닉 입력을 적용할 경우 성능 향상에 효과적임을 보여주었다. 그리고 단순한 단일 하모닉 입력과 분할된 스텝 함수를 성능 향상 및 진동 감소를 위해 최상의 작동 시나리오를 도출하기 위해 particle swarm genetic 알고리즘을 사용한 연구도 수행된 바 있다⁽¹⁹⁾.

일반적으로 단일 하모닉 제어에 비해 다중 하모닉 제어 또는 비 하모닉 제어를 적용하면 보다 우수한 진동 저감 성능을 얻을 수 있을 것으로 예상된다. 그러나 다중 하모닉 또는 비 하모닉 제어 기법을 적용할 경우 알고리즘에 따라 최적의 해를 얻기 위한 계산량이 크게 증가할 수 있다. 헬리콥터의 진동 특성이 선형적인 경우 최적 제어 기법을 적용하여 상대적으로 적은 계산을 통해 최적 제어 입력을 도출할 수 있다. 또한 최적 제어 기법은 비행 시험 데이터를 처리하여 피드백 제어기를 설계할 때 효과적으로 사용할 수 있다. 다중 사이클릭 헬리콥터 진동 제어 알고리즘 유도 및 검토는 Johnson이⁽²⁰⁾ 수행하였고, 이를 활용한 수치 해석 시뮬레이션 연구는 Chopra와 McCloud가⁽²¹⁾ 소개한 바 있다. 다중 사이클릭 진동제어는 헬리콥터를 선형(linear), 준정적(quasi-steady), 주파수 영역(frequency domain) 모델로 표현하는 것에 기반을 둔다. 2차 성능 함수를 최소화하기 위한 최적 제어 해는 간단한 선형 대수로 계산할 수 있다. 그리고 개-루프 또는 폐-루프 제어 시스템의 형태로 구현할 수 있다.

이 연구에서는 동적으로 스케일링된 Bo-105 축소 로터 모델에 다중 사이클릭 제어 기법을 적용하여 시뮬레이션을 수행하고 진동 제어 성능을 분석하였다. 먼저 진동 제어를 수행할 비행 조건을 선정하여 기본 데이터를 생성하고, 시스템 식별을 수행한 다음 최적 제어 해를 도출하여 개-루프 시스템에서 진동 저감 성능을 검토하였다. 폐-루프 시스템으로 운용 가능성을 검토하기 위해 MATLAB/CAMRAD II(comprehensive analytical model of rotorcraft aerodynamics and dynamics II) 연계 해석 시뮬레이션을 수행하였다. 또한 최적 제어 입력 시 로터 발생되는 로터 시스템의 동적 특성 변화에 대해서도 고찰하였다.

2. 다중 사이클릭 진동 제어

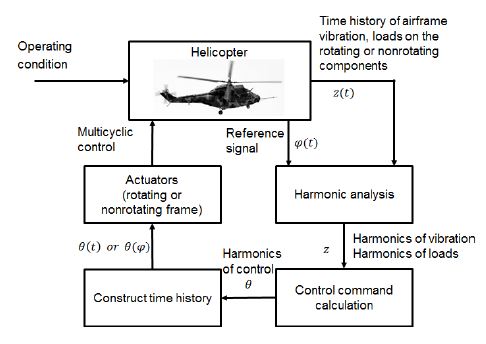
다중 사이클릭 진동제어 시스템의 개략도는 Fig. 1과 같다. 이 시스템은 회전부 또는 비회전부 구성 요소의 진동을 최소화하는 것을 목적으로 한다. 정상 상태 비행에서 헬리콥터 진동 하중은 주기적이며, 회전부에서는 1P(1/rev, one per revolution), 비회전부에서는 NP(N/rev, N은 블레이드 개수)의 기본 주파수를 가진다. 따라서 진동을 완화시키기 위해 필요한 제어 입력 또한 주기적이며 제어 시스템에서 입력 및 출력의 하모닉 성분들을 처리할 수 있다⁽²⁰⁾.

Fig. 1

Schematic of multicyclic vibration control system

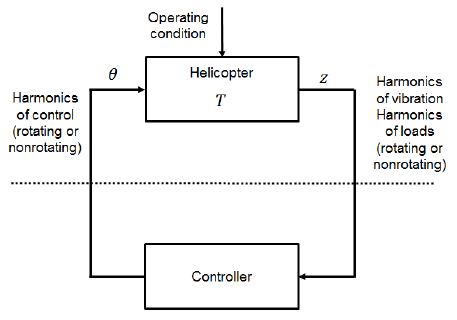
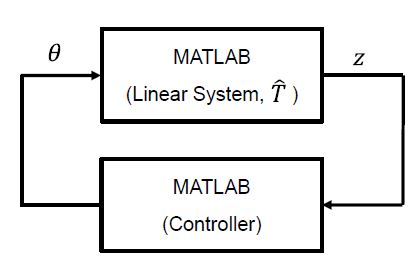
다중 사이클릭 진동 제어 시스템에서는 진동의 하모닉 성분들을 제어기에 제공하기 위해서 헬리콥터의 응답에 대한 하모닉 분석이 수행되어야 하고, 주파수 영역에서 계산된 제어 입력을 시간영역 신호로 구성하여 작동기에 제공되어야하며, 작동기의 동특성 또한 고려되어야한다. 모든 기능 중에서 다중 사이클릭 제어기의 진동 제어 성능에 중점을 두기 위하여 제어기를 제외한 구성 요소를 헬리콥터 모델에 포함시키면 Fig. 2와 같이 단순화된 형태로 표현할 수 있다.

Fig. 2

Simplified schematic of multicyclic vibration control system

2.2 오프라인 시스템 식별

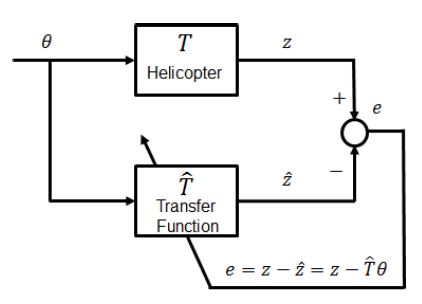
시스템 식별은 Fig. 3과 같이 헬리콥터 모델 T에 대한 수학적 모델 $$ \widehat{T}$$를 구성하는 프로세스이다. 오프라인으로 식별 한다는 것은 시스템을 구성하는 파라미터가 일정하다는 것을 의미한다. 즉, 로컬 모델에는 적용할 수 없고, 글로벌 모델에 적용 가능한 방법이다. 시스템 식별을 위해 미리 정해진 제어 입력을 사용하여 N_t개의 측정 세트를 확보해야 한다. 시스템 식별에 필요한 최소의 독립적인 측정 개수는 제어 입력의 개수와 같다. 시스템 식별 오차는 실제 시스템에서 측정된 출력값과 모델을 이용해 추정된 출력 간의 차이로 정의된다.

$\[ e=z-\widehat{z}=z-\widehat{T}\theta \]$

(2)

Fig. 3

System identification

여기서, z는 측정된 출력이고 $$ \widehat{z}$$는 추정된 출력이다. N_t개의 측정 세트로부터 계산된 N_t개의 오차 벡터를 합쳐서 오차 행렬 E를 다음과 같이 나타낼 수 있다.

$\[ E=Z-\widehat{T}\Theta \]$

(3)

여기서, Z는 N_t 개의 열벡터 z로 구성된 (P×N_t) 크기의 출력 행렬이고, Θ는 N_t개의 열벡터 θ로 구성된 (M×N_t) 크기의 입력 행렬이다. 오프라인 시스템 식별은 최소 제곱 오차 방법으로 수행할 수 있다. 오차 행렬의 j-번째 행의 제곱합을 고려해보자.

$\[ S_j\begin{array}{l}=e_j{e}_j^T\\ =\sum _{n=1}^N{\left(z_{jn}-t_{jn}{\theta }_n\right)}^2=\left(z_j-t_j\theta \right){\left(z_j-t_j\theta \right)}^T\\ \left(n=1,\dots ,N\right)\end{array} \]$

(4)

여기서, 아래첨자 j는 출력 센서의 번호에 해당한다. e_j는 오차 행렬 E의 j번째 행, z_j는 응답 행렬 Z의 j번째 행, t_j는 전달함수 $$ \widehat{T}$$의 j번째 행이다. S_j를 최소화시키는 해 t_j는 ∂S_j/∂t_j= 0으로 구할 수 있다.

$\[ t_j=z_j{\Theta }^T{\left(\Theta {\Theta }^T\right)}^{-1} \]$

(5)

계산된 t_j(j= 1,…,P)를 합치면 전달함수를 다음과 같이 얻게 된다.

$\[ \widehat{T}=Z{\Theta }^T{\left(\Theta {\Theta }^T\right)}^{-1} \]$

(6)

3. 진동 제어 시뮬레이션

헬리콥터 모델을 시뮬레이션하기 위하여 가상의 Bo-105 축소 로터 모델을 CAMRAD II 통합해석 코드로 구현하였다. 대표적인 Bo-105 로터의 축소 모델인 HART II 로터 모델을 수정하여 구성하였다. 반경 2 m, 선형 비틀림 8°, 코드 길이 0.121 m, NACA 23012에어포일을 가지고, 1041 r/min (1P = 17.35 Hz)의 속도로 회전한다. Table 1은 로터 특성과 계산에 사용된 대기 조건을 보여준다. HART II 모델과 다른 특성은 시계 방향으로 회전하고, 관절형 허브로 3.5 %R 위치에 플랩/래그 힌지를 가지며 프리콘이 없다는 점이다.

Table 1

Properties of the rotor and atmospheric conditions

블레이드 구조는 15개의 보 요소로 구성하였으며 각 요소는 15개의 자유도를 가진다. 블레이드 공기역학 특성은 양력선(lifting line) 이론에 기반한 C81 테이블로 모델링하였고, ONERA EDLIN 비정상 공기역학 모델이 적용되었다. 17개의 블레이드 공력 패널을 사용하고 자유후류 해석 기법을 적용하여 공력하중을 계산하였다. 트림 해석은 15° 방위각 간격으로 수행되었다.

3.2 비틀림 작동

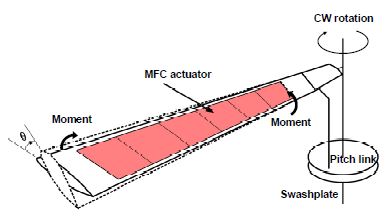
블레이드 상부 및 하부 표면에 MFC 작동기가 부착되어 있어 전기장이 부가되면 비틀림 모멘트와 탄성 비틀림 변형을 생성한다. CAMRAD II에서 이러한 능동 작동 요소를 직접 모델링하는 것은 불가능하다. 따라서 Fig. 4와 같이 작동기에 부가되는 전압에 따라 유발되는 비틀림 모멘트가 블레이드 구조 요소에 작용하도록 CAMRAD II에서 모델링하여 시뮬레이션에 사용하였다. 능동 작동기가 부착된 구조 요소의 경계, 즉 가장 안쪽과 가장 바깥쪽 양쪽에서 비틀림 모멘트가 작용하도록 모델링하였다. 블레이드에 부가되는 제어 입력은 다음과 같이 정의된다.

$\[ A\left(V\right)=A_0+A_m\cos \left(m\psi -\varphi \right) \]$

(15)

Fig. 4

Mechanism of twist actuation

여기서, A₀는 정적 전압 오프셋, A_m은 작동 전압 진폭, ψ는 방위각, ϕ는 작동 위상각, m은 하모닉 차수를 나타낸다. 양의 전압이 부가될 경우 블레이드 압전(leading edge)이 위로 변형되는 nose-up 모멘트가 발생한다. 부가된 전압에 의해 발생되는 비틀림 모멘트의 관계는 정적 또는 준정적 테스트를 통해 식별된다. 블레이드 루트 부를 고정한 다음 모든 MFC 작동기를 작동하여 블레이드 팁에서 발생된 비틀림 각도를 측정한 결과와 간단한 보 이론을 이용하여 작용된 모멘트 값을 계산한다. 이 연구에서는 참고문헌 9의 MFC 작동기 성능과 유사하게 해석 모델에 적용하였다. 부가 전압에 의해 발생되는 비틀림 모멘트는 0.005 Nm/V를 적용하고, MFC 작동기의 허용 작동 전압은 –500 V ~ +1100 V, 오프셋 전압은 +300 V, 최대 작동 진폭은 800 V로 가정하였다.

3.3 시뮬레이션 데이터 생성

다중 사이클릭 진동제어 시뮬레이션을 위해 응답 출력 벡터 z와 제어 입력 벡터 θ를 정의해야 한다. 그리고 제어되지 않은 응답 z₀뿐만 아니라 시스템식별을 위한 N_t개의 입출력 데이터 세트가 필요하다. 4-블레이드 로터의 경우 비회전부에서의 주요 진동 성분은 4P 하모닉이므로 4P 비회전 허브 하중 및 모멘트의 코사인, 사인 성분 12개를 출력 벡터로 지정하였다.

$\[ z=\begin{array}{l}\left[F_{x,4C}{F}_{y,4C}{F}_{z,4C}{M}_{x,4C}{M}_{y,4C}{M}_{z,4C}\right.\\ {\left.F_{x,4S}{F}_{y,4S}{F}_{z,4S}{M}_{x,4S}{M}_{y,4S}{M}_{z,4S}\right]}^T\end{array} \]$

(16)

다중 사이클릭 제어 입력의 경우 2P, 3P, 4P 하모닉 코사인, 사인 성분 6개를 사용하였다.

$\[ \theta ={\left[\mathrm{c}\mathrm{o}\mathrm{s}2\mathrm{P} \mathrm{s}\mathrm{i}\mathrm{n}2\mathrm{P} \mathrm{c}\mathrm{o}\mathrm{s}3\mathrm{P} \mathrm{s}\mathrm{i}\mathrm{n}3\mathrm{P} \mathrm{c}\mathrm{o}\mathrm{s}4\mathrm{P} \mathrm{s}\mathrm{i}\mathrm{n}4\mathrm{P}\right]}^{\mathrm{T}} \]$

(17)

오프셋 전압만 부가되는 제어되지 않은 응답 z₀ 및 오프셋 전압 및 30 %, 60 %, 80 % 3가지 진폭으로 6가지 독립적인 비틀림 작동(cos2P, sin2P, cos3P, sin3P, cos4P, sin4P)을 적용한 18가지 구동 조건을 앞서 설명한 하강 비행 조건에 적용하여 기본 시뮬레이션 데이터를 생성하였다. 각 구동 조건별 부가된 전압 및 모멘트를 Table 2에 정리하였다.

Table 2

Applied moments for baseline cases

3.4 선형성 검토

다중 사이클릭 헬리콥터 진동제어 시스템은 헬리콥터를 선형, 준정적, 주파수 영역 모델로 표현하는 것에 기반을 둔다. 따라서 시스템이 선형일 때 제어 성능을 발휘할 수 있다. 그러므로 헬리콥터 시스템의 선형성을 확인해야 한다. 제어 입력을 구성하는 사이클릭 입력 항목들에 대한 개별 가진에 대한 응답 특성을 통해 선형성을 확인할 수 있다. 선형시스템의 특성을 이용하여 두 가지 점검항목을 선정할 수 있다. 다음의 두 가지 특성이 충족될 때 임의의 진폭과 방향으로 제어 가능한 진동 하중을 생성할 수 있다.

(1) 동일한 개별 사이클릭 입력에 의해 생성된 진동의 크기는 입력 진폭에 비례해야한다.

(2) 동일 주파수의 코사인파 가진과 사인파 가진에 의해 발생되는 진동은 90°의 위상차를 가져야한다.

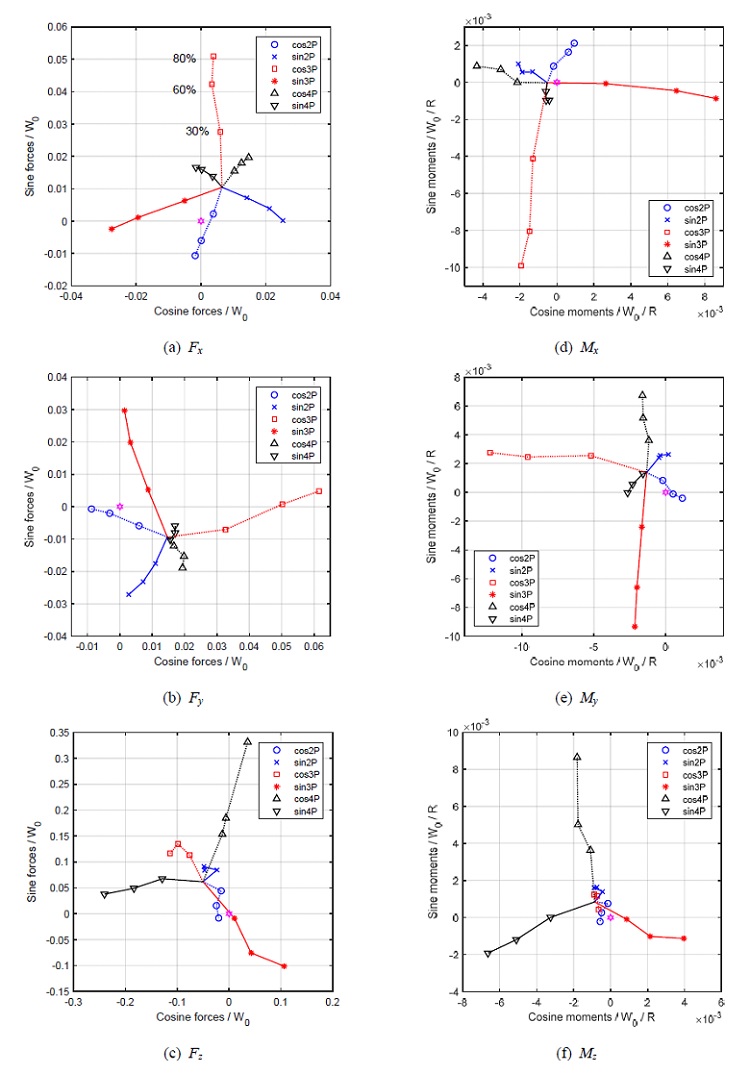
독립적인 제어 입력에 따른 비회전 허브 하중과 모멘트 변화를 Fig. 5에 나타내었다. F_x 응답은 매우 선형적으로 보인다. 가진 진폭이 0 %에서 80 %로 증가함에 따라 출력 응답의 크기가 증가한다. 2P, 4P 주파수로 가진한 경우, 사인 파형의 가진에 의해 유발되는 진동하중은 코사인 파형의 가진에 의해 유발되는 진동하중에 비해 약 90°의 위상 지연을 보여준다. 3P 주파수로 가진한 경우, 코사인파 가진이 사이파 가진에 비해 약 110°의 위상차를 나타내지만 cos3P와 sin3P의 조합으로 임의의 크기와 방향으로 진동하중을 생성 가능하다. 따라서 2P, 3P, 4P의 다중 사이클릭 제어 입력으로 F_x진동 하중을 상쇄할 수 있는 제어 가능한 진동 하중을 생성할 수 있다. F_y의 경우 4P 가진에 대한 응답은 진폭이 증가함에 따라 비선형적 특성을 보여주지만 2P, 3P 입력에 대한 반응 특성이 좋아서 제어 가능하다고 판단된다. F_z의 경우에는 2P, 3P 가진에 의한 응답이 비선형적이어서 2P, 3P 성분의 사이클릭 입력으로는 진동 제어가 불가능해 보인다. 그러나 4P 가진에 따른 응답 특성은 진동 제어에 충분히 활용 가능할 것으로 보인다. M_x, M_y 응답은 특이사항이 없다. M_z의 경우에도 2P, 3P 가진에 따른 응답 특성의 비선형성이 크지만 4P 가진에 의한 응답은 선형에 가까워서 제어 가능하다고 보인다. 전체적으로 F_z및 M_z 응답에서 비선형 특성이 관찰되지만, 다중 사이클릭 입력을 조합하여 진동을 상쇄시킬 제어 가능한 하중을 유발시킬 수 있을 것으로 기대된다.

Fig. 5

Responses to independent control input

생성된 진동 하중이 제어되지 않은 진동의 진폭과 같고 위상이 반대인 경우 원치 않는 진동을 상쇄시킬 수 있다. 그러나 반대 위상의 상쇄 진동을 유발시킬 수 있더라도 작동기의 운용범위 내에서 충분한 진폭을 만들어내지 못할 경우에는 진동 저감 효과가 크지 않다. 따라서 제어되지 않은 진동의 진폭만큼 충분한 제어 하중을 생성시킬 수 있는지도 확인해야 한다. Fig. 5에 진동이 ‘0’인 상태가 별표(✡)로 표시되어 있다. 80 % 미만의 진폭으로 생성된 진동 하중의 크기가 제어되지 않은 상태의 진동보다 충분히 크므로 작동기 운용 범위 내에서 제어되지 않은 진동을 상쇄시킬 충분한 제어 진동 하중을 생성시킬 수 있을 것으로 예상된다.

3.6 개-루프 제어

단순화된 시스템에 대한 시뮬레이션을 수행하기 위해서 W_z= I, W_Δθ= W_θ= 0로 가정하였다. 최적 제어 입력은 식 (11)을 이용해서 계산하며, 다음과 같은 결과를 얻었다.

$\[ {\theta }_{opt}=\begin{array}{l}{\left[40.9 10.5 5.3 11.9 -4.6 -7.4\right]}^T\\ \left(\%\mathrm{a}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{i}\mathrm{t}\mathrm{u}\mathrm{d}\mathrm{e}\right)\end{array} \]$

(19)

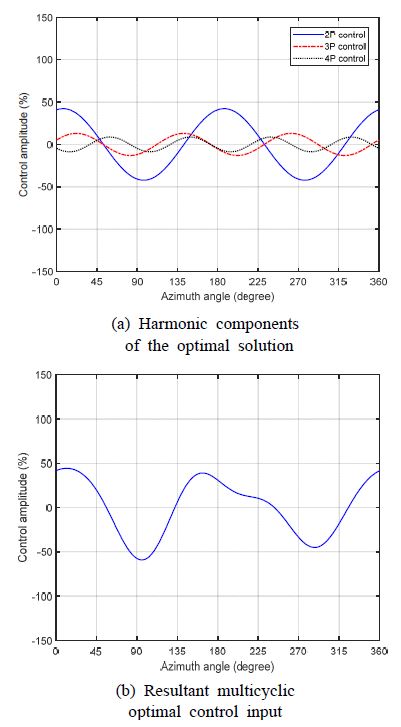
다중 사이클릭 최적 제어 입력의 2P, 3P, 4P 하모닉 성분은 Fig. 6(a)와 같고, 모든 성분이 합쳐진 최적 제어 입력의 파형은 Fig. 6(b)에 나타내었다. 2P, 3P 및 4P 하모닉 성분의 진폭은 각각 42.4 %, 13.0 % 및 8.7 % 이다. 통합된 최적제어 입력에서의 최대 및 최소값은 각각 44.4 % 및 –59.1 % 이다. 이는 작동 전압 +354.9 V 및 – 472.6 V에 해당한다. 최적 제어 입력이 MFC 작동기의 허용 작동 전압 범위를 초과하지 않으므로 추가적인 조치 없이 적용 가능하다.

Fig. 6

Optimal control input for 2P, 3P, 4P multicyclic control

진동 제어 성능을 분석하기 위해 Fig. 7과 같이 두 가지 종류의 시뮬레이션이 수행되었다. 하나는 오프라인으로 식별된 시스템 모델을 이용한 선형시스템 예측이고, 다른 하나는 최적제어 입력을 사용한 CAMRAD II 계산이다. 진동 하중 출력 벡터는 12개의 성분으로 구성되어 있어 어떤 성분은 감소하고 다른 성분이 증가하는 경우 제어 성능을 평가하기 어렵다. 이에 진동 제어 성능을 비교하기 위해 12개의 출력 성분들을 무차원화된 하나의 진동 지수(vibration index, VI)로 나타내어 진동의 크기 변화를 비교하였다.

$\[ VI\begin{array}{l}\frac{=\sqrt{{\left(F_{x,4}\right)}^2+{\left(F_{y,4}\right)}^2+{\left(F_{z,4}\right)}^2}}{W_0}\\ +\frac{\sqrt{{\left(M_{x,4}\right)}^2+{\left(M_{y,4}\right)}^2+{\left(M_{z,4}\right)}^2}}{{RW}_0}\end{array} \]$

(20)

Fig. 7

Open-loop control simulation

여기서, (F_x,4)²= (F_x,4C)²+(F_x,4S)², 힘과 모멘트는 각각 W₀ 와 RW₀ 에 의해 무차원화된다. 각 하중 성분별로 가중치를 적용하여 VI를 구성할 수도 있으나, 이 연구에서는 가중치는 고려하지 않았다. 선형시스템 예측을 통해서는 96 %의 VI 감소가 예측되었으나, CAMRAD II 계산 결과에서는 93 %의 VI 감소가 확인되었다. 이는 헬리콥터 모델이 완벽하게 선형은 아니기 때문이다.

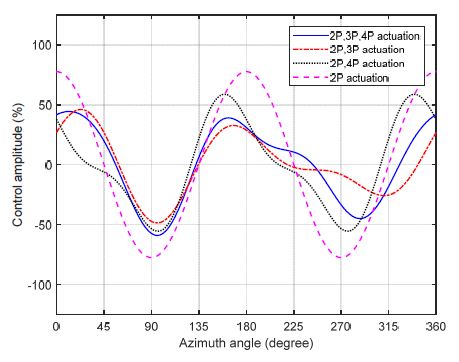
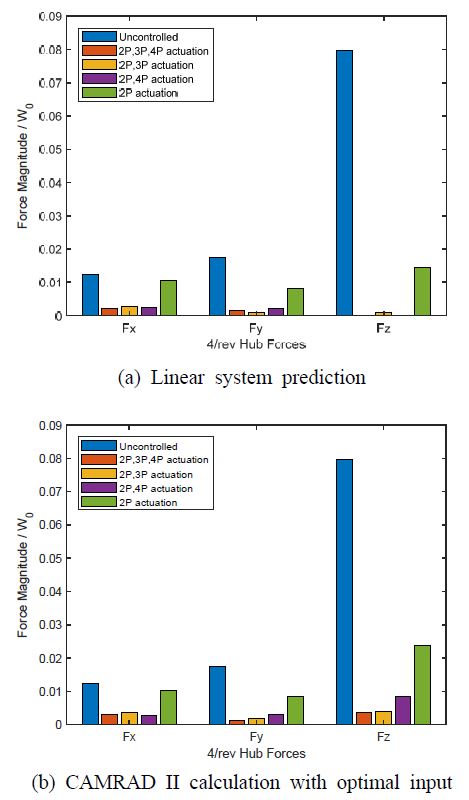
Fig. 6을 살펴보면 2P 주파수 성분이 최적 제어 입력의 주요 구성 요소임을 알 수 있다. 따라서 2P 하모닉만 사용하거나 2P, 3P 또는 2P, 4P 조합으로 제어 입력을 구성한 경우에도 진동 저감 성능이 유지될 것으로 예상된다. 이에 Table 3과 같이 4종류의 다중 사이클립 제어 입력 조합에 대한 시뮬레이션을 수행하여 진동 저감 성능을 비교해 보았다. Case 1이 진동 저감에 가장 효과적이지만 case 2와 case 3도 우수한 성능을 보여준다. 단일 하모닉 성분만 사용한 case 4의 경우에는 상대적으로 진동 저감 성능이 낮다. 전반적으로 단일 하모닉 입력 보다는 다중 사이클릭 입력이 진동 저감에 효과적인 결과를 보여준다.

Table 3

Vibration reduction performance according to multicyclic control input changes

Table 3의 4가지 경우에 대한 최적 제어 입력은 Fig. 8과 같다. 전체적인 파형은 유사한 형태를 보여준다. (+) 제어 입력이 부가되는 작동 범위는 방위각 약 135° ~ 225° 및 320° ~ 45° 범위에 해당한다. 즉 로터디스크 전방과 후방 위치에서 nose-up 모멘트가 크게 부가되고, 전진면과 후퇴면에서는 nose-down 모멘트가 부가된다. 단일 하모닉 입력에 비해 고차의 하모닉 가진 성분이 추가된 경우 제어 입력으로 부가되는 모멘트의 크기가 상대적으로 작다.

Fig. 8

Optimal control solutions according to multicyclic control input changes

Fig. 9는 최적 제어 입력에 대한 선형 시스템 예측 결과와 CAMRAD II 계산 결과 중 허브 하중 성분을 나타낸 그래프이다. F_x와 F_y는 CAMRAD II 계산 결과가 예측 결과와 비슷하지만, F_z는 상대적으로 차이가 크다. 즉, F_z 성분이 선형시스템을 이용한 진동 저감 특성 예측과 진동 제어가 가장 어려운 성분이다. 이는 Fig. 5에서 살펴보았듯이 F_z가 상대적으로 비선형 특성이 큰 특성을 가지고 있기 때문이다.

Fig. 9

Nonrotating hub force responses according to multicyclic control input changes

3.7 폐-루프 제어

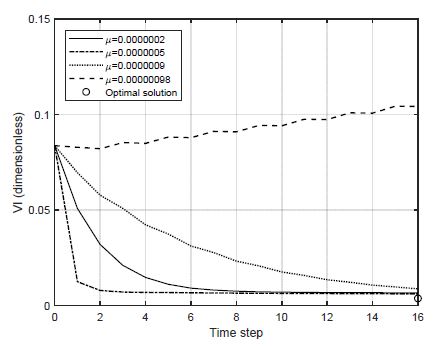
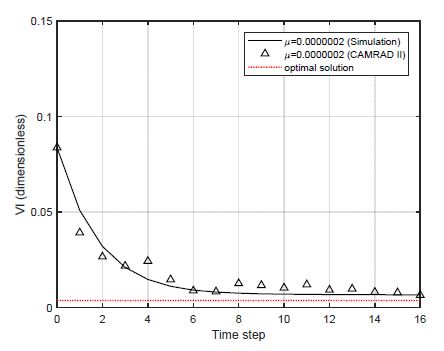
경사하강법을 적용한 폐-루프 제어 시뮬레이션을 수행하였다. 경사하강법 알고리즘을 적용할 때 가장 중요한 사항 중 하나는 학습률 μ를 선택하는 것이다. 적정 학습률에 대한 대략적인 초기 추정값은 최적 제어 해와 첫 번째 스텝에서의 순간 기울기 값을 사용하여 계산할 수 있다. 그런 다음 Fig. 10과 같이 선형시스템 폐루프 시뮬레이션을 수행하여 학습률 변화에 따른 시스템 응답을 분석한다. 학습률 변화에 따른 VI 값 변화를 Fig. 11에 나타내었다. μ > 0.00000098인 경우 시스템이 발산하고, 그보다 작은 학습률을 사용한 경우에는 수렴한다. μ가 0.0000002에서 0.0000005로 증가함에 따라 수렴 속도가 크게 증가하였고, 2번의 스텝 만에 VI 최소값에 수렴하였다. μ가 0.0000005에서 0.0000009로 증가하면 시스템 반응 속도가 느려진다. 학습률이 커짐에 따라 제어 입력의 변동이 크게 발생하기 때문이다. 시스템의 반응 속도와 제어 입력의 변화 수준을 고려하여 0.0000002를 MATLAB/CAMRAD II 연계 폐-루프 시뮬레이션에 대한 학습률 값으로 선정하였다.

Fig. 10

Closed-loop simulation using the identified linear system

Fig. 11

Vibration reduction performance according to learning rate

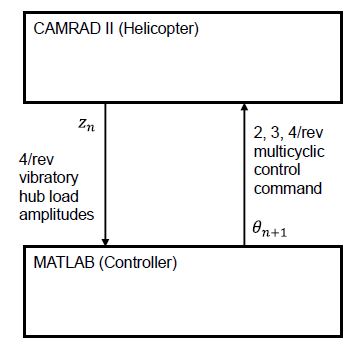
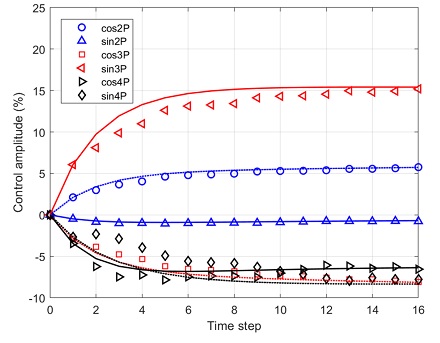
MATLAB/CAMRAD II 연계 폐-루프 제어 시뮬레이션은 Fig. 12에 도식한 것처럼 CFD(computational fluid dynamics)/CA(comprehensive analysis) loose coupling 해석과⁽²²⁾ 동일한 방법으로 수행된다. 현재 시간 스텝에서 비회전 허브 하중의 4P 하모닉 성분이 CAMRAD II에서 계산되어 MATLAB으로 제공되며, 2P, 3P, 및 4P 다중 사이클릭 제어 명령이 식 (14)를 이용하여 계산되고 CAMRAD II에 제공된다. 시간 스텝 0에서 16까지의 시뮬레이션 결과는 Fig. 13과 Fig. 14와 같다. 약간의 차이가 있으나, CAMRAD II 연계 시뮬레이션 결과는 선형시스템 예측 결과와 매우 유사하다. 진동은 10시간 ~ 15시간 스텝 내에 최적의 응답 수준으로 감소되었다. CAMRAD II 연계 시뮬레이션으로 계산된 제어 입력 또한 선형시스템 예측 결과와 유사하다. 학습률이 작기 때문에 제어 입력의 변화가 크기 않고 작동기에 과도한 입력 변화를 초래하지 않는다. 시간 단계가 계속 증가하면 제어 입력은 최적제어 입력 값에 수렴하게 된다.

Fig. 12

MATLAB/CAMRAD II coupled closed-loop simulation

Fig. 13

Vibration reduction performance calculated by MATLAB/CAMRAD II coupled simulation

Fig. 14

Control command history calculated by MATLAB/CAMRAD II coupled simulation

글로벌 모델의 경우 식 (9)로 계산된 최적 제어 입력 값으로 개-루프 제어를 수행하는 것이 가장 단순한 방법이다. 그러나 많은 경우 시스템이 비선형 특성을 가지며, 시스템 잡음, 측정 잡음 등으로 인한 시스템 식별 오차가 존재하고, 또한 항공기 운용 조건이 변경되면 시스템 모델이 변화하게 된다. 이러한 시스템 모델 변화에 대처하기 위해서는 폐-루프 제어 방식이 유용하다. 항공기 운용 조건 변화에 따라 시스템 변화가 있을 경우에 대한 진동 제어는 이 논문에서는 다루고 있지 않지만, 경사하강법에 기반한 폐-루프 제어기를 확장하여 시스템 변화를 고려한 제어기를 설계할 수 있다. 또한 학습률을 조절하여 폐-루프 시스템의 동적 반응 속도를 조절할 수 있어서 제어기의 적용과 해제 시 발생되는 과도 응답 특성을 사용자가 조절 가능한 장점이 있다.

4. 결 론

다중 사이클릭 제어 기법을 능동 비틀림 제어 로터에 적용하여 개-루프 및 폐-루프 진동제어 대한 시뮬레이션 연구를 수행하였다. CAMRAD II를 사용하여 생성된 하강 비행 조건에 대한 데이터는 완벽한 선형시스템은 아니지만 선형 최적 제어 이론을 적용할 수 있다. 다중 하모닉 제어 입력을 사용할 경우 단일 하모닉 제어 입력을 사용하는 것에 비해 우수한 진동 저감 성능을 얻을 수 있다. MATLAB/CAMRAD II 연계 폐-루프 시뮬레이션 결과는 선형 시스템 예측 결과와 유사하다. 따라서 선형 시스템 시뮬레이션을 통해 폐-루프 제어기를 설계하여 진동제어 시스템에 적용할 수 있다.

Acknowledgments

이 연구는 산업통상자원부 소형무장헬기 연계 민수헬기 핵심기술개발사업(과제번호: 10053157)과 한국항공우주연구원 자체연구사업의 지원으로 수행되었습니다.

References

• Gmelin, B. L., Heller, H., Mercker, E., Philippe, J. J., Preisser, J. S. and Yu, Y. H., 1995, The HART Programme - A Quadrilateral Cooperative Research Effort, American Helicopter Society 51st Annual Forum Proceedings, Fort Worth, TX, USA, pp. 695~709.
• Kessler, C., 2011, Active Rotor Control for Helicopters: Motivation and Survey on Higher Harmonic Control, CEAS Aeronautical Journal, Vol. 1, No. 1-4, Article no. 3. [https://doi.org/10.1007/s13272-011-0005-9]
• Kessler, C., 2011, Active Rotor Control for Helicopters: Individual Blade Control and Swashplateless Rotor Designs, CEAS Aeronautical Journal, Vol. 1, No. 1-4, Article no. 23. [https://doi.org/10.1007/s13272-011-0001-0]
• Jacklin, S. A., Blaas, A., Swanson, S. M. and Teves, D., 1995, Second Test of a Helicopter Individual Blade Control System in the NASA Ames 40-by-80 feet Wind Tunnel, In American Helicopter Society 2nd International Aeromechanics Specialists Conference Proceedings, Bridgeport, CT.
• Straub, F. K., Anand, V. R., Lau, B. H. and Birchette, T. S., 2018, Wind Tunnel Test of the SMART Active Flap Rotor, Journal of the American Helicopter Society, Vol. 63, No. 1, pp. 1~16. [https://doi.org/10.4050/JAHS.63.012002]
• Dieterich, O., Rabourdin, A., Maurice, J.-B. and Konstanzer P., 2015, Blue Pulse TM: Active Rotor Control by Trailing Edge Flaps at Airbus Helicopter, 41st European Rotorcraft Forum Proceedings, Munich, Germany.
• Wilbur, M. L., Mirick, P. H., Yaeger Jr., W. T., Langston, C. W., Cesnik, C. E. S. and Shin, S., 2002, Vibratory Loads Reduction Testing of the NASA/ARMY/MIT Active Twist Rotor, Journal of the American Helicopter Society, Vol. 47, No. 2, pp. 123~133. [https://doi.org/10.4050/JAHS.47.123]
• Hoffmann, F., Opitz, S. and Riemenschneider, J., 2009, Validation of Active Twist Modeling on Whirl Tower Tests, in American Helicopter Society 65th Annual Forum Proceedings, Graphvine, TX, USA.
• Lim, J. W., Boyd, D. D., Jr., Hoffmann, F., Van der Wall, B. G., Kim, D.-H. et al., 2014, Aeromechanical Evaluation of Smart-twisting Active Rotor, in 40th European Rotorcraft Forum Proceedings, Southampton, U.K.
• Kobiki, N., Tanabe, Y., Aoyama, T., Kim, D.-H., Kang, H. J. et al., 2019, Design, Analysis and Prototyping of Active Tab Rotor, Transactions of the Japan Society for Aeronautical and Space Sciences, Vol. 62, No. 2, pp. 64~74. [https://doi.org/10.2322/tjsass.62.64]
• Kim, T., Kim, D.-H. and Paek, S.-K., 2015, Active Gurney Flap Design Modification for High Speed Operation and Natural Frequency Estimate, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 25, No. 10, pp. 667~676. [https://doi.org/10.5050/KSNVE.2015.25.10.667]
• Buter, A. and Breitbach, E., 1995, The Main Sources of Helicopter Vibration and Noise Emissions and Adaptive Concepts to Reduce Them, EUROMECH 341 Smart Structures and Materials, Giens, France.
• Kalow, S., Opits, S., Riemenschneider, J. and Hoffmann, F., 2016, Results of a Parametric Study to Adapt Structural Properties and Strain Distribution of Active Twist Blades, Proceedings of the American Helicopter Society 72nd Annual Forum, West Parm Beach, Florida, USA.
• Kalow, S., Van de Kamp, B., Keimer, R. and Riemenschneider, J., 2019, Next Generation Active Twist Helicopter Rotor Blade - Simulated Results Validated by Experimental Invetigation, Proceedings of the European Rotorcraft 45th Forum, Warsaw, Poland.
• Zhang, Q., Hoffmann, F. and Van der Wall, B. G., 2009, Benefit Studies for Rotor with Active Twist Control Using Weak Fluid-structure Coupling, Proceeding of the European Rotorcraft 35th Forum, Hamburg, Germany.
• Bailly, J. and Delrieux, Y., 2009, Improvement of Noise Reduction and Performance for a Helicopter Model Rotor Blade by Active Twist Actuation, Proceedings of the European Rotorcraft 35th Forum, Hamburg, Germany.
• Fogarty, D. E., Wilbur, M. L. and Sekula, M. K., 2011, The Effect of Non-harmonic Active Twist Actuation on BVI Noise, Proceedings of the American Helicopter Society 67th Annual Forum, Virginia Beach, VA, USA.
• Jain, R., Yeo, H. and Chopra, I., 2010, Computational Fluid Dynamics-Computational Structure Dynamics Analysis of Active Control of Helicopter Rotor for Performance Improvement, Journal of the American Helicopter Society, Vol. 55, No. 4, p. 42004. [https://doi.org/10.4050/JAHS.55.042004]
• You, Y. H. and Jung, S. N., 2016, Optimal Active Twist Deployment Schedule of a Rotor for Performance Improvement and Vibration Reduction, Proceedings of the American Helicopter Society 72nd International Annual Forum, West Parm Beach, Florida, USA.
• Johnson, W., 1982, Self-tuning Regulators for Multicyclic Control of Helicopter Vibration, Washington, NASA and Technical Information Branch.
• Chopra, I. and McCloud, J. L., 1983, A Numerical Simulation Study of Open-loop, Closed-loop, and Adaptive Multicyclic Control Systems, Journal of the American Helicopter Society, Vol. 28, No. 1, pp. 63~77. [https://doi.org/10.4050/JAHS.28.1.63]
• Kang, H. J., Kim, D. H. and Wie, S. Y., 2014, Aerodynamic and Noise Calculations of Helicopter Blades Using Loose CFD-CSD Coupling Methodology, Journal of Computational Engineering, Vol. 19, No. 3, pp. 62~68. [https://doi.org/10.6112/kscfe.2014.19.3.062]