균열을 가지는 폭이 테이퍼진 보의 굽힘 진동 해석

1. 서 론

선형적으로 감소하는 단면을 가진 테이퍼진 보는 크게 단면의 높이(type A)⁽¹⁾, 단면의 폭과 높이(type B)⁽²⁾, 그리고 단면의 폭(type C)⁽³⁾이 변화하는 보 구조물로 구분할 수 있다.

Type A와 B의 경우 많은 연구자들에 의하여 블레이드와 구조물의 프레임과 같은 많은 공학적 설계에서 보다 정확한 동특성을 분석하기 위해 다양한 수치적 방법들이 연구되어 왔으나 type C의 경우 앞에서 언급된 두 가지 보 구조물 보다는 상대적으로 적은 연구가 수행되었다.

이러한 보 구조물들에 대해 균열의 영향을 고려한 수치적 방법들도 type A^(4,5)와 B⁽⁶⁾에 대해서는 일부 수행되었으나 type C에 대한 균열의 영향을 분석한 연구논문은 찾기 어렵다.

일반적으로 균열에 대한 연구는 균일 단면을 가진 보에 대한 연구가 대부분이다^(7~9). 테이퍼진 보 구조물에 대한 균열의 영향을 분석한 연구에 대해 Chaudhari 등⁽⁴⁾은 멱급수 중의 하나인 Frobenius법을 사용하여 방정식의 해를 구하였고 분석적 방법을 사용하여 고유진동수에 관한 균열의 영향을 분석하였다. Ma 등⁽⁵⁾은 전달행렬법을 사용하여 균열의 영향을 분석하였다. 이들 연구는 높이에서 선형적으로 감소하는 단면을 가진 테이퍼진 보 구조물을 고려하였다. Lee 등⁽⁶⁾은 전달행렬법을 사용하여 type A와 B에 대한 균열의 영향을 분석하였고 미분방정식의 근을 Frobenius법을 사용하여 결정하였다.

실제 폭이 테이퍼진 보 구조물은 기계, 토목, 건축 등 다양한 분야에서 공학적 설계를 위하여 사용되는 요소이다. 그러나, 폭이 테이퍼진 보 구조물에 대한 균열의 영향을 평가 할 수 있는 수치적 방법론은 Kempe 등⁽¹⁰⁾에 의해 파괴인성치를 측정하기 위한 연구를 제외하고는 폭이 테이퍼진 보 구조물의 고유진동수에 관한 균열의 영향을 분석한 논문은 찾는 것이 어려웠다. 따라서, 현재의 연구는 type C의 구조물의 고유진동수에 대한 균열을 평가 할 수 있는 수치적 방법을 개발하고자 한다.

이 연구에서의 목적은 전달행렬법을 사용하여 보 요소의 길이를 따라 선형적으로 감소하는 폭을 가진 보 구조물에 대한 균열의 영향을 분석하는 것이다. 미분방정식의 해는 Frobenius법을 사용하여 결정하였고 고유진동수를 결정하기 위한 주파수 방정식으로 전달행렬법이 고려되었다. 방법의 정확도를 검증하기 위하여 선행연구에서 검토된 결과들과 비교 하였고 균열 위치 변화에 따른 고유진동수의 변화가 변수 연구를 통하여 조사되었다. 또한, 선행연구에서 토론된 type A와 B의 결과들을 type C에 대하여 예측된 결과들과 비교하여 균열의 영향을 분석하였다.

2. 이 론

2.1 미분방정식

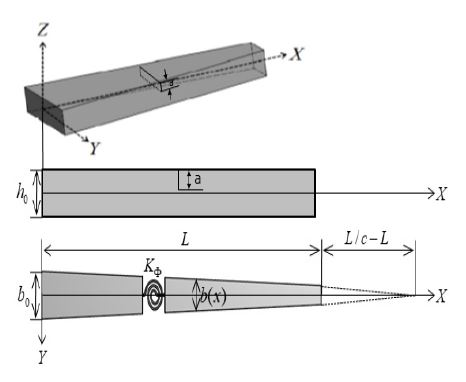
Fig. 1은 균열을 가지는 폭이 테이퍼진 보의 기하학적 형상이고, XYZ는 전체 좌표계이다. h₀와 b₀ 각각 균일한 단면을 가지는 보의 높이와 폭이다. L은 보의 길이, c는 테이퍼 비이며 b(x)는 임의의 위치에서 테이퍼 비에 의해 감소된 단면의 폭이고, a는 균열의 깊이이다. 이 연구에서, 회전관성과 전단변형의 영향은 무시되었고 개방균열(open edge crack)을 고려하였다.

Fig. 1

Geometry of a width-tapered beam with cracking

폭이 테이퍼진 보에 대한 미분방정식과 힘 (전단력과 굽힘모멘트)는 식 (1) ~ (3)과 같다⁽³⁾.

$\[ {\left(EI\left(x\right)w^{″}\right)}^{″}+m\left(x\right)\ddot{w}=0 \]$

(1)

$\[ V={\left(EI\left(x\right)w^{″}\right)}^{\text{'}} \]$

(2)

$\[ M=-EI\left(x\right)w^{″} \]$

(3)

여기서, V는 전단력, M은 굽힘 모멘트이고 EI(x)와 m(x)는 테이퍼비에 의존하여 변화하는 굽힘 강성과 단위 길이당 질량이며 다음과 같이 길이를 따라 변화된다.

$\[ {EI}_{\left(x\right)}={EI}_0\left(1-c\frac{x}{L}\right) \]$

(4)

$\[ m\left(x\right)=m_0\left(1-c\frac{x}{L}\right) \]$

(5)

여기서, EI₀와 m₀는 균일 단면을 가지는 보 요소에 대한 굽힘 강성과 단위 길이 당 질량이다.

각 주파수 ω로 조화 진동을 한다고 가정하면,

$\[ w\left(x,t\right)=W\left(x\right)\mathrm{c}\mathrm{o}\mathrm{s}\omega t \]$

(6)

식 (6)을 식 (1)에 대입하여 변수를 분리하면 무차원 미분방정식은 식 (7)과 같이 된다.

$\[ \left(1-\zeta \right)W^{″″}-2W″’-{\alpha }^2\left(1-\zeta \right)W=0 \]$

(7)

여기서, $$ \zeta =c\overline{x}, \overline{x}=x/L \mathrm{이}\mathrm{고} {\alpha }^2=m_0{\omega }^2{L}^4/E{I}_0{c}^4$$이다.

3. 결과 및 고찰

연구된 방법의 정확도를 검증하기 위하여 문헌에서 토론된 결과들과 비교 되었으며 Table 1에 검증을 위하여 사용된 재료 물성치가 제시되었다⁽⁶⁾. c = 0 일 때 고정-자유 끝 조건이 고려되었으며 1개의 균열을 가지는 보 구조물에서 균열의 위치는 각각 $$ \overline{x} =0.2$$와 $$ \overline{x} =0.6$$에서 s = 0.5의 균열이 있는 것으로 가정하였다. 비교 결과는 Table 2에 제시되었으며 결과들이 잘 일치하여 제안된 방법의 정확도가 논증되었다. Table 2에서 TMM은 전달행렬을 사용하여 얻어진 결과이고 FEA는 유한요소 해석 프로그램을 사용하여 얻어진 결과이다. 또한, 수치적 결과를 논증하기 위하여 사용된 멱급수에서의 항의 수는 60개이다.

Table 1

Material properties of the beam element

Table 2

First three natural frequencies of a beam with a single edge crack: c = 0 and s = 0.5

이와 관련하여 테이퍼 비가 c = 0.1, 0.3, 0.5일 때 s = 0.5를 고려하여 고유진동수에 관한 균열의 영향을 분석하였고, 특히 c = 0.5일 때 s = 0.1, 0.3을 추가로 분석함으로써 동일한 테이퍼 비를 가지는 보 구조물의 고유진동수에 대한 균열의 크기에 대한 영향을 비교하였다. $$ \overline{x} =1$$의 위치에서는 어떤 균열이 존재하더라도 고유진동수의 영향을 주지 않기 때문에 균열의 위치는 $$ \overline{x} =0$$부터 $$ \overline{x} =9$$까지 0.1의 간격에서 위치가 변화하였다. 예측된 결과들은 Table 3에 제시되었다. Table 3에서 보이는 것과 같이 균열의 영향은 균열의 크기와 보의 높이 비(s)의 값이 클수록 고유진동수에 많은 영향을 준다는 것은 잘 알려진 사실이다. 고정-자유조건일 때 $$ \overline{x} =0$$의 위치에서 균열이 존재할 때 균열의 영향이 가장 크게 나타난다. s = 0.1일 때 고유진동수에 관한 균열의 영향은 주파수 비로 확인했을 때 $$ \overline{x} =0$$의 위치에서 1차와 2차는 약 0.9977, 3차는 0.9976으로 균열의 영향이 아주 작은 것을 확인 할 수 있다.

Table 3

First three natural frequencies of cracked beams: c = 0.2, 0.3, 0.5 and s = 0.1, 0.3, 0.5

주파수 비(frequency ratio)는 균열이 있는 보 요소의 고유진동수를 균열이 없는 보요소의 고유진동수로 나눈 값이다.

테이퍼 비 c = 0.1, 0.3, 0.5일 때 테이퍼 비의 변화에 대한 균열의 영향을 분석하기 위하여 세 가지 테이퍼 비에 대하여 동일한 균열 크기 s = 0.5를 가지는 보 구조물의 균열의 위치 변화에 대한 고유진동수의 변화를 주파수 비로 그림으로 나타내었다. Fig. 2는 c = 0.1, Fig. 3은 c = 0.3, Fig. 4는 c = 0.5일 때 균열의 영향이다. 그림들은 curve fitting을 사용하여 그렸다.

Fig. 2

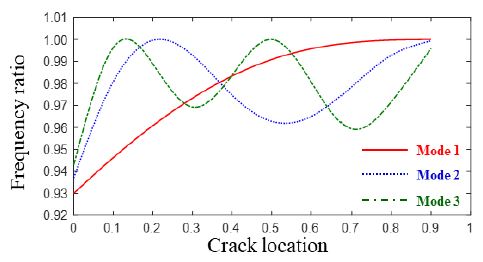
Frequency ratio of the first three natural frequencies of width-tapered beams with respect to the variation of the crack location: c = 0.1

Fig. 3

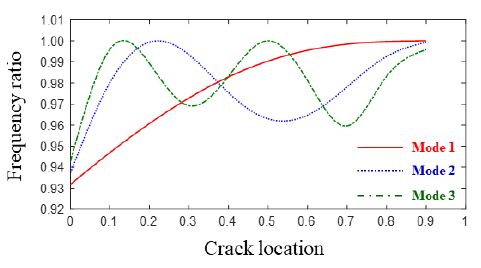
Frequency ratio of the first three natural frequencies of width-tapered beams with respect to the variation of the crack location: c = 0.3

Fig. 4

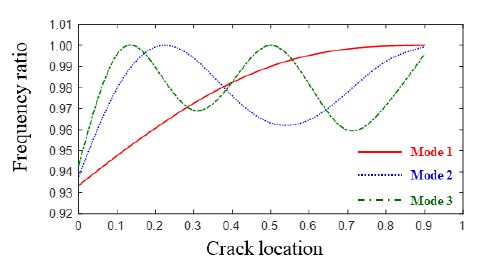
Frequency ratio of the first three natural frequencies of width-tapered beams with respect to the variation of the crack location: c = 0.5

그림들에서 보여진 것과 같이 $$ \overline{x}=0$$에서 1차 고유진동수일 때 c = 0.1에서 균열의 영향이 가장 큰 것으로 나타났으며 테이퍼 비가 작아질수록 눈에 띄는 영향을 보였다. 2차와 3차 고유진동수는 테이퍼 비에 의한 영향이 유사한 것으로 나타났다.

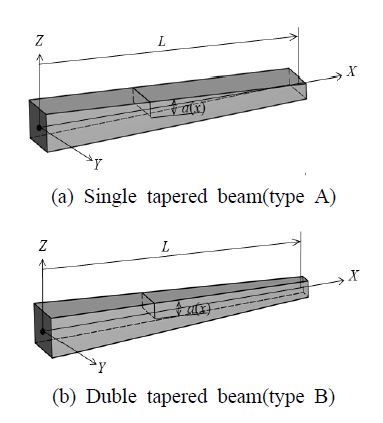
마지막으로 세 가지 유형의 테이퍼진 보 구조물의 고유진동수에 관한 균열의 영향을 비교하였다. Fig. 5(a)는 type A로 임의의 위치에 균열을 가지는 길이를 따라 단면의 높이가 선형적으로 변화하는 테이퍼진 보이고, Fig. 5(b)는 type B로 임의의 위치에 균열을 가지고 단면의 높이와 폭이 동일한 테이퍼 비를 가지고 선형적으로 변화하는 보 구조물이다. Fig. 1에서 제시된 type C는 현재의 연구에서 분석된 단면의 폭이 선형적으로 변화하는 보 구조물이다.

Fig. 5

Geometry of single and double tapered beams with cracking

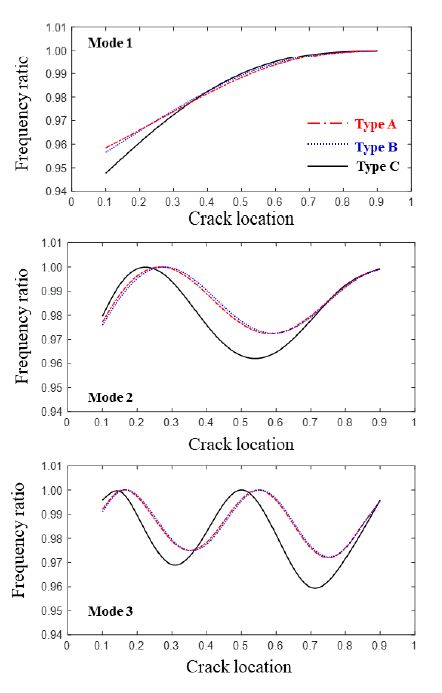
비교를 위하여 사용된 테이퍼 비는 c = 0.5이고 균열의 깊이는 s = 0.5이다. 균열의 위치 변화에 따른 세 가지 유형의 테이퍼진 보에 관한 균열의 영향이 비교되었고 type A와 B에 대한 결과는 Lee 등⁽⁶⁾에 의해 분석된 결과를 사용하였다. 비교 결과는 Fig. 6에 나타난다. 그림에서 보이는 것과 같이 고정단 부근에서 1차 모드에서 균열의 영향에 의하여 type C가 가장 큰 감소를 보였다. 또한, 2차 모드와 3차 모드에서도 type A와 B에 비하여 type C에서 균열의 영향에 의한 고유진동수의 감소폭이 컸으며 고유진동수에서 최대 감소가 일어나는 균열 위치는 type C 비하여 type A와 B는 오른쪽으로 이동하는 것을 볼 수 있다. 또한, 균열의 영향이 없는 노드 점 또한 type A와 B는 type C와 비교하여 오른쪽으로 크게 이동하였다. 결과적으로 type A와 B가 균열의 위치에 따라 유사한 경향성을 보였다면 균열의 영향에 의해 type C는 type A와 B와는 전혀 다른 경향성을 보였다. Type C의 경우 균일한 단면을 가지는 보 구조물과 유사한 균열의 영향을 보였다. 유사한 개념에서 type B는 type A와 동일한 높이에서 변화를 가지고 폭만 감소되었기 때문에 두 가지 타입이 유사한 경향성을 보인 것으로 분석되었다.

Fig. 6

Comparisons between the three type of beams

4. 결 론

폭이 테이퍼진 보 구조물의 고유진동수에 관한 균열의 영향을 분석할 수 있는 수치적 방법이 전달행렬법을 사용하여 개발되었다. 이 방법의 정확도는 문헌에서 검토된 결과들과 비교함으로써 논증하였고 다음과 같은 결론을 도출하였다.

(1) 균열의 위치 변화에 따른 보 구조물의 고유진동수에 관한 균열의 영향을 검토하였고 1차, 2차, 3차 고유진동수 모두 $$ \overline{x}=0$$에서 균열의 영향에 의해 가장 큰 감소를 보였다.

(2) 테이퍼 비 c = 0.1, c = 0.3과 c = 0.5의 조건을 가질 때 $$ \overline{x}=0$$에서 1차 고유진동수의 경우 테이퍼 비의 변화에 따라 눈에 띄는 변화를 보였으나 2차와 3차 고유진동수는 유사한 변화를 보이는 것으로 분석되었다.

(3) 세 가지 유형의 테이퍼진 보의 고유진동수에 대한 균열의 영향을 비교한 결과 type A와 B는 유사한 경향성을 가지고 변화하는 것을 볼 수 있으나 type C는 균열의 영향이 없는 노드 점의 위치나 균열의 영향에 의한 고유진동수의 감소폭에서 다른 두 가지 유형의 테이퍼 보와는 다른 경향성을 가지고 변화하였다.

Acknowledgments

이 연구는 경기도의 경기도 지역협력연구센터 사업의 일환으로 수행하였음(GRRC경기2020-B02, 혁신형 지능제조시스템 연구).

References

• Ryu, B. J., Yim, K. B., Yoon, C. S. and Ryu, D. H., 2000, Vibration and Stability of Tapered Timoshenko Beams on Two-parameter Elastic Foundations, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 10, No. 6, pp. 1075~1082.
• Wang, Z. and Li, R., 2018, Transverse Vibration of Rotating Tapered Cantilever Beam with Hollow Circular Cross-section, Shock and Vibration, Vol. 2018, 1056397. [https://doi.org/10.1155/2018/1056397]
• Lee, J. W., Kim, J. H. and Lee, J. Y., 2015, Exact Solutions for Bending Vibration of Beam with Linearly Reduced Width along Its Length, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 25, No. 6, pp. 420~425. [https://doi.org/10.5050/KSNVE.2015.25.6.420]
• Chaudhari, T. D. and Maiti, S. K., 1999, Modelling of Transverse Vibration of Beam of Linearly Variable Depth with Edge Crack, Engineering Fracture Mechanics, Vol. 63, No. 4, pp. 425~445. [https://doi.org/10.1016/S0013-7944(99)00029-6]
• Ma, Y., Du, X., Wu, J., Chen, G. and Yang, F., 2020, Natural Vibration of a Non-uniform Beam with Multiple Transverse Cracks, Journal of the Brazillian Society of Mechanical Sciences and Engineering, Vol. 42, No. 4, pp. 1~12. [https://doi.org/10.1007/s40430-020-2246-1]
• Lee, J. W. and Lee, J. Y., 2018, A Transfer Matrix Method for In-plane Bending Vibrations of Tapered Beams with Axial Force and Multiple Edge Cracks, Structrual Engineering and Mechanics, Vol. 66, No. 1, pp. 125~138.
• Chondros, T. G., Dimarogonas, A. D. and Yao, J., 1998, A Continuous Cracked Beam Vibration Theory, Journal of Sound Vibration, Vol. 215, No. 1, pp. 17~34. [https://doi.org/10.1006/jsvi.1998.1640]
• Park, H. W. and Lim, T. J., 2020, A Closed-form Frequency Equation of an Arbitrarily Supportedbeam with a Transverse Open Crack considering Axial-bending Modal Coupling, Journal of Sound and Vibration, Vol. 477, 115336. [https://doi.org/10.1016/j.jsv.2020.115336]
• Lee, J. W. and Lee, J. Y., 2017, In-plane Bending Vibration Analysis of a Rotating Beam with Multiple Edge Cracks by Using the Transfer Matrix Method, Meccanica, Vol. 52, pp. 1143~1157. [https://doi.org/10.1007/s11012-016-0449-4]
• Kempe, M. D., Morse, J., Eafanti, J., Julien, S., Wan, K. et al., 2021, Measurement of Crack Length in Width Tapered Beam Experiments, Journal of Adhesion Science and Technology, Vol. 35, No. 4, pp. 357~374. [https://doi.org/10.1080/01694243.2020.1801271]