탐욕 알고리즘 및 특이치 분해를 이용한 프로펠러 초생 캐비테이션의 위치추정

2.1 압축센싱 기반 정위법

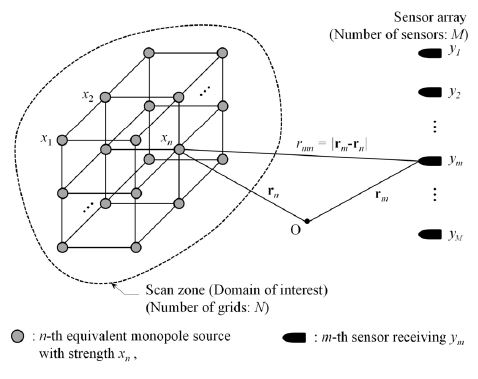
프로펠러 캐비테이션에 의한 음장을 Fig. 1에 나타낸 총 N개 등가단극음원(equivalent monopole source)의 조합을 통해 표현할 수 있다고 가정하자. x_n(n=1, …, N)은 각 음원의 (복소) 강도를 의미한다고 할 때, m(=1, …, M)번째 센서(여기서는 하이드로폰) 응답은 자유음장 그린함수를 이용하여 다음과 같이 쓸 수 있다.

Fig. 1

Equivalent source model consisting of N monopole sources

여기서 r_mn = |r_m-r_n|은 m번째 센서와 n번째 음원간 거리, k = 2πf / c는 파수, f는 주파수 [Hz], c는 음속 (=1502 [m/s])를 의미하며, e_m은 잡음을 의미한다.

식 (1)에 대한 벡터-행렬 표현은 식 (2)와 같다.

y∈₵ ^M와 e∈₵ ^M는 각각 측정벡터, 잡음벡터라 한다. A∈₵ ^M×N는 측정행렬이라 칭하며 그 원소는 a_mn=exp(-jkr_mn)/4πr_mn와 같고, x∈₵ ^M는 미지의 해 벡터이다. 실제의 캐비테이션 소음원은 x에서 0이 아닌 요소로 나타나며, 그것에 대응하는 3차원 공간좌표를 캐비테이션의 발생위치로 볼 수 있다.

일반적으로, 센서의 수 M은 미지수의 개수 N보다 작다고 할 수 있으므로 (M < N), 식 (2)는 과소결정(under-determined) 문제가 됨을 알 수 있다. 그리고, 정위 문제 특성상 x에서 단지 s (« N) 개만 0 아닌 값을 갖는다는 희박성(sparseness)을 가정할 수 있다. 이와 같은 부족조건(ill-posed) 문제는 압축센싱에서 취급할 수 있으며 해법을 위해 전술한 바와 같이 컨벡스 최적화 또는 탐욕 알고리즘을 이용한다.

기저추적(basis pursuit)으로도 불리는 전자의 방법에서는 볼록함수 l₁-norm ||x||₁=$$ {\sum }_{n=1}^N\left|x_n\right|$$을 식 (2)의 구속조건에 대해 최소화한다. 즉,

이며, $$ {‖\mathrm{x}‖}_2={\left({\sum }_{n=1}^N{\left|x_n\right|}^2\right)}^{1/2}$$은 Euclidean norm을 의미한다. CVX⁽¹⁴⁾, l₁-magic⁽¹⁵⁾ 등과 같은 공개 코드에서 이미 구현된 바와 같이 l₁-norm의 볼록성은 전형적인 선형 프로그래밍(linear programming)의 문제로 변환될 수 있는 근거를 제공하며, 전역 수렴성을 보장한다.

기본적으로 식 (3)의 최적화 문제는 어느 한 주파수에 대해 정의되며, 잡음의 영향을 저감하기 위해 관심 여러 주파수에 대해 계산한 결과들을 평균하여 최종결과를 얻는다. 주목할 점은 프로펠러 캐비테이션 소음은 충격음과 유사한 임펄스 신호가 주기적으로 반복되는 진폭변조의 특성을 가진다는 것이며, 이에 이 연구에서는 스펙트럴 커토시스(spectral kurtosis, SK)⁽¹⁶⁾를 이용하여 관심 주파수 대역을 지정하였다.

컨벡스 최적화의 단점은 잡음의 크기 ||e||₂를 알고 있어야 한다는 것인데, 당연히 대부분의 경우 알 수 없으며 현실적으로는 튜닝의 방법을 택한다. 결국, ||e||₂는 라그랑지 승수(Lagrange multiplier)⁽¹⁷⁾와 동일하게 해의 희박성과 잔차(residual) 사이의 균형을 조정하는 역할을 한다고 할 수 있다(이 측면에서 ||e||₂를 정규화 인자(regularization parameter)라 볼 수 있음). 부연하면, ||e||₂가 클 경우 과도한 일반화(generalization)로 인해 너무 희박한 해(음원분포)를 얻는 반면, 그 반대의 경우(즉, 측정치를 신뢰할 경우) 과적합(overfitting)을 초래하여 여러 곳에 산재해 있는 음원분포를 얻을 가능성이 높다. 또한, 컨벡스 최소화 기법은 비교적 많은 반복 연산횟수를 요구하는 편이며, 이는 여러 주파수에 대해 계산할 경우 느린 계산속도의 원인이 된다.

탐욕 알고리즘은 각 반복 단계에서 국소 최소값을 선택해 나가며 궁극적으로는 전역 최소값에 도달하기 희망하는 비교적 단순한 생각에서 출발한 방법이다. 각 반복에서 최적 x를 구하는 방법에 따라 다양한 형태의 탐욕 알고리즘이 구현된다. 서론에서 언급한 바와 같이, 이 연구에서는 빠른 계산이 가능하며 널리 활용되고 있는 OMP(Orthogonal matching pursuit)^(7,13)를 도입하였다. OMP는 해 벡터의 서포트 집합(support set)을 특정 종료조건이 만족될 때까지 갱신하며 최적해를 추정한다(상세알고리즘은 부록 참조).

식 (3)의 잡음에 대한 구속식 즉, ||y-Ax|| ≤ ||e||₂을 OMP 종료조건으로 고려할 수 있지만, 역시 잡음의 특성을 알 수 없으므로, 이를 사용할 수 없다. 대신, 참고문헌(12)에 의하면, 해 벡터의 희박도(sparsity)가 s(나머지 N – s 개 원소는 ‘0’)라면, OMP 방법을 s회만 반복하면 해를 구할 수 있음이 밝혀졌다. 여기서, 희박도 s는 x 가운데 0이 아닌 원소의 개수를 의미하므로, 물리적으로는 음원의 개수로 해석될 수 있다. 3절에서 보이는 예와 같이, 초생 캐비테이션과 관련한 희박도는 대개 한 자리 숫자이며, 이는 기껏해야 10회 이하의 반복만으로도 해를 산출할 수 있음을 예상할 수 있다. 통상 수십 ~ 수백회 반복을 요하는 컨벡스 최적화에 비해 계산속도가 빠를 수 밖에 없다. 그러나, OMP의 시작을 위한 선결조건인 희박도 s는 별도의 방법을 통해 추정해야 하며, 다음절에서 이에 대해 상술하기로 한다.

2.2 특이치 분해를 이용한 희박도(음원개수) 추정

비록 초생 단계라 할지라도, 캐비테이션은 수많은 기포의 붕괴를 수반하며, 이로 인해 다수의 음원이 존재하게 된다. 해당 음원들 사이에는 상관성(coherency)이 존재하며, 그 모든 음원을 규명하는 것은 사실상 불가능하다. 대신, 소음 출력에 독립적으로 기여하는 비상관(incoherent) 음원을 찾는 것이 현실적으로/공학적으로 더 의미있다고 할 수 있으며, 이를 위해 특이치 분해(singular value decomposition, SVD)를 다음과 같이 이용할 수 있다.

우선, x 가운데 상호 독립인 음원의 집합을 x_s∈₵ ^s라 하면 x_s = x(supp(x))로 쓸 수 있다. supp(x) = {n, x_n ≠ 0}는 x의 서포트를 의미하는데, x에서 0이 아닌 원소 번호의 집합이다. 잡음이 없는 경우, 식 (2)는 식 (4)와 같다.

A_s∈₵ ^M×s는 측정행렬 A에서 supp(x)에 해당하는 열(column)을 취해 구성한 부분행렬이다. 식 (4)의 양변의 뒤에 y^H(H: Hermitian transpose)를 곱하고 기대치를 취하면⁽¹⁸⁾, 식 (5)와 같다.

G_yy∈₵ ^M×M와 G_xsxs∈₵ ^s×s는 각각 출력 상호스펙트럼밀도 행렬(output cross spectral density matrix, OSDM), 입력 상호스펙트럼밀도 행렬(input cross spectral density matrix, ISDM)이라 하며 구체적으로는 다음과 같다.

여기서 기호 ‘*’는 켤레 복소수(complex conjugate)를 의미한다.

ISDM은 독립된 s개의 성분(음원)으로 구성된 벡터로부터 정의되므로, 행렬의 계수 즉 rank(G_xsxs) = s이다. 센서의 개수가 음원의 수보다 많음을 가정하면 (M ≥ s), 부분행렬 A_s의 계수 역시 s 라 할 수 있다. 또한, 두 행렬 A, B에 대해, rank(AB) ≤ min(rank(A), rank(B))가 성립한다(단, 등호는 A 또는 B가 non-singular일때 성립)⁽¹⁹⁾. 위 관계를 식 (5)에 적용하면,

식 (8)과 같이 쓸 수 있으며, 이는 OSDM의 계수를 통해 음원개수(희박도) 추정이 가능함을 시사한다.

G_yy에 대한 특이치 분해는 다음과 같다.

여기서 U와 V는 M×M 크기의 유니터리(unitary) 행렬이고, Σ는 대각행렬(diagonal matrix)이며 그 원소 si는 특이치이다. 참고로, OSDM은 허미시언 행렬이므로($$ {\mathrm{G}}_{\mathrm{y}\mathrm{y}}={\mathbf{G}}_{\mathbf{y}\mathbf{y}}^{\mathbf{H}}$$), OSDM의 특이치 분해와 고유치 분해(eigenvalue decomposition)는 서로 차이가 없다. 잡음이 없는 경우, 특이치(또는 고유치)는 σ₁ ≥ σ₂ ≥ … σ_s ≥ 0의 관계로 내림차순 정렬된다. 따라서 0이 아닌 특이치의 개수는 OSDM의 계수(혹은 음원의 수)에 해당한다.

잡음의 존재는 OSDM을 정규화하므로 더 이상 ‘0’인 특이치는 없으며, 대신 다음과 같이 ‘0’보다 약간 큰 특이치가 나타나게 한다.

여기서, ε는 한계치(threshold)를 의미한다. 따라서, 잡음이 존재하는 경우에는, 한계치보다 큰 특이치 개수를 조사하여 ODSM의 유효 계수(effective rank)를 추정해야 한다. 한계치 ε는 사실상 특정하기 어려우므로, 특이치의 급격한 감소가 시작되는 기점을 선택 한계로 본다. 물론, 잡음 수준이 높은 환경에서는 특이치가 완만하게 감소하는 경향을 보이므로 컷오프(cut-off) 방식은 유효하지 않을 수 있다. 그러나, 다음 실험절에서 보이는 바와 같이, 초생 캐비테이션 신호의 경우 신호대잡음비(signal-to-noise ratio, SNR)가 충분히 높아, 이 방법을 도입할 수 있는 것으로 판단된다.

3.1 실험장치

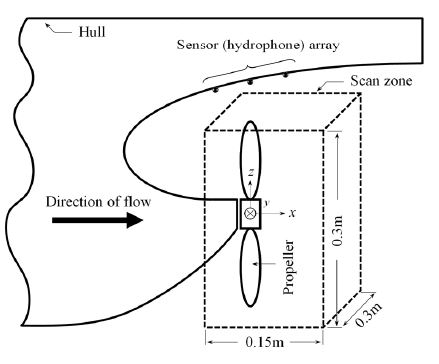
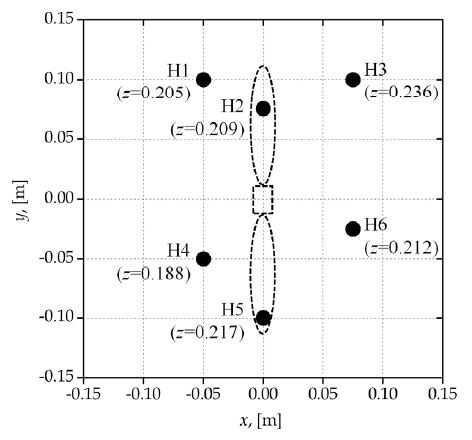
2절에서 설명한 정위법의 검증을 위해 캐비테이션 터널에서 모형실험을 수행하였으며, Fig. 2에 그 개략을 보였다. 모형선 내부에 설치된 동력계가 모형 프로펠러(4익)를 구동하면서 추력, 토크, 회전 속도를 측정한다. 직경 0.238 m인 모형 프로펠러는 후미에서 바라보았을 때 시계 방향으로 회전한다. Fig. 3에 나타낸 바와 같이, 프로펠러 상부 선체 표면에 6개(M = 6)의 하이드로폰 배열을 설치하였으며, 조정/증폭 후 256 kHz의 샘플링 주파수로 신호를 취득하였다.

Fig. 2

Sketch for propeller cavitation test

Fig. 3

Arrangement of sensor (hydrophone) array

캐비테이션 시험은 기본적으로 터널내 물의 유속 V_T, 프로펠러 회전속도 n_s, 터널압력 P_T 세 가지 매개변수를 조정하며 수행한다⁽²⁰⁾. 여기서는, 프로펠러가 발생하는 힘을 유지하기 위해 두 매개변수(V_T, n_s)를 일정하게 유지한 반면, 캐비테이션 발달 정도를 변화시키기 위해 터널압력 P_T를 감소시키며 실험하였다. 즉, 비교적 높은 터널압력에서 캐비테이션이 없음을 소음신호 관찰을 통해 확인하였고, 이후 캐비테이션이 충분히 발달할 때까지 여러 압력 조건(Table 1참조)에 대해 소음신호를 계측하였다. 참고로, 음향적 정위 결과와 비교하기 위해 고속 카메라(SA-5)를 이용한 시각적 관찰도 함께 병행하였다.

Table 1

Conditions of propeller cavitation test

3.2 소음스펙트럼 분석 및 음원개수 추정

시험조건별 소음 스펙트럼 분석 결과를 Fig. 4에 보였다. 시험조건 2의 결과는 1 kHz ~ 4 kHz 및 20 kHz 이상의 주파수 대역에서 약간의 증가(< 3 dB)를 보인다. 그러나, 해당 고속카메라 영상에서는 캐비테이션 관련한 시각적인 징후를 관찰할 수 없었다. 즉, 음향적 초생이 이미 시작했음에도 불구하고, 시각적 초생이 시작하지 않았기에 조건 2를 sub-visual inception이라 지칭하였다. 조건 3에서는, 12시 영역 끝단에서 보오텍스 캐비테이션(tip vortex cavitation, TVC)이 미약하게 발생한다(Fig. 5(a)참조). 관련된 스펙트럼의 변화는 20 kHz 이상 주파수 대역에 국한되고 있으며, 이는 팝형(pop-type) 음향 특성⁽²¹⁾과 유사하다. 충격성 소음을 야기하는 팝 유형의 소음 발생은 초생 캐비테이션의 중요한 징후로 볼 수 있다.

Fig. 4

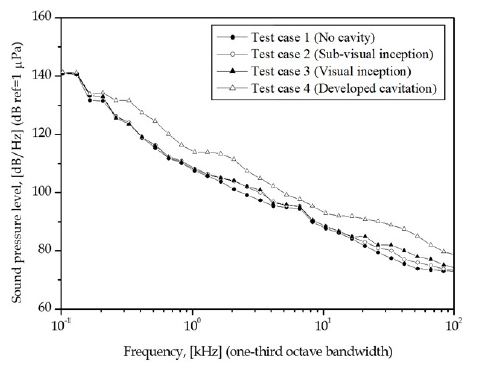
Power spectral densities for the test cases (analysis channel: H4). Estimated by Welch’s method with Hanning window, 500 times ensemble average and 75 % overlapping

Fig. 5

Representative high speed images

조건 4에서는 TVC가 프로펠러 후류선(slip-stream)을 따라 잘 발달하고 있다(Fig. 5(b) 참조). 충분히 성장한 캐비테이션의 경우 체적 진동(volumetric oscillation)이 발생하며, 이때 충격음 뿐만이 아니라 수 kHz 정도로 낮은 주파수 성분의 첩(chirp)소음도 함께 발생하는 것으로 알려져 있다⁽²¹⁾. 따라서, 조건 4에 대응하는 소음 스펙트럼이 전 주파수 대역에 걸쳐 증가하는 양상을 보이게 된다.

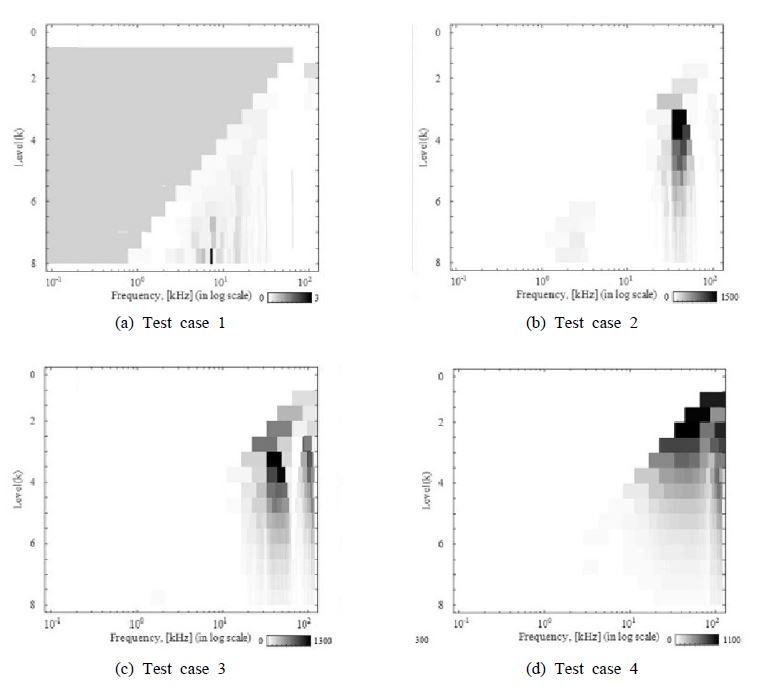
상기의 내용은 Fig. 6에서 보인 SK 해석 결과에서도 잘 나타난다. SK는 충격성 신호가 나타나는 주파수 영역에서 큰 값을 가지는데, 그 최대값이 저주파가 아닌 수십 kHz 대역에서 나타남을 볼 수 있는 것이다. 따라서, 초생(즉, 팝 소음)에 대한 진단 정보는 고주파 대역에 포함되어 있음을 확인할 수 있으며, 또한 이 대역에 대해 소음원 개수 추정 및 정위를 수행해야 함을 알 수 있다.

Fig. 6

Spectral kurtosis (SK) analysis with Fast Kurtogram

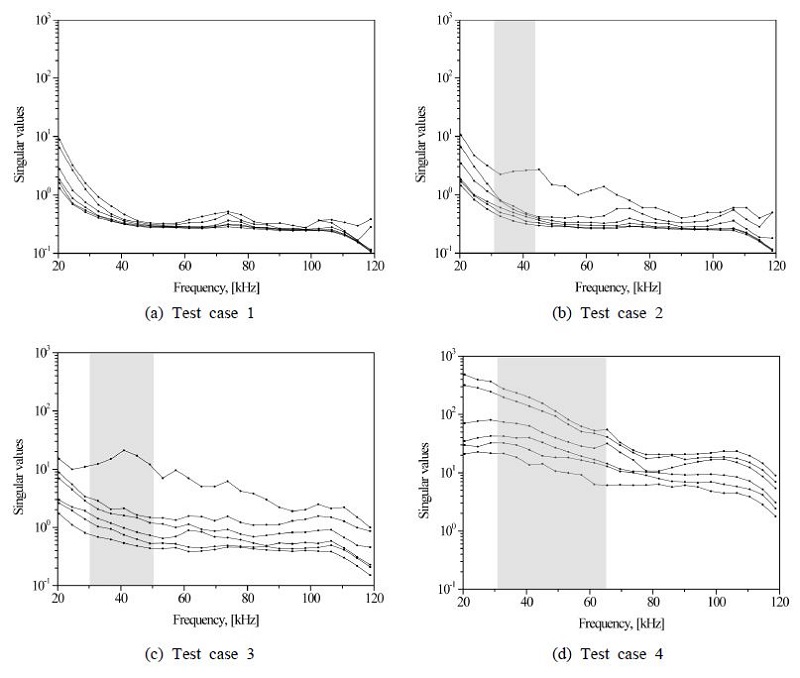
Fig. 7은 OSDM의 특이치를 주파수에 대해 도시한 결과이다. 조건 1(비공동 상황)의 경우, 의미있는 특이치의 변화를 식별하기 어렵다. 반면, 조건 2(sub-visual inception)와 3(visual inception)에 대해서는 하나의 특이치가 나머지 특이치에 비해 큰 주파수 대역을 볼 수 있으며, 특히 SK 값이 커지는 주파수 범위 근방에서(그림에서 음영 표시) 그 양상이 부각되고 있다.

Fig. 7

Singular values of OSDM, Note that the horizontal frequency axis was linear-scaled, not log-scaled.

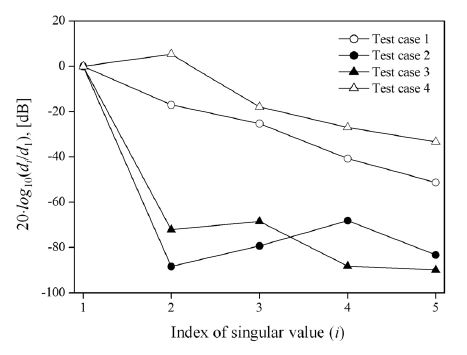
정량적인 계산을 위해 특이치의 변화량을 식 (11)과 같이 정의하였다.

이에 따라 특정 주파수(41 kHz)에 대해 계산한 결과를 Fig. 8에 도시하였다. 조건 2 및 3에 대해, d₁ → d₂ 구간에서 크게 감소하고 있음을 볼 수 있으며, 이를 통해 해당 주파수에서 OSDM의 계수는 ‘1’임과 동시에 독립적인 음원의 수는 ‘1’개임을 알 수 있다.

Fig. 8

Difference of singular value (di = σi − σi+1). Evaluated frequency: f = 41 kHz.

발달된 TVC에 대한 특이치는 그 크기가 모두 전반적으로 증가하였음을 볼 수 있다(Fig. 7(d)). 특이치의 급격한 변화도 나타나지 않아 음원개수를 추정하기 어려움을 알 수 있다. 초생 시점을 지나 크게 발달한 캐비테이션은 무수히 많은 기포를 내포하며, 음장에 기여하는 독립된 음원의 개수는 초생 상황에 비해 많을 것이 자명하다. 따라서, 센서의 개수가 충분히 많지 않는 한, 발달 캐비테이션에 대해, SVD를 이용하여 음원개수를 추정하는 것에는 무리가 따른다고 정리할 수 있겠다.

3.3 정위결과 분석

정위 문제 설정을 위해, Fig. 2 표시한 바와 같이 프로펠러 근방에 지정된 0.15 m × 0.3 m × 0.3 m의 탐색영역을 0.01 m의 해상도로 이산화하였으며, 이에 따른 미지 음원의 총 개수는 N = 15 376(= 16 × 31 × 31)이 된다. 언급한 바와 같이, 잡음의 영향을 억제하기 위해 여러 주파수에 대해 평균한 결과를 도시해야 하겠으나, 여기서는 주파수별 계산결과의 일관성을 보이기 위해 SK에서 도출된 관심 주파수 영역내 5개점 각각의 결과를 (평균을 취하지 않고) 모두 보였다.

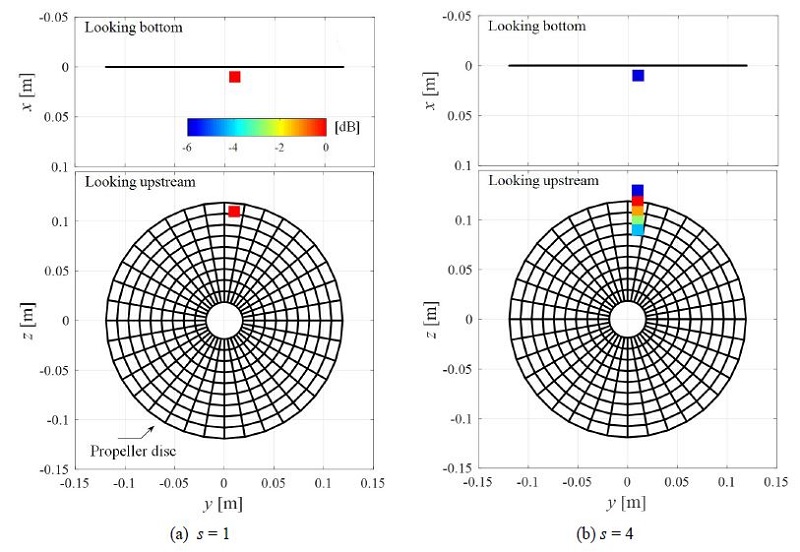
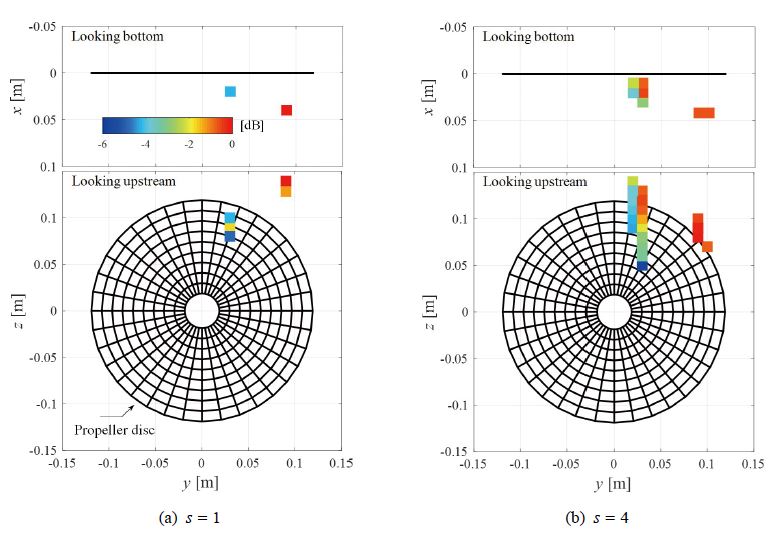
Fig. 9와 Fig. 10은 조건 2 및 3에 대한 OMP 정위결과를 보이고 있다. 음원개수 s의 값을 적절히 설정한 경우(Fig. 9(a), Fig. 10(a)), 정위 결과는 고속 카메라 관찰결과와 상관관계가 크다고 볼 수 있으며 이를 미루어 제안한 방법의 타당성을 검증할 수 있다. OMP 해석 시 음원개수 추정이 잘못된 경우를 가정하여, s = 4로 설정한 경우를 Fig. 9(b)와 Fig. 10(b)에 나타냈다. 이때, 추정된 음원들은 상하방향을 따라 늘어선 형태로 나타나며, 프로펠러 외부 영역에서도 존재하는 음원도 나타나 분석결과의 질을 저해하게 된다. 따라서, 정위과정에 있어 음원개수 추정도 함께 중요함을 강조할 수 있다.

Fig. 9

OMP localization for test case 2 with letting

Fig. 10

OMP localization for test case 3 with letting

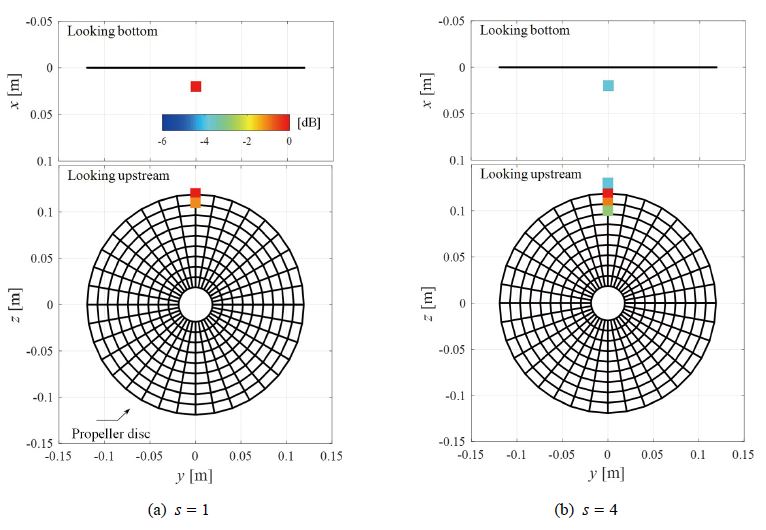
Fig. 11은 조건 4(발달된 TVC)에 대한 해석결과이다. 이 경우 음원 개수를 추정할 수는 없었으나, 앞에서와 마찬가지로 각각 s = 1과 4로 임의 설정하였다. s = 1일 때, 나타나는 두 개군 중 하나의 군이 프로펠러 외부로 벗어나고 있으나, s = 4일 때에는 좀 더 현실적인 위치로 음원이 옮겨가고 있는 것을 알 수 있다. 이는, 앞절의 특이치 해석과 부합하게도, 발달된 캐비테이션을 구성하는 음원수는 적어도 4개 혹은 그 이상임을 의미한다. s를 6까지 늘려 해석하였으나, Fig. 11(b)의 결과와 크게 다르지 않았으며, 센서의 개수는 음원의 수보다는 많아야 한다(M ≥ s)는 제한여건상 더 이상은 시도하지 않았다. 물론, 센서 개수 자체를 늘린다면 더 나은 결과를 얻을 수 있겠으나, 이 연구의 대상이 발달된 캐비테이션이 아닌 초생 캐비테이션에 있었기에 이 역시 시도하지 않았다.

Fig. 11

OMP localization for test case 4 with letting