멤브레인 타입 음향 메타 구조의 흡음 분석
© The Korean Society for Noise and Vibration Engineering
Abstract
In this study, an acoustic metastructure, combined with a thin membrane and a rectangular cavity, was designed to reduce the noise of mechanical structures from 2000 Hz to 4000 Hz. Finite element method (FEM) analysis was performed through COMSOL multiphysics and the sound-absorbing structure was evaluated using the sound absorption coefficient from the 2-microphone method. Subsequently, the acoustic impedance of this metastructure was analyzed to explain the absorption mechanism of the thin film. The target frequency was controlled by carefully designing the size of the cavity to effectively reduce noise in a specific frequency region. Additionally, to determine the sound absorption effect of the thin film, the difference in the sound pressure level owing to the rectangular duct was measured.
Keywords:
Meta-structure, Membrane, Cavity, Absorption Coefficient, Acoustic Impedance, Insertion Loss키워드:
메타 구조, 멤브레인, 빈 공간, 흡음률, 음향 임피던스, 삽입손실1. 서 론
내부의 열원이 존재하는 기계 장치의 경우 내부에 열이 원활하게 순환, 배출되지 않으면 장치의 성능이 저하되고 심한 경우 작동이 멈추거나 장치가 고장이 나는 일이 발생한다(1). 이러한 이유로 주요 소음 원인을 찾더라도 소음 인자를 흡음재 등으로 감싸거나 하는 방법을 사용할 수 없기에 소음 저감에 특히 어려움을 겪는다. 게다가 기계 장치는 구성하는 부품들에 따라 특정한 주파수에서 소음이 도드라지는 경우가 많은데(2) 일반적인 흡음재는 특정 주파수에서만 소음을 줄이지 못하므로 흡음재의 효율이 떨어진다.
이러한 문제점을 해결하기 위해 기존의 흡음 물질이 아닌 음향 메타물질을 활용하려는 시도가 많다(3,4). 특히 특정 주파수 대역의 소음을 흡음 또는 차단하는 연구가 많이 이루어지고 있는데(5~7), 이 연구에서는 격자 구조 위에 멤브레인을 부착하여 cavity를 형성하는 멤브레인 타입 흡음 구조를 설계하였다. 멤브레인 타입 흡음 구조는 멤브레인의 진동에 의한 감쇠(damping)와 유효질량에 의한 임피던스와 cavity 구조의 임피던스가 공기의 임피던스와 매칭되면서 흡음 구조를 형성한다. 이러한 흡음 구조는 소음 인자를 완전히 감싸는 것이 아닌 소음 인자 주변을 흡음 덕트 형식으로 둘러싸기 때문에 열의 순환이나 방출에도 큰 영향을 끼치지 않는다. 또한, cavity의 부피를 조절하면 메타 구조의 임피던스 또한 변하게 되는데 이를 이용하여 목적 주파수를 조율할 수 있다. 이러한 방법으로 기계 장치의 주요 소음 주파수 대역을 파악하고 그 대역의 목적 주파수를 가지는 멤브레인 타입 메타 구조를 설계하면 효과적으로 소음을 줄일 수 있다.
이러한 멤브레인 타입 메타 구조의 흡음 성능을 알아보기 위해 이 연구에서는 멤브레인 타입 메타 구조의 흡음률을 예측하였는데 COMSOL Multiphysics 5.4를 사용하여 finite element method(FEM) 해석을 진행하였다. 시뮬레이션 상에서 2-microphone method를 이용해 음파 분리법을 적용하여 흡음률을 계산하였다. 또한, 멤브레인 타입 메타 구조의 음향 임피던스를 구하여 흡음률과의 관계를 분석하였다.
Cavity의 부피에 따른 목적 주파수의 변화를 알아보기 위해 cavity의 높이에 따른 흡음률 변화를 구하였다. 그리고 Brüel & Kjær사의 임피던스 튜브를 사용하여 실제 흡음률을 측정하고 FEM을 통해 구한 흡음률과 비교해보았다. 최종적으로 멤브레인 타입 메타 구조를 가지는 흡음 덕트를 제작하여 음압레벨을 측정함으로써 실제 소음원에서 소음 저감 효과를 가지는지 확인하였다.
2. 음향 FEM 해석
2.1 멤브레인 타입 흡음 구조 구성
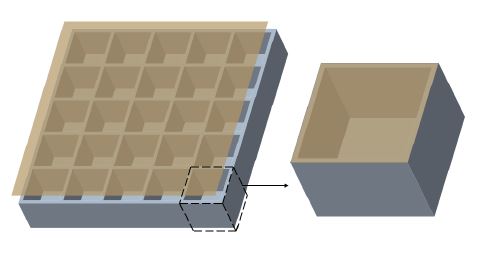
이 연구에서는 2000 Hz ~ 4000 Hz 대역의 소음을 저감하기 위해 멤브레인과 cavity를 결합한 형태인 멤브레인 타입의 흡음 구조를 설계하였다. Fig. 1에 나타난 것과 같이 한 면이 막힌 사각형의 격자 구조에 멤브레인을 부착하여 cavity를 형성하고 이 cavity와 멤브레인이 결합하여 메타 구조를 구성한다. 이때 멤브레인은 50 μm 두께의 내열 테이프인 kapton tape를 사용하였고 이를 구성하는 물질은 polyimide이다. 따라서 Table 1의 polyimide 물성 데이터를 이용한다(8).
이렇게 구성된 멤브레인 타입 메타 구조에서 멤브레인의 진동 때문에 발생하는 점성 감쇠(viscous damping)와 멤브레인의 진동에 영향을 받는 유효질량으로 생성되는 임피던스와 cavity의 구조에 의해 형성되는 임피던스가 합쳐지고 이것이 공기의 임피던스와 매칭되어 흡음 구조를 형성한다.
2.2 2-Microphone method를 이용한 음향해석
이 연구는 멤브레인 타입 메타물질의 흡음률을 계산하여 흡음 성능을 판단하고 고유음향임피던스를 계산하여 흠음률과의 관계를 알아보았다. 이를 위해 FEM 해석(COMSOL Multiphysics 5.4)을 진행하였고 2-microphone method를 이용해 임피던스 튜브 내부에 음파 분리법을 적용하여 흡음률과 임피던스를 계산하였다(9).
임피던스 튜브는 Fig. 2와 같이 upstream과 unit cell로 구분되고 unit cell은 멤브레인과 cavity가 결합한 멤브레인 타입 메타 구조의 single unit을 뜻하며 upstream의 윗부분에서 평면 파의 음원을 생성하여 음압분포를 형성한다. 이때 임피던스 튜브 내부에는 음원에서 발생하는 진행파와 unit cell에서 반사되는 반사파가 중첩된다. 이러한 음압분포를 mic 1과 mic 2로 나타낸 두 지점에서 측정하여 이 두 가지 파동을 분리할 수 있는데 이것이 음파 분리법이다.
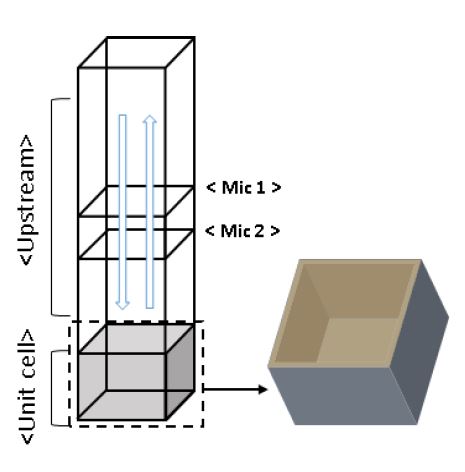
Schematic of impedance tube constructed in COMSOL. It is made up of 3 part, upstream, downstream, unit cell. unit cell means single membrane-cavity structure
Fig. 2에서 2-microphone method를 이용해 계산한 음압은 식 (1)과 같이 나타낼 수 있다. 이때, 식 (1)의 A와 B는 각각 입사파와 반사파의 진폭인데, 이는 두 마이크에서 측정한 음압 P1, P2, wave number k, 그리고 두 마이크까지의 거리 x1, x2를 이용하여 식 (2)와 같이 계산할 수 있다.
| (1) |
| (2) |
또한 식 (1)과 식 (2)를 이용하여 식 (3)과 같이 반사율 γ를 구할 수 있고 이를 통해 흡음률 α를 계산할 수 있다.
| (3) |
2.3 멤브레인 타입 메타 구조해석 및 임피던스 분석
멤브레인 타입 메타 구조는 멤브레인과 cavity의 결합구조이다. 이때 이 두 가지가 결합한 메타 구조의 음향 임피던스는 식 (4)와 같이 멤브레인의 임피던스와 cavity의 임피던스의 합으로 표현할 수 있다.
| (4) |
멤브레인의 임피던스는 멤브레인의 진동으로 발생한 유효질량에 의한 임피던스와 댐핑에 의한 임피던스의 합으로 식 (5)와 같이 표현할 수 있다(10,11).
| (5) |
여기에서는 R은 멤브레인의 진동으로 발생하는 감쇠에 의한 저항임피던스이고, M은 멤브레인의 진동으로 발생하는 유효질량에 의한 임피던스이다.
Cavity 구조의 음향 임피던스는 cavity의 단면적 S와 높이 h로 결정되어 식 (6)과 같이 표현된다.
| (6) |
또한, 이렇게 구한 메타 구조의 음향 임피던스를 통해 식 (7)과 같이 흡음률 α를 계산할 수 있다. 이때 Za는 단면적 S를 가지는 도파관을 지나는 공기의 임피던스로 공기의 고유음향임피던스의 값을 도파관의 단면적 S로 나눈 값을 통해 구할 수 있다. 특히 공기의 고유음향임피던스 Zair는 공기의 밀도와 음속이 곱한 값으로 표현된다. 이때 20 ℃에서 공기는 밀도 ρ가 1.2 kg/mm3, 음속 c가 343 m/s이므로 공기의 고유음향임피던스 Zair는 420 kgm-2m-1의 값을 가진다(12).
| (7) |
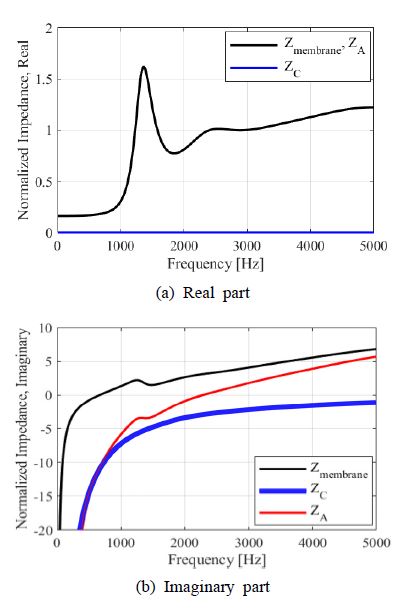
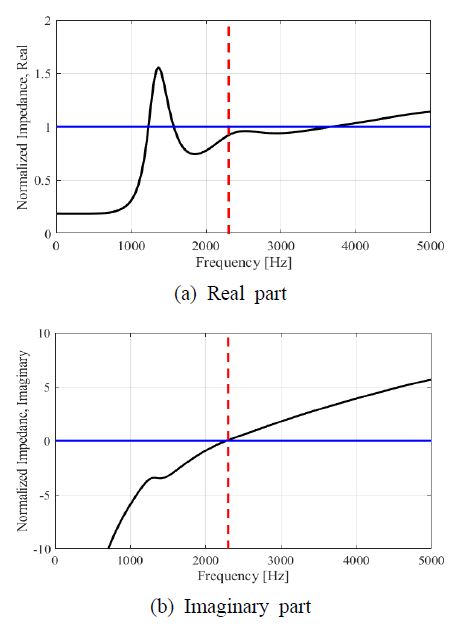
Fig. 3은 식 (4) ~ (6)으로 계산한 정규화된 임피던스의 실수와 허수부 그래프로 멤브레인 타입 메타 구조의 정규화된 임피던스는 식 (4)에 따라 멤브레인과 cavity의 정규화된 임피던스의 합으로 계산한다. 이때 ZC의 실수부는 식 (6)에 따라 존재하지 않기 때문에 ZA의 실수부는 Zmembrane의 실수부와 같다. 따라서 Fig. 3(a)에서는 Zmembrane만 도시한다.
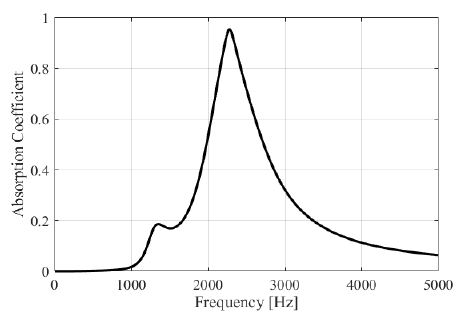
이렇게 계산한 정규화된 임피던스 값을 식 (7)에 대입하여 구한 흡음률을 Fig. 4에 도시하였다. 흡음률은 2300 Hz에서 최대값을 가진다.
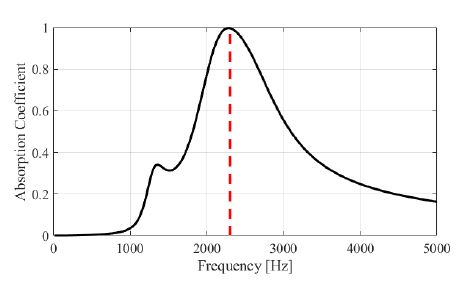
이 연구는 cavity의 높이 h가 10 mm, 한 변의 길이가 20 mm인 흡음 구조를 설계하여 Fig. 3과 같이 임피던스 튜브에 삽입한 형태로, COMSOL multiphysics 5.4 소프트웨어를 통한 FEM 해석을 수행하였다. 이때 멤브레인은 COMSOL multiphysics 내부의 membrane 모듈을 사용하였고, polyimide의 물성을 바탕으로 하여 26.11 N/m의 장력과 rayleigh damping을 사용하여 구현하였다. 그 후 음파 분리법을 이용해 멤브레인 타입 메타 구조의 흡음률을 구하면 Fig. 5와 같은 값을 가진다. 흡음률 그래프는 2300 Hz에서 최대 흡음률을 가지며 그 값은 0.998로 거의 1에 가깝다.
이 흡음률 결과를 임피던스 매칭 관점에서 분석하기 위하여 멤브레인 타입 메타 구조의 정규화된(normalized) 임피던스를 계산하였다. 이때 정규화된 임피던스는 음향 재료의 임피던스와 공기의 임피던스와의 비로, 멤브레인 타입 메타 구조의 정규화된 임피던스를 Fig. 2의 unit cell에서 멤브레인 표면의 입자 속도와 압력을 측정한 결과를 통해 계산하고 도파관 내의 공기의 음향 임피던스로 나눠주면 식 (8)과 같다.
| (8) |
Fig. 6은 membrane-cavity 구조의 정규화된 임피던스값으로 (a)는 임피던스의 real 값 (b)는 imaginary 값이다. Fig. 4의 (a)에서 정규화된 임피던스 Zn의 real 값은 2300 Hz에서 1에 가까운 값을 가진다. 즉, 공기의 음향 임피던스 Za와 흡음 구조의 음향 임피던스 ZA의 real 값이 거의 같아진다. 이를 식 (7)에 대입하면 흡음률 α가 1이 되는 것을 확인할 수 있다. 또한, Fig. 5의 (b)에서 정규화된 임피던스 Zn의 imaginary 값은 2300 Hz에서 0이 되며 위상이 변한다. 이를 통해 Fig. 3의 흡음률 그래프를 분석하면 멤브레인 타입 메타 구조의 음향 임피던스 ZA는 2300 Hz에서 공기의 음향 Za와 매칭되어 멤브레인 타입 메타 구조가 2300 Hz에서 1에 가까운 최대 흡음률을 가지는 것을 확인할 수 있다. 이때 이것을 Fig. 4에서 식 (7)을 통해 계산한 흡음률과 비교하였을 때 동일한 목적 주파수를 가지는 것을 확인할 수 있다.
2.4 Cavity 크기에 따른 흡음률 분석
멤브레인 타입 메타 구조에서 흡음대역의 목적 주파수를 조율하기 위해 변경할 수 있는 parameter들은 멤브레인의 두께, 재질 그리고 cavity의 부피 등이 있다. 이때 임피던스 매칭의 관점에서 볼 때 cavity의 높이를 바꿔 부피를 조절하는 것이 흡음과 상관관계가 크고 parameter의 변화에 따른 목적 주파수 변화를 직관적으로 확인하기 쉽다. 따라서 이 연구에서는 cavity의 높이 변화에 따른 흡음률을 분석한다.
Cavity 높이 h에 따른 흡음률 변화를 알아보기 위하여 h가 각각 15 mm, 10 mm, 5 mm일 때의 흡음률을 계산하였다. Fig. 7는 cavity 높이 h에 따른 흡음률 그래프이다. Fig. 5에서 h = 15 mm일 때 흡음률이 최대가 되는 목적 주파수는 1800 Hz, h = 10 mm일 때 목적 주파수는 2300 Hz, h = 5 mm일 때 목적 주파수는 3100 Hz이다.
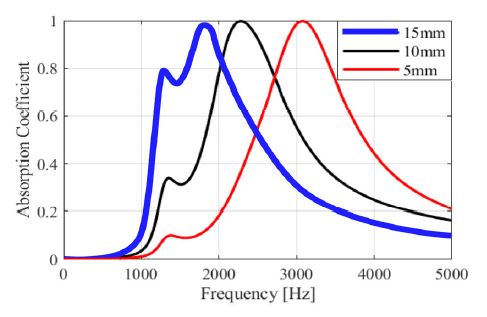
Variation of simulated absorption coefficient of with the intervals 15 mm, 10 mm, 5 mm (the peak frequencies are identically at 800 Hz, 2300 Hz, 3100 Hz)
즉, h가 커질수록 목적 주파수는 저주파에 형성된다고 볼 수 있다. 이는 식 (6)에서 확인할 수 있는데, 멤브레인의 음향 임피던스 Zmembrane과 공기의 음향 임피던스 Zair는 h에 따라 변화가 없는 반면 cavity에 의한 음향 임피던스 Zc는 h에 따라 변한다. 이때, h가 작아지면 음향 컴플라이언스(acoustic compliance)가 작아지고, 이에 따라 음향 스티프니스(acoustic stiffness)이 커짐에 따라, 최대의 흡음률을 구현하기 위한 멤브레인 공진주파수가 커지기 때문에 높은 주파수에서 음향 임피던스가 매칭된다. 반대로 h가 커지면 음향 스티프니스가 작아짐에 따라, 낮은 주파수에서 최대의 흡음률이 구현된다. 이러한 원리로 cavity의 높이 h를 이용해 음향 임피던스를 변경할 수 있고 결과적으로 목적 주파수를 조율할 수 있다.
3. 실 험
3.1 Impedance tube 실험
Fig. 8은 흡음률 측정을 위해 사용한 Brüel & Kjær사의 임피던스 튜브이다. 측정에 사용한 임피던스 튜브의 지름은 29 mm로 식 (9)에 따라 6400 Hz의 cut-off frequency를 가진다. 이 실험은 2000 Hz ~ 4000 Hz 대역에서 흡음 성능을 확인하기 위해 랜덤 신호를 발생시켜 흡음률을 측정하였고, 측정 데이터 중 1000 Hz ~ 5000 Hz 대역을 확인한다.
| (9) |
Fig. 9는 임피던스 튜브를 통해 측정한 흡음률로 점선은 FEM 해석을 통해 계산한 흡음률 그래프이고 실선은 Brüel & Kjær 사의 임피던스 튜브를 통해 실제 측정한 흡음률 그래프이다.
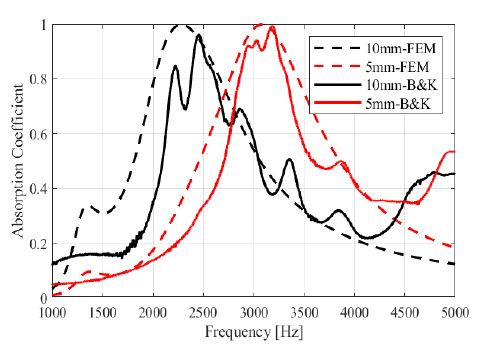
Comparisons of simulated absorption coefficient and measured absorption coefficient (the peak frequencies are similar depending on each height of cavity)
Fig. 9의 실제 측정 흡음률을 보면 cavity의 높이 h가 10 mm일 때는 흡음률이 최대가 되는 목적 주파수가 약 2400 Hz이고 h가 5 mm일 때는 목적 주파수가 약 3150 Hz이다. FEM 해석을 통해 계산한 흡음률의 목적 주파수 2300 Hz, 3100 Hz와 비교했을 때 완전히 일치하지는 않지만, cavity가 작아지면 목적 주파수가 커지는 경향이 그대로 나타나고 그래프의 형태가 유사하며 목적 주파수 또한 근사하는 값을 가지는 것을 확인할 수 있다. 이때 FEM 해석과 실제 측정 흡음률 그래프의 차이는 멤브레인 장력(tension) 및 감쇠(damping)에 대한 해석과 실험의 차이에서 기인한다.
3.2 음압 레벨 실험
이 연구는 기계구조물에서 2000 Hz ~ 4000 Hz 대역의 소음을 효과적으로 저감하는 것을 목적으로 한다. 따라서 멤브레인 타입 메타 구조의 실질적 소음 저감 효과를 확인하기 위해 멤브레인 타입 메타 구조를 기반으로 하는 흡음 덕트를 제작하여 음압 레벨(sound pressure level)을 측정한다.
음압 레벨은 음의 크기를 나타내기 위한 값으로, 특정한 위치에서 측정한 음압과 기준 음압을 통해 계산할 수 있다.
입사파와 반사파의 소음 레벨 차이를 무반사단을 통해 구하는 투과 손실(transmission loss)과는 달리 음압 레벨은 실질적으로 귀에 전달되는 소음을 직관적으로 판단할 수 있으므로(13,14) 이 연구에서는 아무 장치가 없는 상태, 멤브레인이 부착되어 있지 않은 격자 상태의 덕트, 멤브레인을 부착하여 메타 구조를 형성하는 흡음 덕트, 세 가지 상태의 음압 레벨의 비교를 통해 멤브레인 타입 메타 구조의 소음 저감 성능을 판단하였다. 이때 흡음 덕트는 한 변의 길이가 130 mm인 정육면체 형태로, 한 변의 길이가 20 mm이고 h가 10 mm인 cavity 100개를 가진다.
음압 레벨을 측정하기 위해 Fig. 8과 같이 반무향실에서 white noise를 발생시키고 음원의 수직 방향으로 1 m 떨어진 위치에 microphone을 위치시켜 측정을 진행하였다.
Fig. 11의 (a)는 speaker 주변에 아무것도 없이 측정한 음압레벨, speaker를 멤브레인을 부착하여 cavity를 형성한 흡음 덕트와 멤브레인이 없는 상태의 격자 구조 덕트로 감쌌을 때의 음압 레벨 그래프이다. 이때, Fig. 11의 (b)는 멤브레인에 의한 흡음 효과를 직접 비교하기 위해 멤브레인을 부착하여 cavity를 형성한 덕트로 감쌌을 때의 음압 레벨에서 멤브레인을 부착하지 않은 격자 구조 덕트로 감쌌을 때의 음압 레벨을 뺀 그래프이다.
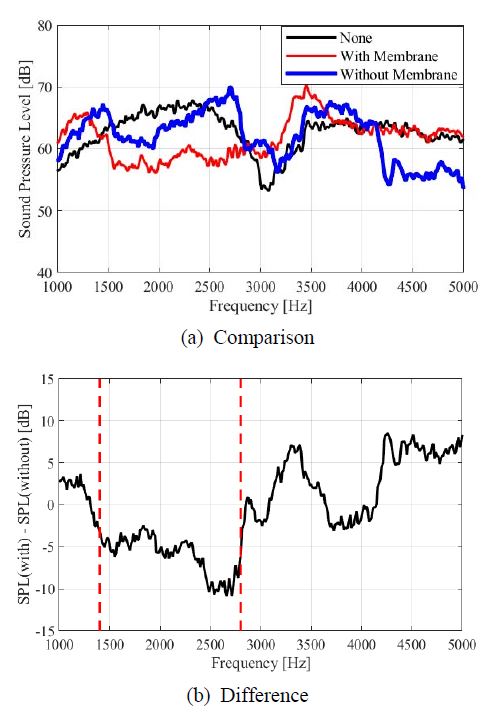
Comparison and difference of sound pressure level of absorption duct with membrane and without membrane
이 그래프들을 앞서 Fig. 5에서 알아본 흡음률 그래프와 비교해서 분석하면 흡음률은 2300 Hz에서 가장 크게 나타났는데, 해당 주파수 주변의 1400 Hz ~ 2800 Hz대역에서 멤브레인을 부착한 상태의 흡음 덕트의 음압 레벨이 더 낮게 측정되었으며 그 값은 평균 6 dB가량이다. 해당 대역 이외의 구간에서는 멤브레인이 없을 때의 소음 저감이 더 큰데 이는 덕트의 구조에 의한 소음 저감 현상으로 보인다. 이를 통해 흡음 덕트의 구조 때문이 아니라 멤브레인 타입의 메타 구조로 인해 해당 대역의 소음이 감소한다고 판단할 수 있다.
4. 결 론
이 논문에서는 2000 Hz ~ 4000 Hz 대역의 소음을 효과적으로 줄이기 위하여 멤브레인과 cavity가 결합한 멤브레인 타입 흡음 구조를 설계하였다. 얇은 박막으로 구성된 멤브레인의 진동으로 발생한 댐핑에 의해 공기와 메타 구조의 임피던스가 특정 주파수에서 매칭되고, 매칭된 주파수에서 완전 흡음률(α = 1)을 거의 구현하였다. 특히 임피던스가 매칭되는 주파수 관점에서 분석하면 cavity의 높이가 커질수록 공기의 임피던스와 매칭되는 주파수가 낮아지고 따라서 저주파 대역에서 최대 흡음률을 가짐을 확인하였다. 또한, 멤브레인 타입 메타 구조의 소음 저감 효과를 직관적으로 확인하기 위해 임피던스 튜브 흡음 실험과 음압 레벨 실험 결과를 통해 멤브레인 타입 메타 구조의 흡음 성능을 확인하였다.
기 호 설 명
| A : | 웨이브 가이드에서 입사파의 진폭 [Pa] |
| α : | 흡음률 |
| B : | 웨이브 가이드에서 반사파의 진폭 [Pa] |
| c : | 공기의 속도 [m/s] |
| d : | 임피던스 튜브의 지름 [m] |
| fcutoff : | 차단 주파수 [Hz] |
| h : | cavity의 높이 [m] |
| k : | 파수 [m-1] |
| M : | 멤브레인의 유효질량 |
| P : | 한 지점에서의 압력 [Pa] |
| Pz : | 특정 위치에서 측정한 음압 [dB] |
| P0 : | 기준 음압 [dB] |
| p : | 음압 [Pa] |
| ρ : | 밀도 [kg/m3] |
| R : | 멤브레인의 viscous damping |
| γ : | 반사 계수 |
| S : | 도파관의 넓이 [mm2] |
| SPL : | 음압 레벨 [dB] |
| υ : | 입자 속도 [m/s] |
| w : | 각 주파수 [rad/m] |
| x : | 기준 면에서 마이크까지의 거리 [m] |
| ZA : | 메타 구조의 음향 임피던스 [kgm-2s-1] |
| Za : | 도파관 내부의 공기 고유음향임피던스 [kgm-2s-1] |
| Zair : | 공기 음향 임피던스 [kgm-2s-1] |
| Zc : | cavity의 음향 임피던스 [kgm-2s-1] |
| Zmembrane : | 멤브레인의 음향 임피던스 [kgm-2s-1] |
| Zn : | 정규화된 임피던스 [kgm-2s-1] |
Acknowledgments
이 논문은 부산대학교 기본 연구지원사업(2년)에 의하여 연구되었음.
References
-
Weber, A. and Resch, K., 2012, Thermotropic Glazings for Overheating Protection, Energy Procedia, Vol. 30, pp. 471~477.
[https://doi.org/10.1016/j.egypro.2012.11.056]

-
Hermans, L. and Van Der Auweraer, H., 1999, Modal Testing and Analysis of Structures under Operational Conditions: Industrial Applications, Mechanical Systems and Signal Processing, Vol. 13, No. 2, pp. 199~216.
[https://doi.org/10.1006/mssp.1998.1211]

-
Kumar, S. and Lee, H. P., 2020, Recent Advances in Acoustic Metamaterials for Simultaneous Sound Attenuation and Air Ventilation Performances, Crystals, Vol. 10, No. 8, pp. 1~22.
[https://doi.org/10.3390/cryst10080686]

-
Xiang, X., Wu, X., Li, X., Wu, P., He, H., Mu, Q., Wang, S., Huang, Y. and Wen, W., 2020, Ultra-open Ventilated Metamaterial Absorbers for Sound-silencing Applications in Environment with Free Air Flows, Extreme Mechanics Letters, Vol. 39, 100786.
[https://doi.org/10.1016/j.eml.2020.100786]

- Jung, J. S. and Wang, S. M., 2015, Topology Optimization of Membrane-type Acoustic Metamaterials for Low Frequency Noise Reduction, Proceedings of the KSNVE 2015 Annual Spring Conference, pp. 503~505.
- Ahn, B. H. and Lee, J. W., 2020, Meta-structure Muffler Design to Reduce Noise in Target Frequency Band, Proceedings of the KSNVE 2020 Annual Autumn Conference, p. 84.
-
Park, Y., Bae, J. and Lee, J. W., 2015, Design of a Perforated Panel for Transmission Noise Reduction, Transactions of the Korean Society of Mechanical Engineers A, Vol. 39, No. 4, pp. 437~445.
[https://doi.org/10.3795/KSME-A.2015.39.4.437]

- Material: Polyimide, Material Property Database, Last Modified n.d., https://www.mit.edu/~6.777/matprops/polyimide.htm, (accessed September 14, 2021).
- Shim, K. H., Jang, J., Kwon, H. J. and Song, K.-J., 2021, Design of Acoustic Meta-material Silencer Based on Coiled Up Space, The Journal of the Acoustical Society of Korea, Vol. 40, No. 1, pp. 31~37.
-
Ren, S. W., Van Belle, L., Claeys, C., Xin, F. X., Lu, T. J., Deckers, E. and Desmet, W., 2019, Improvement of the Sound Absorption of Flexible Micro-perforated Panels by Local Resonances, Mechanical System and Signal Processing, Vol. 117, pp. 138~156.
[https://doi.org/10.1016/j.ymssp.2018.07.046]

-
Lan, J., Zhang, X., Liu, X. and Li, Y., 2018, Wavefront Manipulation Based on Transmissive Acoustic Metasurface with Membrane-type Hybrid Structure, Scientific Reports, Vol. 8, 14171.
[https://doi.org/10.1038/s41598-018-32547-3]

- Acoustic Impedance, Intensity and Power, Unsw, Last Modified n.d., https://www.animations.physics.unsw.edu.au/jw/sound-impedance-intensity.htm, (accessed September 14, 2021).
-
Lee, J. K., Oh, K. S. and Lee, J. W., 2016, Optimal Muffler Design Considering the Insertion Loss Calculated Outside the Duct, Transactions of the Korean Society of Mechanical Engineers A, Vol. 40, No. 5, pp. 497~503.
[https://doi.org/10.3795/KSME-A.2016.40.5.497]

- Im, Y. B. and Kim, M. J., 1996, Sound Insulation Performance of Noise Barriers for Apartment House Site near Road by Field Measurement, Journal of the Architectural Institute of Korea, Vol. 12, No. 8, pp. 185~194.

Seok Gyu Lee received his B.S. and M.S. degrees in mechanical design engineering from Pusan National University, Busan, Korea in 2020 and 2022, respectively. His research interests include His current research interests include noise and vibrations, and acoustic meta-materials.

JunYoung Jang received B.S. and M.S. degree from Pusan National University in 2018 and 2020, respectively. He is currently majoring in noise and vibration in Pusan National University. His current research interests include the acoustic metamaterial, and measurement & signal processing.

Kyungjun Song received B.S. degree from Seoul National University in 2002 and Ph.D. degree from the University of Michigan, Ann arbor, Michigan, USA in 2010. He is an assistant professor in Mechanical Engineering Department of Pusan National University, Busan. Korea. His current research interests include noise and vibrations, and acoustic meta-materials.