FRF 기반 부분구조합성법을 이용한 차량 진동성능 강건설계

1. 서 론

다양한 분야에서 진동의 제어는 중요한 기술 중 하나이다. 특히, 자동차 분야에서 진동은 사고의 원인이 될 수 있으며, 승차감을 저하시키는 원인이 된다. 이러한 진동을 제어하면 승차감이 향상되며, 판매량의 증가를 기대할 수 있다. 운전자에게 전달되는 진동의 크기를 수동제어하기 위해서는 차량의 연결부를 일래스토머로 구성하는 것이 일반적이다. 하지만 일래스토머는 주어진 정하중과 주파수에 의해 동특성이 변하는 불확실성을 지니고 있다⁽¹⁾. 이러한 일래스토머의 불확실성으로 인해 운전자에게 전달되는 진동의 크기를 예측하기 어려운 특징이 있다.

자동차의 진동응답을 최소화하기 위한 설계시 전체 시스템을 유한요소모델로 표현하여 상용화된 해석프로그램을 이용하는 것은 비효율적이다. 따라서 효율적인 계산을 위해서는 전체 시스템을 부분구조와 연결부로 나누고, 부분구조를 동특성 정보로 표현하는 방법이 필요하다. 부분구조를 주파수응답함수의 정보로 표현하여 전체 시스템의 응답을 구하는 주파수응답함수 기반 부분구조합성법은 부분구조 동특성의 정보손실이 없어 유용하게 사용된다⁽²⁾.

설계인자의 변화에 따른 관심응답의 변화의 정도를 민감도라고 부른다. 전역민감도 해석은 각 설계점에서 설계변화의 선형 기울기를 나타내는 국부적 민감도와 다르게 설계영역에서 설계인자의 변화에 따른 관심응답의 전체 변화를 상관관계로 나타낸 것이다. 불확실성을 지닌 일래스토머의 강성을 설계인자로 차량의 진동응답의 변화의 예측하고 영향력을 계산하기 위해서는 전역민감도해석을 사용하는 것이 필요하다^(3,4).

불확실성을 지닌 일래스토머를 고려하여 차량의 진동문제에 대해서 전역민감도해석을 수행하기 위해서는 몬테카를로 해석(monte carlo simulation, MCS)과 같은 샘플링기법을 이용하여 설계인자의 기여도를 계산하는 분산기반의 전역민감도해석이 유리하다^(4~6). 몬테카를로 해석에서 많은 샘플링으로 인한 계산시간 측면에서의 비효율성은 무작위균형설계를 이용하면 효율적인 계산시간으로 전역민감도해석을 할 수 있다^(4,7,8).

일래스토머의 동특성에 따라 변하는 진동응답의 크기와 변동성을 줄이기 위해 평균과 분산을 최소화하는 최적화가 필요하다⁽⁴⁾. 유전자알고리즘은 이와 같은 비선형 문제에 대해 최적화가 가능하다. 그러나 전역 최소화 문제에서 샘플링기반의 함수값 계산이 필요한 경우 계산비용은 설계변수의 수와 함께 기하급수적으로 증가하게 된다. 따라서 이러한 전역최적설계문제에서는 설계변수를 최소화하고 효율적인 샘플링 기반의 평균과 분산의 계산방법이 필요하다. 이 연구에서는 전역민감도 해석법을 이용하여 설계정식화 단계에서 설계변수를 선별하는 방법을 제안하고, 선별된 설계변수를 바탕으로 FRF기반 부분구조합성법과 무작위균형설계법을 이용한 일래스토머의 전역적 강건설계을 제안하고 이를 자동차 진동문제에 적용하였다.

2. 차량 진동응답 계산 및 민감도해석

2.1 주파수응답함수 기반 부분구조합성법

자동차와 같이 복잡한 기계 구조물의 진동응답을 효율적으로 계산하기 위해 전체 시스템을 부분구조와 연결부의 동특성으로 표현하는 방법이 있다. 동특성 정보는 모달 파라메타, 주파수응답함수, 특성행렬 등이 있으며 주파수응답함수를 이용한 부분구조합성법은 부분구조의 정보손실 없이 연결부의 동특성 변화에 따라 전체 시스템을 쉽게 재구성할 수 있어 계산비용이 효율적이다⁽⁹⁾.

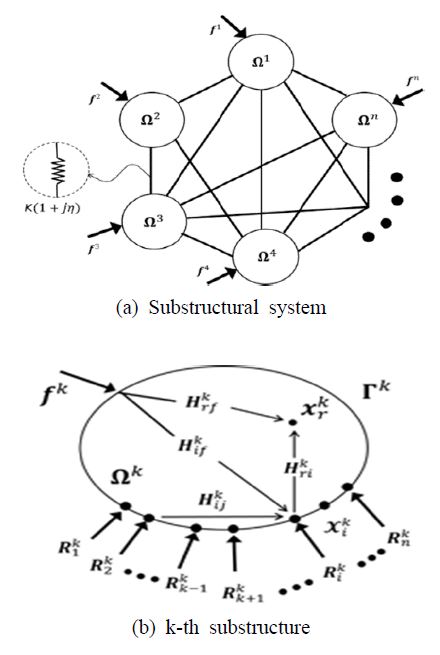
주파수응답함수 기반 부분구조합성법은 Fig. 1(a)와 같이 n개의 부분구조와 외력 그리고 연결부로 이루어진 구조계로 표현되며, Fig. 1(b)는 k번째 부분구조를 표현한다. k번째 부분구조에서 주파수응답함수의 정보는 식 (1)과 같이 정리할 수 있다.

$\[ H^k=\left[\begin{array}{cccc}{H}_{11}^k& H_{12}^k& \cdots & H_{1n}^k\\ H_{21}^k& H_{22}^k& \cdots & H_{2n}^k\\ ⋮& ⋮& \ddots & ⋮\\ H_{n1}^k& H_{n2}^k& \cdots & H_{nn}^k \end{array}\right], n\ne k \]$

(1)

Fig. 1

Substructural system and its FRFs

각 응답점에서 발생되는 반력은 작용과 반작용의 원리에 의해 식 (2)가 성립한다.

$\[ \begin{array}{cccc}{R}_i^k+R_k^i=0,& i,& k=1,\cdots ,n,& i\ne k\end{array} \]$

(2)

이때 각 연결부는 강성과 손실계수로 표현할 수 있으며 식 (3)의 조건을 만족해야한다.

$\[ \begin{array}{cccc}{C}_{ki}·R_i^k=x_i^k-x_k^i,& i, & k=1,\cdots ,n,& i\ne k\end{array} \]$

(3)

식 (3)에서 C_ki는 k번째 구조물과 i번째 구조물을 잇는 연결부의 컴플라이언스 행렬로 식 (4)와 같이 표현된다.

$\[ \begin{array}{l}diag\left(C_{ki}\right)=\frac{1}{K_{ki}\left(1+j{\eta }_{ki}\right)}\\ \begin{array}{ccc}i,& k=1,\cdots ,n, & i\ne k\end{array}\end{array} \]$

(4)

여기서 K_ki와 η_ki는 방향성이 없기 때문에 K_ki = K_ik와 η_ki = η_ik의 특성을 가진다. 식 (2), (3)을 정리하여 나타내면 식 (5)로 나타낼 수 있다.

$\[ H\cdot R=Q \]$

(5)

식 (5)를 이용하여 전체 시스템 행렬의 역행렬을 구하면 반력벡터를 구할 수 있으며, k번째 부분구조에서 임의로 정해진 r점의 응답을 식 (6)과 같이 구할 수 있다.

$\[ \begin{array}{l}{x}_r^k=\sum _{i=1,i\ne k}^n{H}_{ij}^k\cdot R_j^k+H_{if}^k\cdot f^k\\ \begin{array}{cc}i=1,\cdots ,n& i\ne k\end{array}\end{array} \]$

(6)

주파수응답함수 기반 부분구조합성법을 이용하면 컴플라이언스 행렬의 값을 수정하여 부분구조의 정보변화 없이 연결부의 강성 값에 따른 전체 시스템을 재구성할 수 있다.

2.2 전역민감도해석

(1) 분산기반 전역민감도해석

설계인자 X_k(k = 1, ⋯, n)가 관심응답에 영향을 미칠 때, i번째 인자 X_i의 관심응답에 대한 영향도는 E(Y|X_i)의 분산으로 나타낼 수 있다. 따라서 X_i의 영향도를 전체 분산으로 정규화하면 일차 민감도계수를 구할 수 있으며 식 (7)과 같이 정의할 수 있다.

$\[ S_i=\frac{V\left(E\left(Y\left|X_i\right.\right)\right)}{V\left(Y\right)} \]$

(7)

위 식에서 V와 E는 분산과 기대값을 의미한다.

(2) 무작위균형설계

분산기반의 전역민감도해석에서 사용되는 조건부평균을 계산하기 위한 샘플링기법 중 하나이다. 무작위균형설계는 푸리에진폭 감도시험을 개선한 방법으로 식 (8)을 이용하여 설계인자를 계산한다.

$\[ X_i\left(s_{ij}\right)=G_i\left(\mathrm{s}\mathrm{i}\mathrm{n}\omega s_{ij}\right) \]$

(8)

식 (8)에서 G_i는 확률분포함수를, s_ij는 샘플링 포인트를 나타낸다. 무작위균형설계는 다음의 절차로 나타낼 수 있다.

Step 1. 각 인자마다 -π에서 π의 범위에서 샘플링을 통해 N개의 점 s_ij생성

Step 2. 생성된 점을 식 (8)에 대입하여 k개의 설계 인자를 N개씩 계산

Step 3. 각 설계인지를 무작위로 선정하여 N개의 관심응답 계산

Step 4. i번째 인자에서 선택된 점의 순서에 따라 N개의 관심응답 재배치하여 푸리에변환 후 식 (7)을 통해 1차 민감도계수 계산

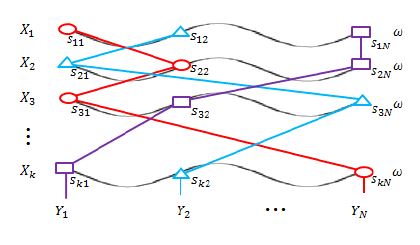
Fig. 2는 무작위균형설계를 표현한 것으로 동그라미, 세모, 네모 표시는 각 설계인자를 무작위로 선정하여 각 표식의 응답을 구한 것을 나타낸다.

Fig. 2

Random balance design (RBD)

무작위균형설계는 푸리에진폭 감도시험에서 발생되는 엘리어싱 문제를 해결할 수 있으며, 단일 각속도를 사용함으로써 계산이 단순하다. 또한, 적은 수의 샘플링으로 많은 경우의 수를 고려할 수 있어 효과적으로 사용할 수 있다.

2.3 유전자알고리즘

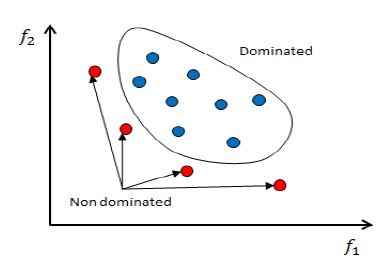
유전자알고리즘은 경계조건 내에서 무작위로 N개의 개체를 가지는 초기 모집단을 생성한 후 각 개체들의 적합성을 판단한다. 두 개체의 접합성에 따라 선택하여 일정한 확률로 각 개체의 특성을 교배 또는 무작위로 변이함으로써 새로운 개체를 생성한다. 생성된 개체를 새로운 모집단에 배치하면 다음 세대의 모집단이 된다. 이러한 계산을 설정한 세대 수 반복하여 최종적으로 선택된 개체들을 파레토 최적해라고 한다. 파레토 최적해들은 서로 지배하지 않는 관계를 가지고 있다. 여기서 ‘비지배한다’는 의미는 다른 개체보다 우월하다는 것이다. 이러한 지배 또는 비지배에 대한 개념을 Fig. 3에서 표현했다. 이러한 비지배 파레토 개체의 집합을 파레토 최적해(pareto optimum)라고 정의하고 함수적으로 파레토 최적선이라 표현한다.

Fig. 3

Dominated and non-dominated solution

3. 자동차 진동성능 강건설계

3.1 강건설계 정식화

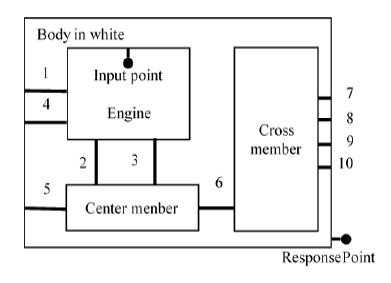
자동차에서 발생되는 진동은 다양한 원인이 있지만, 엔진에서 발생되는 진동은 주행 또는 정차상태에 상관없이 승차감에 영향을 준다. 따라서 자동차 진동성능을 강건설계하기 위해 Fig. 4와 같은 시스템을 다루었다.

Fig. 4

Passenger car for verification

전체 시스템은 엔진, 센터멤버, 크로스멤버 그리고 차체 4개의 부부구조와 10개의 연결부로 구성했으며, 엔진은 강체로 가정하였고, 연결부는 불확실성을 지닌 일래스토머로써 1번 ~ 4번은 엔진마운트, 5번 ~ 10번은 부시로 구성했다. 차체의 FRF는 유한요소 모델을 이용하여 계산하고 차체의 플로어에서 진동을 계산할 수 있는 FBS 모델을 구성하였다.

평균뿐만 아니라 분산을 최소화하는 강건설계 문제를 정식화하기 위해 X, Y, Z 방향을 고려한 일래스토머의 강성 30개를 설계변수로 정의하였으며, 목적함수는 일정한 입력이 있을 때, 설계변수의 불확실성으로 인해 분포를 가지는 응답들의 평균(μ)과 분산(σ)을 최소화하도록 식 (9)와 같이 정의했다⁽¹⁰⁾.

$\[ \begin{array}{l}\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}\left(f_1\left(x\right),f_2\left(x\right)\right)\\ \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} f_1\left(x\right)={\mu }_{acc}, f_2\left(x\right)={\sigma }_{acc}^2, x\in X\end{array} \]$

(9)

이때, acc는 진동성능으로 응답점에서 가속도의 값을 관심주파수 영역(1 Hz ~ 80 Hz)에서 가속도 값과 기준값 사이의 면적이다. 각 연결부의 방향에 따른 설계변수의 번호를 Table 1에 나타내었다.

Table 1

Definition set of design variable

3.2 부분구조합성 모델을 이용한 강건설계

(1) 주파수응답함수 기반 부분구조합성법 검증

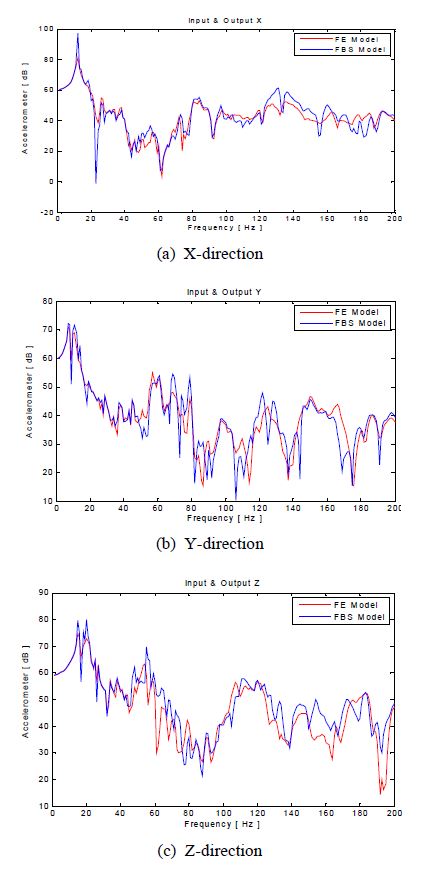
강건설계문제를 해결하기 앞서 주파수응답함수 기반 부분구조합성법으로 계산된 응답을 검증하였다. 검증을 위해 전체시스템을 유한요소모델로 구성하여 해석프로그램을 통해 계산된 응답점에서 진동가속도의 값과 각 부분구조를 해석프로그램을 이용하여 전달함수를 구한 후 주파수응답함수 기반 부분구조합성법을 통해 계산된 응답점에서 진동가속도의 값을 비교하였다. 해석프로그램은 MSC/Nastran의 direct frequency response (Sol.108)를 사용하였으며, 주파수응답함수 기반 부분구조합성법의 계산은 Matlab 7.10.0 (2010a)을 사용했다. 두 가지 방법으로 계산된 비용과 응답을 Table 2와 Fig. 5에 나타내었다.

Table 2

Elapsed CPU time for FRF analysis

Fig. 5

FBS model validation compared with those of FE model

Table 2는 각 프로그램을 이용한 해석시간을 정리했으며, 하나의 샘플링에서 계산시간이 각 4.53시간과 1.35시간이 소요되었다. 연결부의 동특성의 불확실성을 고려하여 많은 수의 샘플링을 사용하여 계산할 때, FE 모델의 해석시간은 샘플링 수가 증가할수록 초기의 해석시간에 비례하여 증가하는 반면, FBS 모델의 해석시간은 FBS계산시간만 추가되기 때문에 1000번의 샘플링에서는 대략 4527시간을 절약할 수 있어 효율적인 계산비용이 든다. Fig. 5(a) ~ (c)는 FE모델과 FBS 모델의 각 방향에 따라 0 Hz ~ 200 Hz의 주파수영역에서 진동가속도의 크기를 데시벨(dB)형식으로 나타내었다. 관심주파수 영역인 0 Hz ~ 80 Hz에서 비교하였을 때 각 피크의 위치와 크기가 일치하는 경향을 확인할 수 있었다. 따라서, 불확실성을 지닌 일래스토머를 고려한 시스템의 해석은 주파수응답함수 기반 부분구조합성법을 이용하는 것이 상용화된 해석프로그램을 이용하는 것보다 효율적인 계산비용으로 응답을 계산할 수 있다. 보다 정확한 응답 계산이 필요한 경우 실험기법으로도 검증된 알고리즘을 사용할 수 있다⁽¹¹⁾.

(2) 일래스토머 강성의 불확실성 모델링

강건설계문제에서 설계인자로 선정된 일래스토머의 강성을 표현하기 위해 2.2절에서 언급한 무작위 균형설계에 적용하여 불확실성을 표현하였다. 이때, 확률분포함수는 상한값과 하한값을 정해져 있을 때 확률밀도함수를 기술하는 베타분포함수를 사용하였으며 다음과 같은 식 (10)으로 정의된다⁽¹²⁾.

$\[ {\rm B}\left(a,b\right)={\int }_0^1{x}^{a-1}{\left(1-x\right)}^{b-1}dx \]$

(10)

식 (10)을 이용하여 확률밀도함수는 식 (11)과 같이 표현된다.

$\[ f\left(x;a,b\right)=\frac{1}{{\rm B}\left(a,b\right)}{x}^{a-1}{\left(1-x\right)}^{b-1} \]$

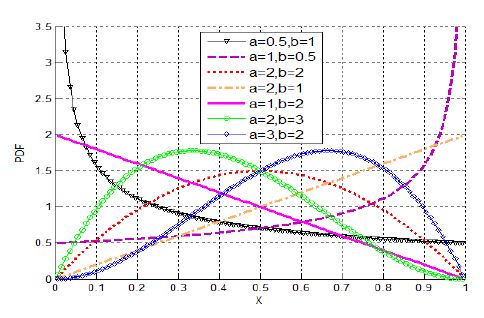
(11)

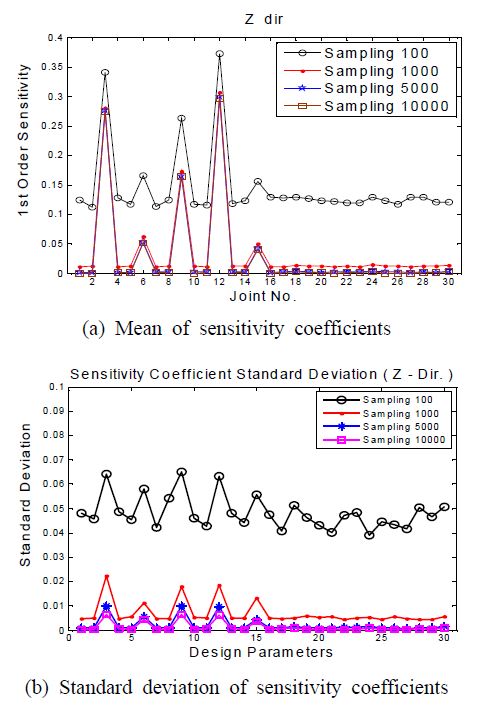
식 (11)에서 x는 구간을 나타내고 a, b의 값에 따라 그 크기가 정해지며, 이에 따른 베타함수의 확률밀도함수는 Fig. 6과 같이 그릴 수 있다. a가 b보다 크면 그래프가 오른쪽으로, a가 b보다 작으면 왼쪽으로 치우치고, a와 b가 같으면 x = 0.5를 기준으로 대칭을 이루는 분포형태를 보인다. 또한, 일래스토머의 강성의 범위는 Table 3에 표현하였다. 이와 같이 정의된 일래스토머 강성의 범위와 분포함수를 적용한 무작위균형설계를 사용하여 1차 민감도 계수를 계산하였다. 1차 민감도계수의 신뢰도를 위해 100, 1000, 5000, 10 000개의 샘플링수를 적용하여 100번 반복하여 계산했다. 샘플링수에 따른 1차 민감도계수의 평균과 표준편차를 다음 Fig. 7에 나타내었다. Fig. 7(a)와 7(b)는 각 샘플링수에 따른 1차 민감도계수의 평균과 분산을 비교한 그래프로서, 샘플링수가 1000개 이상일 때 설계인자의 민감도 결과가 안정되게 수렴하였다. 따라서 일래스토머의 불확실성을 고려하기 위한 최소 샘플링수는 1000으로 결정하였다. 일차 민감도계수의 계산결과는 강건설계시 설계변수를 선택하는 정보로 사용하였다.

Fig. 6

Probability distribution function of beta distribution

Table 3

Assumed distribution of elastomers

Fig. 7

Convergence test for the global sensitivity analysis

(3) NAGA-Ⅱ를 이용한 강건설계

불확실성을 지닌 일래스토머의 특성을 고려한 강건설계문제는 비선형문제이기 때문에 유전자알고리즘 기반의 NSGA-Ⅱ를 이용했다⁽¹³⁾. 이때 80개의 개체를 여러 세대를 거쳐 교배, 돌연변이 계산을 실행하였으며, i번째 세대의 개체가 i-1세대의 개체와 95 % 이상 동일한 경우가 연속 3번 나타났을 때 해를 파레토 최적해로 선정하였다. 또한 파레토 최적해 중 두 개의 목적함수에 0.5의 가중치를 주어 최적의 값을 선정하였다.

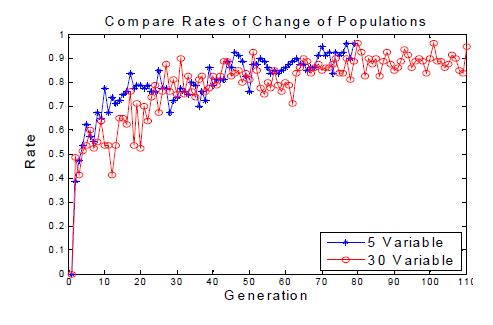
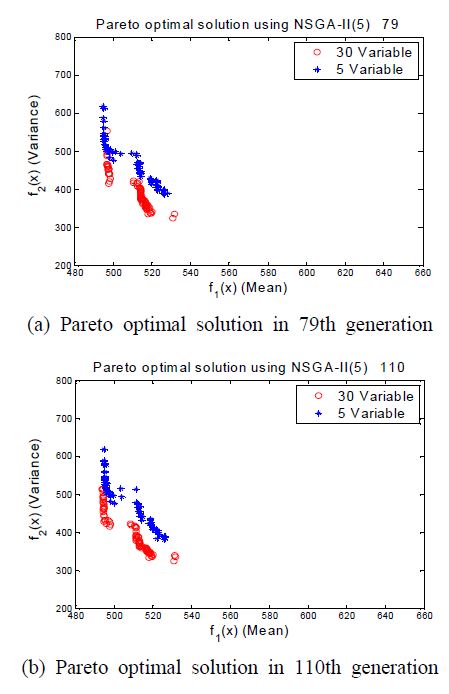
강건설계의 효율성 비교를 위해 1차 민감도계수가 큰 5개의 설계변수를 사용한 설계결과와 30개 전체의 연결부 강성을 설계변수로 선정한 방법을 사용하였다. Fig. 8은 두 가지 경우에 대해서 축차시 세대가 증가함에 따라 변하지 않은 개체의 수의 비를 비교하였다. 5개의 변수와 30개의 변수를 이용한 계산은 각 79세대와 110세대에서 파레토 최적해를 얻을 수 있었다. Fig. 9의 (a)와 (b)에 79세대와 110세대에서 두 가지 경우에 대한 파레토 최적해를 비교하였다. Table 4에 가중값이 0.5인 경우의 최적해를 정리하였다.

Fig. 8

Rate of fixed individuals in populations during the iterations

Fig. 9

Pareto optimal solution using NSGA-Ⅱ

Table 4

Results of multi-objective optimization

결과를 비교하면 5개의 변수를 사용한 방법이 30개의 변수를 사용한 방법보다 적은 수의 세대를 반복하여 최적해를 얻을 수 있었음을 알 수 있다. 소요시간은 30개의 변수를 사용한 방법에 비해 29.33 %의 적었다. 진동성능을 평가할 수 있는 가속도크기 평균은 두 경우에 각각 초기값에 비해 13.59 %, 13.67 % 감소하였고, 분산의 크기는 9.39 %, 23.71 % 감소하였다. 영향도가 큰 주요 설계변수만을 사용하여 강건설계를 하는 경우 평균값은 비슷한 성능을 얻었으나 분산의 경우는 모든 설계변수를 사용하는 경우에 비해 제한적인 결과를 얻었음을 알 수 있다.

4. 결 론

이 연구에서는 분산기반 전역민감도 해석을 위해 주파수응답함수 기반 부분구조합성법을 이용하여 일래스토머 강성의 변화에 따른 진동성능의 민감도를 효율적으로 계산하는 것이 가능했으며, 무작위균형설계를 이용하여 일래스토머의 비선형성을 고려하여 동특성을 확률분포로 나타내어 전역민감도해석을 수행하여 결과를 얻을 수 있었다. 이때 전역민감도 해석은 약 1000번 정도의 적은 수의 샘플링으로 안정적으로 민감도해석을 수행했다.

유전자알고리즘의 계산비용을 효율성을 위해 1차 민감도계수를 이용하여 설계변수의 수를 축소하여 최적화를 수행하는 방법을 제안하였으며 이를 이용한 방법으로 효율인 다목적 최적설계가 가능함을 보였다. 이와 같이 최적화된 일래스토머 강성을 적용하여 1차 민감도계수를 계산하였을 때, 초기의 강성을 적용한 결과보다 감소하였으며, 이를 통해 차량 진동응답의 변동성을 감소시킴으로써 강건설계가 가능함을 보였다.

Acknowledgments

이 연구는 한국연구재단의 지원을 받아 수행된 연구이며(NRF-2021R1H1A2094395), 이에 감사드립니다.

References

• Lee, D., 2008, Optimal Layout Design of Frequency- and Temperature-dependent Viscoelastic Materials for Manximum Loss Factor of Constrained-layer Damping Beam, Transactions of the Korean Society of Noise and Vibration Engineering, Vol. 18, No. 2, pp. 185~191. [https://doi.org/10.5050/KSNVN.2008.18.2.185]
• Lee, D.-H. and Hwang, W.-S., 2003, Parametric Optimization of Complex Systems Using a Multi-domain FRF-based Substructuring Method, Computers & Structures, Vol. 81, No. 22–23, pp. 2249~2257. [https://doi.org/10.1016/S0045-7949(03)00288-8]
• Saltelli, A., Ratto, M., Andres, T., Campolongo, F., Cariboni, J., Gatelli, D., Saisana, M. and Tarantola, S., 2008, Global Sensitivity Analysis: The Primer, John Wiley & Sons, Chichester. [https://doi.org/10.1002/9780470725184]
• Lee, D., Won, Y.-W. and Kwon, J.-H., 2016, Global Sensitivity Analysis of Joints for Plug-in Digital Framework, Transactions of the Korean Society of Mechanical Engineers A, Vol. 40, No. 5, pp. 483~488. [https://doi.org/10.3795/KSME-A.2016.40.5.483]
• Saltelli, A., Annoni, P., Azzini, I., Campolongo, F., Ratto, M. and Tarantola, S., 2010, Variance Based Sensitivity Analysis of Model Output. Design and Estimator for the Total Sensitivity Index, Computer Physics Communications, Vol. 181, No. 2, pp. 259~270. [https://doi.org/10.1016/j.cpc.2009.09.018]
• Cukier, R., Levine, H. and Shuler, K., 1978, Nonlinear Sensitivity Analysis of Multiparameter Model Systems, Journal of Computational Physics, Vol. 26, No. 1, pp. 1~42. [https://doi.org/10.1016/0021-9991(78)90097-9]
• Tarantola, S., Gatelli, D. and Mara, T. A., 2006, Random Balance Designs for the Estimation of First Order Global Sensitivity Indices, Reliability Engineering & System Safety, Vol. 91, No. 6, pp. 717~727. [https://doi.org/10.1016/j.ress.2005.06.003]
• Sobol', I. Y. M., 1990, On Sensitivity Estimation for Nonlinear Mathematical Models, Matematicheskoe Modelirovanie, Vol. 2, No. 1, pp. 112~118.
• Lee, D. H., Hwang, W. S. and Kim, C. M., 2002, Design Sensitivity Analysis and Optimization of an Engine Mount System Using an FRF-based Substructuring Method, Journal of Sound and Vibration, Vol. 255, No. 2, pp. 383~397. [https://doi.org/10.1006/jsvi.2001.4160]
• Jung, B. C., Lee, D., Youn, B. D. and Lee, S., 2011, A Statistical Characterization Method for Damping Material Properties and Its Application to Structural-acoustic System Design, The Journal of Mechanical Science and Technology, Vol. 25, No. 8, pp. 1893~1904. [https://doi.org/10.1007/s12206-011-0517-6]
• Contartese, N., Nijman, E. and Desmet, W., 2022, A Procedure to Restore Measurement Induced Violations of Reciprocity and Passivity for FRF-based Substructuring, Mechanical Systems and Signal Processing, Vol. 167, No. p. 108556. [https://doi.org/10.1016/j.ymssp.2021.108556]
• Montgomery, D. C. and Runger, G. C., 2010, Applied Statistics and Probability for Engineers, John Wiley & Sons, Chichester.
• Deb, K., Pratap, A., Agarwal, S. and Meyarivan, T., 2002, A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II, IEEE Transactions on Evolutionary Computation, Vol. 6, No. 2, pp. 182~197. [https://doi.org/10.1109/4235.996017]