해군 함정 탑재용 전자장비 랙의 수직 기둥 단면 형상 설계에 관한 연구

1. 서 론

기계 구조물에 대한 구조 강성은 초기 기계 시스템을 설계하는 과정에서 가장 우선적으로 검토해야 한다. 통상 구조 강도를 높이기 위해 매우 강성이 큰 부재를 사용하면 되지만 해당 제품을 제작하고 생산하는 입장에서는 요구하는 설계 사양을 만족하는 범위 내에서 최소한의 소재를 사용하여 요구하는 구조 강성을 확보해야 한다. 단순 1차원의 구조 강성의 경우 간단한 구조 강성 관련 수식을 활용하여 강도 계산 후 요구 사항을 최소한으로 만족하는 설계 사양을 도출할 수 있다. 하지만 3차원의 복잡한 형상을 가지는 구조체에 대해서는 효율적 대응을 위해 유한요소 모델을 활용한 구조 강도를 복합적으로 예측하는 기법이 주로 사용된다.

함정에 탑재되는 전자장비 랙(electronic equipment rack, EER)은 통신 및 전술정보 등의 처리, 저장 및 전달 기능을 수행하는 전자장비를 적층 형태로 보관 및 보호하는 구조체이다. 이러한 임무를 수행하는 함정 탑재용 랙은 엔진 구동에 의한 공진 및 수중폭발에 의한 충격하중을 견딜 수 있도록 설계되어야 하며, 충격이 가해진 후에도 전자장비 성능에 이상이 없어야 한다. 기존 연구에서도 함정 탑재용 기계 시스템에 대한 충격이나 진동 관련 연구를 꾸준히 진행했었다^(1~3).

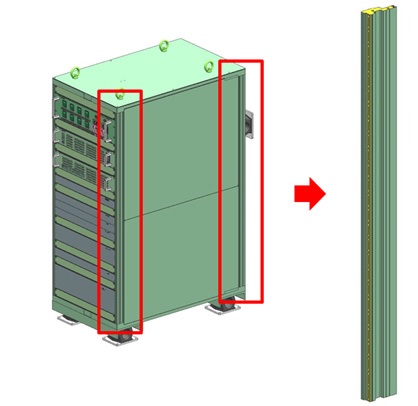
Fig. 1은 실제 해군 함정에 탄성마운트를 부착하여 장착된 EER(제조자: 대양전기, 대한민국)을 보여준다. 전자장비들이 각 층의 랙에 장착되어 있으며 수직 프레임 구조가 전체 구조를 지탱하고 있다. 전자장비를 제외한 프레임 구조(body frame)는 전자장비를 수납하는 랙 부분과 주요 강성을 지탱하는 수직 기둥 부분으로 나눌 수 있다. 통상 랙 부분은 전자장비들을 공정하는 위치를 수행하기 때문에 프레임 구조의 구조 강성과 관련해서는 수직 기둥이 주요한 역할을 수행하게 된다. 수납하는 전자장비는 장비 전면과 프레임 구조 수직기둥 전면에 탭(tap) 가공된 부분에 나사로 조립되며, 장비 인출을 위해 장비의 양옆 슬라이드 레일과 프레임 구조 내부 브라켓 또한 나사로 조립된다. 개별 장비 무게는 통상 5 kg ~ 20 kg 수준이다. 하단은 탄성 마운트를 사용하여 함정 바닥과 연결되며, 정강성이 대략 20 kN/m ~ 150 kN/m 값을 가진다. 이 연구에서 프레임 구조의 구조해석은 해당 탄성 마운트는 제외하고 프레임 구조 자체의 동적 특성만을 이용하여 연구를 수행하였다. 향후 시스템 단위에서 EER 해석을 수행하기 위해서는 반드시 장비의 질량, 탄성마운트 특성값을 활용하여야 한다.

Fig. 1

Example of EER installed in naval ships

이 연구에서는 해군 함정 탑재용 EER 시스템의 구조 강도와 직접적인 영향이 있는 수직 기둥에 대한 최적 설계를 목표로 하였다. EER 시스템의 구조 강도를 결정하는 프레임 구조를 연구대상으로 선정하였고, 특히 랙과 수직 기둥으로 구성된 프레임 구조 중 수직 기둥의 최적 설계에 연구 역량을 집중하였다. EER 시스템의 수직기둥이 동일한 단면 형상을 가지기 때문에 후보군으로 4개의 단면 형상을 선정한 이후 해당 단면들이 적용된 간단한 빔 구조의 유한요소 모델에 대해 충격시험 규격인 BV-043 규격^(4~6) 조건에서 허용 가능한 최소한의 단면 형상을 프레임 구조의 과도응답 해석을 통해 결정하였다. 해당 단면 조건이 프레임 구조 상태에서 설계 요구사항을 만족하는지를 확인하기 위해 유한요소 모델을 통한 모드해석을 수행하여 도출된 최소 공진점들을 평가하였다. 이후 해당 해석의 신뢰성을 평가하기 위해 실제 프레임 구조를 제작한 후 실험적 모델해석을 통해 추가적인 구조 강도에 대한 검증도 실시하였다. 진동 시험 규격(MIL-STD-167-1A)^(7,8)의 주파수 범위가 4 Hz ~ 33 Hz이므로 연구 대상인 프레임 구조의 최소 공진 주파수가 가능한 33 Hz 이상이 되도록 설계하는 것을 목표로 하였다.

2. 수직 기둥 단면 구조 강도

EER 시스템의 수직 기둥은 Fig. 2에 나타낸 바와 같이 통상 4개가 사용되며, 해당 기둥들은 동일한 단면 형상을 가지고 있다. EER 시스템 하부는 탄성마운트를 통해 해군 함정의 바닥에 고정되어 있으며 전자장비들이 수납되는 각 층의 랙들은 전자장비를 고정하는데 한정되어 있어 구조 강도 기여가 작다.

Fig. 2

Configuration of vertical column of EER system

전자장비가 랙에 적층되는 형태로 제작되는 함정용 랙의 특성상 수직 기둥 역시 일정한 단면 형상에서 높이 방향으로 길어지는 형태를 가질 수밖에 없으며, 이와 같은 부재의 강성 및 강도를 검토하기 위해 널리 알려진 단면 2차 모멘트(cross-sectional second moment of inertia)를 주요 인자로 하여 활용하였다.

2.1 단면별 비교 검토

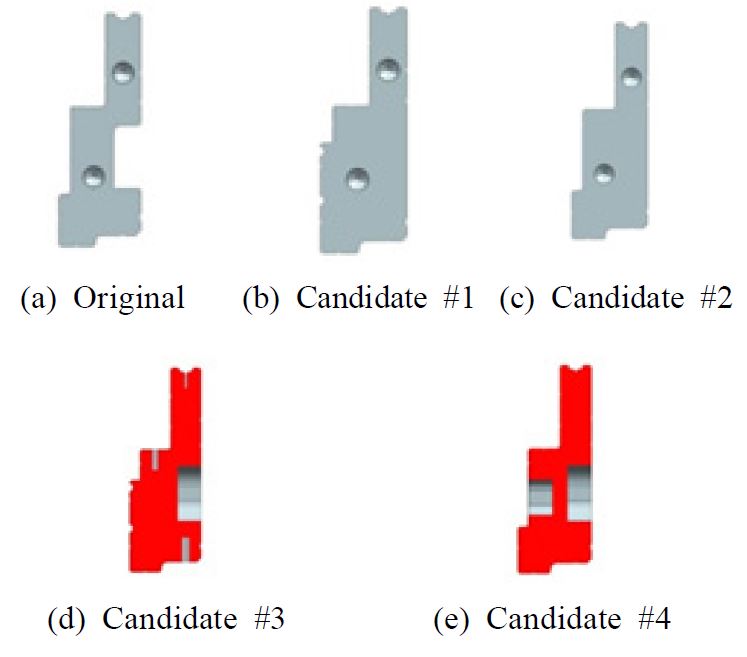
기존 제작 회사에서는 수직 기둥의 충분한 강도를 확보하기 위해 직시각형 형태의 단순한 중실축의 형상을 사용하였다. 하지만 이 연구에서는 실제 제작이 가능한 범위 내에서 기둥의 세로방향 및 측면부 형상을 서로 다르게 설계하여 최소의 단면적(제작비용)으로 동등한 구조 강도를 가지는지를 확인해보고자 하였다. Fig. 3은 기존 형상 및 4가지 후보군의 단면을 보여준다. 후보군 #1, #2는 기존 단면적을 넓힌 경우이며, 빨간색으로 명기된 후보군 #3, #4는 단면의 국부 살빼기를 통해 후보군 #1, #2로부터 단면적을 줄인 형상에 각각 해당한다.

Fig. 3

Configuration of five candidates of cross-section in vertical column

만약 탄성영역 내 순수 굽힘 조건이고 단면 형상이 단순한 대칭 구조를 가지고 있다면 우력이 M이라고 가정할 때 중립면(neutral surface)에서 가장 먼 거리를 c라고 하면 최대 응력(σ_m)은 식 (1)과 같다.

$\[ \frac{{\sigma }_m}{c}\int y^{2}dA=M \]$

(1)

여기서, I는 외팔보 단면의 2차 모멘트 성분이다. 하지만, 검토되는 5개 단면 형상은 순수 굽힘 상태로 하더라도 비대칭의 복잡한 형상을 가지고 있기 때문에 중립면 설정 및 c값을 결정하는 것이 명확하지 않다. 이를 극복하기 위해 5개의 서로 다른 단면 형상을 가지는 단순 빔으로 가정하고 유한요소 모델에 대한 최대 하중 조건을 비교할 필요가 있다.

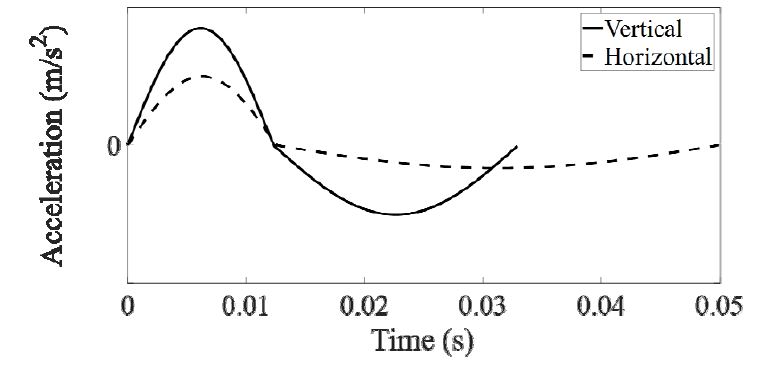
4가지 단면 형상에 대한 구조 강도를 비교하기 위해 최대 하중을 결정해야 한다. 실제 EER 시스템의 강도를 평가하기 위해 수행되는 시험 규정은 반 정현파 형태의 충격과 정현파 형태의 진동 두 가지가 필드에서 사용 중이며, 상대적으로 큰 응력을 발생시키는 충격의 형태를 이 연구에서는 고려하였다. 인가 하중은 수요 기업의 요구 규격인 BV-043을 활용하여 Fig. 4와 같은 임팩트 프로파일을 도출하여 응력 평가에 활용하였다.

Fig. 4

Acceleration spectral input according to BV-043 specification

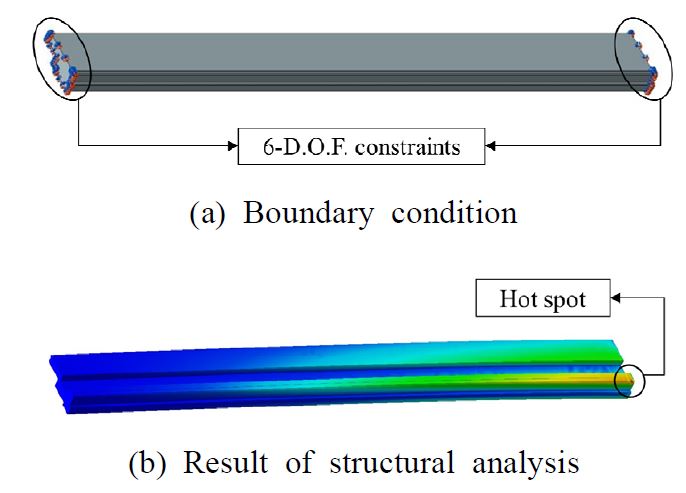
해당 유한요소 모델 생성 및 구조해석은 상용 소프트웨어인 midas NFX(MIDAS, South Korea)를 사용하였다. 해석 모델에 사용된 재료는 Table 1과 같이 프레임 구조에 사용되었던 AL6061-T6을 그대로 사용하였고 해당 소재의 항복 강도는 265 MPa이다. Fig. 5는 단순 빔 형상에 대한 과도응답 해석을 수행하는 모습을 보여준다. 여기서, 실제 충격하중이 인가되는 것과 동일하도록 하부 6-자유도 구속 후 동일면에 충격 하중을 인가하였다.

Table 1

Material property for body frame

Fig. 5

Structural analysis of simple cantilever beam structure

2.2 해석 결과 검토

유한요소 모델에 대한 최대 하중 조건에서 구조해석을 수행하였으며 해당 조건에서 발생된 최대 응력 및 안전율을 Table 2에 정리하였다. 안전율은 사용된 소재의 최대 허용 강도가 265 MPa 값에서 도출한 것이며, 2차 단면 모멘트 값들은 상용 프로그램에서 계산된 값을 명기한 것이다. 안전율은 1.4 ~ 1.6으로 모든 단면 형상에서 안정적이라고 할 수 있다. 실제 산업현장에서의 원가 측면을 고려할 때 무게에서 가장 이득을 보는 #4 조건이 최적이라 할 수 있겠으며, 이 연구에서 #4 형상의 단면으로 해석 및 실험적 검증을 향후 수행할 것이다.

Table 2

Summary of calculation results regarding five different cross-sectional shape cases

3. 프레임 구조 동적 강성 평가

3.1 유한요소 모델을 활용한 동적 강성 평가

선정된 수직 기둥의 단면 형상을 적용한 프레임 구조에 대한 해석을 우선적으로 진행하였다. 실제 EER 시스템이 임팩트 하중에 의한 동적 거동 관련 강건성을 평가받기 때문에 이 연구에서는 동적 강성과 직접적인 연관이 있는 공진점을 확인하여 프레임 구조가 충분히 높은 동적 강성을 보유하는지를 평가하는 것이다.

유한요소 모델(finite element model, FEM)을 구성하고 자유경계(free-free) 상태에서 모드해석을 상용 소프트웨어인 midas NFX(MIDAS, South Korea)를 사용하여 수행하였으며 관심 주파수는 최대 200 Hz로 선정을 하였다. 랙 형상 및 수직 기둥은 개발 설계 모델을 그대로 사용하였으며 수직 기둥의 단면은 2장에서 도출된 허용 가능한 최소 2차 모멘트 값을 가지는 단면을 사용하였다. 설계된 소재는 2장 해석에 사용된 동일 소재인 AL6061-T6를 활용하였으며 유한요소 모델 형상은 Fig. 6과 같다.

Fig. 6

Configuration of finite element mode of body frame

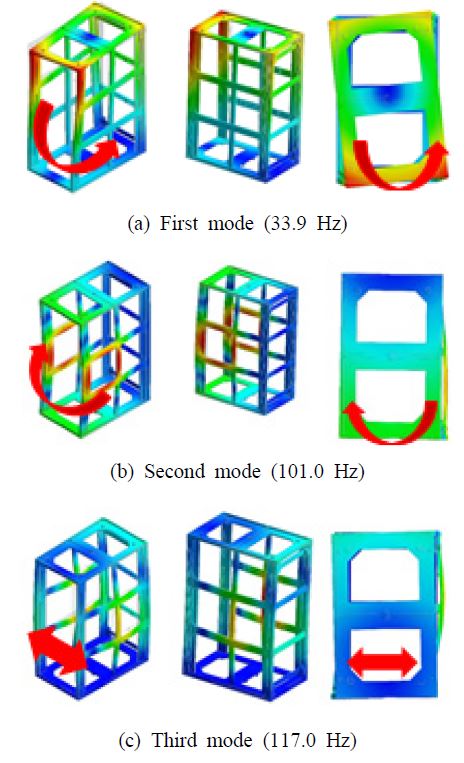
해석 결과 가장 낮은 3개의 공진점은 33.9 Hz, 101.0 Hz, 및 117.0 Hz으로 도출되었다. Fig. 7은 3개의 저차 공진점들에 해당하는 모드 형상이다. 실제 모드해석 결과는 Fig. 7 내의 3개의 모드 이외에도 존재하지만, 시험 결과와 비교 평가를 진행하는 과정에서 해당 모드는 제외하였기 때문에 연관성이 큰 3개 모드만 도시를 하였다.

Fig. 7

Mode shapes corresponding to lowest three

3.2 프레임 구조 시제품에 대한 동적강성 평가

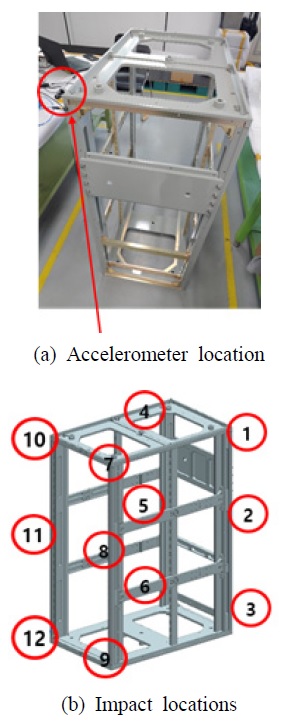
유한요소 모델 생성 시 활용된 설계 도면을 바탕으로 프레임 구조의 시제품에 대한 제작을 실시하였다. 해당 시제품의 재질은 설계 사양과 동일한 AL6061-T6이며 모달 실험(modal testing)^(9,10)은 바닥에 강성이 프레임 구조 대비 낮은 소재 위에 시험 대상을 거치한 후 타격 시험을 진행하여 유사 자유경계 상태가 되도록 하였다. 프레임 구조의 단면 형상은 해석에서 사용된 형상을 그대로 사용하였으며 제작된 시제품은 Fig. 8에 보여준다.

Fig. 8

Prototype of body frame

임팩트 헤머(B&K, Model: LW41571)를 사용하여 roving hammer 방식으로 12개 포인트에서 측정을 실시하였으며, 가속도 센서(PCB, model: KS943B)는 #1 위치에 부착하였다. 동일 가속도 센서와 타격 위치에 대해 5번의 반복시험을 실시하여 평균된 주파수응답함수(frequency response function)들을 측정하였으며, 공진점 근방에서 최소 기여도 함수값(coherence function)이 0.9 이상의 값을 가지는 경우에만 저장하였다. 타격 위치들과 3축 가속도 위치는 Fig. 9에 나타내었다.

Fig. 9

Impact locations and attached 3-axial accelerometer at body frame

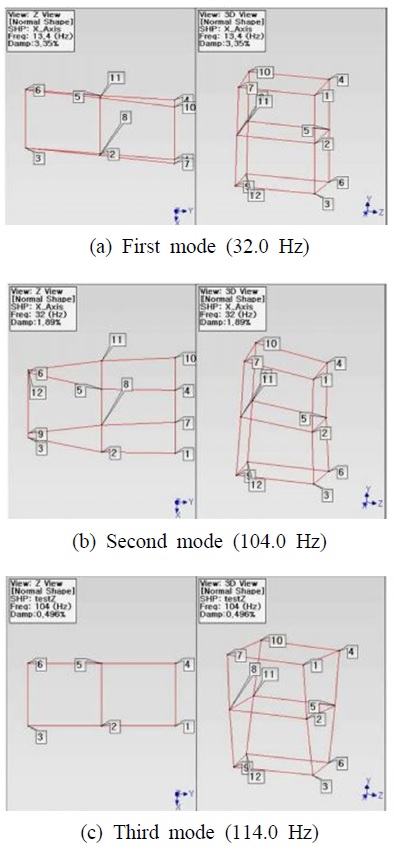
모달 분석은 상용 소프트웨어인 MEscope(vibrant technology, USA)를 사용하여 수행하였다. 모달 해석은 해석과 유사하게 최대 200 Hz 구간에 대해 실시를 하였으며, 분석한 결과를 모드해석 결과와 비교하면 Table 3과 같다. 또한 실험적 모달 해석을 통해 획득된 3개 모드의 모드 형상은 Fig. 10과 같다.

Table 3

Material property for body frame

Fig. 10

Mode shapes corresponding to lowest three resonance frequencies of body frame prototype

Table 3의 결과를 비교할 때 실험적 결과와 해석적 결과는 최대 5.9 % 공진점 오차(실험 결과를 기준으로 한 상대오차) 범위 내로 도출되었기 때문에 해석 결과가 충분한 신뢰성을 가짐을 알 수 있다. 수요 기업에서 요구하는 동적 강도의 요구 사항이 진동 시험(MIL-STD-167-1A, 2015)의 주파수 범위에서 가능한 공진점을 가지지 않은 것이 필요하기 때문에 실험적으로 도출된 최소 주파수인 32.0 Hz는 설계 요구 사항을 대체적으로 만족한다고 판단된다. 이는 동적 구조 강성 측면에서 선정된 수직 기둥의 형상 조건이 프레임 구조의 관점에서 받아들일 수 있는 설계 사양임을 알 수 있다. 좀 더 강도가 높은 단면 형상을 가지는 것이 구조 강도 측면에서는 보다 강건한 설계이지만 생산 단가 절감을 고려할 때 선정된 단면 형상은 최적이라고 판단된다.

4. 결 론

해군 함정에 탑재되는 전자장비 랙의 구조 강도를 최적으로 선정하기 위한 설계 프로세스 과정 중 구조 강도에 지배적인 영향을 주는 프레임 구조에 대한 최적 설계를 수행하였다. 프레임 구조는 전자장비를 수납하는 랙과 수직 기둥으로 이루어져 있으며, 구조 강도와 직접적인 영향이 있는 수직 기둥의 단면 형상 설계에 연구를 집중하였다. 기존 단순한 중실축 구조를 생산비용 등을 고려한 최적형상으로 변경하기 위해 4가지 후보 형상을 설계한 다음 한쪽 끝이 구속되어 있는 단순 빔 형태에서 최대 하중을 견딜 수 있는지를 확인하였다. 해석 결과 2차 모멘트 값이 가장 작은 경우에도 요구 응력을 만족시키는 것을 확인하였기 때문에 해당 단면 형상으로 유한요소 모델을 구성한 다음 동적 강도를 확인하기 위해 모드해석을 수행하였다. 이와 동시에 해당 설계 사양을 바탕으로 시제품을 제작한 다음 동일한 조건에서 모달 실험도 진행하였다. 해석과 실험 결과의 공진점들은 5.9 % 이하의 주파수 오차를 보였기 때문에 수행된 해석은 신뢰성이 높았다. 결과적으로 2가지 해석 결과는 수요자의 요구 사항인 시험주파수 구간인 4 Hz ~ 33 Hz 구간에서 공진점이 가능한 나타나지 않는 조건을 대부분 만족하고 있음을 확인하였다. 따라서 제안된 수직 기둥의 단면은 기존 대비 경제성을 가진 최소한의 2차 모멘트 값의 최적화된 형상 조건으로 요구 구조 강도까지 확보하였기 때문에 제품 경쟁력 측면에서 우수하다고 판단된다. 향후 연구는 이 프레임 구조을 기본으로 하여 EER 시스템 단위에서 해석 및 검증 시험을 진행할 것이다.

Acknowledgments

이 논문은 국방기술진흥연구소 국방벤처지원사업 ‘통합통신체계 콘솔, 랙 형 장비 충격 진동 저감 기술 개발(2019)’에 의해 연구되었습니다.

References

• Shin, C. J., Hong, C. S., Jeong, W. B. and Seo, H. S., 2009, Dynamic Response of Hull Mounted Cylinderical Array Sonars to Shocks, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 19, No. 2, pp. 146~154. [https://doi.org/10.5050/KSNVN.2009.19.2.146]
• Bae, S. W., Hong, C. S., Jeong, W. B., Park, Y. S. and Bin, J. G., 2010, Shock Resistance Analysis of a Propulsion Motor for Naval Vessels, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 20, No. 12, pp. 1183~1189. [https://doi.org/10.5050/KSNVE.2010.20.12.1183]
• Kwon, J. I., Lee, S. G. and Jeong, J. H., 2005, Shock Response Analysis of MIL-S-901D Floating Shock Platform, Journal of Society of Naval Architects of Korea, Vol. 42, No. 5, pp. 493~498. [https://doi.org/10.3744/SNAK.2005.42.5.493]
• Federal German Army Procurement Office, 1985, Shock Resistance Experimental and Mathematical Proof, BV-043.
• Kim, J. H., 2007, Shock Response Analysis under Underwater Explosion for Underwater Ship using ALE Technique, Journal of the Korean Society for Marine Environmental and Energy, Vol. 10, No. 4, pp. 218~226.
• Jeon, S. H., Hong, J. S., Jeong, W. B., Seo, H. S. and Cho, Y. H., 2012, Structural Response and Reliability of a Cylinderical Array Sensor due to Underwater Explosion, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 22, No. 1, pp. 81~87. [https://doi.org/10.5050/KSNVE.2012.22.1.081]
• MIL-STD-167-1A, 2005, Mechanical Vibrations of Shipboard Equipment, Department of Defense Test Method Standad, U.S.A.
• Kim, Y., Han, H., Jeon, S. and Lee, C., 2020, Research for Improvement of Flexible Rotor Vibration Criteria in MIL-STD-167-1A, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 30, No. 6, pp. 581~590. [https://doi.org/10.5050/KSNVE.2020.30.6.581]
• Ewins, D. J., 2000, Modal Testing, 2^nd Edition, Research Studies Press Ltd., Baldock, England.
• Inman, D. J., 2013, Engineering Vibration, 4th Edition, Pearson, Boston.