포락선 대수감소법의 오차 분석
© The Korean Society for Noise and Vibration Engineering
Abstract
The current logarithmic decrement method extracts the damping ratio from a single-frequency signal. However, the envelope logarithmic decrement method(ELDM) can extract the damping ratio from the beat wave containing two adjacent frequencies. In this study, the error factors of the ELDM were analyzed. For the error analysis, various beat waveforms were generated using the first natural frequency and damping ratio of the King Seongdeok Divine Bell. The generated beat waveforms were used to analyze the error of the damping ratio in terms of the sampling frequency, beat clarity, and beat period. We developed a more precise damping ratio extraction technique in applying the ELDM using simulations.
Keywords:
Envelope Logarithmic Decrement Method, Damping Ratio, Beat Wave, Error Analysis키워드:
포락선 대수감소법, 감쇠비, 맥놀이 파동, 오차 분석1. 서 론
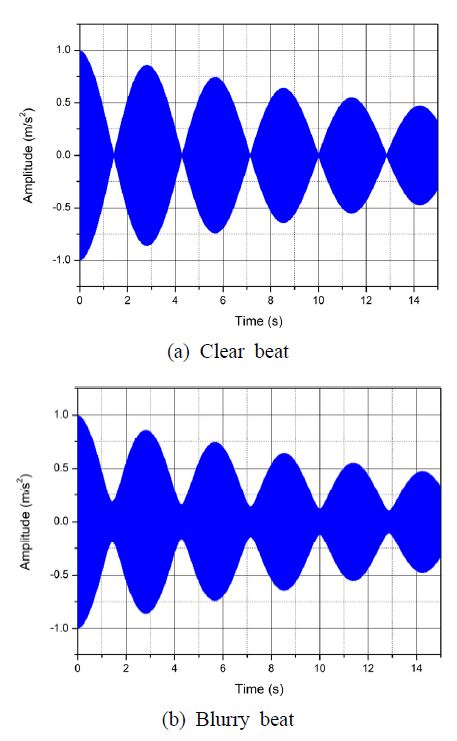
맥놀이는 매우 근접한 두 주파수의 진동이 중첩될 때, 진동이 주기적으로 커졌다 작아지는 현상이다. 회전축이나 회전쉘, 풍력 타워 같은 축 대칭형 구조가 질량이나 강성의 분포 또는 경계조건에서 미세한 비대칭성을 갖는 경우, 하나의 진동모드가 비슷한 주파수를 갖는 진동모드 쌍으로 분리되고 그 간섭으로 맥놀이가 발생한다. 맥놀이가 중요한 의미를 갖는 진동계로 한국 종이 있다. 적절한 주기로 우~웅 우~웅 반복되는 맥놀이는 종소리의 웅장함과 생동감을 높인다(1). 한국 종에서 맥놀이 진동의 감쇠비는 종소리가 얼마나 오래 지속되는가를 결정하는 중요한 음향 성능 인자이며, 내부 균열 등의 구조적 변화를 감지하는 데에도 사용되는 물리적 인자다. 종의 진동과 같이 감쇠가 작은 진동계의 감쇠비를 구하는 데에는 대수감소법(logarithmic decrement method)이 자주 사용된다. 대수감소법은 단일 주파수의 진동 파형으로부터 점성감쇠비를 추출하는 오래된 방법이나 근래에 들어서도 감쇠비 추출 오차를 줄이려는 많은 연구가 있었다. Huang 등(2)은 부분적으로 존재하는 잡음이 대수감소에 주는 큰 오차를 제거하기 위해 면적감소(area decrement)의 개념을 도입했다. Tweten 등(3)은 잡음 오차 감소를 위해 대수감소의 평균화 과정에서 오차를 최소화시키는 최적 싸이클 수를 제시했다. Little 등(4)은 대수감소의 불확도를 최소화시키는 최적 싸이클 수에 대한 이론식을 제시했다. 그러나 이러한 연구들은 모두 단일 주파수 파형에 대한 연구이다. Fig. 1과 같이 매우 근접한 두 개의 주파수 운동이 간섭하여 만드는 맥놀이 파동에는 기존의 대수감소법을 바로 적용할 수가 없다. 주파수 필터링을 통해 두 주파수 성분을 완전히 분리해야 기존의 대수감소법을 적용할 수 있다. 문제는 두 주파수 성분이 매우 근접한 경우, 주파수 필터링이 개별 파형을 상당히 왜곡시킨다는 점이다. Liao and Wells(5)에 의하면, 필터의 대역폭은 목표 주파수 성분을 포함하도록 충분히 커야 함과 동시에 인접한 주파수 성분을 완전히 배제할 정도로 작아야 한다. 따라서 두 주파수 성분이 가까이 붙어있는 종의 맥놀이에서 필터링은 상당한 왜곡을 일으킨다. 대책으로 Nakutis 등(6)은 맥놀이의 포락선 데이터를 사용하는 확장된 대수감소법을 제시하였으나, 이 방법은 Fig. 1(a)와 같이 두 주파수 성분의 진폭이 같을 때 나오는 완벽하게 선명한 맥놀이에만 한정되었다. 인접한 두 주파수 성분의 진폭이 다른 일반적인 경우, (b)와 같이 흐린 맥놀이 파동을 얻게 된다. 선행연구에서 웨이블릿 변환(7)을 사용해서 다자유도 진동계 모드의 감쇠비를 동시에 추출하는 방법을 제시하였다. 현장에서 보다 쉽게 사용 가능한 방법으로 최근에는 일반적인 맥놀이 파형의 감쇠비 추출을 위한 포락선 대수감소법(envelope logarithmic decrement method)(8)를 제시하고 평창 동계올림픽대종에 적용하였다. 이 방법은 필터링 과정 없이 다양한 패턴의 맥놀이 포락선 데이터로부터 감쇠비를 추출할 수 있다. 그러나 포락선 대수감소법을 사용할 때, 측정 조건에 따라 오차가 발생할 수가 있다. 파형 측정시 사용하는 샘플링 주파수, 측정 파형의 선명도, 맥놀이를 만드는 주파수 쌍의 차이가 중요한 오차 요인이다.
이 연구에서는 주어진 맥놀이 조건과 감쇠비 참값을 사용하여 맥놀이 파형을 만든 후, 위 세 가지 오차 요인에 따른 감쇠비 추출 오차를 시뮬레이션을 통해 분석한다. 그 결과로부터 포락선 대수감소법의 오차 범위를 파악하고 측정 오차를 감소시키기 위한 정보를 제공하는 것이 이 연구의 목적이다.
2. 포락선 대수감소법
미세한 주파수 차이를 갖는 두 개의 점성감쇠 진동이 중첩될 때 발생하는 맥놀이 파동은 식 (1)로 표현된다.
| (1) |
ωL은 미세하게 낮은 주파수 성분이고, ωH는 미세하게 높은 주파수 성분이다. ζL과 ζH는 ωL, ωH 두 주파수 진동의 감쇠비다. 동일한 진동모드가 ωL, ωH의 매우 근접한 주파수로 분리된 경우, 두 감쇠비는 같다고 보고, 식 (1)을 식 (2)로 단순화시킬 수 있다.
| (2) |
여기서 ζL과 ζH는 동일한 값 ζ로 표시하였고, 평균 주파수 ω=(ωL+ωH)/2를 사용하였다.
식 (2)의 괄호 안의 맥놀이 파동을 미세한 주파수 차이 Δω=ωH-ωL을 사용하여 표시하면 식 (3)과 같다.
| (3) |
식 (3)은 삼각함수 합성 공식에 의해 식 (4)로 표시 가능하다.
| (4) |
| (5) |
| (6) |
| (7) |
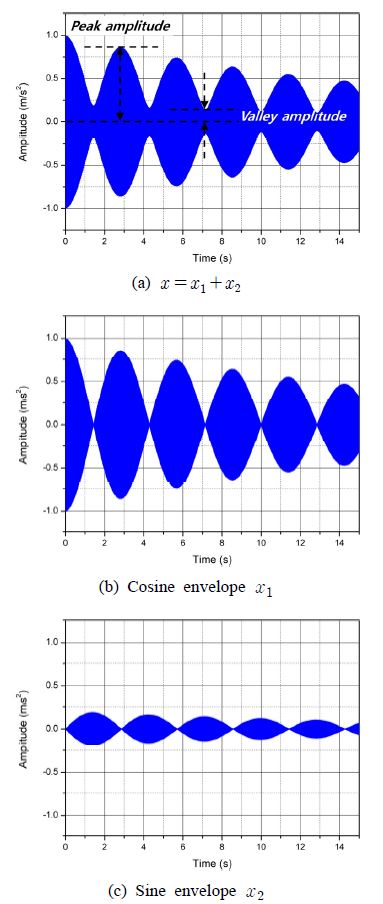
식 (6)은 완벽하게 선명한 코싸인 포락선 맥놀이고 식 (7)은 싸인 포락선 맥놀이다. 즉, Fig. 2(a)의 임의의 맥놀이는 (b)의 코싸인 맥놀이와 (c)의 싸인 맥놀이의 합이다. 이때 맥놀이 포락선의 정점에서의 진폭은 코싸인 맥놀이 진폭이고, 골에서의 진폭은 싸인 맥놀이 진폭이 된다.
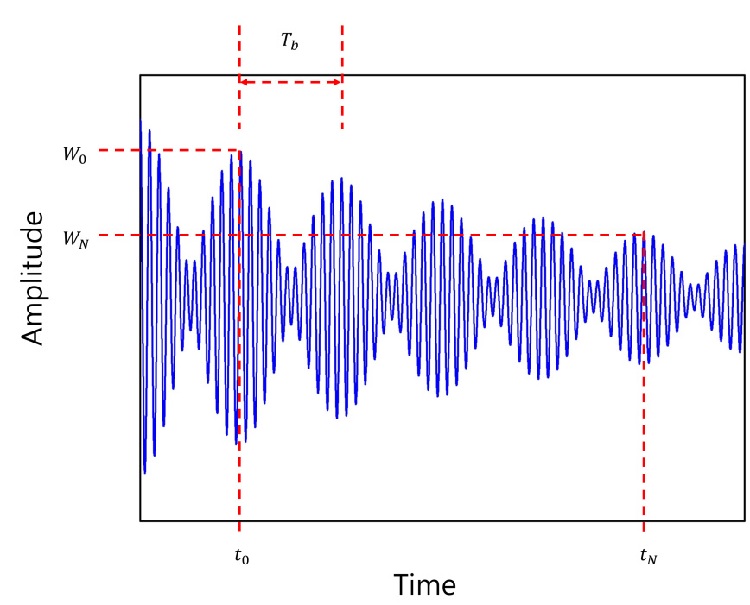
포락선 대수감소를 구하기 위해 Fig. 3의 확대된 맥놀이 파형을 사용한다. Fig. 3의 포락선 간격은 Tb = 2π/Δω이고, tN = t0 + NTb 이다. 두 시점 t0, tN 에서 포락선 정점의 진폭비를 취하면, 식 (8)과 같다.
| (8) |
따라서 포락선 대수감소를 식 (9)와 같이 구할 수 있다.
| (9) |
식 (9)로부터 감쇠비를 식 (10)과 같이 구할 수 있다.
| (10) |
3. 시뮬레이션
3.1 파형의 생성
Fig. 4는 성덕대왕신종의 원주상 위치에 따른 1차 맥놀이 포락선 분포다(9). 위치에 따라 맥놀이 포락선은 큰 차이를 보인다. 시뮬레이션을 위해 성덕대왕신종의 1차 고유진동수와 감쇠비 데이타로 맥놀이 파형을 만들었다. 고유주파수로 fL = 64.07 Hz와fH = 64.42 Hz의 쌍을, 감쇠비로 0.00013을 사용했다. 감쇠비 추출 오차 요인으로 샘플링 주파수, 선명도, 주파수 쌍의 3가지 효과를 검토했다. 대수감소 추출을 위해 모든 시뮬레이션에서 식 (9)에 N=7, 즉 7개의 맥놀이 정점 값을 사용했다.
3.2 샘플링 오차
단일 주파수 파형을 샘플링하는 과정에서 Liao and Wells(5)는 감쇠비 추출치의 불확도 제거를 위해 목표주파수 대비 샘플링 주파수를 10배로 할 때, 감쇠비 추출 오차는 2 % 이내 이고, 샘플링 주파수의 제곱에 비례해서 오차가 감소함을 이론적으로 증명했다. 샘플링 오차를 보기 위해 식 (1)을 목표 주파수인 64 Hz의 2배 ~ 100배로 샘플링하여 만든 파형 데이타로 감쇠비 추출 오차를 관찰했다. 포락선 파형으로는 가장 선명한 맥놀이를 사용했고, 감쇠비의 백분율 오차는 식 (11)로 구하였다.
| (11) |
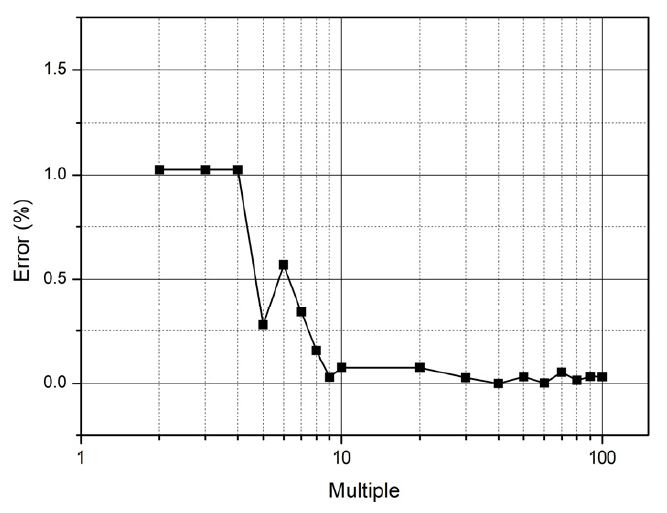
Fig. 5는 샘플링 주파수의 증가에 따른 오차를 보인다. 횡축은 목표 주파수의 몇 배(multiple)로 샘플링했는가를 의미한다. 실험에서 많이 사용하는 2.56배 샘플링 주파수에서 오차율은 1 % 정도이며, 10배 이상으로 샘플링하면 오차율은 0.2 % 이내로 확인되었다.
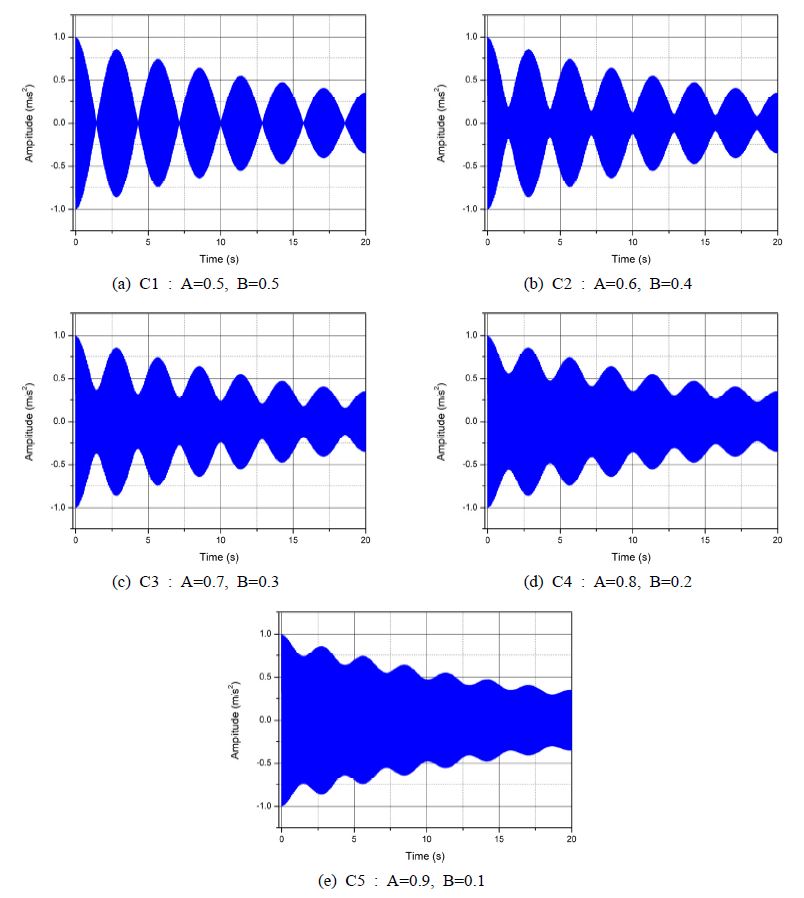
3.3 선명도 오차
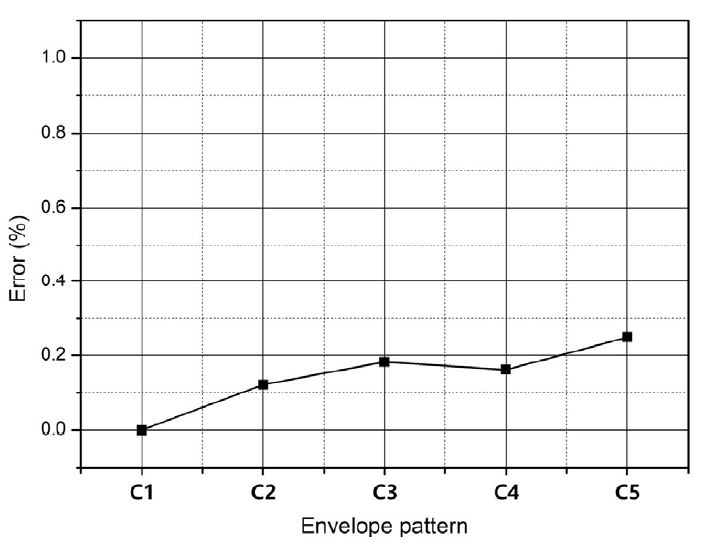
Fig. 2에서 포락선이 선명하지 못하면 포락선의 정점 값을 취하는 데에 오차가 발생할 수가 있다. 따라서 맥놀이 포락선의 선명도에 따라 감쇠비 추출치는 미세하게 차이 날 수 있다. Fig. 6과 같이 맥놀이 선명도가 다른 5개의 파형을 만들어 감쇠비 추출치와 참값을 비교했다. C1은 맥놀이가 완벽하게 선명한 경우, C5는 선명하지 못한 경우다. 이때 목표주파수의 40배로 샘플링하여 샘플링 오차를 제거했다. Fig. 7은 선명도에 따른 오차를 보인다. 맥놀이가 선명할수록 오차는 감소한다. 완벽하게 선명한 포락선 C1의 경우 오차율은 0이다. 식 (7)에서 완벽하게 선명한 포락선에서는 맥놀이의 정점 값을 정확하게 취할 수 있어 식 (8)은 오차를 만들지 않는다. 가장 흐린 포락선 C5에서도 오차율은 0.25 %로, 선명도에 따른 오차는 매우 작다. 이는 Fig. 4에서 임의의 위치에서 측정한 파형으로 감쇠비를 추출해도 그 차이는 매우 작음을 의미한다.
3.4 주파수 쌍 오차
주파수 쌍 오차는 식 (1)에 주파수 쌍의 평균치를 적용하여 식 (2)로 단순화시킬 때 발생하는 오차다. 종형 구조물이나 풍력 타워에서는 주파수 쌍 fL, fH 의 차이가 매우 작고, 회전축이나 교량 구조에서는 상대적으로 크다. 비대칭의 정도에 따라 주파수 쌍의 차이 Δf와 맥놀이 주기가 다르다.
대형 한국종의 맥놀이 주기는 대부분 1초에서 10초 범위이므로, 주파수 쌍의 차이는 그 역수인 0.1 Hz ~ 1 Hz 범위다(10). 이를 고려하여 성덕대왕신종의 1차 고유주파수 쌍의 평균치 64.245 Hz를 기준으로, 주파수 쌍의 차이 Δf를 0.1 Hz ~ 1 Hz 범위로 주고 오차를 검토했다.
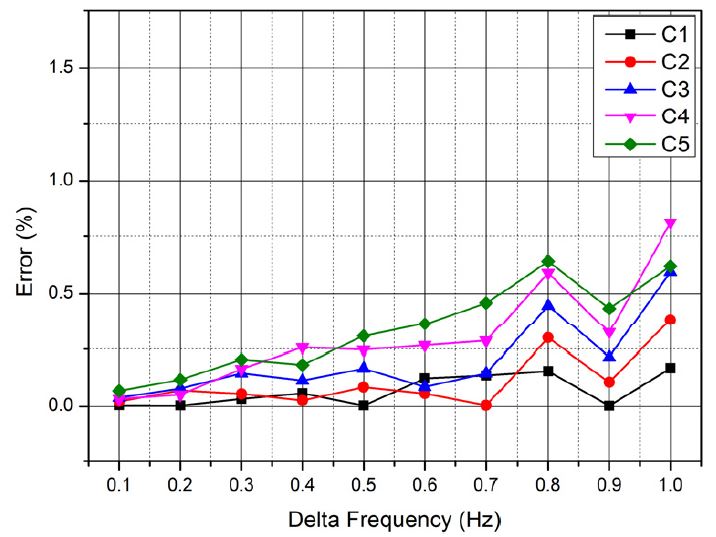
Fig. 8은 주파수 차이에 따른 오차로, 선명도가 다른 맥놀이 파형별로 검토했다. 예상대로 주파수 차이가 증가하면 오차율도 증가한다. 또, 선명도가 떨어지면 오차율은 더 커진다. 그러나 1 Hz의 큰 차이에서도 최대 오차율은 0.8 % 이내다. 성덕대왕신종의 경우 1차 맥놀이에서 0.35 Hz의 주파수 쌍 차이를 보인다. Fig. 8에서 이 정도의 주파수 차이에서는 C1 ~ C5의 어떠한 맥놀이 파형을 사용해도 0.25 % 이내의 오차율을 보인다. 이러한 결과는 포락선 대수감소법을 이용하여 다양한 포락선 파형으로 감쇠비 추출이 가능함을 의미한다.
4. 결 론
포락선 대수감소법으로 감쇠비를 추출하는 과정에서 발생 가능한 오차를 분석하였다. 성덕대왕신종의 1차 고유주파수 쌍과 감쇠비를 사용해서 다양한 패턴의 맥놀이 파형을 만들어 포락선 대수감소법을 적용하였다. 샘플링 주파수, 선명도, 주파수 쌍의 차이에 의한 오차를 검토했다. 목표주파수의 10배 이상으로 샘플링하면 오차율은 0.2 % 이내로 수렴하였다. 포락선의 선명도가 높아지면서 오차율은 영으로 수렴하였고, 선명도가 떨어져도 오차율은 0.25 % 수준이었다. 주파수 쌍의 차이가 증가하면 오차율도 증가하나, 성덕대왕신종의 주파수와 감쇠 수준에서는 임의의 맥놀이 파형을 사용하여 감쇠비를 추출하더라도 0.25 % 이내의 작은 오차율을 보였다.
References
-
Kim, S. H., Kim, J. H., Jung, J. D. and Lee, J. M., 2002, Vibration and Sound Characteristics of King Seongdeok Bell, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 12, No. 7, pp. 534~541.
[https://doi.org/10.5050/KSNVN.2002.12.7.534]

-
Huang, F., Wang, X., Chen, Z., He, X. and Ni, Y., 2007, A New Approach to Identification of Structural Damping Ratios, Journal of Sound and Vibration, Vol. 303, No. 1-2, pp. 144~153.
[https://doi.org/10.1016/j.jsv.2006.12.026]

-
Tweten, D. J., Ballard, Z. and Mann, B. P., 2014, Minimizing Error in the Logarithmic Decrement Method Through Uncertainty Propagation, Journal of Sound and Vibration, Vol. 333, No. 13, pp. 2804~2811.
[https://doi.org/10.1016/j.jsv.2014.02.024]

-
Little, J. A. and Mann, B. P., 2019, Optimizing Logarithmic Decrement Damping Estimation through Uncertainty Propagation, Journal of Sound and Vibration, Vol. 457, pp. 368~376.
[https://doi.org/10.1016/j.jsv.2019.05.040]

-
Liao, Y. and Wells, V., 2011, Modal Parameter Identification using the Log Decrement Method and Band-pass Filters, Journal of Sound and Vibration, Vol. 330, No. 21, pp. 5014~5023.
[https://doi.org/10.1016/j.jsv.2011.05.017]

-
Nakutis, Ž. and Kaškonas, P., 2011, Bridge Vibration Logarithmic Decrement Estimation at the Presence of Amplitude Beat, Measurement, Vol. 44, No. 2, pp. 487~492.
[https://doi.org/10.1016/j.measurement.2010.11.012]

-
Park, S. Y., Kang, Y. J. and Kim, S. H., 2009, Identification of Beat Characteristics and Damping Ratios of Bell Type Structures using Wavelet Transform, Journal of Sound and Vibration, Vol. 326, No. 1-2, pp. 367~382.
[https://doi.org/10.1016/j.jsv.2009.04.039]

-
Byeon, J. H. and Kim, S. H., 2022, Extraction of the Damping Ratio of a Beat Wave using Envelope Logarithmic Decrement, Journal of Mechanical Science and Technology, Vol. 36, No. 6.
[https://doi.org/10.1007/s12206-022-0506-y]

-
Kim, S. H., Lee, C. W. and Lee, J. M., 2005, Beat Characteristics and Beat Maps of the King Seongdeok Divine Bell, Journal of Sound and Vibration, Vol. 281, No. 1-2, pp. 21~44.
[https://doi.org/10.1016/j.jsv.2004.01.038]

- Kim, S. H. and Lee, J. H., 2021, Beat Control Method of Korean Bells using Artificial Dumshoi, Journal of the Acoustical Society of Korea, Vol. 40, No. 3, pp. 192~200.

Seockhyun Kim received B.S. and Ph.D. degree in Mechanical Engineering from Seoul National University (Seoul, Korea) in 1980 and 1987 respectively. In 1988, he joined the faculty of Kangwon National University, where he is currently a professor in the department of Mechatronics Engineering. His main research areas include Korean bells, sound insulation of the railway vehicle, vibration and noise analysis of the wind turbine, and so on.

Junho Byeon received his B.S., M.S. degree from Kang- won National University, Korea in 2014, 2016, respectively. He is currently a Ph.D. student of Noise and Vibration Engineering lab. at the department of Mechatronics Engineering, Kangwon National University, Korea.