슈라우드 접촉에 따른 증기터빈 블레이드의 진동모드 해석과 실험적 검증
© The Korean Society for Noise and Vibration Engineering
Abstract
An integral shrouded blade with a gas turbine dovetail that is robust against the stress of the dovetail has been applied in large steam turbines to achieve high efficiency by minimizing the steam leakage of the tip. Further, the natural frequency of the blade has been calculated with high accuracy considering the contact condition of the shrouded blade for the avoidance design of resonance. This paper compares the analysis and measurement results for the shrouded blade with a gas turbine dovetail. To realize a valid analysis model, a full-scaled mock-up with blades and a rotor was manufactured and assembled, and a spin test was conducted in balancing shop up to 120 % overspeed of the rated speed. The spin test procedure was described, and a Campbell diagram was obtained as the test result. The FE model and boundary conditions of the shrouded blade were observed to agree well with the measured Campbell diagram. The model is expected to be applicable for the vibration design of the shrouded blade for gas turbine blades and steam turbines.
Keywords:
Gas Turbine Dovetail Blade, Shrouded Blade, Campbell Diagram키워드:
가스터빈 도브테일 블레이드, 슈라우드 블레이드, 캠벨 선도1. 서 론
최근에 증기터빈의 대용량 고효율 요구에 따라 증기 온도의 상승과 증기유로 면적 증가는 필수적이다. 고온고압의 증기조건에서 안정적이고 신뢰성 있는 운전이 가능한 터빈 회전체 설계 기술 개발이 요구되며, 특히, 고속의 회전체인 블레이드는 고온으로 갈수록 급격한 소재 인성강도의 저하로 고온용 소재 개발과 함께 신뢰성 있는 구조설계가 필요하다.
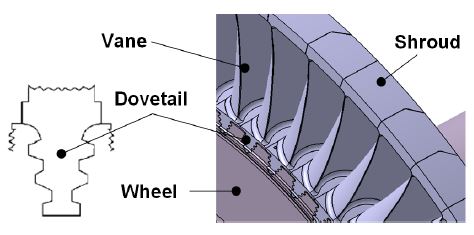
블레이드는 크게 3가지로 구성되는데, 고온고압 증기의 열에너지를 기계적 회전력으로 변환시키는 베인(vane), 베인을 로터에 고정시키는 도브테일(dovetail) 그리고 베인 끝단부를 통해 증기누설 최소화와 진동 저감을 위한 슈라우드(shroud)가 설치된다. 증기터빈 블레이드 설계시 다양한 도브테일이 적용되고 있고, 이 중 Fig. 1과 같이 가스터빈에서 유래되어 증기터빈에 적용되고 있는 가스터빈형 도브테일은 블레이드와 휠(wheel) 사이의 접촉 면적이 넓어 응력을 작게 받아 고온부 블레이드 설계에 적용된다.
블레이드는 슈라우드가 없는 경우(free standing type)와 슈라우드가 있는 블레이드(shrouded blade)로 구분되며, 최근에는 터빈효율 향상을 위해 블레이드 팁(tip)에서 누설증기 최소화할 수 있도록 슈라우드 블레이드가 널리 사용되고 있다. 슈라우드 블레이드는 베인과 슈라우드가 각각 따로 제작하여 조립되는 리벳 슈라우드(riveted shroud)와 베인과 일체로 제작하는 일체형 슈라우드(integral shroud)가 있다. 리벳 슈라우드는 두 개 이상의 여러 블레이드와 연결하여 조립함으로써 블레이드의 진동 안정성을 향상시킨다. 반면, 일체형 슈라우드는 리벳 슈라우드에 비해 구조가 간단하고 제작이 용이한 장점이 있다. 특히 인접 슈라우드 간에 마찰로 진동감쇠 효과를 증가시킬 수 있어, 슈라우드 접촉압력을 적절히 설계함으로써 블레이드 진동 마찰 감쇠를 극대화할 수 있다. 본 논문에서는 가스터빈형 도브테일로 구성된 일체형 슈라우드 블레이드의 진동해석 연구에 대해 다루었다.
일체형 슈라우드 블레이드는 회전 시 원심력으로 인해 비틀림 형상이 풀어지며 슈라우드 간의 접촉압력이 회전수에 따라 변한다. 이에 따라 정지 상태와 다른 조건으로 인해 블레이드의 진동 특성은 완전히 달라진다. 이와 같이 블레이드의 운전 조건을 잘 반영한 블레이드의 동적 거동 예측이 필요하다. 특히, 블레이드의 고유진동수는 가진력인 회전수 배수 성분 및 노즐통과주파수(nozzle passing frequency)와 적절히 이격되도록 공진회피 설계가 필요하며, 이를 위해서는 정확한 고유진동수 예측이 무엇보다 중요하다(1).
슈라우드 블레이드의 슈라우드간의 마찰 접촉을 고려한 동적 모델 연구는 최근에 해외에서 많이 연구되고 있다. 비선형 마찰 접촉 모델을 선형화하여 자유 진동 및 강제 진동해석을 수행하고 슈라우드의 접촉 각도에 따른 고유진동수를 비교하였다(2). 다양한 로터 회전속도를 고려한 슈라우드 접촉부의 압력과 마찰 응력을 해석적인 방법으로 계산하고, 진동 가진 크기의 변화에 따른 블레이드의 비선형 거동을 관찰하고 공진 주파수와 마찰 감쇠비의 영향을 연구하였다(3).
블레이드 진동해석 FE모델(finite element model)의 타당성 검증은 일반적으로 정지 상태로 개별 블레이드에 대해 충격 시험(impact testing)을 실시하여 블레이드 고유진동수를 측정하지만(4), 실제 회전 조건에서 블레이드와 도브테일간의 체결, 슈라우드간의 접촉 영향 및 회전 효과 등이 반영되지 않아 블레이드의 진동특성을 확인하는 데 한계를 갖고 있다. 실제 운전 조건을 반영한 진동 특성 분석하는 가장 효과적인 방법은 블레이드의 베인에 스트레인 게이지를 부착하고 회전하면서 블레이드를 가진시켜 블레이드에서 발생하는 진동 변형률 응답 신호를 획득하여 회전수별 공진점을 측정하는 회전 블레이드 진동시험(spin test)이다. 이와 같이 운전 조건을 잘 반영하는 회전 블레이드 진동시험을 본 연구에서 수행하였다.
이 논문에서는 여러 가지 장점으로 인해 증기터빈의 고압(high pressure turbine) 및 중압터빈(intermediate pressure turbine)에서 널리 사용되고 있는 가스터빈 도브테일형 블레이드의 슈라우드 접촉부의 모델링에 따른 블레이드 고유진동수 변화를 파악하고, 회전하는 블레이드의 진동시험 결과로부터 타당한 블레이드 진동해석 모델을 도출하였다.
2. 본 론
2.1 블레이드 진동모드 해석
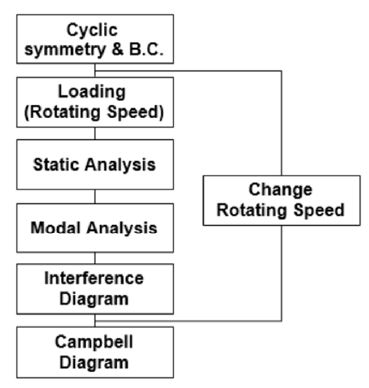
회전 원심력에 의해 블레이드 내에서 작용하는 응력이 증가함에 따라 블레이드 강성 증가 효과에 따라 고유진동수가 증가한다. 이를 응력의 강성보강효과(stress stiffening)라고 하며, 진동모드 해석에 고려되는 것이 필수적이다. 한편, 원심력이 작용하는 방향으로 변형량 증가로 인해 블레이드 강성이 감소하며, 이를 회전 연화효과(spin softening)라고 하며, 블레이드 진동해석시 고려된다. 이와 같이 회전 원심력 효과에 의한 블레이드의 강성변화를 고려하기 위해서는 Fig. 2의 해석절차와 같이 진동모드 해석 수행 전에 정적구조해석이 요구된다.
증기터빈 블레이드와 같이 동일 모델이 블레이드 개수만큼 반복적으로 구성된 터보기계의 구조해석시 전체 모델링하는 대신 주기적 대칭(cyclic symmetry) 조건 적용으로 해석모델을 최소화하여 계산 자원 감소와 계산 시간을 단축할 수 있다(5).
이 논문에서는 Fig. 2의 해석절차에 따라 슈라우드 접촉부의 경계조건에 따른 블레이드 진동모드 해석을 수행하여 고유진동수 변화를 파악하였다. 이 연구에서는 구조해석에 널리 활용되고 있는 상용 유한요소 코드인 ANSYS를 사용하여 해석을 수행하였다.
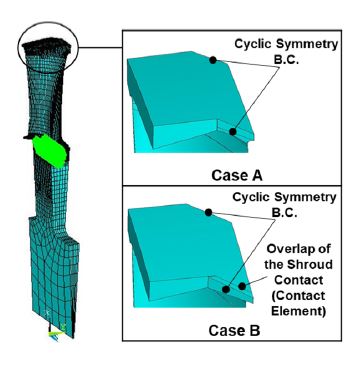
Fig. 3은 총 60개로 구성된 블레이드 중 한 개의 FE모델을 나타낸 것으로 블레이드와 휠 사이의 연결부인 도브테일은 고정시키고, 휠과 슈라우드는 주기적 대칭 조건을 적용하는 반면, 슈라우드간의 접촉부는 2가지 경계 조건에 따라 해석 결과값을 비교하였다. A의 경우는 인접한 슈라우드 간의 접촉하는 부분을 주기적 대칭 조건을 적용하였다. 이 조건은 이상적인 상태이며 블레이드가 회전 시 슈라우드 전체가 접촉되지 않고 일부 영역만 접촉될 가능성을 배제하였다.
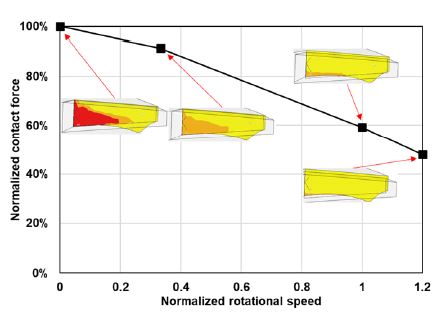
B의 경우는 블레이드의 슈라우드가 접촉하는 면에 접촉요소(contact element) 적용하고, 블레이드의 조립시 적용되는 슈라우드간의 간섭량(interference fit)을 접촉요소의 입력값으로 주어 슈라우드에서 예하중(preload)을 받도록 모델링 된다. 사용된 접촉요소는 ANSYS에서 제공되는 CONTA174와 TARGE170로서, CONTA174는 3차원 8절점의 고차 사각형(higher-order quadrilateral) 요소이며 솔리드 및 쉘의 표면에 접촉해석이 가능하다(6). 이 해석에서는 표면 대 표면(surface-to-surface) 접촉 경계조건을 사용하였다. 접촉 해석의 결과에 영향을 주는 인자는 간섭량, 회전 원심력 및 마찰계수이며, 이 논문에서는 간섭량과 마찰계수는 고정된 값을 사용하였다. 이와 같이 접촉요소 모델이 포함된 블레이드에 회전 원심력이 적용한 비선형 정적 해석을 수행하면, Fig. 4와 같이 접촉영역에 접촉력을 얻을 수 있다. 그림으로부터 회전수가 증가할수록 슈라우드 접촉력은 줄어들며, 정지상태 대비 정격회전수에서 접촉력은 약 60 %까지 감소함을 알 수 있다. 접촉면의 상태는 정지 상태에서는 빨간색의 고착영역(stick)이 보이지만, 회전수가 증가할수록 주황색의 슬립영역(slip)이 감소하면서 노란색의 근접 슬립영역(near slip)이 증가한다. 접촉면에서 발생한 접촉응력을 선형화하고 강성행렬에 반영시킨 FE모델로부터 블레이드 진동모드해석을 수행한다.
터빈 블레이드와 휠이 결합된 원판 형상의 진동모드는 진동 변위가 없는 선 형태가 발생하는 데 이를 노달 직경(nodal diameter)이라 하고, 블레이드가 동일한 굽힘 모드형을 갖더라도 다른 노달 직경을 갖는 원판 형 진동모드가 발생한다. 전체 블레이드가 N개로 구성될 때, 노달 직경은 N의 값이 짝수일 경우 0부터 N/2의 값을 가질 수 있으며, N의 값이 홀수일 경우 0부터 (N-1)/2의 값을 갖는다. 노달 직경에 따른 블레이드의 고유진동수를 그래프로 나타낸 것을 간섭 선도(interference diagram) 또는 안전 선도(safe diagram)라 부르며, 가진 성분인 회전수의 배수 성분을 함께 표시함으로써 쉽게 공진여부를 판단할 수 있다(7).
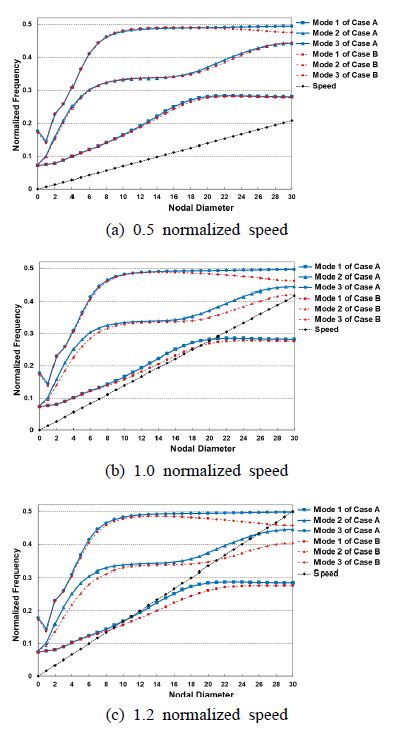
이 논문에서 고려된 슈라우드 접촉부의 2가지 조건에 대해 회전속도에 따른 해석 결과를 Fig. 5의 간섭 선도로 나타내고 있다. 간섭 선도에서 알 수 있듯이 회전속도가 증가할수록 두 가지 해석 조건의 결과 차이는 더욱 많이 발생하고, 또한 같은 회전속도에서는 노달 직경이 증가할수록 해석 결과 차이가 많이 나타난다. 이와 같이 고유진동수의 차이는 슈라우드 접촉에 따른 영향으로 볼 수 있다. 해석 조건 A의 고유진동수 값이 전반적으로 해석 조건 B보다 높으며, 슈라우드의 접촉 영역에서 강성이 크다는 것을 알 수 있다. 즉, 해석 조건 A의 경우는 슈라우드 전체가 이상적으로 접촉된다는 가정으로 인접 슈라우드의 절점이 서로 결합되는 주기적 대칭 경계조건이 적용된 반면, 해석 조건 B는 접촉 해석을 통해 접촉면에서 발생하는 강성만 반영한 것으로 슈라우드 강성 차이인 것으로 알 수 있다.
노달 직경별 고유진동수를 나타낸 간섭 선도는 블레이드 진동특성을 이해하는 데 도움이 된다. 노달 직경별 고유진동수 변화는 휠 모드와 블레이드 모드에 의해 결정되고, 낮은 노달 직경에서 급격한 고유진동수 변화는 휠 모드에 의한 영향이고, 높은 노달 직경에서 고유진동수 변화는 블레이드 강성 영향을 많이 받는다. Fig. 5의 간섭 선도로부터 1차 모드의 경우에 노달 직경 20차까지는 휠 강성에 의한 영역으로 이해할 수 있다. 특히, 3차 모드에서 노달 직경 0의 고유진동수가 노달 직경 1보다 큰 이유는 노달 직경 0의 휠모드 강성이 크기 때문이다.
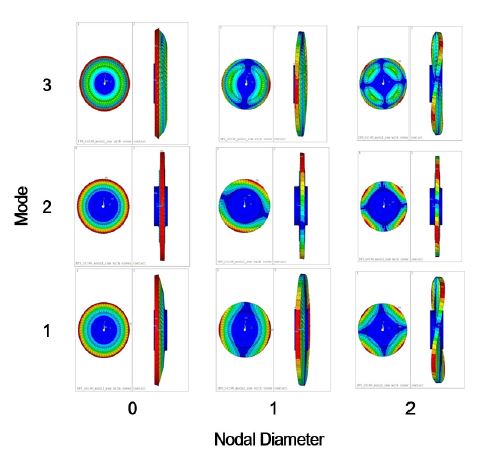
블레이드의 진동모드형을 Fig. 6에 해석 조건 B의 경우에 대해 나타내었고, 해석 조건에 따른 진동모드형은 거의 유사하여 조건 A의 결과는 생략하였다. Fig. 6에 나타낸 진동모드는 모두 굽힘 모드이며, 첫 번째와 세 번째 진동모드는 회전 축방향으로 진동이 발생하는 굽힘모드로서 각각 축방향 굽힘 1차 및 2차모드이며, 두 번째 모드는 회전 접선방향의 1차 굽힘모드이다. 블레이드 개별로 진동모드형은 동일하지만, 원판 진동모드형과 유사하게 원주별로 노달 직경 수에 따른 직경절 모드가 나타난다. 앞서 서술한 것과 같이 N개 블레이드는 짝수 개의 블레이드는 N/2개, 홀수 개의 경우는 (N-1)/2개의 직경 절 모드가 나타나며, Fig. 6에서는 0, 1, 2개의 직경 절 모드만 나타내고 있다.
블레이드 슈라우드 접촉부의 타당한 모델은 회전 블레이드의 진동시험을 통해 도출되며, 회전 블레이드의 진동시험 결과는 일반적으로 캠벨 선도(Campbell diagram)(8,9)으로부터 비교할 수 있다. 해석적인 캠벨 선도는 Fig. 2와 같이 블레이드 회전수를 변경하면서 진동모드해석을 반복적으로 수행하여 회전수별 고유진동수를 얻을 수 있다. 이 논문에서는 3가지 다른 회전수에서 각각 진동모드 해석을 수행하고, 회전수별로 고유진동수 값을 선형 보간하여 회전수 차수 성분과 만나는 공진점을 찾아 캠벨 선도를 작성하였다.
2.2 회전 블레이드 진동시험
가스터빈형 도브테일이 적용된 블레이드의 슈라우드 접촉부 경계조건 타당성을 확인하기 위해 실물 크기의 중압터빈 최종단 블레이드를 제작하고, 로터에 조립하였다. 블레이드의 회전에 따른 강성변화 효과와 슈라우드 접촉 영향은 회전하는 블레이드의 고유진동수 측정을 통해 확인할 수 있다. 회전하는 블레이드의 진동시험은 Fig. 7과 같이 발란싱 벙커(balancing bunker) 내의 블레이드가 조립된 터빈 로터를 설치하고 진공 상태에서 정격회전수의 120 % 과속도까지 회전시켰다.
회전하는 블레이드의 응답을 측정하기 위해서는 적절한 가진이 필요하며, Table 1과 같이 다양한 가진 방법이 있다.
이 연구에서는 설치하기가 쉽고, 적용상 제한이 크게 없어 산업계에서 널리 사용되고 있는 공기 분사 노즐을 사용하였다.
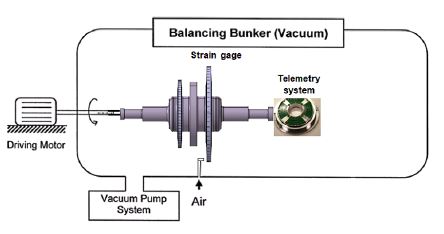
Fig. 8은 발란싱 벙커에 설치한 블레이드가 조립된 로터, 회전시 블레이드를 가진하기 위한 공기 분사 노즐 및 무선 데이터 송수신 안테나를 나타내고 있다. 압축기를 이용하여 약 10 bar이상의 압축공기를 만들어 발란싱 벙커 내에 유입시키고, 블레이드의 앞부분에 공기 분사 노즐을 설치하여 회전 중인 블레이드에 압축 공기를 분사시키는 방법으로 블레이드를 가진하였다. 정격 회전수의 120 % 과속도로부터 측정하고자 하는 회전수 범위까지 천천히 일정속도로 로터를 감속시키면서 동시에 압축 공기로 가진하면서 회전수에 따른 블레이드 진동응답을 측정하였다.
회전 블레이드 진동시험을 위한 측정 시스템은 센서, 무선 데이터 송수신 및 신호 분석으로 구성된다. 블레이드의 진동 거동을 분석하기 위하여 측정하는 물리량인 진동 변형률을 감지하기 위한 센서로 스트레인 게이지가 설치된다. 스트레인 게이지의 부착위치는 블레이드의 변형률 진동모드 해석 결과를 통해 측정하고자 하는 진동모드까지 모두 포함하는 진동 변형률 모드가 가장 큰 위치를 선정한다. 본 연구에서는 블레이드 베인 하단부에 등 간격으로 총 6개의 블레이드에 스트레인 게이지를 부착하였다. 회전하는 블레이드에 설치된 스트레인 게이지의 신호 데이터는 무선 전송 방식에 의한 신호 송수신 시스템이 적용되었다. 진동 신호는 데이터 취득/분석 시스템을 통해 신호처리, 저장 및 분석되었다.
발란싱 벙커 내부를 진공상태로 유지하여 블레이드 회전시 공기 저항을 최소화하였지만, 블레이드 가진을 위한 압축 공기 분사로 인해 블레이드 온도가 상승한다. 시험시 과도한 온도 상승 감시와 온도 효과를 고려하기 위해 블레이드 표면에 열전대(thermal couples)를 부착하여 진동신호와 함께 무선 송수신으로 동시에 온도를 측정하였다. 측정된 온도 결과는 해석 모델의 기계적 물성치에 영향을 미치나, 온도 변화율이 작아 블레이드의 진동수 변화량은 0.1 % 이하였다.
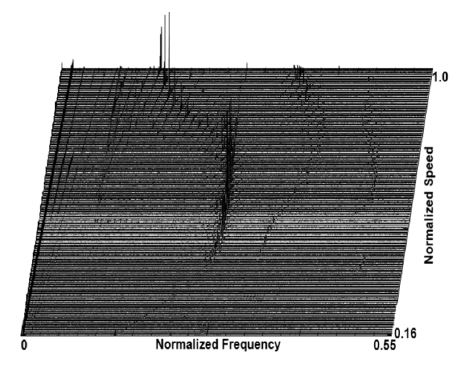
이와 같은 방법으로 회전하는 블레이드의 진동 응답 측정한 후, 신호처리를 통해 측정한 블레이드의 캠벨 선도를 Fig. 9에 나타내고 있다.
2.3 해석 모델의 검증
앞서 서술된 회전에 의한 블레이드 강성 변화 효과 및 해석 절차를 반영하여 블레이드 진동모드 해석 수행한 결과와 회전 블레이드 진동시험 결과를 비교하였다. 회전 블레이드 진동시험에서 진동과 동시에 측정된 블레이드 온도 데이터를 블레이드 진동모드 해석시 온도에 따른 기계적 물성치에 반영하였다.
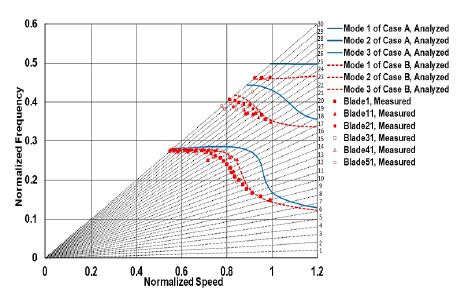
블레이드 슈라우드의 접촉부에 고려된 2가지 경계조건에 따라 수행한 결과와 회전 블레이드 시험 결과를 Fig. 10의 캠벨 선도에 함께 나타내고 있다. 그림으로부터 슈라우드의 접촉 해석을 통해 접촉강성을 반영하여 해석한 조건 B의 경우가 3차 모드까지 잘 일치하고 있음을 알 수 있다. 해석 조건 A의 경우는 블레이드 슈라우드 접촉면의 전체 절점이 인접 슈라우드와 서로 결합되어 있다고 가정된 것으로 측정된 3차 진동모드의 공진점보다 높게 나타나며, 이는 해석시 슈라우드 접촉부의 강성이 높게 고려되었음을 의미한다. 블레이드가 회전시 슈라우드 접촉면에서 발생하는 접촉 강성은 해석 조건 B가 타당함을 시험 결과로부터 확인할 수 있었다.
캠벨 선도로부터 1차 모드의 공진점이 상대적으로 많이 변화는 구간은 Fig. 5의 간섭 선도에서 노달 직경별 고유진동수 변화가 큰 영역과 일치한다. 노달 직경 20차까지인 이 영역은 휠 강성의 영향을 주로 받는다. 캠벨 선도는 노달 직경별 고유진동수와 회전수 차수와 일치하는 공진점을 나타낸 것(8,9)으로 Fig. 5의 간섭 선도에서 기울기가 큰 영역인 8 ~ 20차 노달 직경에서 회전수 성분과 만난다. 이는 Fig. 10의 캠벨 선도에서는 0.8 ~ 1인 회전속도 구간에서 공진점 변화를 크게 나타나게 하였다. 캠벨 선도의 높은 회전수 영역에서 공진점 변화가 크게 나타난 것은 휠 강성의 변화가 크게 미친다는 것으로 이해할 수 있다.
3. 결 론
이 논문에서 대형 증기터빈에 적용되고 있는 가스터빈 도브테일형 슈라우드 블레이드의 진동모드 해석 절차를 제시하고 슈라우드 접촉부의 경계조건에 따른 해석을 수행하였다. 이 연구에서 제시된 2가지 해석 모델의 경계조건 타당성을 확인하기 위해 회전 블레이드 진동 시험을 수행하였다.
회전 블레이드 진동 시험 방법과 절차에 대해 서술하고, 시험 결과인 캠벨 선도를 획득하였다. 측정된 캠벨 선도와 해석 조건에 따른 결과를 비교한 결과, 슈라우드 접촉영역의 강성변화를 고려한 해석 조건 B의 결과가 보다 정확함을 확인하였다. 슈라우드 간의 접촉부에서 발생하는 강성을 보다 정확히 반영할 수 있는 해석모델을 도출하였고, 해석 모델의 타당성이 확인하였다.
향후, 이 연구를 통해 제시된 슈라우드 블레이드의 해석 절차와 방법은 유사 모델인 증기터빈의 최종단 블레이드(last stage blade) 및 가스터빈 블레이드의 공진 회피 설계를 위한 해석 정확성 향상에 기대된다.
References
- Park, J. P., Shin, E. T. and Kim, H. J., 1998, Running Bucket Vibration Test of Steam Turbines, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 8, No. 2, pp. 331~335.
-
Szwedowicz, J., Visser, R., Sextro, W. and Masserey, P. A., 2003, On Forced Vibrations of Shrouded Turbine Blades, Proceedings of ASME Turbo Expo 2003, Vol. 4, pp. 257~266.
[https://doi.org/10.1115/GT2003-38808]

-
Kaptan, F., Scheidt, L. P. -V. and Wallaschek, J., 2018, Numerical and Experimental Study of Shrouded Blade Dynamics Considering Variable Operating Points, Proceedings of ASME Turbo Expo 2018, Vol. 2018, No. 7C, V07CT35A034.
[https://doi.org/10.1115/GT2018-76692]

-
Lee, D. Y., Bae, Y. C., Kim, H. S., Lee, Y. R. and Kim, D. Y., 2010, Vibration Analysis for the L-1 Stage Bladed-disk of a LP Steam Turbine, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 20, No. 1, pp. 29~35.
[https://doi.org/10.5050/KSNVE.2010.20.1.029]

- Rao, J. S., 1991, Turbomachine Blade Vibration, John Wiley & Sons, New York, NY.
- ANSYS, 2018, ANSYS Manual.
- Singh, M. P., Vargo, J. J., Schiffer, D. M. and Dello, J. D., 1988, SAFE Diagram-A Design and Reliability Tool for Turbine Blading, Proceedings of the 17th Turbomachinery Symposium, Turbomachinery Laboratory, Texas A&M University, College Station, Texas, pp. 93~102.
- Campbell, W., 1924, The Protection of Steam Turbine Disk Wheels from Axial Vibration, General electric, New York, NY.
- Campbell, W. and Heckman, W. C., 1925, Tangential Vibration of Steam Turbine Buckets. Transactions of ASME, Vol. 47, pp. 643~654.

YoungHo Ju received his M.S. and Ph.D. degree in Dept. of Mechanical Engineering from GyeongSang National University in 1997 and 2021 respectively, he joined Doosan Enerbility as R&PD engineer, in 1997. He has over 25 years of experience in development of thermal turbomachinery as engineer or project leader. His professional interests include blade mechanical design, spin testing of blade, mistuning, damping and flutter in blade aeromechanics of turbomachinery.

JungChan Kim received a B.S. and M.S. degree from Pusan National University, Busan, South Korea, in 2005 and 2007, respectively. He was a Research Engineer at LG Electronics, South Korea. He is currently a Senior Research Engineer at Turbomachinery Technology Development Team in Doosan Enerbility, South Korea, since 2011. His research interests include blade design, aeromechanics and vibration diagnosis of turbomachinery.