스프링 양단 지지 케이블의 고유진동 해석을 위한 허용함수와 준 비교함수의 선택에 대한 고찰
© The Korean Society for Noise and Vibration Engineering
Abstract
Natural vibration analysis of cables is required in various fields, such as transmission lines and elevator ropes. Actual cables are often non-uniform. Because an exact solution is difficult to calculate in this case, an approximate solution must be calculated through numerical analysis. It is important to define the admissible function in the assumed method, which is widely used among numerical analysis methods. However, selecting an admissible function for a problem in which only geometric boundary conditions exist, such as spring-end support cable, is difficult. In this study, we propose the admissible and quasi-comparison functions for the addressed problem and compare the results to the finite element method results. This study can be used for the analysis of various structures in which cables are used.
Keywords:
Assumed Mode Method, Admissible Function, Quasi-comparison Function, Finite Element Method, Spring-end Support Cable키워드:
가정모드법, 허용함수, 준 비교함수, 유한요소법, 스프링 지지 케이블1. 서 론
진동 해석이 필요한 구조물들은 대부분 연속계이다. 연속계의 대표적인 예로는 봉(bar), 보(beam), 평판(plate), 케이블(cable) 혹은 스트링(string)이 있다. 이러한 연속계는 복잡한 구조물의 고유진동 해석의 기초가 되기 때문에 중요하다. 그중 케이블의 경우 송전선, 엘리베이터의 로프, 기계에 사용되는 벨트 등을 표현하는데 사용되기 때문에 다양한 경우의 케이블 진동 해석은 많은 구조물의 진동 해석에 기초 연구로써 사용되고 있다. Rao(1)는 변분법을 사용해 스트링의 운동방정식을 유도하고, 다양한 경우의 경계조건을 소개했다. Lee and Park(2)은 길이가 변하는 현에 대해 이동파 방법을 사용하여 운동방정식과 고유진동수의 엄밀해를 계산했다. Shin 등(3)은 축방향으로 이송되는 현의 운동방정식을 유도하기 위해 기하학적 비선형성을 고려하여 von Karman 변위-변형률 관계식과 확장 해밀턴 원리를 사용했다.
수학적으로 엄밀해를 구하게 되면 모든 변수에 대해 정답을 계산할 수 있게 된다. 즉, 해당 문제에 대한 통찰력을 제공하기 때문에 많은 연구가 엄밀해를 구하기 위해 진행되었다. 하지만 엄밀해를 구할 수 있는 경우는 매우 한정적으로, 강성과 질량이 균일하게 분포되어 있는 균일한 구조물이어야 한다. 실제 송전선의 경우 스톡브릿지 댐퍼(stock bridge damper)와 같은 추가적인 질량이 부착되는 경우가 많다. 엘리베이터의 로프는 다양한 장치들이 부착되어 있어 균일한 케이블로 볼 수 없다. 예인음탐케이블은 4종류의 단면으로 구성되어 엄밀해 계산이 어렵다. 이런 경우에는 수치해석법으로 근사해를 계산해야 한다. 수치해석법으로는 대표적으로 Rayleigh-Ritz 방법, 가정모드법(AMM, Assumed mode method), 유한요소법(FEM, Finite element method)이 있다.
먼저 유한요소법은 Rayleigh-Ritz 방법에 기반을 두고 있는 방법이다. 하지만 시스템을 여러 요소로 나누어 전역함수가 아닌 국부함수를 사용한다는 것이 Rayleigh-Ritz 방법과 가정모드법과의 차이점이다. 많은 요소로 나눌수록 정확도가 증가하기에 많은 계산량이 필요하지만 단순한 함수를 사용하기 때문에 컴퓨터를 사용한 계산에 매우 적합하다. 따라서 컴퓨터의 발달과 더불어 주목을 받게 된 수치해석법이다.
가정모드법과 Rayleigh-Ritz 방법은 자유진동 문제의 경우 동일한 운동방정식이 유도된다. 그러나 강제진동 응답 계산까지 고려한다면 가정모드법이 유리하다(4). 가정모드법은 수치해석법임에도 불구하고 수학을 사용하는 정성적인 방법에 가깝기 때문에 의미가 있는 방법이다. 가정모드법에서 근사해의 정확도는 허용함수의 선택에 좌우된다. 사용가능한 허용함수에는 3가지가 있다. 첫번째는 미분 방정식과 경계조건을 모두 만족하는 고유함수, 두번째는 경계조건만 만족하는 비교함수, 마지막은 기하학적인 경계조건만 만족하는 허용함수이다. 여기서 경계조건은 기하학적 경계조건과 동역학적 경계조건으로 구성되어 있다. 기하학적 경계조건은 변위나 기울기에 대한 경계조건을 의미한다. 동역학적 경계조건은 힘이나 굽힘 모멘트에 대한 경계조건을 의미한다. 일반적으로 가정모드법의 허용함수로 기하학적 경계조건을 만족하는 균일한 시스템의 고유함수를 사용한다. Talib 등(5)은 양 끝이 고정된 송전선에 스프링 스페이서가 연결되어 있는 경우의 진동 해석을 위해 에너지 방법과 가정모드법을 사용했다. Koo 등(6)은 스톡브릿지 댐퍼가 장착된 양 끝 고정 송전선의 진동해석을 위해 가정모드법을 사용했다. 두 연구 모두 허용함수로 양 끝 고정 균일 스트링의 고유함수를 사용했다. Yang 등(7)은 건물과 승강기 로프의 연성 진동을 해석하기 위해 가정모드법과 해밀턴 원리를 함께 사용했다. 로프의 허용함수로 양 끝 고정 균일 스트링의 고유 함수를 사용했다. 이처럼 가정모드법은 복잡하고 불균일한 구조물에 대한 근사해를 제공한다.
지금까지의 연구들은 적어도 하나의 기하학적 경계조건을 갖는 구조물에 대해서만 가정모드법을 사용했다. 양 끝단이 모두 스프링으로 지지되어 있는 케이블은 동역학적 경계조건만을 가지고 있기 때문에 허용함수의 설정이 어려워 이에 대한 연구는 아직 이루어지지 않았다. 이런 경계조건은 송배전선에서 나타난다.
이 연구에서는 양 끝단이 스프링으로 지지되어 있는 케이블이 균일하지 않아 엄밀해를 구할 수 없는 경우에 가정모드법을 사용해 고유진동 해석을 진행하기위해 두가지 형태의 허용함수를 제안한다. 유한요소법과 결과를 비교함으로써 타당성을 조사한다.
2. 엄밀해
2.1 스프링 지지 케이블
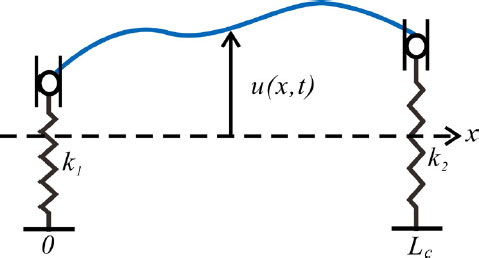
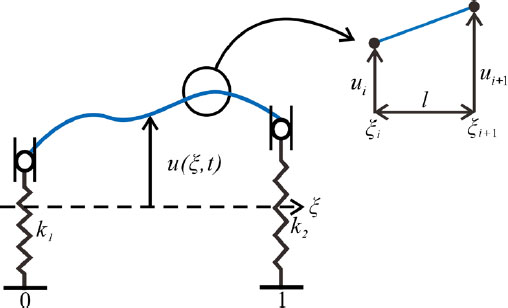
이 연구에서 다루고자 하는 시스템은 Fig. 1과 같다. x축 방향이 그림에서 보이는 바와 같을 때, x축으로 길이가 Lc인 케이블이 강성 k1, k2를 가지는 스프링으로 양 끝단이 지지 되어있고, 수직방향으로 u의 변위를 가진다. 케이블의 단위 길이당 질량은 , 케이블 내부 장력은 Tc를 사용해 표현했다.
2.2 확장 해밀턴 원리
수치해석 방법에 대한 연구를 진행하기 앞서, 수치해석 방법의 정확도를 확인하기 위해 엄밀해를 계산했다. 엄밀해 계산을 위해 균일한 케이블이라는 가정을 사용했고, 확장 해밀턴 원리를 사용하여 운동방정식과 초기 조건을 유도했다. Fig. 1의 케이블의 운동 에너지와 위치 에너지는 각각 식 (1), 식 (2)와 같다.
| (1) |
| (2) |
여기서 •는 시간에 대한 미분을 나타낸다. 식 (1)과 식 (2)를 사용해 표현한 라그랑지안(L = T – V)은 식 (3)과 같다.
| (3) |
라그랑지안은 라그랑지안 밀도 함수 를 사용해 식 (4)와 같이 표현 가능하다.
| (4) |
따라서 식 (3)과 식 (4)를 비교하면 라그랑지안 밀도 함수는 다음과 같다.
| (5) |
확장 해밀턴 원리는 다음과 같다.
| (6) |
여기서 δ은 변분을 의미하고, 는 비보존력에 의한 일을 의미한다. 케이블에 분포하중 f(x, t)이 작용한다고 하면 비보존일은 다음과 같다.
| (7) |
식 (5)와 식 (7)을 확장 해밀턴 원리인 식 (6)에 대입하고 정리하면 다음과 같은 식이 계산된다.
| (8) |
가상변위 δu가 임의의 값을 가지기에 식 (8)이 성립하기 위해서는 적분의 내부 부분이 0이 되어야 하고, 이로부터 운동방정식과 경계 조건을 유도할 수 있다. 운동방정식은 다음과 같다.
| (9) |
경계 조건은 다음과 같다.
| (10) |
이 연구에서는 케이블의 고유 특성에 대해 살펴보고자 자유 진동의 상태라고 가정했다. 길이 방향으로 무차원화 해주기 위해 ξ = x/Lc라는 변수를 도입했다. 운동방정식 및 경계 조건을 다시 표현하면 다음과 같다.
| (11) |
| (12) |
여기서 '은 ξ에 대한 미분을 나타낸다. 변수분리법을 사용해 다음과 같이 u(ξ, t)를 ξ와 t에 대한 함수로 각각 분리할 수 있다.
| (13) |
변수분리법을 적용해 식 (11)과 식 (12)를 다시 표현하면 다음과 같다.
| (14) |
| (15) |
식 (14)가 변수 ξ, t에 상관없이 항상 식이 성립하고, 진동하는 시스템이기 위해서는 다음과 같아야 한다.
| (16) |
여기서 ω는 x방향으로의 케이블 고유 진동수를 의미한다. 식 (16)을 두개의 식으로 분리하여 얻은 상미분 방정식의 일반해 형태는 다음과 같이 표현된다.
| (17) |
| (18) |
여기서
| (19) |
식 (17)의 A와 B는 초기조건으로부터, 식 (18)의 C와 D는 경계조건으로부터 계산된다. 경계조건 식 (15)에 식 (18)을 대입하면 다음과 같은 결과를 얻을 수 있다.
| (20) |
여기서
| (21) |
으로 무차원화된 시스템의 특성을 의미한다. 식 (20)으로부터 β를 계산하면 스프링 지지 케이블의 고유모드는 다음과 같다.
| (22) |
여기서 Ui는 i번째 고유모드를 의미하고, βi는 i번째 고유진동수에 대한 β를 의미한다.
이처럼 엄밀해를 구하는 과정은 복잡하고 특수한 경우에만 구할 수 있다. 수치해석법을 사용해 근사해를 구하는 방법은 다음과 같다.
3. 가정모드법을 사용한 근사해
이 연구에서는 수치해석 방법으로 가정모드법과 유한요소법을 사용했다. 두 방법은 모두 연속계를 다자유도 이산계로 이산화하여 문제를 해결한다. 가정모드법의 정확도는 허용함수 선택에 영향을 받는다. 이 연구에서는 허용함수와 비교함수에 준하는 준 비교함수를 사용했다. 허용함수는 기하학적인 경계조건을 만족하는 함수이다. 준 비교함수는 Meirovitch와 Kwak(8)에 의해 소개되었는데, 각각의 함수들은 동역학적 경계조건을 만족하지 않지만, 함수들의 결합은 동역학적 경계조건을 만족하게 되면서 비교함수에 가까운 성질을 갖는 함수를 의미한다.
가정모드법을 사용해 근사해를 구하는 방법은 다음과 같다. 먼저 식 (1)의 운동에너지와 식 (2)의 위치에너지를 ξ를 사용해 x에 대해 무차원화하고 다음의 가정모드법을 적용한다.
| (23) |
여기서 Φ (ξ)는 케이블 변위에 대한 허용함수 ϕ로 이루어진 1 × na크기의 행렬이다. q(t)는 케이블 변위에 대한 일반화된 좌표 q(t)로 구성된 na × 1크기의 벡터이다. na 는 케이블 변위에 대한 허용함수의 개수를 의미한다. 즉 다음과 같다.
| (24a) |
| (24b) |
가정모드법을 적용해 이산화한 운동에너지와 위치에너지는 다음과 같다.
| (25) |
| (26) |
여기서
| (27) |
| (28) |
자유진동일 때의 라그랑지 방정식(Lagrangian equation)은 다음과 같다.
| (29) |
| (30) |
q(t) = q0eiwt을 식 (30)에 대입하면 다음과 같은 방정식을 얻을 수 있다.
| (31) |
식 (31)의 고유치문제를 풀면 β를 계산할 수 있는데, 행렬이 식 (27), 식 (28)에서와 같이 허용함수로 표현되어 있기 때문에 식 (31)의 고유치문제를 풀기 위해서는 허용함수를 먼저 설정해야 한다.
3.1 허용함수를 사용한 가정모드법
먼저 허용함수로 기하학적인 경계조건을 만족하는 허용함수를 사용했다. Fig. 1의 기하학적 경계조건은 다음과 같이 표현할 수 있다.
| (32) |
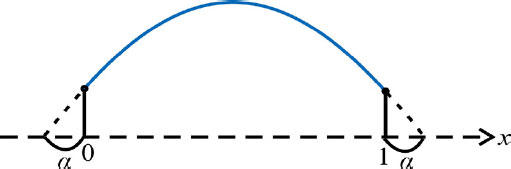
이 연구에서는 끝점이 고정된 균일한 케이블의 고유함수를 끝점에서 α만큼을 제외한 함수로 수정해 허용함수로 사용했다. 수식으로 표현하면 식 (33)과 같다.
| (33) |
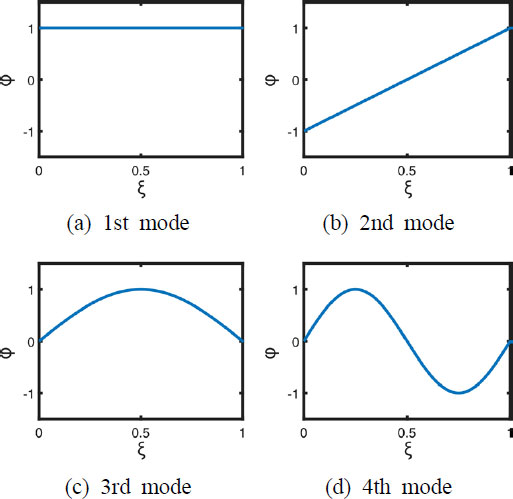
허용함수를 도식화하면 Fig. 2와 같다.
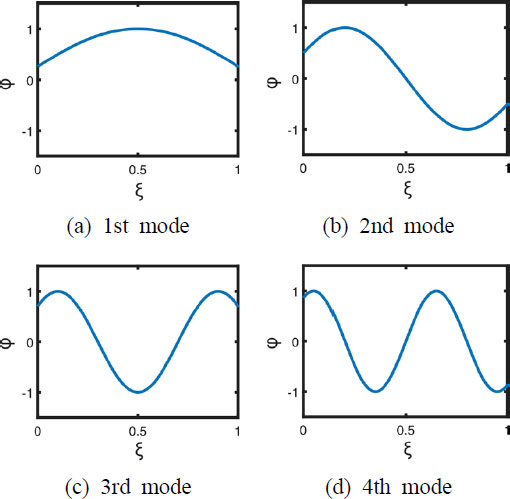
α = 0.1로 작게 설정하여 4차 허용함수까지 그래프로 표현하면 Fig. 3와 같다. 여기서 α값의 선택이 수치해석의 정확도에 영향을 준다. α를 0에서부터 0.1씩 증가시키며 β를 계산하고 엄밀해인 βexact와 비교하여 적절한 α의 값을 찾고자 했다. 그 결과 0에 가까운 아주 작은 α에서는 β의 오차가 컸지만, 1에 가까운 α에서는 β의 정확도가 매우 높아짐을 확인했다. α = 1로 크게 설정하여 4차 허용함수까지 그래프로 표현하면 Fig. 4와 같다.
이는 끝이 고정된 케이블의 고유함수와는 다른 형상을 보여준다. 기존 고유함수의 1차 고유모드가 Fig. 4의 (c)와 같이 허용함수의 3차 모드에서 나타나기 시작한다. 허용함수의 1차, 2차 허용함수는 마치 상수, 직선 함수의 형태와 비슷하다. 이러한 함수가 추가되었는데 오히려 정확도가 높아진 이유는 준 비교함수에 가까워졌기 때문이다. 단, α가 1에 가까워질수록 수렴 안정성에서 문제가 발생할 가능성이 커지는 문제가 발생했다.
이와 같이 허용함수는 α의 선택이 정확성과 수렴 안정성에 영향을 주게 된다. 해석 결과값이 안정적으로 수렴하는 한에서 α를 크게 설정해주는 방법이 있지만, 이는 추가적인 계산 과정이 필요하기 때문에 다음과 같은 준 비교함수를 제안한다.
3.2 준 비교함수를 사용한 가정모드법
준 비교함수는 각각의 함수들은 동역학적 경계조건을 만족하지 않지만, 함수들의 결합은 동역학적 경계조건을 만족하게 되면서 비교함수에 가까운 성질을 갖는 함수를 의미한다. 이 연구에서 사용한 준 비교함수는 다음과 같다.
| (34a) |
| (34b) |
| (34c) |
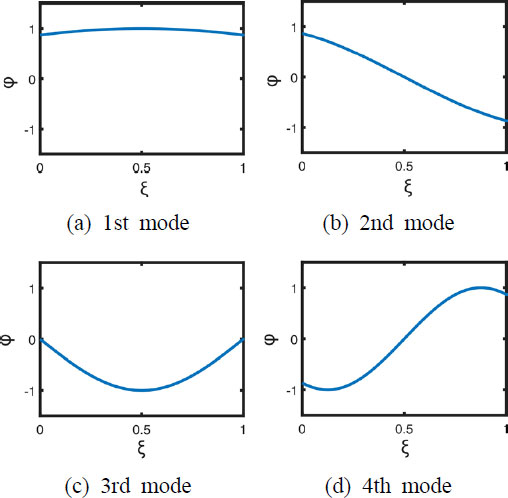
첫 번째 허용함수는 스프링이 같은 방향으로 변형되었을 때의 형상을 의미하는 1이라는 상수 값을 사용했고, 두 번째 허용함수는 스프링이 반대 방향으로 변형되었을 때의 형상을 의미하는 1차 함수를 사용했다. 세 번째 이후의 허용함수는 끝이 고정된 균일 케이블의 고유 함수이다. 4차까지의 준 비교함수를 그래프로 표현하면 Fig. 5와 같다.
이 연구에서 도입한 준 비교함수는 양단의 변위가 0인 함수와 강체 모드가 결합된 형태라고 할 수 있다.
4. 유한요소법을 사용한 근사해
유한요소법은 Fig. 6과 같이 구조물을 작은 요소로 나눈 후 각 요소에 대해 간단한 형태의 국부함수를 사용한다. 유한요소법에서 사용된 함수를 수식으로 표현하면 다음과 같다.
| (35a) |
| (35b,c) |
여기서 아래 첨자 i는 요소의 순서, ui는 i번째 요소의 변위를 의미한다. l은 요소의 길이를 의미하고, nf는 요소의 개수를 의미한다. 식 (35)를 사용해 식 (1), 식 (2)를 각 요소에 대해 다시 표현하면 다음과 같다.
| (36) |
| (37) |
여기서
| (38) |
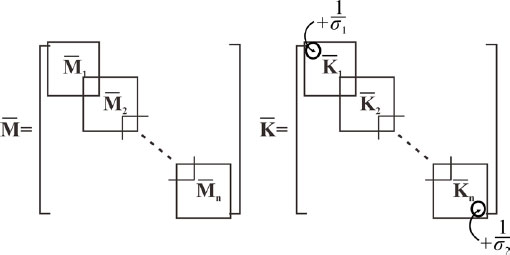
유한요소법은 각 요소에 대해 계산한 후 조립하는 과정이 필요하다. 요소들이 순차적으로 연결되어 있기에 Fig. 7과 같이 조립된다.
유한요소법 또한 질량행렬과 강성행렬을 사용해 다음의 고유치문제를 해결함으로써 β를 계산할 수 있다.
| (39) |
5. 해석 결과
수치해석으로 구한 근사해와 수학으로 구한 엄밀해를 비교하여 수치해석의 정확성을 비교해보기 위해서 균일한 케이블이라고 가정했다. 두 가지 함수를 사용한 가정모드법과 유한요소법으로 계산한 β와, 해밀턴 원리를 사용해 구한 엄밀해인 βexact을 비교했다. 해석에는 Tc = 2000 N, k1 = 100 N/m, k2 = 200 N/m, Lc = 1 m, = 1 kg/m의 값을 사용했다. 양 끝단이 비대칭의 형상을 가지게 함으로써 대칭의 경우보다는 특수한 경우에 대해 결과를 비교해 보고자 양 스프링 상수를 다르게 설정했다.
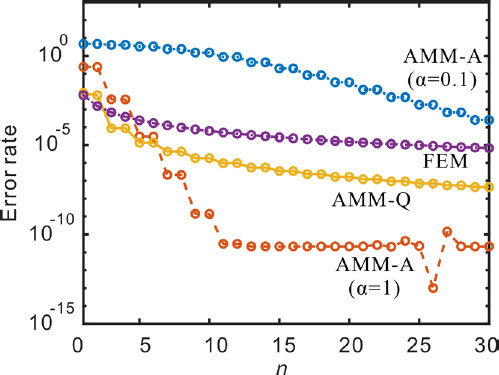
Table 1은 허용함수 개수나 요소의 개수에 따른 수치해석으로 계산한 β1, β2을 정리한 표이다. n은 가정모드법의 경우 허용함수의 개수를, 유한요소법의 경우 요소의 개수를 의미한다. 이는 가정모드법과 유한요소법의 수렴성 및 정확성을 보여준다. AMM-A는 허용함수를 사용한 가정모드법을, AMM-Q는 준 비교함수를 사용한 가정모드법을, FEM은 유한요소법을 의미한다. 추가적으로 Fig. 8과 같이 n의 범위를 증가시켜 β1의 오차율을 확인함으로써 수렴 안정성을 확인했다.
식 (20)으로 계산한 β1, β2의 엄밀해인 0.38412, 3.18862와 비교했을 때 α = 0.1으로 설정한 AMM-A는 작은 α를 설정했기 때문에 안정적으로 수렴하긴 했지만 가장 느린 수렴성을 보여줬다. α = 1로 설정한 AMM-A는 큰 α를 설정했기에 준 비교함수에 가까워져 수렴이 빨라졌지만, Fig. 8과 같이 수렴 안정성이 악화되는 부분이 발생했다. 물론 매우 작은 값이지만 이런 문제는 고차 β에서 더 크게 발생했기 때문에 결코 무시할 수 없다. 준 비교함수를 사용한 방법은 안정적이면서도 우수한 수렴성을 보여줬다. 유한요소법도 좋은 수렴성을 보여줬지만 특히 β2에 대해서는 가정모드법 보다는 수렴의 속도가 느렸다.
결론적으로 정확성, 수렴성, 수렴 안정성을 종합적으로 비교한 결과 준 비교함수를 사용한 가정모드법이 가장 적합한 수치해석법으로 생각된다.
6. 결 론
이 연구에서는 양 끝단이 스프링으로 지지된 케이블이 불균일하여 엄밀해를 구할 수 없는 경우에 고유진동을 해석하기 위한 수치해석 방법에 대해 연구하고, 특히 가정모드법의 적절한 허용함수의 형태를 연구했다. 수치해석법으로는 가정모드법과 유한요소법을 사용했고, 각 수치해석법으로 구한 근사해의 정확성과 수렴성을 확인하고자 확장 해밀턴 원리를 사용해 구한 엄밀해와 비교했다.
유한요소법의 정밀도는 요소의 개수에 좌우되어 비교적 많은 계산량이 필요했다. 하지만 유한요소법은 국부 허용함수 설정이 단순하기에 컴퓨터 연산에 적합하다는 특징이 있다. 가정모드법은 허용함수의 설정이 쉽지 않다. 하지만 수치해석법임에도 불구하고 수학의 정성적인 성질을 가지고 있기에 의미가 있다.
가정모드법은 허용함수를 사용하여 연속계를 이산화하는 수치해석방법으로 결과의 정확성에 있어 허용함수의 선택이 큰 영향을 끼친다. 이 연구에서 다룬 양 끝단 스프링 지지 케이블은 동역학적 경계조건만을 가지기 때문에 기존 기하학적 경계조건을 가지는 문제에 사용하던 가정모드법을 적용하기에는 허용함수 설정에 어려움이 있었다. 따라서 이 연구에서는 두가지의 함수를 제안했다. 첫번째는 기하학적인 경계조건만을 만족하도록 양끝 고정 케이블의 고유함수를 수정한 허용함수이다. 두번째는 여러 허용함수가 결합되었을 때 비교함수의 성질을 갖는 준 비교함수이다. 양단의 변위가 0인 함수와 강체 모드가 결합된 형태로 구성되어 있다. 유한요소법은 구조물을 작은 요소로 나누어 요소의 변위를 단순한 함수로 표현해준다. 이 연구에서는 단순한 직선형태의 함수를 사용해주었다.
수치해석법으로 계산한 β값들과 β의 엄밀해의 비교를 통해 각 방법의 수렴성과 정확성을 확인했다. 먼저 허용함수를 사용한 가정모드법은 α값에 따라 수렴성이 달라졌다. α값이 작은 경우 수렴성이 가장 느렸고, α값이 1에 가깝게 커지면 정확도가 높아졌다. 이유는 α가 커지면 준 비교함수와 매우 유사해지기 때문이다. 단, α가 1에 가까워질수록 수렴 안정성에서 문제가 발생할 가능성이 커지는 문제가 발생했다. 준 비교함수의 계산 결과는 안정적이면서도 빠르게 수렴하는 것을 확인했다. 유한요소법은 가정모드법과 비교하여 수렴성이 낮은 것을 확인했다. 따라서 이 연구에서 제안한 준 비교함수를 사용하는 가정모드법이 가장 적합한 수치해석법이라고 판단된다.
동역학적 경계조건만을 가진 케이블에 대해 이 연구에서 제안한 허용함수를 사용하면 기존에 사용하지 못했던 가정모드법으로 고유진동 해석이 가능하다. 특히 송배전선의 고유진동 해석에 활용될 수 있을 것으로 판단된다.
기 호 설 명
| α : | 끝점이 고정된 균일한 케이블의 고유함수에서 제외되는 길이 |
| β : | 무차원 고유진동수 () |
| βexact : | β의 엄밀해 |
| k1, k2 : | 케이블 양단 고정 케이블 강성 |
| L : | 라그랑지안 |
| : | 라그랑지안 밀도 함수 |
| Lc : | 케이블의 x축 방향으로의 길이 |
| : | 케이블의 단위 길이당 질량 |
| na : | 케이블 변위에 대한 허용함수 개수 |
| nf : | 유한요소법에서 요소의 개수 |
| q(t) : | 케이블 변위에 대한 일반화된 좌표 |
| q(t) : | 케이블 변위에 대한 일반화된 좌표 벡터 |
| T : | 운동 에너지 |
| Tc : | 케이블 내부 장력 |
| u(x, t) : | 수직방향 케이블 변위 |
| σi : | 무차원 시스템 특성 변수 (= Tc/Lcki(i = 1, 2)) |
| ϕ(ξ) : | 케이블 변위에 대한 허용함수 |
| Φ(ξ) : | 케이블 변위에 대한 허용함수 행렬 |
| V : | 위치 에너지 |
| : | 비보존력에 의한 일 |
| ξ : | 길이방향 무차원 변수(= x/Lc) |
Acknowledgments
이 연구는 한국전력공사의 2022년 착수 사외공모 기초 연구 사업에 의해 지원되었음(과제번호: R21XO01-42).
References
-
Rao, S. S., 2006, Vibration of Continuous Systems, John Wiley & Sons, Inc., Chap. 8.
[https://doi.org/10.1002/9780470117866]

- Lee, S.-Y. and Park, S. G., 1999, Free Vibration Characteristics of a String with Time-varying Length, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 9, No. 5, pp. 906~913.
- Shin, C. H., Haw, J. W., Chung, J. T. and Han, C. S., 1999, Dynamic Analysis for an Axially Moving String, Proceedings of the KSNVE Annual Autumn Conference, pp. 365~369.
-
Kwak, M. K., 2022, Dynamic Modeling and Active Vibration Control of Structures, Springer, Dordrecht, Chap. 4.
[https://doi.org/10.1007/978-94-024-2120-0]

-
Talib, E., Shin, J.-H., Kwak, M. K. and Koo, J. R., 2019, Dynamic Modeling and Simulation for Transmission Line Galloping, Journal of Mechanical Science and Technology, Vol. 33, No. 9, pp. 4173~4181.
[https://doi.org/10.1007/s12206-019-0812-1]

-
Koo, J.-R. and Song, O.-S., 2019, Vibration Analysis of Transmission Line with Stockbridge Dampers, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 29, No. 4, pp. 470~476.
[https://doi.org/10.5050/KSNVE.2019.29.4.470]

-
Yang, D.-H., Kim, K.-Y., Kwak, M. K. and Lee, S., 2017, Dynamic Modeling and Experiments on the Coupled Vibrations of Building and Elevator Ropes, Journal of Sound and Vibration, Vol. 390, pp. 164~191.
[https://doi.org/10.1016/j.jsv.2016.10.045]

-
Meirovitch, L. and Kwak, M. K., 1990, Convergence of the Classical Rayleigh-Ritz Method and the Finite Element Method, AIAA Journal, Vol. 28, No. 8, pp. 1509~1516.
[https://doi.org/10.2514/3.25246]


Soo-Min Kim received B.S. in Mechanical Engineering from Dongguk University in 2020. She is currently a doctoral student in the Dept. of Mechanical Engineering in Dongguk University. Her research interests are active vibration control and fluid-structure interaction.

Moon Kyu Kwak received B.S. and M.S. degrees in Naval Architecture from Seoul National University in 1981 and 1983. He received his Ph.D. degree from the Dept. of Engineering Science and Mechanics of Virginia Tech in 1989. He is currently a Professor at the Department of Mechanical, Robotics and Energy Engineering of Dongguk University in Seoul, Korea. His research interests are dynamics and control of flexible multibody system and active vibration control of smart structure.

Dae Woong Kim received B.S. in Mechanical Engineering from Dongguk University in 2022. He is currently a graduate student in the Dept. of Mechanical Engineering in Dongguk University.