방음용 실링재 유무에 따른 틈새 소음 영향에 대한 연구

1. 서 론

삶의 질 개선과 개인 공간의 프라이버시를 중요시하는 니즈를 충족하기 위해 주거 환경에서 소음 문제에 대한 개선 욕구는 지속적으로 증대되어왔다. 이에 차음 성능이 뛰어난 벽체 재료와 흡 ∙ 차음재 등 건설 재료 및 시공법 개선으로 이어졌다.

실내 공간에서 인접하고 있는 두 공간에서 음향 전달경로는 두 가지로 나눌 수 있다. 직접적인 방법은 벽에 의한 투과이며, 간접적인 방법은 천정, 바닥, 문, 창문 등의 틈새를 통해 전달되는 측면 투과이다. 특히 측면 투과는 벽의 차음효과에 악영향을 미치기 때문에 실링재를 이용하여 틈새를 채워 차음효과를 얻는다.

틈새 용어는 포괄적으로 사용하지만 크기와 모양에 따라 분류된다. 틈새 크기가 음파 파장보다 작을 경우 ‘leak’라 정의하며, 그 반대인 경우는 ‘opening’라 한다. 주로 이 두 가지 경우를 모두 일컬어서 ‘aperture’라 할 수 있다⁽¹⁾. 또한 모양에 다른 분류에서 직사각형으로 된 틈새를 ‘slit’이라 한다.

틈새 투과손실에 대한 연구는 다양한 각도에서 진행되어 왔다. 이론적 연구는 Gomperts⁽²⁾, Gomperts and Kihlman⁽³⁾, Wilson and Soroka⁽⁴⁾, Sauter and Soroka⁽⁵⁾, Mechel⁽⁶⁾, Chen⁽⁷⁾, Yang 등⁽⁸⁾ 등에 의해 진행되었고, 수치적 접근으로 Park and Eom⁽⁹⁾, Sgard 등⁽¹⁾, Poblet-Puig and Rodriguez-Ferran⁽¹⁰⁾ 등이 있다. 실험적 접근으로는 Oldham and Jhao⁽¹¹⁾, Hongisto 등⁽¹²⁾, Uris 등⁽¹³⁾, Kim⁽¹⁴⁾ 등이 있다.

틈새에 대한 다양한 이론적, 실험적 접근법이 있었지만 틈새 실링에 대한 연구는 거의 없었다. 또한 기존 연구들은 대부분 Gomperts와 Kihlman에 의한 예측모델⁽³⁾을 이용했던 반면, 이 연구에서는 Mechel의 예측모델⁽⁶⁾을 이용하였다.

이 연구는 직사각형 틈새(slit)가 있는 석고 보드에 대한 투과손실 예측 모델을 검토하고, 틈새를 방음용 실링재로 채움으로써 얻어지는 효과를 확인하는 것이 목적이다. 또한 이 예측 모델과 실험과의 일치성을 확인하는 것이 주된 목적이다.

2. 이론적 접근 및 실험개요

2.1 음향 투과에 대한 이론적 모델

이론적 접근을 쉽게 하기 위해 다음과 같이 가정을 하였다. 먼저 3차원 공간에서 무한한 벽에 두께가 한정적이나, 너비 길이가 무한한 직사각형 틈새(slit)를 벽 가운데 위치시켰다. 틈새 내부 매질은 등방성과 균일성을 갖춘 단일 매질로 구성되어, 매질의 종류에 따라 파수가 달라지게 된다. 또한 틈새 폭 길이가 음파의 파장보다 작다고 가정하였고, 틈새 표면은 밴드 모양으로 피스톤 운동을 한다. 평면파가 벽과 틈새와 비스듬히 입사한다고 하였다.

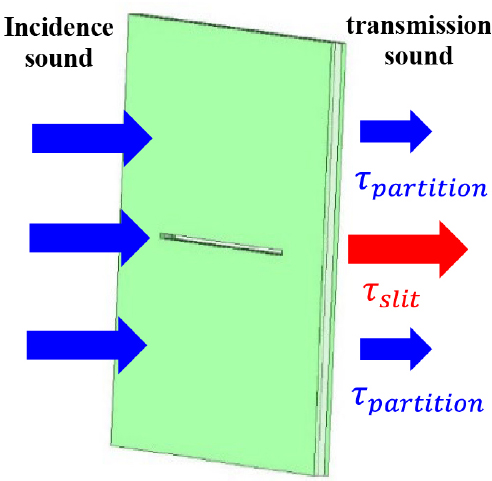
Fig. 1은 벽의 음향 투과 전달경로를 나타낸 것이다. 전체 음향투과율은 식 (1)과 같이 각 구역의 음향투과율과 면적비 곱의 합으로 구할 수 있다.

Fig. 1

Configuration of sound transmission

$\[ {\tau }_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l} }={\tau }_{\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n} }\left(\frac{A_{\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{ }}}{A_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}\mathrm{ }}}\right)+{\tau }_{\mathrm{s}\mathrm{l}\mathrm{i}\mathrm{t} }\left(\frac{A_{\mathrm{s}\mathrm{l}\mathrm{i}\mathrm{t} }}{A_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}\mathrm{ }}}\right) \]$

(1)

이 논문에서는 틈새의 음향투과율 τ_slit은 Table 1에 제시된 두 가지 해석모델 중 Mechel 모델⁽⁶⁾을 이용하였고, 벽의 음향투과율 τ_partition은 식 (2)와 같이 Fahy 모델⁽¹⁵⁾을 통해 예측하였다.

Table 1

The analytical models of slit transmission loss

$\[ \begin{array}{l}{\tau }_{\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}=\\ \frac{{\left(2{\rho }_{0}c/\omega m\right)}^2{\mathrm{s}\mathrm{e}\mathrm{c}}^2{\theta }_i}{{\left[\left(2{\rho }_{0}c\mathrm{s}\mathrm{e}\mathrm{c}{\theta }_i/\omega m\right)+{\left(k_0\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_i/k_b\right)}^4\eta \right]}^2+{\left[1-{\left(k_0\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_i/k_b\right)}^4\right]}^2}\end{array} \]$

(2)

여기서 k_b = (ω²m/D)^1/4는 벽의 굽힘파를 나타내고, D는 휨 강성, η는 댐핑 손실계수를 나타낸다. 벽의 전체 음향투과율은 식 (1)에 각각의 음향투과율과 면적비를 대입하여 구할 수 있다.

2.2 Mechel 모델을 이용한 음향 투과

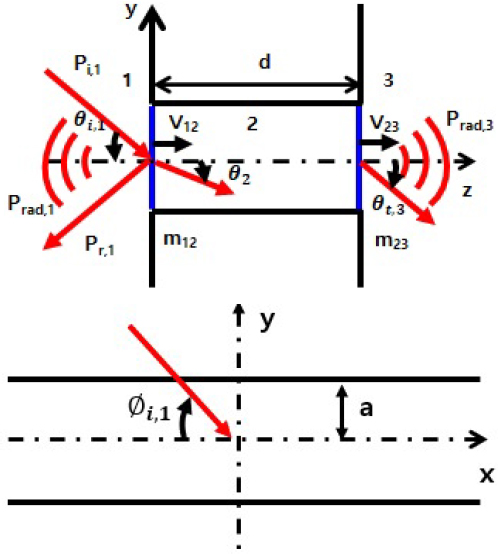
단일 매질로 이루어진 틈새 내부에 대해 비스듬히 입사한 음이 투과한 모습을 도식한 것이 Fig. 2가 되겠다. 입사파 p_i,1와 틈새 표면과 수직 방향이 이루는 각을 θ_i,1라 하고, 틈새 표면과 평행하게 이루는 각을 Φ_i,1라 하자. 또한 m₁₂, m₂₃은 각각 틈새 내 매질 1, 2 사이, 매질 2, 3 사이 경계면에서의 면밀도를 나타내며, 틈새 내부 매질에 따라 달라지게 된다. 만약 공기일 경우는 면밀도는 0으로 가정한다.

Fig. 2

A schematic representation of cross section of a slit

각 구역별로 음장에 대한 방정식은 식 (3) ~ (5)와 같으며 시간에 대한 성분 e^jwt은 여기서 생략하였다. 1번 매질에서 음장은 입사, 반사로 인해 발생한 blocked pressure와 가상의 baffled piston에 의해 발생하는 radiated pressure의 중첩으로 결정된다.

$\[ p_1=p_{i,1}+p_{r,1}+p_{rad, 1}=p_{\mathrm{b}\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{k}}+p_{\mathrm{r}\mathrm{a}\mathrm{d}, 1} \]$

(3)

$\[ p_{i,1}\left(x,y,z\right)={\widehat{p}}_1{e}^{-j{k}_0\left(x \mathrm{s}\mathrm{i}\mathrm{n}{\theta }_1\mathrm{c}\mathrm{o}\mathrm{s}{\varnothing }_1+y \mathrm{s}\mathrm{i}\mathrm{n}{\theta }_1\mathrm{c}\mathrm{o}\mathrm{s}{\varnothing }_1+z \mathrm{c}\mathrm{o}\mathrm{s}{\theta }_1\right)} \]$

(4)

$\[ p_{r,1}\left(x,y,z\right)={\widehat{p}}_1{e}^{-j{k}_0\left(x \mathrm{s}\mathrm{i}\mathrm{n}{\theta }_1\mathrm{c}\mathrm{o}\mathrm{s}{\varnothing }_1+y \mathrm{s}\mathrm{i}\mathrm{n}{\theta }_1\mathrm{c}\mathrm{o}\mathrm{s}{\varnothing }_1-z \mathrm{c}\mathrm{o}\mathrm{s}{\theta }_1\right)} \]$

(5)

여기서 p_i,1, p_r,1은 매질 1에서 입사 압력과 반사 압력이 되겠다. p_rad,1 식 (6)과 같이 Rayleigh integral⁽¹⁵⁾을 통해 얻을 수 있다.

$\[ \begin{array}{c}{p}_{\mathrm{r}\mathrm{a}\mathrm{d},1}=-\frac{j\omega {\rho }_0{V}_{12}2a}{2\pi }{e}^{-j{k}_{x}x}\\ {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }} \frac{\mathrm{s}\mathrm{i}\mathrm{n}\alpha a}{\alpha a}\frac{e^{-j\alpha y+z\sqrt{{\alpha }^2-{\gamma }^2}}}{\sqrt{{\alpha }^2-{\gamma }^2}}d\alpha \end{array} \]$

(6)

여기서 V₁₂는 매질 1, 2 사이의 경계면에서 표면 속도의 크기, 2a는 틈새 폭의 길이, $$ {\gamma }^2=k_0^2-k_x^2$$이 되겠다. 매질 2에서 식 (7), (8)과 같이 음장은 들어가는 파와 나가는 파로 이루어져 있고, 매질 1에서 매질 2로 y축 방향으로 전파되는 것은 일정하다고 가정한다.

$\[ p_{i,2}\left(x,z\right)={\widehat{p}}_{i,2}{e}^{-j{k}_a\left(x \mathrm{s}\mathrm{i}\mathrm{n}{\theta }_2+z \mathrm{c}\mathrm{o}\mathrm{s}{\theta }_2\right)} \]$

(7)

$\[ p_{r,2}\left(x,z\right)={\widehat{p}}_{r,2}{e}^{-j{k}_a\left(x \mathrm{s}\mathrm{i}\mathrm{n}{\theta }_2-z \mathrm{c}\mathrm{o}\mathrm{s}{\theta }_2\right)} \]$

(8)

매질 3에서는 매질 1에서 radiated pressure와 동일하게 식 (9)와 같이 Rayleigh integral⁽¹⁵⁾을 통해 구할 수 있다.

$\[ \begin{array}{c}{p}_{rad,3}=-\frac{j\omega {\rho }_0{V}_{23}2a}{2\pi }{e}^{-j{k}_{x}x}\\ {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }} \frac{\mathrm{s}\mathrm{i}\mathrm{n}\alpha a}{\alpha a}\frac{e^{-j\alpha y+z\sqrt{{\alpha }^2-{\gamma }^2}}}{\sqrt{{\alpha }^2-{\gamma }^2}}d\alpha \end{array} \]$

(9)

식 (6)과 (9)를 음향 임피던스의 관계식을 통해 다음과 같이 변환할 수 있다.

$\[ p_{\mathrm{r}\mathrm{a}\mathrm{d},1}=-Z_{\mathrm{r}\mathrm{a}\mathrm{d},1}{V}_{12}{e}^{-j{k}_{x}x} \]$

(10)

$\[ p_{\mathrm{r}\mathrm{a}\mathrm{d},3}=Z_{\mathrm{r}\mathrm{a}\mathrm{d},3}{V}_{23}{e}^{-j{k}_{x}x} \]$

(11)

$\[ \begin{array}{c}{Z}_{\mathrm{r}\mathrm{a}\mathrm{d},1}=Z_{\mathrm{r}\mathrm{a}\mathrm{d},3}\\ =Z_0\left[\begin{array}{c}{H}_0^2\left(2\gamma a\right)+\frac{\pi }{2}\left(\begin{array}{c}{H}_1^2\left(2\gamma a\right)S_0\left(2\gamma a\right)\\ -H_0^2\left(2\gamma a\right)S_1\left(2\gamma a\right)\end{array}\right)\\ -\frac{1}{2k_{0}a}{H}_1^2\left(2k_{0}a\right)+\frac{2j}{\pi {\left(2k_{0}a\right)}^2}\end{array}\right]\end{array} \]$

(12)

여기서 $$ H_i^2, S_j\left(i,j=0.1\right)$$는 각각 2차 Hankel, Struve 함수이다.

인접한 매질 사이의 경계조건인 힘의 평형과 속도의 연속성을 통해 각 매질의 음압과 매질 사이 경계면에서의 표면속도를 식 (13), (14)와 같이 구할 수 있다. 먼저 힘의 평형 조건을 각각의 인접하고 있는 매질 경계면에 적용한다.

$\[ \left(2{\widehat{p}}_1-Z_{\mathrm{r}\mathrm{a}\mathrm{d},1}{V}_{12}-{\widehat{p}}_{i,2}-{\widehat{p}}_{r,2}\right)A=m_{12}A{\dot{V}}_{12} \]$

(13)

$\[ \begin{array}{c}\left({\widehat{p}}_{i,2}{e}^{-j{k}_{a}d\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_2}+{\widehat{p}}_{r,2}{e}^{j{k}_{a}d\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_2}-Z_{\mathrm{r}\mathrm{a}\mathrm{d},3}{V}_{23}\right)A\\ =m_{23}A{\dot{V}}_{23}\end{array} \]$

(14)

다음은 속도의 연속성 조건을 식 (15), (16)과 같은 방식으로 적용한다.

$\[ \frac{{\widehat{p}}_{i,2}-{\widehat{p}}_{r,2}}{Z_{12}}=\frac{V_{12}}{\cos {\theta }_2} \]$

(15)

$\[ \frac{{\widehat{p}}_{i,2}{e}^{-j{k}_{a}d\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_2}-{\widehat{p}}_{r,2}{e}^{j{k}_{a}d\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_2}}{Z_{23}}=\frac{V_{23}}{\cos {\theta }_2} \]$

(16)

여기서 Z₁₂, Z₂₃은 각각 틈새 내부 매질의 경계면에서의 wave impedance를 나타내며, 식 (17)과 같이 틈새 표면의 방사 임피던스와 특성 임피던스의 합으로 나타낼 수 있다. 틈새 매질의 특성 임피던스 Z_a는 틈새 내부가 비워있는 공기로 이루어진 상태이면 Z₀로 나타낼 수 있다. 틈새 내부를 실란트로 채우게 된다면 실란트를 elastic solid로 가정하에 단위면적당 mechanical impedance로 나타낼 수 있다.

$\[ Z_{12}=Z_{\mathrm{r}\mathrm{a}\mathrm{d},1}+j\omega m_{12}-\frac{s}{\omega } \]$

(17)

여기서 s는 실란트의 단위면적당 강성이며, 댐핑계수는 생략하였다. 식 (13) ~ (16)에 식 (3) ~ (12)을 대입하여 다음과 같은 행렬 형태로 나타낼 수 있다.

$\[ \begin{array}{l}\mathbf{A}\mathbf{X}=\mathbf{B}\\ \mathbf{A}=\left[\begin{array}{cccc}1& 1& a_{13}& 0\\ 1& -1& a_{23}& 0\\ a_{31}& a_{32}& 0& a_{34}\\ a_{41}& a_{42}& 0& a_{45}\end{array}\right]\\ {\mathbf{B}}^T=\left[\begin{array}{cccc}{b}_{11}& 0& 0& 0\end{array}\right]\\ {\mathbf{X}}^T=\left[\begin{array}{cccc}{\widehat{p}}_{i,2}& {\widehat{p}}_{r,2}& V_{12}& V_{23}\end{array}\right]\end{array} \]$

(18)

[A], [B]의 성분은 다음과 같다.

$\[ \begin{array}{c}{a}_{13}=Z_{\mathrm{r}\mathrm{a}\mathrm{d},1}+j\omega m_{12},a_{23}=-Z_{12}/cos{\theta }_2\\ a_{31}=e^{-j{k}_{a}d\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_2},a_{32}=e^{j{k}_{a}d\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_2}\\ a_{41}=e^{-j{k}_{a}d\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_2},a_{42}=-e^{j{k}_{a}d\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_2}\\ a_{34}=-Z_{\mathrm{r}\mathrm{a}\mathrm{d},3}-j\omega m_{23},a_{45}=-Z_{23}/cos{\theta }_2\\ b_{11}=2{\widehat{p}}_i\mathrm{s}\mathrm{i}\mathrm{n}\left(k_{0}a\mathrm{s}\mathrm{i}\mathrm{n}\theta sin\varphi \right)/k_{0}a\mathrm{s}\mathrm{i}\mathrm{n}\theta sin\varphi \end{array} \]$

(19)

틈새의 음향투과율은 다음과 같이 정의할 수 있다.

$\[ {\tau }_{\mathrm{s}\mathrm{l}\mathrm{i}\mathrm{t}}\left({\theta }_{\mathrm{i},1},{\varphi }_{\mathrm{i},1}\right)=\frac{{\Pi }_t\left({\theta }_{\mathrm{i},1},{\mathrm{\varphi }}_{\mathrm{i},1}\right)}{{\Pi }_i\left({\theta }_{\mathrm{i},1},{\mathrm{\varphi }}_{\mathrm{i},1}\right)} \]$

(20)

여기서 ∏_i(θ_i,1,ϕ_i,1), ∏_t(θ_i,1,ϕ_i,1)는 각도 (θ_i,1,ϕ_i,1)에 대한 틈새 입사 음향파워와 투과 음향파워이며, 식 (20), (21)와 같은 방식으로 나타낼 수 있다.

$\[ {\Pi }_i\left({\theta }_{i,1},{\varphi }_{i,1}\right)=\frac{2a}{\left({\left|{\widehat{p}}_i\right|}^2/2\right)/Z_0}\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{i,1} \]$

(21)

$\[ {\Pi }_t\left({\theta }_{i,1},{\varphi }_{i,1}\right)=\frac{1}{2}2a\times Re\left(Z_{\mathrm{r}\mathrm{a}\mathrm{d},3}\right){\left|V_{34}\right|}^2 \]$

(22)

현실에서는 실내의 고유 모드와 정재파의 위상차 등에 의해 이상적인 이론적 조건과 달라서, 그 영향을 최대한 줄이기 위해 확산음장을 도입하였다. 확산음장 음향투과율은 수치적으로 다음과 같이 나타낼 수 있다.

$\[ {\tau }_d={\int }_0^{2\pi } {\int }_0^{{\theta }_{\mathrm{l}\mathrm{i}\mathrm{m}}} \frac{\tau \left({\theta }_i,{\varnothing }_i\right)\mathrm{s}\mathrm{i}\mathrm{n}{\theta }_i\mathrm{c}\mathrm{o}\mathrm{s}{\varnothing }_{i}d{\theta }_{i}d{\varnothing }_i}{\pi {\mathrm{s}\mathrm{i}\mathrm{n}}^2{\theta }_{\mathrm{l}\mathrm{i}\mathrm{m}}} \]$

(23)

여기서 θ_lim은 실험실 환경에 따라 결정되는 limit angle이다. 단일 벽의 투과 손실 측정값과 예측 결과 비교를 통해 limit angle θ_lim을 구할 수 있다.

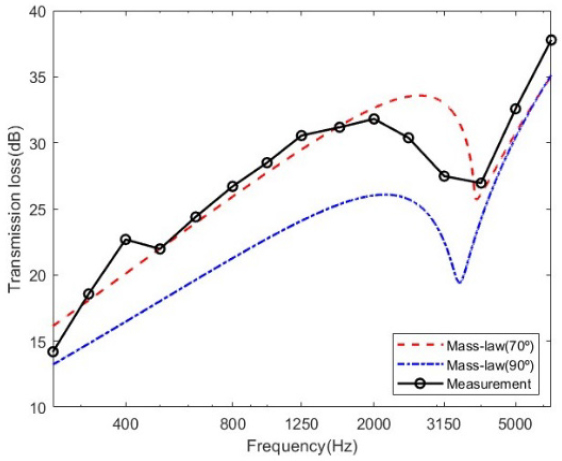
Fig. 3은 limit angle을 구하기 위해 단일 석고보드에 대해 투과손실을 측정하여 mass-law curve와 비교한 결과이며, limit angle은 70°가 되겠다. 따라서 확산음장에서 투과손실은 다음과 같이 구할 수 있다.

Fig. 3

The comparison between measured TL and mass law curve

$\[ TL=10{\mathrm{l}\mathrm{o}\mathrm{g}}_{10}\left(\frac{1}{{\tau }_d}\right) \]$

(24)

2.3 실험개요

틈새 실링재 유무에 따른 벽의 투과손실을 구하기 위해 음향 인텐시티 방법(sound intensity method)을 사용하였다. 여기서 실링재는 3M SS 100 sealant를 사용하였다. 측정은 잔향실과 반무향실 사이에서 이루어졌으며, 잔향실 체적은 241 m³이고, cut-off frequency는 100 Hz가 되겠다.

Fig. 4에서 잔향실 내 3개의 diffuse microphone과 2개의 active loudspeaker를 설치하였고, 특히 벽과 2 m 이상 거리를 이격하여 실험실 내에서 중첩효과가 발생하지 않도록 위치시켰다.

Fig. 4

Reverberant room with experimental equipment

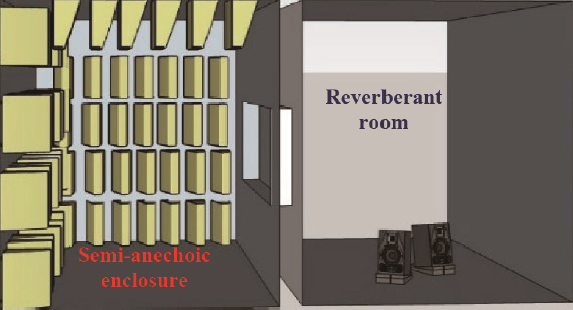
Fig. 5에서 반무향실에서 sound intensity probe를 통해 틈새로 전달되는 음향 인텐시티(sound intensity)를 측정하였다. 반무향실 체적은 45 m³으로 반사파에 대해 저주파수 대역에서 오차가 발생할 수 있으나, 벽에 흡음마감 처리와 표면이 천으로 이루어져 오차를 최소화하려 노력하였다. Fig. 6은 실험시설에 대한 도면을 개략적으로 나타낸 것이다.

Fig. 5

Semi-anechoic enclosure with test sample

Fig. 6

Geometric configuration of test room

잔향실과 반무향실 인접한 공간에 측정 샘플을 두었고, 인접한 공간의 벽 크기는 0.84 m² × 0.84 m²가 되어 국내외 시험규격에서 요구하는 최소 10 m²인 면적으로 저주파에서 모드 중첩에 의해 발생하는 실험적 오차가 발생할 수 있다. 측정 샘플의 틈새 길이는 너비 500 mm, 두께는 9.5 mm, 폭에 차이를 두어 5 mm, 10 mm로 제작하였다. 샘플의 물성치는 Table 2에 나타내었다.

Table 2

The properties of test samples

3. 실험결과 및 분석

3.1 음향 투과손실 측정

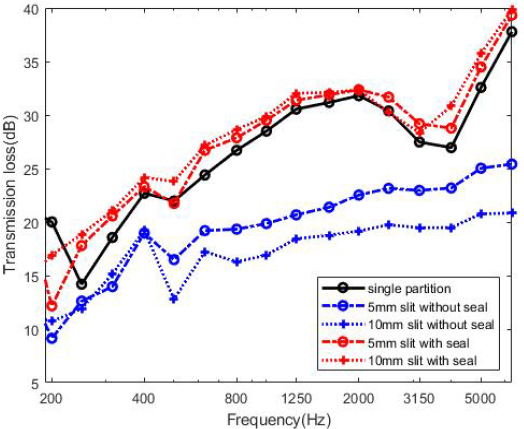
Fig. 7은 각각 실링 유무에 따른 단일벽에 대한 투과손실을 나타낸 그래프이다. 그래프에서 검은 선은 틈새가 없는 벽에 대한 투과손실이고, 파란색 선은 틈새가 있는 벽, 빨간색 선은 틈새에 실란트를 채운 벽에 대한 투과손실을 나타낸 것이다.

Fig. 7

The measured transmission loss of the single partition

Fig. 7에서 틈새가 있는 단일벽은 틈새가 없는 벽에 비해 현저히 투과손실이 낮아졌으며, 틈새 폭 길이에 비례하여 투과손실이 더 낮아졌다. 반면 틈새에 실란트를 채운 벽의 투과손실은 기존 석고보드 벽체보다 증가하였는데, 실란트의 면밀도가 석고보드 면밀도보다 크기 때문에 틈새 폭이 커질수록 미미한 증가폭을 보였다.

실험 조건상 샘플크기가 무한평판을 가정한 최소 시험규격인 10 mm²에 미치지 못하여, 200 Hz 인근 저주파수에서 모드 중첩으로 인한 오차가 발생하였다. 이 실험에서 석고보드 판에 대한 임계주파수에서 공진(resonance) 효과는 식 (25)에서 유도된 4000 Hz에서 동일하게 발생함을 알 수 있었다.

$\[ f_{cr}=\frac{1}{2\pi }{c}^2{\left(\frac{m}{D}\right)}^{1/2} \]$

(25)

3.2 음향 투과손실 해석 및 비교

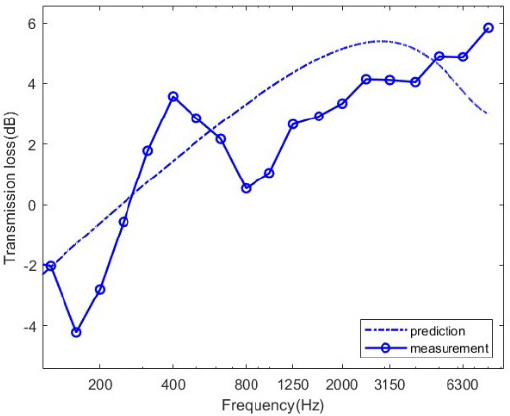
틈새가 있는 벽에 대한 음향 투과손실 해석에 앞서 벽체와 틈새에 대한 해석 결과가 각각 타당한지 여부를 확인하였다. 먼저 단일 벽체인 석고보드에 대한 해석결과는 Fig. 3에서 음향 투과손실 측정결과와 limit angle이 70°에서 예측결과인 mass-law curve를 비교를 통해 확인할 수 있다. 또한 틈새에 대한 해석결과는 Fig. 8에서 확인할 수 있는데, Fig. 8은 폭 10 mm, 두께 9.5 mm인 공기로 채워진 틈새에 대한 음향 투과손실 측정결과와 Mechel의 예측모델을 비교한 그래프가 되겠다. 이 그래프에서 저주파수에서 투과 손실이 음수가 되는 경우는 fluid-loading에 의한 fundamental resonance가 발생하는 주파수에서 투과계수가 1보다 큰 값이 유도되기 때문이다⁽¹⁶⁾. 측정결과와 예측결과를 비교했을 때 대부분 2 dB 이내의 오차가 발생하였고, 유효주파수는 실험조건과 측정장비에 따라 상이할 수 있으나 이 연구에서는 측정결과와 해석결과 오차를 통해 200 Hz ~ 6300 Hz로 판단하였다.

Fig. 8

The comparison between measured and predicted transmission loss in a slit

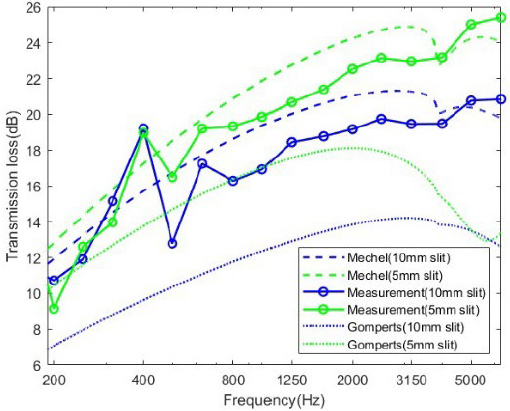
Fig. 9는 틈새가 있는 단일벽에 대해 Gomperts and Kihlman에 의한 예측모델⁽³⁾과 Mechel의 예측모델⁽⁶⁾ 로 투과손실을 예측하고, 실험을 통해 측정한 결과를 비교한 그래프이다. 실제 측정값과 비교했을 때 Mechel의 예측 모델이 Gomperts and Kihlman의 예측 모델보다 오차가 작다는 것을 알 수 있다. 특히 Mechel의 예측 모델이 저주파 대역보다 중 ∙ 고주파 대역부분에서 더 근접하게 일치하였고, 대부분 2 dB 이내의 오차를 보였다. 두 모델 모두 측정값과 동일하게 4000 Hz에서 공진 효과를 보였다.

Fig. 9

The comparison between measured and predicted transmission loss in the single partition with a slit

Fig. 10은 Mechel의 예측 모델을 통해서 틈새에 실란트를 채운 단일벽에 대해 예측한 값과 측정결과를 비교한 그래프이다. 이 경우에는 측정값에는 틈새 폭 길이 즉, 실란트로 대체된 면적에 따라 미세하지만 투과손실 증가하는 경향을 보였지만, 예측 모델에서는 틈새가 없는 벽과 동일한 효과만 보였고 틈새 폭 길이에 따른 변화가 거의 없었다.

Fig. 10

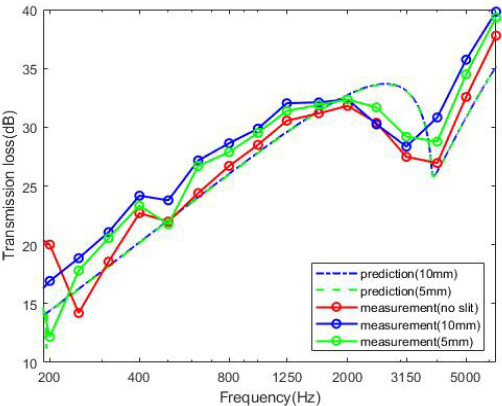
The comparison between measured and predicted transmission loss in the single partition with a sealant

이는 식 (1)을 통해 설명할 수 있는데, 식 (1)을 변형하면 식 (26)으로 나타낼 수 있다.

$\[ {\tau }_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}={\tau }_{\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}+\left({\tau }_{\mathrm{s}\mathrm{l}\mathrm{i}\mathrm{t}}-{\tau }_{\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}\right)\left(\frac{A_{\mathrm{s}\mathrm{l}\mathrm{i}\mathrm{t}}}{A_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}}\right) \]$

(26)

식 (26)에서 우측 두번째 항이 전체 음향투과율의 실제적인 변화량이 되겠으며, 그 변화량은 벽체와 틈새의 음향투과율 차이와 틈새의 면적에 의해 좌우된다. 따라서 틈새가 실란트로 채워진다면 벽체와 음향투과율 차이가 현저히 나지 않기 때문에 전체 벽의 음향투과율은 벽체 석고보드의 음향투과율에 근사하게 된다.

4. 결 론

이 연구를 통해 벽 내부의 직사각형 틈새로 인해 벽의 투과손실이 저하되고, 그 틈새를 방음용 실란트로 채우게 되면 벽과 동일시되는 차음 효과를 얻을 수 있음을 알 수 있었다.

해석적으로는 직사각형 틈새가 있는 석고보드에 대해 기존의 Gomperts의 예측모델이 아닌 Mechel의 예측모델을 통해서 투과손실 예측하였고, 측정결과 비교시 중 ∙ 고주파 대역에서 2 dB 이내의 오차가 발생하여 매우 잘 일치하는 결과를 얻었다.

향후 연구에서는 벽의 종류, 틈새 두께 및 위치 등 여러가지 조건을 달리하여 해당 예측모델에 대한 검증이 필요하겠으며, 위 연구에서 예측하지 못한 이중벽에 대한 투과손실 예측모델과 식 (1)에 대한 틈새와 벽에 대한 기여도 분석이 필요하겠다.

Acknowledgments

이 연구는 서울대학교 공학연구원의 지원을 통해 진행되었으며, 2022년도 추계 소음진동 학술대회에서 발표한 내용을 토대로 작성되었다.

References

• Sgard, F., Nelisse, H. and Atalla, N., 2007, On the Modeling of the Diffuse Field Sound Transmission Loss of Finite Thickness Apertures, Journal of the Acoustical Society of America, Vol. 122, No. 1, pp. 302~313. [https://doi.org/10.1121/1.2735109]
• Gomperts, M. C., 1964, The “Sound Insulation” of Circular and Slit-shaped Apertures, Acta Acustica United with Acustica, Vol. 14, No. 1, pp. 1~16.
• Gomperts, M. C. and Kihlman, T., 1967, The Sound Transmission Loss of Circular and Slit-shaped Apertures in Walls, Acta Acustica united with Acustica, Vol. 18, No. 3, pp. 144~150.
• Wilson, G. P. and Soroka, W. W., 1965, Approximation to the Diffraction of Sound by a Circular Aperture in a Rigid Wall of Finite Thickness, Journal of the Acoustical Society of America, Vol. 37, No. 2, pp. 286~297. [https://doi.org/10.1121/1.1909325]
• Sauter, A. Jr. and Soroka, W. W., 1970, Sound Transmission through Rectangular Slots of Finite Depth between Reverberant Rooms, Journal of the Acoustical Society of America, Vol. 47, No. 1A, pp. 5~11. [https://doi.org/10.1121/1.1911442]
• Mechel, F. P., 1986, The Acoustic Sealing of Holes and Slits in Walls, Journal of Sound and Vibration, Vol. 111, No. 2, pp. 297~336. [https://doi.org/10.1016/S0022-460X(86)80163-8]
• Chen, K.-T., 1995, Study of Acoustic Transmission through Apertures in Wall, Applied Acoustics, Vol. 46, No. 2, pp. 131~151. [https://doi.org/10.1016/0003-682X(95)00009-X]
• Yang, C., Zhang, X., Tao, F. and Lam, D. C., 2017, A Study of the Sound Transmission Mechanisms of a Finite Thickness Opening without or with an Acoustic Seal, Applied Acoustics, Vol. 122, pp. 156~166. [https://doi.org/10.1016/j.apacoust.2017.02.012]
• Park, H. H. and Eom, H. J., 1997, Acoustic Scattering from a Rectangular Aperture in a Thick Hard Screen, Journal of Acoustical Society of America, Vol. 101, No. 1, pp. 595~598. [https://doi.org/10.1121/1.417971]
• Poblet-Puig, J. and Rodríguez-Ferran, A., 2013, Modal-based Prediction of Sound Transmission through Slits and Openings between Rooms, Journal of Sound and Vibration, Vol. 332, No. 5, pp. 1265~1287. [https://doi.org/10.1016/j.jsv.2012.09.044]
• Oldham, D. J. and Zhao, X., 1993, Measurement of the Sound Transmission Loss of Circular and Slit-shaped Apertures in Rigid Walls of Finite Thickness by Intensimetry, Journal of Sound and Vibration, Vol. 161, No. 1, pp. 119~135. [https://doi.org/10.1016/0022-460X(93)90359-J]
• Hongisto, V., Keränen, J. and Lindgren, M., 2000, Sound Insulation of Doors-Part 2: Comparison between Measurement Results and Predictions, Journal of Sound and Vibration, Vol. 230, No. 1, pp. 149~170. [https://doi.org/10.1006/jsvi.1999.2610]
• Uris, A., Bravo, J. M., Llinares, J. and Estelles, H., 2004, The Influence of Slits on Sound Transmission through a Lightweight Partition, Applied Acoustics, Vol. 65, No. 4, pp. 421~430. [https://doi.org/10.1016/j.apacoust.2003.11.006]
• Kim, M.-J., 2010, Sound Reduction Index of Interior Door by Aperture Size at Door’s Bottom, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 20, No. 9, pp. 834~840. [https://doi.org/10.5050/KSNVE.2010.20.9.834]
• Fahy, F. J. and Gardonio, P., 2007, Sound and Structural Vibration: Radiation, Transmission and Response, 2nd Edition, Academic Press, Cambridge. [https://doi.org/10.3397/1.2741307]
• Thompson, D. J., Gardonio, P. and Rohlfing, J., 2009, Can a Transmission Coefficient Be Greater Than Unity?, Applied Acoustics, Vol. 70, No. 5, pp. 681~688. [https://doi.org/10.1016/j.apacoust.2008.08.001]