[ Article ]

Transactions of the Korean Society for Noise and Vibration Engineering - Vol. 33, No. 5, pp.516-530

ISSN: 1598-2785 (Print) 2287-5476 (Online)

Print publication date 20 Oct 2023

Received 02 May 2023 Revised 28 Jun 2023 Accepted 07 Jul 2023

DOI: https://doi.org/10.5050/KSNVE.2023.33.5.516

재료의 점탄성과 공기의 점성을 고려한 보의 복소 모드해석을 위한 정식화

김용우^†

Formulation for Complex Modal Analysis of Beam with Internal and Air Viscous Damping

Yong-Woo Kim^†

Correspondence to: ^†Member, School of Mechanical and Aerospace Engineering, Sunchon National University, Professor E-mail : kyw@scnu.ac.kr ‡ Recommended by Editor Gunwoo Noh

Abstract

This paper presents a state space formulation for complex modal analysis of a beam with internal viscous damping and air viscous damping. Equation of motion and boundary conditions are derived by utilizing the extended Hamilton’s principle, and orthogonal conditions are derived. Decoupled modal equations of motion and the relation between initial conditions in modal coordinates and those in physical coordinates are obtained by employing the orthogonal conditions. The theory of complex modal analysis of continuous systems is applied to a clamped-clamped beam, and the examples for the time responses due to initial displacement as well as the responses due to an impulse are exemplified in relation to modal damping ratios.

Keywords:

Complex Modal Analysis, Internal Viscous Damping, Air Viscous Damping, Complex Eigenvalue, Complex Eigenfunction, Orthogonal Condition, Modal Damping Ratio

키워드:

복소 모드해석, 재료의 점성감쇠, 공기 점성감쇠, 복소 고유값, 복소 고유진동형, 직교조건, 모드 감쇠비

1. 서 론

자동차, 항공기, 토목구조물 등의 복잡한 구조물에서 피로파괴를 예방하거나 진동을 억제하는 기술을 개발하기 위해서는 구조물의 진동 특성을 이해하는 것이 매우 중요하다. 고분자재료 및 복합재료는 재료의 감쇠 특성 때문에 진동제어에 많이 적용되고 있다. 고분자 재료나 복합재료는 탄성과 점성이 혼합된 특성을 보이므로 이들을 흔히 점탄성 재료라고 일컫는다. 이러한 특성 때문에 점탄성재료는 공학적으로 다양하게 응용되고 있다. 그러나 점탄성재료로 만든 구조물의 정적 및 동적 거동을 연구하기 위해서는 수학적 모델을 개발해야 하며 모델에 대한 해를 구할 수 있어야 한다.

Banks and Inman⁽¹⁾은 복합재로 만든 보를 모델로 네 가지의 감쇠 모델을 고려하였다. 즉, 공기점성에 의한 감쇠(viscous air damping), 재료의 점탄성에 의한 감쇠(Kelvin-Voigt damping 또는 internal viscous damping), 시간이력 감쇠(time hysteresis damping), 그리고 공간이력 감쇠(spatial hysteresis damping)를 고려하였다. 이러한 감쇠 모델의 도입으로 인하여 보의 해석은 더욱 복잡하게 되었다.

전통적으로는 이러한 감쇠를 고려한 문제를 풀기 위해 비례감쇠(proportional damping)을 가정하였다. 그러나 왜 비례감쇠를 가정하는지에 대한 일반적인 물리적 이유는 없으며, 단지 비감쇠의 경우와 같이 단순화시켜 해석할 수 있기에 사용해왔었다. 그러나 모드 실험(modal testing)에 의하면 대부분의 실제 구조물은 비례감쇠계에서의 실수의 고유진동형을 갖는 것이 아니고 복소 고유진동형(complex mode)을 갖는 것으로 알려져 있다. 즉, 일반적으로 선형 시스템들은 비례감쇠가 아닌 비비례감쇠(non-proportional damping)인 것으로 알려져 있다. 비비례감쇠계에서는 고유값과 고유진동형들이 실수가 아닐 뿐만 아니라 전통적인 직교조건을 만족시키기 못하기 때문에 문제 풀이를 더욱 복잡하게 만든다. 이로 인해 복소 고유값 문제에 관한 일반적인 수식화에 관한 연구가 계속되고 있다.

Prater and Singh⁽²⁾는 비비례 점성감쇠를 갖는 보의 복소 고유값과 고유진동형을 결정하는 기법을 개발하였다. Oliveto 등⁽³⁾은 양단에 회전 점성감쇠기(rotational viscous damper)가 부착된 단순지지보의 복소 고유값과 고유진동형을 수치적 방법을 사용하여 구하였다. 운동 방정식을 비연성화 시키기 위한 직교조건을 유도하고 복소 모드 중첩법(complex mode superposition method)를 사용하여 양단의 지반으로부터 가해지는 가속도 충격(acceleration impulse) 및 조화적 지반 가진(harmonic ground motions)에 대한 응답을 구하였다. Krenk⁽⁴⁾은 시간에 관해 2계 편미분방정식인 보의 운동방정식을 상태변수(state variables)를 사용하여 2개의 1계미분방정식으로 표현하고 변수분리법을 적용하여 얻은 고유값 문제들(점성감쇠기가 있는 팽팽한 케이블, 양단에 회전감쇠기가 있는 단순보)의 파수(wave number)들을 단순반복법을 사용하여 구하였다. 그리고 케이블의 충격 응답(impulse response)과 보의 최적 점성감쇠에 대한 예제를 검토하였다.

Gürgöze and Erol⁽⁵⁾은 균일분포 점성감쇠 및 자유단에서 단일 점성감쇠기가 부착된 외팔보에 대하여 동적강성법을 적용하여 진동특성값들을 구하고, 시간에 관해 2계 미분방정식의 운동방정식의 직교조건들을 구하여 모드좌표계에서의 비연성화된 모드 운동방정식을 유도하여 복소 주파수 함수와 동적 충격응답함수를 구하였다. 그러나 가진력에 초점을 둔 분석으로서 초기조건에 의한 자유진동은 고려하지 않았다. Rosa 등⁽⁶⁾은 왼쪽 단이 탄성지지되어 있고 오른쪽 단에 집중질량이 있으며 임의 위치에 단일 점성감쇠기가 있는 테이퍼진 보의 복소 고유값을 구하였다. Xing 등⁽⁷⁾은 외팔보의 자유단에 점성감쇠기가 부착된 보에 대해, 실수로 가정한 모드(real assumed-mode trial functions)를 사용하여 이산화된 고유값 문제로 표현하고, 이산화된 고유값 문제의 고유값과 고유벡터를 구하기 위해 이산화된 고유값 문제를 상태변수로 표현된 운동방정식을 사용하였다. Svedholm 등⁽⁸⁾은 비비례 감쇠가 있는 오일러-베르누이 보에서 이동하중에 의한 보의 동적거동에 관한 이론해를 유도하였다. 적절한 직교조건을 유도하고 직교조건과 중첩법을 이용하여 이동 하중에 대한 모드좌표계에서의 2계 미분 운동방정식과 단위충격 응답함수를 유도하여 이동 하중에 대한 시간응답을 제시하였다. 그러나 이동하중에 의한 자유진동해석에 초점을 둔 연구로서 초기조건에 의한 자유진동은 고려하지 않았다. Singh⁽⁹⁾는 점탄성 재료로 구성된 이산계 및 연속계의 고유값 문제에 대한 고유값 및 고유진동형을 계산하는 수치계산법을 제안하고, 이 방법의 정확성을 보이기 위해 다자유도의 점탄성 시스템, 점탄성 지지의 축방향으로 진동하는 봉, 양단 사이에 맥스웰 요소가 있는 단순지지 보 등에 적용하였다. Zangeneh 등⁽¹⁰⁾은 양단이 점탄성 지지된 보의 이동하중에 의한 최대 공진 응답을 구하기 위해 보의 변위를 단순지지 보의 변위와 점탄성 지점의 강체변위의 합으로 가정하여 닫힌 형태로 표현되는 최대 공진 응답의 근사해(closed-form approximate expression)를 구하였다. 이들도 초기에 정지해있는 보의 이동하중에 의한 자유진동을 다룸으로써 초기조건에 의한 자유진동은 취급하지 않았다.

위에서 보는 바와 같이 대부분의 연구가 복소 고유값 문제의 고유값과 고유진동형을 구하거나 충격하중에 의한 응답을 얻는데 초점을 두고 있다. 그러나 보의 초기 변형조건에 의한 자유진동을 위한 수식화 및 응답에 관한 연구는 찾아보기 어렵다. 이는 주어진 물리적 좌표계에서의 초기조건을 모드좌표계에서의 초기조건으로 표현하는 것이 점성이 없는 경우⁽¹¹⁾에 비해 간단하지 않기 때문인 것으로 판단된다.

초기조건에 의한 자유진동은 구조물의 거동을 분석하는데 매우 중요하다. 예를 들면 구조물이 지진하중을 받는 동안 초기 변위와 속도는 구조물의 응답을 결정한데 중요한 역할을 한다. 따라서 이 연구에서는 점탄성재료로 만든 보가 진동하면서 공기의 점성저항을 받을 때, 외력에 의한 자유 진동뿐만 아니라 초기조건에 의한 자유진동의 시간 응답을 얻기 위하여 복소 모드해석 방법을 정식화한다. 이를 위해 운동방정식을 비연성화 시키기 위한 직교조건을 유도하고, 직교조건을 이용하여 모드좌표계의 초기조건을 주어진 물리적 좌표계의 초기조건으로 표현한다. 그리고 복소 모드중첩법을 사용하여, 외력에 의한 자유 진동뿐만 아니라 초기조건에 의한 자유진동의 시간응답을 구한다.

2. 본 론

2.1 운동방정식

Fig. 1과 같은 점탄성재료로 만든 보가 분포하중 f(x,t)를 받아 운동하면서 공기의 점성 저항을 받을 때, 보의 운동방정식은 확장된 Hamilton 원리를 적용하여 얻을 수 있다. 즉,

δ ∫ t 1 t 2 T - U + W d t - ∫ t 1 t 2 ∫ 0 L ∂ F d ∂ y ˙'' δ y'' d x d t - ∫ t 1 t 2 ∫ 0 L ∂ F a ∂ y ˙ δ y d x d t = 0

(1)

Fig. 1

A beam subjected to a distributed force f(x,t)

식 (1)에서 T는 계의 운동에너지를, U는 계의 변형에너지를, W는 외력에 의한 일을 나타내며, F_d와 F_a는 각각 재료의 점성과 공기 점성에 의한 Rayleigh의 소산함수들로서 식 (2) ~ 식 (6)과 같이 표현된다.

T = ∫ 0 L m 2 y ˙ 2 d x

(2)

U = ∫ 0 L E I 2 y'' 2 d x

(3)

W = ∫ 0 L f x, t y d x

(4)

F d = c d I 2 ∂ 2 y ˙ ∂ x 2 2

(5)

F a = γ 2 y ˙ 2

(6)

앞선 식들에서 $y ˙$ 는 변위 y(x,t)를 시간에 관해 미분한 것이고 y″는 변위 y를 x에 관해 두 번 미분한 것을 나타낸다. 또한, m은 단위길이 당 질량을, E는 탄성계수를, I는 중립축에 대한 단면 2차모멘트를, c_d는 재료의 점성계수를, γ는 공기 점성계수를, f(x,t)는 단위길이 당 힘을 나타낸다.

식 (1)로부터 다음과 같은 운동방정식과 경계조건을 얻는다. 운동방정식은 다음과 같고,

m y ¨ + E I y'''' + c d I ˙ y ˙'''' + γ y ˙ = f x, t

(7)

경계조건은 x=0 또는 x=L에서 다음과 같다.

E I y'' + c d I y ˙'' = 0 o r y' = 0 E I y''' + c d I y ˙''' = 0 o r y = 0

(8)

c_d=0, γ=0이면, 식 (7)과 식 (8)은 감쇠가 없는 보의 운동방정식과 경계조건으로 된다.

2.2 고유값과 고유진동형

자유진동방정식은 식 (7)로부터 식 (9)와 같다.

m y ¨ + E I y'''' + c d I y'' ˙'' + γ y ˙ = 0

(9)

위 식의 해를 식 (10)과 같이 가정한다.

y x, t = U x e λ t

(10)

여기서 U(x)는 복소함수이며, λ는 계의 복소 고유값(complex eigenvalue)을 나타낸다. 가정한 해를 식 (9)에 대입하여 식 (11)을 얻는다.

U i v - β 4 U = 0

(11)

여기서 U^ⅳ는 U(x)를 x에 관해 네 번 미분한 것을 나타내며, β⁴은 식 (12)와 같다.

β 4 = - m λ 2 + γ λ c d I λ + E I

(12)

미분방정식 (11)의 일반해는 식 (13)과 같다.

U x = C 1 sin ⁡ β x + C 2 cos ⁡ β x + C 3 sinh ⁡ β x + C 4 cosh ⁡ β x

(13)

여기서 C_i(i=1,2,3,4)는 경계조건에 의해 결정되는 복소 상수들(complex constants)이다. 경계조건들은 다음과 같다. 단순지지단에서의 경계조건은 식 (14)

E I U'' + c d I λ U'' = 0 and U = 0

(14)

이고 자유단에서의 경계조건은 식 (15)이며,

E I U'' + c d I λ U'' = 0 a n d E I U''' + c d I λ U''' = 0

(15)

고정단에서의 경계조건은 식 (16)이다.

U = 0 a n d U' = 0

(16)

단순지지단이나 자유단을 갖는 보는 경계조건에 고유값이 포함되어 고유값에 의존하는 경계조건을 갖는다.

위의 경계조건을 이용하여 식 (13)의 고유진동형 U(x)를 결정할 수 있다. 예를 들면 양단이 고정단인 보의 고유진동형은 식 (17)과 같다.

U x = cosh ⁡ β x - cos ⁡ β x - cosh ⁡ β L - cos ⁡ β L sinh ⁡ β L - sin ⁡ β L sinh ⁡ β x - sin ⁡ β x

(17)

또한, 경계조건을 이용하여 고유값을 결정하기 위한 복소 고유값 방정식을 얻을 수 있으며, 고유값 방정식으로부터 β를 계산하고 β를 식 (12)에 대입하여 고유값을 얻는다. 이때 산출되는 다수의 고유값 중 실수부가 음수인 것들을 고유값으로 선택한다.

일반적으로 고유값 λ는 켤레복소수(complex conjugate numbers)의 형태(즉, λ₁= $λ 2 -$ )로 나타난다. 그러므로 r번째 모드의 두 개의 고유값을 $λ r 1, λ r 2$ 이라고 하면 $λ r 1 = λ r 2 -$ 이다. 그리고 $λ r 1$ 과 $λ r 2$ 에 대응하는 β는 식 (12)로부터 각각 식 (18)과 식 (19)와 같다.

β r 1 4 = - m λ r 1 2 + γ λ r 1 c d λ r 1 + E I

(18)

β r 2 4 = - m λ r 2 2 + γ λ r 2 c d I λ r 2 + E I

(19)

$β r 1 4$ 과 $β r 2 4$ 의 관계는 식 (20)과 같다(부록 A 참조).

β r 1 4 = β r 2 4 ¯

(20)

따라서 $β r 1$ 과 $β r 1$ 의 관계는 식 (21)과 같다(부록 B 참조).

β r 1 = β r 2 - .

(21)

그리고 $β r 1$ 과 $β r 2$ 에 대응하는 고유진동형 $U r 1 x$ 와 $U r 2 x$ 사이의 관계는 식 (22)과 같다(부록 C 참조).

U r 1 x = U r 2 - x

(22)

2.3 직교조건

식 (7)의 운동방정식을 상태변수를 이용하여 식 (23)과 같이 쓸 수 있다.

D y ˙ y ¨ + E y y ˙ = f x, t 0

(23)

여기서

D = ∂ 2 ∂ x 2 c d I ∂ 2 ∂ x 2 + γ m m 0

(24)

E = ∂ 2 ∂ x 2 E I ∂ 2 ∂ x 2 0 0 - m

(25)

식 (23)에 대한 자유진동방정식에, 식 (10)과 $y ˙ = λ U x e λ t = V x e λ t$ 를 대입하여 식 (26)을 얻는다.

λ D + E U x V x = 00

(26)

여기서 V(x)=λU(x)이다.

고유값 $λ r m$ 과 $λ s n$ (r,s=1,2,3, ...; m, n=1,2)에 대하여 식 (26)은 각각 식 (27)과 식 (28)과 같이 쓸 수 있다.

λ r m D U r m x V r m x = - E U r m x V r m x

(27)

λ s n D U s n x V s n x = - E U s n x V s n x

(28)

식 (27)의 양변에 $U s n x V s n x$ 을 앞에서 곱하고 적분하여 식 (29)를 얻고

λ r m ∫ 0 L U s n V s n D U r m V r m d x = - ∫ 0 L U s n V s n E U r m V r m d x

(29)

또한, 식 (28)의 양변에 $U r m x V r m x$ 을 앞에서 곱하고 적분하여 식 (30)을 얻는다.

λ s n ∫ 0 L U r m V r m D U s n V s n d x = - ∫ 0 L U r m V r m E U s n V s n d x

(30)

식 (29)에서 식 (30)을 뺀 결과를 정리하면 식 (31)과 같다.

λ r m - λ s n ∫ 0 L c d I U r m'' U s n'' d x + λ r m + λ s n ∫ 0 L m U r m U s n d x = - U s n c d I λ r m U r m''' + U s n E I U r m''' 0 L + U r m c d I λ s n U s n''' + U r m E I U s n''' 0 L + U s n' ⋅ c d I λ r m U r m'' + U s n' ⋅ E I ⁡ U r m'' 0 L - U r m' ⋅ c d I λ s n U s n'' + U r m' ⋅ E I U s n'' 0 L

(31)

위 식의 우변은 전통적인 경계조건(단순지지단, 자유단, 고정단 등)에 대하여 영이 된다(식 (14) ~ (16) 참조). 따라서 식 (32)와 같은 첫 번째 직교조건을 얻는다.

λ r m + λ s n ∫ 0 L m U r m U s n d x + ∫ 0 L c d I U r m'' U s n'' d x = A s n f o r s = r a n d n = m 0 f o r s ≠ r o r n ≠ m

(32)

위의 직교조건을 Kronecker delta를 사용하여 표현하면 식 (33)과 같다.

λ r m + λ s n ∫ 0 L m U r m U s n d x + ∫ 0 L c d I U r m'' U s n'' d x = A s n δ r s δ m n

(33)

여기서 식 (33)은 텐서 식(tensor equation)이 아님에 유의한다. 따라서 한 항에 2번씩 나오는 상첨자 및 하첨자는 합을 의미하지 아니한다. 이후의 식들도 텐서 식이 아니다.

식 (29)의 우변의 적분을 첫 번째 직교조건식 (33)을 이용하여 표현하면 식 (34)와 같다.

∫ 0 L U s n V s n D U r m V r m d x = A s n δ r s δ m n + ∫ 0 L γ U r m U s n d x + U s n c d I U r m''' 0 L - U s n' ⋅ c d I U r m'' 0 L

(34)

또한, 식 (29)의 좌변의 적분은 식 (35)와 같다.

∫ 0 L U s n V s n E U r m V r m d x = ∫ 0 L E I U s n'' U r m'' d x - λ r m λ s n ∫ 0 L m U r m U s n d x + U s n E I U r m''' 0 L - U s n' ⋅ E I U r m'' 0 L

(35)

식 (34)와 식 (35)를 식 (29)에 대입하여 식 (36)과 같은 두 번째 직교조건을 얻는다.

∫ 0 L E I U r m'' U s n'' d x - λ r m λ s n ∫ 0 L m U r m U s n d x + λ r m ∫ 0 L γ U r m U s n d x = B s n f o r r = s a n d m = n 0 f o r r ≠ s o r m ≠ n

(36)

여기서 $B s n = - λ s n A s n$ 이다. 식 (36)을 Kronecker delta를 이용하여 다시 쓰면 식 (37)과 같다.

∫ 0 L E I U r m'' U s n'' d x - λ r m λ s n ∫ 0 L m U r m U s n d x + λ r m ∫ 0 L γ U r m U s n d x = B s n δ r s δ m n

(37)

식 (35)를 두 번째 직교조건 식 (37)을 이용하여 다시 쓰면 식 (38)과 같다.

∫ 0 L U s n V s n E U r m V r m d x = B s n δ r s δ m n - λ r m ∫ 0 L γ U r m U s n d x + U s n E I U r m''' 0 L - U s n' ⋅ E I U r m'' 0 L

(38)

2.4 모드좌표에서의 운동방정식의 해

모드 중첩법을 이용하여 식 (23)의 해는 식 (39)와 같이 쓸 수 있다.

y y ˙ = ∑ r = 1 ∞ ∑ m = 1 2 U r m x V r m x q r m t

(39)

여기서 $q r m t$ 는 식 (40)과 같다.

q r m t = e λ r m t

(40)

식 (23)의 운동방정식에 식 (39)를 대입하면 식 (41)과 같다.

∑ r = 1 ∞ ∑ m = 1 2 D U r m x V r m x q ˙ r m t + E U r m x V r m x q r m t = f x, t 0

(41)

위 식의 양변에 $U s n V s n$ 을 앞에서 곱하고 적분하면 식 (42)와 같다.

∑ r = 1 ∞ ∑ m = 1 2 ∫ 0 L U s n V s n D U r m x V r m x d x q ˙ r m t + ∫ 0 L U s n V s n E U r m x V r m x d x q r m t = ∫ 0 L U s n V s n f x, t 0 d x

(42)

식 (34)와 식 (38)을 식 (42)에 대입하면 식 (43)과 같다.

∑ r = 1 ∞ ∑ m = 1 2 A s n δ r s δ m n + ∫ 0 L γ U r m U s n d x + U s n c d I U r m''' 0 L - U s n' ⋅ c d I U r m'' 0 L q ˙ r m t + B s n δ r s δ m n - λ r m ∫ 0 L γ U r m U s n d x + U s n E I U r m''' 0 L - U s n' ⋅ E I U r m'' 0 L q r m t = ∫ 0 L U s n f x, t d x

(43)

식 (43)에 $q ˙ r m t = λ r m q r m t$ 의 관계와 경계조건을 적용하면 식 (43)은 식 (44)와 같이 된다.

∑ r = 1 ∞ ∑ m = 1 2 A s n δ r s δ m n q ˙ r m t + B s n δ r s δ m n q r m t = ∫ 0 L U s n f x, t d x

(44)

식 (44)는 s=r, n=m일 때 식 (45)와 같이 된다.

A r m q ˙ r m t + B r m q r m t = ∫ 0 L U r m f x, t d x

(45)

그런데 $B r m = - λ r m A r m$ 이므로 식 (45)는 식 (46)과 같다.

q ˙ r m t - λ r m q r m t = 1 A r m ∫ 0 L U r m f x, t d x

(46)

여기서 $A r m$ 은 식 (33)로부터 식 (47)과 같다.

A r m = 2 λ r m ∫ 0 L m U r m 2 d x + ∫ 0 L c d I U r m'' 2 d x

(47)

식 (45)는 모드좌표(modal coordinates)에서의 운동방정식이다. 식 (45)의 해는 Laplace 변환을 이용하여 구하면 식 (48)과 같다.

q r m t = 1 A r m ∫ 0 t e λ r m t - τ ∫ 0 L U r m x f x, τ d x d τ + q r m 0 e λ r m t

(48)

식 (48)의 초기조건 $q r m 0$ 는 첫 번째 직교조건 식 (33)을 이용하여 식 (49)와 같이 표현된다(부록 D 참조).

q r m 0 = 1 A r m λ r m ∫ 0 L m U r m y x, 0 d x + ∫ 0 L m U r m y ˙ x, 0 d x + ∫ 0 L c d I U r m'' y'' x, 0 d x

(49)

2.5 고유진동형의 정규화

$A r m$ 과 $B r m$ 은 직교조건들에 의해 정의되는 상수들로서 서로 연관되어 있다. 2.3절의 직교조건들이 감쇠가 없을 때의 직교조건 형태로 일관성 있게 표현되도록 첫 번째 직교조건 식 (33)을 고려해보자. c_dI=0, γ=0이고 r=s, m=n일 때, 식 (33)은 식 (50)과 같다.

2 λ r m ∫ 0 L m U r m 2 d x = A r m

(50)

한편, 감쇠가 없을 경우에 정의된 전통적인 모드 질량(modal mass)은 식 (51)과 같다⁽¹¹⁾.

∫ 0 L m U r m 2 d x = M r m

(51)

식 (50)과 식 (51)을 비교하면 $A r m$ 과 $M r m$ 의 관계는 식 (52)와 같다.

2 λ r m M r m = A r m or M r m = A r m / 2 λ r m

(52)

따라서 첫 번째 직교조건 식 (33)은 식 (53)과 같이 쓸 수 있다.

λ r m + λ s n ∫ 0 L m U r m U s n d x + ∫ 0 L c d I U r m'' U s n'' d x = 2 λ r m M r m δ r s δ m n

(53)

또한, $B r m = - λ r m A r m = - 2 λ r m 2 M r m$ 이므로 두 번째 직교조건 식 (37)을 식 (54)와 같이 쓸 수 있다.

∫ 0 L E I U r m'' U s n'' d x - λ r m λ s n ∫ 0 L m U r m U s n d x + λ r m ∫ 0 L γ U r m U s n d x = - 2 λ r m 2 M r m δ r s δ m n

(54)

감쇠가 없는 경우(c_d=0, γ=0)에 순허수로서 $λ r 1 = j ω r ω r > 0$ 이라면 $λ r 2 = - j ω r$ (여기서 ω_r은 r번째 고유진동수이고 j는 허수단위)이다. 이때, r=s, m=n일 때 식 (54)는 식 (55)와 같이 되어 감쇠가 없을 때의 전통적인 두 번째 직교조건이 됨을 알 수 있다.

∫ 0 L E I U r m'' 2 d x = ω r 2 M r m

(55)

그러므로 첫 번째 직교조건 식 (53)을 이용하여 고유진동형을 정규화하면, 감쇠가 있는 경우나 감쇠가 없는 경우에 대해 일관성 있게 모드해석을 할 수 있다. 따라서 양단이 고정된 보의 고유진동형(식 (17))에 식 (53)을 이용하여 $M r m = 1$ 로 정규화시키면 고유진동형(normalized eigenfunction)은 식 (56)과 같다.

U^r m x = C r m cosh ⁡ β r m x - cos ⁡ β r m x - cosh ⁡ β r m L - cos ⁡ β r m L sinh ⁡ β r m L - sin ⁡ β r m L sinh ⁡ β r m x - sin ⁡ β r m x

(56)

여기서 계수 $C r m$ 은 식 (57)과 같다.

C r m = 2 λ r m 2 λ r m ∫ 0 L m U r m 2 d x + ∫ 0 L c d I (U r m'' 2 d x

(57)

식 (57)에서 $U r m$ 은 식 (58)과 같다.

U r m x = cosh ⁡ β r m x - cos ⁡ β r m x - cosh ⁡ β r m L - cos ⁡ β r m L sinh ⁡ β r m L - sin ⁡ β r m L sinh ⁡ β r m x - sin ⁡ β r m x

(58)

2.6 운동방정식의 해

(1) 운동방정식의 해

식 (53)을 이용하여 $M r m = 1$ 로 정규화된 고유진동형과 직교조건을 사용하여, 식 (48)과 식 (49)를 다시 쓰면 각각 식 (59)와 식 (60)과 같다.

q r m t = 1 2 λ r m ∫ 0 t e λ r m t - τ ∫ 0 L U^r m x f x, τ d x d τ + q r m 0 e λ r m t

(59)

q r m 0 = 1 2 λ r m λ r m ∫ 0 L m U^r n y x, 0 d x + ∫ 0 L m U^r m y ˙ x, 0 d x + ∫ 0 L c d I U^r m'' y'' x, 0 d x

(60)

그러므로 식 (7)의 해는 모드중첩법을 이용하여 식 (61)과 같이 표현된다.

y x, t = ∑ r = 1 ∞ ∑ m = 1 2 U^r m x q r m t = ∑ r = 1 ∞ U^r 1 x q r 1 t + U^r 2 x q r 2 t = ∑ r = 1 ∞ U^r 1 x q r 1 t + U^r 1 x q r 1 t - = ∑ r = 1 ∞ 2 R e ⁡ U^r 1 x q r 1 t = ∑ r = 1 ∞ R e ⁡ U^r 1 x λ r 1 ∫ 0 t e λ r 1 t - τ ∫ 0 L U r 1^x f x, τ d x d τ + e λ r 1 t λ r 1 ∫ 0 L m U^r 1 y x, 0 d x + ∫ 0 L m U^r 1 y ˙ x, 0 d x + ∫ 0 L c d I U^r 1'' y'' x, 0 d x

(61)

여기서 Re[‧‧‧]는 대괄호 안의 복소수의 실수부를 의미한다.

(2) 운동방정식의 해에 대한 검토

식 (61)이 잘 알려져 있는 감쇠가 없는 경우(c_dI=0, γ=0)의 해를 주는지 검토해 보자. 감쇠가 없는 경우 $λ r 1 = j ω r ω r > 0$ 이라면 $λ r 2 = - j ω r$ 이고, $λ r 1$ 과 $λ r 2$ 에 대응하는 파라미터 β를 각각 $β r 1 = j β r, β r 2 = - j β r$ 라고 할 때(여기서 β_r=(m(ω_r)²/EI)^1/4의 실수), 이에 대응하는 고유진동형들( $U^r 1 x$ 과 $U^r 2 x$ 은 동일하며 실함수(real-valued function)이다. 즉, $U^r 1 = U^r 2$ 이므로 이들을 $U^r x$ 로 표기하면, c_dI=0, γ=0일 때 식 (61)은 식 (62)와 같이 된다.

y x, t = ∑ r = 1 ∞ U^r 1 ω r ∫ 0 L sin ⁡ ω r t - τ ∫ 0 L U^r f x, τ d x d τ + ∫ 0 L m U r^y x, 0 d x cos ⁡ ω r t + 1 ω r ∫ 0 L m U r^y ˙ x, 0 d x sin ⁡ ω r t

(62)

위 식은 감쇠가 없는 경우의 해⁽¹¹⁾와 일치한다.

3. 수치해석 및 검토

본론에서의 모드해석을 위한 수식을 이용하여, Fig. 2의 양단이 고정된 보에 대하여 충격하중에 의한 자유진동과 초기조건에 의한 자유진동에 대해 검토하고자 한다. 이를 위해, Table 1과 같은 물성을 갖는 보의 자유진동을 비교하고자 한다. Table 1의 데이터는 참고문헌⁽¹⁾의 실험값들이다.

Fig. 2

A clamped-clamped beam(L=1 m, m=1.02 kg/m and I=1.64×10-9 m4)

Table 1

Two sets of data for simulation

Table 1의 data-Ⅰ은 Cudney and Inman⁽¹²⁾의 실험결과를 Banks and Inman⁽¹⁾이 처음 9개의 모드에 대해 그들이 제안하는 이론에 적용하여 얻은 값들이고, data-Ⅱ는 Cudney and Inman의 실험 결과를 Banks and Inman⁽¹⁾이 처음 2개 모드, 처음 3개 모드, ..., 처음 9개 모드에 대하여 연속적으로 최소자승법을 적용하여 얻은 값들이다.

3.1 감쇠고유진동수와 점성감쇠비의 관계

식 (12)로부터 식 (63)의 관계식을 얻는다.

λ r m 2 + c d I β r m 4 + γ m λ r m + E I β r m 4 m = 0

(63)

그런데 양단 고정보의 경우 $β r 1 4 = β r 2 4$ 이므로 이들을 (β⁴)_r로 나타내면 식 (63)은 식 (64)와 같이 쓸 수 있다.

λ r m 2 + c d I β 4 r + γ m λ r m + E I β 4 r m = 0

(64)

그러므로 고유값은 식 (65)와 같이 표현된다.

λ r m = 12 - b ± b 2 - 4 c

(65)

여기서 b와 c는 식 (66)과 식 (67)과 같다.

b = c d I β 4 r + γ / m.

(66)

c = E I β 4 r / m

(67)

1-자유도 스프링-댐퍼-질량 시스템의 고유값과 감쇠비 및 고유진동수의 관계, 즉 $λ r 1 + λ r 2 = - 2 ζ r ω r$ 와 $λ r 1 λ r 2 = ω r 2$ 를 이용하면 양단 고정보의 r번째 모드 감쇠비(modal damping ratio)는 식 (68)과 같이 표현된다.

ζ r = c d I 2 E I ω r + γ 2 m 1 ω r

(68)

여기서 ω_r은 감쇠가 없는 경우의 r번째 고유진동수로서 식 (69)와 같다.

ω r = E I β 4 r / m

(69)

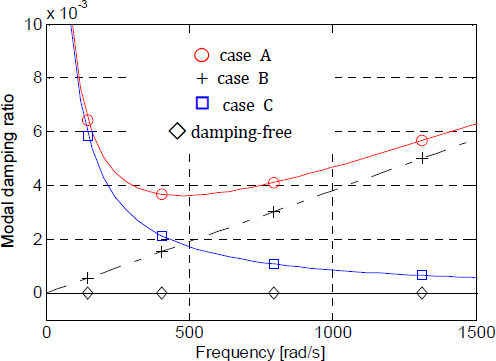
식 (68)의 모드 감쇠비(ζ_r)는 고유진동수(ω_r)에 비례하는 첫 번째 항과 반비례하는 두 번째 항의 합으로 구성되어 있다. 이로부터 재료의 점성으로부터 유래되는 모드 감쇠비는 ω_r에 비례하고, 공기 점성으로부터 유래되는 모드 감쇠비는 ω_r에 반비례함을 알 수 있다. 이러한 사실을 모드별로 나타내기 위하여, Table 1의 data-Ⅰ에 대하여 Table 2와 같이 네 가지 경우로 분해하고, 각 경우에 대한 모드 감쇠비를 계산하여 Fig. 3에 도시한다.

Table 2

Four cases of damping coefficients of the Data-Ⅰ in Table 1(E=2.68×1010 N/m2)

Fig. 3

Modal damped natural frequency versus modal damping ratio for the data in Table 2

Fig. 3에서 맨 위의 곡선은 식 (68)에서 재료의 점성과 공기 점성을 모두 고려한 경우(Case A)의 것이고, 일점쇄선의 직선은 재료의 점성(식 (68))의 첫 번째 항)만을 고려한 경우(Case B)의 것이며, 쌍곡선 형태의 곡선은 공기 점성(식 (68)의 두 번째 항)만을 고려한 경우(Case C)의 것이다. 그리고 맨 아래의 수평선은 c_d=0, γ=0일 때(damping-free)의 것이다. 따라서 맨 위의 곡선은 점선과 쌍곡선 형태의 곡선을 중첩시킨 것에 해당된다. 그리고 ○, +, □, ◊ 등은 각 경우의 첫 번째부터 네 번째 모드의 고유진동수 및 감쇠비를 나타낸다.

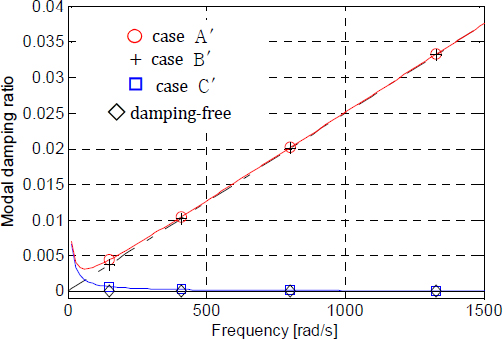
또한 Table 1의 data-Ⅱ에 대해서도 Table 3과 같이 네 가지 경우로 분해하고, 각 경우에 대한 모드 감쇠비를 계산하여 Fig. 4에 도시한다.

Table 3

Four cases of damping coefficients of the Data-Ⅱ in Table 1(E=2.75×1010 N/m2)

Fig. 4

Modal damped natural frequency versus modal damping ratio for the data in Table 3

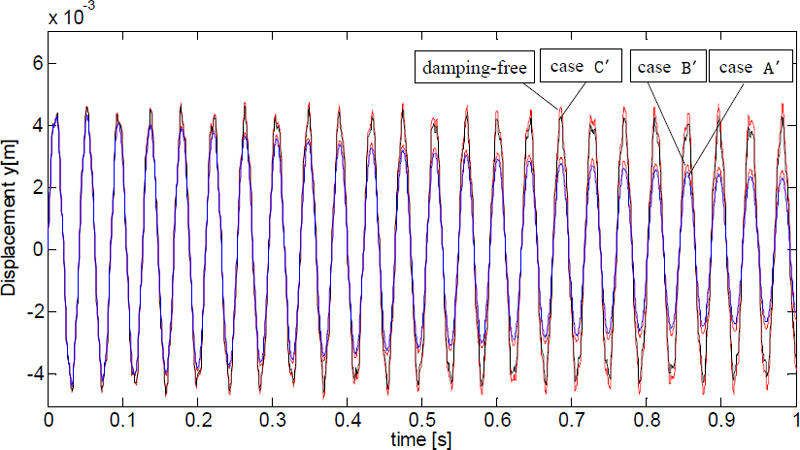
Fig. 3과 Fig. 4를 비교해보면, Fig. 3의 경우 첫 번째 모드의 감쇠비의 크기는 case A > case C > case B > damping-free의 순서인데 반해, Fig. 4의 경우에는 case A′ > case B′ > case C′ > damping-free이다. 이러한 정보는 다음 절의 수치해석 결과에 대한 검토 자료로 사용된다. Fig. 3과 Fig. 4의 결과가 상이한 것은 앞에서 언급한 것처럼 모드실험에서 적용한 파라메터 추출방법이 다르기 때문이다.

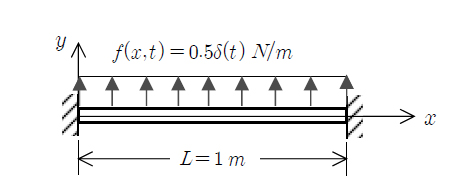
3.2 충격하중에 의한 자유진동

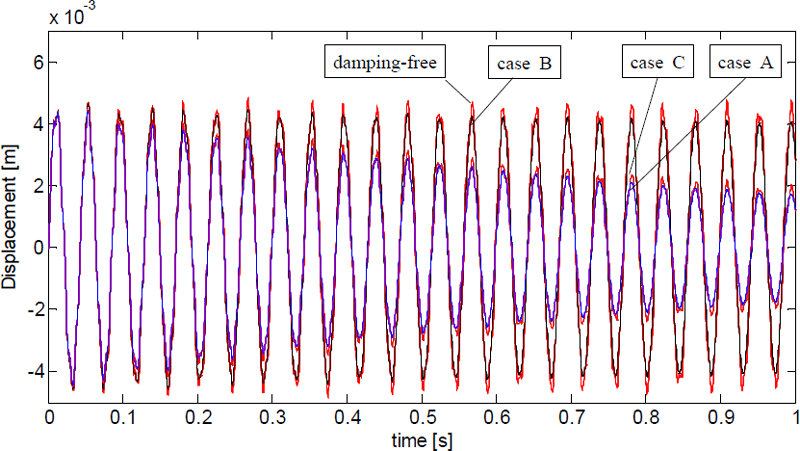
초기에 정지해 있는 보가 Fig. 5와 같은 충격하중(f(x,t)=0.5δ(t) [N/m], 여기서 δ(t)는 Dirac delta function이다)을 받는 경우의 응답을 구하기 위하여 Table 2 및 Table 3의 8가지 경우에 대한 충격응답들을 각각 Fig. 6과 Fig. 7에 도시한다. 이 응답들은 8개의 모드를 사용하여 계산한 것이다.

Fig. 5

A clamped-clamped beam subjected to an impulse load of f(x,t)=0.5δ(t) [N/m]

Fig. 6

Response of the displacement at x=0/5 m of the four cases in Table 2

Fig. 7

Response of the displacement at x=0/5 m of the four cases in Table 3

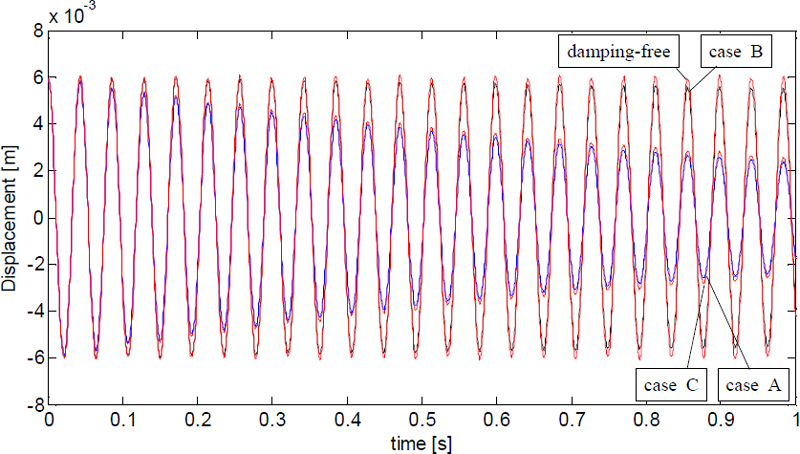
Fig. 6에서 진폭의 감소율이 가장 큰 것부터 차례로 보면 case A > case C > case B > damping-free의 순이다. 이에 반해, Fig. 7에서는 case A′ > case B′ > case C′ > damping-free의 순이다. 그런데 이들의 응답은 모드 한 개만 사용하여도 8개를 사용한 응답에 거의 수렴한다. 따라서 응답은 첫 번째 모드가 지배적임을 알 수 있다. 그러므로 응답의 진폭 감소율은 첫 번째 모드 감쇠비의 크기에 지배적인 영향을 받는다. 즉, Figs. 3과 4에서의 첫 번째 모드의 감쇠비가 클수록 Figs. 6과 7에서 보는 바와 같이 응답 진폭의 감소율이 크다는 사실을 알 수 있다.

3.3 초기조건에 의한 자유진동

이 절에서는 Table 2 및 Table 3과 같은 데이터를 갖는 양단 고정보가 처음에 초기변위(y(x,0))로 구속되어 있다가 그 구속을 풀어줌으로써 발생하는 자유진동을 고려한다. 초기변위가 식 (70)과 같다면

y x, 0 = 100 24 E I x 4 - 2 L x 3 + L 2 x 2

(70)

이 처짐의 초기곡률은 식 (71)과 같다.

y'' x, 0 = 100 12 E I 6 x 2 - 6 L x + L 2

(71)

위의 초기변위는 균일분포하중(하중의 세기는 100 N/m)을 받는 양단고정보의 처짐곡선으로서 경계조건들(y|_x=0=0, y′|_x=0=0, y|_x=L=0, y′|_x=L=0)을 만족시킨다.

Fig. 8에서 진폭의 감소율이 가장 큰 것부터 차례로 보면 case A > case C > case B > damping-free의 순이다. 이에 반해, Fig. 9에서는 case A′ > case B′ > case C′ > damping-free의 순이다. 이에 대한 이유는 3.2절에서의 설명과 동일하다.

Fig. 8

Response of the displacement at x=0.5 m of the four cases in Table 2

Fig. 9

Response of the displacement at x=0.5 of the four cases in Table 3

4. 결 론

이 연구에서는 점탄성재료로 만든 보가 진동하면서 공기의 점성저항을 받을 때, 외력에 의한 자유 진동뿐만 아니라 초기조건(초기 변위)에 의한 자유진동의 시간 응답을 얻기 위한 복소 모드해석 정식화를 제시하였다. 이를 위해 확장된 해밀톤 원리를 적용하여 운동방정식과 경계조건을 유도하고, 상태변수를 사용한 운동방정식을 비연성화 시키기 위한 직교조건을 유도하고, 이 직교조건을 이용하여 모드좌표계에서의 초기조건을 구하였으며, 복소 모드 중첩법을 사용하여, 외력에 의한 자유 진동뿐만 아니라 초기조건(초기 변위)에 의한 자유진동의 시간 응답을 구하였다. 특히 본 연구에서 사용한 정규화된 고유진동형은 점성 감쇠가 없는 보에서도 일관되게 사용할 수 있도록 정규화 하였다. 또한 재료의 점탄성과 공기 점성이 응답에 미치는 영향을 검토하기 위하여, 재료 및 공기의 점성이 없는 경우, 공기의 점성만 고려한 경우, 재료의 점성만 고려한 경우, 재료 및 공기의 점성을 모두 고려한 경우 등의 진폭 감소율의 차이를 모드 감쇠비를 사용하여 설명하였다.

References

Banks, H. T. and Inman, D. J., 1991, On Damping Mechanisms in Beams, Journal of Applied Mechanics, Vol. 58, No. 3, pp. 716~723. [https://doi.org/10.1115/1.2897253]
Prater, G. Jr. and Singh, R., 1990, Eigenproblem Formulation, Solution and Interpretation for Non-proportionally Damped Continuous Beams, Journal of Sound and Vibration, Vol. 143, No. 1, pp. 125~142. [https://doi.org/10.1016/0022-460X(90)90572-H]
Oliveto, G., Santini, A. and Tripodi, E., 1997, Complex Modal Analysis of a Flexural Vibrating Beam with Viscous End Conditions, Journal of Sound and Vibration, Vol. 200, No. 3, pp. 327~345. [https://doi.org/10.1006/jsvi.1996.0717]
Krenk, S., 2004, Complex Modes and Frequencies in Damped Structural Vibrations, Journal of Sound and Vibration, Vol. 270, No. 4-5, pp. 981~996. [https://doi.org/10.1016/S0022-460X(03)00768-5]
Gürgöze, M. and Erol, H., 2006, Dynamic Response of a Viscously Damped Cantilever with a Viscous End Condition, Journal of Sound and Vibration, Vol. 298, No. 1-2, pp. 132~153. [https://doi.org/10.1016/j.jsv.2006.04.042]
De Rosa, M. A., Lippiello, M., Maurizi, M. J. and Martin, H. D., 2010, Free Vibration of Elastically Restrained Cantilever Tapered Beams with Concentrated Viscous Damping and Mass, Mechanics Research Communications, Vol. 37, No. 2, pp. 261~264. [https://doi.org/10.1016/j.mechrescom.2009.11.006]
Xing, X. and Feeny, B. F., 2015, Complex Modal Analysis of a Nonmodally Damped Continuous Beam, Journal of Vibration and Acoustics, Vol. 137, No. 4, 041006. [https://doi.org/10.1115/1.4029899]
Svedholm, C., Zangeneh, A., Pacoste, C., François, S. and Karoumi, R., 2016, Vibration of Damped Uniform Beams with General End Conditions under Moving Loads, Engineering Structures, Vol. 126, pp. 40~52. [https://doi.org/10.1016/j.engstruct.2016.07.037]
Singh, K. V., 2016, Eigenvalue and Eigenvector Computation for Discrete and Continuous Structures Composed of Viscoelastic Materials, International Journal of Mechanical Sciences, Vol. 110, pp. 127~137. [https://doi.org/10.1016/j.ijmecsci.2016.03.009]
Zangeneh, A., Museros, P., Pacoste, C. and Karoumi, R., 2021, Free Vibration of Viscoelastically Supported Beam Bridges under Moving Loads: Closed-Form Formula for Maximum Resonant Response, Engineering Structures, Vol. 244, 112759. [https://doi.org/10.1016/j.engstruct.2021.112759]
Meirovitch, L., 1975, Elements of Vibration Analysis, McGraw-Hill, New York.
Cudney, H. H. and Inman, D. J., 1989, Experimental Verification of Damping Mechanisms in a Composite Beam, Proceedings of the 7th International Modal Analysis Conference, pp. 704~710.

Appendix

부 록 A

$λ r 1 = λ r 2 -$ 이므로

β r 1 4 = - m λ r 1 2 + γ λ r 1 c d I λ r 1 + E I = - m λ r 2 ¯ 2 + γ λ r 2 ¯ c d I λ r 2 ¯ + E I = β r 2 4 ¯

(A-1)

그러므로 $β r 1 4 = β r 2 4 ¯$ 이다.

부 록 B

$β r 1 4 = X + j Y$ 라 하고(여기서 X, Y는 실수이고 j는 허수단위이다), 이를 극좌표 형태(polar from)로 표현하면 다음과 같다.

β r 1 4 = M {c os ⁡ 2 k π + θ + j sin ⁡ 2 k π + θ}

(B-1)

여기서 $M = X 2 + Y 2$ 이고 θ=tan^-1(Y/X)이며 k=0,1,2,...이다. 그러므로

β r 1 = M 1 / 4 cos ⁡ k π / 2 + θ / 4 + j sin ⁡ k π / 2 + θ / 4, (k = 0,1, 2,3)

(B-2)

이다. 또한 $β r 2 4 = β r 1 4 ¯$ 이므로

β r 2 = M 1 / 4 cos ⁡ k π / 2 + θ / 4 - j sin ⁡ k π / 2 + θ / 4, (k = 0,1, 2,3)

(B-3)

식 (B-2)와 식 (B-3)를 비교하면 $β r 1 = β r 2 -$ 이다.

부 록 C

양단 고정인 보의 고유진동형은 다음과 같다.

U r m x = cosh ⁡ β r m x - cos ⁡ β r m x - σ r m sinh ⁡ β r m x - sin ⁡ β r m x

(C-1)

여기서

σ r m = cosh ⁡ β r m L - cos ⁡ β r m L sinh ⁡ β r m L - sin ⁡ β r m L

(C-2)

그러므로, $U r 1 x, U r 2 x$ 는 다음과 같다.

U r 1 x = cosh ⁡ β r 1 x - cos ⁡ β r 1 x - σ r 1 sinh ⁡ β r 1 x - sin ⁡ β r 1 x

(C-3)

U r 2 x = cosh ⁡ β r 2 x - cos ⁡ β r 2 x - σ r 2 sinh ⁡ β r 2 x - sin ⁡ β r 2 x

(C-4)

그런데,

$s i n ⁡ β r 1 x = s i n ⁡ β r 2 ¯ x = s i n ⁡ β r 2 x ¯, c o s ⁡ β r 1 x = c o s ⁡ β r 2 ¯ x = c o s ⁡ β r 2 x ¯ s i n h ⁡ β r 1 x = s i n h ⁡ β r 2 ¯ x = s i n h ⁡ β r 2 x ¯, c o s h ⁡ β r 1 x = c o s h ⁡ β r 2 ¯ x = c o s h ⁡ β r 2 x ¯, σ r 1 = σ r 2 ¯$

이므로 식 (C-3)로부터,

$U r 1 ¯ x = cosh ⁡ β r 1 x ¯ - cos ⁡ β r 1 x ¯ - σ r 1 ¯ sinh ⁡ β r 1 x ¯ - sin ⁡ β r 1 x ¯ = cosh ⁡ β r 1 - x - cos ⁡ β r 1 - x - σ r 1 - sinh ⁡ β r 1 - x - sin ⁡ β r 1 - x = cosh ⁡ β r 2 x - cos ⁡ β r 2 x - σ r 2 sinh ⁡ β r 2 x - sin ⁡ β r 2 x = U r 2 x$

이므로 $U r 1 x = U r 2 - x$ 이다.

다른 경계조건을 갖는 보의 고유진동형들에 대하여도 동일한 방식으로 증명할 수 있다.

부 록 D

식 (34)의 양변에 $η s n t$ 를 곱하여 다시 쓰면 다음과 같다.

λ r m ∫ 0 L m U r m U s n η s n t d x + λ s n ∫ 0 L m U r m U s n η s n t d x + ∫ 0 L c d I U r m'' U s n'' η s n t d x = A s n δ r s δ m n η s n t

(D-1)

임의의 r과 m에 대하여, s≠r 또는 n≠m일 때 식 (D-1)의 우변은 항상 영이다. 그리고 s=r과 n=m인 경우에만 식 (D-1)의 우변은 영이 아니다. 이를 고려하여 식 (D-1)을 네 가지 경우에 대해 각각 다시 쓰면 다음과 같다.

s ≠ r, n = m 일 때; λ r m ∫ 0 L m U r m U s m η s m t d x + λ s m ∫ 0 L m U r m U s m η s m t d x + ∫ 0 L c d I U r m'' U s m'' η s m t d x = 0 s ≠ r, n ≠ m 일 때; λ r m ∫ 0 L m U r m U s n η s n t d x + λ s n ∫ 0 L m U r m U s n η s n t d x + ∫ 0 L c d I U r m'' U s n'' η s n t d x = 0 s = r, n = m 일 때; λ r m ∫ 0 L m U r m U r m η r m t d x + λ r m ∫ 0 L m U r m U r m η r m t d x + ∫ 0 L c d I U r m'' U r m'' η r m t d x = A r m η r m t s = r, n ≠ m 일 때; λ r m ∫ 0 L m U r m U r n η r n t d x + λ r n ∫ 0 L m U r m U r n η r n t d x + ∫ 0 L c d I U r m'' U r n'' η r n t d x = 0

(D-2)

식 (D-2)의 식들을 s와 n(s=1, 2, 3,...,∞과 n=1,2)에 대하여 좌변은 좌변끼리, 우변은 우변끼리 모두 더하면 다음과 같다.

λ r m ∫ 0 L m U r m ∑ s = 1 ∞ ∑ n = 1 2 U s n η s n t d x + ∫ 0 L m U r m ∑ s = 1 ∞ ∑ n = 1 2 U s n λ s n η s n t d x + ∫ 0 L c d I U r m'' ∑ s = 1 ∞ ∑ n = 1 2 U s n'' η s n t d x = A r m η r m t

(D-3)

그런데 $y x, t = ∑ s = 1 ∞ ∑ n = 1 2 U s n η s n t$ 이고 $η s n t = e λ s n t$ 이므로, $y ˙ x, t = ∑ s = 1 ∞ ∑ n = 1 2 U s n λ s n η s n t$ 이며 $y'' x, t = ∑ s = 1 ∞ ∑ n = 1 2 U s n'' η s n t$ 이다. 그러므로 식 (D-3)는 식 (D-4)와 같이 쓸 수 있다.

λ r m ∫ 0 L m U r m y x, t d x + ∫ 0 L m U r m y ˙ x, t d x + ∫ 0 L c d I U r m'' y'' x, t d x = A r m η r m t

(D-4)

위 식은 t=0일 때 식 (D-5)와 같다.

λ r m ∫ 0 L m U r m y x, 0 d x + ∫ 0 L m U r m y ˙ x, 0 d x + ∫ 0 L c d I U r m'' y'' x, 0 d x = A r m η r m 0

(D-5)

그러므로 모드좌표계에서의 초기조건 $η r m 0$ 은 식 (D-6)과 같다.

η r m 0 = 1 A r m λ r m ∫ 0 L m U r m y x, 0 d x + ∫ 0 L m U r m y ˙ x, 0 d x + ∫ 0 L c d I U r m'' y'' x, 0 d x

(D-6)

Yong-Woo Kim His recent research areas are complex modal analysis of continuous system and dynamic analysis of the structures made of viscoelastic materials.

Data-Ⅰ	Data-Ⅱ
E=2.68×10¹⁰ N/m²	E=2.75×10¹⁰ N/m²
c_d=2.05×10⁵ kg/m‧s	c_d=1.375×10⁶ kg/m‧s
γ=1.7561 kg/m·s	γ=0.2025 kg/m·s

	c_d [kg/ms]	γ [kg/ms]
Case A	2.05×10⁵	1.7561
Case B	2.05×10⁵	0.0
Case C	0.0	1.7561
Damping-free	0.0	0.0

	c_d [kg/ms]	γ [kg/ms]
Case A'	1.375×10⁶	0.2025
Case B'	1.375×10⁶	0.0
Case C'	0.0	0.2025
Damping-free	0.0	0.0