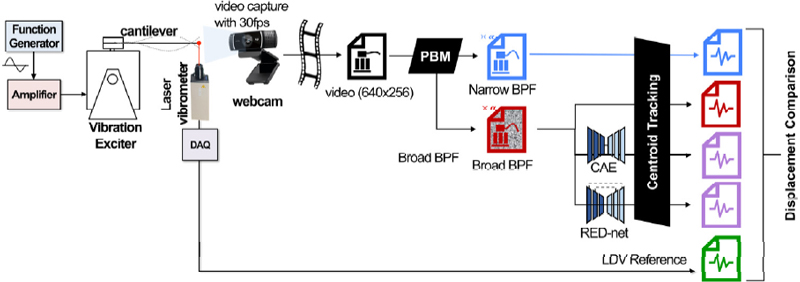
Application of Autoencoder Models to Replace Band-pass Filters in Image Vibrometry Utilizing Phase-based Motion Magnification

1. Introduction

Conventionally, piezoelectric accelerometers or laser Doppler vibrometers are utilized to monitor the vibration of mechanical structures. However, recent research has focused on applying image processing techniques to vibration monitoring. Image processing includes techniques for point tracking and digital image correlation.

Small vibrations that cannot be observed with the naked eye can overcome the limitation of small displacement through the image-magnification technique. In particular, phase-based video magnification (PBM)⁽¹⁾ is used in various image-based vibration measurement research^{(2 ~ 5)} since it linearly magnifies the dynamic behavior. On the other hand, temporal band-pass filtering is employed to reduce image artifacts caused by the magnification. However, it is difficult to set the band-pass filter’s frequency in a real-world measuring situation because the magnification technique is performed without knowing the object’s dynamic frequency range. When the entire frequency band is magnified, unnecessary motion is also magnified, resulting in image artifacts. Therefore, it is difficult to obtain exact vibration data, as it is challenging to measure accurate data on structural vibration.

Assume that the image artifacts induced by the magnification technique are considered to be image noise. In this instance, noise removal can be addressed for a single-frame image independently, regardless of other image frames in the time domain. Filters^(6,7) and orthogonal transformation^(8,9) are fundamental noise removal techniques in image frames. Due to the inconsistent noise, parameter optimization is essential to use the aforementioned rule-based approaches, such as filters or orthogonal transforms. Autoencoder neural networks for image noise removal were recently introduced to address these optimization issues.

As a result, in this study, we proposed a method to use an autoencoder instead of a predetermined temporal band-pass filter to eliminate artifacts caused by the full-frequency band phase-based magnification. The autoencoder model was trained to receive an image frame without band-pass filtering as input and return an image frame with appropriate band-pass filtering. Then, a dataset was generated using online phase-based magnification⁽¹⁰⁾, and the model was trained. The verification confirmed the artifact reduction of the results of applying the autoencoder model based on the accuracy of the extracted displacement.

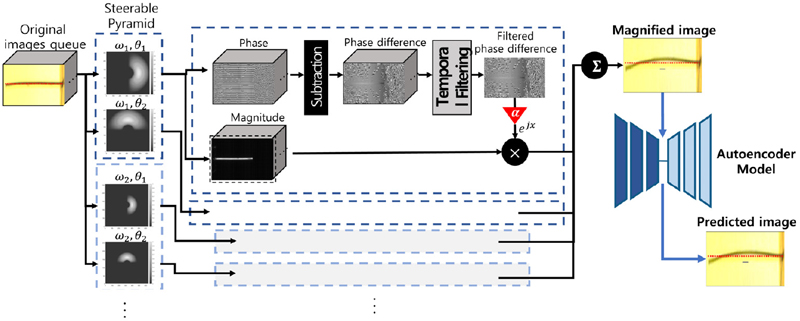
2. Phase-based Magnification

Phase-based magnification employs a complex steerable pyramid⁽¹¹⁾ to extract motion components. The magnification image frames are generated by merging each level of magnified images. The complex steerable filter, which is a partial component of complex steerable pyramid at specific spatial frequency, is a spatial sinusoid applied windowing, therefore can be noted as W(x)e^jωx. where x and ω respectively represent a positional coordinate and a specific frequency in the spatial domain. A spatially decomposed image S_ω(x) can be described as follows as Eq. (1):

where the ⊗ represents convolution on spatial domain. As the purpose of reconstructing an image is to collect all frequency image components, S_ω(x), the image notation can be represented as an infinite series as Eq.(2)

where δ_x(t) represents the sparse motion. The phase difference between the first and current image frames is equivalent to the sparse motion at specific spatial frequency, denoted as ωδ_x(t). This shows the difference in the complex phase angle of an image matches closely with the position change of a motion in the corresponding image⁽¹²⁾. Applying magnification factor α, which is simple ratio, to the phase difference and set Eulerian term as exp(jαωδ_x(t)), multiplication to Eq. (2) results in the magnified image as Eq. (3)

Therefore, multiplying α to the difference of extracted phase angle leads to motion amplitude increasing in proportion to the value set.

However, because the phase angle difference does not perfectly match the image’s motion information, temporal band-pass filtering is conducted by a finite impulse response (FIR) filter to filter out uncertain data and determine the motion in the frequency domain of interest. The filtered phase angle is multiplied by the magnification factor  and then merged back into the image to provide a partial image with magnified motion. By recombining the magnified partial images in this approach, the previously undetectable motion is significantly magnified. This procedure is illustrated in Fig. 1.

Fig. 1

Phase-based motion magnification with post-filtering by pre-trained autoencoder model

The time-domain band-pass filtering procedure requires a discrete Fourier transform, which can only be applied to finite data and cannot be performed by continually accumulating real-time streaming video. In this instance, the discrete Fourier transform can be replaced by a convolution with a filter coefficient for each frame in the time domain, providing frame-by-frame processing. In addition, this approach can perform online phase-based magnification⁽¹⁰⁾. Due to this feature, the image result can be observed in real-time by changing the frequency range of the time domain filter and the magnification factor α. The magnified output of the streaming video in real-time can be checked immediately. In addition, whereas with the conventional phase-based magnification technique, the filter order must be equal to the total number of video frames, in online time-domain convolution processing, an appropriate value can be adjusted during the process.

3. Image Artifact Reduction with Autoencoder

The displacement is extracted from the image with amplified motion using the phase-based magnification method. The actual displacement value can be estimated through the camera-object distance and scale calibration by applying the reciprocal of the magnification factor. However, for effective displacement extraction, the band-pass filtering frequency must be adjusted to an appropriate value, which is only possible with the information on the object’s dynamic characteristics. When a broad-band frequency is applied to determine dynamic characteristics without knowing the particular frequency of motion, artifacts appear in the image, limiting the displacement measurement algorithm’s application. Fig. 2(a) and Fig. 2(b) shows the results of displacement extraction by the centroid tracking method⁽¹³⁾ when the frequency of band-pass filtering is applied narrowly to broadly. When the frequency band is not specified (Fig. 2(b)), displacement extraction is not generally accomplished due to edge artifacts in the image.

Fig. 2

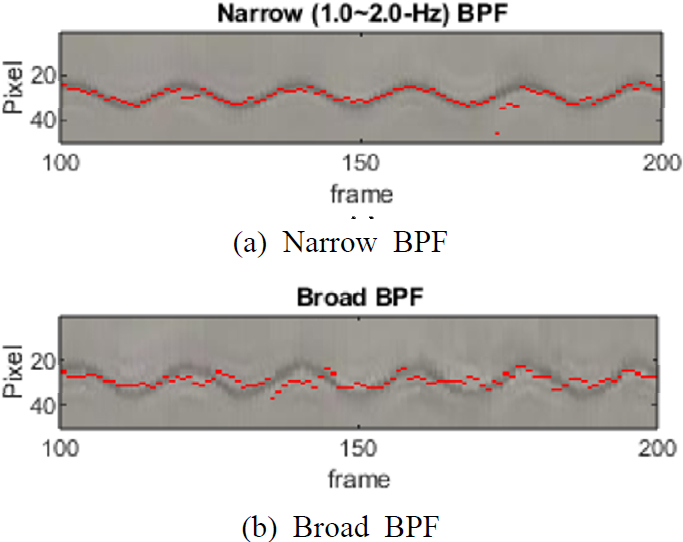
Displacement extraction results from the vibrationimage frames with phase-based magnification according to band-pass filtering

If these edge artifacts are considered a sort of image noise, a method for eliminating the artifacts from a single frame can be investigated. As mentioned in the introduction, the method employing a filter or orthogonal transformation is not applicable to this study because it requires a separate parameter optimization procedure. Instead, phase-based magnification processing incorporates an autoencoder to decrease edge artifacts, as it is well-known that an autoencoder is an efficient tool for image restoration.

3.1 Autoencoder Models

The denoise autoencoder model⁽¹⁴⁾ is a deep neural network (DNN). It consists of fully-connected layers, which are accompanied by reprocessing inputs and outputs into one-dimensional vectors. When applied to real images, the vectorized data becomes excessively long and the performance is potentially degraded depending on the duplication of learning parameters. Therefore, a convolutional autoencoder (CAE) was proposed⁽¹⁵⁾, in which fully-connected layers were replaced with convolution layers while conforming to the encoder-decoder configuration appropriate for the 2D image data format.

A convolutional autoencoder (CAE) is like a deep neural network because it consists of many layers stacked on top of each other. The image data compressed by the convolutional layer are restored to the original size through a deconvolutional layer. While passing through the convolution layer, the existing image loses its fine details, which are not conveyed to the deconvolution layer. Gradient vanishing occurs throughout the backpropagation process due to this information loss, making it challenging for the model to converge to the globally optimal solution.

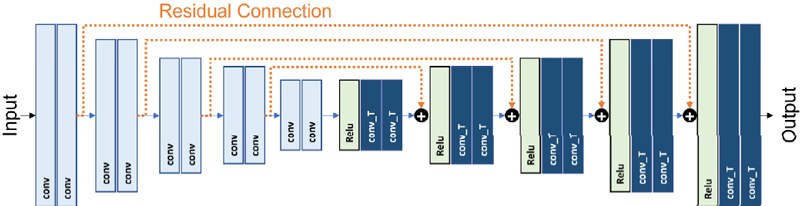
The residual encoder-decoder network (RED-Net) Fig. 3 is a structure in which skip connections are inserted between the convolution layer and the deconvolution layer to solve this optimal solution problem⁽¹⁶⁾. This residual connection structure preserves information before the information is lost as the dimensionality is reduced in the convolution layer, so that the detailed information of the existing image can be referred to when reconstructed in the deconvolution layer. As a result, it is easier to train the optimal solution by mitigating the gradient loss in backpropagation.

Fig. 3

Residual encoder-decoder network (RED-net) model

3.2 Datasets and Model Training

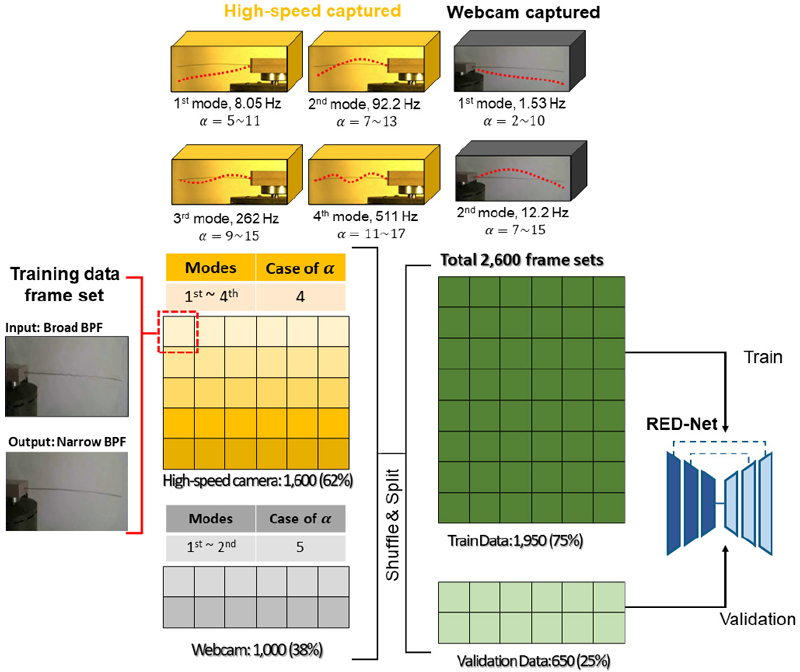
This study used the structural vibration images of two steel cantilevers to generate a training dataset. The training model receives a magnified image with severe artifacts because the band-pass filter is usually not applied. However, according to the typical application, the model delivers an image with the artifacts eliminated. The magnification factor of each magnified image frame should operate independently. Figure. 4 illustrates this procedure. For the diversity of training data, the left and right shooting angles and the lighting color were set differently. For uniformity of input to the learning model, however, the image dimensions were set at 640 × 256. The cantilevers photographed by the two types of cameras have the same thickness and width of 0.5 mm and 15 mm, respectively. However, the length for the high-speed camera is 240 mm that represents relatively high natural frequency, and the length for the webcam is 480 mm that represents relatively low natural frequency. Based on the sampling theory, images with modes up to the maximum frequency that can be captured at the speed of each recording device among the mode frequencies of the two cantilevers were taken, and a total of 26 types of videos were created by applying different magnification coefficients. A frame of broad BPF and the respective frame of narrow BPF are combined as single pair, and a total of 2600 pairs of images were made as a dataset by extracting 100 random pairs of images for a pair of video pairs. An autoencoder model is trained to predict a narrow BPF by receiving a broad BPF for a pair of data in this dataset. It was trained for a total of 500 epochs, and the number of training batches was set to 12 to utilize the memory capacity limit of the workstation GPU. It was set up to stop training and save the last optimal model if the training loss did not improve within 50 epochs during training.

Fig. 4

Datasets (total 2600 image frames) for model training and validation

A simple CAE and a RED-net were employed to construct the model used in this study. The RED-net utilized in the study contains 20 layers, no separate pooling layer, and a skip connection between every two layers. By eliminating the skip connection, a simple convolutional autoencoder is implemented.

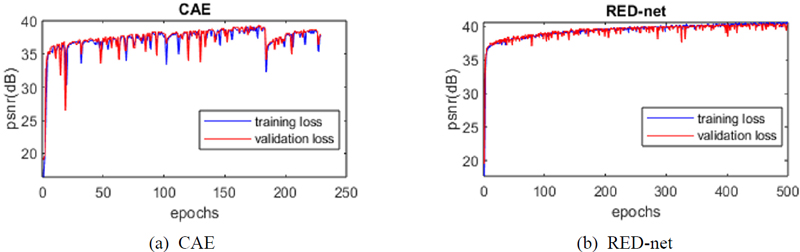
Model training was performed on a workstation with an Intel Xeon Silver 4210R CPU and NVIDIA RTX3090 GPU. The models were trained with a total training epoch of 500 by applying the same dataset and learning parameters, and each result was saved as a model. The number of training batches was set to 12 to utilize up to the limit of the memory capacity of the GPU of the workstation. If there is no improvement even after 50 epochs during training, the training is stopped and the last optimal model is saved. The backpropagation loss between the training of the two models is also presented in Fig. 5(a) and Fig. 5(b).

Fig. 5

Backpropagation loss in autoencoder models

Model training was performed on a workstation with an Intel Xeon Silver 4210R CPU and NVIDIA RTX3090 GPU. The models were trained with a total training epoch of 500 by applying the same dataset and learning parameters, and each result was saved as a model. The number of training batches was set to 12 to utilize up to the limit of the memory capacity of the GPU of the workstation. If there is no improvement even after 50 epochs during training, the training is stopped and the last optimal model is saved. The backpropagation loss between the training of the two models is also presented in Fig. 5.

4. Results and discussion

The data acquisition and experiment details are depicted in Fig. 6; while the 0.5 mm-thick, 15 mm-width, 480 mm-length cantilever is weakly excited with its mode frequency, video is recorded up to 500 frames using a 30 fps webcam, and the displacement of the cantilever tip was simultaneously acquired as a reference signal by LDV. The data acquisition occurred twice for excitation at 1.53 Hz and 12.2 Hz, respectively 1st and 2nd modes of the specimen, satisfying the sampling theorem. While broad BPF is set to 0.01 Hz ~ 14.99 Hz for both excitation cases, narrow BPF was set 1.0 Hz ~ 2.0 Hz and 11.0 Hz ~ 13.0 Hz for the two cases, respectively. Two learning models were used as post-filters in addition to a broad BPF to reduce image artifacts. Even when the band-pass filter was not correctly applied to the image acquired by the webcam, the vibration displacement was extracted with less noise using the autoencoder models.

Fig. 6

Experiment procedure for the comparison of results due to the BPFs, CAE and RED-net models

Figure 7 shows the obtained displacement compared to the case where band-pass filters are applied. As such, in general, the position of the cantilever tip cannot be appropriately tracked unless a band-pass filter is adequately applied to remove edge artifacts from the image. On the other hand, removing the noise via the autoencoder model tracks the displacement well.

Fig. 7

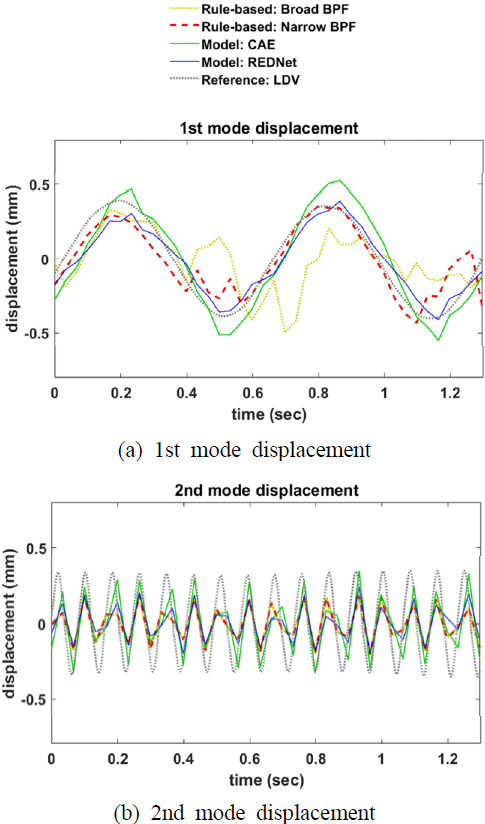
Extracted displacement of the 1st and 2nd mode response from the magnified images according to the band-pass filters and autoencoder models

Table 1 also shows the root-mean-squared (RMS) error to the reference displacement for the extracted displacement of the magnified image due to the applied band-pass filters and the autoencoder models, respectively. In the case of the first mode vibration displacement, the autoencoder model shows a relatively close result to the reference LDV value. In the second mode displacement, especially in the RED-net model, there is no significant difference from the conventional band-pass filter.

Table 1

RMS errors to reference LDV displacement amplitude (mm) and the relative RMSE ratio (%) to the case of conventional narrow BPF

On the other hand, there are cases in which the simple CAE cannot track the displacement, although RED-net does correctly. This can be quantitatively confirmed through the smaller RMS error. The poor artifact reduction performance of the model can be seen as a failure to converge to the global optimal solution. For example, in Fig. 5, CAE assumes that it converges to the local optimal solution because learning is stopped. Though the total learning time of RED-net is longer than CAE as shown in Table 2, the prediction processing time spent on a single frame is not different; but the RMS error of the result using RED-net is much smaller. Therefore, the RED-net model is still beneficial.

Table 2

Training time per epoch of the autoencoder models and post-filtering prediction time per frame

Since the proposed learning models can be applied to a single image frame, they can also be applied to video streaming, such as online phase-based image magnification⁽¹⁰⁾, if the computational capability is available. Additionally, it is superior, as it does not require the additional parameter adjustments necessary for a band-pass filter. Consequently, it was confirmed that model-based image restoration could be applied to image artifacts generated by phase-based magnification using RED-net beyond image noise reduction. This study confirmed that the proposed approach is only effective in the first- and second-mode of vibrations. It is extended to the higher modes of vibration and has been demonstrated⁽¹⁷⁾.

5. Conclusion

This study presented a deep learning autoencoder model to reduce edge artifacts caused by the inappropriate band-pass frequency filter configuration in phase-based magnification. The autoencoder model reduced the estimation errors when conventional band-pass filtering was not optimally applied. For learning the autoencoder model, the training datasets comprised online phase-based magnification images for each magnification factor, size, direction, FPS, and frequency. The residual autoencoder and the conventional autoencoder neural networks were trained using the prepared training dataset. As a result, the residual autoencoder model exhibited improved edge artifact reduction performance. The autoencoder model delivers substantially better results than applying broad band-pass filtering. Moreover, it can be executed immediately, even if the dynamic characteristics of the structure are not identifiable. This autoencoder model enables an additional benefit to the online phase-based magnification technique.

Acknowledgments

This work was supported by the 2020 sabbatical year research grant of the University of Seoul.

References

• Wadhwa, N., Rubinstein, M., Durand, F. and Freeman, W. T., 2013, Phase-based Video Motion Processing, ACM Transactions on Graphics, Vol. 32, No. 4, pp. 1~10. [https://doi.org/10.1145/2461912.2461966]
• Son, K.-S., Jeon, H.-S., Park, J.-H. and Park, J. W., 2013, A Technique for Measuring Vibration Displacement Using Camera Image, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 23, No. 9, pp. 789~796. [https://doi.org/10.5050/KSNVE.2013.23.9.789]
• Kong, Y., Miao, Y., Jeon, J. Y. and Park, G., 2021, Motion Phase-based 2-dimensional Displacement Measurements under Various Illumination Conditions with Maker and Filter Design, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 31, No. 4, pp. 408~418. [https://doi.org/10.5050/KSNVE.2021.31.4.408]
• Eitner, M., Miller, B., Sirohi, J. and Tinney, C., 2021, Effect of Broad-band Phase-based Motion Magnification on Modal Parameter Estimation, Mechanical Systems and Signal Processing, Vol. 146, 106995. [https://doi.org/10.1016/j.ymssp.2020.106995]
• Kim, H., Chung, Y., Jin, J. and Park, J., 2021, Manifestation of Flexural Vibration Modes of Rails by the Phase-based Magnification Method, IEEE Access, Vol. 9, pp. 98121~98131. [https://doi.org/10.1109/ACCESS.2021.3095619]
• Tomasi, C. and Manduchi, R., 1998, Bilateral Filtering for Gray and Color Images, Proceedings of the 6th International Conference on Computer Vision, pp. 839~846.
• Buades, A., Coll, B. and Morel, J.-M., 2005, A Non-local Algorithm for Image Denoising, Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition, pp. 60~65.
• Sendur, L. and Selesnick, I. W., 2002, Bivariate Shrinkage Functions for Wavelet-based Denoising Exploiting Interscale Dependency, IEEE Transactions on Signal Processing, Vol. 50, No. 11, pp. 2744~2756. [https://doi.org/10.1109/TSP.2002.804091]
• Portilla, J., Strela, V., Wainwright, M. J. and Simoncelli, E. P., 2003, Image Denoising Using Scale Mixtures of Gaussians in the Wavelet Domain, IEEE Transactions on Image Processing, Vol. 12, No. 11, pp. 1338~1351. [https://doi.org/10.1109/TIP.2003.818640]
• An, J. Y. and Lee, S. I., 2022, Phase-based Motion Magnification for Structural Vibration Monitoring at a Video Streaming Rate, IEEE Access, Vol. 10, pp. 123423~123435. [https://doi.org/10.1109/ACCESS.2022.3224601]
• Simoncelli, E. P. and Freeman, W. T., 1995, The Steerable Pyramid: A Flexible Architecture for Multi-scale Derivative Computation, Proceedings of International Conference on Image Processing, pp. 444~447.
• Gautama, T. and Van Hulle, M. A., 2002, A Phase-based Approach to the Estimation of the Optical Flow Field Using Spatial Filtering, IEEE Transactions on Neural Networks, Vol. 13, No. 5, pp. 1127~1136. [https://doi.org/10.1109/TNN.2002.1031944]
• Fu, G., Bo, W., Pang, X., Wang, Z., Chen, L., Song, Y., Zhang, Z., Li, J. and Wu, R., 2013, Mapping Shape Quantitative Trait Loci Using a Radius-centroid-Contour Model, Heredity, Vol. 110, pp. 511~519. [https://doi.org/10.1038/hdy.2012.97]
• Vincent, P., Hugo, L., Bengio, Y. and Manzagol, P.-A., 2008, Extracting and Composing Robust Features with Denoising Autoencoders, Proceedings of the 25th International Conference on Machine Learning, pp. 1096~1103. [https://doi.org/10.1145/1390156.1390294]
• Masci, J., Meier, U., Cireşan, D. and Schmidhuber, J., 2011, Stacked Convolutional Auto-encoders for Hierarchical Feature Extraction, Proceedings of the 21st International Conference on Artificial Neural Networks, pp. 52~59. [https://doi.org/10.1007/978-3-642-21735-7_7]
• Mao, X., Shen, C. and Yang, Y.-B., 2016, Image Restoration Using Very Deep Convolutional Encoder-decoder Networks with Symmetric Skip Connections, Proceedings of the 30th International Conference on Neural Information Processing Systems, pp. 2810~2818.
• An, J. Y., 2023, Vibration Measurement and Monitoring Using Online Image Processing and AI Vision, Master’s Thesis, University of Seoul, Seoul.