충격 하중의 주파수 특성을 고려한 안테나 구조물의 모드 기반 구조 경량화

1. 서 론

현대 해전 환경에서는 고도화된 대함유도탄의 위협이 증가하고 있으며, 이에 대한 효과적인 대응이 필요하다. 특히 기습 공격이 가능한 소형 및 고속 수상 함정과 근접 해상테러의 위협은 근거리 대함 방어 능력을 강화하는 필요성이 제기되고 있다. 이러한 요구에 부합하는 대함방어 시스템 중 하나인 능동위상배열레이더(active electronically scanned array, AESA)를 장착한 근접방어무기체계(close-in weapon system, CIWS)의 개발이 이루어졌다. AESA는 적대적인 행위자를 탐지하고 추적하기 위해 능동적으로 레이더의 빔을 형성하는 기술로, 이를 활용하여 목표물을 탐지하고 추적하는 안테나가 개발되고 있다. 기존의 능동위상배열레이더는 대부분 고정된 시스템에서 운용하고 있지만, 근접방어무기체계의 경우 고속 구동하는 기관포에 탑재되어 운용하기 때문에 안테나 장치의 동특성과 경량화 설계가 중요하다. 구축함에 탑재되는 안테나 구조물은 다양한 해양 환경과 전투 환경에 노출되기 때문에 경량화 설계된 안테나 구조물에 대한 구조 건전성 또한 확보되어야 한다^(1,2).

함정의 탑재장비의 구조 건전성 평가 방법은 실선 폭발 시험과 M&S(modeling and simulation) 기반 해석 방법이 있다. 중중량 탑재 장비의 경우, 시험 장비의 부재로 인해 국내에서는 시험이 불가능하기 때문에 중중량 함정 탑재장비의 구조 건전성 검증은 대부분 유한요소해석에 의존하고 있다. 이와 같은 M&S 기반의 해석 절차로는 독일 해군 규정인 BV043과 미국 NRL(naval research laboratory)에서 제시한 DDAM(dynamic design analysis method) 등이 있다⁽³⁾.

위상 최적화는 안테나 구조물과 같이 구조 건전성을 확보하면서 경량화된 디자인이 필요할 때 많이 사용되는 방법으로, 구조물의 제약 조건을 만족하면서 목표 함수를 최소화하는 디자인을 제공할 수 있다. 최근에는 구조물의 밀도 기반 최적화를 통해 최적의 형상을 구할 수 있는 SIMP(solid isotropic material with penalization) 방법 등이 많이 사용되고 있으며 ANSYS 등 다양한 해석 프로그램에 적용되고 있다⁽⁴⁾. 하지만 대부분의 위상 최적화 연구는 정적 하중에 대해서만 연구되었고, 시간 영역에서의 동적 하중에 대한 연구는 복잡성과 계산 부하 등으로 인해 등가의 정해석 등을 통해 대체되었다^(5~8). 동적 하중을 주파수 영역으로 변환하여 최적화를 진행한 연구도 있었지만, 구조물의 동적 거동을 충분히 반영하지 못하고 있다^(9,10). 따라서 BV043과 같이 시간 영역에서의 과도응답해석을 요구하는 규정을 만족해야 하는 구조물의 동적 거동을 충분히 반영하는 위상 최적화에 대한 연구가 필요하다.

이 연구에서는 BV043에 대한 구조 건전성을 확보하면서 경량화된 안테나 구조물을 제시하는 모드 기반 위상 최적화 방법을 제안하고자 한다. 이를 위해 유한요소해석 프로그램을 통해 안테나 구조물에 대한 모드해석을 진행하였고, 구조물의 주요 모드를 BV043의 충격 하중의 주파수 특성과 비교하였다. 구조물의 주요 모드의 고유진동수가 충격 하중의 주파수 범위를 피하는 제약 조건과 구조물의 질량을 줄이는 목표 함수에 대한 최적화 문제를 통해 공진 회피 설계가 고려된 경량화 디자인을 제시하였다. 마지막으로 기존 구조물과 경량화 구조물에 대하여 과도응답해석을 진행하여 구조 건전성을 평가하였다.

2. 안테나 구조물과 충격 하중 분석

2.1 안테나 구조물의 주요 모드 분석

(1) 유한요소 해석 모델 구축

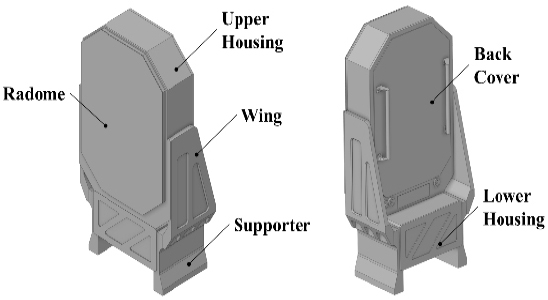
이 연구의 대상 구조물인 안테나 구조물은 Fig. 1과 같으며, 전체 높이는 약 1.67 m이고 크게 상부 하우징(upper housing)과 하부 하우징(lower housing) 그리고 지지 구조물로 구성되어 있다. 상부 하우징에는 다양한 전자 장비와 레이돔(radome), 냉각판, 후면 커버(back cover) 등이 포함되어 있다. 하부 하우징에도 다양한 전자 장비가 포함되어 있으며 지지대(supporter)와 날개(wing)를 통해 상부 하우징과 결합된다. 안테나 구조물은 지지대를 통해 기관포에 고정되어 기관포의 거동에 따라 함께 움직인다.

Fig. 1

Schematic diagram of antenna structure

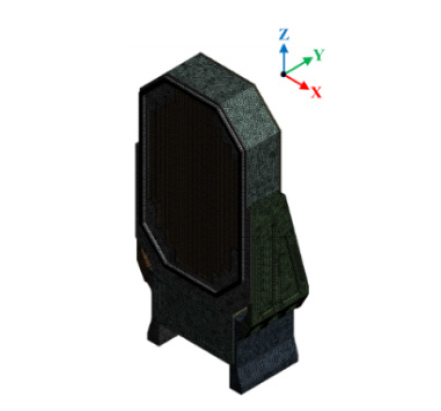
안테나 구조물에 대한 효과적인 유한요소 해석을 위해 내부의 복잡한 형상의 전자장비와 레이돔은 집중 질량으로 치환하였다. 경계조건은 지지대의 바닥면을 고정조건으로 설정하였으며, 볼트는 빔 구조로 치환하였다. 최종 유한요소해석 모델은 총 1 711 732개의 요소와 1 650 412개의 절점으로 구축하였으며 Fig. 2와 같다. 안테나의 각 구조물에 대한 크기와 물성치 등은 Table 1과 같다.

Fig. 2

Finite element model of antenna structure

Table 1

Details of finite element model

(2) 모드해석 결과

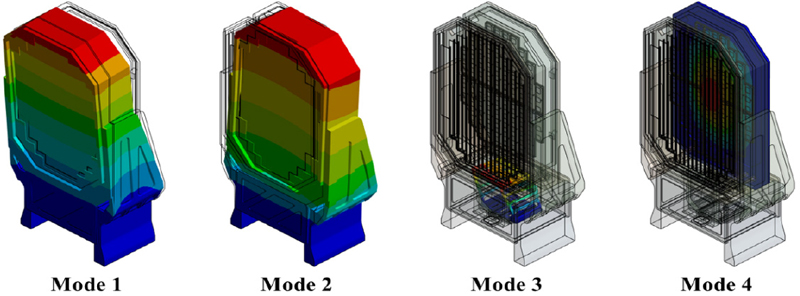
안테나 구조물의 진동 특성을 파악하기 위해 유한요소 해석 모델에 대한 모드해석을 진행하였다. 모드해석 결과는 Table 2와 Fig. 3과 같이 나타났다. 1차 모드는 60.00 Hz로 구조물의 Y축 방향 굽힘 모드이고, 2차 모드는 73.91 Hz로 구조물의 X축 방향 굽힘 모드이다. 3차 모드는 112.9 Hz로 하부 하우징의 내부 프레임의 X축 방향 굽힘 모드이고, 4차 모드는 123.7 Hz로 상부 하우징의 후면 커버의 Y축 방향 굽힘 모드이다.

Table 2

Dynamic characteristics of antenna structure

Fig. 3

Mode shapes of antenna structure

2.2 BV043의 주파수 특성 분석

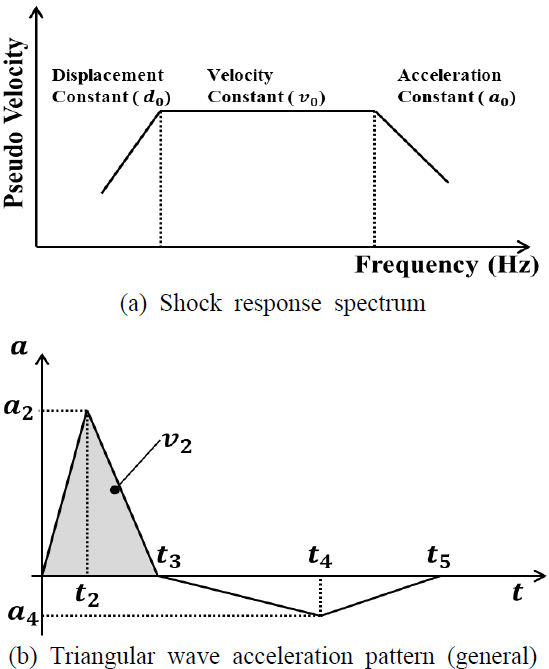
안테나 구조물과 같이 다양한 해전 환경에서 운용이 되는 함정에 탑재된 장비는 장비 운용 환경에서의 구조적 안정성도 요구되지만, 수중 폭발에 의한 충격에 대한 구조적 안정성도 요구된다. BV043은 독일 해군의 함정의 내충격성능과 관련한 규격으로, BV043에서 제시한 충격파에 함정이 노출되었을 때 함정의 장비들이 정상적으로 작동이 가능해야 한다. BV043에서 제시한 충격파에 노출된 장비의 내충격해석을 위한 충격응답스펙트럼(shock response spectrum)은 Fig. 4(a)와 같다. BV043의 충격응답스펙트럼은 함정의 종류나 장비의 탑재 위치, 충격 방향, 함정의 배수량, 그리고 장비 중량에 따라 분류된다. 여기서 d₀는 변위 스펙트럼의 기준값, v₀는 의사속도스펙트럼의 기준값, a₀는 가속도스펙트럼의 기준값을 나타낸다.

Fig. 4

Shock response spectrum and corresponding triangular wave acceleration pattern in time domain

BV043은 충격응답스펙트럼을 시간 영역에서의 가진 신호로 변환시켜 해석모델에 가진원으로 적용하는데, 충격응답스펙트럼에 대한 등가의 삼각파형 충격파(triangular wave acceleration pattern)는 Fig. 4(b)와 같다. 충격파의 세부값은 충격응답스펙트럼을 통해 식 (1) ~ 식 (7)과 같이 계산할 수 있다⁽³⁾.

$\[ a_2=0.6a_0 \]$

(1)

$\[ v_2=\frac{3}{4}{v}_0 \]$

(2)

$\[ t_3=\frac{2v_2}{a_2} \]$

(3)

$\[ t_2=0.4\times t_3 \]$

(4)

$\[ \left(t_5-t_3\right)=\frac{6d_0\times 1.05-1.6a_2{t}_3^2}{1.6a_2{t}_3} \]$

(5)

$\[ a_4=-\frac{a_2{t}_3}{\left(t_5-t_3\right)} \]$

(6)

$\[ t_4=t_3+0.6\left(t_5-t_3\right) \]$

(7)

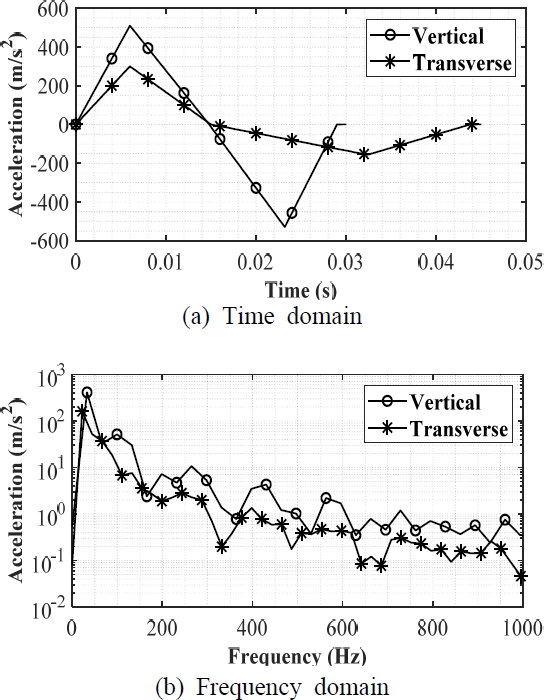
BV043의 삼각파형 충격파의 시간(t₂, t₃, t₄, t₅)과 가속도 크기(a₂, a₄)는 Table 3에 나타난 기준값을 통해 구할 수 있으며, 이 연구의 대상이 되는 안테나 구조물은 Table 3의 mounting location III에 해당하는 기준값을 적용하였다. 식 (1) ~ (7)을 통해 구한 안테나 구조물에서의 시간이력 충격 하중은 Fig. 5(a)와 같다. 여기서 vertical 방향의 충격 하중은 Z축 방향으로 입력되고, transverse 방향 충격 하중은 X축과 Y축 방향으로 입력된다. 충격하중을 주파수영역에서 살펴보면 Fig. 5(b)와 같은데, 충격하중의 주요 주파수 영역이 vertical 방향의 경우 약 33 Hz 이내이고, transverse 방향의 경우 약 45 Hz 이내인 것을 알 수 있다.

Table 3

BV043 Shock response spectrum value

Fig. 5

Triangular wave acceleration pattern for antenna structure

Table 2와 같이, 안테나 구조물의 1차 모드가 60 Hz에서 발생하기 때문에, 기존의 안테나 구조물의 진동특성이 BV043의 충격하중의 주요 주파수 영역과 겹치지 않으며 공진 회피 설계를 만족한다.

3. 모드 기반 구조 최적화

3.1 최적화 문제의 목표 함수 및 제약 조건

안테나 구조물의 주요 전자 장비들의 파손은 함정의 전투능력에 치명적인 영향을 주기 때문에 전자 장비를 보호하는 상부 및 하부 하우징의 구조안정성이 매우 중요하다. 따라서 안테나 구조물의 경량화를 위한 구조 최적화 대상 구조물은 하우징을 제외한 하부 구조물 중 지지대로 선정하였다.

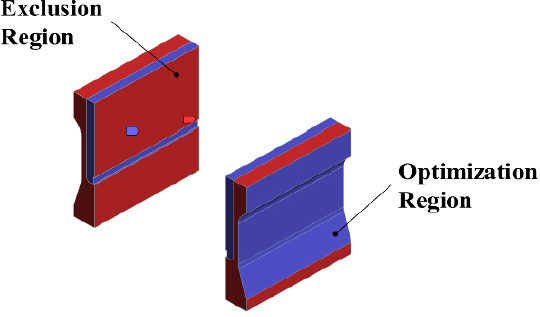
안테나 구조물의 저주파 주요 모드는 모두 지지대를 기준으로 구조물 전체의 굽힘 모드로, 지지대의 경량화 설계 방향에 따라 시스템의 고유진동수가 크게 낮아질 수 있다. 시스템의 고유진동수가 지나치게 낮아지게 되어 충격하중의 주요 주파수 영역 내에 포함되면 구조물이 충격하중에 의해 공진하여 구조적 안정성이 떨어지게 된다. 따라서 이 연구에서는 안테나 구조물의 주요 모드의 고유진동수가 충격하중의 주파수 영역에 포함되지 않도록 제약 조건을 설정하고, 지지대의 질량을 감소하는 목표 함수를 통해 구조 최적화를 진행하였다. 제약 조건의 경우, 최적화 구조물의 1차 모드 고유진동수가 기존 구조물의 1차 모드의 고유 진동수인 60 Hz와 크거나 같아지도록 설정하였다. 목표 함수의 경우, 지지대 구조물의 질량이 감소하도록 설정하였으며, 최적화로 인해 구조물에 구멍이 생겨 내부 전자 장비가 드러나지 않도록 Fig. 6과 같이 접촉면과 경계조건 부분은 최적화 대상에서 제외하였다. 최적화 문제의 목표 함수와 제약 조건에 대한 식은 식 (8)과 같다.

$\[ \begin{array}{l}\min { M}_{\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{t}\mathrm{e}\mathrm{r}}= \mathrm{M}\mathrm{a}\mathrm{s}\mathrm{s}\mathrm{ }\mathrm{o}\mathrm{f}\mathrm{ }\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{t}\mathrm{e}\mathrm{r}\\ s.t. f_1\ge f_1^{\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l}}\end{array} \]$

(8)

Fig. 6

Optimization region of antenna structure

여기서 M_supporter는 지지대 구조물의 전체 질량이고, f₁은 최적화 구조물의 1차 고유 진동수, $$ f_1^{\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l}}$$은 기존 구조물의 1차 고유 진동수이다.

3.2 구조 최적화 결과

(1) 최적화 결과 및 최종 경량화 모델

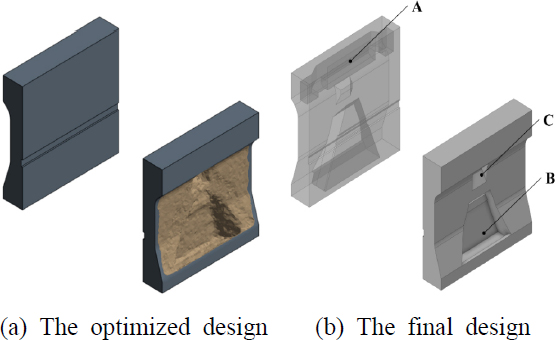
안테나 구조물의 제약 조건과 목표 함수로 정의된 최적화 문제를 해결하기 위해 ANSYS의 structural optimization 툴을 사용하였고, 밀도 기반의 최적화 방법인 SIMP 방법을 사용하였다. 최적화 결과, Fig. 7과 같이 지지대의 최적 형상을 얻었다. 지지대의 A 위치에서는 내부에 빈 공간이 생겼으며, B 위치에서는 겉면으로부터 내부를 향해 삼각형 모양으로 공간이 생겼다. 또한, C 부분에서도 내부를 향해 약간의 공간이 생겼다. 안테나 구조물의 1차 모드가 Y축 방향 굽힘 모드이기 때문에, 해당 거동에 대해 가장 주요한 위치인 지지대 하부의 양쪽 부분을 제외한 부분의 질량이 감소하는 방향으로 최적화 결과가 나타났다고 판단된다. 최적화 결과를 토대로 설계된 최종 형상은 Fig. 7(b)와 같다. 기존 모델의 지지대의 질량에 비해 경량화 모델의 지지대의 부피와 질량이 약 25 % 감소하였고, 감소한 부피와 질량은 Table 4와 같다.

Fig. 7

Optimization result of antenna structure

Table 4

Comparison of mass and volume of the model

(2) 경량화 모델의 모드해석 결과

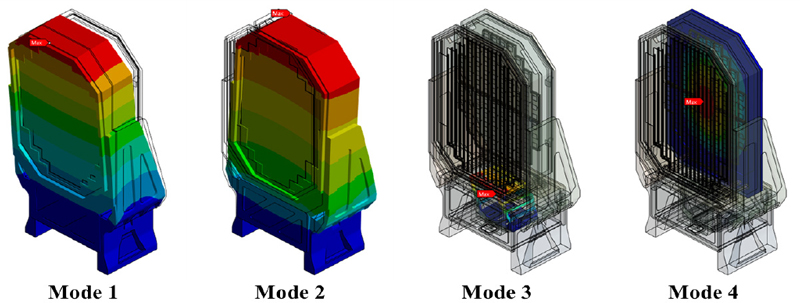
최종 경량화 모델이 제약 조건은 만족하는지 확인하기 위해 최종 모델에 대한 모드해석을 진행하였다. 유한요소해석 모델의 지지대 부분을 제외한 다른 구조물과 경계조건은 모두 동일하게 설정하였다. 모드해석 결과, 1차 모드가 58.62 Hz, 2차 모드가 70.40 Hz, 3차 모드가 112.7 Hz, 4차 모드가 123.7 Hz에서 발생하였고 이를 Table 5와 Fig. 8에 나타내었다. 최적화 문제의 제약 조건에서 구조물의 고유진동수가 60 Hz보다 크거나 같도록 설정하였는데 모드해석 결과에서 1차 모드가 더 낮게 나온 이유는 최종 경량화 모델의 형상이 모델 구축 과정에서 최적화 형상과 정확히 일치하지 않기 때문으로 판단된다.

Table 5

Comparison of dynamic characteristics

Fig. 8

Mode shapes of the optimization model

4. 구조 건전성 평가

4.1 BV043에 의한 충격응답해석

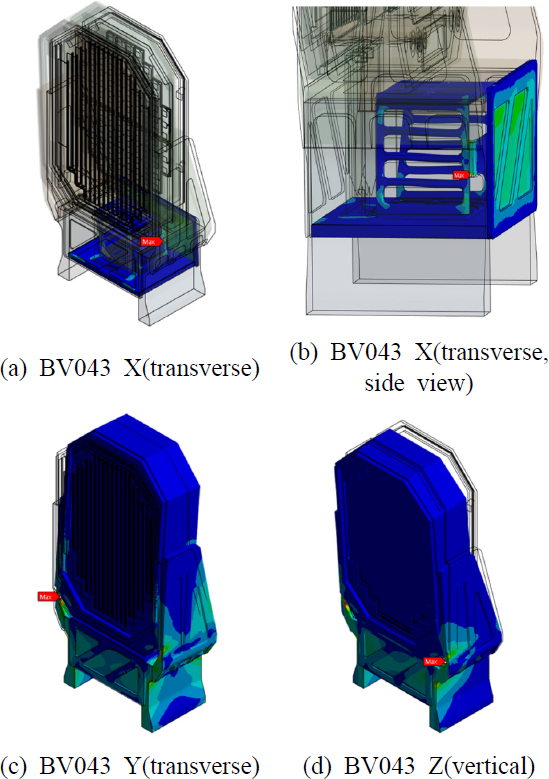
모드해석을 기반으로 정의한 최적화 문제를 통해 얻은 최종 경량화 모델이 실제로 충격하중에 대해서도 구조 건전성을 만족하는지 확인하기 위하여, BV043 시간이력 충격하중에 대한 과도응답해석을 진행하였다. Fig. 5(a)의 BV043의 vertical 방향과 transverse 방향에 대한 삼각파형 충격파를 X, Y, Z축 방향으로 입력한 후, 기존 모델과 최종 경량화 모델에 대하여 응력 기반으로 구조 건전성을 평가하였다. 먼저 기존 안테나 구조물 모델에 충격 하중이 가해졌을 때 응력 분포는 Fig. 9와 같다. X축 방향으로 BV043의 transverse 충격파가 가해졌을 때에는 Fig. 9(a)와 같이 하부 하우징 내부의 전자 장비 프레임에서 약 155 MPa의 최대 응력이 발생하였다. Y축 방향으로 같은 충격이 가해졌을 때에는 Fig. 9(c)와 같이 왼쪽 날개 부분에서 약 125 MPa의 최대 응력이 발생하였다. Z축 방향으로 BV043의 vertical 충격파가 가해졌을 때에는 Fig. 9(d)와 같이 오른쪽 날개 부분에서 약 51 MPa의 최대 응력이 발생하였다.

Fig. 9

Stress distribution of original model for shock loads

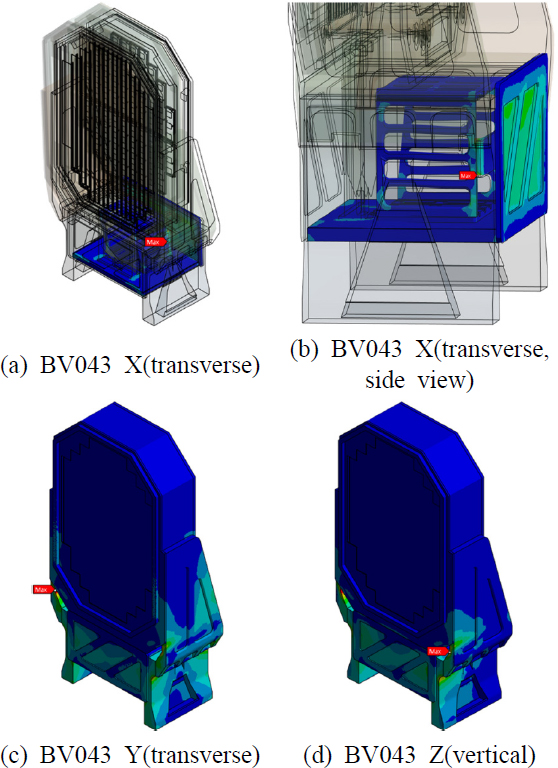
경량화 안테나 구조물에 대해서도 동일한 충격 하중을 인가하였고, 이로 인해 나타난 응력 분포는 Fig. 10과 같다. Fig. 10(a)에서 볼 수 있듯이, X축 방향 충격 하중에 대해 경량화 모델도 기존 모델과 마찬가지로 전자 장비 프레임에서 최대 응력이 발생하였다. 또한, Y축 방향 충격 하중에 대한 최대 응력 위치는 왼쪽 날개, Z축 방향 충격 하중에 대한 최대 응력 위치는 오른쪽 날개에서 나타났다.

Fig. 10

Stress distribution of optimization model for shock loads

기존 모델과 경량화 모델의 최대 응력 위치에서 응력의 크기는 Table 6과 같이 나타나는데, 경량화 모델에서 최대 응력이 발생한 위치와 응력의 크기가 기존 모델과 유사하게 나타났고 BV043에 대한 구조 건전성을 충분히 만족하는 것을 확인하였다. 따라서 모드 기반 최적화를 통해 충격 하중에 대한 공진을 회피하여 구조 건전성을 확보하는 경량화 설계가 가능함을 확인하였다.

Table 6

Comparison of maximum of equivalent stress

5. 결 론

이 연구는 다양한 해전 환경에서 사용되는 안테나 구조물을 구조 건전성을 만족하면서 구조 최적화를 통해 경량화하는 방안을 제시하였다. 먼저, 안테나 구조물의 유한요소해석 모델을 구축하여 모드해석을 통해 구조물의 동특성을 분석하고, 안테나 구조물의 충격 하중에 대한 주파수 특성과 비교하였다. 안테나 구조물의 주요 모드는 60 Hz 이상에서 나타나며 BV043 규정의 충격 하중의 주파수 범위는 45 Hz 이내이기 때문에 공진 회피 설계를 만족하는 것을 확인하였다.

다음으로, 안테나 구조물의 경량화를 위한 구조 최적화를 진행하였다. 경량화 모델이 충격 하중에 대한 구조 건전성을 만족해야 하기 때문에, 충격 하중의 주파수 특성과 구조물의 모드를 고려한 모드 기반 위상 최적화 방법을 적용하였다. 최적화 대상 구조물은 지지대로 선정하였고, 최적화 모델의 고유진동수가 기존 모델의 고유진동수보다 크거나 같으면서 지지대의 질량이 감소하도록 최적화 문제를 정의하였다. 최적화 결과, 지지대의 질량이 약 25 % 감소한 경량화 모델을 얻었으며, 모드해석 결과 1차 모드가 58.62 Hz에서 발생하였다.

마지막으로, 기존 모델과 경량화 모델에 대한 구조 건전성 평가를 위해 BV043 규정의 시간 이력 충격 하중에 대한 과도응답해석을 진행하여 비교하였다. 과도응답해석 결과, 경량화 모델의 최대 응력 발생 위치와 기존 모델과 같은 위치에서 발생했고, 최대 응력의 크기도 유사하게 나타나 두 모델 모두 구조 건전성을 만족하는 것을 확인하였다. 따라서 구조물의 동특성과 충격 하중의 주파수특성을 고려하여 적절한 제약조건과 목표 함수를 설정한다면 모드 기반 최적화를 통해 충격 하중에 대한 구조건전성을 확보하는 경량화 설계가 가능함을 확인하였고, 다른 구조물에 대한 경량화 설계에도 충분히 활용 가능할 것으로 기대된다.

Acknowledgments

이 연구는 LIG Nex1 산학협력과제 지원으로 수행되었습니다.

References

• Moon, S. J. and Kim, H. S., 2010, Noise, Vibration and Impacted Testing Methods for Shipboard and Their Current Status (Focused on the Korea Institute of Machinery & Materials), Defense & Technology, Vol. 380, pp. 58~65.
• Lee, J.-H., Son, D., Lee, K., Kim, D., Park, S. and Park, N.-C., 2020, A Method of Evaluating Structural Integrity of Integrated Mast with Scaled Model, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 30, No. 2, pp. 179~188. [https://doi.org/10.5050/KSNVE.2020.30.2.179]
• Federal German Army Procurement Office, 1985, Shock Resistance Experimental and Mathematical Proof, Federal German Army Procurement Office, BV043.
• Jung, J., Jensen, J. S., Jeong, C.-H., Jeon, O. and Wang, S., 2021, Optimizing a Distribution of Resonators on a Thin Plate for the Desired Sound Radiation, Journal of Sound and Vibration, Vol. 496, 115926. [https://doi.org/10.1016/j.jsv.2020.115926]
• Behrou, R. and Guest, J. K., 2017, Topology Optimization for Transient Response of Structures Subjected to Dynamic Loads, Proceedings of the 18th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, 3657. [https://doi.org/10.2514/6.2017-3657]
• Choi, W. S. and Park, G. J., 2002, Structural Optimization Using Equivalent Static Loads at All Time Intervals, Computer Methods in Applied Mechanics and Engineering, Vol. 191, No. 19-20, pp. 2105~2122. [https://doi.org/10.1016/S0045-7825(01)00373-5]
• Zhao, J. and Wang, C., 2016, Dynamic Response Topology Optimization in the Time Domain Using Model Reduction Method, Structural and Multidisciplinary Optimization, Vol. 53, No. 1, pp. 101~114. [https://doi.org/10.1007/s00158-015-1328-7]
• Kim, Y.-I. and Park, G.-J., 2010, Nonlinear Dynamic Response Structural Optimization Using Equivalent Static Loads, Computer Methods in Applied Mechanics and Engineering, Vol. 199, No. 9-12, pp. 660~676. [https://doi.org/10.1016/j.cma.2009.10.014]
• Venini, P., 2016, Dynamic Compliance Optimization: Time vs Frequency Domain Strategies, Computers & Structures, Vol. 177, pp. 12~22. [https://doi.org/10.1016/j.compstruc.2016.07.012]
• Jang, H. H., Lee, H. A., Lee, J. Y. and Park, G. J., 2012, Dynamic Response Topology Optimization in the Time Domain Using Equivalent Static Loads, AIAA Journal, Vol. 50, No. 1, pp. 226~234. [https://doi.org/10.2514/1.J051256]